Tema 3 Estimació puntual

L’objectiu principal de la inferència estadística és obtenir informació sobre tota una població a partir de només una mostra, com quan volem saber si un brou és fat o salat tastant-ne només una cullerada. El primer tipus d’informació que ens sol interessar és què val qualque paràmetre d’alguna variable aleatòria poblacional (una proporció, una mitjana…), per exemple per poder escriure un titular com el següent:

Figura 3.1: https://www.efesalud.com/miopia-estudio-universitarios

Aquest 60% no s’ha obtingut fent passar a tots els universitaris espanyols un test de miopia, ni tan sols demanant-los a tots si són miops o no, sinó que simplement s’ha pres una mostra d’universitaris, s’hi ha observat un 60% de miops i s’ha extrapolat aquesta proporció a tot el col·lectiu d’universitaris espanyols.

El procés d’intentar endevinar el valor d’un paràmetre d’una població a partir d’una mostra se’n diu estimació puntual, i és el que tractarem en aquest tema.

En aquest curs, sempre suposarem que empram mostres aleatòries i gairebé sempre que aquestes mostres aleatòries són a més simples. Per tant, si no diem el contrari, d’ara endavant quan parlem de mostres sempre suposarem que són mostres aleatòries simples, encara que no ho diguem explícitament per no carregar massa el text.

3.1 Estimadors

Per estimar el valor d’un paràmetre d’una variable aleatòria poblacional, en prenem una mostra (aleatòria simple) i calculam qualque cosa amb els valors que la formen. Què calculam? Doncs un estimador: alguna funció adequada aplicada als valors de la mostra, i que dependrà del que volguem estimar.

Per exemple:

Si volem estimar l’alçada mitjana dels estudiants de la UIB, prendrem una mostra d’estudiants de la UIB, els amidarem i calcularem la mitjana aritmètica de les seves alçades.
Si volem estimar la proporció d’estudiants de la UIB que tenen la COVID-19, prendrem una mostra d’estudiants de la UIB, els farem un test de COVID i calcularem la proporció mostral de positius en la mostra.

Formalment:

Tenim una variable aleatòria poblacional $X$, definida sobre una població.
Una mostra aleatòria simple de mida $n$ de $X$ és un vector $(X_1,\ldots,X_n)$ format per $n$ còpies independents de $X$.

Cada variable $X_i$ és una còpia de “Prenem un subjecte de la població i hi mesuram $X$”.
Una realització de la mostra aleatòria simple $(X_1,\ldots,X_n)$ és un vector $(x_1,\ldots,x_n)\in \mathbb{R}^n$ de valors presos per aquestes variables aleatòries.

És a dir, amb $(X_1,\ldots,X_n)$ repetim $n$ vegades (independents les unes de les altres) el procés de prendre un subjecte de la població i mesurar-hi $X$. Cada vegada que ho fem, obtenim un vector de números, al que diem una realització de la mostra.

A la lliçó anterior a aquestes realitzacions les déiem directament “mostres aleatòries simples de valors de $X$”; no passeu ànsia, en sortir d’aquest “formalment” els ho tornarem a dir.
Un estimador és una variable aleatòria $f(X_1,\ldots,X_n)$ obtinguda aplicant una funció $f$ a una mostra aleatòria simple $(X_1,\ldots,X_n)$.

Aquest estimador s’aplica a les realitzacions de la mostra i dóna nombres reals.

Un estimador és una variable aleatòria, definida sobre la població formada per les mostres aleatòries simples de la població de partida. Per tant, té funció de densitat, funció de distribució (que genèricament anomenarem distribució mostral, per indicar que refereix a la probabilitat que li passi qualque cosa al valor del estimador sobre una mostra), esperança, desviació típica, etc.

Com ja us hem dit, i com que no hi ha necessitat de filar tan prim, d’ara endavant cometrem l’abús de llenguatge de dir mostra (aleatòria simple) de $X$ tant al vector de variables aleatòries $(X_1,\ldots,X_n)$ com a una realització $(x_1,\ldots,x_n)$ i hi ometrem els parèntesis.

Com ja hem comentat a la Secció 1.5, si la mida $N$ de la població és MOLT més gran que la mida $n$ de la mostra (per fixar idees, hem dit que si $N\geqslant 1000n$), els resultats per a mostres aleatòries simples valen (aproximadament) per a mostres aleatòries sense reposició, perquè les variables aleatòries que formen la mostra sense reposició són gairebé idèntiques i independents i les repeticions són improbables.

3.2 Mitjana mostral

Quan volem estimar el valor mitjà d’una variable sobre una població, en prenem una mostra de valors i calculam la seva mitjana aritmètica, no és ver? Doncs això és la mitjana mostral.

Donada una variable aleatòria $X$, la seva mitjana mostral (de mostres aleatòries simples) de mida $n$ és la variable aleatòria $\overline{X}$ “Prenem una mostra aleatòria simple de mida $n$ de $X$ i calculam la mitjana aritmètica dels seus valors”. És a dir, formalment, la mitjana mostral de mida $n$ de $X$ és la variable aleatòria obtinguda prenent $n$ còpies independents $X_1,\ldots,X_n$ de la variable aleatòria $X$ i calculant \[ \overline{X}=\frac{X_1+\cdots+X_n}{n} \]

Fixau-vos que definim la mitjana mostral només per a mostres aleatòries simples. Naturalment, té sentit definir-la per a mostres qualssevol, però llavors la seva distribució mostral deixa de complir les propietats que donarem en aquesta secció. El mateix advertiment val per als estimadors que definim en les pròximes seccions.

Com a conseqüència del comportament d’esperances i variàncies de combinacions lineals, tenim el resultat següent:

Teorema 3.1 Siguin $X$ una variable aleatòria d’esperança $\mu_X$ i desviació típica $\sigma_X$, i $\overline{X}$ la seva mitjana mostral (de mostres aleatòries simples) de mida $n$. Aleshores

El valor esperat de $\overline{X}$ és $E(\overline{X})=\mu_X$.
La desviació típica de $\overline{X}$ és $\sigma(\overline{X})={\sigma_X}/{\sqrt{n}}$.

En efecte, com que \[ \overline{X}=\frac{1}{n}X_1+\cdots +\frac{1}{n}X_n \] i les variables $X_1,\ldots,X_n$ són còpies de $X$, i per tant tenen totes esperança $\mu_X$ i variància $\sigma^2_X$, tenim que \[ \mu_{\overline{X}}=\overbrace{\frac{1}{n}\mu_X+\cdots +\frac{1}{n}\mu_X}^n=\mu_X \] i, si $X_1,\ldots,X_n$ són independents, \[ \sigma_{\overline{X}}=\sqrt{\overbrace{\frac{1}{n^2}\sigma^2_X+\cdots+ \frac{1}{n^2}\sigma^2_X}^n}=\sqrt{\frac{n}{n^2}\sigma^2_X}=\frac{\sigma_X}{\sqrt{n}} \]

Si us hi fixau, per demostrar que $E(\overline{X})=\mu_X$ no hem fet servir que $X_1,\ldots,X_n$ siguin independents. De fet, la igualtat $E(\overline{X})=\mu_X$ també és vertadera per a mitjanes mostrals de mostres aleatòries sense reposició. En canvi, la igualtat $\sigma_{\overline{X}}={\sigma_X}/{\sqrt{n}}$ sí que requereix que les mostres aleatòries siguin simples.

Per tant:

$\overline{X}$ és un estimador puntual de $\mu_X$.
$E(\overline{X})=\mu_X$, la qual cosa significa que:
- La mitjana de les mitjanes mostrals de totes les mostres aleatòries de mida $n$ de $X$ és igual a la mitjana $\mu_X$ de $X$.
- Esperam que la mitjana mostral doni $\mu_X$: si repetíssim moltes vegades el procés de prendre una mostra aleatòria de mida $n$ i calcular-ne la mitjana mostral, molt probablement el valor mitjà d’aquestes mitjanes s’acostaria molt a $\mu_X$.
$\sigma(\overline{X})= \sigma_X/\sqrt{n}$ indica que la dispersió de les mitjanes mostrals creix amb la dispersió de $X$ i decreix amb la mida $n$ de la mostra, tendint a 0 quan $n\to\infty$.

L’efecte de la mida de les mostres sobre la variabilitat de $\overline{X}$ és raonable. Quan prenem mostres aleatòries grans d’una variable i en calculam la mitjana, el més normal és que dins cada mostra els valors més petits se compensin amb els més grans, i que com a conseqüència les mitjanes siguin més homogènies que els valors de la variable.

Vaja: si triam una persona a l’atzar, no és molt improbable que faci, jo què sé, 2.10 m. Però si prenem una mostra aleatòria de 50 persones, és molt més difícil que la mitjana de les seves alçades sigui 2.10 m. El que hi esperaríem és que les alçades dels més alts s’hi compensin amb les alçades dels més baixos i tot plegat doni una mitjana més… “mitjana”.

A la desviació típica de $\overline{X}$ li diem l’error estàndard, o típic, de $\overline{X}$. Per tant, l’error estàndard de la mitjana mostral de mida $n$ de $X$ és $\sigma_X/\sqrt{n}$.

Exemple 3.1 El fitxer tests.txt que trobareu a l’url https://raw.githubusercontent.com/AprendeR-UIB/MatesII/master/Dades/tests.txt conté les notes (sobre 100) de tests dels estudiants de Matemàtiques I de fa uns cursos. El guardam en un vector anomenat tests:

tests=scan("https://raw.githubusercontent.com/AprendeR-UIB/MatesII/master/Dades/tests.txt")

Considerarem la població dels estudiants de Matemàtiques I d’aquell curs i com a variable aleatòria d’interès $X$ la seva nota de tests sobre 100. Per tant, aquest vector tests conté els valors de la variable aleatòria d’interès sobre tots els individus de la població. La seva mida és

N=length(tests)
N

## [1] 185

La seva mitjana, que és la mitjana poblacional $\mu_X$, és

mu=mean(tests)
mu

## [1] 55.43243

Si en prenem una mostra aleatòria simple, per exemple de mida $n=40$, la seva mitjana mostral no té per què coincidir amb la mitjana poblacional:

n=40
MAS=sample(tests,n,replace=TRUE) # Una mostra aleatòria simple
x.barra=mean(MAS) # La seva mitjana mostral
x.barra

## [1] 53.5

Però si prenem moltes mostres aleatòries simples, la mitjana de les seves mitjanes és molt probable que sí que s’acosti a la mitjana poblacional. Vegem si tenim sort amb cent mil mostres:

mitjanes=replicate(10^5,mean(sample(tests,n,replace=TRUE)))
mean(mitjanes)

## [1] 55.4187

Vegem ara que la desviació típica d’aquesta mostra de mitjanes s’acosta a l’error típic de la mitjana mostral, no a la desviació típica de la població:

La desviació típica poblacional:

sigma=sd(tests)*sqrt((N-1)/N)
sigma

## [1] 21.38241

La desviació típica de la mostra de mitjanes:

sd(mitjanes)*sqrt(99999/100000)

## [1] 3.384666

L’error típic de la mitjana mostral:

sigma/sqrt(n)

## [1] 3.380856

Veiem que les mitjanes mostrals presenten una dispersió molt més petita que la variable poblacional original. Gràficament, als histogrames de les Figures 3.2 i 3.3 hi podeu veure com les mitjanes estan més concentrades al voltant de 55 que les notes originals.

La veritat és que ens haguéssim pogut estalviar el factor corrector $\sqrt{99999/100000}$, que val 0.999995, quan hem calculat la desviació típica de la mostra de cent mil mitjanes. Als propers exemples on emprem mostres d’aquesta mida ja no el farem servir.

Recordau del Teorema 2.6 que una combinació lineal de variables aleatòries normals independents torna a ser normal. Com que la mitjana mostral de mostres aleatòries simples és una combinació lineal de variables aleatòries independents, obtenim el resultat següent:

Teorema 3.2 Si $X$ és una variable aleatòria normal $N(\mu_X,\sigma_X)$, la seva mitjana mostral $\overline{X}$ de mostres aleatòries simples de mida $n$ és normal \[ N\big(\mu_X,\sigma_X/\sqrt{n}\big). \]

El teorema següent diu que la conclusió del teorema anterior és aproximadament vertadera si la mida $n$ de les mostres aleatòries simples és gran:

Teorema 3.3 \iffalse (Teorema Central del Límit) Siguin $X$ una variable aleatòria qualsevol d’esperança $\mu_X$ i desviació típica $\sigma_X$. Quan $n\to \infty$, la funció de distribució de la seva mitjana mostral $\overline{X}$ de mostres aleatòries simples de mida $n$ tendeix a la d’una variable normal \[ N\big(\mu_X,\sigma_X/\sqrt{n}\big). \]

Com us podeu imaginar, quan un resultat l’anomenen Teorema Central de qualque cosa és perquè és molt important.

Normalment aplicarem el Teorema Central del Límit de la manera següent:

Siguin $X$ una variable aleatòria qualsevol d’esperança $\mu_X$ i desviació típica $\sigma_X$. Si la mida $n$ de les mostres (aleatòries simples) és gran, la mitjana mostral $\overline{X}$ és aproximadament normal $N(\mu_X,\sigma_X/\sqrt{n})$.

Per fixar una fita, en aquest curs entendrem que $n$ és prou gran com per poder aplicar aquest “resultat” quan és més gran o igual que 40, potser menys com més se sembli $X$ a una normal i potser més si la $X$ és molt diferent d’una normal.

A partir d’ara, sovint cometrem l’abús de llenguatge d’ometre l’adverbi “aproximadament” de l’expressió anterior, i direm simplement que si $n$ és gran, $\overline{X}$ és normal. Però heu de tenir present que aquest “és normal” en realitat vol dir “la seva distribució és aproximadament la d’una variable normal”.

Per qualque motiu que no entenem, alguns estudiants teniu tendència a invocar el Teorema Central del Límit dient coses de l’estil de “La variable poblacional $X$ no és normal, però com que la mostra és molt gran, $X$ és aproximadament normal”. Si ho llegiu amb calma, veureu que això és un doi. $X$ no és normal, però si en preneu una mostra gran, $X$ passa a ser aproximadament normal? En sèrio? Qui serà aproximadament normal és la mitjana mostral $\overline{X}$, no $X$!

Exemple 3.2 Suposem que tenim una variable aleatòria $X$ de mitjana poblacional $\mu_X=3$ i desviació típica poblacional $\sigma_X=0.2$ i que en prenem mostres aleatòries simples de mida 100. Pel Teorema Central del Límit, la distribució de la mitjana mostral $\overline{X}$ és (aproximadament) \[ NN\big(\mu_X,0.2/\sqrt{100}\big)=N(3,0.02) \]

Exemple 3.3 Tornem a la situació de l’Exemple 3.1. Teníem les notes guardades en un vector anomenat tests. Amb l’histograma següent podem veure que aquestes notes no tenen pinta de seguir una distribució normal.

fact.trans=hist(tests,plot=FALSE)$counts[1]/hist(tests,plot=FALSE)$density[1]
hist(tests,col="light blue",xlab="Notes dels tests",
     ylab="Freqüències",main="")
curve(fact.trans*dnorm(x,mean(tests),sd(tests)),col="red",lwd=2,add=TRUE)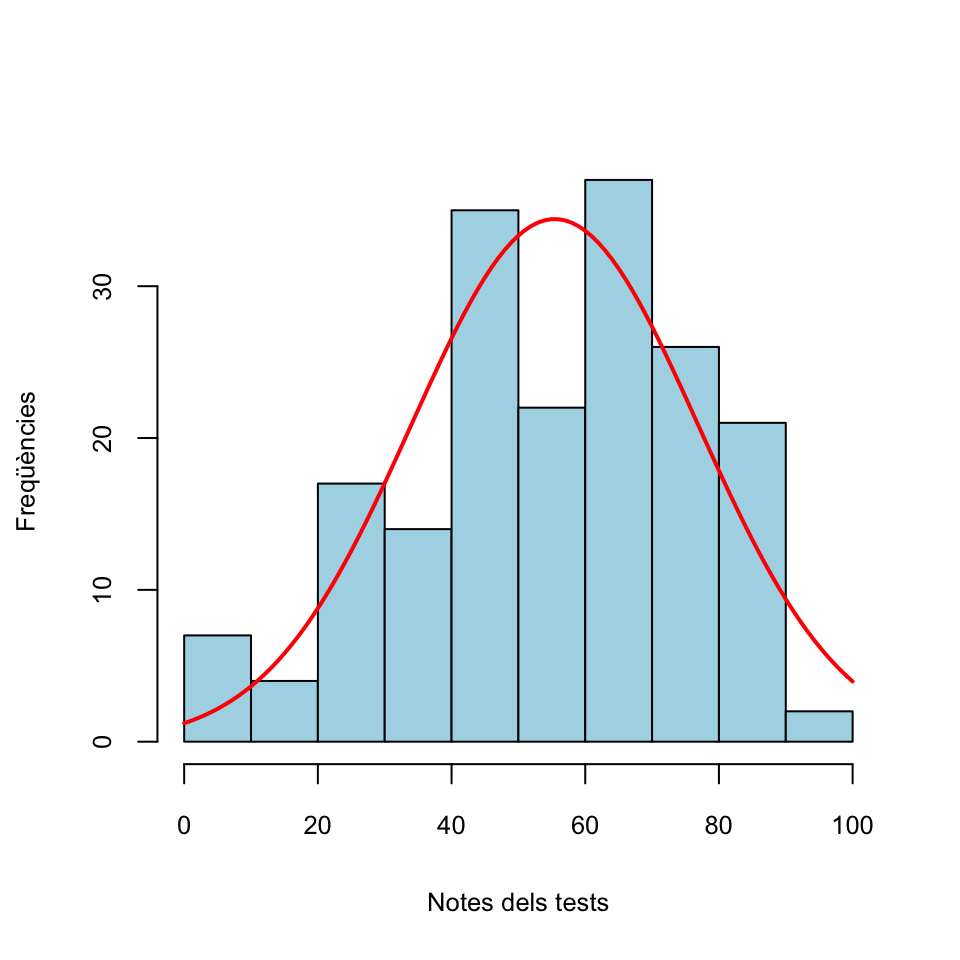

Figura 3.2: Histograma de les notes de tests

A l’Exemple 3.1 també hem construït un vector anomenat mitjanes format per 10⁵ mitjanes mostrals de mostres aleatòries simples de notes de mida 40. Pel Teorema Central del Límit, aquestes mitjanes mostrals haurien de seguir aproximadament una distribució normal, malgrat que la “població original” (les notes dels tests) no sigui normal. Vegem-ho amb un histograma, on hem afegit la densitat de la normal $N(\mu_X,\sigma_X/\sqrt{n})$ predita pel Teorema Central del Límit.

fact.trans.m=hist(mitjanes,plot=FALSE)$counts[1]/hist(mitjanes,plot=FALSE)$density[1]
hist(mitjanes,col="light blue",xlab="Mitjanes",
     ylab="Freqüències",main="")
curve(fact.trans.m*dnorm(x,mu,sigma/sqrt(n)),col="red",lwd=2,add=TRUE)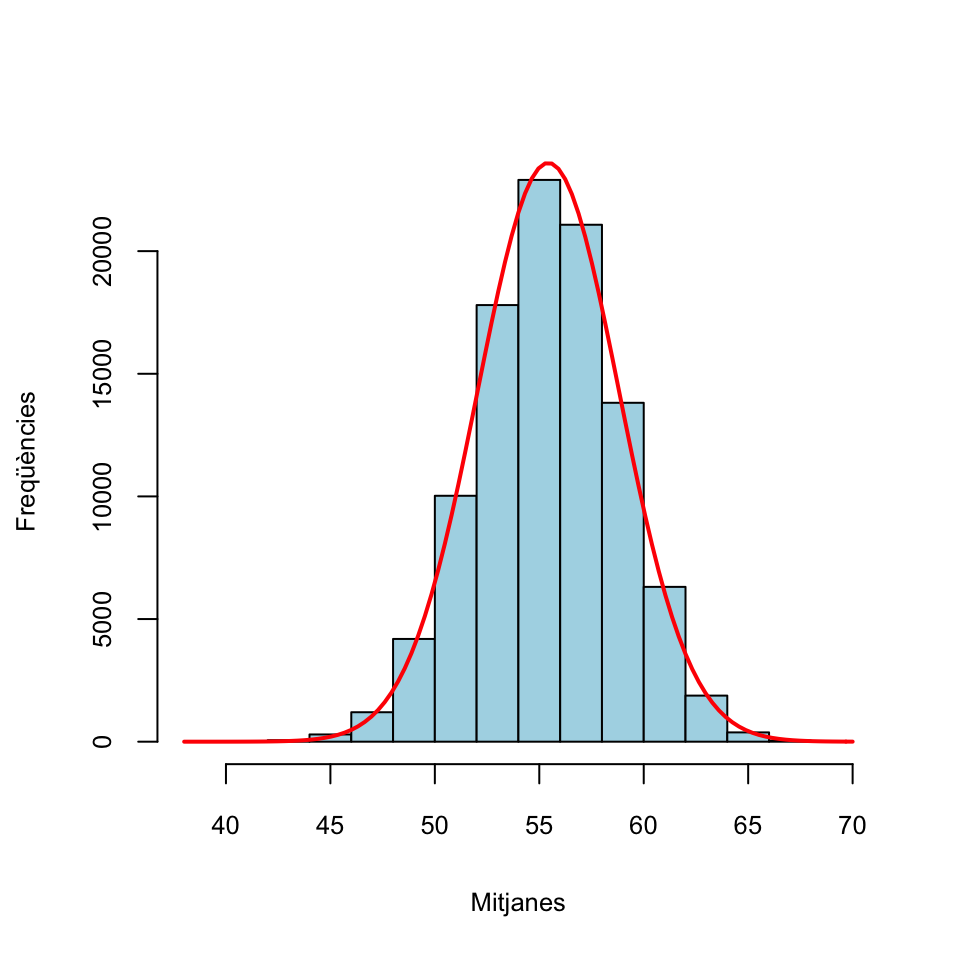

Figura 3.3: Histograma de les mitjanes de mostres de notes de tests

L’exemple següent és un tipus de pregunta que més endavant ens preocuparà molt.

Exemple 3.4 L’alçada d’una espècie de matolls té valor mitjà 115 cm, amb una desviació típica de 25 cm. Si prenem una mostra aleatòria simple de 100 matolls d’aquesta espècie, quina és la probabilitat que la mitjana mostral de les alçades sigui més petita que 110 cm?

Diguem $X$ a la variable aleatòria definida per les alçades d’aquests matolls. Pel Teorema Central del Límit, podem suposar que la mitjana mostral $\overline{X}$ de mostres aleatòries simples de 100 alçades segueix una distribució $N(115,25/\sqrt{100})=N(115,2.5)$. Llavors, la probabilitat que ens demanen és \[ P(\overline{X}< 110) \] que podem calcular amb

round(pnorm(110,115,2.5),4)

## [1] 0.0228

Un 2.28% de les mostra aleatòries simples de 100 matolls d’aquesta espècie tenen la mitjana de les alçades més petita que 110 cm.

3.3 Proporció mostral

Quan volem estimar la proporció d’individus d’una població que tenen una determinada característica, en prenem una mostra i hi calculam la proporció de membres amb aquesta característica. Aquesta serà la proporció mostral de subjectes amb aquesta característica en la nostra mostra.

Sigui $X$ una variable aleatòria poblacional de Bernoulli amb probabilitat d’èxit $p_X$. És a dir, $X$ pren els valors 1 (èxit) o 0 (fracàs) i $p_X$ és la proporció de subjectes de la població en els quals val 1. Recordau que $E(X)=p_X$ i $\sigma_X=\sqrt{p_X(1-p_X)}$.

La proporció mostral (de mostres aleatòries simples) de mida $n$ de $X$, $\widehat{p}_X$, és la variable aleatòria que consisteix a prendre una mostra aleatòria simple de mida $n$ de $X$ i calcular-ne la proporció d’èxits: és a dir, comptar-hi el nombre total d’èxits i dividir el resultat per $n$.

Formalment, sigui $X_1,\ldots,X_n$ una mostra aleatòria simple de mida $n$ de $X$. Sigui $S_n=\sum_{i=1}^n X_i$, que és la variable aleatòria que compta el nombre d’èxits en una mostra aleatòria simple de mida $n$. Aleshores, la proporció mostral de mida $n$ de $X$ és \[ \widehat{p}_X=\frac{S_n}{n}=\frac{X_1+\cdots+X_n}{n}. \]

Recordau que si prenem mostres aleatòries simples, $S_n$ és una variable aleatòria binomial $B(n,p_X)$. Però no digueu que la proporció mostral $\widehat{p}_X$ és una variable aleatòria binomial, ni que només sigui perquè les variables aleatòries binomials prenen valors nombres naturals i els valors que pot prendre $\widehat{p}_X$ són fraccions entre 0 i 1.

Fixau-vos que $\widehat{p}_X$ és un cas particular de la mitjana mostral $\overline{X}$, per tant per a les proporcions mostrals val tot el que hem dit per a mitjanes mostrals:

Teorema 3.4 Sigui $X$ una variable aleatòria de Bernoulli amb probabilitat d’èxit $p_X$. Aleshores, la proporció mostral de mostres aleatòries simples de mida $n$ de $X$, $\widehat{p}_X$, satisfà que:

$E(\widehat{p}_X)=p_X$
$\sigma(\widehat{p}_X)=\sqrt{\dfrac{p_X(1-p_X)}{n}}$
Pel Teorema Central del Límit, si la mida $n$ de la mostra és gran, la distribució de $\widehat{p}_X$ és aproximadament la d’una variable normal \[ N\big({p}_X,\sqrt{{p}_X(1-{p}_X)/n}\big) \] i per tant \[ \frac{\widehat{p}_X-p_X}{\sqrt{{p}_X(1-{p}_X)/n}} \] és aproximadament $N(0,1)$.

Els valors de l’esperança i la desviació típica de $\widehat{p}_X$ es poden deduir dels de $S_n$ sense necessitat d’invocar els de la mitjana mostral. Com que $S_n$ és $B(n,p_X)$, sabem que $E(S_n)=np_X$ i $\sigma(S_n)^2=np_X(1-p_X)$ i per tant \[ \begin{array}{l} \displaystyle E(\widehat{p}_X)=E\Big(\frac{S_n}{n}\Big)=\frac{E(S_n)}{n}=\frac{np_X}{n}=p_X\\ \displaystyle \sigma(\widehat{p}_X)=\sigma\Big(\frac{S_n}{n}\Big)=\frac{\sigma(S_n)}{n}=\frac{\sqrt{np_X(1-p_X)}}{n}=\sqrt{\frac{p_X(1-p_X)}{n}} \end{array} \]

Alguns comentaris:

$E(\widehat{p}_X)=p_X$: Esperam que la proporció mostral sigui igual a la proporció poblacional d’èxits (si hi ha, diguem, un 20% d’èxits a la població, quin percentatge d’èxits “esperau” trobar a la mostra? Un 20%, no?).

És a dir, si repetíssim moltes vegades el procés de prendre una mostra aleatòria simple de mida $n$ d’una variable aleatòria de Bernoulli $X$ i calcular-ne la proporció mostral d’èxits, molt probablement la mitjana d’aquestes proporcions mostrals s’acostaria molt a $p_X$.
En particular, $\widehat{p}_X$ és un estimador de $p_X$, naturalment.
$\sigma(\widehat{p}_X)= \sqrt{{p_X(1-p_X)}/{n}}$: la variabilitat dels resultats de $\widehat{p}_X$ decreix amb $n$ i tendeix a 0 quan $n\to \infty$.

Pel que fa a la dependència de $\sigma(\widehat{p}_X)$ respecte de $p_X$ si la $n$ és fixada, observau a la Figura 3.4 que $\sqrt{p_X(1-p_X)}$ creix entre 0 i 0.5 i decreix entre 0.5 i 1, assolint el valor màxim a $p_X=0.5$.

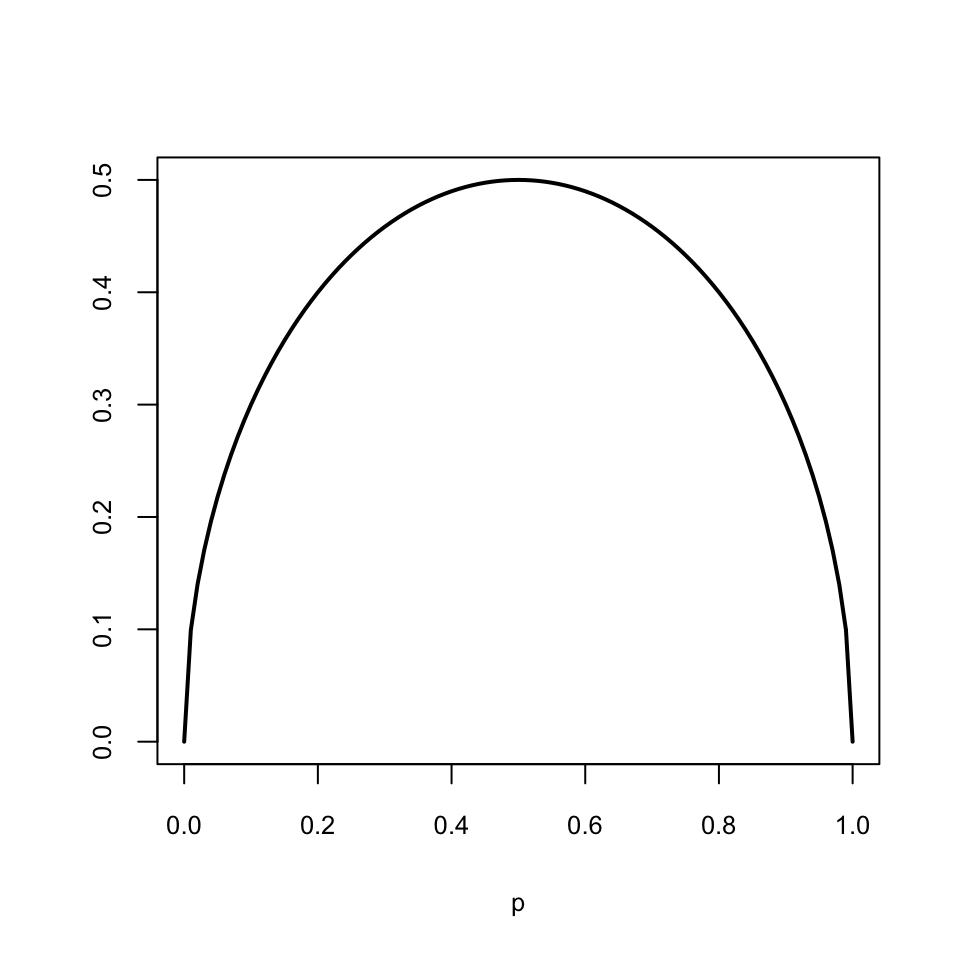
$Gràfica de $\sqrt{p(1-p)}$$

Figura 3.4: Gràfica de $\sqrt{p(1-p)}$

$\sqrt{{p_X(1-p_X)}/{n}}$ és l’error estándard, o típic, de $\widehat{p}_X$. L’estimam amb l’error estándard, o típic, de la mostra $\sqrt{{\widehat{p}_X(1-\widehat{p}_X)}/{n}}$.
Sovint cometrem l’abús de llenguatge d’ometre l’adverbi “aproximadament” de l’apartat (3) del teorema anterior, i direm simplement que si $n$ és gran, $\widehat{p}_X$ és normal. Però, repetim, hem de recordar que aquest “és normal” en realitat vol dir “la seva distribució és aproximadament la d’una variable normal”.

Exemple 3.5 Tornem una altra vegada a la situació dels Exemples 3.1 i 3.3. Traduïm el fitxer de notes de tests en un vector binari: 0 per suspens (haver tret menys de 50) i 1 per aprovat (haver tret 50 o més):

# Iniciam totes les notes a 1
aprovs=rep(1,length(tests))
# Posam 0 on la nota del test és suspesa
aprovs[which(tests<50)]=0

Aquest vector aprovs el podem entendre com els valors sobre la nostra població d’estudiants de la variable poblacional de Bernoulli $Y$ que ens diu si un estudiant aprovà o suspengué els tests. La seva probabilitat poblacional d’èxit (aprovat) $p_Y$ serà la proporció d’estudiants aprovats:

p_Y=sum(aprovs)/N
round(p_Y,4)

## [1] 0.5946

Ara n’extreurem 10⁵ mostres aleatòries simples de mida $n=40$, en calcularem les proporcions mostrals d’aprovats i comprovarem si es confirmen les conclusions del teorema anterior.

n=40
props.mostrals=replicate(10^5,mean(sample(aprovs,n,rep=TRUE)))

La mitjana d’aquest vector de proporcions hauria de ser propera a la proporció poblacional d’aprovats $p_Y=0.5946$.

round(mean(props.mostrals),4)

## [1] 0.5954

Vegem ara la seva desviació típica:

round(sd(props.mostrals),4)

## [1] 0.0775

Pel Teorema 3.4, sabem que això hauria de ser proper a $\sqrt{p_Y(1-p_Y)/n}$

round(sqrt(p_Y*(1-p_Y)/n),4)

## [1] 0.0776

I pel Teorema Central del Límit, aquestes proporcions mostrals haurien de seguir aproximadament una distribució normal $N(p_Y,\sqrt{p_Y(1-p_Y)/n})$. Vegem-ho amb un histograma:

fact.trans.p=hist(props.mostrals,plot=FALSE)$counts[1]/hist(props.mostrals,plot=FALSE)$density[1]
hist(props.mostrals,col="light blue",xlab="Proporcions mostrals",
     ylab="Freqüències",main="Histograma de la mostra de proporcions")
curve(fact.trans.p*dnorm(x,p_Y,sqrt(p_Y*(1-p_Y)/n)),
      col="red",lwd=2,add=TRUE)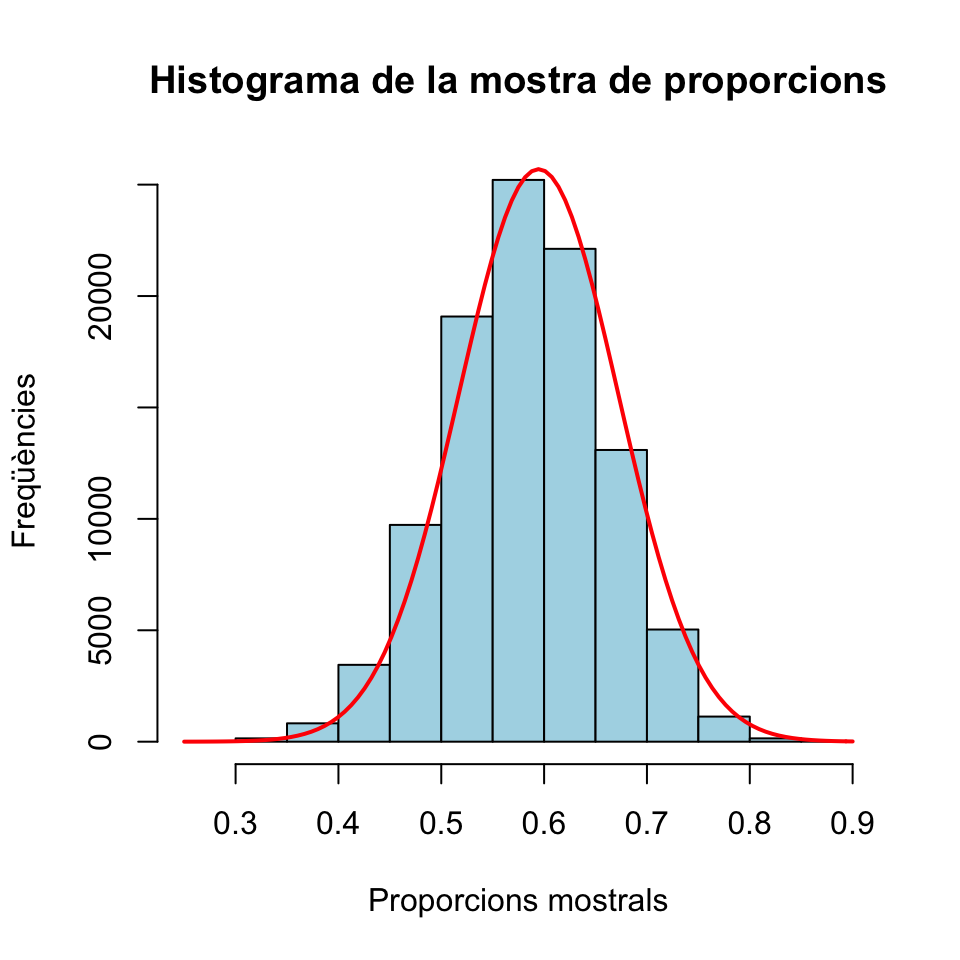

I això que la mida de les mostres, 40, no és especialment gran.

Exemple 3.6 Un 59.1% dels estudiants de la UIB són dones. Hem pres una mostra més o menys aleatòria de 60 estudiants de la UIB i hi hem trobat 40 dones, dos terços. Ens demanam si 40 de 60 és una quantitat raonable de dones en una mostra aleatòria simple d’estudiants de la UIB, o si són moltes (atès que hi esperaríem al voltant d’un 59% de dones).

Aquesta pregunta, que serà molt típica d’aquí a pocs temes, la traduïm en la pregunta següent:

Si prenem una mostra aleatòria simple de 60 estudiants, quina és la probabilitat que la proporció mostral de dones sigui més gran o igual que 2/3?

La manera més correcta de respondre aquesta qüestió és emprar que el nombre $S_{60}$ de dones en mostres aleatòries simples de 60 estudiants de la UIB segueix de manera exacta una distribució binomial $B(60,0.591)$. Com que el 2/3 de la pregunta en realitat representa 40 dones, la probabilitat demanada és exactament

round(1-pbinom(39,60,0.591),4)

## [1] 0.1441

Recordau que si $X$ és una variable aleatòria discreta que pren valors enters, com ara la binomial, $P(X\geqslant 40)=1-P(X\leqslant 39)$.

Això ens diu que un 14.41% de les mostres aleatòries simples de 60 estudiants de la UIB contenen almenys 40 dones. Naturalment, aquesta probabilitat només és “l’exacta” si la proporció poblacional “59.1%” és exacta.

Una altra opció seria aprofitar el Teorema Central del Límit, segons el qual la proporció mostral $\widehat{p}_X$ de dones en mostres aleatòries simples de 60 estudiants de la UIB segueix una distribució aproximadament normal amb $\mu=0.591$ i \[ \sigma=\sqrt{\dfrac{0.591(1-0.591)}{60}}=0.0635 \] Per tant, la probabilitat que $\widehat{p}_X\geqslant 2/3$ és (ara, aproximadament)

round(1-pnorm(2/3,0.591,sqrt(0.591*(1-0.591)/60)),4)

## [1] 0.1166

L’aproximació seria més bona si haguéssim emprat la correcció de continuïtat. Diguem $Y$ a la normal $N(0.591,0.0635)$. Com que $\widehat{p}_X=S_{60}/60$, seria millor aproximar \[ P(S_{60}\geqslant 40)=1-P(S_{60}\leqslant 39) \] per \[ 1-P(Y\leqslant 39.5/60) \]

round(1-pnorm(39.5/60,0.591,sqrt(0.591*(1-0.591)/60)),4)

## [1] 0.1444

En el cas de la proporció mostral, de vegades considerarem que s’han pres mostres aleatòries sense reposició. En aquest cas, la distribució del nombre d’èxits $S_n$ en una mostra segueix una distribució hipergeomètrica. D’aquí deduïm, exactament igual que en el cas de mostres aleatòries simples, que seguim tenint que $E(\widehat{p}_X)=p_X$, però ara, si $N$ és la mida de la població, \[ \sigma({\widehat{p}_X})=\sqrt{\frac{p_X(1-p_X)}{n}}\cdot \sqrt{\frac{\vphantom{(p_X}N-n}{N-1}}. \] Recordau que al factor \[ \sqrt{\frac{N-n}{N-1}} \] que transforma $\sigma({\widehat{p}_X})$ per a mostres aleatòries simples en la desviació típica de ${\widehat{p}_X}$ per a mostres aleatòries sense reposició li diem el factor de població finita, i és el que transformava la desviació típica d’una variable binomial (que compta èxits en mostres aleatòries simples) en la desviació típica d’una variable hipergeomètrica (que compta èxits en mostres aleatòries sense reposició).

Però recordau que si la mida de la població $N$ és molt gran comparat amb $n$, podem suposar que una mostra aleatòria sense reposició és simple.

Exemple 3.7 Tornem a la situació de l’Exemple 3.5. Què passa si prenem les mostres aleatòries de notes de tests sense reposició?

Prenguem ara 10⁵ mostres aleatòries sense reposició de 40 notes de tests.

props.norep=replicate(10^5,mean(sample(aprovs,n)))

Un altre cop, la mitjana d’aquest vector de proporcions mostrals hauria de ser propera a la proporció poblacional d’aprovats $p_Y=0.5946$.

round(mean(props.norep),4)

## [1] 0.5946

Calculem ara la desviació típica d’aquest vector:

round(sd(props.norep),4)

## [1] 0.069

Pel que acabam d’explicar, la desviació típica d’aquest vector de proporcions mostrals de mostres sense reposició hauria de ser molt propera a \[ \sqrt{\frac{p_Y(1-p_Y)}{n}}\cdot\sqrt{\frac{\vphantom{(p_Y}N-n}{N-1}} \] on $N$ és la mida de la població, és a dir, la longitud del vector aprovs, i $n$ la mida de les mostres. Vegem si és veritat:

round(sqrt(p_Y*(1-p_Y)/n)*sqrt((N-n)/(N-1)),4)

## [1] 0.0689

Però si prenem mostres aleatòries sense reposició i la població no és molt més gran que les mostres, ja no es pot aplicar el Teorema Central del Límit: encara que les mostres siguin grans, la proporció mostral no té per què ser aproximadament normal.

3.4 Variància mostral

Donada una variable aleatòria $X$:

La seva variància mostral (de mostres aleatòries simples) de mida $n$, $\widetilde{S}_{X}^2$, és la variable aleatòria que consisteix a prendre una mostra aleatòria simple de mida $n$ de $X$ i calcular la variància mostral dels seus valors.
La seva desviació típica mostral (de mostres aleatòries simples) de mida $n$, $\widetilde{S}_{X}$, és la variable aleatòria que consisteix a prendre una mostra aleatòria simple de mida $n$ de $X$ i calcular la desviació típica mostral dels seus valors.

Formalment, sigui $X_1,\ldots, X_n$ una mostra aleatòria simple de mida $n\geqslant 2$ d’una variable aleatòria $X$. Aleshores \[ \widetilde{S}_{X}^2=\frac{\sum_{i=1}^n (X_{i}-\overline{X})^2}{n-1},\quad \widetilde{S}_{X}=+\sqrt{\widetilde{S}_{X}^2} \] A més, de tant en tant també farem servir la variància i la desviació típica “a seques”:

La variància (de mostres aleatòries simples) de mida $n$ de $X$, $S_{X}^2$, és la variable aleatòria que consisteix a prendre una mostra aleatòria simple de mida $n$ de $X$ i calcular la variància dels seus valors: \[ S^2_{X}=\frac{\sum_{i=1}^n (X_{i}-\overline{X})^2}{n}=\frac{(n-1)}{n}\widetilde{S}^2_{X} \]
La desviació típica (de mostres aleatòries simples) de mida $n$ de $X$, ${S}_{X}$, és la variable aleatòria que consisteix a prendre una mostra aleatòria simple de mida $n$ de $X$ i calcular la desviació típica dels seus valors: \[ S_X=+\sqrt{S_X^2} \]

La variància (a seques) admet la expressió senzilla següent: \[ S^2_X=\frac{\sum_{i=1}^n X_{i}^2}{n}-\overline{X}^2 \]

En efecte: \[ \begin{array}{l} \displaystyle \frac{\sum_{i=1}^n (X_{i}-\overline{X})^2}{n}=\frac{1}{n}\sum_{i=1}^n (X_{i}^2-2\overline{X}X_i+\overline{X}^2)\\ \displaystyle\qquad = \frac{1}{n}\Big(\sum_{i=1}^n X_{i}^2-2\overline{X}\sum_{i=1}^n X_{i}+n\overline{X}^2\Big)\\ \displaystyle\qquad =\frac{\sum_{i=1}^n X_{i}^2}{n}-2\overline{X}\frac{\sum_{i=1}^n X_{i}}{n}+\frac{n\overline{X}^2}{n}\\ \displaystyle\qquad =\frac{\sum_{i=1}^n X_{i}^2}{n}-2\overline{X}\cdot\overline{X} + \overline{X}^2=\frac{\sum_{i=1}^n X_{i}^2}{n}- \overline{X}^2 \end{array} \]

Tenim els dos resultats següents. El primer ens diu que esperam que la variància mostral d’una mostra aleatòria simple de $X$ valgui la variància $\sigma_{X}^2$ de $X$, en el sentit usual que si prenem mostres aleatòries simples de $X$ de mida $n$ gran i calculam les seves variàncies mostrals, molt probablement obtenim de mitjana un valor molt proper a $\sigma_{X}^2$.

Teorema 3.5 Si $X$ és una variable aleatòria de variància $\sigma_X^2$ i $\widetilde{S}_{X}^2$ és la seva variància mostral de mida $n$, \[ E(\widetilde{S}_{X}^2)=\sigma_{X}^2 \] per a qualsevol $n$.

I per tant no esperam que la variància “a seques” d’una mostra aleatòria simple valgui $\sigma_{X}^2$. Això ho podeu comprovar fàcilment, perquè $S_X^2$ s’obté a partir de $\widetilde{S}_{X}^2$ canviant el denominador, \[ S_X^2=\frac{n-1}{n} \widetilde{S}_{X}^2 \] i per tant \[ E(S_X^2)=\frac{n-1}{n}E(\widetilde{S}_{X}^2)=\frac{n-1}{n}\sigma^2_{X}\neq \sigma^2_{X} \]

El segon resultat ens diu que si la variable $X$ és normal, un múltiple adequat de $\widetilde{S}_{X}^2$ té distribució mostral coneguda, la qual cosa ens permetrà calcular probabilitats d’esdeveniments relatius a $\widetilde{S}_{X}^2$.

Teorema 3.6 Si $X$ es $N(\mu_X,\sigma_X)$ i $\widetilde{S}_{X}$ és la seva variància mostral de mida $n$, la variable aleatòria \[ \frac{(n-1)\widetilde{S}_{X}^2}{\sigma_{X}^2} \] té distribució coneguda: $\chi_{n-1}^2$ (es llegeix khi quadrat amb $n-1$ graus de llibertat).

La lletra $\chi$ en català es llegeix khi; en castellà, ji; i en anglès, chi, pronunciat xai.

Figura 3.5: En Chi és un moixet, la distribució és khi.

De la distribució $\chi_\nu^2$, on $\nu$ són els graus de llibertat, heu de saber que:

És una distribució contínua
Per definició, és la distribució de la suma dels quadrats de $\nu$ variables aleatòries normals estàndard independents. És a dir, si $Z_{1},Z_{2},\ldots, Z_{\nu}$ són variables $N(0,1)$ independents, la variable \[ Z_{1}^{2}+Z_{2}^{2}+\cdots +Z_{\nu}^{2} \] té distribució $\chi_\nu^2$.
El nombre de graus de llibertat $\nu$ és el paràmetre del que depèn la seva densitat
Amb R és chisq
Si $X_\nu$ és una variable aleatòria amb distribució $\chi_\nu^2$, aleshores $E(X_\nu)=\nu$ i $\sigma(X_\nu)^2=2 \nu$
Per a valors petits de $\nu$, la distribució d’una $\chi_{\nu}^2$ és asimètrica amb una cua a la dreta.

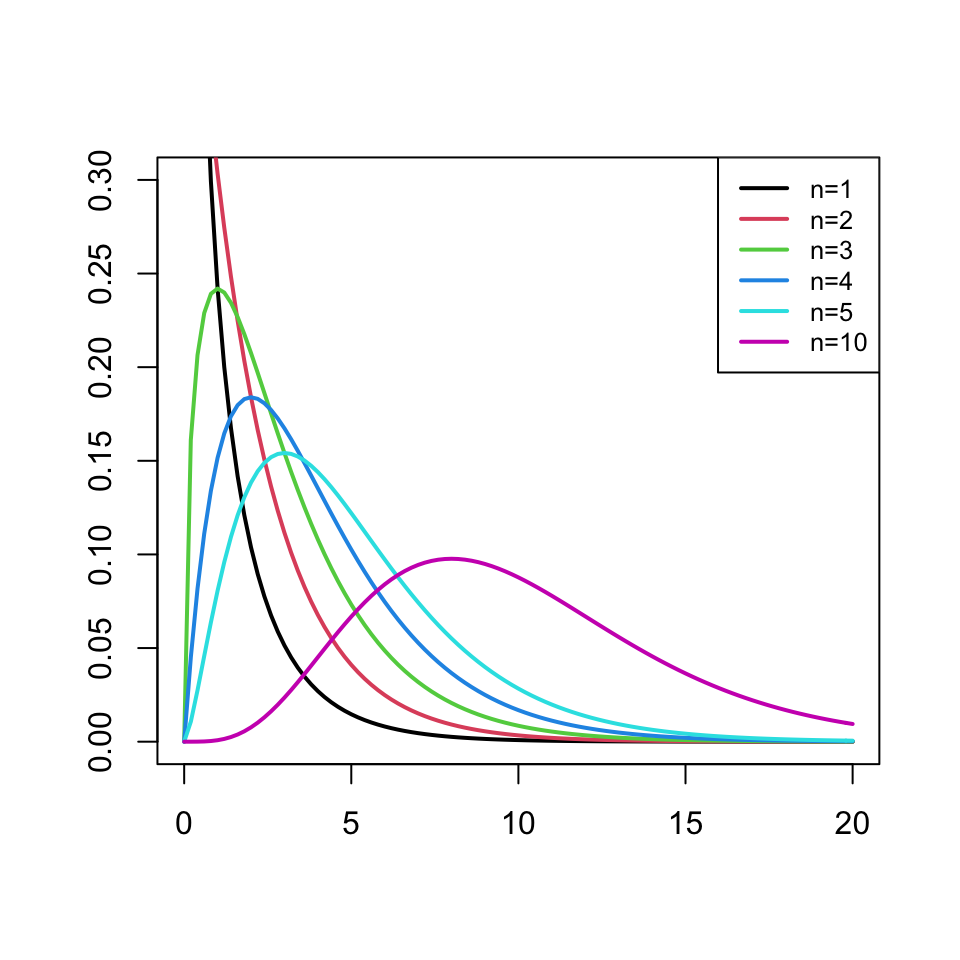
$Algunes densitats de variables $\chi^2$$

Figura 3.6: Algunes densitats de variables $\chi^2$

A mida que $\nu$ creix, i atès que és la distribució d’una suma de $\nu$ variables aleatòries independents, pel Teorema Central del Límit es va aproximant a una distribució normal $N(\nu,\sqrt{2\nu})$.

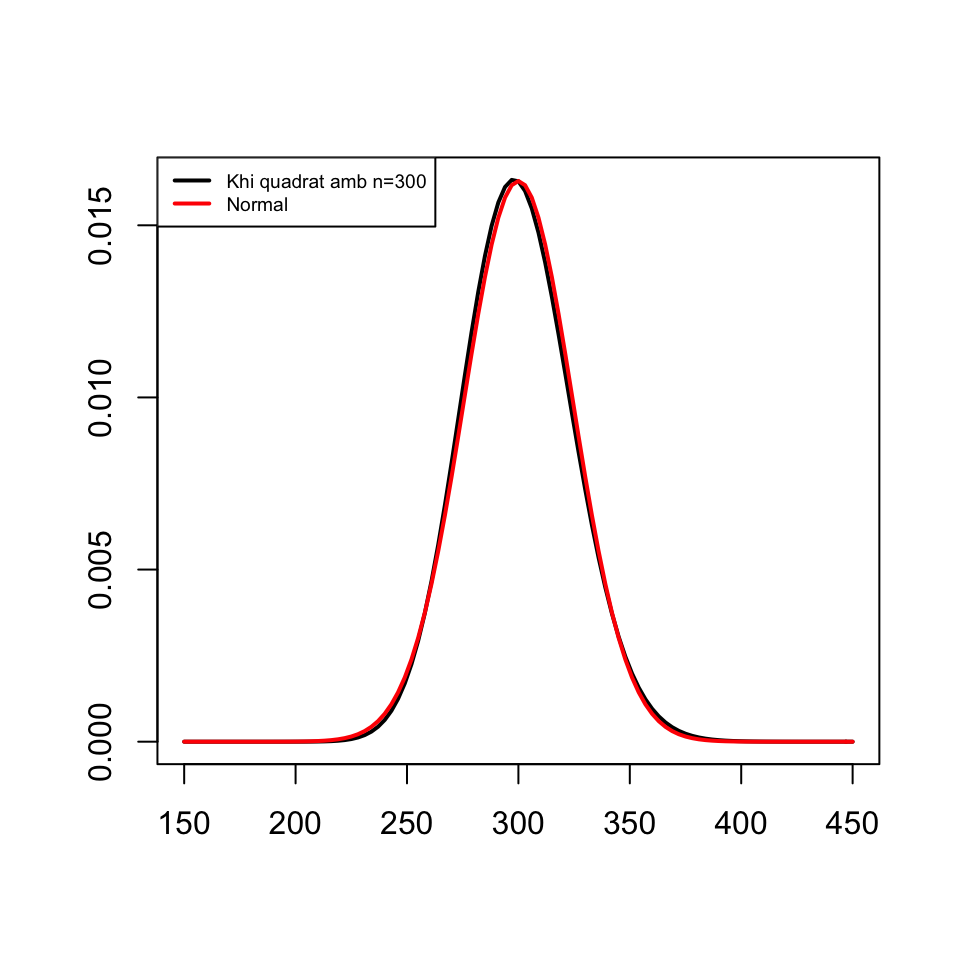
$$\chi^2$ vs normal$

Figura 3.7: $\chi^2$ vs normal

Per si no hi heu caigut, fixau-vos que \[ (n-1)\widetilde{S}_{X}^2=\sum_{i=1}^n (X_i-\mu_X)^2=nS_{X}^2 \] i per tant
\[ \frac{nS_{X}^2}{\sigma_{X}^2}=\frac{(n-1)\widetilde{S}_{X}^2}{\sigma_{X}^2}. \] Així doncs, també podem dir que si $X$ és normal, $nS_{X}^2/\sigma_{X}^2$ té distribució $\chi_{n-1}^2$.

Tornem un instant a això dels graus de llibertat. Per què diem que la variància de mostres de mida $n$ té $n-1$ graus de llibertat?

Doncs perquè si volem construir un conjunt de $n$ nombres $x_1,\ldots,x_n$ que tenguin variància un valor donat, posem $y_0$, en principi podem escollir com volguem $n-1$ d’ells, $x_1,\ldots,x_{n-1}$, i aleshores el darrer, $x_n$, queda bastant fixat. En matemàtiques això se sol expressar dient que “tenim $n-1$ graus de llibertat a l’hora d’escollir $x_1,\ldots,x_n$ amb variància fixada $y_0$”.

En efecte, si fixam el valor $y_0\geqslant 0$ de la variància i volem trobar $x_1,\ldots,x_{n}$ tals que \[ y_0=\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n}=\frac{\sum_{i=1}^n x_i^2}{n}-\overline{x}^2 \] vegem que per a qualssevol valors de $x_1,\ldots,x_{n-1}$, el valor de $x_n$ queda fixat per una equació quadràtica: \[ \begin{array}{l} n y_0 & =\displaystyle \sum_{i=1}^n x_i^2-n\overline{x}^2= \sum_{i=1}^n x_i^2-n\Big(\frac{\sum_{i=1}^n x_i}{n}\Big)^2\\ & =\displaystyle \sum_{i=1}^n x_i^2-\frac{(\sum_{i=1}^n x_i)^2}{n}\\ & \displaystyle =\frac{1}{n}\left(n\sum_{i=1}^n x_i^2-\Big(\sum_{i=1}^{n} x_i\Big)^2\right)\\ & =\displaystyle \frac{1}{n}\left(n\sum_{i=1}^{n-1} x_i^2+n\mathbf{x_n}^2-\Big(\sum_{i=1}^{n-1} x_i\Big)^2-2\Big(\sum_{i=1}^{n-1} x_i\Big)\mathbf{x_n}-\mathbf{x_n}^2\right)\\ & =\displaystyle \frac{1}{n}\left((n-1)\mathbf{x_n}^2-2\Big(\sum_{i=1}^{n-1} x_i\Big)\mathbf{x_n}+n\sum_{i=1}^{n-1} x_i^2-\Big(\sum_{i=1}^{n-1} x_i\Big)^2 \right) \end{array} \] d’on (multiplicant els dos costats de la igualtat per $n$ i dividint-los per $n-1$) obtenim, finalment, l’equació de segon grau en $\mathbf{x_n}$ \[ \mathbf{x_n}^2-\frac{2\sum_{i=1}^{n-1} x_i}{n-1}\mathbf{x_n}+\frac{n\sum_{i=1}^{n-1} x_i^2-\Big(\sum_{i=1}^{n-1} x_i\Big)^2-n^2y_0^2}{n-1}=0 \] Per tant, fixat $y_0$ i un cop escollits $x_1,\ldots,x_{n-1}$, el darrer valor $x_n$ ha de ser per força una solució d’aquesta equació de segon grau.

Fixau-vos que aquesta equació no sempre té solució real, perquè pot tenir el discriminant negatiu. Per tant exageràvem un poc dient que podíem triar $x_1,\ldots,x_{n-1}$ “com volguem”. Per exemple, si voleu que la variància sigui 0 i preneu $x_1,\ldots,x_{n-1}$ no tots iguals, podeu estar ben segurs que no trobareu cap $x_n$ que satisfaci aquesta equació: per tenir variància 0, els nombres $x_1,\ldots,x_n$ han de ser tots iguals. Però el que ha de quedar clar és que un cop escollits $x_1,\ldots,x_{n-1}$, el valor de $x_n$ ja no pot ser qualsevol, pot prendre com a màxim dos valors diferents.

Anau alerta:

Si la variable poblacional $X$ no és normal, la conclusió del Teorema 3.6 no és vertadera.
Encara que $X$ sigui normal, $E(\widetilde{S}_{X})\neq \sigma_{X}$.
Ja ho hem comentat abans, però ho repetim: si $S^2_{X}$ és la variància “a seques” (dividint per $n$ en comptes de per $n-1$), $E(S^2_{X})\neq \sigma^2_{X}$.

Exemple 3.8 Suposem que el pes en néixer dels nadons segueix una distribució normal, i s’estima que la seva desviació típica (en g) és 800. Hem anotat els pesos de tots els recent nats VIH positius d’una ciutat durant 2 anys. El teniu al vector pesos.VIH següent:

pesos.VIH=c(2466,3941,2807,3118,2098,3175,3515,3317,3742,3062,
             3033,2353,2013,3515,3260,2892,1616,4423,3572,2750,
             2807,2807,3005,3374,2722,2495,3459,3374,1984,2495,
             3062,3005,2608,2353,4394,3232,2013,2551,2977,3118,
             2637,1503,2438,2722,2863,2013,3232,2863)

Quina és la probabilitat que una mostra (aleatòria simple) de pesos de recent nats de la mateixa mida que aquesta tengui una desviació típica mostral tan petita o més que la d’aquesta mostra?

La variable d’interès és $X$: “Prenem un recent nat i pesam el seu pes en g”. Ens diuen que és normal amb $\sigma=800$. Pel que fa a la nostra mostra de pesos, la seva mida $n$ és

n=length(pesos.VIH)
n

## [1] 48

i la seva desviació típica mostral és

s.tilda=round(sd(pesos.VIH),1)
s.tilda

## [1] 623.4

Sigui $\widetilde{S}_X$ la desviació típica mostral de mida 48 de la variable $X$. Ens demanen $P(\widetilde{S}_X \leqslant 623.4)$. Això tal qual no ho sabem calcular, perquè no sabem la funció de distribució de $\widetilde{S}_X$. Però sí que sabem la de \[ \frac{(n-1)\widetilde{S}_{X}^2}{\sigma_{X}^2}= \frac{47\widetilde{S}_{X}^2}{800^2} \] Aquesta variable té distribució $\chi_{47}^2$. Per tant el que hem de fer és traduir la probabilitat que volem calcular en termes d’aquesta variable: \[ P(\widetilde{S}_X\leqslant 623.4)=P\Big(\frac{47\widetilde{S}_{X}^2}{800^2}\leqslant \frac{47\cdot 623.4^2}{800^2}\Big)=P(\chi_{47}^2\leqslant 28.54) \] i això val

round(pchisq(round((n-1)*s.tilda^2/800^2,2),n-1),4)

## [1] 0.0153

Per tant, només un 1.5% de les mostres aleatòries simples de 48 recent nats tenen una desviació típica mostral més petita o igual que la de la nostra mostra de recent nats VIH positius.

3.5 La distribució t de Student

Recordau que si la variable poblacional $X$ és $N(\mu_X,\sigma_X)$ i prenem mostres aleatòries simples de mida $n$, la variable \[ \frac{\overline{X}-\mu_X}{\sigma_{X}/\sqrt{n}} \] és normal estàndard. Des del punt de vista teòric això és útil per obtenir fórmules, però normalment no ens serveix per calcular la probabilitat que a $\overline{X}$ li passi qualque cosa, perquè gairebé mai sabrem la desviació típica poblacional $\sigma_{X}$. Què passa si l’estimam per mitjà de $\widetilde{S}_{X}$ amb la mateixa mostra amb la qual calculam $\overline{X}$? Doncs que el resultat següent ens salva el dia, perquè la variable que obtenim té distribució coneguda.

Teorema 3.7 Sigui $X$ una variable $N(\mu_X, \sigma_X)$. Siguin $\overline{X}$ i $\widetilde{S}_{X}$ les seves mitjana mostral i desviació típica mostral de mostres aleatòries simples de mida $n$, respectivament. Aleshores, la variable aleatòria \[ T=\frac{\overline{X}-\mu_X}{\widetilde{S}_{X}/\sqrt{n}} \] té una distribució coneguda, anomenada t de Student amb $n-1$ graus de llibertat, $t_{n-1}$.

Al denominador $\widetilde{S}_{X}/\sqrt{n}$ li diem l’error estàndard, o típic, de la mostra: estima l’error estàndard $\sigma_X/\sqrt{n}$ de $\overline{X}$.

De la distribució t de Student amb $\nu$ graus de llibertat, $t_{\nu}$, heu de saber que:

És contínua
Amb R és t
El nombre de graus de llibertat $\nu$ és el paràmetre del que depèn la seva densitat
Si $T_{\nu}$ és una variable amb distribució $t_{\nu}$, aleshores $E(T_{\nu})=0$ i $\sigma(T_{\nu})^2=\nu/(\nu-2)$ (en realitat aquestes dues igualtats només són veritat si $\nu\geqslant 3$, però no fa falta recordar-ho).
La funció de densitat d’una variable $t_{\nu}$ és simètrica al voltant de 0 (com la d’una $N(0,1)$): \[ P(T_{\nu}\leqslant -x)=P(T_{\nu}\geqslant x)=1-P(T_{\nu}\leqslant x) \] Per tant 0 també és la seva mediana.

Figura 3.8: Densitats d’algunes t de Student

Si $\nu$ és gran, la distribució d’una variable $t_{\nu}$ és aproximadament la d’una $N(0,1)$ però amb una mica més de variància, perquè $\nu/(\nu-2)>1$, i per tant un poc més aplatada.

Figura 3.9: t amb molts graus de llibertat vs Normal estàndard

El fet que una t de Student sigui més aplatada que una normal estàndard $Z$ implica que les cues de la t tenen major probabilitat que les de $Z$ (fixau-vos que als gràfics anteriors els extrems de les densitats de les t estan per damunt dels de la de $Z$), la qual cosa es tradueix en el fet que és més probable obtenir valors lluny del 0 amb una t de Student que amb una $N(0,1)$.

Indicarem amb $t_{\nu,q}$ el $q$-quantil d’una variable aleatòria $T_{\nu}$ que segueix una distribució $t_\nu$. És a dir, $t_{\nu,q}$ és el valor tal que \[ P(T_{\nu}\leqslant t_{\nu,q})=q \] Per la simetria de la distribució $t_\nu$, \[ t_{\nu,q}=-t_{\nu,1-q}. \]

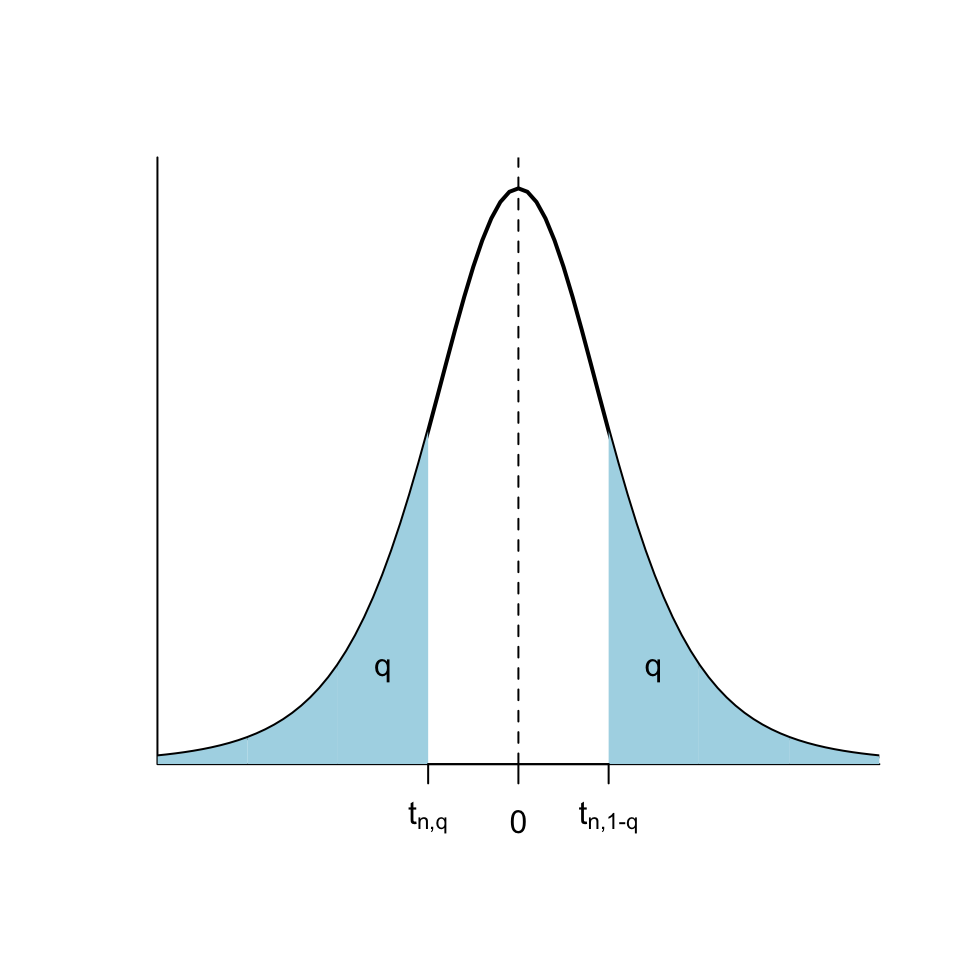
Hi ha algunes propietats dels quantils de la t de Student que heu de saber, per poder aplicar-les quan no tengueu a l’abast R o una apli per calcular quantils:

$t_{\nu ,q}\approx z_{q}$ si $\nu$ és molt gran, posem $\nu \geqslant 200$. Per exemple

qt(0.975,200) # t_{200,0.975}

## [1] 1.971896

qnorm(0.975)  # z_0.975

## [1] 1.959964

$t_{\nu,0.95}$ (per a $10\leqslant \nu\leqslant 200$) està entre 1.65 i 1.8; ho podeu aproximar $t_{\nu,0.95}\approx 1.7$
$t_{\nu,0.975}$ (per a $10\leqslant \nu\leqslant 200$) està entre 1.97 i 2.2; ho podeu aproximar $t_{\nu,0.975}\approx 2$

Comprovau amb R les afirmacions sobr els quantils de la t de Student dels darrers dos punts.

Abans de tancar aquesta secció, recordau que, donada una variable aleatòria $X$, no heu de confondre:

Desviació típica (o estàndard) de la variable aleatòria, $\sigma_X$: El paràmetre poblacional, normalment desconegut.
Desviació típica (o estàndard) (sigui mostral, $\widetilde{S}_X$, o a seques, $S_X$) d’una mostra: L’estadístic que calculam sobre la mostra i que quantifica la dispersió de la mostra.
Error típic (o estàndard) d’un estimador: La desviació típica de la variable aleatòria que defineix l’estimador, normalment desconeguda.
Error típic (o estàndard) d’una mostra: Estimació de l’error típic de la mitjana mostral (o de la proporció mostral) a partir d’una mostra; servirà per calcular intervals de confiança. És $\widetilde{S}_X/\sqrt{n}$ (o $\sqrt{\widehat{p}_X(1-\widehat{p}_X)/n}$ si es tracta de proporcions).

3.6 Biaix i precisió

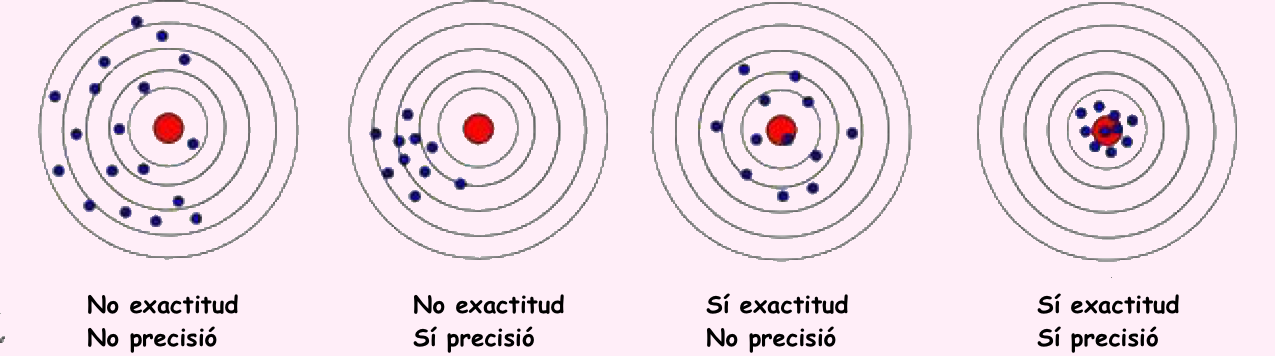
En una primera aproximació, la bondat d’un estimador es descriu en termes de dues propietats: la seva exactitud i la seva precisió.

L’exactitud d’un estimador refereix al fet que el seu valor esperat sigui el valor real del paràmetre que es vol estimar.
La precisió d’un estimador refereix al fet que els seus valors estiguin molt concentrats.

Per tant, un estimador és exacte i precís quan els seus valors es concentren molt al voltant del valor real del paràmetre. La combinació d’exactitud i precisió disminueix la probabilitat que una estimació caigui enfora del valor real que volem estimar.

Aquests dos conceptes se solen il·lustrar amb una diana, així que nosaltres també ho farem:

3.6.1 Estimadors no esbiaixats

Un estimador puntual $\widehat{\theta}$ d’un paràmetre poblacional $\theta$ és exacte, o no esbiaixat (insesgado, en castellà), quan el seu valor esperat és el valor poblacional del paràmetre, és a dir, quan \[ E(\widehat{\theta})=\theta \] El biaix d’un estimador $\widehat{\theta}$ d’un paràmetre $\theta$ és la diferència $E(\widehat{\theta})-\theta$. L’exactitud de l’estimador també es mesura amb aquesta diferència $E(\widehat{\theta})-\theta$, però hem de tenir en compte a l’hora d’expressar-nos que, com més petit sigui el valor absolut d’aquesta diferència, $|E(\widehat{\theta})-\theta|$, menys esbiaixat i més exacte és l’estimador. Per tant, “augmentar l’exactitud” és reduir el valor absolut del biaix.

Exemples: Ja hem vist a les seccions anteriors que

$E(\overline{X})=\mu_X$. Per tant, $\overline{X}$ és un estimador no esbiaixat de $\mu_X$.
$E(\widehat{p}_X)=p_X$. Per tant, $\widehat{p}_X$ és un estimador no esbiaixat de $p_X$.
$E(\widetilde{S}_{X}^2)=\sigma_X^2$. Per tant, $\widetilde{S}_{X}^2$ és un estimador no esbiaixat de $\sigma_X^2$.
Com que ${S}_{X}^2=\dfrac{n-1}{n}\widetilde{S}_{X}^2$, tenim que $E({S}_{X}^2)=\dfrac{n-1}{n}\sigma_X^2$. Per tant, en aquest cas, ${S}_{X}^2$ és un estimador esbiaixat de $\sigma_X^2$, amb biaix \[ \mu_{{S}_{X}^2}-\sigma_X^2=\dfrac{n-1}{n}\sigma_X^2-\sigma_X^2=-\dfrac{\sigma_X^2}{n}\ \mathop{\longrightarrow}_{\scriptscriptstyle n\to\infty}\ 0 \] En aquest cas diem que el seu biaix tendeix a 0.
$E(\widetilde{S}_{X}), E({S}_{X})\neq \sigma_X$ ni tan sols quan $X$ és normal. Per tant, $\widetilde{S}_{X}$ i ${S}_{X}$ són estimadors esbiaixats de $\sigma_X$. Quan $X$ és normal, el seu biaix tendeix a 0.

Recordau que, en general, $E(X^2)\neq E(X)^2$. Per tant, no hauríem d’esperar que $E(\widetilde{S}_{X})=\sqrt{E(\widetilde{S}_{X}^2)}$.

Per si qualque dia us cal saber-ho, si $X$ és normal \[ E(\widetilde{S}_X)=\left\{\begin{array}{ll} \sigma_X\sqrt{\dfrac{2}{(n-1)\pi}}\cdot \dfrac{2^{n-2}(\frac{n}{2}-1)!^2}{(n-2)!} & \text{ si $n$ és parell}\\ \sigma_X\sqrt{\dfrac{2\pi}{n-1}}\cdot \dfrac{(n-2)!}{2^{n-2}(\frac{n-1}{2}-1)!^2} & \text{ si $n$ és imparell} \end{array}\right. \] Per tant, per obtenir un estimador no esbiaixat per a la desviació típica $\sigma_X$ d’una variable normal, només heu de dividir $\widetilde{S}_X$ pel factor que acompanyi la $\sigma_X$ a la dreta d’aquesta fórmula, segons quina sigui la mida $n$ de les mostres.

3.6.2 Estimadors precisos

Donats dos estimadors $\widehat{\theta}_1$, $\widehat{\theta}_2$ del mateix paràmetre $\theta$, direm que $\widehat{\theta}_1$ és més eficient, o més precís, que $\widehat{\theta}_2$ quan la desviació típica de $\widehat{\theta}_1$ és més petita que la de $\widehat{\theta}_2$: \[ \sigma(\widehat{\theta}_1)< \sigma(\widehat{\theta}_2). \]
Quan $\widehat{\theta}_1$ i $\widehat{\theta}_2$ són no esbiaixats, que $\widehat{\theta}_1$ sigui més eficient que $\widehat{\theta}_2$ significa que els seus valors es concentren més al voltant del paràmetre $\theta$ que volem estimar.

Normalment, només comparam l’eficiència de dos estimadors quan són no esbiaixats o amb el biaix que tendeixi a 0. De res ens serveix tenir un estimador molt precís però que sistemàticament dóna un valor llunyà del valor real del paràmetre.

Exemples:

Si $X$ és normal, $\overline{X}$ és l’estimador no esbiaixat més eficient de la mitjana poblacional $\mu_X$.
Si $X$ és Bernoulli, $\widehat{p}_X$ és l’estimador no esbiaixat més eficient de la proporció poblacional $p_X$.
Si $X$ és normal, $\widetilde{S}_X^2$ és l’estimador no esbiaixat més eficient de la variància poblacional $\sigma_X^2$.

Exemple 3.9 Sigui $X$ una variable aleatòria normal $N(\mu_X,\sigma_X)$. Per la simetria de les variables normals, sabem que $\mu_X$ és també la seva mediana. Se’ns podria ocórrer llavors emprar la mediana $\mathit{Me}=Q_{0.5}$ d’una mostra aleatòria simple de mida $n$ de $X$ per estimar $\mu_X$.

Resulta que $E(\mathit{Me})=\mu_X$ però \[ \sigma^2(\mathit{Me})\approx \dfrac{\pi}{2}\cdot \dfrac{\sigma_{X}^2}{n}\approx 1.57 \cdot \frac{\sigma_{X}^2}{n}=1.57\sigma^2_{\overline{X}} \]

Per tant, si $X$ és normal, la mediana $\mathit{Me}$ també és un estimador no esbiaixat de $\mu_X$, però és menys eficient que $\overline{X}$. Per això preferim emprar la mitjana mostral per estimar $\mu_X$.

Hem dit que si la població és normal, $\widetilde{S}_X^2$ és l’estimador no esbiaixat més eficient de la variància poblacional $\sigma_X^2$. La variància a seques \[ S_X^2=\frac{(n-1)}{n} \widetilde{S}_X^2 \]
és més eficient, perquè \[ \sigma(S_X^2)=\sqrt{\frac{(n-1)}{n}}\sigma(\widetilde{S}_X^2)<\sigma(\widetilde{S}_X^2), \]
però és un estimador esbiaixat de $\sigma_X^2$, amb biaix que tendeix a 0.

Si $n$ és petit, és millor fer servir la variància mostral $\widetilde{S}_X^2$ per estimar la variància, ja que el biaix pot desplaçar substancialment l’estimació, però si $n$ és gran, el biaix de $S_X^2$ ja és petit i es pot fer servir $S_X^2$. De totes formes, si $n$ és molt gran, dividir per $n$ o per $n-1$ no varia gaire el resultat i per tant $\widetilde{S}_X^2$ i $S_X^2$ donen valors molt semblants.

3.7 Estimadors màxim versemblants

Un estimador d’un paràmetre és màxim versemblant quan, aplicat a una mostra aleatòria simple, dóna el valor del paràmetre que fa màxima la probabilitat d’obtenir aquesta mostra.

En realitat, l’estimació màxim versemblant d’un paràmetre el que fa màxim és el producte dels valors de la funció densitat de la variable aleatòria poblacional aplicada als elements de la mostra. Quan la variable aleatòria és discreta, això coincideix amb el que hem dit, perquè la probabilitat d’obtenir un valor concret és la funció densitat aplicada a aquest valor. Però quan la variable aleatòria poblacional és contínua, la probabilitat d’obtenir una mostra concreta és sempre 0 i no té sentit parlar de maximitzar aquest 0. Per això es pren la funció densitat.

Aquí no ens complicarem la vida i entendrem que el que maximitzam és la probabilitat d’obtenir la mostra.

Exemple 3.10 Suposem que tenim una variable aleatòria Bernoulli $X$ de probabilitat d’èxit $p_X$ desconeguda. Donada una mostra aleatòria simple $x_1,\ldots,x_n$ de $X$, siguin $\widehat{p}_x$ la seva proporció mostral i
\[ P(x_1,\ldots,x_n\mid p_X=p) \] la probabilitat d’obtenir la mostra quan la probabilitat poblacional $p_X$ és igual $p$. Un estimador per a $p_X$ és màxim versemblant quan, aplicat a cada mostra aleatòria simple $x_1,\ldots,x_n$ de $X$, ens dóna el valor de $p$ que fa que \[ P(x_1,\ldots,x_n\mid p_X=p) \] sigui el màxim possible.

Quin creieu que és l’estimador màxim versemblant de $p_X$? Vegem un exemple concret. Suposau en 20 llançaments d’una moneda obtenim 5 cares. Quina creieu que és la probabilitat d’obtenir cara amb aquesta moneda que fa màxima la probabilitat que en 20 llançaments obtinguem 5 cares? La intuïció ens diu que hauria de ser la proporció mostral $\widehat{p}_X=5/20=0.25$, no? Confirmem-ho amb el gràfic de la probabilitat que una binomial $B(20,p)$ doni 5 en funció de $p$:

plot((0:200)/200,dbinom(5,20,(0:200)/200),type="h",xlab="p",ylab="",xaxp=c(0,1,20))
points(0.25,dbinom(5,20,0.25),type="h",col="red")

Figura 3.10: Probabilitat que una B(20,p) valgui 5

El resultat següent mostra que això sempre és així.

Teorema 3.8 El valor de $p$ per al qual $P(x_1,\ldots,x_n\mid p_X=p)$ és màxim és $\widehat{p}_x$.

La demostració és senzilla. Suposau que dins $x_1,\ldots,x_n$ hi ha $m$ 1s i $n-m$ 0s, de manera que $\widehat{p}_X=m/n$. Aleshores, la probabilitat d’obtenir $x_1,\ldots,x_n$ és \[ P(x_1,\ldots,x_n\mid p_X=p)=p^m(1-p)^{n-m} \] Per trobar el valor de $p$ que fa aquest probabilitat màxima, derivau respecte de $p$ i estudiau el signe de la derivada, i concloureu que el màxim es dóna efectivament a $p=m/n$.

La proporció $\widehat{p}_x$ és el valor de $p_X$ que fa màxima la probabilitat d’obtenir la nostra mostra, no a l’enrevés: No és el valor més probable de $p_X$ condicionat a la nostra mostra. Vaja, no confongueu \[ P(x_1,\ldots,x_n\mid p_X=p)\text{ amb }P(p_X=p\mid x_1,\ldots,x_n). \] D’això darrer no en sabem trobar el màxim sense alguna hipòtesi sobre la distribució de probabilitat dels valors possibles de $p_X$.

Si la proporció $\widehat{p}_x$ fos el valor més probable de $p_X$ condicionat a la nostra mostra, en díríem un estimador màxim probable, no un estimador màxim versemblant, no ho trobau?

Alguns altres estimadors màxim versemblants:

$\overline{X}$ és l’estimador màxim versemblant del paràmetre $\lambda$ d’una variable aleatòria Poisson
$\overline{X}$ és l’estimador màxim versemblant de la mitjana $\mu_X$ d’una variable aleatòria normal
$S_X^2$ i $S_X$ (sí, la variància i desviació típica a seques, no les mostrals!) són els estimadors màxim versemblants de la variància $\sigma_X^2$ i la desviació típica $\sigma_X$ d’una variable aleatòria normal

3.8 Estimació de poblacions

3.8.1 Estimació de poblacions numerades

Exemple 3.11 Un dia vaig voler estimar quants taxis hi havia a Palma. Per fer-ho, assegut en un bar del Passeig Marítim vaig apuntar les llicències dels 40 primers taxis que passaren. Els entraré directament en un vector de R.

taxis=c(1217,600,883,1026,150,715,297,137,508,134,38,961,538,1154,
        314,1121,823,158,940,99,977,286,1006,1207,264,1183,1120,
        498,606,566,1239,860,114,701,381,836,561,494,858,187)
sort(taxis)

##  [1]   38   99  114  134  137  150  158  187  264  286  297  314  381  494  498
## [16]  508  538  561  566  600  606  701  715  823  836  858  860  883  940  961
## [31]  977 1006 1026 1120 1121 1154 1183 1207 1217 1239

Puc estimar quants taxis hi ha a Palma a partir d’aquesta mostra? Us pot semblar una beneitura de pregunta, però aquest és un problema de rellevància històrica, com podeu consultar en aquest article.

La solució d’aquest problema és donada pel resultat següent:

Teorema 3.9 Sigui $X$ una variable aleatòria uniforme sobre $\{1,2,\ldots,N\}$ (és a dir, $X$ pot prendre tots els valors entre 1 i N, tots amb la mateixa probabilitat 1/N), i sigui $x_1,\ldots,x_n$ una mostra aleatòria sense reposició de $X$. Sigui $m=\max(x_1,\ldots,x_n)$. Aleshores, l’estimador no esbiaixat més eficient de $N$ és \[ \widehat{N}=m+\frac{m-n}{n} \]

Vegem la idea intuïtiva que hi ha al darrere d’aquesta fórmula. Suposau que teniu $x_1,\ldots,x_n$ ordenats en ordre creixent, $x_1<\cdots<x_n$, de manera que $x_n=m$. Calculem la longitud mitjana dels “forats” a l’esquerra de cada valor $x_i$.

A l’esquerra de $x_1$ hi “falten” els nombres $1,2,\ldots,x_1-1$, per tant hi ha un forat de $x_1-1$ nombres.
Entre $x_1$ i $x_2$ hi “falten” els nombres $x_1+1,\ldots,x_2-1$, per tant hi ha un forat de $x_2-x_1-1$ nombres.
En general, entre cada $x_{i-1}$ i $x_{i}$ hi ha un forat de $x_{i}-x_{i-1}-1$ nombres (hi “falten” els nombres $x_{i-1}+1,\ldots,x_i-1$).

Per tant, la mitjana de les longituds d’aquests “forats” és \[ \begin{array}{l} \displaystyle \frac{(x_1-1)+(x_2-x_1-1)+\cdots+(x_{n}-x_{n-1}-1)}{n}\\ \displaystyle \qquad\quad =\frac{x_n-n}{n}=\frac{m-n}{n} \end{array} \]

El que fa l’estimador $\widehat{N}$ és sumar al màxim de la mostra, $m$, aquesta longitud mitjana dels forats entre membres de la mostra. És a dir, estimam que la mida de la població és tal que a la dreta del màxim de la nostra mostra hi ha un “forat” de mida la mitjana dels forats de la mostra menys 1.

Exemple 3.12 Continuem amb l’Exemple 3.11. Emprant la fórmula anterior, obtenim

max(taxis)+(max(taxis)-length(taxis))/length(taxis)

## [1] 1268.975

la qual cosa em permeté estimar que hi havia 1269 taxis a Palma. En realitat, consultant la web de l’Ajuntament, després vaig saber que en aquell moment n’hi havia 1246.

Exemple 3.13 Fem un experiment. Generarem a l’atzar una mida N d’una població grandeta, i suposarem que els individus de la població estan numerats de l’1 al N. A continuació, prendrem 100 mostres aleaòries sense reposició de la nostra població i amb cada una d’aquestes mostres estimarem la N emprant la fórmula que hem donat. Al final, calcularem la mitjana d’aquestes estimacions i la compararem amb el valor real de N, que no descobrirem fins el final.

Perquè l’experiment sigui reproduïble, fixarem la llavor d’aleatorietat, però perquè no cregueu que fem trampes amb aquesta llavor, el que farem serà generar a l’atzar la llavor d’aleatorietat amb la funció sample.

Llavor=sample(1000,1)
Llavor

## [1] 580

set.seed(Llavor)

Ara generam la mida N de la població com un nombre a l’atzar entre 5000 i 10000.

N=sample(5000:10000,1)

Suposarem per tant que hi ha N individus a la nostra població, numerats de l’1 al N. Ara generarem 100 mostres aleatòries sense reposició d’aquesta població, i ens quedarem amb la mida i el valor màxim de cada una d’elles, que és l’únic que necessitam saber. Les mides les generarem a l’atzar entre, posem, 25 i 75:

Mostra=function(a,b,P){
  # a i b: mides màxima i mínima de la mostra; P: mida de la població
  n=sample(a:b,1)  # Mida de la mostra
  X=sample(P,n)  # Mostra aleatòria de mida n
  c(n,max(X)) # Parell (mida, màxim)
}
Mostres=replicate(100,Mostra(25,75,N))
Mostres

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
## [1,]   43   53   53   40   67   44   40   73   67    67    61    26    37    30
## [2,] 6682 6684 6684 6652 6673 6623 6607 6540 6670  6657  6657  6455  6528  6667
##      [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
## [1,]    75    29    56    29    33    74    51    64    42    61    39    68
## [2,]  6686  6651  6632  6617  6671  6470  6379  6565  6637  6684  6423  6522
##      [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
## [1,]    48    28    57    28    63    46    32    31    44    69    31    31
## [2,]  6105  6522  6293  6327  6691  6498  6464  6522  6652  6606  6298  6262
##      [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49] [,50]
## [1,]    27    65    70    30    42    56    53    40    33    25    61    63
## [2,]  6562  6676  6509  5655  6370  6641  6653  6674  6341  6612  6641  6693
##      [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61] [,62]
## [1,]    59    42    60    52    64    38    26    71    75    48    39    47
## [2,]  6657  6596  6545  6681  6528  6583  6656  6692  6588  6603  6569  6583
##      [,63] [,64] [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72] [,73] [,74]
## [1,]    41    37    57    70    51    29    69    46    52    64    56    54
## [2,]  6480  6535  6693  6694  6422  6665  6630  6654  6679  6414  6609  6672
##      [,75] [,76] [,77] [,78] [,79] [,80] [,81] [,82] [,83] [,84] [,85] [,86]
## [1,]    59    57    56    69    39    70    58    59    48    50    37    68
## [2,]  6675  6624  6223  6618  6480  6664  6681  6536  6525  6671  6669  6686
##      [,87] [,88] [,89] [,90] [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98]
## [1,]    70    44    39    47    56    65    43    32    60    57    42    55
## [2,]  6697  6490  6677  6619  6492  6609  6587  6653  6564  6674  6152  6585
##      [,99] [,100]
## [1,]    75     36
## [2,]  6398   6623

En aquesta matriu Mostres, cada columna correspon a una mostra aleatòria: la primera filera és la seva mida $n$ i la segona filera el màxim $m$. Ara, amb cada una d’aquestes mostres, podem estimar la mida N de la població per mitjà de la fórmula $m+(m-n)/n$. Dibuixarem un histograma d’aquestes estimacions, per veure què ens ha sortit.

Estimacions=Mostres[2,]+(Mostres[2,]-Mostres[1,])/Mostres[1,]
round(range(Estimacions),1) # Estimacions mínima i màxima

## [1] 5842.5 6911.0

hist(Estimacions, breaks=20,col="light blue",
     xlab="Estimacions de N",ylab="Freqüències",main="")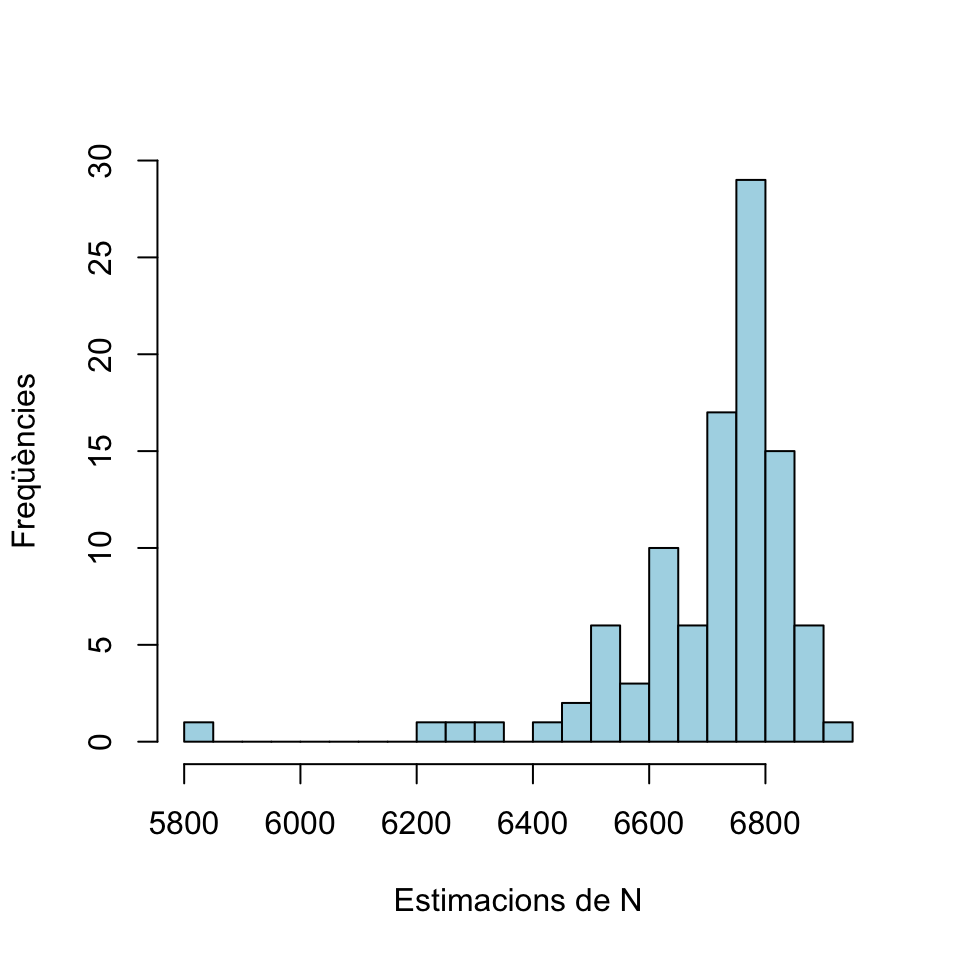

Com veieu, obtenim estimacions que van de 5842.5 a 6911. La mitjana d’aquestes estimacions és

round(mean(Estimacions),1)

## [1] 6704.5

És hora de descobrir el valor de N, per veure si hi hem fet a prop:

## [1] 6701

No hem fet molt enfora, com veieu.

3.8.2 Marca-recaptura

Suposem que en una població hi ha $N$ individus, en capturam $K$ (tots diferents), els marcam i els tornam a amollar. Al cap de poc temps, en capturam $n$, dels quals resulta que $k$ estan marcats. A partir d’aquestes dades, volem estimar el valor de $N$.

Si suposam que $N$ i $K$ no han canviat de la primera a la segona captura (cap individu no ha abandonat la població ni se n’hi ha incorporat cap de nou), aleshores la variable aleatòria $X$ definida per “Capturam un individu i miram si està marcat” és Bernoulli $Be(p)$ amb $p=K/N$, on coneixem la $K$ i volem estimar la $N$.

Sigui ara $x_1,\ldots,x_n$ la mostra capturada en segon lloc. La seva proporció mostral d’individus marcats és $\widehat{p}_X=k/n$. Com que $\widehat{p}_X$ és l’estimador màxim versemblant de $p$, estimam que \[ \dfrac{K}{N}=\dfrac{k}{n} \] d’on, aïllant la $N$, estimam que \[ N=\frac{n\cdot K}{k}. \]

En resum, l’estimador \[ \widehat{N}=\frac{n\cdot K}{k} \] maximitza la probabilitat d’obtenir $k$ individus marcats en una mostra aleatòria de $n$ individus. És l’estimador màxim versemblant de $N$ a partir de $K$, $k$ i $n$; també se li diu estimador de Lincoln-Petersen. Fixau-vos que aquest estimador no fa res més que traduir la proporció “Si he trobat $k$ individus marcats en un conjunt de $n$ individus, què ha de valer el nombre total $N$ de individus perquè hi hagi en total $K$ individus marcats?”

Exemple 3.14 Suposem que hem marcat 15 peixos d’un llac, i que en una captura posterior de 10 peixos, n’hi ha 4 de marcats. Quants peixos conté el llac?

Ho estimarem amb l’estimador de Lincoln-Petersen: \[ \widehat{N}=\frac{15\cdot 10}{4}=37.5 \] Per tant, estimam que hi haurà entre 37 i 38 peixos al llac.

En aquest cas podem comprovar la màxima versemblança d’aquesta estimació, calculant la probabilitat d’obtenir 4 individus marcats en una mostra aleatòria de 10 individus d’una població de $N$ individus on n’hi ha 15 de marcats i trobant la $N$ que maximitza aquesta probabilitat. Per fer-ho, recordem que si una població està formada per $K$ subjectes marcats i $N-K$ subjectes no marcats, el nombre de subjectes marcats en mostres aleatòries sense reposició de mida $n$ segueix una distribució hipergeomètrica $H(K, N-K,n)$. Per tant, per a cada possible $N$, la probabilitat que en una mostra de 10 peixos del nostre llac n’hi hagi 4 de marcats serà dhyper(4,15,N-15,10).

N=15:1000  # Rang de possibles valors de N
p=dhyper(4,15,N-15,10)  # Probabilitats de 4 marcats en 10
Nmax=N[which(p==max(p))] # N que maximitza la probabilitat
Nmax

## [1] 37

Aquest Nmax és la $N$ que fa màxima la probabilitat que en una mostra de 10 peixos del nostre llac n’hi hagi 4 de marcats. Vegem-ho amb un gràfic:

plot(N[1:86],p[1:86],type="h",xaxp=c(15,100,17),xlab="N",ylab="p")
points(Nmax,dhyper(4,15,Nmax-15,10),type="h",col="red",lwd=1.5)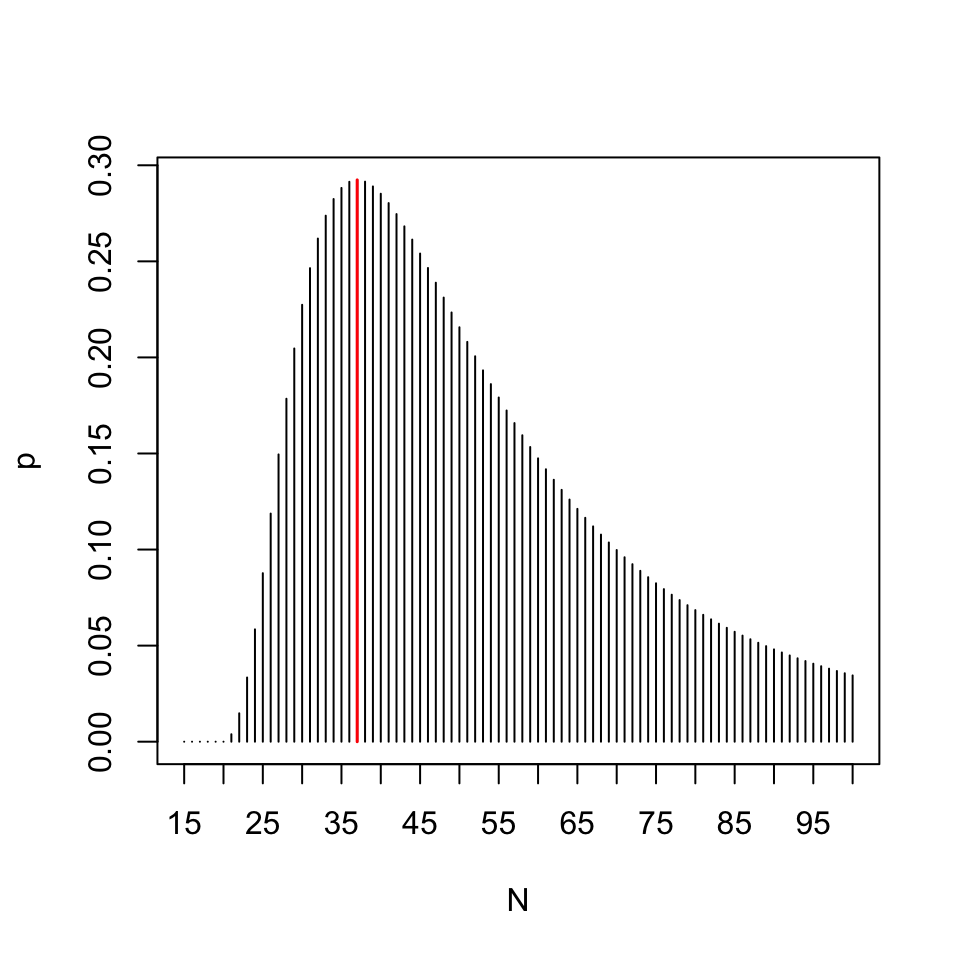

I què hagués passat si no haguéssim trobat cap peix marcat a la mostra?

Quan la mida de la mostra és petita, és més convenient emprar l’estimador de Chapman: \[ \widehat{N}=\frac{(n+1)\cdot (K+1)}{k+1}-1 \]

La idea és que afegim a la població un individu extra i marcat, que suposam que també capturam a la segona mostra. Llavors, aplicam l’estimador de Lincoln-Petersen i finalment restam 1, per descomptar l’individu marcat extra que realment no pertany a la població que volem estimar. D’aquesta manera ja no tenim el problema de dividir per 0 si $k$ ens dóna 0.

En la situació de l’Exemple 3.14, aquest estimador dóna \[ \widehat{N}=\frac{16\cdot 11}{5}-1=34.2 \] i ens fa estimar una població total d’uns 34 peixos. Abans hem obtingut entre 37 i 38 peixos.

Quina de les dues estimacions s’acosta més a la realitat? Ni idea, no ho podem saber. Amb una altra recaptura segurament haguéssim obtingut resultats diferents.

L’estimador de Lincoln-Petersen \[ \widehat{N}=\frac{n\cdot K}{k} \] és esbiaixat, amb biaix que tendeix a 0. L’estimador de Chapman és menys esbiaixat però no és màxim versemblant.

Exemple 3.15 Fem un experiment similar al de l’Exemple 3.13. Generarem a l’atzar una mida N d’una població grandeta i en marcarem una certa quantitat K. A continuació, prendrem 50 mostres aleaòries sense reposició de la nostra població i amb cada una d’aquestes mostres estimarem la N emprant els dos estimadors que hem explicat en aquesta subsecció. Al final, calcularem les mitjanes d’aquestes estimacions i les compararem amb el valor real de N, que no descobrirem fins el final. Com a l’Exemple 3.13, fixarem la llavor d’aleatorietat a l’atzar.

Llavor2=sample(1000,1)
Llavor2

## [1] 206

set.seed(Llavor2)

Ara generam la mida N de la població com un nombre a l’atzar entre 5000 i 10000.

N=sample(5000:10000,1)

Ara en capturam i marcam K; per fixar idees, prendrem K=200.

K=200

Per simplificar, suposarem que els N individus de la nostra població estan numerats de l’1 a l’N i que els marcats són els K primers. Ara generarem 100 mostres aleatòries sense reposició d’aquesta població, i ens quedarem amb la mida de la mostra i el nombre d’individus marcats (és a dir, el nombre de valors $\leqslant K=200$ en la mostra). Les mides les generarem a l’atzar entre, posem, 100 i 150:

Mostra=function(a,b,P,M){
  # a i b: mides màxima i mínima de la mostra; P: mida de la població;
  # M: nombre de marcats
  n=sample(a:b,1)  # Mida de la mostra
  X=sample(P,n,rep=FALSE)  # Mostra aleatòria 
  c(n,length(which(X<=M))) # Parell (mida, nombre de marcats)
}
Mostres=replicate(100, Mostra(100,150,N,K))
Mostres

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
## [1,]  119  101  101  109  130  121  129  107  136   108   120   146   124   134
## [2,]    5    2    5    1    5    4    6    3    4     3     2     5     3     4
##      [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
## [1,]   106   131   120   149   113   143   117   125   132   101   109   108
## [2,]     1     3     4     5     2     3     4     5     1     4     3     2
##      [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
## [1,]   138   143   109   105   141   110   125   150   109   103   141   115
## [2,]     4     3     8     2     3     1     5     3     2     6     8     3
##      [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49] [,50]
## [1,]   107   132   135   118   131   117   110   115   135   138   127   121
## [2,]     2     4     3     4     3     5     1     3     6     2     6     5
##      [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61] [,62]
## [1,]   124   144   134   115   129   102   111   130   102   107   111   123
## [2,]     2     4     4     1     5     6     5     5     2     1     4     4
##      [,63] [,64] [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72] [,73] [,74]
## [1,]   119   131   115   150   145   125   119   149   129   112   146   135
## [2,]     4     3     2     1     7     1     3     1     5     4     7     4
##      [,75] [,76] [,77] [,78] [,79] [,80] [,81] [,82] [,83] [,84] [,85] [,86]
## [1,]   119   128   124   147   148   135   139   150   123   142   108   138
## [2,]     2     5     4     4     5     6     4     6     5     8     2     2
##      [,87] [,88] [,89] [,90] [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98]
## [1,]   112   141   131   144   111   112   147   103   112   108   107   133
## [2,]     2     7     5     4     1     6     3     4     4     1     2     5
##      [,99] [,100]
## [1,]   139    149
## [2,]     1      5

En aquesta matriu Mostres, cada columna correspon a una mostra aleatòria: la primera filera és la seva mida $n$ i la segona filera el nombre d’individus marcats a la mostra. Ara, amb cada una d’aquestes mostres, podem estimar la mida N de la població per mitjà de l’estimador de Lincoln-Petersen.

EstimacionsLP=Mostres[1,]*K/Mostres[2,]
round(range(EstimacionsLP),1)

## [1]  2725 30000

hist(EstimacionsLP, breaks=20,col="light blue",
     xlab="Estimacions de N",ylab="Freqüències",
     main="Estimador de Lincoln-Petersen")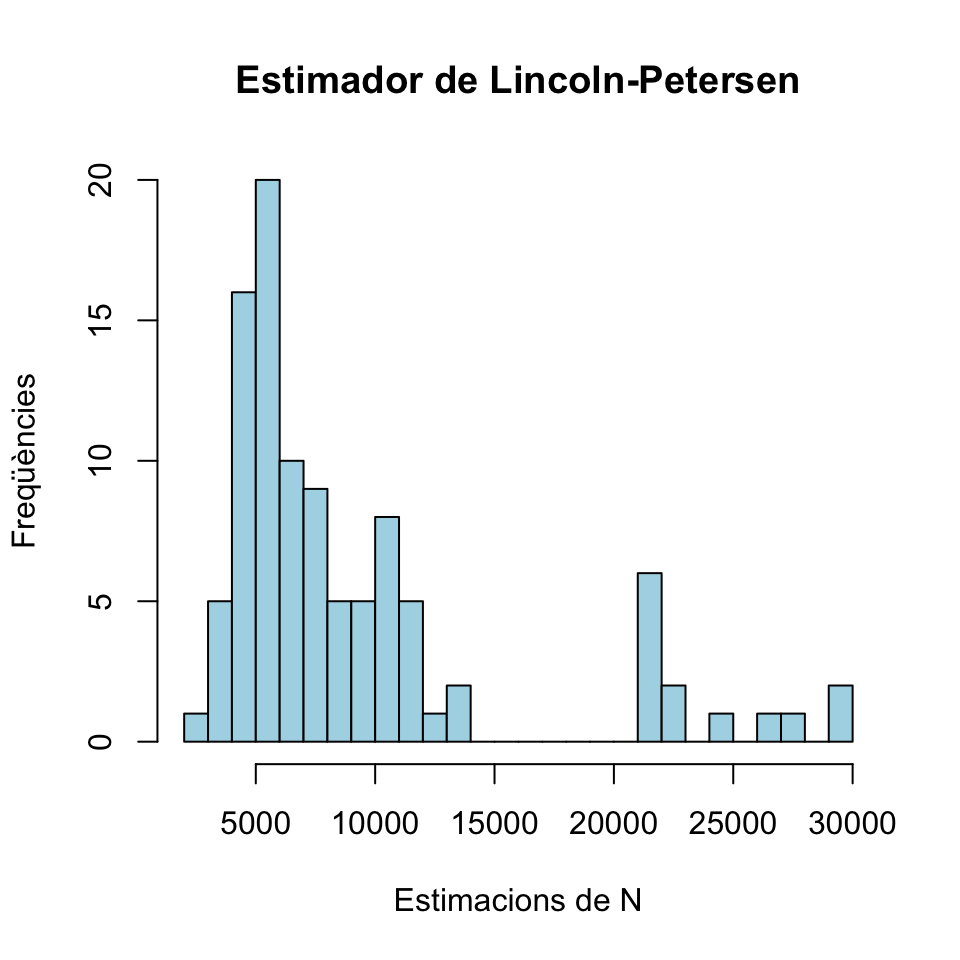

Com veieu, obtenim estimacions que van de 2725 a 30000. La mitjana de les estimacions és

round(mean(EstimacionsLP),1)

## [1] 9246

També podem emprar l’estimador de Chapman:

EstimacionsCh=(Mostres[1,]+1)*(K+1)/(Mostres[2,]+1)-1
round(range(EstimacionsCh),1)

## [1]  2455.7 15174.5

hist(EstimacionsCh, breaks=20,col="light blue",xlab="Estimacions de N",ylab="Freqüències",main="Estimador de Chapman")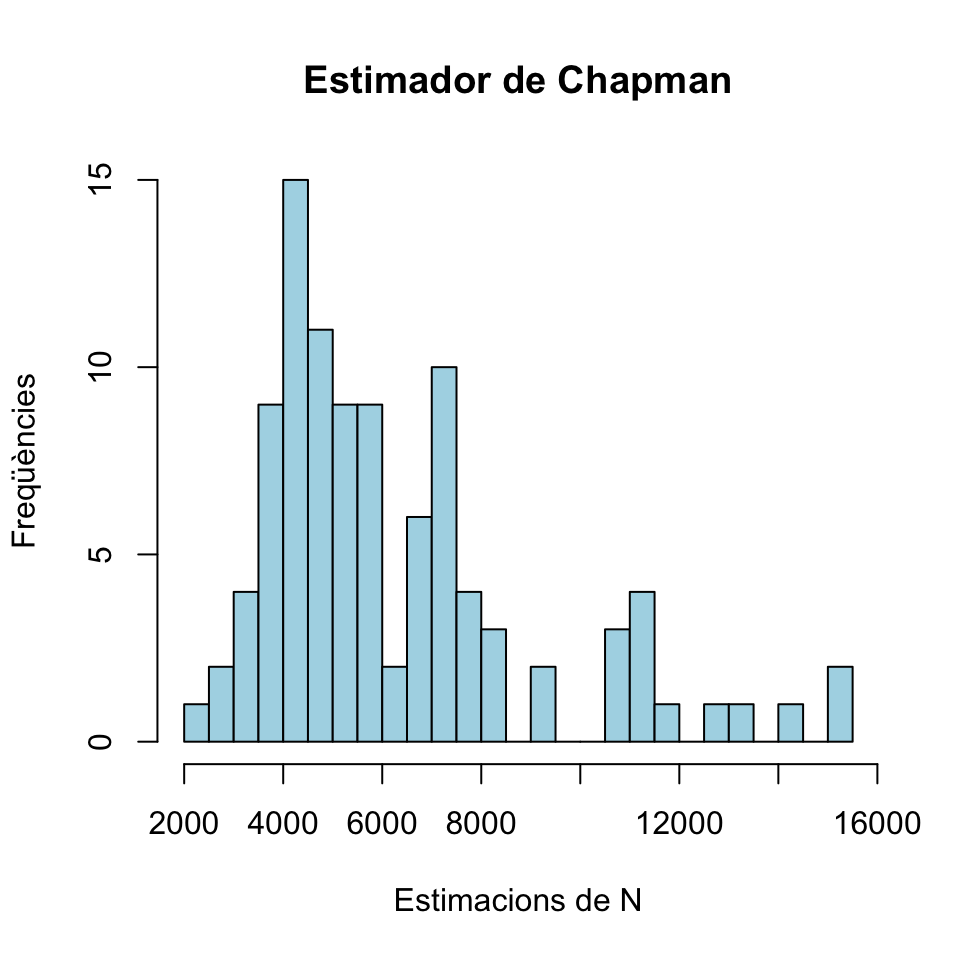

Com veieu, obtenim estimacions que van de 2455.7 a 15174.5. La mitjana d’aquestes estimacions és

round(mean(EstimacionsCh),1)

## [1] 6292.7

És hora de descobrir el valor de N, per veure si hi hem fet a prop:

## [1] 7225

Com veieu, amb l’estimador de Chapman ens hem fet més a prop del valor real de $N$ que amb el màxim versemblant. Però amb cap d’ells ens hi hem fet molt a prop.

3.9 Test de la lliçó 3

(1) Tenim una variable aleatòria $X$ normal de mitjana $\mu$ i desviació típica $\sigma$. Prenem mostres aleatòries simples de mida $n$, i indicam amb $\widetilde{S}_X$ la seva desviació típica mostral. Quina o quines de les afirmacions següents són vertaderes?

$E(\widetilde{S}_X^2)=\sigma^2$.
$E(\widetilde{S}_X)=\sigma$.
$\widetilde{S}_X^2$ segueix una distribució $\chi^2$ amb $n-1$ graus de llibertat.
$(n-1)\widetilde{S}_X^2/\sigma^2$ segueix una distribució $\chi^2$ amb $n-1$ graus de llibertat.
Totes les altres respostes són falses.

(2) Quina o quines de les afirmacions següents sobre la mitjana mostral són vertaderes?

Si la distribució poblacional és normal, sempre coincideix amb la mediana de la mostra.
Sempre serveix per estimar la mitjana poblacional.
Sempre serveix per estimar la mediana poblacional.
Si la distribució poblacional és normal, serveix per estimar la mediana poblacional.
Cap de les altres respostes és correcta.

(3) L’error estàndard de la mitjana mostral de mida $n\geqslant 2$ (marca totes les continuacions correctes):

Mesura la variabilitat de les observacions que formen la mostra.
És l’exactitud amb què es mesura cada observació de la mostra.
Mesura la variabilitat de les mitjanes mostrals de mostres aleatòries simples.
Mesura la precisió amb què les mitjanes mostrals de mostres aleatòries simples estimen la mitjana poblacional.
És proporcional a la mitjana mostral.
És més gran que la desviació típica de la població.
Sobre cada mostra val la desviació típica de la mostra.
Cap de les altres respostes és correcta.

(4) La proporció d’afectats per una determinada malaltia en una població és del 10%. Si estimam aquesta proporció poblacional repetidament a partir de mostres de mida 1000, aquestes estimacions segueixen una distribució que (marca totes les afirmacions correctes):

És una distribució mostral.
És aproximadament normal.
Té mitjana 0.1.
Té variància 90.
És binomial.
Cap de les altres respostes és correcta.

(5) Què hem de fer per disminuir a la meitat l’error estàndard d’una proporció?

Hem d’augmentar en un 50% la mida de la mostra
Hem de doblar la mida de la mostra.
Hem de quadruplicar la mida de la mostra.
Hem de dividir per 2 la mida de la mostra.
Hem de dividir per 4 la mida de la mostra.
Cap de les altres respostes és correcta.

(6) La probabilitat que els individus d’una determinada població tenguin una determinada característica $C$ és $p$. Prenem mostres aleatòries simples de mida $n$ d’aquesta població, i indicam amb $\widehat{p}_X$ la seva proporció mostral. Quina o quines de les afirmacions següents són vertaderes?

$\widehat{p}_X$ té sempre distribució binomial $B(n,p)$.
$\widehat{p}_X$ té sempre distribució normal.
Si $n$ és gran, $\widehat{p}_X$ té distribució aproximadament binomial $B(n,p)$.
Si $n$ és gran, $\widehat{p}_X$ té distribució aproximadament normal.
L’error estàndard de $\widehat{p}_X$ és $\sqrt{p(1-p)/n}$.

(7) Sigui $X$ una variable aleatòria que no és constant. Si en prenem mostres aleatòries simples més grans (marca totes les continuacions correctes):

La mitjana mostral sempre disminueix.
L’error estàndard de la mitjana sempre disminueix.
L’error estàndard de la mitjana sempre augmenta.
La variància mostral sempre augmenta.
El nombre de graus de llibertat de l’estimador $\chi^2$ associat a la variància mostral sempre augmenta.
Cap de les altres respostes és correcta.

(8) La longitud d’una determinada espècie d’animalons té un valor mitjà de $\mu$ cm. Si prenem mostres aleatòries simples de 20 exemplars, calculam la seva mitjana mostral $\overline{X}$ i la seva desviació típica mostral $\widetilde{S}_X$ (marca la continuació més correcta):

L’estadístic $\frac{\overline{X}-\mu}{\widetilde{S}_X/\sqrt{20}}$ segueix sempre una llei normal.
L’estadístic $\frac{\overline{X}-\mu}{\widetilde{S}_X/\sqrt{20}}$ segueix sempre una llei t de Student.
L’estadístic $\frac{\overline{X}-\mu}{\widetilde{S}_X/\sqrt{20}}$ segueix una llei normal si la longitud segueix una llei normal.
L’estadístic $\frac{\overline{X}-\mu}{\widetilde{S}_X/\sqrt{20}}$ segueix una llei t de Student si la longitud segueix una llei normal.
L’estadístic $\frac{\overline{X}-\mu}{\widetilde{S}_X/\sqrt{20}}$ no segueix mai ni una llei normal ni una llei t de Student, perquè les mostres no són prou grans.

(9) En una mostra de 100 dones es va obtenir una concentració mitjana d’hemoglobina en sang de 10 amb una desviació típica de 2. Quin és l’error típic de la mostra?

0.02
0.04
0.2
0.4
1
Cap dels valors anteriors

(10) Què significa que un estimador d’un paràmetre d’una variable aleatòria sigui no esbiaixat?

Que la distribució mostral de l’estimador és normal.
Que aplicat a una mostra aleatòria simple sempre dóna el valor poblacional del paràmetre.
Que el seu valor esperat és igual al valor poblacional del paràmetre.
Que aplicat a una mostra aleatòria simple sempre dóna el valor esperat del paràmetre.
Que el seu error típic és petit.

(11) La concentració en sang a les persones d’un determinat metabolit (en mg/ml) té una distribució $N(23,3)$. Quina de les afirmacions següents és vertadera?

Aproximadament un 90% de les mostres aleatòries de 100 individus tendran la seva mitjana entre 22.4 i 23.6 mg/ml.
Aproximadament un 95% de les mostres aleatòries de 100 individus tendran la seva mitjana entre 22.4 i 23.6 mg/ml.
Aproximadament un 99% de les mostres aleatòries de 100 individus tendran la seva mitjana entre 22.4 i 23.6 mg/ml.
Més d’un 99% de les mostres aleatòries de 100 individus tendran mitjana igual a 23.
Cap de les afirmacions anteriors és vertadera.

(12) Sigui $X$ una variable aleatòria $N(\mu_X,2)$ i sigui $\overline{X}$ la mitjana mostral de mida $10$ de $X$. Quina de les afirmacions següents és vertadera?

La desviació típica de $\overline{X}$ és igual a 2.
La desviació típica de $\overline{X}$ és menor que 2.
La desviació típica de $\overline{X}$ és major que 2.
Que la desviació típica de $\overline{X}$ sigui major, menor o igual que 2 depèn de $\mu_X$.
Cap de les afirmacions anteriors és vertadera.

(13) Quan un estimador és màxim versemblant?

Quan, aplicat a una mostra, sempre dóna el valor real del paràmetre.
Quan tots els estadístics el consideren versemblant
Quan, aplicat a una mostra, dóna el valor que fa màxima la probabilitat del paràmetre.
Quan, aplicat a una mostra, dóna el valor del paràmetre que fa màxima la probabilitat de la mostra.
Quan el seu valor esperat és el valor real del paràmetre.