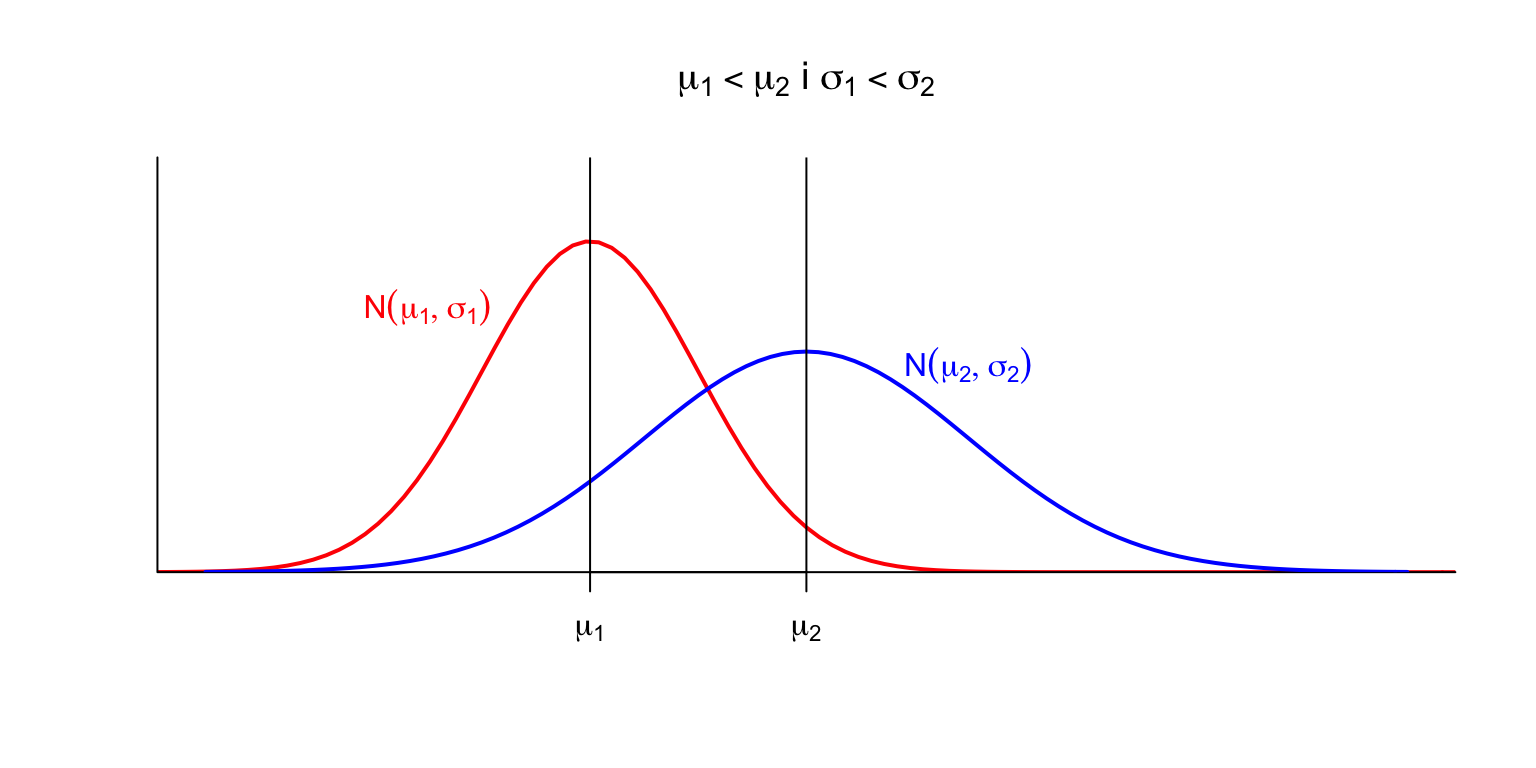
Tema 2 Variables aleatòries

2.1 Generalitats sobre variables aleatòries

Una variable aleatòria definida sobre una població \(\Omega\) és simplement una funció \[ X: \Omega\to \mathbb{R} \] que assigna a cada subjecte de \(\Omega\) un nombre real. La idea intuïtiva que hi ha al darrera d’aquesta definició és que una variable aleatòria mesura una característica dels subjectes de \(\Omega\) que varia a l’atzar d’un subjecte a un altre. Per exemple:

• Prenem una persona d’una població i mesuram el seu nivell de colesterol, o la seva alçada, o el seu nombre de fills… En aquest cas, \(\Omega\) és la població baix estudi, de la qual prenem la persona que mesuram.

• Llançam una moneda equilibrada 3 vegades i comptam les cares que obtenim. En aquest cas, \(\Omega\) és la població formada per totes les seqüències de 3 llançaments d’una moneda equilibrada passades, presents i futures.

El que més ens interessarà d’una variable aleatòria són les probabilitats dels esdeveniments que defineix. I quin tipus d’esdeveniments són els que més ens interessen quan mesuram característiques numèriques? Doncs bàsicament esdeveniments definits mitjançant igualtats i desigualtats. Per exemple, si \(X\) és la variable aleatòria “Prenem una persona i mesuram el seu nivell de colesterol en plasma (en mg/dl)”, ens poden interessar esdeveniments de l’estil de:

• El conjunt de les persones amb nivell de colesterol entre 200 i 240. la indicarem amb \[ 200\leqslant X\leqslant 240 \]

• El conjunt de les persones amb nivell de colesterol més petit o igual que 200: \[ X\leqslant 200 \]

• El conjunt de les persones amb nivell de colesterol més gran que 180: \[ X>180 \]

• El conjunt de les persones amb nivell de colesterol exactament 180: \[ X=180 \]

• Etc.

Com dèiem, el que ens interessarà d’aquests esdeveniments serà la seva probabilitat, i llavors emprarem notacions de l’estil de les següents:

• \(P(200\leqslant X\leqslant 240)\). Això indica la probabilitat que una persona tengui el nivell de colesterol entre 200 i 240. Per abreujar, ho llegirem la “probabilitat que \(X\) estigui entre 200 i 240” i representa la proporció de persones (de la població \(\Omega\) on hàgim definit la variable \(X\)) amb nivell de colesterol entre 200 i 240.

• \(P(X\leqslant 200)\). Això indica la probabilitat que una persona tengui el nivell de colesterol més petit o igual que 200 (per abreujar, la probabilitat que “\(X\) sigui més petit o igual que 200”). Representa la proporció de persones amb nivell de colesterol més petit o igual que 200.

• Etc.

En aquest context, indicarem normalment la unió amb una o i la intersecció amb una coma. Per exemple, si \(X\) és la variable aleatòria “Llançam una moneda 6 vegades i comptam les cares que obtenim”:

• \(P(X\leqslant 2\text{ o }X\geqslant 5)\): Probabilitat de treure com a màxim 2 cares o com a mínim 5.

• \(P(2\leqslant X, X< 5)\): Probabilitat de treure un nombre de cares que sigui més gran o igual que 2 i més petit que 5; és a dir, \(P(2\leqslant X< 5)\).

Dues variables aleatòries \(X,Y\) definides sobre una mateixa població són independents quan, per a tots els parells de valors \(a,b\in \mathbb{R}\), els esdeveniments \[ X\leqslant a, Y\leqslant b \] són independents. És a dir, intuïtivament, quan el valor que pren \(X\) sobre un subjecte no afecta per res el valor que hi pren \(Y\), i viceversa.

Per exemple, si prenem una persona i:

• \(X\): li demanam que llanci una moneda 3 vegades i comptam les cares

• \(Y\): mesuram el seu nivell de colesterol en plasma (en mg/dl)

(segurament) \(X\) i \(Y\) són independents.

Recordau que els esdeveniments \(X\leqslant a\) i \(Y\leqslant b\) són independents quan satisfan les tres condicions equivalents següents: \[ \begin{array}{l} P(X\leqslant a|Y\leqslant b)=P(X\leqslant a)\\ P(Y\leqslant b|X\leqslant a)=P(Y\leqslant b)\\ P(X\leqslant a, Y\leqslant b)=P(X\leqslant a)\cdot P(Y\leqslant b) \end{array} \]

Més en general, unes variables aleatòries \(X_1,X_2,\ldots,X_n\) definides sobre una mateixa població són independents quan, per a tots \(a_1,a_2,\ldots,a_n\in \mathbb{R}\), els esdeveniments \[ X_1\leqslant a_1, X_2\leqslant a_2,\ldots, X_n\leqslant a_n \] són independents. És a dir, quan el valor que pren una d’aquestes variables sobre un subjecte no afecta per res els valors que hi prenen les altres.

2.2 Variables aleatòries discretes

Una variable aleatòria és discreta quan els seus possibles valors són dades quantitatives discretes. Per exemple,

• Nombre de cares en 3 llançaments d’una moneda
• Nombre de fills d’una dona
• Nombre de casos nous de COVID-19 en un dia a Mallorca

2.2.1 Densitat i distribució

Sigui \(X: \Omega\to \mathbb{R}\) una variable aleatòria discreta.

• El seu domini \(D_X\) és el conjunt dels valors que pot prendre: més concretament, és el conjunt dels \(x\in \mathbb{R}\) tals que \(P(X=x)>0\).

• La seva funció de densitat és la funció \(f_X:\mathbb{R}\to [0,1]\) que assigna a cada \(x\in \mathbb{R}\) la probabilitat que \(X\) valgui \(x\): \[ f_X(x)=P(X=x) \] És a dir, \(f_X(x)\) és la proporció de subjectes de la població en els quals \(X\) val \(x\).

• La seva funció de distribució és la funció \(F_X:\mathbb{R}\to [0,1]\) que assigna a cada \(x\in \mathbb{R}\) la probabilitat que \(X\) sigui més petit o igual que \(x\): \[ F_X(x)=P(X\leqslant x) \] És a dir, \(F_X(x)\) és la proporció de subjectes de la població en els quals \(X\) pren un valor \(\leqslant x\).

  A la funció de distribució també se li sol dir funció de probabilitat acumulada per posar èmfasi en el fet que \(F_X(x)\) mesura la “freqüència relativa acumulada” de \(x\) en el total de la població.

Exemple 2.1 Sigui \(X\) la variable aleatòria “Llançam 3 vegades una moneda equilibrada i comptam les cares que obtenim”. Aleshores:

• El seu domini és el conjunt dels seus possibles valors: \(D_X=\{0,1,2,3\}\).

• La seva funció de densitat és definida per \(f_X(x)=P(X=x)\):

  • \(f_X(0)=P(X=0)=1/8\) (la probabilitat de treure 0 cares en 3 llançaments)
  • \(f_X(1)=P(X=1)=3/8\) (la probabilitat de treure 1 cara en 3 llançaments)
  • \(f_X(2)=P(X=2)=3/8\) (la probabilitat de treure 2 cares en 3 llançaments)
  • \(f_X(3)=P(X=3)=1/8\) (la probabilitat de treure 3 cares en 3 llançaments)
  • \(f_X(x)=P(X=x)=0\) per a qualsevol altre valor de \(x\) (si \(x\notin\{0,1,2,3\}\), la probabilitat de treure \(x\) cares en 3 llançaments és 0)

  En resum, la funció de densitat de \(X\) és \[ f_X(x) =\left\{ \begin{array}{ll} 1/8 & \text{ si $x=0$}\\ 3/8 & \text{ si $x=1$}\\ 3/8 & \text{ si $x=2$}\\ 1/8 & \text{ si $x=3$}\\ 0 & \text{ si $x\neq 0,1,2,3$} \end{array} \right. \]

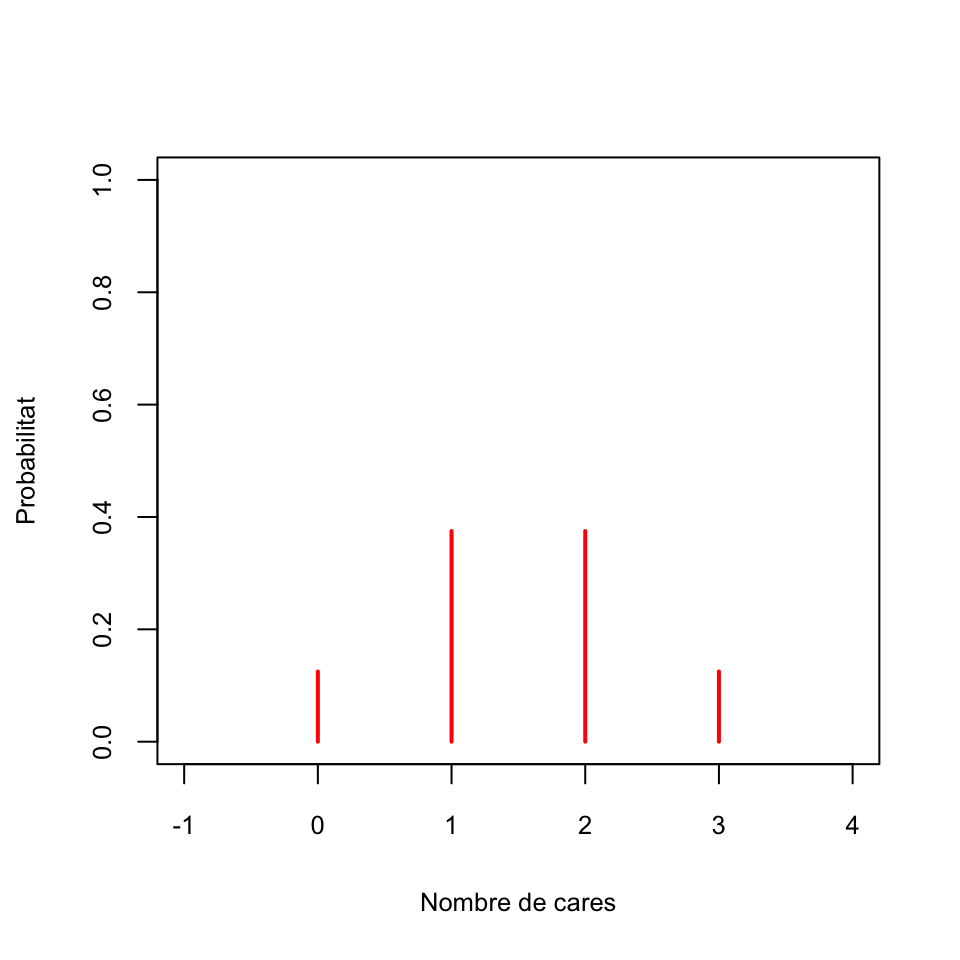
Figura 2.1: Funció de densitat de la variable aleatòria que compta el nombre de cares en 3 llançaments

Si \(X\) és una variable aleatòria discreta, \(P(X\in A)=0\) per a qualsevol subconjunt \(A\) disjunt amb \(D_X\), perquè, per la definició del domini \(D_X\), \(X\) no pot prendre cap valor fora de \(D_X\). Per exemple, quina és la probabilitat de treure entre 2.5 i 2.7 cares en llançar 3 vegades una moneda? 0. I la de treure \(\pi\) cares? 0 un altre cop.

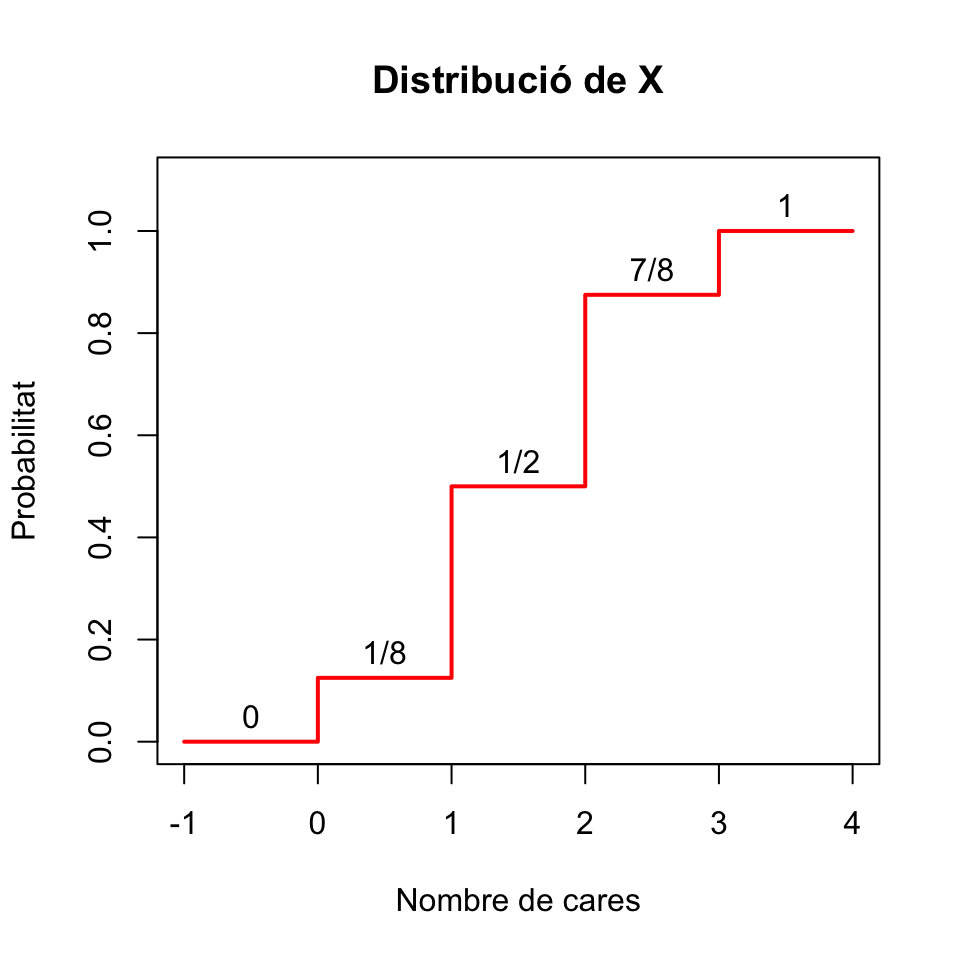
• Vegem ara la seva funció de distribució \(F_X\). Recordau que \(F_X(x)=P(X\leqslant x)\) i que la nostra variable només pot prendre els valors 0, 1, 2 i 3.

  • Si \(x<0\), \(F_X(x)=P(X\leqslant x)=0\), perquè \(X\) no pot prendre cap valor estrictament negatiu.

  • Si \(0\leqslant x<1\), \(F_X(x)=P(X\leqslant x)=P(X=0)=f_X(0)=1/8\), perquè si \(0\leqslant x<1\), l’únic valor \(\leqslant x\) que pot prendre \(X\) és el 0.

  • Si \(1\leqslant x<2\), \(F_X(x)=P(X\leqslant x)=P(X=0\text{ o }X=1)\) \(=f_X(0)+f_X(1)=4/8=1/2\), perquè si \(1\leqslant x<2\), els únics valors \(\leqslant x\) que pot prendre \(X\) són 0 i 1.

  • Si \(2\leqslant x<3\), \(F_X(x)=P(X\leqslant x)=P(X=0\text{ o }X=1\text{ o }X=2)\) \(=f_X(0)+f_X(1)+f_X(2)=7/8\), perquè si \(2\leqslant x<3\), els únics valors \(\leqslant x\) que pot prendre \(X\) són 0, 1 i 2.

  • Si \(3\leqslant x\), \(F_X(x)=P(X\leqslant x)=1\), perquè si \(x\geqslant 3\), segur que obtenim un nombre de cares \(\leqslant x\).

  Per tant, la funció \(F_X\) és la funció \[ F_X(x) =\left\{ \begin{array}{ll} 0 & \text{ si $x<0$}\\ 1/8 & \text{ si $0\leqslant x< 1$}\\ 4/8 & \text{ si $1\leqslant x< 2$}\\ 7/8 & \text{ si $2\leqslant x< 3$}\\ 1 & \text{ si $3\leqslant x$} \end{array} \right. \] El seu gràfic és el següent:

Figura 2.2: Funció de distribució de la variable aleatòria que compta el nombre de cares en 3 llançaments

Observau en aquest gràfic que aquesta funció de distribució \(F_X\) és creixent i escalonada. Això és general. Si \(X\) és una variable aleatòria discreta:

• \(F_X\) és una funció escalonada, amb bots en els valors de \(D_X\), que són els únics amb probabilitat estrictament més gran que 0 i per tant els únics que “sumen” probabilitat. Més en concret:

  • Si \(x_0,y_0\in D_X\) i \(x_0<y_0\), llavors \(F_X(x_0)< F_X(y_0)\), perquè, com que \(P(X=y_0)>0\), \[ \begin{array}{rl} F_X(x_0)\!\!\!\!\! & =P(X\leqslant x_0)<P(X\leqslant x_0)+P(X=y_0)\\ & =P(X\leqslant x_0\text{ o }X=y_0)\leqslant P(X\leqslant y_0)=F_X(y_0) \end{array} \]

  • Si \(x_0\in D_X\) i dins \((x_0,x]\) no hi ha cap element de \(D_X\), aleshores \(F_X(x_0)=F_X(x)\), perquè \[ \begin{array}{rl} F_X(x)\!\!\!\!\! & =P(X\leqslant x)=P(X\leqslant x_0)+P(x_0<X\leqslant x)\\ & =P(X\leqslant x_0)+0= P(X\leqslant x_0)=F_X(x_0) \end{array} \] ja que, com que \((x_0,x]\cap D_X=\emptyset\), \(P(x_0<X\leqslant x)=0\).

  • Si \(x_0\in D_X\), \(P(X<x_0)<P(X\leqslant x_0)\), perquè \[ P(X\leqslant x_0)=P(X<x_0)+P(X=x_0)>P(X<x_0) \]

• \(F_X\) és creixent, perquè si \(x\leqslant y\), tots els subjectes que compleixen que \(X\leqslant x\) també compleixen que \(X\leqslant y\), i per tant \[ P(X\leqslant x)\leqslant P(X\leqslant y). \]

• Com que els valors que pren \(F_X\) són probabilitats, no poden ser ni més petits que 0 ni més grans que 1.

El coneixement de \(f_X\), més les regles del càlcul de probabilitats, permet calcular la probabilitat de qualsevol esdeveniment relacionat amb \(X\): \[ P(X\in A) =\sum_{x\in A} P(X=x) = \sum_{x\in A} f_X(x) \] En particular \[ F_X(x_0)=P(X\leqslant x_0)=\sum_{x\leqslant x_0} f_X(x) \]

La moda d’una variable aleatòria discreta \(X\) és el valor (o els valors) \(x_0\) tal que \(f_X(x_0)=P(X=x_0)\) és màxim. Per tant, la moda és el valor de \(X\) més probable o més freqüent en la població. Per exemple, per a la nostra variable aleatòria que compta el nombre de cares en 3 llançaments d’una moneda equilibrada, la moda són els valors 1 i 2.

Exemple 2.2 Una variable aleatòria discreta \(X\) és uniforme quan el seu domini \(D_X\) és finit i tots els seus elements tenen la mateixa probabilitat. És a dir, si \(D_X\) té \(m\) elements, aleshores \(P(X=x)=1/m\) per a cada \(x\in D_X\). Per exemple, el resultat de llançar un dau equilibrat és una variable aleatòria discreta.

Com que tots els resultats del domini d’una variable aleatòria discreta uniforme tenen la mateixa probabilitat, tots en són la moda (o cap no ho és, depèn de si veieu el tassó mig ple o mig buit).

Considerau la variable aleatòria \(X\) “Llançam una moneda equilibrada tantes vegades com sigui necessari fins que surti una cara per primera vegada, i comptam quantes vegades l’hem haguda de llançar”.

1. Quin és el seu domini?
2. Quina és la seva funció de densitat?
3. Quina és la seva moda? Què significa?
4. Quina és la seva funció de distribució? (Indicació: Calculau primer \(P(X>x)\), tenint en compte que \(X>x\) significa que en els primer \(x\) llançaments ha sortit creu, i per això hem hagut de llançar la moneda més de \(x\) vegades per obtenir una cara.)

2.2.2 Esperança

Quan prenem una mostra d’una variable aleatòria \(X\) definida sobre una població, podem calcular la mitjana i la desviació típica dels seus valors a fi i efecte d’obtenir una idea de quin és el valor central de la mostra i si els seus valors estan tots molt a prop d’aquest valor central o no. Naturalment, també ens podem preguntar per aquesta mena d’informació per al total de la població: Quin és el “valor mitjà” de \(X\) sobre tota la població? Aquesta variable, pren valors molt dispersos, o més aviat els pren concentrats al voltant del seu valor mitjà? La primera pregunta la responem amb la mitjana, o esperança, de \(X\), i la segona amb la seva variància i la seva desviació típica. Comencem amb la primera.

La mitjana, o esperança (o valor esperat, valor mitjà…), d’una variable aleatòria discreta \(X\) amb densitat \(f_X:D_X\to [0,1]\) és \[ E(X)=\sum_{x\in D_X} x\cdot f_X(x) \] Sovint també la indicarem amb \(\mu_X\).

La interpretació natural de \(E(X)\) és que és la mitjana dels valors de la variable \(X\) en el total de la població \(\Omega\). En efecte, com que \(P(X=x)\) és la proporció de subjectes de \(\Omega\) en els quals \(X\) val \(x\), \[ E(X)=\sum_{x\in D_X} x\cdot P(X=x) \] és la mitjana dels valors de \(X\) sobre tots els subjectes de \(\Omega\). Comparau-ho amb l’exemple següent.

Exemple 2.3 Si, en una classe, un 10% dels estudiants han tret un 4 en un examen, un 20% un 6, un 50% un 8 i un 20% un 10, quina ha estat la nota mitjana obtenguda?

Segurament calcularíeu aquesta mitjana de la manera següent: \[ 4\cdot 0.1+6\cdot 0.2+8\cdot 0.5+10\cdot 0.2=7.6 \] Doncs aquest valor és la mitjana de la variable aleatòria \(X\) “Prenc un estudiant d’aquesta classe i mir quina nota ha tret en aquest examen”: \[ \begin{array}{rl} E(X)\!\!\!\!\! &=4\cdot P(X=4)+6\cdot P(X=6)+8\cdot P(X=8)+10\cdot P(X=10)\\ & = 4\cdot 0.1+6\cdot 0.2+8\cdot 0.5+10\cdot 0.2=7.6 \end{array} \]

A banda de la seva interpretació com a “la mitjana de \(X\) en el total de la població”, \(E(X)\) és també el valor esperat de \(X\), en el sentit següent:

Suposau que prenem a l’atzar una mostra de \(n\) subjectes de la població, mesuram \(X\) sobre ells i calculam la mitjana aritmètica dels \(n\) valors obtenguts. Aleshores, quan la mida \(n\) de la mostra tendeix a \(\infty\), aquesta mitjana aritmètica tendeix a valer \(E(X)\) “gairebé sempre”, en el sentit que la probabilitat que el seu límit sigui \(E(X)\) és 1.

És a dir: si mesuràssim \(X\) sobre molts subjectes triats a l’atzar i calculàssim la mitjana dels valors obtenguts, és gairebé segur que obtendríem un valor molt proper a \(E(X)\).

Exemple 2.4 Seguim amb la variable aleatòria \(X\) “Llançam una moneda equilibrada 3 vegades i comptam les cares que obtenim”. La seva esperança és \[ E(X)= 0\cdot \frac{1}{8}+1\cdot \frac{3}{8}+2\cdot \frac{3}{8}+3\cdot \frac{1}{8}=1.5 \]

Això ens diu que:

• La mitjana de \(X\) és 1.5: El valor mitjà de la variable \(X\) sobre tota la població de seqüències de 3 llançaments d’una moneda equilibrada és 1.5.

• El valor esperat de \(X\) és 1.5: Si repetíssim moltes vegades l’experiment de llançar la moneda 3 vegades i comptar les cares, de mitjana obtendríem, molt probablement, un valor molt pròxim a 1.5. Abreujam això dient que si llançam la moneda 3 vegades, esperam treure 1.5 cares.

Més en general, si \(X\) és una variable aleatòria i \(g:\mathbb{R}\to \mathbb{R}\) és una funció, l’esperança de \(g(X)\) és \[ E(g(X))=\sum_{x\in D_X} g(x)\cdot f_X(x). \] Un altre cop, la interpretació natural d’aquest valor és que és la mitjana de \(g(X)\) sobre la població, i també que és el valor “esperat” de \(g(X)\) en el sentit anterior.

Exemple 2.5 Si llançam una moneda equilibrada 3 vegades, comptam les cares i elevam aquest nombre de cares al quadrat, quin valor esperam obtenir?

Serà l’esperança de \(X^2\), on \(X\) és la variable aleatòria “Llançam una moneda equilibrada 3 vegades i comptam les cares que obtenim” (és a dir, aquesta \(X^2\) és la variable aleatòria “Llançam una moneda equilibrada 3 vegades, comptam les cares i elevam aquest número al quadrat”):

\[ E(X^2)= 0\cdot \frac{1}{8}+1\cdot \frac{3}{8}+2^2\cdot \frac{3}{8}+3^2\cdot \frac{1}{8}=3 \]

Fixau-vos que \(E(X^2) \neq E(X)^2\). Per exemple, en els dos darrers exemples hem vist que si \(X\) és la variable aleatòria que compta el nombre de cares en 3 llançaments d’una moneda equilibrada, \(E(X^2)=3\) però \(E(X)^2=1.5^2=2.25\).

En general, donades una variable aleatòria \(X\) i una aplicació \(g:\mathbb{R}\to \mathbb{R}\), el més habitual és que \(E(g(X))\neq g(E(X))\).

L’esperança de les variables aleatòries discretes té les propietats següents, totes molt raonables si les interpretau en termes del valor mitjà de \(X\) sobre la població:

• Sigui \(b\) una variable aleatòria constant, que sobre tots els individus de la població pren el mateix valor \(b\in \mathbb{R}\). Aleshores, \(E(b)=b\).

  Si en una classe tothom treu un 8 d’un examen, la nota mitjana és un 8, no?

Sí, ja sabem que parlar de variables constants és un oxímoron, però de vegades una variable aleatòria pren el mateix valor sobre tots els subjectes d’una població.

• L’esperança és lineal:

  • Si \(X\) és una variable aleatòria i \(a,b\in \mathbb{R}\), \(E(aX+b)=aE(X)+b\)

    Si en una classe la mitjana d’un examen ha estat un 6 i decidim multiplicar per 1.2 totes les notes i sumar-les 1 punt, la mitjana de la nova nota serà 1.2·6+1=8.2, no?

  • Si \(X,Y\) són dues variables aleatòries, \(E(X+Y)=E(X)+E(Y)\).

    Si en una classe la mitjana de la part de qüestions d’un examen ha estat un 3.5 i la de la part d’exercicis ha estat un 3, i la nota de l’examen és la suma de les notes de les dues parts, la nota mitjana de l’examen serà un 3.5+3=6.5, no?

  • Combinant les dues propietats anteriors, si \(X_1,\ldots,X_n\) són variables aleatòries i \(a_1,\ldots,a_n,b\in \mathbb{R}\), \[ E(a_1X_1+\cdots+a_nX_n+b)=a_1E(X_1)+\cdots+a_nE(X_n)+b \]

• L’esperança és monòtona creixent: Si \(X\leqslant Y\) (en el sentit que el valor de \(X\) sobre cada subjecte de la població \(\Omega\) és més petit o igual que el valor de \(Y\) sobre ell), llavors \(E(X)\leqslant E(Y)\).

  Si tots traieu millor nota de Matemàtiques II que de Matemàtiques I, la nota mitjana de Matemàtiques II serà més gran que la de Matemàtiques I, no?

Siguin \(N\) un nombre natural estrictament positiu i \(X\) una variable aleatòria discreta uniforme amb domini \(D_X=\{1,\ldots,N\}\). Què val el seu valor esperat?

2.2.3 Variància i desviació típica

La variància d’una variable aleatòria discreta \(X\) és \[ \sigma(X)^2 =E((X-\mu_X)^2) =\sum_{x\in D_X} (x-\mu_X)^2\cdot f_X(x) \] És a dir, és el valor esperat del quadrat de la diferència entre \(X\) i la seva mitjana \(\mu_X\). També la indicarem amb \(\sigma_X^2\).

Fixau-vos que es tracta de la traducció “poblacional” de la definició de variància per a una mostra, i per tant serveix per mesurar el mateix que aquella: la dispersió dels resultats de \(X\) respecte de la mitjana. Només que ara és per a tota la població, i no per a una mostra.

La identitat següent vos pot ser útil.

Teorema 2.1 \(\sigma(X)^2=E(X^2)-\mu_X^2\).

Operem (i recordau que \(E(X)=\mu_X\)) \[ \begin{array}{rl} \sigma(X)^2\!\!\!\!\! & =E((X-\mu_X)^2)=E(X^2-2\mu_X\cdot X+\mu_X^2)\\ & = E(X^2)-2\mu_X\cdot E(X)+\mu_X^2\\ & \text{(per la linealitat d'$E$)}\\ & = E(X^2)-2\mu_X^2+\mu_X^2=E(X^2)-\mu_X^2 \end{array} \]

La desviació típica (o desviació estàndard) d’una variable aleatòria discreta \(X\) és l’arrel quadrada positiva de la seva variància: \[ \sigma(X)=+\sqrt{\sigma(X)^2} \] També mesura la dispersió dels valors de \(X\) respecte de la mitjana. Sovint la indicarem amb \(\sigma_X\).

En el context de les variables aleatòries, no hi ha “variància” i “variància mostral”, només “variància”. El mateix nom us hauria de donar la pista que la “variància mostral” està definida només per a mostres.

El motiu per introduir la variància i la desviació típica per mesurar la dispersió dels valors de \(X\) és la mateixa que en estadística descriptiva: la variància és més fàcil de manejar (no involucra arrels quadrades) però les seves unitats són les de \(X\) al quadrat, mentre que les unitats de la desviació típica són les de \(X\), i per tant el seu valor és més fàcil d’interpretar.

Exemple 2.6 Seguim amb la variable aleatòria \(X\) “Llançam una moneda equilibrada 3 vegades i comptam les cares que obtenim”. Recordem que \(\mu_X=E(X)=1.5\). Aleshores, la seva variància és:

\[ \begin{array}{rl} \sigma(X)^2 \!\!\!\!\! & \displaystyle=(0-1.5)^2\cdot \frac{1}{8}+(1-1.5)^2\cdot \frac{3}{8}\\ &\displaystyle\qquad +(2-1.5)^2\cdot \frac{3}{8}+(3-1.5)^2\cdot \frac{1}{8}=0.75 \end{array} \] Si recordam que \(E(X^2)=3\), podem veure que \[ E(X^2)-\mu_X^2=3-1.5^2=0.75=\sigma(X)^2 \] La seva desviació típica és \[ \sigma(X) =\sqrt{\sigma(X)^2}=\sqrt{0.75}= 0.866 \]

Vegem algunes propietats de la variància i la desviació típica:

• Si \(b\) és una variable aleatòria constant que sobre tots els individus de la població pren el valor \(b\in \mathbb{R}\), aleshores \(\sigma(b)^2=\sigma(b)=0\).

  Una variable aleatòria constant té zero dispersió.

• El recíproc també és cert: si \(\sigma(X)^2=0\), la variable \(X\) és constant.

  En efecte, observau a \[ \sigma(X)^2 =\sum_{x\in D_X} (x-\mu_X)^2\cdot f_X(x) \] que \(\sigma(X)^2\) és una suma de nombres positius. Per tant, si és 0, tots els sumands \((x-\mu_X)^2\cdot f_X(x)\) han de ser 0. Però \(f_X(x)>0\) per a cada \(x\in D_X\). Per tant, si \(\sigma(X)^2=0\), tots els \(x-\mu_X\), amb \(x\in D_X\), han de ser 0, és a dir, \(D_X=\{\mu_X\}\): \(X\) només pot prendre un valor.

• \(\sigma(aX+b)^2=a^2\cdot \sigma(X)^2\).

En efecte \[ \begin{array}{l} \sigma(aX+b)^2 =E((aX+b)^2)-E(aX+b)^2\\ \quad = E(a^2X^2+2abX+b^2)-(aE(X)+b)^2\\ \quad \text{(per la linealitat de $E$)}\\ \quad = a^2E(X^2)+2abE(X)+b^2-a^2E(X)^2-2abE(X)-b^2\\ \quad \text{(una altre cop, per la linealitat de $E$)}\\ \quad = a^2(E(X^2)-E(X)^2)=a^2\sigma(X)^2 \end{array} \]

• \(\sigma(aX+b)=|a|\cdot \sigma(X)\) (recordau que la desviació típica és positiva, i \(+\sqrt{a^2}=|a|\)).

• Si \(X,Y\) són variables aleatòries independents, \[ \sigma(X+Y)^2=\sigma(X)^2+\sigma(Y)^2 \] i per tant \[ \sigma(X+Y)=\sqrt{\sigma(X)^2+\sigma(Y)^2} \] Si no són independents, en general aquesta igualtat és falsa. Per posar un exemple extrem, \[ \sigma(X+X)^2=4\sigma(X)^2 \neq \sigma(X)^2+\sigma(X)^2. \]

• Més en general, si \(X_1,\ldots,X_n\) són variables aleatòries independents (i, en principi, només en aquest cas) i \(a_1,\ldots,a_n,b\in \mathbb{R}\), \[ \begin{array}{l} \sigma(a_1X_1+\cdots+a_nX_n+b)^2=a_1^2\cdot\sigma(X_1)^2+\cdots+a_n^2\cdot\sigma(X_n)^2\\ \sigma(a_1X_1+\cdots+a_nX_n+b)=\sqrt{a_1^2\cdot\sigma(X_1)^2+\cdots+a_n^2\cdot\sigma(X_n)^2} \end{array} \]

2.2.4 Quantils

Sigui \(p\in [0,1]\). El quantil d’ordre \(p\) (o \(p\)-quantil) d’una variable aleatòria discreta \(X\) és el valor \(x_p\in D_X\) més petit tal que \(P(X\leqslant x_p)\geqslant p\).

Per exemple, que el 0.25-quantil d’una variable aleatòria discreta \(X\) sigui, jo què sé, 8, significa 8 és el valor més petit per al qual la probabilitat acumulada arriba al 25%. És a dir, que almenys un 25% de la població té un valor de \(X\) més petit o igual que 8, però menys d’un 25% de la població té un valor de \(X\) estrictament més petit que 8.

Si existeix algun \(x_p\in D_X\) tal que \(P(X\leqslant x_p)=p\), llavors el \(p\)-quantil és aquest \(x_p\), perquè, per a tot altre \(x\in D_x\):

• Si \(x<x_p\), \(P(X\leqslant x)<P(X\leqslant x_p)=F_X(x_p)=p\) i per tant \(x\) no pot ser el \(p\)-quantil de \(X\).
• Si \(x>x_p\), \(p=P(X\leqslant x_p)< P(X\leqslant x)\), i per tant \(x\) tampoc no pot ser el \(p\)-quantil de \(X\).

Com en estadística descriptiva, alguns quantils de variables aleatòries tenen noms propis. Per exemple:

• La mediana de \(X\) és el seu 0.5-quantil.

• El primer i el tercer quartils de \(X\) són els seus \(0.25\)-quantil i \(0.75\)-quantil, respectivament.

• Etc.

Exemple 2.7 Seguim amb la variable aleatòria \(X\) “Llançam una moneda equilibrada 3 vegades i comptam les cares que obtenim”. Recordem que la seva funció de distribució és

\[ F_X(x)=\left\{ \begin{array}{ll} 0 & \text{ si $x<0$}\\ 0.125 & \text{ si $0\leqslant x<1$}\\ 0.5 & \text{ si $1\leqslant x<2$}\\ 0.875 & \text{ si $2\leqslant x<3$}\\ 1 & \text{ si $3\leqslant x $} \end{array} \right. \]

Llavors, per exemple:

• El seu 0.125-quantil és 0

• El seu 0.25-quantil és 1

• La seva mediana és 1

• El seu 0.75-quantil és 2

Siguin \(N\) un nombre natural estrictament positiu i \(X\) una variable aleatòria discreta uniforme amb domini \(D_X=\{1,\ldots,N\}\). Què val la seva mediana?

Encara que emprem “mitjana”, “variància”, “quantils”, etc. tant per a variables aleatòries com per a mostres, no heu de confondre-les.

• Una variable aleatòria representa una característica numèrica dels subjectes d’una població:

  • “Prenem un estudiant de la UIB i mesuram la seva alçada en m.”

    La mitjana i la variància d’aquesta variable són les de tota la població d’estudiants de la UIB i descriuen propietats de tota la població d’estudiants de la UIB.

• Una mostra d’una variable aleatòria són els valors de la variable sobre un subconjunt de la població.

  • Mesuram les alçades (en m) de 50 estudiants de la UIB d’aquest curs.

    La mitjana i la variància d’aquesta mostra són només les d’aquestes 50 alçades, i poden servir per descriure aquest conjunt de 50 alçades o per estimar els valors de la mitjana i la variància de la població d’estudiants de la UIB

Quan volguem destacar que una mitjana, una variància etc. són les d’una variable aleatòria sobre tota una població, les qualificarem de poblacionals.

Tenim dos daus cúbics equilibrats, amb les cares enumerades de l’1 al 6. Considerem la variable aleatòria \(X\) consistent en llançar els dos daus i sumar els resultats de les cares que queden en l’aire.

1. Dóna la seva funció de densitat.
2. Dóna la seva funció de distribució.
3. Si llançàssim moltes vegades els dos daus, què hauríem d’esperar obtenir de mitjana com a suma de les dues cares?
4. Sigui \(Y\) la variable aleatòria consistent en llançar un dau cúbic equilibrat i anotar el resultat de la cara que queda en l’aire. És el valor esperat de \(X\) el doble del valor esperat de \(Y\)? Hi ha qualque motiu teòric pel qual ho hagi de ser?
5. Calcula la variància de \(X\) i la de \(Y\). Hi ha qualque relació numérica visible entre elles? Hi ha qualque motiu teòric que faci que aquesta relació existeixi?
6. Què val el primer quartil de \(X\)? Quin és el seu significat?
7. Què val la mediana de \(X\)? Quin és el seu significat?
8. És la mediana de \(X\) el doble de la mediana de \(Y\)? Hi ha qualque motiu teòric pel qual ho hagi de ser?

2.3 Famílies importants de variables aleatòries discretes

En aquesta secció descriurem tres famílies de variables aleatòries “distingides” que heu de conèixer:

• Binomial
• Hipergeomètrica
• Poisson

Cadascuna d’aquestes famílies tenen un tipus específic de funció de densitat que depèn d’un o diversos paràmetres.

De cadascuna d’aquestes famílies de variables heu de saber:

• Distingir quan una variable aleatòria és d’aquest tipus.
• Les seves propietats bàsiques, com ara quins són els seus paràmetres, quin és el seu valor esperat i si la seva densitat és simètrica o té una cua a qualque costat.
• Emprar R per calcular coses quan sigui necessari.

2.3.1 Variables aleatòries binomials

Un experiment de Bernoulli és una acció amb només dos resultats possibles, que identificam amb “Èxit” (\(E\)) i “Fracàs” (\(F\)), i de la qual, en principi, no podem predir el seu resultat per mor de la influència de l’atzar. Per exemple, llançar un dau cúbic i mirar si ha sortit un 6 (\(E\): treure un 6; \(F\): no treure un 6).

La probabilitat d’èxit \(p\) d’un experiment de Bernoulli és la probabilitat d’obtenir un èxit \(E\). És a dir, \(P(E)=p\). Naturalment, llavors, \(P(F)=1-p\). A l’exemple del llançament d’un dau, on \(E\) és treure un 6, \(p=1/6\).

Més exemples d’experiments de Bernoulli:

• Llançar una moneda equilibrada i mirar si dóna cara.

  • \(E\): donar cara
  • \(p=1/2\)

• Demanar a una persona si l’estadística l’avorreix.

  • \(E\): que l’estadística l’avorreixi
  • \(p\): la proporció de persones a qui avorreix l’estadística

Figura 2.3: Qui dels dos ets?

Una variable aleatòria de Bernoulli de paràmetre \(p\) (abreujadament, \(Be(p)\)) és una variable aleatòria \(X\) que consisteix a efectuar un experiment de Bernoulli i donar 1 si s’obté un èxit i 0 si s’obté un fracàs.

Una variable aleatòria binomial de paràmetres \(n\) i \(p\) (abreujadament, \(B(n,p)\)) és una variable aleatòria \(X\) que compta el nombre d’èxits \(E\) en una seqüència de \(n\) repeticions independents d’un mateix experiment de Bernoulli de probabilitat d’èxit \(p\). Independents significa que les \(n\) variables aleatòries de Bernoulli, una per a cada repetició de l’experiment de Bernoulli, són independents; és a dir, que el resultat de cada experiment en la seqüència no depèn dels resultats dels altres.

Direm a \(n\) la mida de les mostres i a \(p\) la probabilitat (poblacional) d’èxit. De vegades també direm d’una variable \(X\) de tipus \(B(n,p)\) que té distribució binomial de paràmetres \(n\) i \(p\).

Per exemple:

• Una variable de Bernoulli \(Be(p)\) és una variable binomial \(B(1,p)\).

• Llançar una moneda equilibrada 10 vegades i comptar les cares que surten és una variable binomial \(B(10,0.5)\).

• Triar 20 estudiants de la UIB a l’atzar, l’un rere l’altre, permetent repeticions i cada tria independent de les altres, i mirar si al primer semestre han aprovat totes les assignatures o no, és una variable binomial \(B(20,p)\) amb \(p\) la proporció d’estudiants de la UIB que han aprovat totes les assignatures del primer semestre.

El tipus més comú de variables binomials que ens interessaran és aquest darrer:

Tenim un subconjunt \(E\) d’una població \(\Omega\) (per exemple, \(\Omega\) els estudiants de la UIB i \(E\) els que han aprovat totes les assignatures del primer semestre). Sigui \(p\) la proporció poblacional d’individus de la població que pertanyen a \(E\), és a dir \(p=P(E)\). Prenem mostres aleatòries simples de mida \(n\) de la població i comptam quants subjectes de la mostra són de \(E\). Aquesta variable aleatòria és binomial \(B(n,p)\).

Tenim el resultat següent.

Teorema 2.2 Si \(X\) és una variable \(B(n,p)\):

• El seu domini és \(D_X=\{0,1,\ldots,n\}\)

• La seva funció de densitat és \[ f_X(k)=\left\{\begin{array}{ll} \displaystyle\binom{n}{k}p^k(1-p)^{n-k} & \text{ si $k\in D_X$}\\ 0 & \text{ si $k \notin D_X$} \end{array} \right. \]

• El seu valor esperat és \(E(X)=np\)

• La seva variància és \(\sigma(X)^2=np(1-p)\)

Recordau que:

• El factorial \(m!\) d’un nombre natural \(m\) és \(m!=m(m-1)\cdots 2\cdot 1\) si \(m\geqslant 1\). Si \(m=0\), es pren \(0!=1\).

• El nombre combinatori \(\binom{n}{k}\), amb \(k,n\) nombres naturals tals que \(0\leqslant k\leqslant n\), és \[ \binom{n}{k}=\frac{\overbrace{n\cdot (n-1)\cdots (n-k+1)}^k}{k\cdot (k-1)\cdots 2\cdot 1}=\frac{n!}{k!(n-k)!} \] i ens dóna el nombre de subconjunts de \(k\) elements de \(\{1,\ldots,n\}\). Si \(k>n\) o \(k<0\), es pren \(\binom{n}{k}=0\).

Suposem que efectuam \(n\) repeticions consecutives i independents d’un experiment de Bernoulli de probabilitat d’èxit \(p\) i comptam el nombre d’\(E\)’s; direm \(X\) a la variable aleatòria resultant. Per seguir la demostració, si no us sentiu molt còmodes amb el raonament amb enes i kas abstractes, anau repetint-lo prenent, per exemple, \(n=4\).

Els possibles resultats són totes les paraules possibles de \(n\) lletres formades per \(E\)’s i \(F\)’s. Com que els experiments successius són independents, la probabilitat de cadascuna d’aquestes paraules és el producte de les probabilitats dels seus resultats individuals. Per tant, si una paraula concreta té \(k\) lletres \(E\) i \(n-k\) lletres \(F\) (s’han obtengut \(k\) èxits i \(n-k\) fracassos), la seva probabilitat és \(p^k(1-p)^{n-k}\), independentment de l’ordre en el qual hàgim obtengut els resultats.

Per calcular la probabilitat d’obtenir una seqüència amb \(k\) èxits, sumarem les probabilitats d’obtenir cadascuna de les seqüències de \(n\) lletres amb \(k\) \(E\)’s. Com que totes tenen la mateixa probabilitat, el resultat serà la probabilitat \(p^k(1-p)^{n-k}\) d’una paraula amb \(k\) \(E\)’s i \(n-k\) \(F\)’s multiplicada pel nombre total de paraules diferents amb \(k\) \(E\)’s i \(n-k\) \(F\)’s.

Ara, quantes paraules hi ha amb \(k\) \(E\)’s i \(n-k\) \(F\)’s? Cada una d’elles queda caracteritzada per les posicions de les \(k\) \(E\)’s, per tant hi ha tantes paraules d’aquestes com possibles eleccions de conjunts de \(k\) posicions per a les \(E\)’s. El nombre d’això darrer és el de possibles subconjunts de \(k\) elements (les posicions on hi haurà les \(E\)’s) de \(\{1,\ldots,n\}\), que és el nombre combinatori \(\binom{n}{k}\). Per tant ja tenim \[ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}. \]

A partir d’aquí, el càlcul del valor esperat i la variància és sumar \[ \begin{array}{l} \displaystyle E(X)=\sum_{k=0}^n k\cdot \binom{n}{k}p^k(1-p)^{n-k}\\ \displaystyle \sigma(X)^2=\sum_{k=0}^n k^2\cdot \binom{n}{k}p^k(1-p)^{n-k}-\Big(\sum_{k=0}^n k\cdot \binom{n}{k}p^k(1-p)^{n-k})^2 \end{array} \] Us podeu fiar de nosaltres, donen \(np\) i \(np(1-p)\), respectivament.

Si ho pensau, veureu que el valor de \(E(X)\) és l’“esperat”. Vegem, si preneu una mostra aleatòria de \(n\) subjectes d’una població en la qual la proporció de subjectes \(E\) és \(p\), quants subjectes \(E\) “esperau” obtenir en la vostra mostra? Doncs una proporció \(p\) de la mostra, és a dir \(p\cdot n\), no?

La funció de distribució d’una variable binomial no té una fórmula explícita. Només podem dir que si \(X\) és \(B(n,p)\), \[ F_X(x)=\sum_{k=0}^{\lfloor x\rfloor} \binom{n}{k}p^k(1-p)^{n-k} \]

És un doi, però, per si de cas, us volem fer observar que si \(X\) és \(B(n,p)\), \(P(X=k)\) no només depèn de \(k\) sinó també dels paràmetres \(n\) i \(p\). Això serà general. Totes les variables aleatòries d’una mateixa família tenen la funció de densitat de la mateixa forma, i només hi varien els valors dels paràmetres.

El tipus de teorema anterior és el que fa que ens interessi conèixer algunes famílies distingides freqüents de variables aleatòries. Si, per exemple, reconeixem que una variable aleatòria és binomial i coneixem els seus valors de \(n\) i \(p\) i sabem el teorema anterior, automàticament sabem la seva funció de densitat, i amb ella la seva funció de distribució, el seu valor esperat, la seva variància etc., sense necessitat de deduir tota aquesta informació cada vegada que trobem una variable d’aquestes.

El coneixement estalvia temps.

Naturalment, conèixer les propietats de les variables aleatòries binomials només és útil si sabem reconèixer quan estam al davant d’una. Fixau-vos que en una variable aleatòria binomial:

• Comptam quantes vegades ocorre un esdeveniment (l’èxit \(E\)) en una seqüència d’intents.

• En cada intent, l’esdeveniment que ens interessa passa o no passa, sense grisos.

• El nombre d’intents és fix, \(n\).

• Cada intent és independent dels altres.

• En cada intent, la probabilitat que passi l’esdeveniment que ens interessa és sempre la mateixa, \(p\).

Així, per exemple:

• Una dona té 4 fills. La probabilitat que un fill sigui nina és fixa, 0.51. El sexe de cada fill és independent dels altres. Comptam quantes filles té.

  És una variable binomial \(B(4,0.51)\).

• En una aula hi ha 5 homes i 45 dones. Triam 10 estudiants, un rere l’altre i sense repetir-los, per fer-los una pregunta. Cada elecció és independent de les altres. Comptam quants homes hem interrogat.

  No és una variable binomial: com que no podem repetir estudiants, en cada ronda la probabilitat de triar un home depèn del sexe dels estudiants triats abans que ell. Per tant la \(p\) no és la mateixa en cada elecció.

  Per exemple, en la primera ronda la probabilitat de triar un home és 5/50=0.1. Ara, si en la primera ronda surt triat un home, la probabilitat que en la segona ronda tornem a triar un home es redueix a 4/49=0.0816, mentre que si en la primera elecció surt una dona, la probabilitat de triar un home en la segona ronda puja a 5/49=0.102.

• En una aula hi ha 5 homes i 45 dones. Triam 10 estudiants, un rere l’altre però cada estudiant pot ser triat més d’una vegada, per a fer-los una pregunta. Cada elecció és independent de les altres. Comptam quants homes hem interrogat.

  Ara sí que és una variable binomial \(B(10,0.1)\), ja que la probabilitat de triar un home no varia d’una ronda a la següent.

• En una aula hi ha 5 homes i 45 dones. Triam estudiants un rere l’altre i cada estudiant pot ser triat més d’una vegada, per fer-los una pregunta. Cada elecció és independent de les altres. Comptam quants estudiants hem hagut de triar per arribar a interrogar 5 homes.

  No és una variable binomial: no compta el nombre d’èxits en una seqüència d’un nombre fix d’intents, sinó quants intents hem necessitat per arribar a un nombre fix d’èxits.

• En una aula hi ha 5 homes i 45 dones. Llançam una moneda equilibrada: si surt cara triam 10 estudiants i si surt creu en triam 20, per a fer-los una pregunta. Tant en un cas com en l’altre, els triarem un rere l’altre, cada estudiant podrà ser triat més d’una vegada i cada elecció serà independent de les altres. Comptam quants homes hem interrogat.

  No és una variable binomial: el nombre d’intents no és fix.

• La probabilitat que un dia de novembre plogui és d’un 32%. Triam una setmana de novembre i comptam quants dies ha plogut.

  No és d’una variable binomial. Encara que a priori cada dia tengui la mateixa probabilitat de pluja, que plogui un dia no és independent que plogui l’anterior. Perquè fos binomial, hauríem d’haver triat 7 dies de novembre a l’atzar, permetent que sortissin repetits.

• A Espanya hi ha 46,700,000 persones, de les quals un 11.7% són diabètics. Triam 100 espanyols diferents a l’atzar (de manera independent els uns dels altres) i comptam quants són diabètics.

  No és binomial, pel mateix motiu que no ho era quan escollíem estudiants sense permetre repeticions. Però pràcticament sí que ho és, perquè les probabilitats gairebé no varien d’una elecció a la següent.

  Per exemple, quan ja duim 99 individus escollits, la probabilitat de triar un individu concret dels que queden és \(1/(46700000-99)=2.141332\times 10^{-8}\) mentre que si permetem repeticions, aquesta probabilitat és \(1/46700000=2.141328\times 10^{-8}\). Coincideixen fins la dotzena xifra decimal.

  En aquest cas farem la trampa de considerar-la binomial.

Vegem alguns gràfics de la funció de densitat de variables aleatòries binomials. Primer, per a \(n=10\) i diferents valors de \(p\).

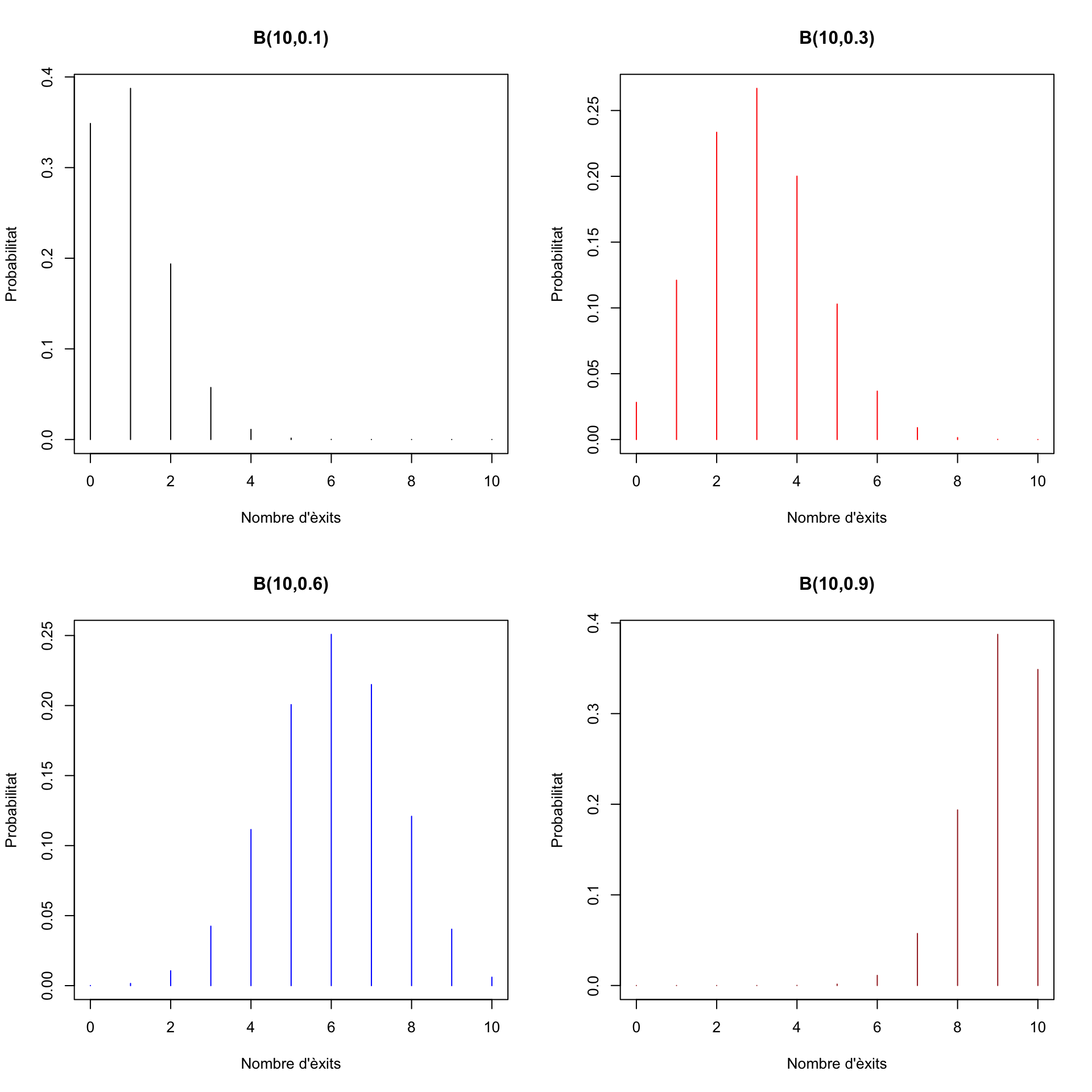
Ara per a \(n=100\):

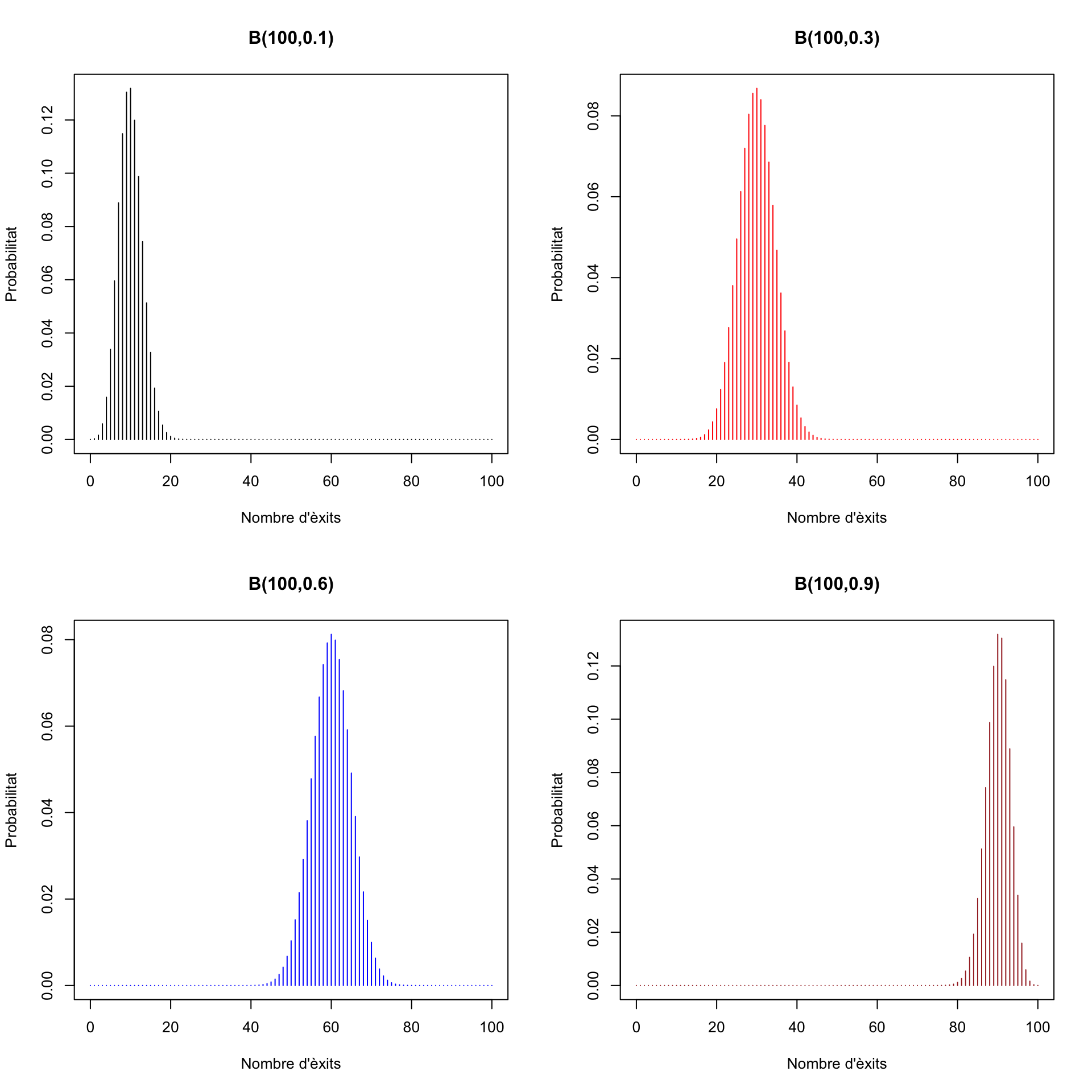
Com podeu veure, la moda d’una binomial \(B(n,p)\) és la seva mitjana \(np\) o, si aquest nombre no és enter, un dels dos enters que l’envolten.

Si \(p=0.5\), la funció de densitat és simètrica respecte de \(n/2\): com que \(E\) i \(F\) tenen la mateixa probabilitat, 0.5, la probabilitat de treure \(k\) \(E\)’s és la mateixa que la de treure \(k\) \(F\)’s, és a dir, la de treure \(n-k\) \(E\)’s.

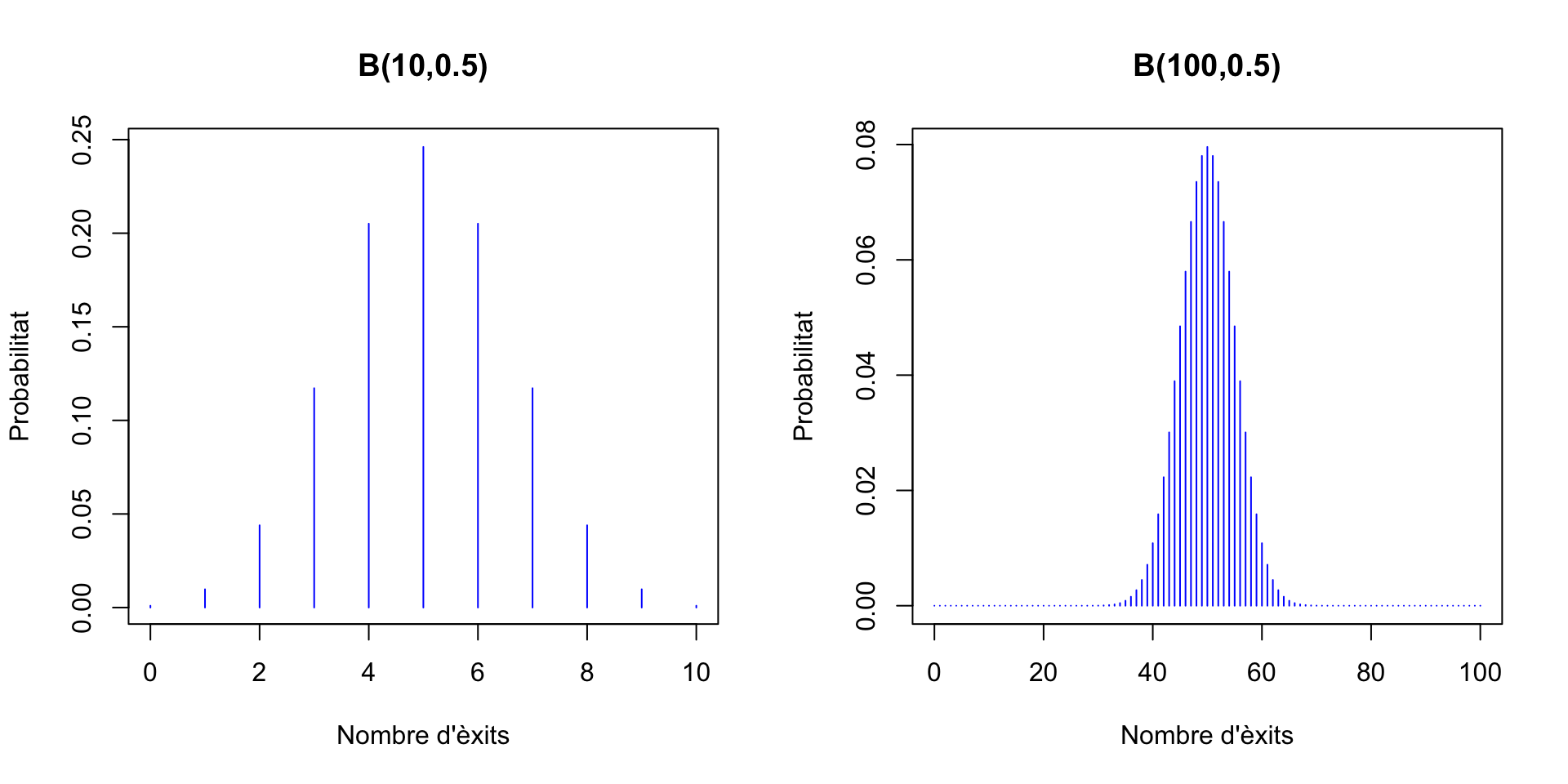
En canvi, si \(p\neq 0.5\), la funció de densitat no és simètrica, com podeu veure als gràfics de més a dalt.

Per agilitzar els tests de COVID-19, es proposà l’estratègia següent (anomenada pooled sample testing o simplement pooling). Unim grups de 10 mostres en una sola mostra i l’analitzam. Si dóna negatiu, serà senyal que totes la mostres originals eren negatives. Declararem llavors negatius els 10 subjectes de les mostres originals. Si dóna positiu, serà perquè almenys una de les mostres originals era positiva. En aquest cas, analitzarem les 10 mostres per separat.

Observau llavors que si les 10 mostres eren negatives, fem un sol test, mentre que si alguna mostra és positiva, en fem 11. Amb l’enfocament tradicional, un test per mostra i per avall, faríem sempre 10 tests.

Suposem que el test és exacte: dóna positiu sempre que ha de donar positiu i negatiu sempre que ha de donar negatiu. Sigui \(p\) la prevalença de la COVID-19 en un moment i població donats. Donades 10 mostres preses en aquest moment en aquesta població, quin és el valor esperat de tests que hem de realitzar? Si \(p\) fos petita, de l’ordre de l’1% al 5%, significaria el pooling un estalvi esperat considerable de tests?

Suposem un examen tipus test amb 10 preguntes d’opció múltiple. Cada una té 5 apartats, dels qual un, i només un, és la resposta correcta.

1. Si un estudiant respon totes les preguntes a l’atzar i cada pregunta encertada val 1 punt, quina nota esperes que tregui?

2. Cada pregunta encertada val 1 punt. Què hauria de restar cada resposta equivocada perquè la nota esperada d’un estudiant que respongués totes les preguntes a l’atzar fos un 0?

3. Suposem que les respostes correctes sumen 1, les equivocades resten el que hagis decidit a l’apartat anterior, i les no contestades no sumen ni resten res. Escriu una funció de R que simuli un estudiant que davant cada pregunta de l’examen la deixa en blanc o escull a l’atzar una de les respostes, amb les 6 opcions (en blanc i les 5 respostes) totes amb la mateixa probabilitat 1/6, i doni la nota que obté.

   Simula una mostra aleatòria de 10000 notes d’estudiants d’aquests. Comprova que la seva mitjana és aproximadament 0 (si no ho és, segurament és perquè la penalització per resposta equivocada que has donat no és la correcta). Quin percentatge de la població ha tret una nota \(\leqslant -1\)?

Com efectuar càlculs amb una variable aleatòria d’una família donada?

Una possibilitat és usar una aplicació de mòbil o tauleta. La nostra preferida és Probability distributions, disponible tant per a Android com per a iOS.

Figura 2.4: L’apli Probability Distributions.

Una altra possibilitat és usar R. R coneix totes la distribucions de variables aleatòries importants; per exemple, per a R la binomial és binom. Aleshores

• Afegint al nom de la distribució el prefix d, tenim la seva funció de densitat: de la binomial serà dbinom.

• Afegint al nom de la distribució el prefix p, tenim la seva funció de distribució: de la binomial, pbinom.

• Afegint al nom de la distribució el prefix q, tenim els seus quantils: per a la binomial, qbinom.

• Afegint al nom de la distribució el prefix r, tenim una funció que produeix mostres aleatòries de nombres amb aquesta distribució de probabilitat: per a la binomial, rbinom.

Aquestes funcions s’apliquen a l’argument de la funció i els paràmetres de la variable aleatòria en el seu ordre usual. Per exemple, per a la binomial, s’apliquen a (argument, \(n\), \(p\)). Per a més detalls sobre tot això, consultau la lliçó de R sobre el tema.

Vegem alguns exemples.

• Si llançam 20 vegades un dau cúbic equilibrat, quina és la probabilitat de treure exactament 5 uns?

  Diguem \(X\) a la variable aleatòria que compta el nombre d’uns en seqüències de 20 llançaments d’un dau equilibrat. És una variable binomial \(B(20,1/6)\). Ens demanen \(P(X=5)\), i aquesta probabilitat ens la dóna la funció de densitat de \(X\). És \(f_X(5)\):

dbinom(5,20,1/6)

## [1] 0.1294103

• Si llançam 20 vegades un dau cúbic equilibrat, quina és la probabilitat de treure com a màxim 5 uns?

  Amb les notacions anteriors, ens demanen \(P(X\leqslant 5)\), i aquesta probabilitat ens la dóna la funció de distribució de \(X\). És \(F_X(5)\):

pbinom(5,20,1/6)

## [1] 0.8981595

• Si llançam 20 vegades un dau cúbic equilibrat, quina és la probabilitat de treure menys de 5 uns?

  Amb les notacions anteriors, ens demanen \(P(X< 5)\), és a dir, \(P(X\leqslant 4)=F_X(4)\):

pbinom(4,20,1/6)

## [1] 0.7687492

• Si llançam 20 vegades un dau cúbic equilibrat, quina és la probabilitat de treure 8 uns o més?

  Amb les notacions anteriors, ens demanen \(P(X\geqslant 8)\). Com que el contrari de treure 8 uns o més és treure 7 uns o menys, tenim que \(P(X\geqslant 8)=1-P(X\leqslant 7)=1-F_X(7)\):

1-pbinom(7,20,1/6)

## [1] 0.01125328

• Si llançam 20 vegades un dau equilibrat, quin és el més petit nombre \(N\) d’uns per al qual la probabilitat de treure com a màxim \(N\) uns arriba al 25%? Ens demanen el més petit valor \(N\) tal que \(P(X\leqslant N)\geqslant 0.25\), i això per definició és el 0.25-quantil de \(X\):

qbinom(0.25,20,1/6)

## [1] 2

Vegem que en efecte \(N=2\) compleix el demanat: la probabilitat de treure com a màxim 2 uns és

pbinom(2,20,1/6)

## [1] 0.3286591

i la probabilitat de treure’n com a màxim 1 és

pbinom(1,20,1/6)

## [1] 0.1304203

Veiem per tant que amb 1 no arribam al 25% de probabilitat i amb 2 sí.

• Volem simular 50 rondes de llançar 20 vegades un dau equilibrat i comptar els uns, és a dir, volem una mostra aleatòria de mida 50 de la nostra variable \(X\):

rbinom(50,20,1/6)

##  [1] 6 4 4 2 4 2 2 4 2 2 7 7 4 3 5 2 2 5 3 2 5 3 2 3 1 3 4 0 2 5 0 5 0 4 3 2 1 1
## [39] 1 4 7 2 4 4 3 1 1 2 5 4

Cada vegada que repetim aquesta instrucció segurament obtendrem una mostra aleatòria nova:

rbinom(50,20,1/6)

##  [1] 1 3 2 2 3 5 4 2 4 4 1 4 4 2 3 2 4 6 1 2 7 4 3 5 5 1 4 2 4 2 4 3 2 3 2 7 2 2
## [39] 3 1 0 4 2 2 2 4 1 3 1 2

rbinom(50,20,1/6)

##  [1] 5 4 6 6 3 2 6 4 5 2 1 2 3 2 3 3 1 3 4 4 3 4 4 4 2 2 2 5 6 2 4 3 4 3 0 4 2 4
## [39] 5 4 4 2 3 3 6 2 3 3 4 4

rbinom(50,20,1/6)

##  [1] 2 3 5 4 3 4 2 0 3 1 0 2 1 2 4 3 4 5 5 4 2 3 3 5 3 8 3 2 4 3 5 5 5 5 4 3 4 4
## [39] 2 2 2 1 3 2 3 1 4 5 2 6

2.3.2 Variables aleatòries hipergeomètriques

Recordau que el paradigma de variable aleatòria binomial és: tenc una població amb una proporció \(p\) de subjectes que satisfan una condició \(E\), en prenc una mostra aleatòria simple de mida \(n\) i compt el nombre de subjectes \(E\) en la meva mostra. Si canviam “mostra aleatòria simple” per “mostra aleatòria sense reposició”, la distribució de la variable aleatòria que obtenim és una altra: és hipergeomètrica.

Una variable aleatòria és hipergeomètrica (o té distribució hipergeomètrica) de paràmetres \(N\), \(M\) i \(n\) (abreujadament, \(H(N,M,n)\)) quan es pot identificar amb el procés següent. Tenim una població formada per \(N\) subjectes que satisfan una condició \(E\) i \(M\) subjectes que no la satisfan (per tant, en total, \(N+M\) subjectes), prenem una mostra aleatòria sense reposició de mida \(n\) i comptam el nombre de subjectes \(E\) en aquesta mostra.

Direm a \(N\) el nombre poblacional d’èxits, a \(M\) el nombre poblacional de fracassos i a \(n\) la mida de les mostres. Fixau-vos llavors que \(N+M\) és la mida total de la població i que \(N/(N+M)\) és la probabilitat poblacional d’èxit (la fracció de subjectes que satisfan \(E\) en el total de la població). Amb R, igual que la distribució binomial era binom, la distribució hipergeomètrica és hyper.

Tenim el resultat següent:

Teorema 2.3 Si \(X\) és una variable \(H(N,M,n)\):

• El seu domini és \(D_X=\{0,1,\ldots,\text{min}(N,n)\}\)

• La seva funció de densitat és \[ f_X(k)=\left\{\begin{array}{ll} \displaystyle\dfrac{\binom{N}{k}\cdot \binom{M}{n-k}}{\binom{N+M}{n}} & \text{ si $k\in D_X$}\\ 0 & \text{ si $k\notin D_X$} \end{array} \right. \]

• El seu valor esperat és \(E(X)=\dfrac{nN}{N+M}\)

• La seva variància és \(\sigma(X)^2=\dfrac{nNM(N+M-n)}{(N+M)^2(N+M-1)}\)

La demostració de la fórmula per a la densitat és senzilla, en termes de casos favorables partit per casos possibles. Vegem: \(f_X(k)\) és la probabilitat que un subconjunt de \(n\) subjectes (diferents) de la població contengui \(k\) subjectes \(E\) i \(n-k\) subjectes dels altres (en direm \(F\)).

• Casos possibles: Tots els possibles subconjunts de \(n\) elements de la població. El nombre de tots els subconjunts de \(n\) elements d’una població de mida \(N+M\) és \(\binom{N+M}{n}\). Ja tenim el denominador.

• Casos favorables: Tots els possibles subconjunts formats per \(k\) subjectes \(E\) i \(n-k\) subjectes \(F\). Cada un d’aquests subconjunts s’obté

  • Triant un subconjunt de \(k\) subjectes \(E\): com que hi ha \(N\) subjectes \(E\), d’aquests subconjunts n’hi ha \(\binom{N}{k}\)
  • Triant un subconjunt de \(n-k\) subjectes \(F\): com que hi ha \(M\) subjectes \(F\), d’aquests subconjunts n’hi ha \(\binom{M}{n-k}\)
  • Per cada tria d’un subconjunt de \(k\) subjectes \(E\) i un subconjunt de \(n-k\) subjectes \(F\), obtenim un subconjunt “favorable” diferent. Per tant, el seu nombre és el producte \(\binom{N}{k}\cdot\binom{M}{n-k}\)

  Això ens dóna el numerador.

Fixau-vos que si diem \(p\) a la probabilitat poblacional d’èxit, \(p=N/(N+M)\), llavors \[ E(X)=np. \] És la mateixa fórmula que per a les variables binomials \(B(n,p)\) (i si ho pensau una estona veureu que, un altre cop i pel mateix argument, és el que la intuïció ens diu que ha de valer). D’altra banda, si diem \(\mathbf{P}\) a la mida total de la població, \(\mathbf{P}=N+M\), llavors \[ \sigma(X)^2=n\cdot\dfrac{N}{N+M}\cdot\dfrac{M}{N+M}\cdot\frac{N+M-n}{N+M-1}=np(1-p)\cdot\dfrac{\mathbf{P}-n}{\mathbf{P}-1} \] que és la variància d’una variable \(B(n,p)\) multiplicada per un factor de correcció a causa del fet que ara prenem mostres sense repetició i la variància és més petita que si les prenem amb repetició. A l’arrel quadrada d’aquest factor \[ \sqrt{\frac{\mathbf{P}-n}{\mathbf{P}-1}} \] se l’anomena factor de població finita.

Un exemple extrem que mostra que si permetem repeticions els resultats són, en principi, més variats és el següent. Considerau una població de \(P\) individus i en preneu una mostra aleatòria de mida aquest mateix \(P\). Si no permeteu repeticions, només n’hi ha una: no teniu més remei que triar la població sencera. Però si permeteu repeticions n’hi ha moltíssimes.

Fixau-vos que si \(\mathbf{P}\) és molt més gran que \(n\), tendrem que \(\mathbf{P}-n\approx \mathbf{P}-1\) i per tant \((\mathbf{P}-n)/(\mathbf{P}-1)\approx 1\) i la variància de la hipergeomètrica serà aproximadament la de la binomial. Això és consistent amb el que ja hem comentat: si la població és molt més gran que la mostra, prendre les mostres amb o sense reposició no afecta massa a les mostres obtengudes, per la qual cosa la distribució de probabilitat ha de ser molt semblant. Recordau els exemples següents:

• En una aula hi ha 5 homes i 45 dones. Triam 10 estudiants, un rere l’altre i sense repetir-los, per fer-los una pregunta. Cada elecció és independent de les altres. Comptam quants homes hem interrogat.

  Aquesta variable és \(H(5,45,10)\). El quocient \((\mathbf{P}-n)/(\mathbf{P}-1)\) en aquesta cas no és aproximadament 1: dóna \[ \frac{50-10}{50-1}=0.8163 \] No és correcte aproximar-la per una binomial \(B(10,0.1)\).

• A Espanya hi ha 46,700,000 persones, de les quals un 11.7% són diabètics. Triam 100 espanyols diferents i comptam quants són diabètics.

  Aquesta variable és, en realitat, hipergeomètrica amb (si les dades donades són exactes) \(N=0.117\cdot 46700000=5463900\), \(M=46700000-N=41236100\) i \(n=100\), però en la pràctica la consideram binomial \(B(100,0.117)\). El quocient \((\mathbf{P}-n)/(\mathbf{P}-1)\) és \[ \frac{46700000-100}{46700000-1}=0.9999979 \] Pràcticament 1.

I com que el nombre d’espanyols i la proporció de diabètics són només aproximats, no perdem res si aproximam un poquet més i consideram la variable com a binomial.

El gràfic següent compara la funció de densitat d’una variable \(B(10,0.1)\) amb les de variables hipergeomètriques \(H(5,45,10)\), \(H(50,450,10)\) i \(H(5000,45000,10)\) perquè vegeu com a mesura que la mida de la població creix (mantenint constant la proporció poblacional d’èxits 0.1), la distribució hipergeomètrica s’aproxima a la binomial.

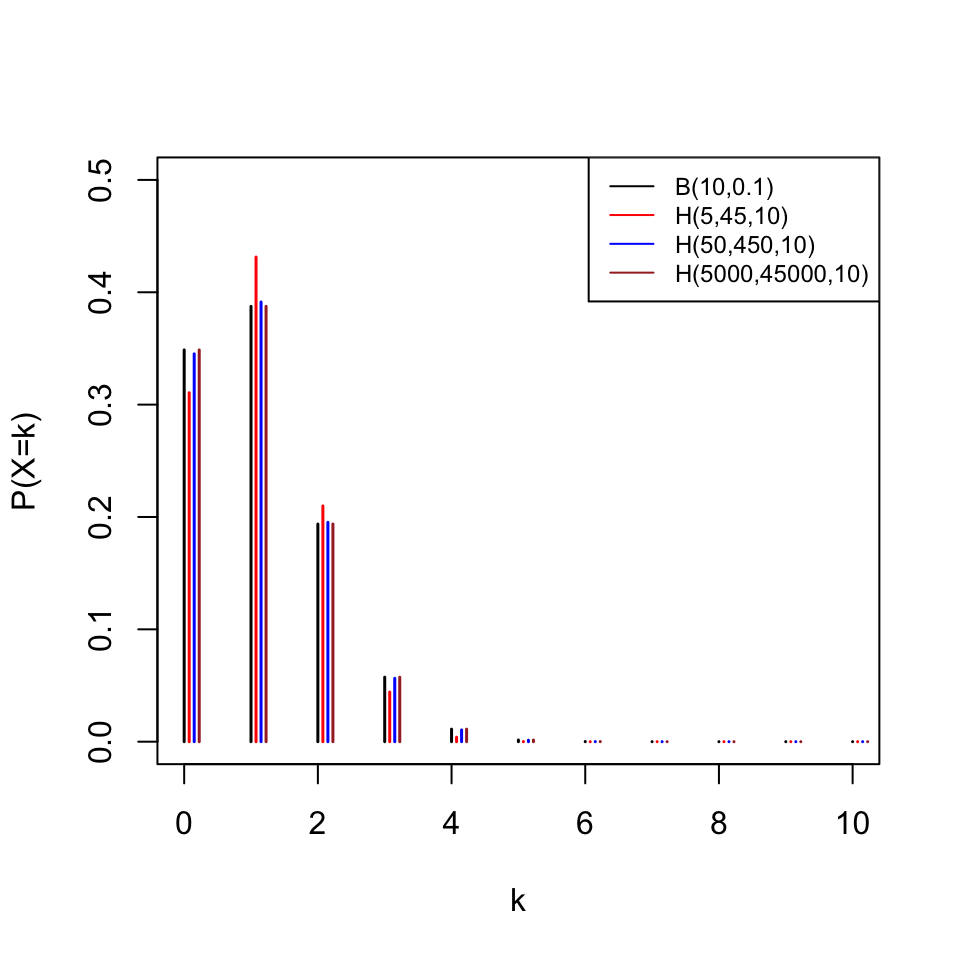
2.3.3 Variables aleatòries de Poisson

Una variable aleatòria \(X\) és de Poisson (o té distribució de Poisson) de paràmetre \(\lambda>0\) (abreujadament, \(Po(\lambda)\)) quan:

• El seu domini és \(D_X=\mathbb{N}\), el conjunt de tots els nombres naturals.

• La seva funció de densitat és \[ f_X(k)=\left\{\begin{array}{ll} e^{-\lambda}\cdot \dfrac{\lambda^k}{k!} & \text{ si $k\in \mathbb{N}$}\\ 0 & \text{ si $k \notin \mathbb{N}$} \end{array} \right. \]

Per a R, la distribució de Poisson és pois.

Teorema 2.4 Si \(X\) és una variable \(Po(\lambda)\), aleshores \(E(X)= \sigma(X)^2= \lambda\).

És a dir, el paràmetre \(\lambda\) d’una variable de Poisson és el seu valor esperat, i coincideix amb la seva variància.

Us deveu estar demanant: de què ens serveix definir una variable de Poisson mitjançant la seva densitat, si el que ens interessa és poder classificar una variable com a Poisson (o binomial, o hipergeomètrica etc.) per a així saber “gratis” la seva densitat? La resposta és que la família de Poisson inclou un tipus de variables aleatòries molt freqüent que tot seguit descrivim.

Suposem que tenim un tipus d’objectes que poden donar-se en una regió contínua de temps o espai. Per exemple, defuncions de persones per una determinada malaltia en el decurs del temps, exemplars d’una espècie de planta en un terreny o bacteris en una superfície.

Suposem a més que les aparicions d’aquests objectes satisfan les propietats següents (per simplificar el llenguatge, hi suposarem que observam aparicions d’aquests objectes en el temps; si es tracta d’una variable que compta objectes en regions de l’espai, canviau-hi “instant” per “punt”):

• Les aparicions dels objectes són aleatòries: en cada instant, un objecte es dóna, o no, a l’atzar, amb una probabilitat fixa i constant.

• Les aparicions dels objectes són independents: que es doni un objecte en un instant concret, no depèn que s’hagi donat o no un objecte en un altre instant.

• Les aparicions dels objectes no són simultànies: és pràcticament impossible que dos objectes d’aquests es donin en el mateix instant exacte, mesurat amb precisió infinita.

En aquesta situació, la variable \(X_t\) que pren un interval de temps de durada \(t\) i compta el nombre d’objectes que s’hi donen és de Poisson \(Po(\lambda_t)\), amb \(\lambda_t\) el nombre esperat d’objectes en aquest interval de temps, és a dir, el nombre mitjà d’objectes en intervals de temps d’aquesta mida.

Per exemple, quan el que compten ocorre a l’atzar, són variables de Poisson:

• El nombre de malalts admesos en urgències en un dia (o en 12 hores, o en una setmana…)

• El nombre de defuncions per una malaltia concreta en un dia (o en una setmana, o en un any…)

• El nombre d’albiraments de dofins en una hora (o en qualsevol altre període fixat de temps) durant un vol d’inspecció

• El nombre de bacteris en un quadrat d’1 cm de costat (o d’1 m de costat…)

Fixau-vos que aquest tipus de coneixement ens serveix per a dues coses:

• Si sabem que aquestes variables són de Poisson, coneixem la seva densitat i per tant podem calcular el que volguem per a elles.

• Si les dades que observam haurien de seguir una distribució de Poisson però sembla que no (per exemple, perquè la seva variància sigui molt diferent de la seva mitjana, tan diferent que sigui difícil de creure que la mitjana i la variància poblacionals siguin iguals), llavors és senyal que qualque cosa “estranya” està passant que afecta la seva aparició.

Exemple 2.8 Observau la diferència entre les dues variables següents:

• Nombres mensuals de defuncions per un tipus de càncer en un país. El moment exacte de les defuncions es produeix a l’atzar, segurament mai no es donen dues defuncions exactament en el mateix instant amb precisió infinita, i les defuncions es produeixen de manera independent. És de Poisson.

• Nombres mensuals de defuncions per una malatia infecciosa en un país. Un altre cop, el moment exacte de les defuncions es produeix a l’atzar i segurament mai no es donen dues defuncions exactament en el mateix instant amb precisió infinita. Però les infeccions no són independents, precisament perquè es tracta d’una malaltia infecciosa, i per tant les defuncions tampoc: com ens hem cansat d’observar amb la COVID-19, en un mateix cluster de la malaltia es poden produir diverses morts associades. No és de Poisson.

Com que les aparicions dels objectes que compta una variable de Poisson són aleatòries i independents, el nombre mitjà d’objectes és lineal en la mida de la regió. És a dir, per exemple, en un interval de dos dies esperam veure el doble d’objectes que en un dia, i en una setmana 7 vegades els d’un dia.

Vegem alguns gràfics de la funció de densitat de variables aleatòries de Poisson.

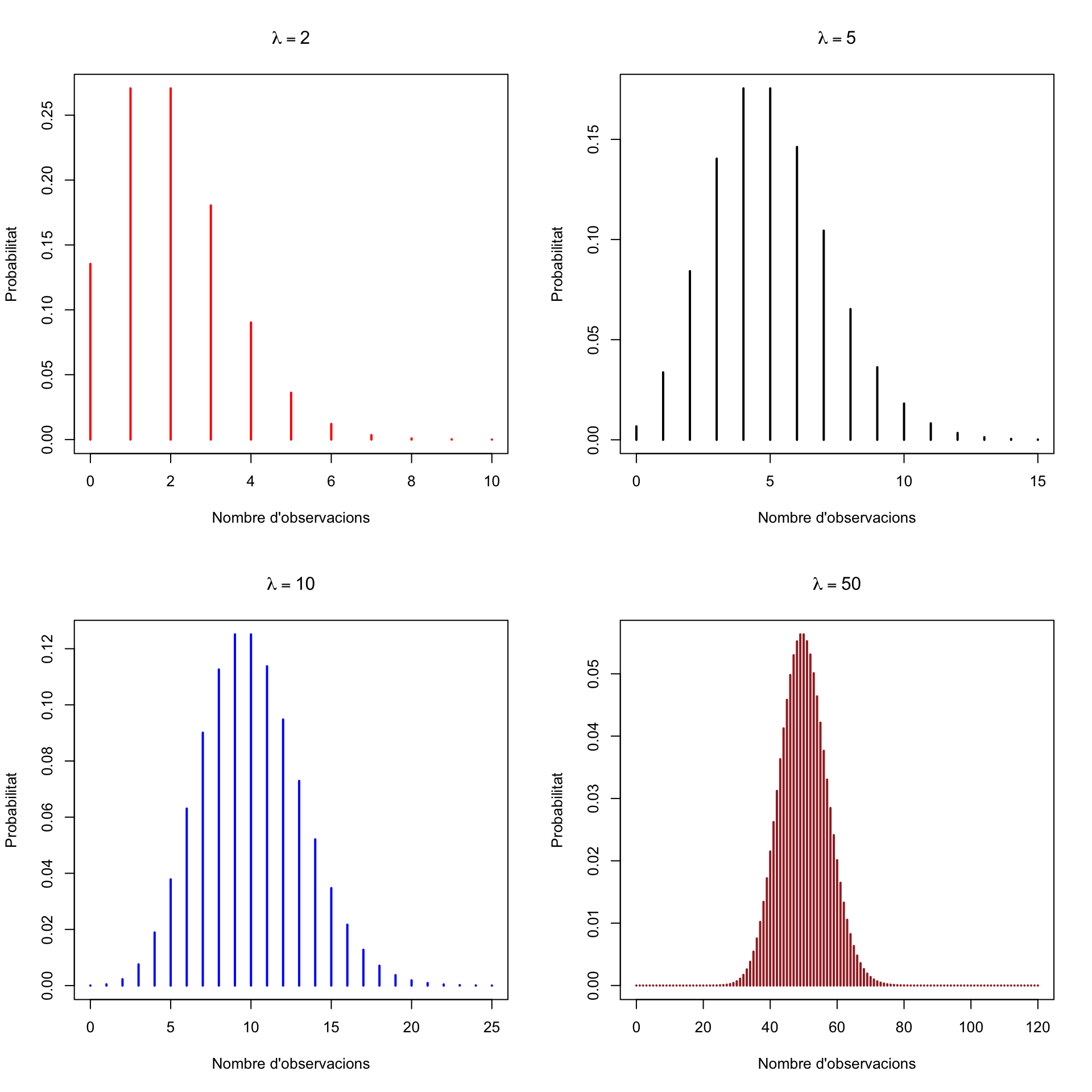
Com veieu, la densitat d’una variable Poisson és asimètrica, amb un màxim al voltant de \(\lambda\) i una cua a la dreta, però a mida que \(\lambda\) creix, l’asimetria va minvant.

El nombre d’estudiants que entren en el bar del vostre edifici al Campus en un interval de 5 minuts, creieu que segueix una distribució de Poisson?

2.4 Variables aleatòries contínues

Una variable aleatòria és contínua quan els seus possibles valors són dades quantitatives contínues. Per exemple:

• Pes
• Nivell de colesterol en sang
• Diàmetre d’un tumor

En aquest curs ens restringirem a variables aleatòries contínues \(X: \Omega\to \mathbb{R}\) que satisfan la propietat extra següent: la seva funció de distribució \[ \begin{array}{rcl} F_X: \mathbb{R} & \to & [0,1]\\ x &\mapsto &P(X\leqslant x) \end{array} \] és contínua. Totes les variables aleatòries contínues que us puguin interessar en algun moment satisfan aquesta propietat, així que no perdem res imposant-la. I el que hi guanyam és que:

Si \(X\) és una variable aleatòria contínua amb funció de distribució contínua, la probabilitat que prengui cada valor concret és 0: \[ P(X=a)=0 \text{ per a tot $a \in \mathbb{R}$}. \]

Per si passa per aquí qualcú que en necessiti una demostració: \[ \begin{array}{l} \displaystyle P(X=a) = P(X\leqslant a)-P(X<a)=P(X\leqslant a)-P\Big(\bigcup_{n\geqslant 1} \Big(X\leqslant a-\frac{1}{n}\Big)\Big)\\ \displaystyle \qquad= P(X\leqslant a)-\lim_{n\geqslant 1}P\Big(X\leqslant a-\frac{1}{n}\Big)= F_X(a)-\lim_{n\geqslant 1}F_X\Big(a-\frac{1}{n}\Big)=0 \end{array} \] perquè \(F_X\) és contínua.

En particular:

Per a una variable aleatòria contínua, probabilitat 0 no significa impossible.

Cada valor de \(X\) té probabilitat 0, però si prenem un subjecte de la població, \(X\) tendrà qualque valor sobre ell, no? Per tant, aquest valor de \(X\) és possible, malgrat tengui probabilitat 0.

De \(P(X=a)=0\) es dedueix que la probabilitat d’un esdeveniment definit amb una desigualtat és exactament la mateixa que la de l’esdeveniment corresponent definit amb una desigualtat estricta. En particular, contràriament al que passava a les variables aleatòries discretes, per a una variable aleatòria contínua sempre tenim que \[ P(X\leqslant a)=P(X<a) \] perquè \[ P(X\leqslant a)=P(X<a)+P(X=a)=P(X<a)+0=P(X<a). \]

Més exemples:

• \(P(X\geqslant a)=P(X> a)+P(X=a)=P(X> a)\)
• \(P(a \leqslant X\leqslant b)=P(a<X <b)+P(X=a)+P(X=b)\) \(=P(a<X <b)\)

2.4.1 Densitat i distribució

Sigui \(X\) una variable aleatòria contínua. Com ja hem dit, la seva funció de distribució \(F_X\) torna a ser \[ x\mapsto F_X(x)=P(X\leqslant x) \]

Però com que ara tenim que \(P(X=x)=0\) per a tot \(x\in \mathbb{R}\), no podem definir la funció de densitat de \(X\) com a \(f_X(x)=P(X=x)\). Què podem fer?

Recordau que, a les variables aleatòries discretes, \[ F_X(a)=\sum_{x\leqslant a} f_X(x) \]

En el context de matemàtiques “contínues”, la suma \(\sum\) es tradueix en una integral \(\int\). Definim aleshores la funció de densitat d’una variable aleatòria contínua \(X\) com la funció \(f_X:\mathbb{R}\to \mathbb{R}\) tal que:

• \(f_X(x)\geqslant 0\), per a tot \(x\in \mathbb{R}\)

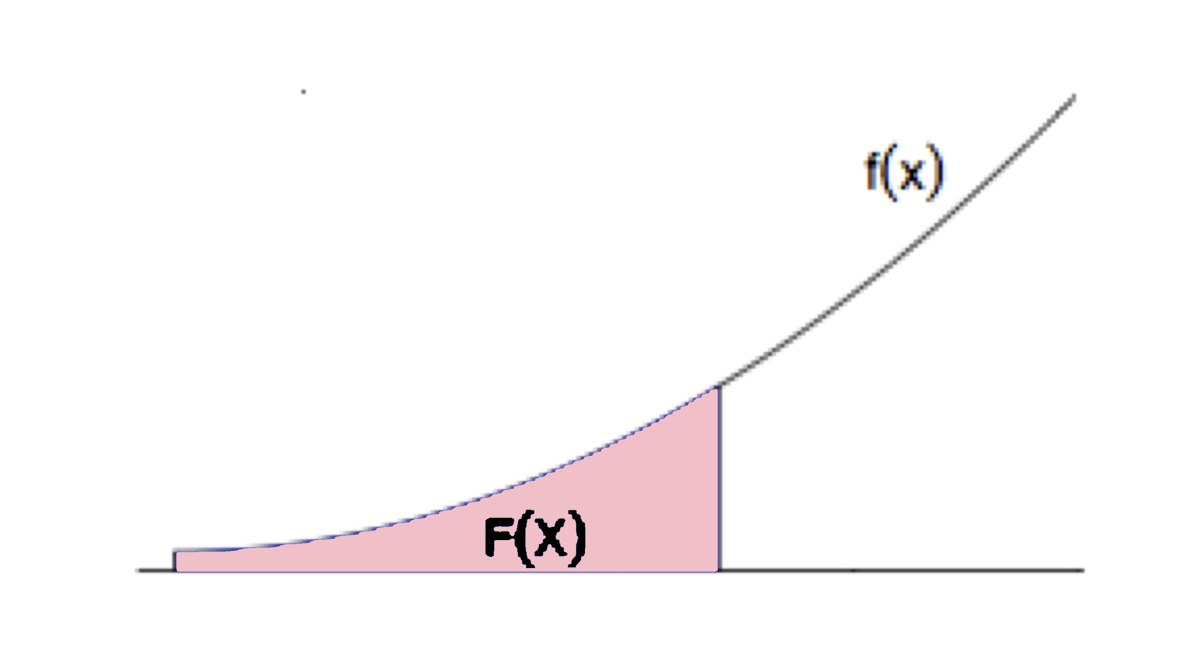
• \(\displaystyle F_X(a)=\int_{-\infty}^a f_{X}(x)\, dx\) per a tot \(a \in \mathbb{R}\).

Recordau que la integral té una interpretació senzilla en termes d’àrees. En concret, donats \(a \in \mathbb{R}\) i una funció \(f(x)\), el valor de la integral \[ \int_{-\infty}^a f(x)\, dx \] és igual a l’àrea de la regió compresa entre la corba \(y=f(x)\) i l’eix d’abscisses \(y=0\) a l’esquerra de la recta vertical \(x=a\). Per tant, la funció de densitat \(f_X\) de \(X\) és la funció positiva tal que, per a tot \(a\in \mathbb{R}\), \(F_X(a)\) és igual a l’àrea davall de la corba \(y=f_X(x)\) (és a dir, entre aquesta corba i l’eix d’abscisses) a l’esquerra de \(x=a\).

Quina és la idea intuïtiva que hi ha al darrere d’aquesta definició de densitat? Suposau que dibuixam histogrames de freqüències relatives dels valors de \(X\) sobre tota la població. Com que estam parlant de tota la població, la freqüència relativa de cada classe és la proporció d’individus de la població en els quals el valor de \(X\) pertany a aquesta classe: és a dir, la probabilitat que \(X\) caigui dins la classe.

Recordau que, en un histograma de freqüències relatives:

• La freqüència relativa (ara, la probabilitat) de cada classe és l’àrea de la seva barra, és a dir, l’amplada de la classe per l’alçada de la barra.
• Diem a l’alçada d’una barra la densitat de la classe (i per tant, qualque cosa tendrà a veure amb la densitat de \(X\), no ho trobau?).
  
• Si \(a\) és un extrem d’una classe, la freqüència relativa acumulada fins \(a\) (la probabilitat que \(X\leqslant a\)) és la suma de les àrees de les barres a l’esquerra d’\(a\).

Si dibuixam els histogrames de \(X\) prenent classes cada vegada més estretes, els seus polígons de freqüències (en vermell) tendeixen a dibuixar una corba:

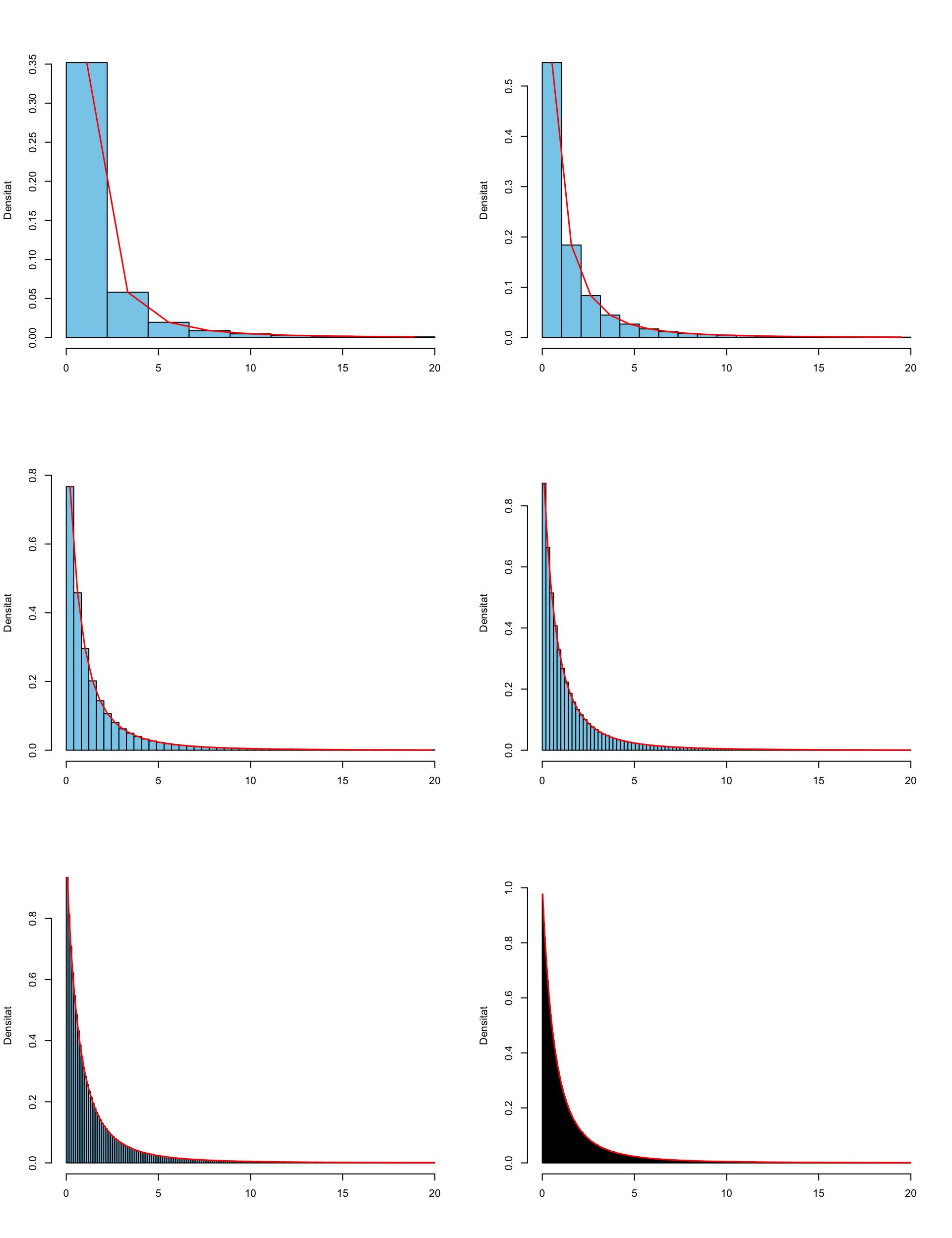
Quan l’amplada de les classes tendeix a 0, obtenim una corba que és el límit d’aquests polígons de freqüències:

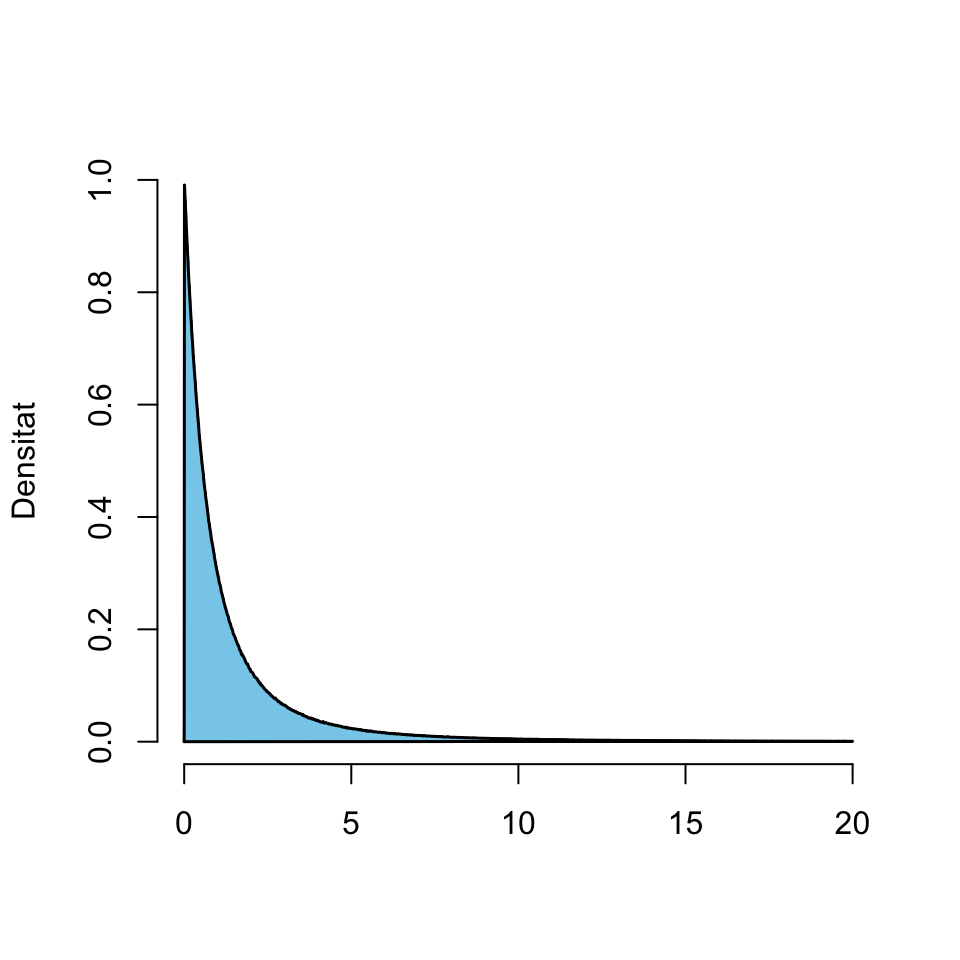
En el límit, la probabilitat que \(X\leqslant a\) serà el límit de les sumes de les àrees de les barres a l’esquerra d’\(a\), i per tant l’àrea davall d’aquesta corba límit a l’esquerra d’\(a\). Això ens diu que aquesta corba és precisament la funció de densitat \(y=f_X(x)\).

La funció de densitat \(f_X\) d’una variable aleatòria contínua \(X\) és la funció límit dels polígons de freqüències d’histogrames de \(X\) quan l’amplada de les classes tendeix a 0.

Vegem algunes propietats que es dedueixen del fet que \(F_X(a)=P(X\leqslant a)\) sigui igual a l’àrea davall de la corba \(y=f_X(x)\) a l’esquerra de \(x=a\):

• Com que \(P(X<\infty)=1\), l’àrea davall de tota la corba \(y=f_X(x)\) és 1.

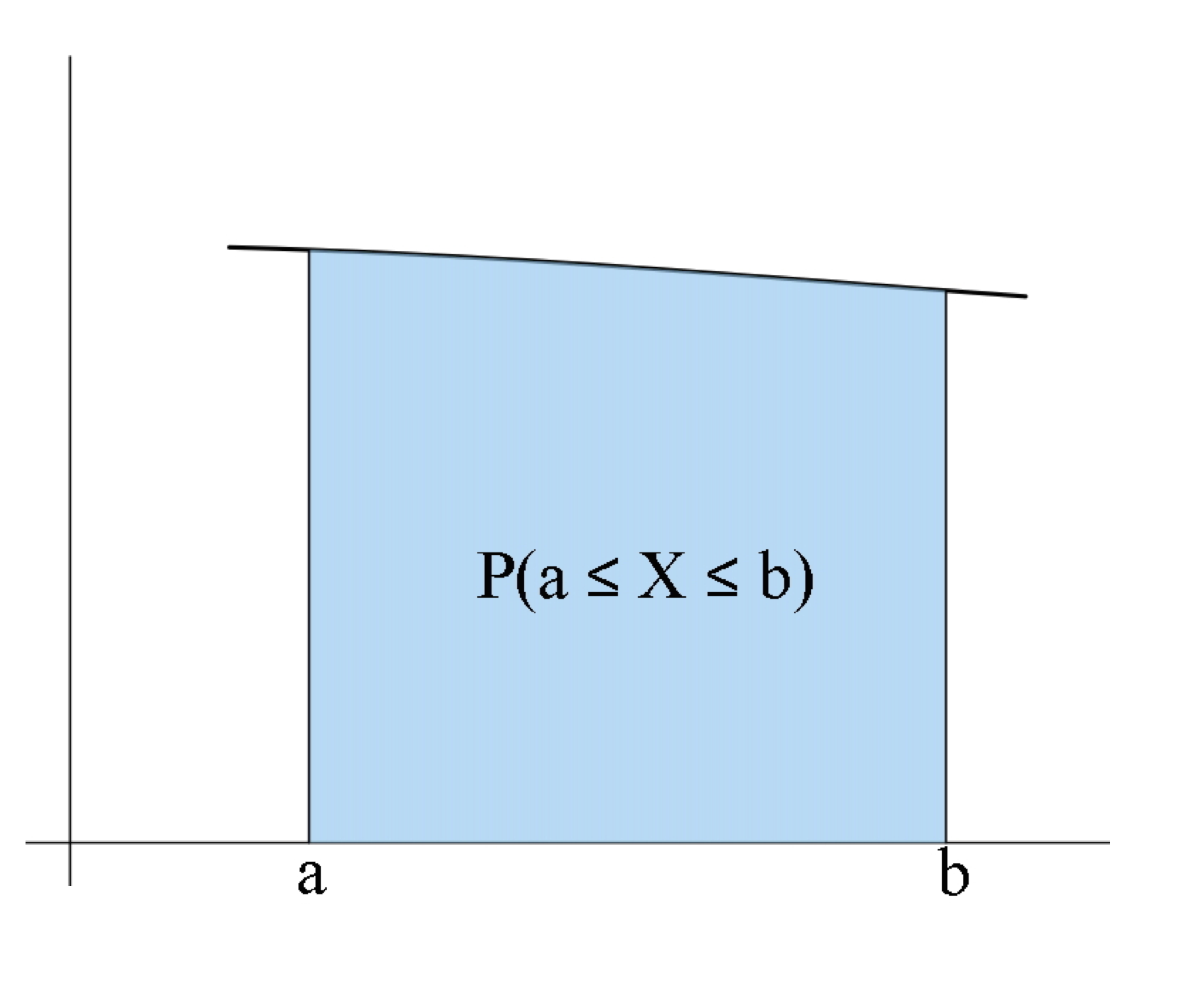
• \(P(a\leqslant X\leqslant b)=P(X\leqslant b)-P(X<a)\) és l’àrea davall de la corba \(y=f_X(x)\) a l’esquerra de \(x=b\) menys l’àrea davall de la corba \(y=f_X(x)\) a l’esquerra de \(x=a\). Per tant, \(P(a\leqslant X\leqslant b)\) és igual a l’àrea davall de la corba \(y=f_X(x)\) entre \(x=a\) i \(x=b\).

• Si \(\varepsilon>0\) és molt, molt petit, l’àrea davall de la corba \(y=f_X(x)\) entre \(a-\varepsilon\) i \(a+\varepsilon\) és aproximadament igual a la del rectangle de base l’interval \([a-\varepsilon,a+\varepsilon]\) i alçada \(f_X(a)\), és a dir, a \(2\varepsilon\cdot f_X(a)\) (vegeu la Figura 2.5). És a dir, \[ P(a-\varepsilon\leqslant X\leqslant a+\varepsilon)\approx 2\varepsilon\cdot f_X(a). \]

  Per tant, \(f_X(a)\) ens dóna una indicació de la probabilitat que \(X\) valgui aproximadament \(a\) (però no és \(P(X=a)\), que val 0). És a dir, per exemple, si \(f_X(a)=0.1\) i \(f_X(b)=0.5\), la probabilitat que \(X\) prengui un valor proper a \(b\) és 5 vegades més gran que la probabilitat que prengui un valor proper a \(a\).

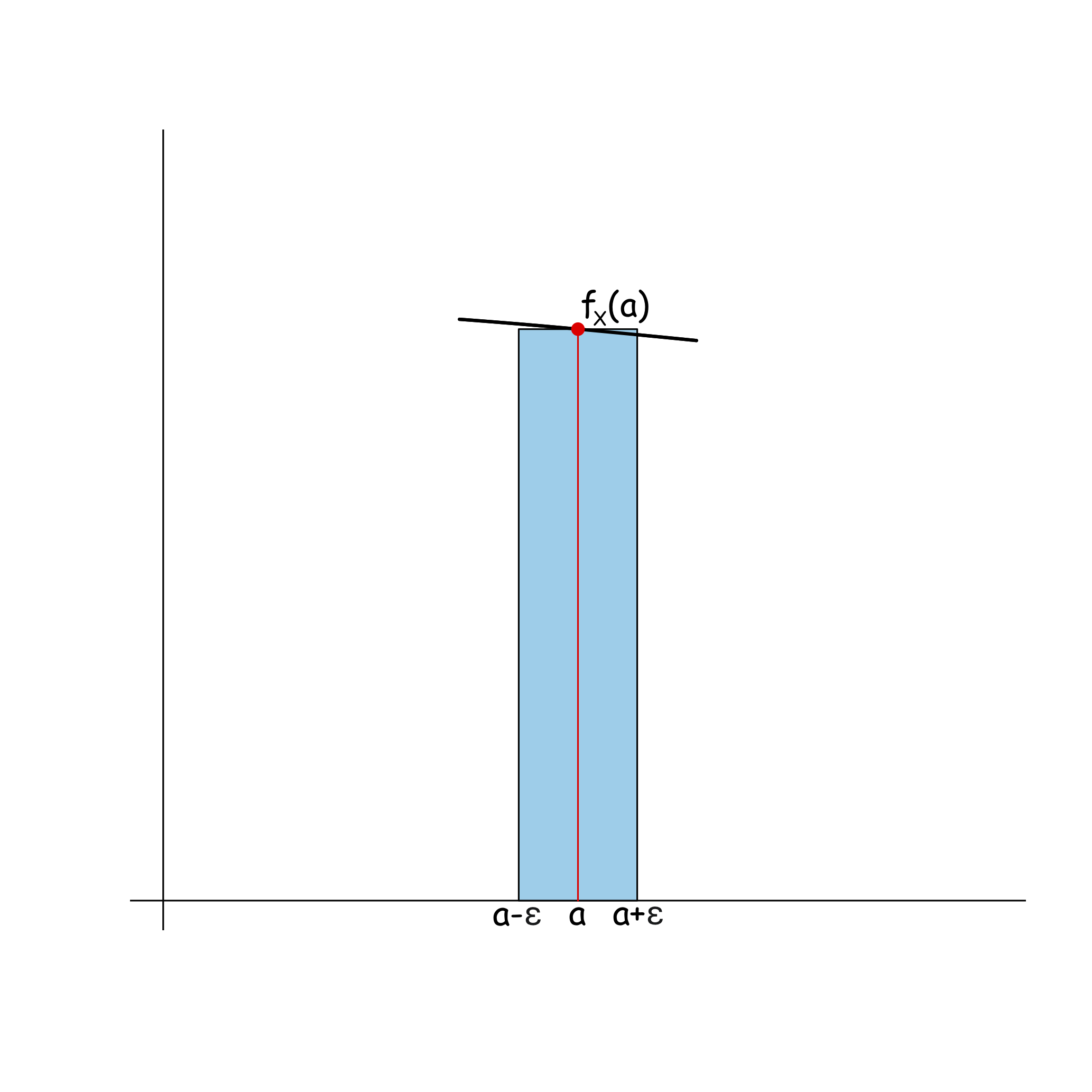
Figura 2.5: L’àrea davall de la corba al voltant d’\(a\) és aproximadament igual a la del rectangle d’alçada f_X(a)

Però \(P(X=a)=P(X=b)=0\), així que, per favor, evitau dir que “la probabilitat que \(X\) valgui \(b\) és 5 vegades més gran que la probabilitat que valgui \(a\)”. Sí, ja sabem que \(5\cdot 0=0\), però la frase és enganyosa: la probabilitat que \(X\) valgui \(b\) no és més gran que la probabilitat que valgui \(a\).

A les variables aleatòries discretes, hi definíem la moda com el valor (o els valors) més probable. Però ara no té sentit definir la moda d’una variable contínua \(X\) com el valor \(x_0\) tal que \(P(X=x_0)\) sigui màxim, perquè… en efecte, perquè \(P(X=x)=0\) per a tot \(x\in \mathbb{R}\). Aleshores, es defineix la moda d’una variable aleatòria contínua \(X\) com el valor (o els valors) \(x_0\) tal que \(f_X(x_0)\) és màxim. Com que \(f_X(x_0)\) mesura la probabilitat que \(X\) valgui “aproximadament” \(x_0\), tenim que la moda de \(X\) és el valor prop del qual és més probable que caigui el valor de \(X\).

Unes consideracions finals:

• Ho hem dit en la definició, i ho hem emprat implícitament en tota la secció, però ho tornam a repetir: \(f_X(x)\geqslant 0\) per a tot \(x\in \mathbb{R}\).

En realitat, que \(f_X(x)\) sigui \(\geqslant 0\) per a tot \(x\in \mathbb{R}\) és conseqüència del fet que la funció \(F_X(x)\) sigui positiva i creixent (les funcions de distribució són sempre creixents, perquè si \(x<y\), \(F_X(x)=P(X\leqslant x)\leqslant P(X\leqslant y)=F_X(y)\)) i coincideixi amb \(\int_{-\infty}^x f_X(x)\,dx\). Però és més senzill donar-ho com a part de la definició i així ens estalviam la demostració.

• \(f_X(x)\) no és una probabilitat, i per tant pot ser més gran que 1. Per exemple, el gràfic següent mostra la densitat d’una variable normal \(N(0,0.01)\) (vegeu la Secció 2.5), que arriba a valer gairebé 40.

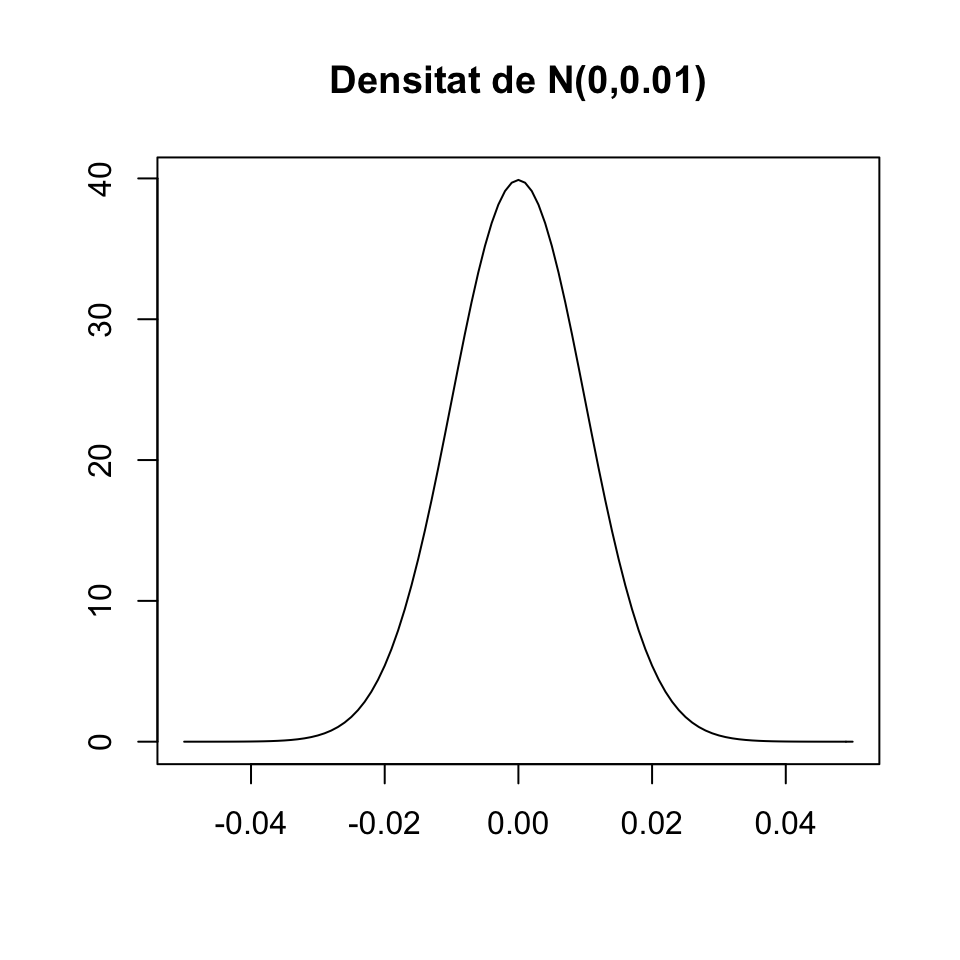
• La funció de densitat \(f_X\) no té per què ser contínua, malgrat la funció de distribució \(F_X\) ho sigui.

2.4.2 Esperança, variància, quantils…

L’esperança i la variància d’una variable aleatòria contínua \(X\), amb funció de densitat \(f_X\), es defineixen com en el cas discret, substituint la suma \(\sum_{x\in D_x}\) per una integral, i tenen les mateixes propietats.

La mitjana, o esperança (o valor mitjà, valor esperat…), de \(X\) és \[ E(X)=\int_{-\infty}^{\infty}x \cdot f_{X}(x)\, dx \] És a dir, és l’àrea compresa entre l’eix d’abscisses i la corba \(y=xf_X(x)\). Com en el cas discret, també la indicarem de vegades amb \(\mu_X\).

Aquest valor té la mateixa interpretació que en el cas discret:

• Representa el valor mitjà de \(X\) sobre el total de la població.

• És (amb probabilitat 1) el límit de les mitjanes aritmètiques de mostres aleatòries de mida \(n\) de valors de \(X\), quan \(n\to \infty\).

Si \(g:\mathbb{R}\to \mathbb{R}\) és una funció contínua, l’esperança de \(g(X)\) és \[ E(g(X))=\int_{-\infty}^{+\infty} g(x) f_X(x)dx \]

La variància de \(X\) és \[ \sigma(X)^2=E((X-\mu_X)^2)=\int_{-\infty}^{+\infty} (x-\mu_X)^2 f_X(x)dx \] i es pot demostrar que és igual a \[ \sigma(X)^2=E(X^2)-\mu_X^2. \] També la indicarem de vegades amb \(\sigma_X^2\).

La desviació típica de \(X\) és \[ \sigma(X)=+\sqrt{\sigma(X)^2} \] i també la indicarem de vegades amb \(\sigma_X\).

Com en el cas discret, la variància i la desviació típica quantifiquen la variabilitat dels resultats de \(X\).

Aquests paràmetres de \(X\) tenen les mateixes propietats en el cas continu que en el discret. Les recordam:

• Si \(b\) és una variable aleatòria constant, \(E(b)=b\) i \(\sigma(b)^2=0\).

• Si \(\sigma(X)^2=0\), \(X\) és constant.

I és clar, si \(X\) només pot prendre un valor, aleshores ja no és contínua, sino discreta. Per tant, per conveni, d’ara endavant suposarem que les nostres variables aleatòries contínues sempre tenen variància no nul·la.

• Si \(X_1,\ldots,X_n\) són variables aleatòries i \(a_1,\ldots,a_n,b\in \mathbb{R}\), \[ E(a_1X_1+\cdots+a_nX_n+b)=a_1E(X_1)+\cdots+a_nE(X_n)+b \]

• Si \(X\leqslant Y\), aleshores \(E(X)\leqslant E(Y)\).

• Si \(a,b\in \mathbb{R}\), \(\sigma(aX+b)^2=a^2 \sigma(X)^2\) i \(\sigma(aX+b)=|a|\cdot \sigma(X)\).

• Si \(X_1,\ldots,X_n\) són variables aleatòries independents (i, en principi, només en aquest cas) i \(a_1,\ldots,a_n,b\in \mathbb{R}\), \[ \begin{array}{l} \sigma(a_1X_1+\cdots+a_nX_n+b)^2=a_1^2\cdot\sigma(X_1)^2+\cdots+a_n^2\cdot\sigma(X_n)^2\\ \sigma(a_1X_1+\cdots+a_nX_n+b)=\sqrt{a_1^2\cdot\sigma(X_1)^2+\cdots+a_n^2\cdot\sigma(X_n)^2} \end{array} \] Si no són independents, aquestes igualtats poden ser falses.

El quantil d’ordre \(p\) (o \(p\)-quantil) d’una variable aleatòria contínua \(X\) és el valor \(x_p\in \mathbb{R}\) més petit tal que \[ F_X(x_p)=P(X\leqslant x_p)=p \]

Observau que, com que \(F_X(x)\) tendeix a 0 (la probabilitat del conjunt buit) quan \(x\to -\infty\) i tendeix a 1 (la probabilitat de tot \(\mathbb{R}\)) quan \(x\to +\infty\) i és contínua (no pega bots), pren tots els valors de l’interval \((0,1)\) i per tant, per a qualsevol \(p\in (0,1)\), existeix qualque \(x\) tal que \(F_X(x)=p\).

La mediana de \(X\) és el seu 0.5-quantil, el primer i tercer quartils són el seu 0.25-quantil i el seu 0.75-quantil, etc.

2.5 Variables aleatòries normals

Una variable aleatòria contínua \(X\) és normal (o té distribució normal) de paràmetres \(\mu\) i \(\sigma\) (per abreujar, \(N(\mu,\sigma)\)) quan la seva funció de densitat és \[ f_{X}(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{{-(x-\mu)^2}/(2\sigma^{2})} \]

Naturalment, no us heu de saber aquesta fórmula.

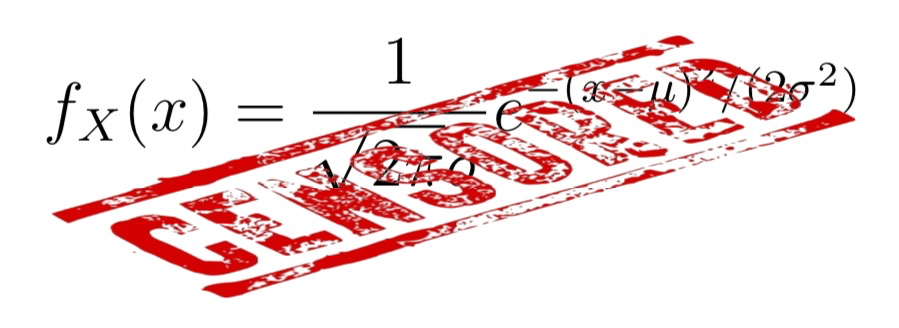
Però sí que heu de saber que:

• Una variable aleatòria normal \(X\) és contínua, i per tant \(P(X=x)=0\), \(P(X\leqslant x)=P(X<x)\) etc.

• Si \(X\) és normal, la seva funció de distribució \(F_X\) és injectiva i estrictament creixent: si \(x<y\), \(F_X(x)<F_X(y)\).

• Si \(X\) és \(N(\mu,\sigma)\), aleshores \(\mu_X=\mu\) i \(\sigma_X=\sigma\).

Una variable aleatòria normal diem que és estàndard (o típica) quan és \(N(0,1)\). Normalment indicarem les variables normals estàndard amb \(Z\). Observau, doncs, que si \(Z\) és normal estàndard, \(\mu_Z=0\) i \(\sigma_Z=1\).

La gràfica de la densitat d’una variable aleatòria normal és la famosa campana de Gauss:

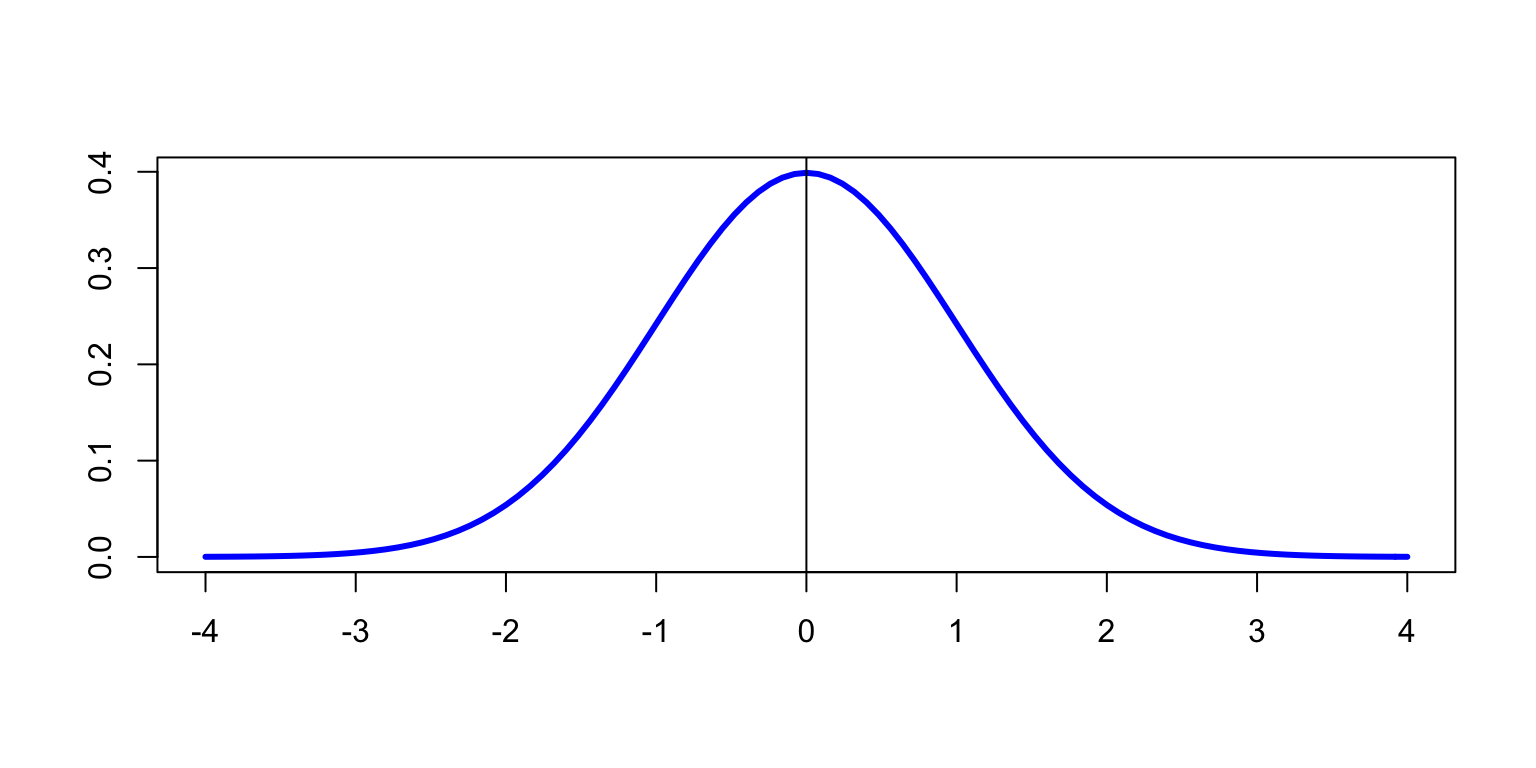
Figura 2.6: Densitat d’una variable normal estàndard

La distribució normal és una distribució teòrica, no la trobareu exacta en la vida real. I malgrat el seu nom, no és més “normal” que altres distribucions contínues.

Però és molt important perquè moltes distribucions de la vida real són aproximadament normals. El motiu és que:

Si una variable aleatòria consisteix a prendre un nombre molt gran \(n\) de mesures independents d’una o diverses variables aleatòries i sumar-les, aleshores té distribució aproximadament normal, encara que les variables aleatòries de partida no ho siguin.

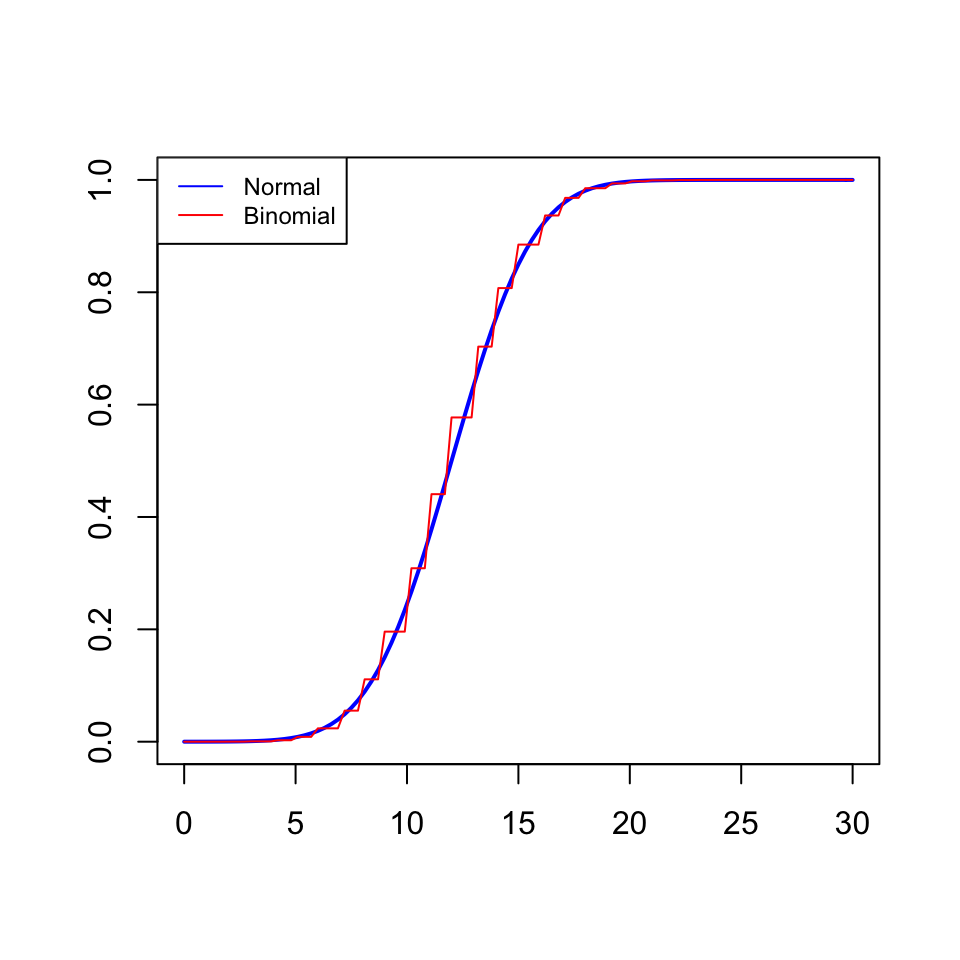
Exemple 2.9 Una variable binomial \(B(n,p)\) s’obté prenent \(n\) mesures independents d’una variable Bernoulli \(Be(p)\) i sumant-les. Per tant, per la “regla” anterior, una \(B(n,p)\) hauria de ser aproximadament normal si \(n\) és gran. Doncs sí, si \(n\) és gran (posem a partir de 40, encara que si \(p\) és molt propera a 0 o 1, la mida de les mostres ha de ser més gran), una variable \(X\) binomial \(B(n,p)\) és aproximadament normal \(N(np,\sqrt{np(1-p)})\); recordau que, si \(X\) és \(B(n,p)\), aleshores \(\mu_X=np\) i \(\sigma_X=\sqrt{np(1-p)}\). Aquest “aproximadament” significa que la funció de distribució de \(X\) és aproximadament la de la normal.

Per exemple, el gràfic següent compara les funcions de distribució d’una binomial \(B(40,0.3)\) i una normal \(N(40\cdot 0.3,\sqrt{40\cdot 0.3\cdot 0.7})\).

En els propers temes emprarem sovint que una variable \(B(n,p)\) amb \(n\) gran és aproximadament \(N(np,\sqrt{np(1-p)})\).

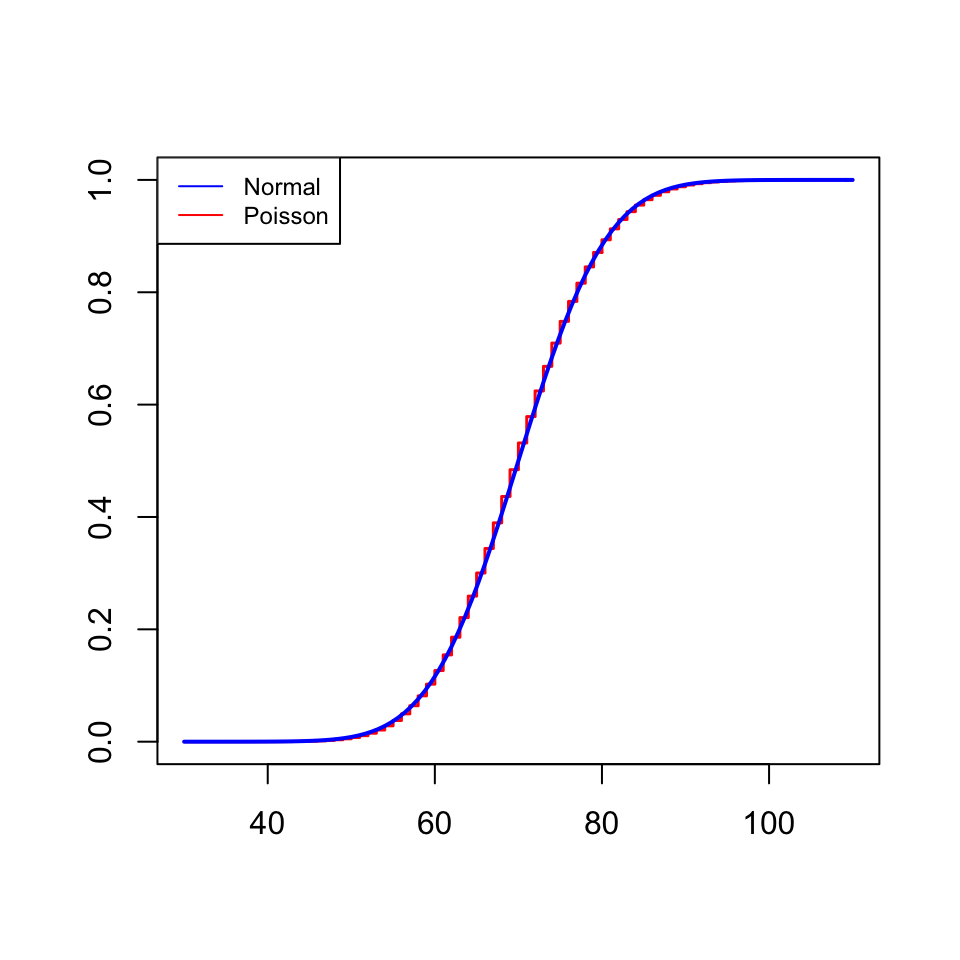
Exemple 2.10 Si \(X\) és una variable aleatòria de Poisson \(Po(\lambda)\) i \(\lambda\) és gran, aleshores \(X\) també és aproximadament \(N(\lambda,\sqrt{\lambda})\).

Per exemple, el gràfic següent compara les funcions de distribució d’una Poisson \(Po(70)\) i una normal \(N(70,\sqrt{70})\).

Sigui \(X\) una variable discreta que només pot prendre com a valors nombres naturals, com ara una binomial o una Poisson. Quan l’aproximam per mitjà d’una variable normal \(Y\), és convenient aplicar alguna correcció de continuïtat. La més senzilla és, per a cada \(n\in \mathbb{N}\), aproximar:

• \(P(X\leqslant n)\) per mitjà de \(P(Y< n+1/2)\)

• \(P(X=n)\) per mitjà de \(P(n-1/2< Y< n+1/2)\)

Vegeu l’Exemple 2.11 més a baix.

2.5.1 Amb R

Per calcular probabilitats d’una \(N(\mu,\sigma)\), cal calcular les integrals a mà.

O podeu emprar R, per a qui la normal és norm. Per tant, si \(X\) és \(N(\mu,\sigma)\):

• dnorm(x,mu,sigma) dóna el valor de la densitat \(f_X(x)\)

• pnorm(x,mu,sigma) dóna el valor de la distribució \(F_X(x)=P(X\leqslant x)\)

• qnorm(q,mu,sigma) dóna el \(q\)-quantil de \(X\)

• rnorm(n,mu,sigma) dóna un vector de \(n\) nombres aleatoris generats amb aquesta distribució

Així, per exemple, si \(X\) és \(N(1,2)\)

• \(P(X\leqslant 1.5)\) és

pnorm(1.5,1,2)

## [1] 0.5987063

• El 0.4-quantil de \(X\), és a dir, el valor \(q\) tal que \(P(X\leqslant q)=0.4\) és

qnorm(0.4,1,2)

## [1] 0.4933058

• \(P(X=1.5)\) és

dnorm(1.5,1,2)

## [1] 0.1933341

No! Com que \(X\) és contínua, \(P(X=1.5)=0\). El que us dóna dnorm(1.5,1,2) és el valor de la funció de densitat de \(X\) en 1.5, que no creiem que us interessi gaire.

Si la normal és estàndard, no fa falta entrar la \(\mu=0\) i la \(\sigma=1\) (són els valors per defecte d’aquests paràmetres per a norm). Així, si \(Z\) és \(N(0,1)\):

• \(P(Z\leqslant 1.5)\) és

pnorm(1.5)

## [1] 0.9331928

• El seu 0.95-quantil és

qnorm(0.95)

## [1] 1.644854

• Què val \(P(-1\leqslant Z\leqslant 1)\)? Com que \(P(-1\leqslant Z\leqslant 1)=P(Z\leqslant 1)-P(Z\leqslant -1)\), és

pnorm(1)-pnorm(-1)

## [1] 0.6826895

Exemple 2.11 A la secció anterior, us hem dit que una variable binomial \(B(n,p)\) amb \(n\) gran s’aproxima per mitjà d’una variable normal \(N(np,\sqrt{np(1-p)})\). Així, per exemple, una variable \(X\) binomial \(B(400,0.2)\) s’aproxima per mitjà d’una variable \(Y\) normal \(N(400\cdot 0.2,\sqrt{400\cdot 0.2\cdot 0.8})=N(80,8)\). Vegem amb alguns exemples que aquesta aproximació és millor aplicant-hi la correcció de continuïtat:

• \(F_X(70)=P(X\leqslant 70)\):

pbinom(70,400,0.2)

## [1] 0.1163917

• \(F_Y(70)=P(Y\leqslant 70)\):

pnorm(70,80,8)

## [1] 0.1056498

• La correcció de continuïtat ens diu que és millor aproximar \(P(X\leqslant 70)\) per mitjà de \(P(Y< 70+1/2)\):

pnorm(70.5,80,8)

## [1] 0.1175152

• \(f_X(70)=P(X=70)\):

dbinom(70,400,0.2) 

## [1] 0.02338443

• \(f_Y(70)\) (que no és \(P(Y=70)\)):

dnorm(70,80,8) 

## [1] 0.02283114

• La correcció de continuïtat ens diu que és millor aproximar \(P(X=70)\) per mitjà de \(P(70-1/2<Y< 70+1/2)\):

pnorm(70.5,80,8)-pnorm(69.5,80,8)

## [1] 0.02283949

Exemple 2.12 La pressió sistòlica, mesurada en mm Hg, es distribueix com una variable normal amb valor mitjà i desviació típica que depenen del sexe i l’edat. Per a la franja d’edat 16-24 anys, aquests valors (s’estima que) són:

• Per a homes, \(\mu=124\) i \(\sigma=13.7\)
• Per a dones, \(\mu=117\) i \(\sigma=13.7\)

El model d’hipertensió-hipotensió acceptat és el descrit en la Figura 2.7. Volem calcular els límits de cada classe per a cada sexe en aquest grup d’edat.

Figura 2.7: Model d’hipertensió-hipotensió.

Vegem:

• El límit superior del grup d’hipotensió serà el valor que deixa a l’esquerra un 5% de les tensions: el 0.05-quantil de la distribució.
• El límit superior del grup de risc d’hipotensió serà el valor que deixa a l’esquerra un 10% de les tensions: el 0.1-quantil de la distribució.
• El límit inferior del grup de risc d’hipertensió serà el valor que deixa a l’esquerra un 90% de les tensions: el 0.9-quantil de la distribució.
• El límit inferior del grup d’hipertensió serà el valor que deixa a l’esquerra un 95% de les tensions: el 0.95-quantil de la distribució.

En els homes, la tensió sistòlica és una variable aleatòria \(N(124,13.7)\). Aleshores, aquests quantils són:

• El 0.05-quantil:

round(qnorm(0.05,124,13.7),1)

## [1] 101.5

• El 0.1-quantil:

round(qnorm(0.1,124,13.7),1)

## [1] 106.4

• El 0.9-quantil:

round(qnorm(0.9,124,13.7),1)

## [1] 141.6

• El 0.95-quantil:

round(qnorm(0.95,124,13.7),1)

## [1] 146.5

En resum, per als homes de 16 a 24 anys tenim els límits de la Taula 2.1.

Taula 2.1: Límits d’hipotensió-hipertensió en homes joves.

Grup	Interval
Hipotens	<101.5
Prehipotens	101.5 a 106.4
Normotens	106.4 a 141.6
Prehipertens	141.6 a 146.5
Hipertens	> 146.5

Calculau els límits per a les dones.

2.5.2 Propietats bàsiques

Ja hem explicat el significat dels paràmetres \(\mu\) i \(\sigma\), però el tornam a repetir:

Si \(X\) és \(N(\mu,\sigma)\), aleshores \(\mu_X=\mu\) i \(\sigma_X=\sigma\).

Una de les propietats clau de la distribució normal és la seva simetria:

Si \(X\) és \(N(\mu,\sigma)\), la seva densitat \(f_X\) és simètrica respecte de \(\mu\), és a dir, \[ f_{X}(\mu-x)=f_{X}(\mu+x), \] i pren el valor màxim a \(x=\mu\). És a dir, \(\mu\) és la moda de \(X\).

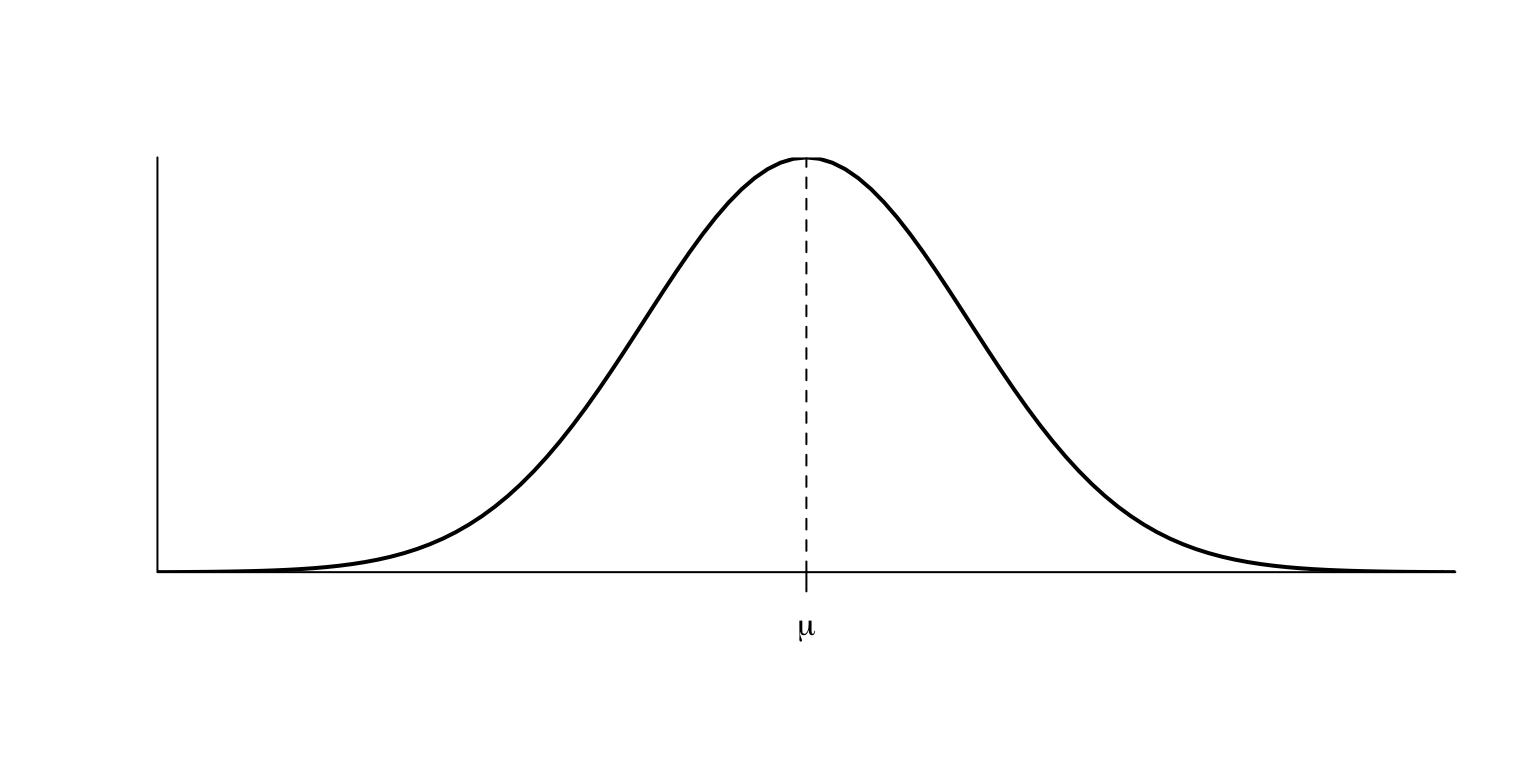
Per tant, el valor al voltant del qual és més probable que una variable normal \(N(\mu,\sigma)\) caigui és justament el seu valor esperat \(\mu\).

En particular, si \(Z\) és \(N(0,1)\), llavors \(f_Z\) és simètrica al voltant de 0, és a dir, \(f_{Z}(-x)=f_{Z}(x)\), i la moda de \(Z\) és \(x=0\).

Recordau que la funció de distribució d’una variable aleatòria contínua \(X\), \[ F_X(x)=P(X\leqslant x) \] és l’àrea compresa entre la densitat \(y=f_X(x)\) i l’eix d’abscisses a l’esquerra de \(x\).

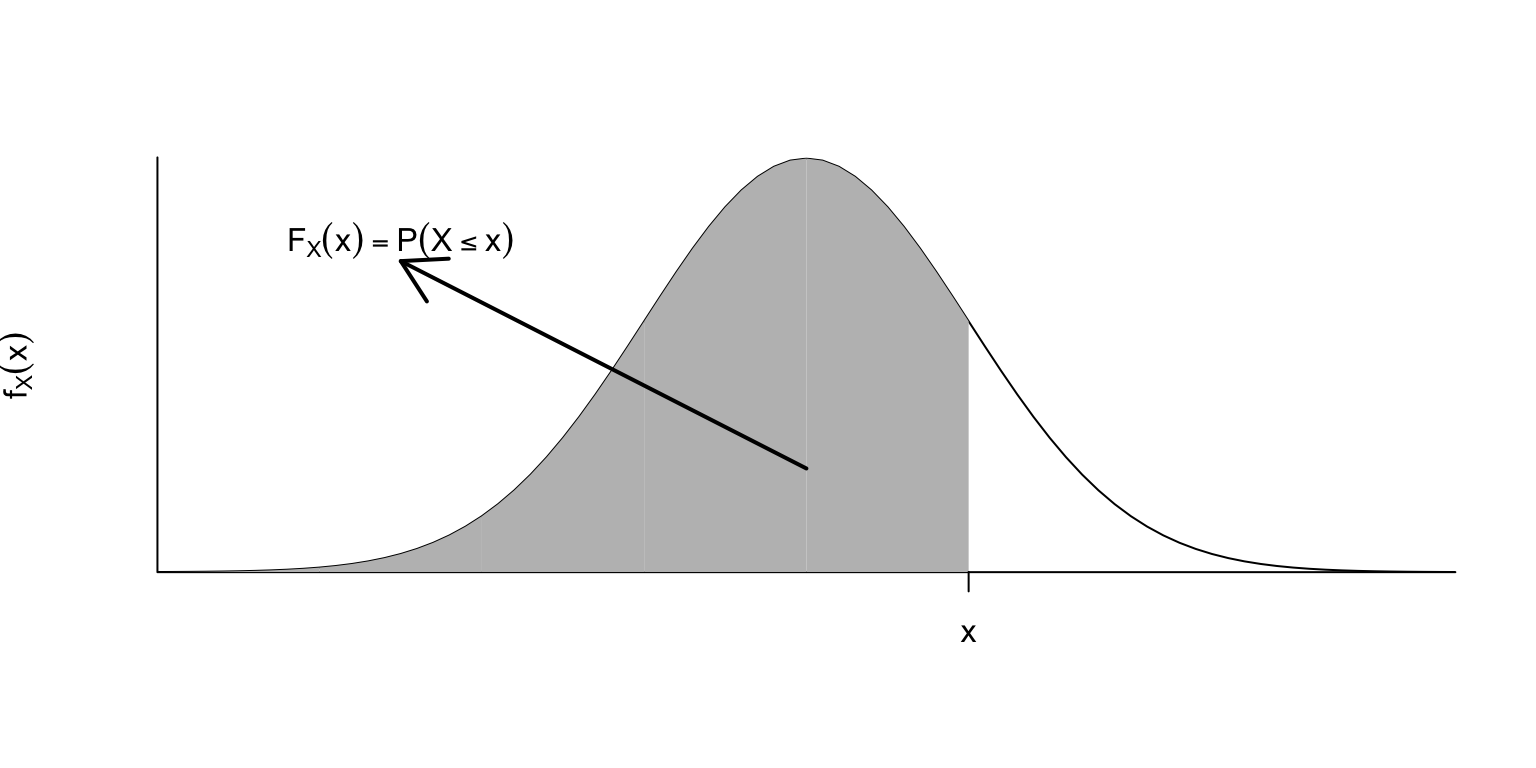
Llavors, la simetria de \(f_X\) fa que, per a tot \(x\geqslant 0\), les àrees davall de la densitat a l’esquerra de \(\mu-x\) i a la dreta de \(\mu+x\) siguin iguals.

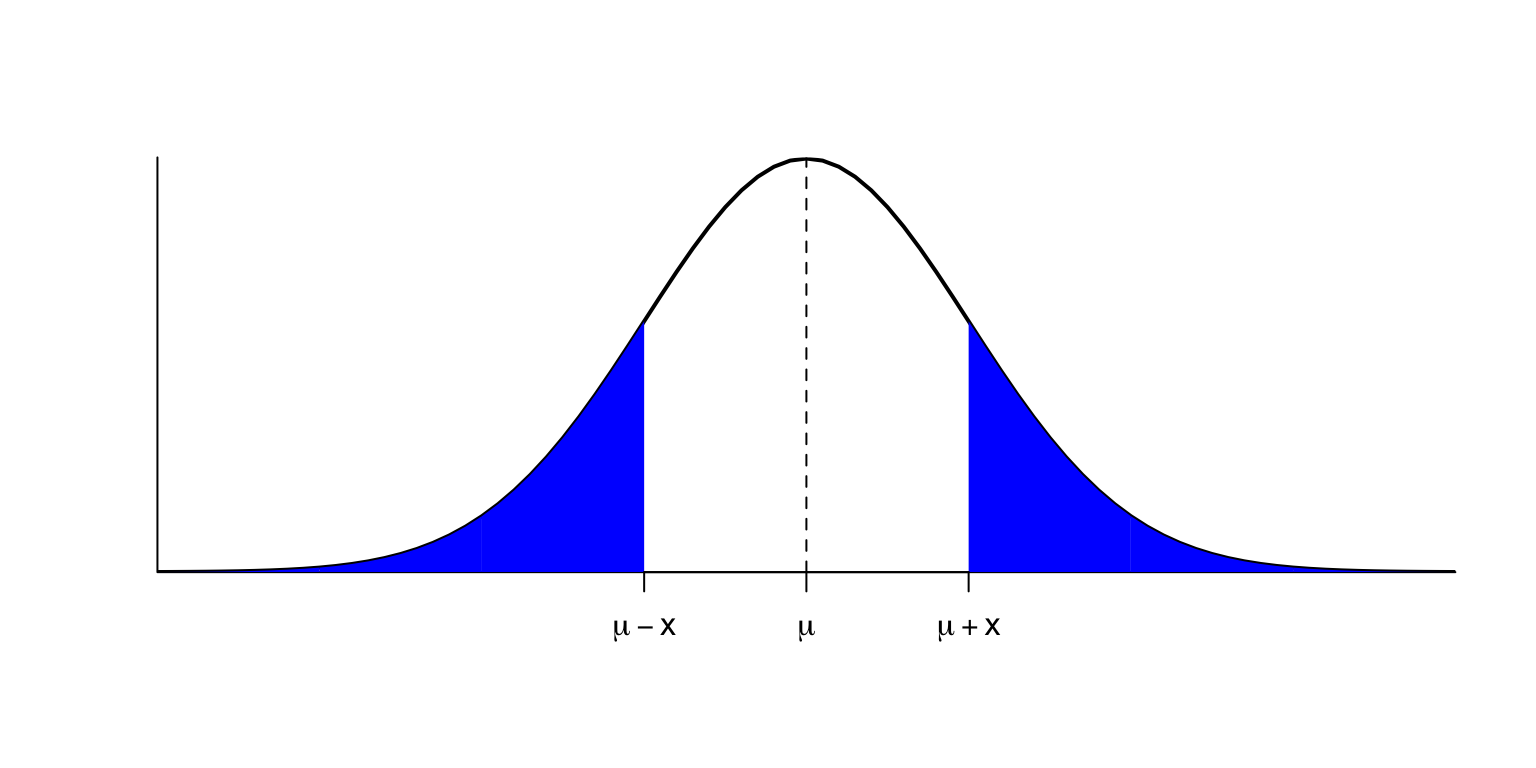
És a dir, \[ P(X\leqslant \mu-x)=P(X\geqslant \mu+x)=1-P(X\leqslant \mu+x) \]

En particular (prenent \(x=0\)) \[ P(X\leqslant \mu)=1-P(X\leqslant \mu)\Rightarrow P(X\leqslant \mu)=0.5 \] i per tant, \(\mu\) és també la mediana de \(X\).

Si \(X\) és \(N(\mu,\sigma)\), \(\mu\) és la mitjana, la mediana i la moda de \(X\).

En el cas concret de la normal estàndard \(Z\), per a qualsevol \(z\geqslant 0\) es té que les àrees davall de la densitat a l’esquerra de \(-z\) i a la dreta de \(z\) són iguals \[ P(Z\leqslant -z)=P(Z\geqslant z)=1-P(Z\leqslant z) \] i la mediana de \(Z\) és 0.

Ara que sabem més coses de la normal, a l’Exemple 2.12 ens haguéssim pogut estalviar la meitat de la feina. Diguem \(X\) a la variable aleatòria que ens dóna la pressió arterial, en mm Hg, d’un home d’entre 16 i 24 anys. Ens diuen que \(X\) és \(N(124,13.7)\).

Per la simetria de \(X\) al voltant de \(\mu=124\), si escrivim el 0.05-quantil com \(124-x\), aleshores \(P(X\geqslant 124+x)=P(X\leqslant 124-x)=0.05\) i per tant \(P(X\leqslant 124+x)=1-P(X\geqslant 124+x)=0.95\), és a dir, \(124+x\) serà el 0.95-quantil de \(X\).

El 0.05-quantil ha estat 101.5. Escrivint \(101.5=124-x\), obtenim \(x=22.5\). Per tant, el 0.95-quantil ha de ser \(124+22.5=146.5\).

El mateix passa amb el 0.9-quantil i el 0.1-quantil, raonau-ho i comprovau-ho.

L’argument que hem desenvolupat a la nota anterior mostra en general que si \(X\) és \(N(\mu,\sigma)\), si el seu \(q\)-quantil és \(\mu-x\), aleshores el seu \((1-q)\)-quantil és \(\mu+x\).

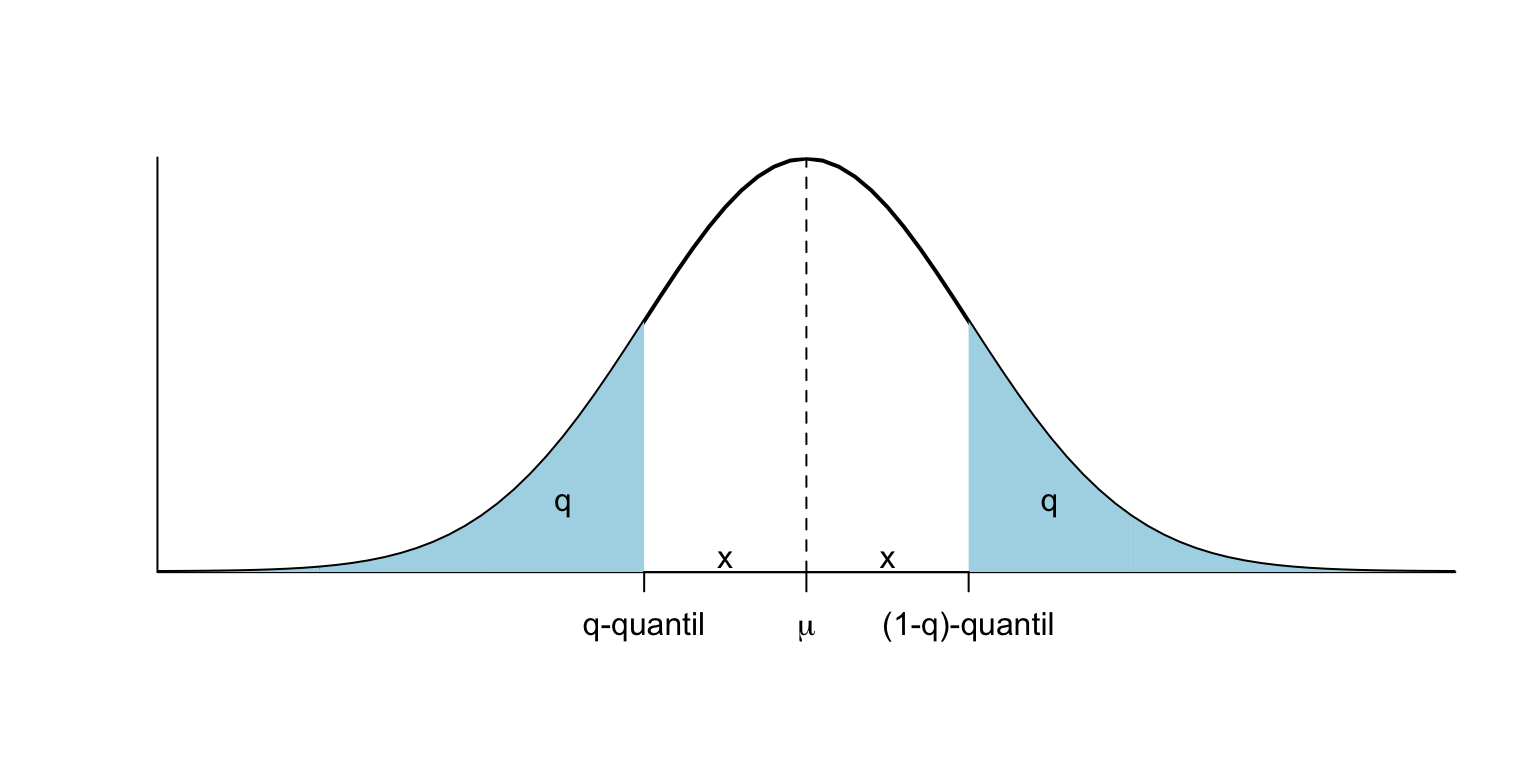
Figura 2.8: Quantils gratis!

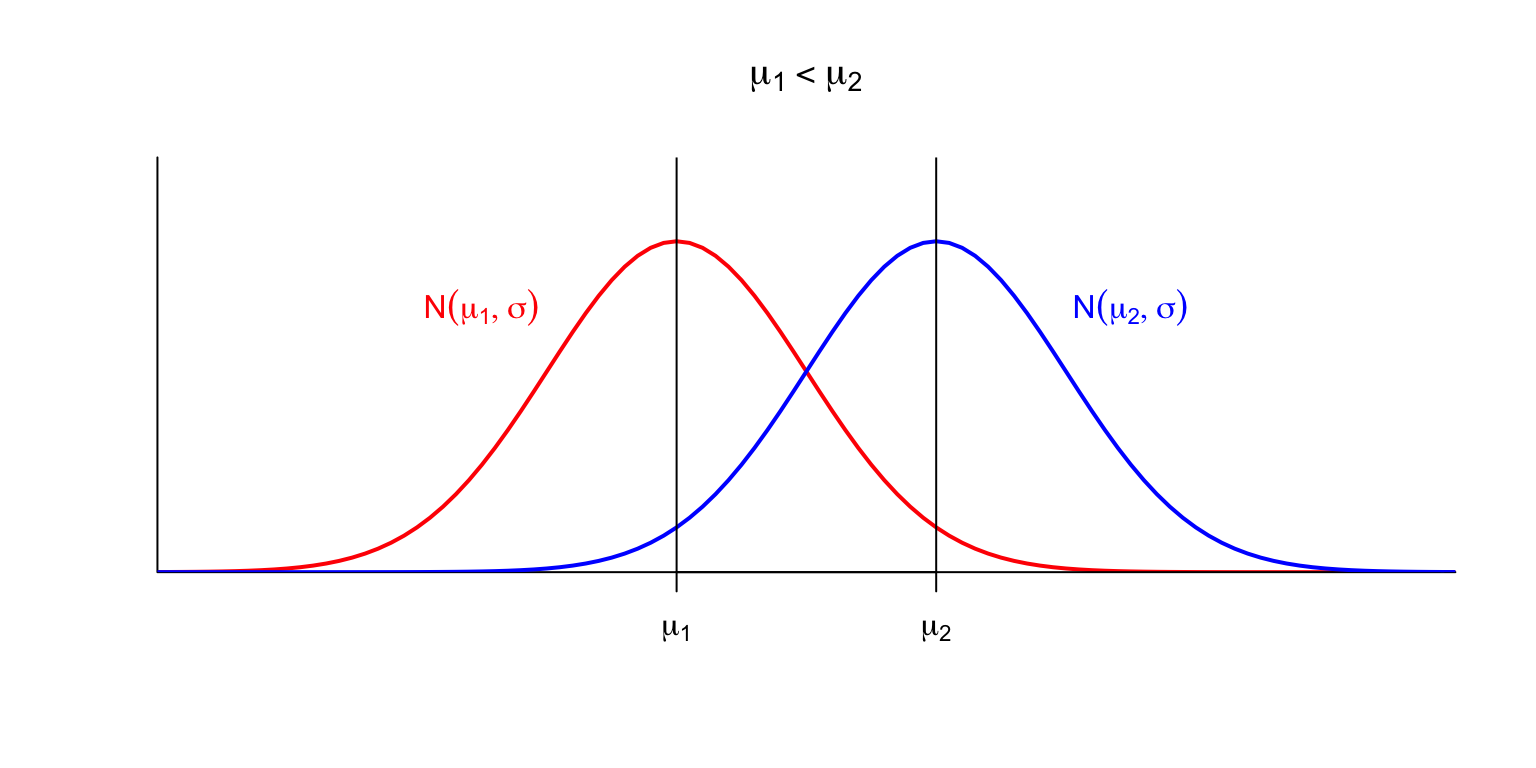
Si \(\mu\) creix, desplaça a la dreta l’eix vertical de simetria de la densitat, i amb ell tota la corba.

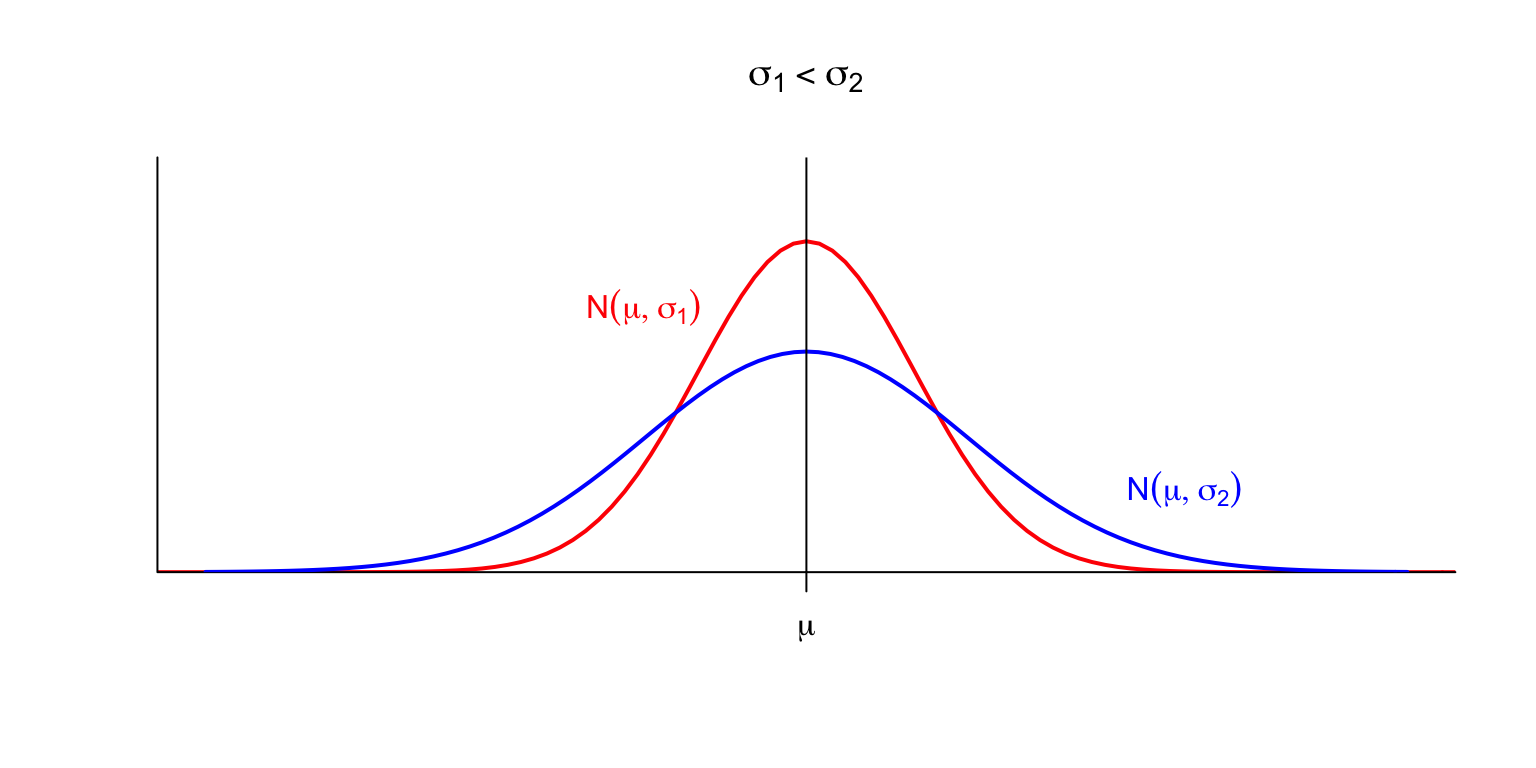
Si la desviació típica \(\sigma\) creix, els valors que pren la variable són més variats i augmenta la probabilitat que prengui valors més llunyans de \(\mu\). Com que l’àrea baix de la corba ha de seguir valent 1, la corba s’aplana.

El gràfic següent mostra l’efecte combinat:

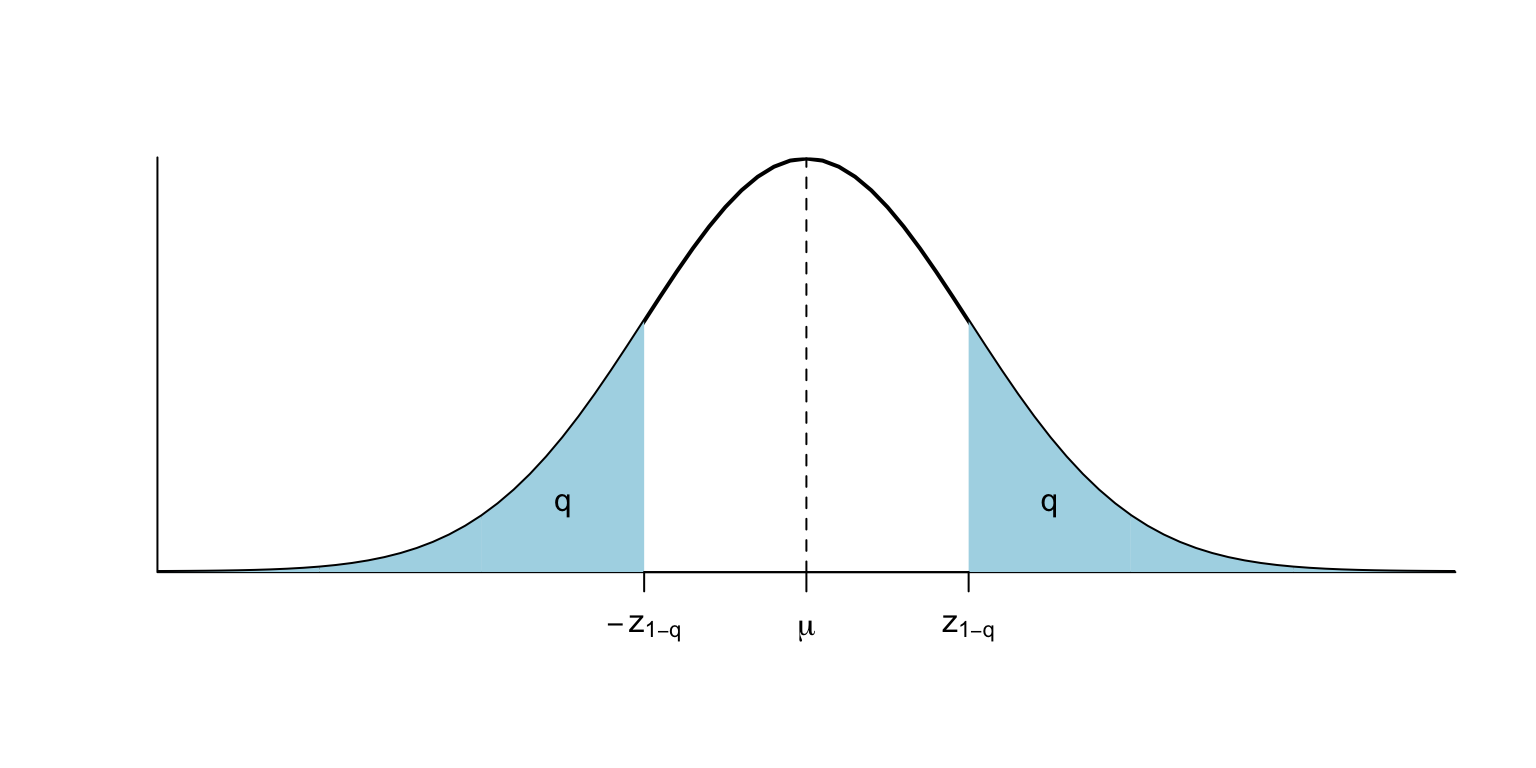
Indicarem amb \(z_q\) el \(q\)-quantil d’una variable normal estàndard \(Z\). És a dir, \(z_q\) és el valor tal que \(P(Z\leqslant z_q)=q\).

A banda del fet que \(z_{0.5}=0\) (la mediana de \(Z\) és 0), hi ha dos quantils més de la normal estàndard \(Z\) que hauríeu de recordar:

• \(z_{0.95}=1.64\); és a dir, \(P(Z\leqslant 1.64)=0.95\) i per tant \(P(Z\leqslant -1.64)=P(Z\geqslant 1.64)=0.05\) (és a dir, \(z_{0.05}=-1.64\)) i \[ P(-1.64\leqslant Z\leqslant 1.64)=0.9. \]

• \(z_{0.975}=1.96\); és a dir, \(P(Z\leqslant 1.96)=0.975\) i per tant \(P(Z\leqslant -1.96)=P(Z\geqslant 1.96)=0.025\) (és a dir, \(z_{0.025}=-1.96\)) i \[ P(-1.96\leqslant Z\leqslant 1.96)=0.95. \]

Molt sovint el valor 1.96 de \(z_{0.975}\) s’aproxima per 2. Teniu permís per a fer-ho quan no disposeu de mitjans (R, aplis de mòbil) per a calcular quantils i us considereu incapaços de recordar “1.96”. Però només en aquest cas.

Pel que hem comentat fa un moment, la simetria de la normal estàndard implica que \(z_{1-q}=-z_{q}\), perquè si \(P(Z\leqslant z_{q})=q\), aleshores \(P(Z\geqslant -z_{q})=q\) i per tant \(P(Z\leqslant -z_{q})=1-q\).

Una de les propietats més útils de la distribució normal és que tota combinació lineal de variables aleatòries normals independents és normal. En concret, tenim els dos resultats següents:

Teorema 2.5 Sigui \(X\) una variable \(N(\mu,\sigma)\).

1. Per a tots \(a,b\in \mathbb{R}\), \(aX+b\) és normal \(N(a\mu+b,|a|\cdot\sigma)\).

2. En particular, la tipificada de \(X\) \[ Z=\dfrac{X-\mu}{\sigma} \] és normal estàndard.

Més en general:

Teorema 2.6 Si \(X_1,\ldots,X_n\) són variables aleatòries normals independents i \(a_1,\ldots,a_n,b\in \mathbb{R}\), llavors \(a_1X_1+\cdots +a_nX_n+b\) és \(N(\mu,\sigma)\) amb \[ \begin{array}{l} \mu=a_1\mu_{X_1}+\cdots +a_n\mu_{X_n}+b\\ \sigma=\sqrt{a_1^2\sigma^2_{X_1}+\cdots +a_n^2\sigma^2_{X_n}} \end{array} \]

Que tota combinació lineal de variables normals independents torni a ser del mateix tipus, és a dir, normal, és una propietat molt útil de les variables normals que poques famílies de distribucions comparteixen. Per exemple, si \(X\) és una variable binomial \(B(n,p)\) amb \(p\neq 0\), la variable \(2X\) no és binomial, perquè només pren valors parells, mentre que una variable binomial \(B(m,q)\) ha de poder prendre tots els valors entre 0 i \(m\). En canvi, si \(X\) és \(N(\mu,\sigma)\), \(2X\) és \(N(2\mu,2\sigma)\).

Les probabilitats de la normal tipificada \(Z\) determinen les de la normal original, perquè si \(X\) és \(N(\mu,\sigma)\): \[ \begin{array}{rl} P(a\leqslant X\leqslant b)\!\!\!\!\! & \displaystyle =P\Big( \frac{a-\mu}{\sigma}\leqslant \frac{X-\mu}{\sigma}\leqslant \frac{b-\mu}{\sigma}\Big)\\ & \displaystyle =P\Big(\frac{a-\mu}{\sigma}\leqslant Z\leqslant \frac{b-\mu}{\sigma}\Big) \end{array} \] Això serveix per deduir fórmules o resoldre problemes com el següent, i els vostres pares ho empraven per calcular probabilitats de normals (amb taules de probabilitats de la normal estàndard), però ara és més còmode usar una apli.

Exemple 2.13 Les alçades de les nordamericanes de 20 anys segueixen una distribució normal. S’ha estimat que un 10% d’elles fan menys de 1.55 m, i un 30.5% fan menys de 1.60 m. Per a quina alçada \(h\) es té que un 95% de les nordamericanes de 18 anys fan menys de \(h\) metres?

Diguem \(X\) a la variable “Prenc una nord americana de 20 anys i mesur la seva alçada en m”. Sabem que és \(N(\mu,\sigma)\), però desconeixem \(\mu\) i \(\sigma\).

Ens diuen que \[ P(X< 1.55)=0.1,\ P(X< 1.60)=0.305 \] i amb això volem calcular la \(h\) tal que \(P(X\leqslant h)=0.95\), és a dir, el 0.95-quantil de \(X\). El que farem serà, tipificant la \(X\), traduir la informació que ens han donat a quantils d’una normal estàndard \(Z\): \[ \begin{array}{l} \displaystyle 0.1=P(X< 1.55)=P\Big(\frac{X-\mu}{\sigma}<\frac{1.55-\mu}{\sigma}\Big)=P\Big(Z<\frac{1.55-\mu}{\sigma}\Big)\\ \displaystyle \qquad \Longrightarrow \frac{1.55-\mu}{\sigma}=z_{0.1}\\ \displaystyle 0.305=P(X< 1.6)=P\Big(\frac{X-\mu}{\sigma}<\frac{1.6-\mu}{\sigma}\Big)=P\Big(Z<\frac{1.6-\mu}{\sigma}\Big)\\ \displaystyle \qquad \Longrightarrow \frac{1.6-\mu}{\sigma}=z_{0.305} \end{array} \] Ara podem calcular aquests dos quantils \(z_{0.1}\) i \(z_{0.305}\):

qnorm(0.1)

## [1] -1.281552

qnorm(0.305)

## [1] -0.5100735

Obtenim d’aquesta manera el sistema d’equacions lineals \[ \left. \begin{array}{ll} 1.55-\mu=-1.282\sigma\\ 1.6-\mu=-0.51\sigma \end{array}\right\} \] El resolem i obtenim \[ \mu=1.633,\ \sigma=0.065 \] I ara ja podem calcular la \(h\) com el 0.95-quantil d’una \(N(1.633,0.065)\):

qnorm(0.95,1.633,0.065)

## [1] 1.739915

Concloem que un 95% de les nord americanes de 20 anys fan menys de 1.74 m.

2.5.3 Intervals de referència

Un interval de referència del Q% per a una variable aleatòria contínua \(X\) és un interval \([a,b]\) tal que \[ P(a\leqslant X\leqslant b)=\frac{Q}{100}. \] És a dir, un interval de referència del Q% per a \(X\) és un interval que conté els valors de \(X\) del Q% dels subjectes de la població.

Per exemple, hem vist en la secció anterior que [-1.64,1.64] i [-1.96,1.96] són intervals de referència del 90% i del 95%, respectivament, per a una variable normal estàndard \(Z\).

Els més comuns són els intervals de referència del 95%, que satisfan que \[ P(a\leqslant X\leqslant b)=0.95 \] i són els, que per exemple, us donen com a valors de referència en les analítiques:

Quan es parla d’un interval de referència sense donar la probabilitat, se sobreentén sempre que és l’interval de referència del 95%.

Quan \(X\) és \(N(\mu,\sigma)\), aquests intervals de referència es prenen sempre centrats en la mitjana \(\mu\), és a dir, de la forma \[ [\mu-\text{alguna cosa},\mu+\text{aquesta mateixa cosa}]. \] Es calculen amb el resultat següent:

Teorema 2.7 Si \(X\) és \(N(\mu,\sigma)\), un interval de referència del Q% per a \(X\) és \[ [\mu- z_{(1+q)/2}\cdot \sigma, \mu+ z_{(1+q)/2}\cdot \sigma] \] on \(q=Q/100\) i \(z_{(1+q)/2}\) és el \((1+q)/2\)-quantil de la normal estàndard \(Z\). Normalment escriurem aquest interval \[ \mu\pm z_{(1+q)/2}\cdot \sigma. \]

La demostració és un exemple d’ús de la tipificació de la normal: \[ \begin{array}{l} P(\mu-x\leqslant X\leqslant \mu+x)=q\\ \qquad \Longleftrightarrow \displaystyle P\Big(\frac{\mu-x-\mu}{\sigma}\leqslant \frac{X-\mu}{\sigma}\leqslant \frac{\mu+x-\mu}{\sigma}\Big)=q\\ \qquad \Longleftrightarrow \displaystyle P(-x/{\sigma}\leqslant Z\leqslant {x}/{\sigma})=q\\ \qquad \Longleftrightarrow \displaystyle P(Z\leqslant {x}/{\sigma})-P(Z\leqslant -{x}/{\sigma})=q\\ \qquad \Longleftrightarrow \displaystyle P(Z\leqslant {x}/{\sigma})-(1-P(Z\leqslant {x}/{\sigma}))=q\\ \qquad \text{(per la simetria de $f_Z$ al voltant de 0)}\\ \qquad \Longleftrightarrow \displaystyle 2P(Z\leqslant {x}/{\sigma})=q+1\\ \qquad \Longleftrightarrow P(Z\leqslant {x}/{\sigma})=(1+q)/2\\ \qquad \Longleftrightarrow x/\sigma= z_{(1+q)/2}\\ \qquad \Longleftrightarrow x=z_{(1+q)/2}\cdot \sigma \end{array} \]

Si \(q=0.95\), llavors \((1+q)/2=0.975\) i \(z_{0.975}=1.96\). Per tant, l’interval de referència del 95% per a una variable \(X\) normal \(N(\mu,\sigma)\) és \[ \mu\pm 1.96\sigma. \] I com que aquest 1.96 sovint s’aproxima per 2, l’interval de referència del 95% d’una \(N(\mu,\sigma)\) se sol simplificar a \[ \mu\pm 2\sigma. \] Això diu, bàsicament, que

Si una variable aleatòria definida sobre una població segueix una distribució normal \(N(\mu,\sigma)\), un 95% dels seus individus tenen el seu valor de \(X\) a distància com a màxim \(2\sigma\) (“a dues sigmes”) de \(\mu\).

Exemple 2.14 Segons l’OMS, les altures (en cm) de les dones europees de 18 anys segueixen una llei \(N(163.1,18.53)\). Quin és l’interval d’altures centrat en la mitjana que conté a la meitat de les europees de 18 anys?

Fixau-vos que, si diem \(X\) a la variable aleatòria “Altura d’una dona europea de 18 anys en cm”, el que volem saber és l’interval centrat en la seva mitjana, 163.1, tal que la probabilitat que l’alçada d’una europea de 18 anys triada a l’atzar pertanyi a aquest interval sigui 0.5. És a dir, l’interval de referència del 50% per a \(X\).

Ens diuen que \(X\) és \(N(163.1,18.53)\). Si \(q=0.5\), llavors \((1+q)/2=0.75\). El 0.75-quantil \(z_{0.75}\) d’una normal estàndard és

qnorm(0.75)

## [1] 0.6744898

Per tant, l’interval de referència demanat és \(163.1\pm 0.6745\cdot 18.53\), és a dir, arrodonint a mm, \([150.6, 175.6]\). Això ens diu que la meitat de les dones europees de 18 anys fan entre 150.6 i 175.6 cm.

El z-score d’un valor \(x_0\in \mathbb{R}\) respecte d’una distribució \(N(\mu,\sigma)\) és \[ \frac{x_0-\mu}{\sigma} \]

És a dir, el z-score de \(x_0\) és el resultat de “tipificar” \(x_0\) en el sentit del Teorema 2.5.2.

Si la variable poblacional és normal, com més gran és el valor absolut del z-score de \(x_0\), més “rar” és \(x_0\); el signe ens diu si és més gran o més petit que el valor esperat \(\mu\).

Exemple 2.15 Recordau que, segons l’OMS, les altures de les dones europees de 18 anys segueixen una llei \(N(163.1,18.53)\). Quin seria el z-score d’una jugadora de bàsquet de 18 anys que fes 191 cm?

Seria \[ \frac{191-163.1}{18.53}=1.5 \]

Això se sol llegir dient que l’alçada d’aquesta jugadora està 1.5 sigmes per sobre de l’alçada mitjana.

2.5.4 Variables log-normals

Direm que \(X\) és una variable log-normal quan el seu logaritme neperià \(\ln(X)\) és una variable normal. O, si ho preferiu, quan és una variable de la forma \(e^Y\) amb \(Y\) normal. Moltes concentracions d’enzims o anticossos tenen distribucions aproximadament log-normals.

Si \(a>1\), \(\log_a(X)=\ln(X)/\ln(a)\) i per tant, pel Teorema 2.5.1, les tres afirmacions següents són equivalents:

1. \(X\) és log-normal
2. \(\log_a(X)\) és normal, per a qualque base \(a>1\).
3. \(\log_a(X)\) és normal per a tota base \(a>1\).

La densitat d’una variable log-normal és asimètrica, amb una cua a la dreta, com mostra la Figura 2.9.

Figura 2.9: Densitat de \(e^Z\) amb \(Z\) normal estàndard.

Recíprocament, molt sovint una variable la densitat de la qual mostri una pujada ràpida des del 0 a la moda i després una cua a la dreta, satisfà que el seu logaritme segueix una distribució aproximadament normal. Això ens serà útil més endavant.

Amb R, la distribució log-normal és lnorm. Els paràmetres que s’empren per descriure-la són els de la variable normal definida pel seu logaritme:

• La mitjana en escala logarítmica de \(X\): \(\mu_{\ln(X)}\)

• La desviació típica en escala logarítmica de \(X\): \(\sigma_{\ln(X)}\)

Exemple 2.16 La dosi letal \(Y\) de la digitalina en ratolins (és la dir, la variable aleatòria que dóna la quantitat de digitalina que cal administrar a un ratolí per matar-lo) té distribució log-normal. Se sap que una injecció de 1cc de digitalina mata un 10% dels ratolins (és a dir, que la probabilitat que una dosi de 1cc o menys mati un ratolí és de 0.1: \(P(Y\leqslant 1)=0.1\)) i que una injecció de 2cc mata un 75% dels ratolins (\(P(Y\leqslant 2)=0.75\)).

Volem saber la dosi de digitalina (en cc) que és letal per al 95% dels ratolins. Aquest tipus d’experiments és la base de l’anomenat mètode probit per determinar la letalitat de substàncies.

Així doncs, volem calcular el valor \(a\) tal que \(P(Y\leqslant a)=0.95\), que no és res més que el 0.95-quantil de \(Y\).

Com que el logaritme és injectiu, \(P(Y\leqslant x)=P(\ln(Y)\leqslant \ln(x))\). Per tant el pla és trobar el 0.95-quantil de \(\ln(Y)\), diguem-li \(b\), i aleshores tendrem \(a=e^b\).

Per simplificar, diguem \(X\) a \(\ln(Y)\). Sabem que \(X\) és normal, per tant només ens cal saber la seva \(\mu\) i la seva \(\sigma\) i podrem calcular el seu 0.95-quantil.

El que sabem és que \[ \begin{array}{l} 0.1=P(Y\leqslant 1)=P(X\leqslant \ln(1))=P(X\leqslant 0)\\ 0.75=P(Y\leqslant 2)=P(X\leqslant \ln(2)) \end{array} \] Com podem determinar la \(\mu\) i la \(\sigma\) de \(X\) a partir d’aquests dos valors? Ja ens hem trobat en una situació semblant a l’Exemple 2.13. El que fem és traduir aquesta informació en termes de quantils de la normal estàndard.

\[ \begin{array}{l} \displaystyle 0.1=P(X\leqslant 0)=P\Big(\frac{X-\mu}{\sigma}\leqslant \frac{-\mu}{\sigma}\Big)=P\Big(Z\leqslant -\frac{\mu}{\sigma}\Big)\\ \displaystyle\qquad \Longrightarrow -\frac{\mu}{\sigma}=z_{0.1}=\texttt{qnorm(0.1)}=-1.2816\\ \displaystyle 0.75=P(X\leqslant \ln(2))=P\Big(\frac{X-\mu}{\sigma}\leqslant \frac{\ln(2)-\mu}{\sigma}\Big)=P\Big(Z\leqslant \frac{\ln(2)-\mu}{\sigma}\Big)\\ \displaystyle\qquad \Longrightarrow \frac{\ln(2)-\mu}{\sigma}=z_{0.75}=\texttt{qnorm(0.75)}=0.6745 \end{array} \] Obtenim el sistema d’equacions \[ \left. \begin{array}{l} \mu=1.2816\sigma\\ \ln(2)-\mu=0.6745\sigma \end{array} \right\} \] i resolent-lo obtenim \[ \mu=0.4541,\quad \sigma=0.3544 \]

Ara podem calcular el 0.95-quantil de \(X\):

qnorm(0.95,0.4541,0.3544)

## [1] 1.037036

Per tant \(P(X\leqslant 1.037)=0.95\). D’aquí deduïm que \(P(Y\leqslant e^{1.037})=0.95\). Com que \(e^{1.037}=2.82\), concloem que 2.82 cc de digitalina són letals pel 95% dels ratolins.

Ho podem comprovar (amb R, no escabetxant ratolins, malpensats!):

plnorm(2.82,0.4541,0.3544)

## [1] 0.9499129

2.6 Test de la lliçó 2

(1) Sigui \(X\) una variable aleatòria de mitjana \(\mu\) i desviació típica \(\sigma\). Quina o quines de les afirmacions següents són sempre vertaderes?

1. \(E(X+2)=\mu+2\).
2. \(\sigma(X+2)=\sigma+2\).
3. \(\sigma(-X)=-\sigma\).
4. \(\sigma(-X)=\sigma\).
5. \(\sigma(X/2)=\sigma/2\).
6. Cap de les altres afirmacions és vertadera.

(2) La funció de distribució \(F_X(x)\) d’una variable aleatòria \(X\) ens dóna:

1. La probabilitat d’obtenir el valor \(x\).
2. La probabilitat d’obtenir un valor entre \(-x\) i \(x\), tots dos extrems inclosos.
3. La probabilitat d’obtenir un valor entre 0 i \(x\), tots dos extrems inclosos.
4. La probabilitat d’obtenir un valor més petit o igual que \(x\).
5. La probabilitat d’obtenir un valor estrictament més petit que \(x\).

(3) Quina o quines de les variables següents tenen distribució binomial?

1. El pes d’una persona triada a l’atzar.
2. Llançam un dau cúbic, llançam una moneda el nombre de vegades que ens hagi sortit al dau, i comptam el nombre de cares.
3. El nombre de glòbuls vermells en 1 mm³ de sang.
4. La proporció d’hipertensos en una mostra aleatòria de 50 individus.
5. Triam 10 estudiants diferents en una classe de 20, i comptam quantes dones han sortit.
6. Triam un grup d’estudiants en una classe de 100, permetent repeticions, i comptam quantes dones han sortit.
7. Cap d’elles.

(4) Quina o quines de les variables següents tenen una distribució de Poisson?

1. El pes d’una persona.
2. El nombre de casos diaris de COVID-19 a Mallorca.
3. El nombre de glòbuls vermells en 1 mm³ de sang.
4. La proporció d’hipertensos en una mostra aleatòria de 50 individus.
5. Triam 10 estudiants diferents en una classe de 20, i comptam quantes dones han sortit.
6. Cap d’elles.

(5) El nombre anual d’accidents laborals d’un tipus concret segueix una distribució de Poisson. Al llarg del temps s’ha observat que el 55% dels anys no es produeix cap accident d’aquests. Quin valor estimes que té el paràmetre \(\lambda\) d’aquesta distribució de Poisson?

1. 0.55
2. \(e^{-0.55}\)
3. \(\ln(0.55)\)
4. \(-\ln(0.55)\)
5. Un valor que no és cap dels proposats en les altres respostes.

(6) Sigui \(X\) una variable aleatòria contínua de funció de densitat: \[ f_X(x)=\left\{\begin{array}{ll} 0 & \mbox{si $x<0$}\\ \frac{2\sqrt{2}}{\sqrt{\pi}} e^{-2x^2} & \mbox{si $x\geqslant 0$} \end{array} \right. \] És cert que \(P(X=1)=2\sqrt{2}e^{-2}/\sqrt{\pi}\)?

1. Sí
2. No: en realitat \(P(X=1)=\int_{-\infty}^1 \frac{2\sqrt{2}}{\sqrt{\pi}} e^{-2x^2}\,dx\) però no sé calcular aquesta integral, o sí que sé calcular-la, però em fa mandra fer-ho.
3. Això no és la funció de densitat d’una variable aleatòria contínua, perquè no és una funció contínua (en el 0 bota de 0 a \(2\sqrt{2}/\sqrt{\pi}\))
4. Totes les altres respostes són incorrectes

(7) Sigui \(X\) una variable aleatòria contínua de mitjana \(\mu\). Què val \(P(X=\mu)\)?

1. 0.5
2. \(\mu\)
3. 0
4. Depèn de la variable aleatòria
5. Totes les altres respostes són falses

(8) Sigui \(X\) una variable aleatòria contínua de moda \(M\). Què val \(P(X=M)\)?

1. 1
2. 0.5
3. 0
4. Depèn de la variable aleatòria, però és estrictament més gran que tots els altres valors de \(P(X=x)\)
5. Depèn de la variable aleatòria, però és el valor màxim de la funció de densitat de \(X\).
6. Totes les altres respostes són falses

(9) Sigui \(Z\) una variable aleatòria normal estàndard. Marca les afirmacions vertaderes.

1. És asimètrica a l’esquerra.
2. La seva mitjana és 1.
3. La seva desviació típica és 0.
4. La seva variància és 1.
5. La seva mediana és 0.

(10) Sigui \(X\) una variable aleatòria \(N(\mu,\sigma)\) i \(f_X\) la seva funció de densitat. Què val l’àrea entre la corba \(y=f_X(x)\) i l’eix d’abscisses?

1. 0
2. \(\mu\)
3. \(\sigma\)
4. En general, no és ni \(\mu\) ni \(\sigma\), però sí que depèn de \(\mu\) i \(\sigma\)
5. Totes les altres respostes són falses

(11) Siguin \(X\) una variable aleatòria \(N(\mu,\sigma)\). Quina de les afirmacions següents és vertadera?

1. \(\mu\) és la mitjana de \(X\), però no la seva mediana
2. \(\mu\) és la mitjana i la mediana de \(X\), però no la seva moda
3. \(\mu\) és la mitjana, la mediana i la moda de \(X\), però no és veritat que \(P(X=\mu)>P(X=a)\) per a tot \(a\neq \mu\)
4. \(\mu\) és la mitjana, la mediana i la moda de \(X\) i \(P(X=\mu)>P(X=a)\) per a tot \(a\neq \mu\)
5. Totes les altres respostes són falses

(12) El FME (Flux Màxim d’Expiració) de les al·lotes d’11 anys segueix una distribució aproximadament normal de mitjana 300 l/min i desviació típica 20 l/min. Marca les afirmacions vertaderes:

1. Aproximadament la meitat de les al·lotes d’11 anys tenen el FME entre 280 l/min i 320 l/min.
2. Al voltant del 95% de les al·lotes d’11 anys tenen el FME entre 280 l/min i 320 l/min.
3. Al voltant del 95% de les al·lotes d’11 anys tenen el FME entre 260 l/min i 340 l/min.
4. Al voltant del 5% de les al·lotes d’11 anys tenen el FME inferior a 260 l/min.
5. Cap al·lota d’11 anys té el FME superior a 360 l/min.

(13) Se sap que una variable bioquímica té mitjana 90 i desviació típica 10. Si prenem una mostra d’individus sans, és raonable esperar que aproximadament el 95% d’ells tenguin un valor d’aquesta variable comprès entre 70 i 110? (marca totes les respostes correctes):

1. Sí, sempre.
2. No, mai.
3. Si la variable té distribució normal, sí.
4. Si la mostra és prou gran, sí.
5. Si la variable té distribució normal i la mostra és prou gran, sí.

(14) En una variable aleatòria contínua, la seva funció de densitat (marca una sola resposta):

1. És sempre contínua
2. Mesura com és de dens el seu domini.
3. Aplicada a un nombre real, ens dóna la probabilitat d’obtenir-lo.
4. Aplicada a un nombre real, ens dóna la probabilitat d’obtenir un valor menor o igual que ell.
5. Totes les altres respostes són falses

(15) Sigui \(X\) una variable aleatòria contínua de desviació típica \(\sigma\). Què val la variància de la variable aleatòria \(-X/2\)?

1. \(\sigma(-X/2)^2=-\sigma^2/2\).
2. \(\sigma(-X/2)^2=\sigma^2/2\).
3. \(\sigma(-X/2)^2=-\sigma^2/4\).
4. \(\sigma(-X/2)^2=\sigma^2/4\).
5. Totes les altres respostes són falses

(16) El temps que tarda a produir-se una determinada reacció bioquímica es distribueix segons una variable normal de mitjana 17 segons i desviació típica 3 segons. Sense fer cap càlcul, què podem deduir d’aquesta afirmació? Marca totes les respostes correctes:

1. Tots aquests temps se situen entre 8 i 26 segons.
2. Gairebé tots aquests temps se situen entre 11 i 23 segons.
3. És estrictament més probable que una reacció d’aquestes tardi entre 16 i 18 segons que tardi entre 18 i 20 segons.
4. És estrictament més probable que una reacció d’aquestes tardi entre 18 i 20 segons que tardi entre 16 i 18 segons.
5. És estrictament més probable que una reacció d’aquestes tardi entre 18 i 20 segons que tardi entre 14 i 16 segons.

(17) El temps que tarda a produir-se una determinada reacció bioquímica es distribueix segons una variable normal de mitjana 17 segons i desviació típica 3 segons. Quina és la probabilitat que tardi menys de 17 segons?

1. 0
2. 0.5
3. 1
4. 17/3
5. Cap de les afirmacions anteriors és correcta.

(18) El temps que tarda a produir-se una determinada reacció bioquímica es distribueix segons una variable normal de mitjana 17 segons i desviació típica 3 segons. Quina o quines de les afirmacions següents són vertaderes?

1. Si poguéssim mesurar els temps amb precisió infinita, observaríem que el temps que tarda més sovint és exactament 17 segons.
2. El temps al voltant del qual tarda més sovint és 17 segons.
3. En un 95% de les ocasions tarda aproximadament entre 14 i 20 segons.
4. Tarda més de 20 segons amb la mateixa freqüència amb la qual tarda menys de 14 segons.
5. Tarda més de 20 segons amb la mateixa freqüència amb la qual tarda menys de 20 segons.
6. En un 95% de les ocasions tarda 23 segons o menys.

(19) Quina de les tres afirmacions és vertadera per a les tres distribucions normals de la figura inferior? (\(\sigma_1\), \(\sigma_2\) i \(\sigma_3\) indiquen les desviacions típiques de les corbes 1, 2 i 3, respectivament).

1. \(\sigma_1> \sigma_2> \sigma_3\)
2. \(\sigma_1< \sigma_2< \sigma_3\)
3. \(\sigma_1= \sigma_2= \sigma_3\)
4. Del gràfic no es pot deduir la relació entre les tres desviacions típiques
5. Cap de les altres afirmacions és veritable.

(20) El pes mitjà d’una bossa de patates d’una determinada marca és de 150 grams amb una desviació típica de 5.6 grams. Quin és el z-score d’una bossa que pesa 147 grams (arrodonit a 2 xifres decimals)?

1. -0.54
2. 0.30
3. 0.54
4. 0.70
5. Cap de les respostes anteriors és correcta

(21) Si una variable aleatòria normal té mitjana 18.1 i desviació típica 1.2, què val el seu 3er quartil (arrodonit a una xifra decimal)? (Empra R o una apli per calcular-lo)

1. 18.1
2. 18.9
3. 19.3
4. 20.5
5. Cap de les respostes anteriors és correcta

(23) L’interval de referència (del 95%) de la concentració de creatinina en sèrum de les persones és 0.66-1.09 mg/dl. Què en podem deduir? (Marca només una resposta.)

1. Que la probabilitat que la concentració mitjana de creatinina en sèrum d’una persona estigui entre 0.66 i 1.09 mg/dl és del 95%.

2. Que si prenem una mostra aleatòria de persones i calculam la mitjana de les seves concentracions de creatinina, en un 95% de les ocasions aquesta mitjana estarà entre 0.66 i 1.09 mg/dl.

3. Que un 5% de les persones tenen una concentració de creatinina en sèrum superior a 1.09 mg/dl.

4. Que un 95% de les persones tenen una concentració de creatinina en sèrum entre 0.66 i 1.09 mg/dl.
   

5. Que si prenem una mostra aleatòria de persones, en un 95% de les ocasions tots els valors estaran entre 0.66 i 1.09 mg/dl.

6. Cap de les altres respostes és correcta.

(24) Quin és l’efecte sobre la mitjana, la desviació típica i la mediana d’una variable aleatòria si sumam 1 al seu valor sobre tots els individus de la població?

1. Cap d’aquests paràmetres varia.
2. La mitjana i la mediana canvien, la desviació típica no.
   
3. La mitjana varia, la resta no.
4. La mitjana no varia, la resta sí.
5. Tots tres paràmetres varien.
6. Cap de les altres respostes és correcta.

(25) Sigui \(X\) una variable aleatòria normal amb \(\mu=0\) i \(\sigma\) desconeguda. ¿Quina de les afirmacions següents segur que és FALSA?

1. \(P(X\leqslant 0)=0.5\)
2. \(P(X< 0)=0.5\)
3. \(P(X\leqslant -1)=0.2\)
4. \(P(X\leqslant 1)=0.2\)
5. \(P(X\leqslant 1)=0.8\)

(26) Siguin \(X\) i \(Y\) dues variables aleatòries discretes. Quina o quines de les afirmacions següents són sempre vertaderes?

1. Sempre és cert que \(E(2X+3Y)=2E(X)+3E(Y)\)
2. No sempre és cert que \(E(2X+3Y)=2E(X)+3E(Y)\), però sí que és cert si \(X\) i \(Y\) són independents
3. Sempre és cert que \(\sigma(2X+3Y)^2=2\sigma(X)^2+3\sigma(Y)^2\)
4. No sempre és cert que \(\sigma(2X+3Y)^2=2\sigma(X)^2+3\sigma(Y)^2\), però sí que és cert si \(X\) i \(Y\) són independents
5. Sempre és cert que \(\sigma(2X+3Y)^2=4\sigma(X)^2+9\sigma(Y)^2\)
6. No sempre és cert que \(\sigma(2X+3Y)^2=4\sigma(X)^2+9\sigma(Y)^2\), però sí que és cert si \(X\) i \(Y\) són independents
7. Sempre és cert que \(\sigma(2X+3Y)=2\sigma(X)+3\sigma(Y)\)
8. No sempre és cert que \(\sigma(2X+3Y)=2\sigma(X)+3\sigma(Y)\), però sí que és cert si \(X\) i \(Y\) són independents
9. Cap de les altres afirmacions és vertadera.

(27) Teniu una població amb una proporció \(0<p<1\) d’individus que tenen una certa malaltia. Preneu mostres aleatòries de mida \(n\) de la població i hi comptau quants individus tenen aquesta malaltia. Quina o quines de les afirmacions següents són vertaderes?

1. Si preneu les mostres sense permetre individus repetits, els resultats surten més variats que si les preneu permetent repeticions.
2. Si preneu les mostres sense permetre individus repetits, els resultats surten menys variats que si les preneu permetent repeticions.
3. Si preneu les mostres permetent que hi surtin individus repetits, com més grans preneu les mostres més variats surten els resultats.
4. Si preneu les mostres permetent que hi surtin individus repetits, com més grans preneu les mostres menys variats surten els resultats.
5. Si preneu les mostres sense permetre individus repetits, com més grans preneu les mostres més variats surten els resultats.
6. Si preneu les mostres sense permetre individus repetits, com més grans preneu les mostres menys variats surten els resultats.
7. Cap de les altres afirmacions és vertadera.