Tema 9 Introducció a l’estadística multidimensional

En general, les dades que es recullen en experiments són multidimensionals: mesuram diverses variables aleatòries sobre una mateixa mostra d’individus i organitzam aquesta informació en taules de dades on les fileres representen els individus observats i cada columna correspon a una variable diferent. És a dir, el que fem és avaluar un vector de variables aleatòries (en direm un vector aleatori) sobre els individus d’una població. En aquesta lliçó introduïm alguns conceptes sobre vectors de variables aleatòries i taules multidimensionals de dades quantitatives.

9.1 Poblacions: vectors aleatoris

Un vector aleatori de dimensió $p$ és un vector format per $p$ variables aleatòries \[ \underline{X}=(X_1,X_2,\ldots,X_p). \] Una realització de $\underline{X}$ és un vector $(x_1,\ldots,x_p)$ format pels valors de $X_1,\ldots,X_p$ sobre un individu. Una mostra de $\underline{X}$ és un conjunt de realitzacions. Usualment, organitzam una mostra de $\underline{X}$ per mitjà d’una taula de dades amb les columnes definides per les variables $X_1,\ldots,X_p$ i on cada filera és una realització d’aquestes variables, és a dir, un vector format pels valors de $X_1,\ldots,X_p$ sobre un individu de la mostra.

Exemple 9.1 Si diem $\textit{BMI}$ a la variable aleatòria que dóna l’Índex de Massa Corporal (BMI) d’una persona, $C$ a la variable aleatòria que dóna el nivell de colesterol en mg/dl d’una persona i $E$ a la variable aleatòria que dóna l’edat d’una persona en anys, llavors \[ \underline{X}=(\textit{BMI},C,E) \] és un vector aleatori de dimensió 3. Cada cop que prenem una persona i n’anotam el BMI, el nivell de colesterol i l’edat i organitzam aquestes mesures en aquest ordre en un vector, obtenim una realització d’aquest vector aleatori $\underline{X}$. Llavors,una mostra de $\underline{X}$ serà un conjunt de vectors amb el BMI, el nivell de colesterol i l’edat d’un grup de persones de la població. Per exemple

BMI	C	E
18.3	170	49
24.4	202	39
24.6	215	50
24.4	218	44
22.2	210	40
19.5	210	36

Siguin $\underline{X}=(X_1,X_2,\ldots,X_p)$ un vector aleatori i $\mu_i$ i $\sigma_i$ la mitjana i la desviació típica, respectivament, de cada $X_i$.

El valor esperat, o vector de mitjanes, de $\underline{X}$ és el vector format pels valors esperats, o mitjanes, de les seves components: \[ E(\underline{X})=(\mu_1,\ldots,\mu_p). \] Per abreviar, de vegades indicarem aquest vector simplement amb $\boldsymbol\mu$.
El vector de variàncies de $\underline{X}$ és el vector format per les variàncies de les seves components: \[ \sigma^2(\underline{X})=(\sigma_1^2,\ldots,\sigma_p^2). \]
El vector de desviacions típiques de $\underline{X}$ és el vector format per les desviacions típiques de les seves components: \[ \sigma(\underline{X})=(\sigma_1,\ldots,\sigma_p). \]

9.1.1 Covariància

La covariància de dues variables $X$ i $Y$ és una mesura del seu comportament conjunt. Formalment, donades dues variables aleatòries $X,Y$ de mitjanes $\mu_X$ i $\mu_Y$, respectivament, la seva covariància és \[ \sigma_{X,Y}=E((X-\mu_X)\cdot ( Y-\mu_Y)). \] És fàcil comprovar que \[ \sigma_{X,Y}=E(X\cdot Y) -\mu_X\cdot \mu_Y. \]

En efecte, \[ \begin{array}{rl} \sigma_{X,Y} & =E((X-\mu_X) ( Y-\mu_Y))= E(XY-\mu_XY-\mu_YX+\mu_X\mu_Y)\\ & =E(XY)-\mu_XE(Y)-\mu_YE(X)+\mu_X\mu_Y\\ &= E(XY)-\mu_X\mu_Y-\mu_Y\mu_X+\mu_X\mu_Y =E(XY)-\mu_X\mu_Y \end{array} \]

La covariància de $X$ i $Y$ pot prendre qualsevol valor real (no com la variància, que sempre és positiva), i mesura el grau de variació conjunta de les variables en el sentit següent:

$\sigma_{X,Y}>0$ significa que quan $X$ és més gran en un individu 1 que en un individu 2, $Y$ tendeix a també ser més gran en l’individu 1 que en l’individu 2.

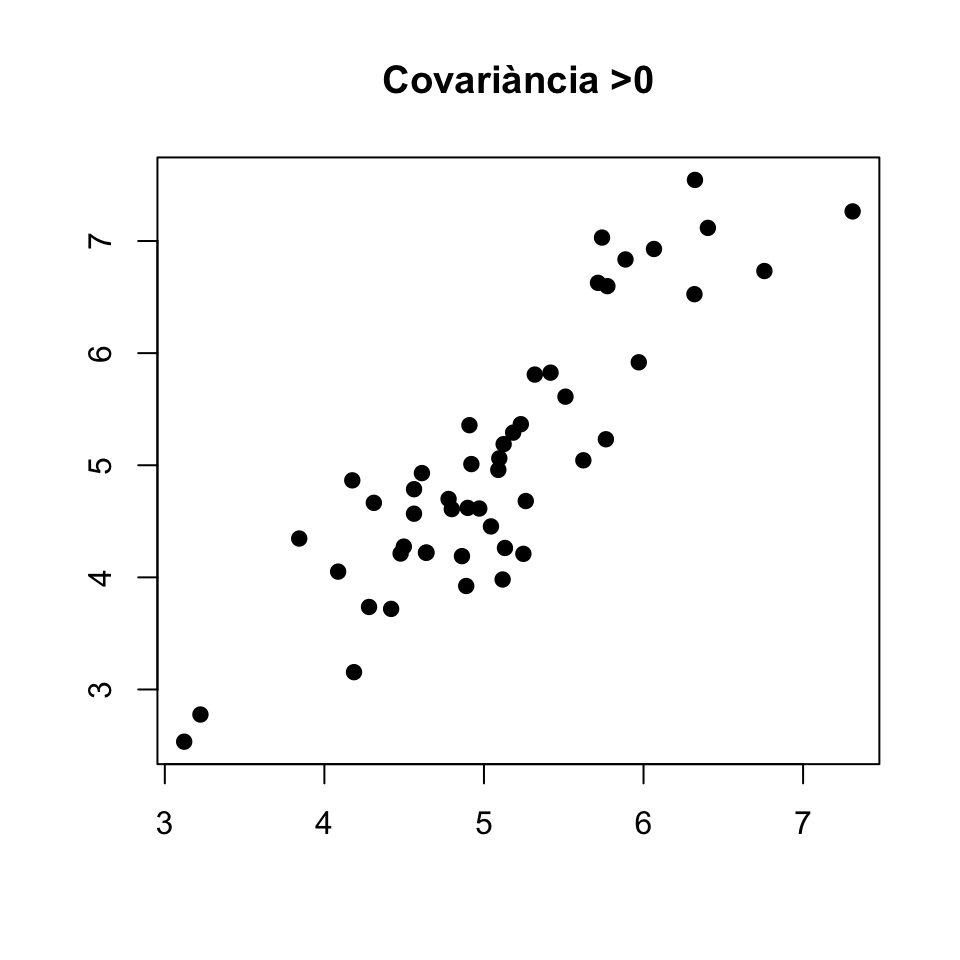
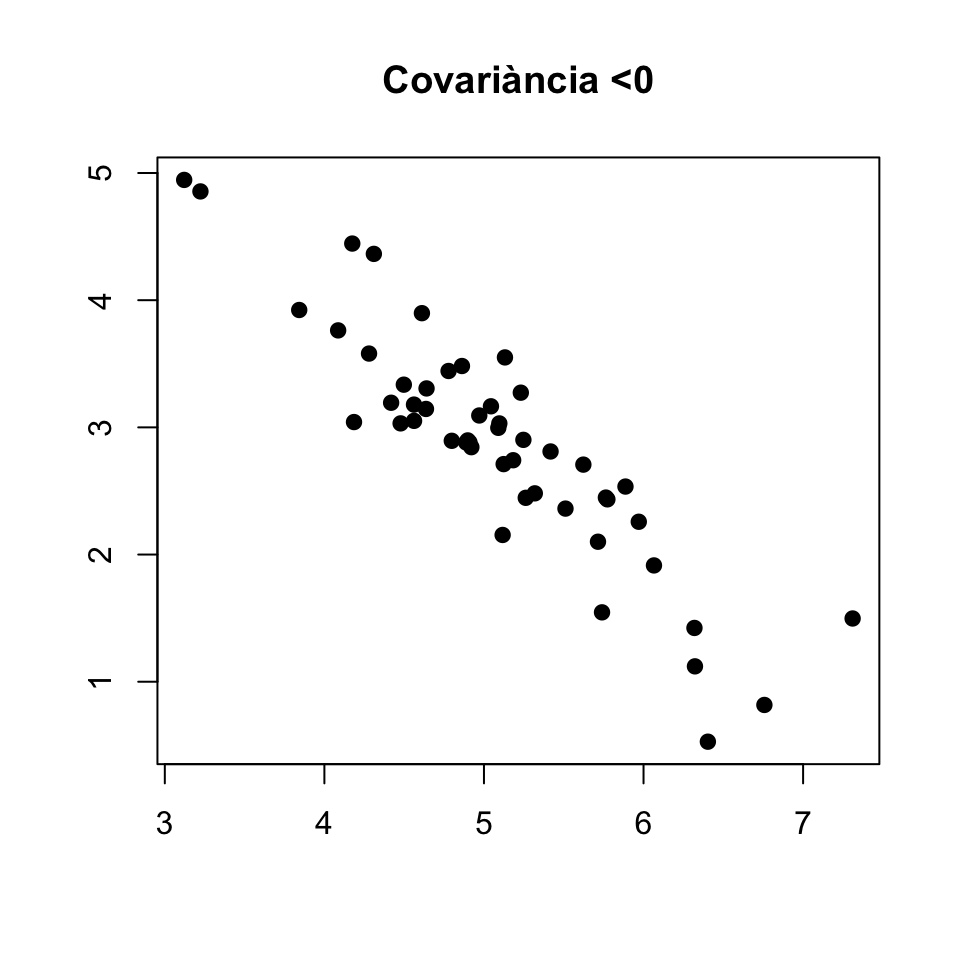
$\sigma_{X,Y}<0$ significa que quan $X$ és més gran en un individu 1 que en un individu 2, $Y$ tendeix a ser més petit en l’individu 1 que en l’individu 2.

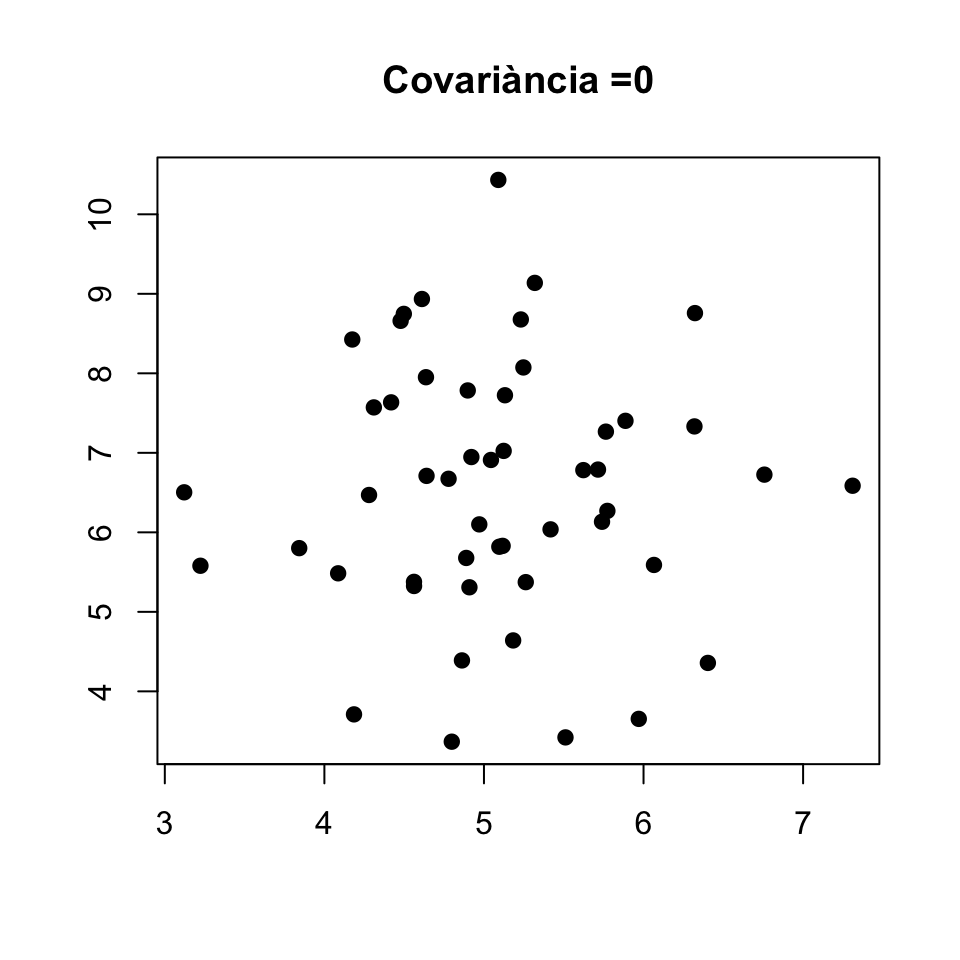
$\sigma_{X,Y}=0$ significa que no hi ha cap tendència en aquest sentit.

El signe de la covariància reflecteix la “tendència del creixement conjunt” de les variables:

Covariància positiva significa la mateixa tendència: Si $X$ augmenta, $Y$ tendeix a augmentar. Això també se sol expressar dient que hi ha associació positiva entre $X$ i $Y$.
Covariància negativa significa la tendència inversa: Si $X$ augmenta, $Y$ tendeix a minvar. Això també se sol expressar dient que hi ha associació negativa entre $X$ i $Y$.

Si $X$ i $Y$ són variables independents, la seva covariància es 0, perquè en aquest cas $E(X\cdot Y) =\mu_X\mu_Y$ i per tant \[ \sigma_{X,Y}=E(X\cdot Y) -\mu_X\cdot \mu_Y=\mu_X\cdot \mu_Y-\mu_X\cdot \mu_Y=0. \] Intuïtivament, si $X$ i $Y$ són independents, que el valor de $X$ augmenti d’un individu a un altre no té cap efecte sobre el valor de $Y$.

Ups, aquesta és nova! Per què, si $X$ i $Y$ són independents, $E(X\cdot Y) =\mu_X\mu_Y$? Us ho demostrarem en el cas discret; l’argument en el cas continu és el mateix canviant sumatoris per integrals. \[ \begin{array}{rl} E(X\cdot Y)\!\!\! &\displaystyle =\sum_{x\in D_X,y\in D_Y} xyP(X=x,Y=y)\\ &\displaystyle =\sum_{x\in D_X,y\in D_Y} xyP(X=x)P(Y=y)\\ &\text{(per la independència de $X$ i $Y$)}\\ &\displaystyle =\Big(\sum_{x\in D_X}xP(X=x)\Big)\Big(\sum_{y\in D_Y} yP(Y=y)\Big)=E(X)E(Y) \end{array} \]

És important remarcar que la igualtat $E(X\cdot Y) =\mu_X\mu_Y$ és equivalent a la igualtat $\sigma(X+Y)^2 =\sigma(X)^2+\sigma(Y)^2$ que dèiem que satisfan les variables independents. En efecte \[ \begin{array}{l} \sigma(X+Y)^2 -(\sigma(X)^2+\sigma(Y)^2)\\ \quad = E((X+Y)^2)-E(X+Y)^2-(E(X^2)-E(X)^2+E(Y^2)-E(Y)^2)\\ \quad = E(X^2+2XY+Y^2)-(E(X)+E(Y))^2\\ \qquad\qquad -E(X^2)+E(X)^2-E(Y^2)+E(Y)^2\\ \quad = E(X^2)+2E(XY)+E(Y^2)-E(X)^2-2E(X)E(Y)-E(Y)^2\\ \qquad\qquad -E(X^2)+E(X)^2-E(Y^2)+E(Y)^2\\ \quad = 2E(XY)-2E(X)E(Y)=2(E(XY)-\mu_X\mu_Y) \end{array} \] i per tant \[ \sigma(X+Y)^2 -(\sigma(X)^2+\sigma(Y)^2)=0 \Longleftrightarrow E(XY)-\mu_X\mu_Y=0 \]

Si $X$ i $Y$ són variables independents, la seva covariància es 0, però la implicació a l’inrevés és falsa: Dues variables aleatòries poden tenir covariància 0 i no ser independents.

Vegem un exemple d’aquest darrer fet:

Exemple 9.2 Suposem que tenim un dau tetraèdric no trucat amb les cares marcades amb els valors -2, -1, 1 i 2. Siguin $X$ la variable aleatòria que consisteix a llançar el dau i anotar el resultat (la cara que queda en terra), i $Y$ la variable aleatòria que consisteix a llançar el dau i anotar el quadrat del resultat obtingut. Com que les quatre cares del dau són equiprobables, \[ \begin{array}{l} \displaystyle P(X=-2)=P(X=-1)=P(X=1)=P(X=2)=\frac{1}{4}\\ \displaystyle P(Y=1)=P(Y=4)=\frac{1}{2} \end{array} \]

Com que $Y$ és funció de $X$, ja que $Y=X^2$, $X$ i $Y$ no poden ser mai independents. Vegem que, en efecte, no ho són. Observau que els únics possibles valors per al vector $(X,Y)$ en una tirada del dau són (-2,4), (-1,1), (1,1) i (2,4), cadascun amb probabilitat 1/4. Llavors, per exemple, la probabilitat d’obtenir en una tirada $X=-1$ i $Y=4$ és 0, perquè és impossible, mentre que \[ P(X=-1)\cdot P(Y=4)=\frac{1}{4}\cdot\frac{1}{2}=\frac{1}{8}\neq 0. \]

Vegem ara que la covariància de $X$ i $Y$ es 0. Per calcular-la, primer necessitam calcular els valors esperats de les variables: \[ \begin{array}{l} \displaystyle \mu_X=(-2)\cdot \frac{1}{4}+(-1)\cdot \frac{1}{4}+1\cdot \frac{1}{4}+2\cdot \frac{1}{4}=0\\ \displaystyle \mu_Y=1\cdot \frac{1}{2}+4\cdot \frac{1}{2}=2.5 \end{array} \] Per tant \[ \begin{array}{l} \sigma_{X,Y}=E\big(X\cdot Y\big)-\mu_X\cdot \mu_Y=E\big(X\cdot Y\big)-0\cdot 2.5=E\big(X\cdot Y\big)\\ \qquad =P\big(X=-2,Y=4\big)\cdot (-2\cdot 4)+P\big(X=-1,Y=1\big)\cdot (-1\cdot 1)\\ \qquad\qquad\qquad +P\big(X=1,Y=1\big)\cdot (1\cdot 1)+P\big(X=2,Y=4\big)\cdot (2\cdot 4)\\ \qquad =\displaystyle \frac{1}{4}\cdot (-8)+\frac{1}{4}\cdot (-1)+\frac{1}{4}\cdot 1+\frac{1}{4}\cdot 8=0. \end{array} \] Així doncs, $X$ i $Y$ són variables dependents, però la seva covariància és 0.

Dues propietats importants més de la covariància:

La covariància és simètrica: \[ \begin{array}{rl} \sigma_{X,Y}\!\!\! & =E((X-\mu_X)\cdot ( Y-\mu_Y))\\ & =E(( Y-\mu_Y)\cdot (X-\mu_X))=\sigma_{Y,X} \end{array} \]
La covariància d’una variable aleatòria amb ella mateixa és la seva variància: \[ \sigma_{X,X}=E((X-\mu_X)^2)=\sigma^2(X) \]

La matriu de covariàncies d’un vector aleatori $\underline{X}=(X_1,\ldots,X_p)$ és la matriu formada per les covariàncies dels parells de variables que la formen: \[ \sigma_{\underline{X},\underline{X}}=\begin{pmatrix} \sigma_{X_1,X_1} & \sigma_{X_1,X_2} & \ldots & \sigma_{X_1,X_p}\\ \sigma_{X_2,X_1} & \sigma_{X_2,X_2} & \ldots & \sigma_{X_2,X_p}\\ \vdots & \vdots &\ddots & \vdots\\ \sigma_{X_p,X_1} & \sigma_{X_p,X_2} & \ldots & \sigma_{X_p,X_p}\\ \end{pmatrix} \]

Aquesta matriu és simètrica i les entrades de la diagonal són les variàncies de les variables del vector, perquè $\sigma_{X_i,X_i}=\sigma^2_{X_i}$.

9.1.2 Correlació

Com hem dit, el signe de la covariància té una interpretació senzilla, ja que reflecteix la tendència del creixement conjunt de les variables. Emperò, la seva magnitud no té una interpretació senzilla. Com a alternativa, es pot mesurar la tendència que hi hagi una relació lineal entre dues variables aleatòries contínues emprant l’anomenat coeficient de correlació lineal de Pearson (o, per abreviar, la correlació), que ve a ser una versió normalitzada de la covariància. En concret, la correlació de les variables $X$ i $Y$ es defineix com el quocient de la seva covariància pel producte de les seves desviacions típiques: \[ \rho_{X,Y}=\frac{\sigma_{X,Y}}{\sigma_{X} \sigma_{Y}} \]

La correlació té les propietats importants següents:

No té unitats (perquè les unitats de $\sigma_X$ són les de $X$, les unitats de $\sigma_Y$ són les de $Y$, i les unitats de $\sigma_{X,Y}$ són les de $X$ per les de $Y$)
Pren valors entre -1 i 1: $-1\leqslant \rho_{X,Y}\leqslant 1$
És simètrica, $\rho_{X,Y}= \rho_{Y,X}$
La correlació d’una variable amb ella mateixa és 1: $\rho_{X,X}=1$
$\rho_{X,Y}=\pm 1$ si, i només si, les variables $X,Y$ tenen una relació lineal perfecta. És a dir, $\rho_{X,Y}=\pm 1$ si, i només si, existeixen $a,b\in \mathbb{R}$ amb $a\neq 0$ i tals que $Y=a X+b$. La pendent $a$ d’aquesta recta té el mateix signe que $\rho_{X,Y}$.
Com més s’acosta $|\rho_{X,Y}|$ a 1, més s’acosta $Y$ a ser funció lineal de $X$.
- Si $\rho_{X,Y}>0$, la funció és creixent
- Si $\rho_{X,Y}<0$, la funció és decreixent
Si $\rho_{X,Y}=0$, diem que les variables $X$ i $Y$ són incorrelades. Notem que la correlació és 0 si, i només si, la covariància és 0. Per tant, si $X$ i $Y$ són independents, també són incorrelades. El recíproc en general és fals, com mostra l’Exemple 9.2.

Si una de les dues variables té desviació típica 0, en la fórmula de la correlació apareix un 0 en el denominador i no la podem calcular. En aquest cas, es pren $\rho_{X,Y}=0$. El motiu intuïtiu és que una variable constant és sempre independent de qualsevol altra variable (faci el que faci l’altra, sempre pren el mateix valor) i hem quedat que les variables independents són incorrelades.

La matriu de correlacions d’un vector aleatori $\underline{X}=(X_1,\ldots,X_p)$ és la matriu formada per les correlacions de parells de les seves variables: \[ \rho(\underline{X}) =\begin{pmatrix} 1 & \rho_{X_1,X_2} & \ldots & \rho_{X_1,X_p}\\ \rho_{X_2,X_1} & 1 & \ldots & \rho_{X_2,X_p}\\ \vdots & \vdots & \ddots & \vdots\\ \rho_{X_p,X_1} & \rho_{X_p,X_2} & \ldots & 1\\ \end{pmatrix}. \] Aquesta matriu és simètrica per la simetria de la correlació.

La correlació de Pearson de dues variables contínues mesura la tendència de les variables a variar conjuntament de manera lineal. En particular, per exemple, si $\rho_{X,Y}>0$, $Y$ tendeix a créixer quan $X$ creix. Però això no significa que un augment del valor de $X$ causi que el valor de $Y$ tendeixi a augmentar:

Correlació no implica causalitat!

La tendencia al creixement simultani de $X$ i $Y$ es pot deure a una tercera variable que les faci créixer totes dues, o pot ser purament espúria.

Figura 9.1: Correlació no implica causalitat (https://xkcd.com/552/ (CC-BY-NC 2.5))

O millor:

Figura 9.2: Correlació no implica causalitat, segons Dilbert

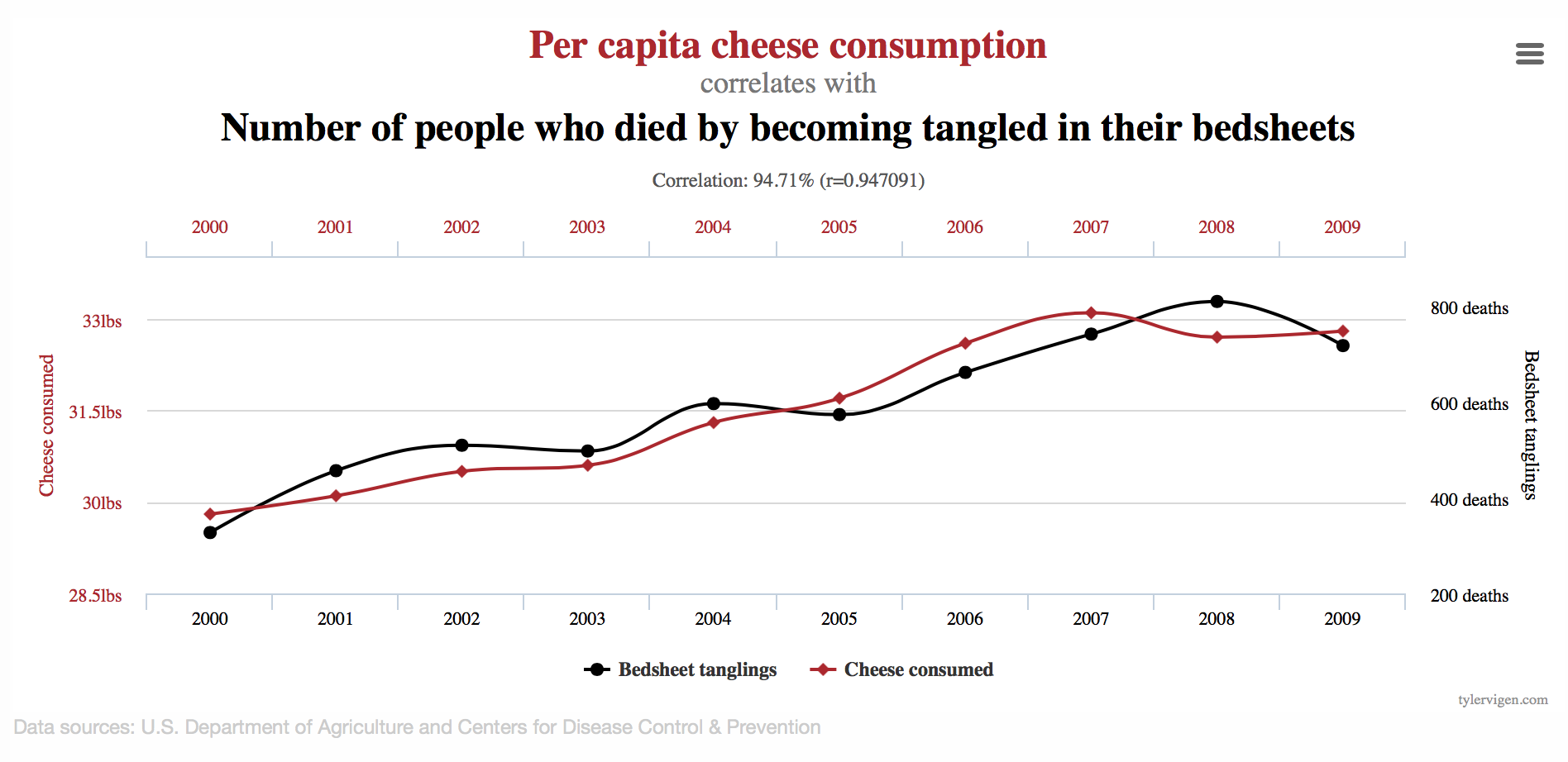
Si entrau a la pàgina web Spurious Correlations podreu explorar un munt de correlacions espúries molt grans. La nostra preferida és una correlació de 0.947 entre la variable $X$ “Prenc un any i anot el consum per capita de formatge als EEUU” i $Y$ “Prenc un any i anot el nombre de morts per estrangulament accidental amb els llençols del llit als EEUU”.

Hi ha un exemple de correlació negativa que és important tenir present per no deixar-se enganar.

Teorema 9.1 Si $X_1$, $X_2$ són dues còpies independents d’una mateixa variable aleatòria $X$, \[ \rho_{X_1,X_2-X_1}=-\frac{1}{\sqrt{2}}\approx -0.71 \]

Això ens diu que, sigui quina sigui la variable $X$, si la mesuram en dos moments independents o sobre dos individus triats de manera independent, la diferència entre els dos valors té una tendència destacada a decréixer linealment en el primer valor. Per exemple:

Feu un test i traieu una nota molt baixa ($X_1$). L’endemà feu un altre test similar ($X_2$) sense haver estudiat més. El més probable és que, per pur atzar, tengueu una nota més alta (que $X_2-X_1$ sigui gran, per tant positiu).
Feu un test i traieu una nota molt alta ($X_1$). L’endemà feu un altre test ($X_2$) sense haver estudiat més. El més probable és que, per pur atzar, tengueu una nota més baixa (que $X_2-X_1$ sigui petit, per tant negatiu).

Per si qualcú necessita una demostració del teorema anterior, recordem que \[ \rho_{X_1,X_2-X_1}=\dfrac{\sigma_{X_1,X_2-X_1}}{\sigma_{X_1}\sigma_{X_2-X_1}} \] Ara \[ \begin{array}{l} \sigma_{X_2-X_1}=\sqrt{\sigma^2_{X_2-X_1}}\\[2ex] \quad =\sqrt{\sigma^2_{X_1}+\sigma^2_{X_2}}\ \text{(perquè són independents)}\\[2ex] \quad =\sqrt{\sigma^2_{X}+\sigma^2_{X}}\ \text{(perquè $X_1,X_2$ són còpies de $X$)}\\[2ex] \quad =\sqrt{2\sigma^2_{X}}=\sigma_{X}\sqrt{2} \end{array} \] I \[ \begin{array}{l} \sigma_{X_1,X_2-X_1}=E(X_1(X_2-X_1))-E(X_1)E(X_2-X_1)\\[1ex] \quad =E(X_1X_2-X_1^2)-E(X_1)(E(X_2-E(X_1))\\[1ex] \quad =E(X_1X_2)-E(X_1^2)-E(X_1)E(X_2)+E(X_1)E(X_1)\\[1ex] \quad =E(X_1)E(X_2)-E(X_1^2)-E(X_1)E(X_2)+E(X_1)E(X_1)\\[1ex] \quad \text{(perquè $X_1,X_2$ són independents)}\\[1ex] \quad =-E(X_1^2)+E(X_1)E(X_1)=-\sigma^2_{X_1}=-\sigma^2_{X} \end{array} \] Combinant-ho: \[ \rho_{X_1,X_2-X_1}=\dfrac{\sigma_{X_1,X_2-X_1}}{\sigma_{X_1}\sigma_{X_2-X_1}}=\dfrac{-\sigma^2_{X}}{\sigma_{X}\cdot \sigma_{X}\sqrt{2}} =-\frac{1}{\sqrt{2}} \]

Exemple 9.3 Com a exemple, generarem una mostra $X$ de 101 “notes” aleatòries entre 0 i 100 amb distribució binomial $B(100,0.5)$. Prendrem com a $X_1$ el vector de les primeres 100 notes, \[ X_1=(x_1,x_2,\ldots,x_{100}) \] i com a $X_2-X_1$ el vector de les diferències de cada nota $x_i$, $i\geqslant 2$, amb l’anterior: \[ X_2-X_1=(x_2-x_1,x_3-x_2,\ldots,x_{101}-x_{100}). \] Calcularem la correlació entre $X_1$ i $X_2-X_1$, i ho il·lustrarem amb un gràfic.

X=rbinom(101,100,0.5)
X1=X[-101]
X2.menys.X1=diff(X)
plot(X1,X2.menys.X1,pch=20,xlab=expression(X[1]),ylab=expression(X[2]-X[1]))
cor(X1,X2.menys.X1)

## [1] -0.7068097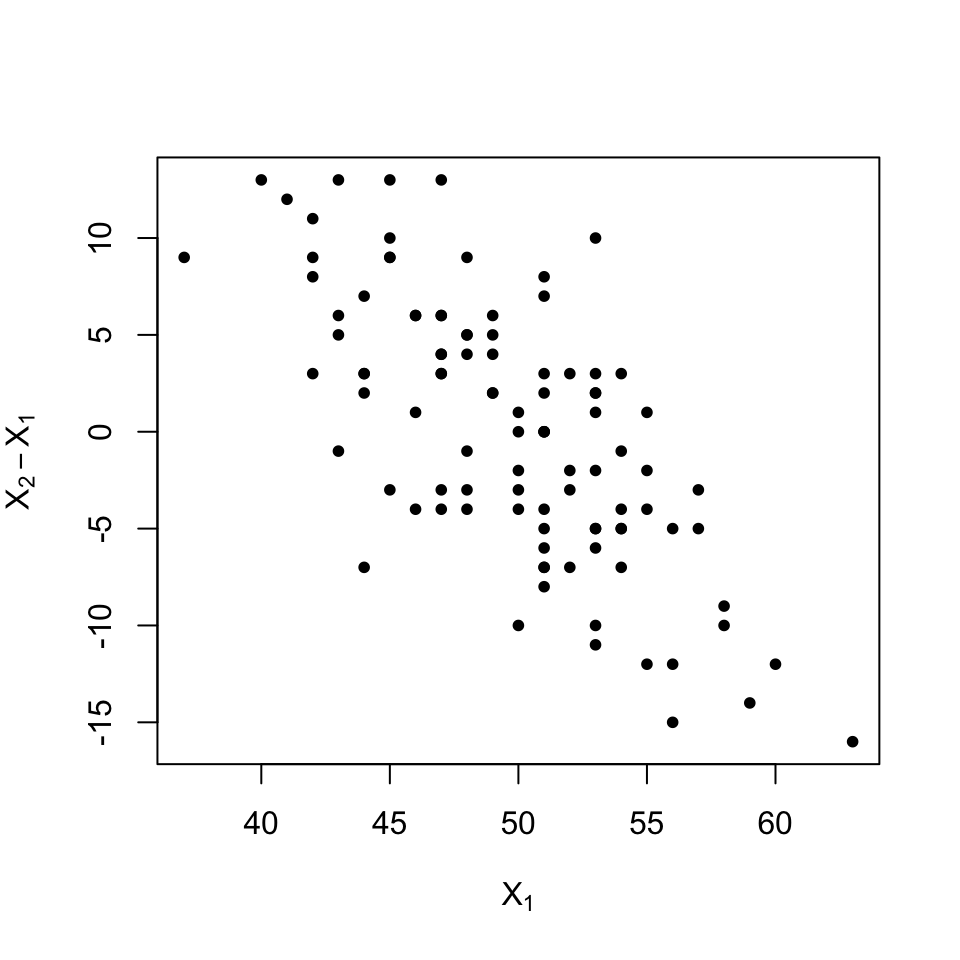

La correlació predita pel teorema anterior és

-1/sqrt(2)

## [1] -0.7071068

9.2 Estadística descriptiva: Mostres

9.2.1 Covariàncies

Siguin $X=(x_1,\ldots,x_n)$ i $Y=(y_1,\ldots,y_n)$ dos vectors obtinguts mesurant dues variables aleatòries quantitatives sobre una mateixa mostra ordenada d’individus de mida $n$ d’una població. Siguin $\overline{X}$ i $\overline{Y}$ les seves mitjanes mostrals. Aleshores la seva covariància mostral és \[ \widetilde{S}_{X,Y} =\frac{1}{n-1} \sum_{i =1}^n\big((x_{i}-\overline{{X}})(y_i-\overline{Y})\big) \] i la seva covariància (a seques) és \[ {S}_{X,Y} =\frac{1}{n} \sum_{i =1}^n\big((x_{i}-\overline{{X}})(y_i-\overline{Y})\big)=\frac{n-1}{n}\widetilde{S}_{X,Y}. \] És a dir, com sempre, la diferència entre la versió “mostral” i la versió “a seques” rau en el denominador, $n-1$ i $n$ respectivament.

La covariància de dos vectors només té sentit quan aquests vectors representen els valors de dues variables quantitatives sobre els mateixos individus, o sobre dues mostres aparellades, i en el mateix ordre. En particular, els dos vectors han de tenir la mateixa longitud.

Com en el cas poblacional, la covariància entre dos vectors mesura la tendència que tenen les seves dades a variar conjuntament:

Quan $\widetilde{S}_{X,Y}>0$, si $x_i>x_j$, $y_i$ tendeix a ser més gran que $y_j$
Quan $\widetilde{S}_{X,Y}<0$, si $x_i>x_j$, $y_i$ tendeix a ser més petit que $y_j$
Quan $\widetilde{S}=0$, no hi ha cap tendència en aquest sentit

És fàcil comprovar que:

Les dues covariàncies són simètriques \[ \widetilde{S}_{X,Y}=\widetilde{S}_{Y,X},\ {S}_{X,Y}={S}_{Y,X} \]
La variància d’un vector és la seva covariància amb ell mateix \[ \widetilde{S}_{X,X}=\widetilde{S}^2_{X},\ {S}_{X,X}={S}^2_{X}. \]

Exemple 9.4 Hem mesurat l’índex de massa corporal, BMI, i el nivell de colesterol en 5 individus sans. Guardam els resultats en un dataframe i en calculam les mitjanes:

BMI= c(18.3,24.4,24.6,24.4,22.2,19.5)
Chol=c(170,202,215,218,210,210)
DF=data.frame(BMI,Chol)
mean(BMI)

## [1] 22.23333

mean(Chol)

## [1] 204.1667

Aleshores la covariància mostral d’aquests dos vectors és \[ \begin{array}{l} \dfrac{1}{5}\Big((18.3-22.23)(170-204.17)+(24.4-22.23)(202-204.17)\\ \qquad +(24.6-22.23)(215-204.17)+(24.4-22.23)(218-204.17)\\ \qquad +(22.2-22.23)(210-204.17)+(19.5-22.23)(210-204.17)\Big)=33.8333 \end{array} \]

i la seva covariància a seques és \[ \begin{array}{l} \dfrac{1}{6}\Big((18.3-22.23)(170-204.17)+(24.4-22.23)(202-204.17)\\ \qquad +(24.6-22.23)(215-204.17) +(24.4-22.23)(218-204.17)\\ \qquad +(22.2-22.23)(210-204.17)+(19.5-22.23)(210-204.17)\Big)=28.1944 \end{array} \]

La covariància mostral de dos vectors numèrics de la mateixa longitud $n$ es calcula amb R amb la funció cov.

cov(BMI,Chol)

## [1] 33.83333

Per obtenir la seva covariància a seques, cal multiplicar el resultat de cov per $(n-1)/n$.

n=length(BMI)
cov(BMI,Chol)*(n-1)/n

## [1] 28.19444

Considerem una taula de dades quantitatives de la forma \[ \begin{array}{cccc} X_1 & X_2 & \ldots & X_p\\ \hline x_{1 1} & x_{1 2} &\ldots & x_{1 p}\\ x_{2 1} & x_{2 2} &\ldots & x_{2 p}\\ \vdots & \vdots & \ddots &\vdots\\ x_{n 1} & x_{n 2} &\ldots & x_{n p} \end{array} \] on cada columna representa els valors d’una certa variable $X_i$ i cada filera un individu d’una mostra de la població, de manera que l’entrada $x_{ij}$ d’aquesta taula és el valor de $X_j$ sobre l’individu $i$-èssim de la mostra.

La matriu de covariàncies mostrals d’aquesta taula és la matriu \[ \widetilde{{S}}= \begin{pmatrix} \widetilde{S}^2_{X_1} & \widetilde{S}_{X_1,X_2} & \ldots & \widetilde{S}_{X_1,X_p}\\ \widetilde{S}_{X_2,X_1} & \widetilde{S}^2_{X_2} & \ldots & \widetilde{S}_{X_2,X_p}\\ \vdots & \vdots & \ddots & \vdots\\ \widetilde{S}_{X_p,X_1} & \widetilde{S}_{X_p,X_2} & \ldots & \widetilde{S}^2_{X_p} \end{pmatrix} \] i la matriu de covariàncies (a seques) es defineix de manera similar, però amb les covariàncies a seques: \[ {S}= \begin{pmatrix} S^2_{X_1} & S_{X_1,X_2} & \ldots & S_{X_1,X_p}\\ S_{X_2,X_1} & S^2_{X_2} & \ldots & S_{X_2,X_p}\\ \vdots & \vdots & \ddots & \vdots\\ S_{X_p,X_1} & S_{X_p,X_2} & \ldots & S^2_{X_p} \end{pmatrix} \] Totes dues són simètriques.

La matriu de covariàncies mostrals es calcula amb la funció cov aplicada a la matriu o el data frame de variables numèriques que emmagatzema la taula de dades. Per calcular la matriu de covariàncies a seques, es multiplica el resultat de cov per $(n-1)/n$, on $n$ és el nombre de fileres de la taula.

Exemple 9.5 Afegirem a les dades de l’Exemple 9.4 una tercera variable amb les edats dels 6 individus.

DF$Edats=c(49,39,50,44,40,36)
DF

##    BMI Chol Edats
## 1 18.3  170    49
## 2 24.4  202    39
## 3 24.6  215    50
## 4 24.4  218    44
## 5 22.2  210    40
## 6 19.5  210    36

La matriu de covariàncies mostrals d’aquesta taula és

cov(DF)

##             BMI      Chol  Edats
## BMI    7.586667  33.83333   1.14
## Chol  33.833333 309.76667 -33.00
## Edats  1.140000 -33.00000  32.00

Podreu observar que és simètrica, que l’entrada (2,1) coincideix amb la covariància de BMI i Chol que hem calculat abans, i que a la diagonal hi obtenim les variàncies mostrals de les variables de la taula:

apply(DF,MARGIN=2,FUN=var)

##        BMI       Chol      Edats 
##   7.586667 309.766667  32.000000

9.2.2 Correlació de Pearson

Siguin $X=(x_1,\ldots,x_n)$ i $Y=(y_1,\ldots,y_n)$ dos vectors obtinguts mesurant dues variables aleatòries contínues sobre una mateixa mostra d’individus de mida $n$ d’una població.

La correlació de Pearson de $X$ i $Y$ és la seva covariància mostral dividida pel producte de les seves desviacions típiques mostrals: \[ R_{X,Y}=\frac{\widetilde{S}_{X,Y}}{\widetilde{S}_X\cdot \widetilde{S}_Y}. \]

La correlació de Pearson de $X$ i $Y$ també és igual a la seva covariància a seques dividida pel producte de les seves desviacions típiques a seques, perquè els canvis de denominador se cancel·len: \[ R_{X,Y}=\frac{\widetilde{S}_{X,Y}}{\widetilde{S}_X\cdot \widetilde{S}_Y}= \frac{\frac{n}{n-1}\cdot {S}_{X,Y}}{\sqrt{\frac{n}{n-1}}\cdot {S}_X \cdot\sqrt{\frac{n}{n-1}}\cdot{S}_Y}= \frac{S_{X,Y}}{S_X \cdot S_Y}=R_{X,Y}. \]

Exemple 9.6 Tornem a la situació de l’Exemple 9.4. La covariància mostral i les desviacions típiques mostrals dels vectors BMI i Chol són

cov(BMI,Chol)

## [1] 33.83333

sd(BMI)

## [1] 2.75439

sd(Chol)

## [1] 17.60019

i per tant la seva correlació de Pearson és \[ R_{BMI,Chol}=\frac{33.833}{2.754\cdot 17.6}= 0.698 \]

Algunes propietats importants de la correlació de Pearson:

La correlació de Pearson és simètrica: \[ R_{X,Y}=R_{Y,X} \]
La correlació de Pearson pren valors només entre -1 i 1: \[ -1\leqslant R_{X,Y}\leqslant 1 \]
La correlació de Pearson d’un vector amb ell mateix és 1: \[ R_{X,X}=1 \]
$R_{X,Y}$ té el mateix signe que $S_{X,Y}$, i per tant aquest signe té el mateix significat que a la covariància:
- Si $R_{X,Y}>0$ i si $x_i>x_j$, $y_i$ tendeix a ser més gran que $y_j$
- Si $R_{X,Y}<0$ i si $x_i>x_j$, $y_i$ tendeix a ser més petit que $y_j$
- Si $R=0$, no hi ha cap tendència en aquest sentit
$R_{X,Y}=\pm 1$ si, i només si, tots els punts $(x_i,y_i)$ estan sobre una recta $y=ax+b$ amb $a\neq 0$. La pendent $a$ d’aquesta relació lineal té el mateix signe que $R_{X,Y}$. Per tant, la recta és creixent si $R_{X,Y}=1$ i decreixent si $R_{X,Y}=- 1$.
El coeficient de determinació $R^2$ de la regressió lineal per mínims quadrats de $Y$ respecte de $X$ és igual al quadrat de la seva correlació de Pearson: \[ R^2=R_{X,Y}^2 \]

Per tant, com més s’acosta la correlació de Pearson de $X$ i $Y$ a 1 o a -1, més s’acosten els punts $(x_i,y_i)$ a estar sobre una recta. El signe de $R_{X,Y}$ indica si aquesta recta és creixent ($R_{X,Y}>0$) o decreixent ($R_{X,Y}<0$).

Com al cas poblacional, quan un dels vectors és constant, la correlació es pren igual a 0.

Amb R, la correlació de Pearson de dos vectors es pot calcular amb la funció cor. Per exemple, la correlació del Pearson dels vectors BMI i Chol s’obté amb

cor(BMI,Chol)

## [1] 0.6979141

Vegem que el seu quadrat és igual al $R^2$ de la regressió lineal de Chol en funció de BMI:

cor(BMI,Chol)^2

## [1] 0.487084

summary(lm(Chol~BMI))$r.squared

## [1] 0.487084

Per fer-nos una idea de què representa aquest valor de la correlació, vegem el gràfic dels punts (BMI,Chol) amb la seva recta de regressió lineal:

plot(BMI,Chol,pch=20)
abline(lm(Chol~BMI),col="red",lwd=1.5)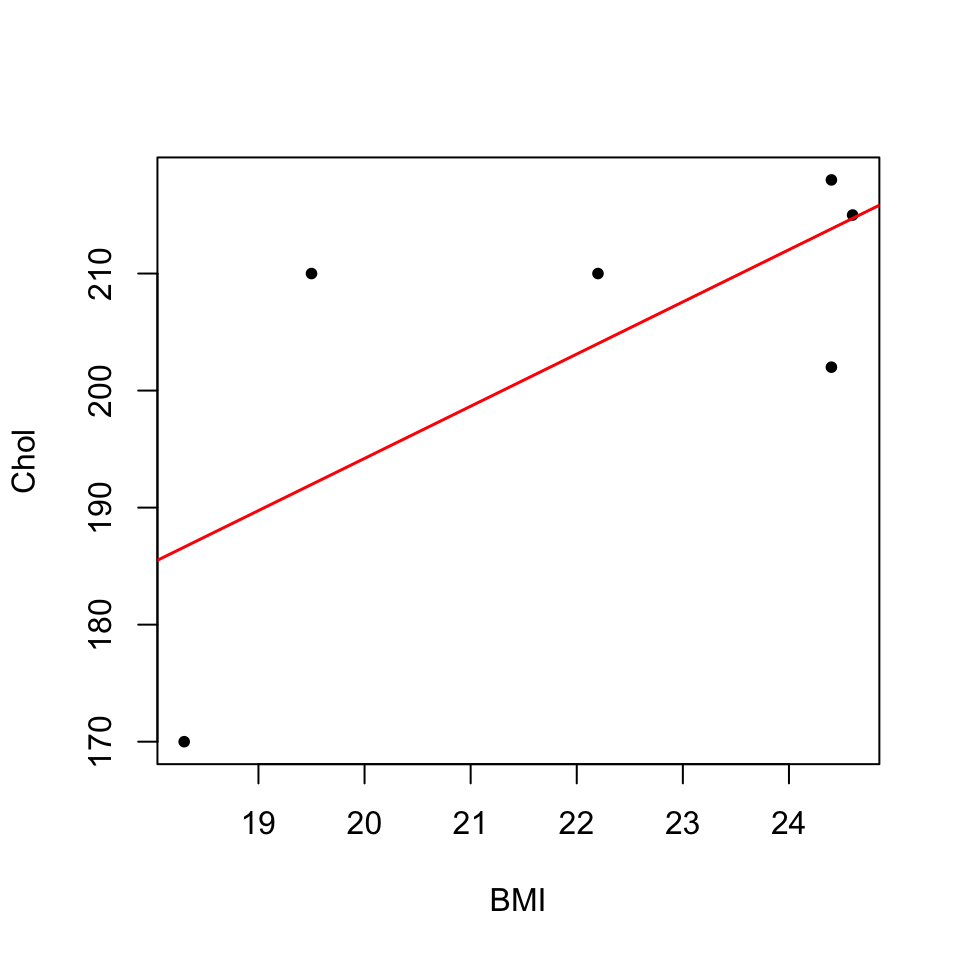

Hi podem observar com Chol tendeix a créixer quan BMI creix, però els punts (BMI,Chol) no tendeixen a estar sobre una recta.

És convenient acompanyar un càlcul de correlació o covariància de dos vectors $x,y$ amb un gràfic dels punts $(x_i,y_i)$, perquè conjunts molt diferents de punts poden donar lloc a la mateixa correlació.

Un exemple clàssic d’aquest fet són els quatre conjunts de dades $(x_{1,i},y_{1,i})_{i=1,\ldots,11}$, $(x_{2,i},y_{2,i})_{i=1,\ldots,11}$, $(x_{3,i},y_{3,i})_{i=1,\ldots,11}$, $(x_{4,i},y_{4,i})_{i=1,\ldots,11}$ que formen el dataframe anscombe de R:

str(anscombe)

## 'data.frame':    11 obs. of  8 variables:
##  $ x1: num  10 8 13 9 11 14 6 4 12 7 ...
##  $ x2: num  10 8 13 9 11 14 6 4 12 7 ...
##  $ x3: num  10 8 13 9 11 14 6 4 12 7 ...
##  $ x4: num  8 8 8 8 8 8 8 19 8 8 ...
##  $ y1: num  8.04 6.95 7.58 8.81 8.33 ...
##  $ y2: num  9.14 8.14 8.74 8.77 9.26 8.1 6.13 3.1 9.13 7.26 ...
##  $ y3: num  7.46 6.77 12.74 7.11 7.81 ...
##  $ y4: num  6.58 5.76 7.71 8.84 8.47 7.04 5.25 12.5 5.56 7.91 ...

Les correlacions dels quatre parells de vectors són molt semblants:

cor(anscombe$x1,anscombe$y1)

## [1] 0.8164205

cor(anscombe$x2,anscombe$y2)

## [1] 0.8162365

cor(anscombe$x3,anscombe$y3)

## [1] 0.8162867

cor(anscombe$x4,anscombe$y4)

## [1] 0.8165214

Però si els dibuixam veureu que els quatre conjunts de punts són molt diferents:

plot(anscombe$x1,anscombe$y1,pch=20,main="Conjunt de dades 1",cex=1.25)
abline(lm(y1~x1,data=anscombe),col="red",lwd=1.5)
plot(anscombe$x2,anscombe$y2,pch=20,main="Conjunt de dades 2",cex=1.25)
abline(lm(y2~x2,data=anscombe),col="red",lwd=1.5)
plot(anscombe$x3,anscombe$y3,pch=20,main="Conjunt de dades 3",cex=1.25)
abline(lm(y3~x3,data=anscombe),col="red",lwd=1.5)
plot(anscombe$x4,anscombe$y4,pch=20,main="Conjunt de dades 4",cex=1.25)
abline(lm(y4~x4,data=anscombe),col="red",lwd=1.5)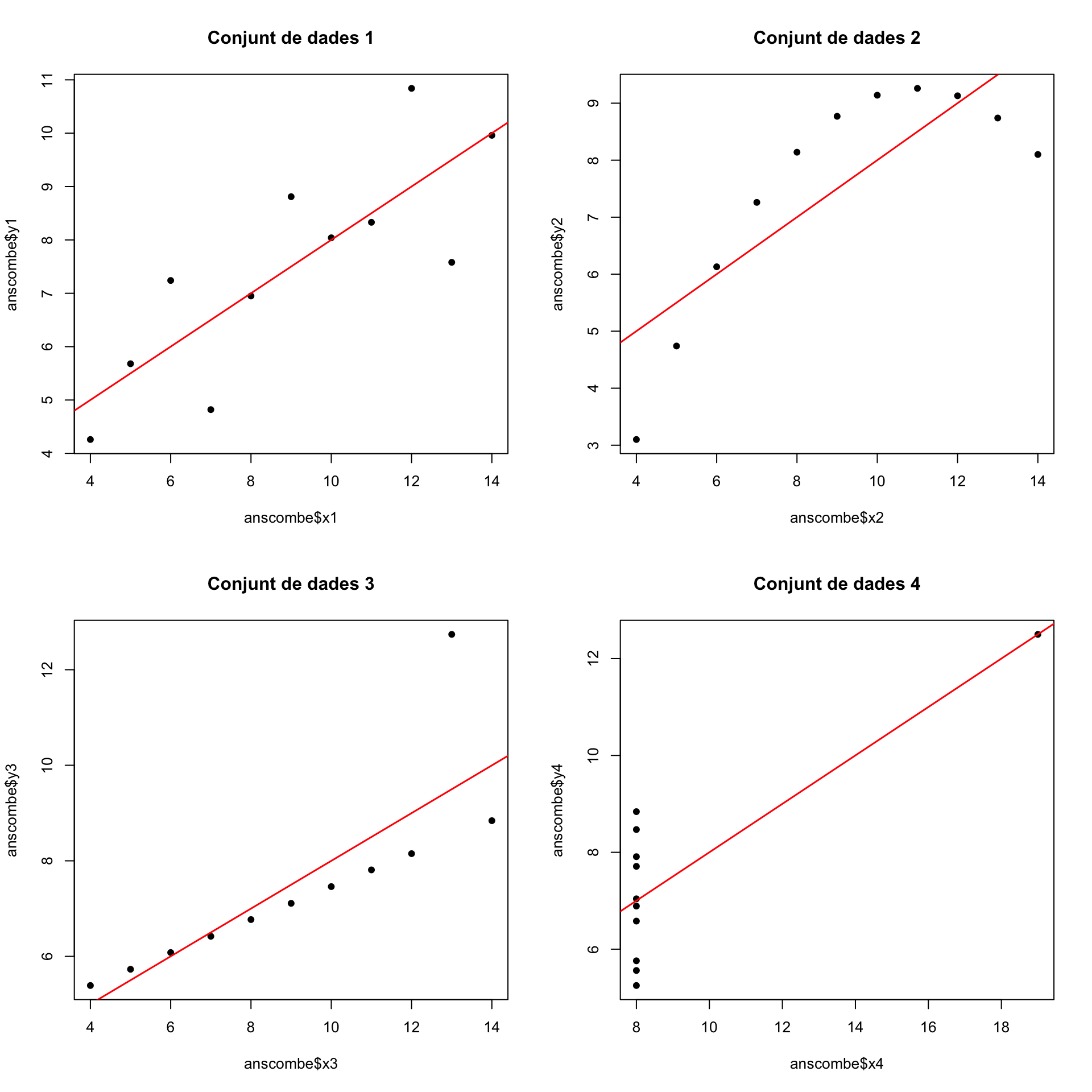

Exemples més espectaculars es poden obtenir amb les funcions del paquet datasaurus, que permeten crear conjunts de punts de “formes” diferents i mateixos estadístics, i en particular la mateixa correlació. Emprant aquest paquet, hem creat dos parells de vectors de dades dino i star, que hem recollit a la taula de dades https://raw.githubusercontent.com/AprendeR-UIB/MatesII/master/Dades/Datasaurus.txt. Aquesta taula de dades té tres variables: una variable dataset que indica el conjunt de dades, i les variables x i y que donen les coordenades dels punts que formen cada conjunt de dades. Comprovarem que els dos parells de vectors de dades el mateix coeficient de correlació (almenys fins a la setena xifra decimal) i els dibuixarem.

datasaure=read.table("https://raw.githubusercontent.com/AprendeR-UIB/MatesII/master/Dades/Datasaurus.txt",header=TRUE,sep="\t")
str(datasaure)

## 'data.frame':    284 obs. of  3 variables:
##  $ dataset: chr  "dino" "dino" "dino" "dino" ...
##  $ x      : num  55.4 51.5 46.2 42.8 40.8 ...
##  $ y      : num  97.2 96 94.5 91.4 88.3 ...

dino=datasaure[datasaure$dataset=="dino",2:3]
star=datasaure[datasaure$dataset=="star",2:3]
cor(dino$x,dino$y)

## [1] -0.0629611

cor(star$x,star$y)

## [1] -0.0629611

plot(dino,pch=20,cex=1.25)
plot(star,pch=20,cex=1.25)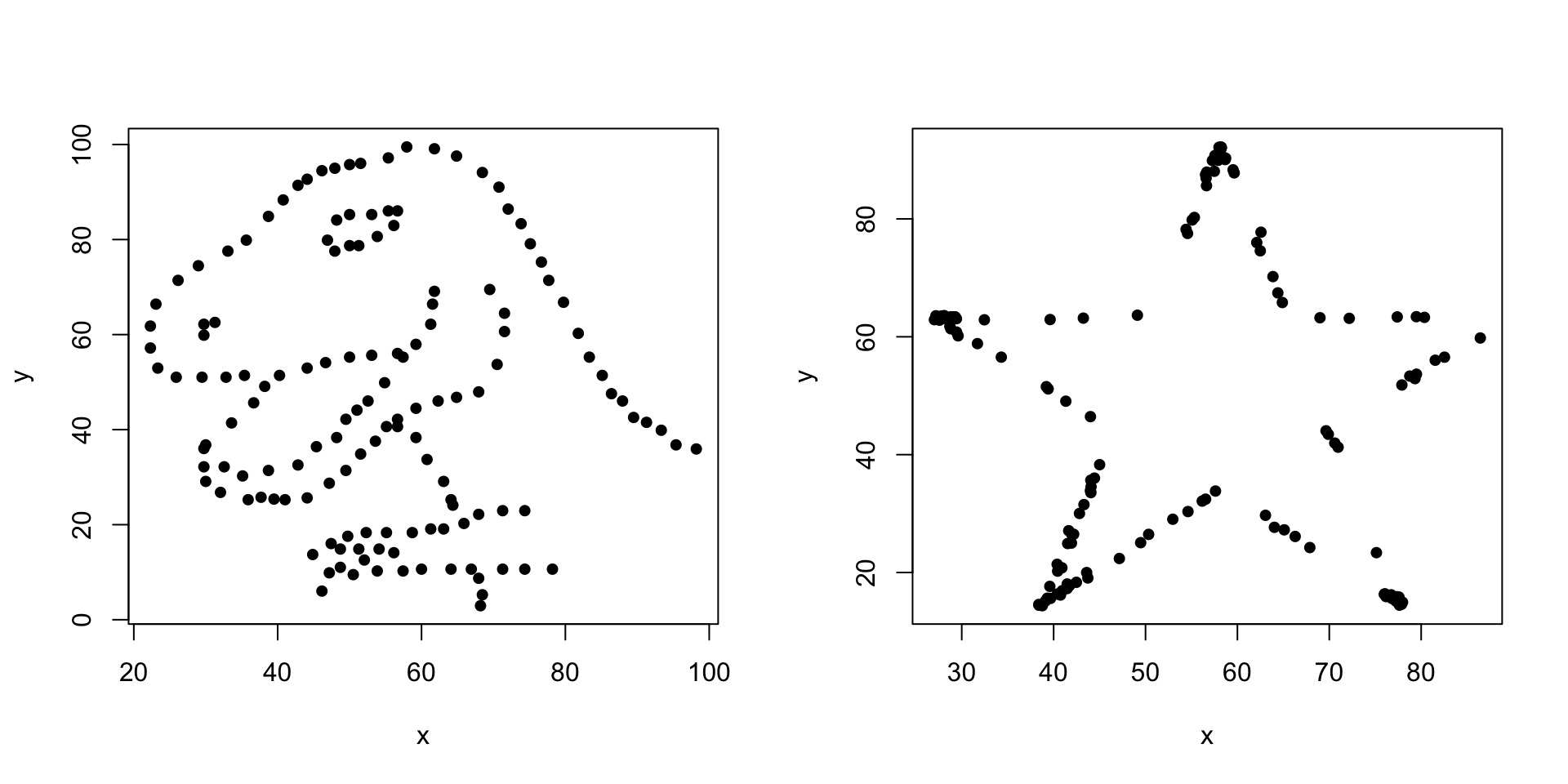

Suposem ara que tenim una taula de dades numèriques de la forma \[ \begin{array}{cccc} X_1 & X_2 & \ldots & X_p\\ \hline x_{1 1} & x_{1 2} &\ldots & x_{1 p}\\ x_{2 1} & x_{2 2} &\ldots & x_{2 p}\\ \vdots & \vdots & \ddots &\vdots\\ x_{n 1} & x_{n 2} &\ldots & x_{n p} \end{array} \] on cada columna representa els valors d’una certa variable $X_i$ i cada filera un individu d’una mostra de la població, de manera que l’entrada $x_{ij}$ d’aquesta taula és el valor de $X_j$ sobre l’individu $i$-èssim de la mostra.

La seva matriu de correlacions de Pearson és la matriu simètrica \[ \begin{pmatrix} 1 & R_{X_1,X_2} & \ldots & R_{X_1,X_p}\\ R_{X_2,X_1} & 1 & \ldots & R_{X_2,X_p}\\ \vdots & \vdots & \ddots & \vdots\\ R_{X_p,X_1} & R_{X_p,X_2} & \ldots & 1 \end{pmatrix} \]

Aquesta matriu de correlacions es calcula amb la funció cor aplicada a la matriu o el data frame de variables numèriques que emmagatzema la taula de dades. Per exemple, la matriu de correlacions de Pearson de la taula de dades DF de l’Exemple 9.5 és

cor(DF)

##              BMI       Chol       Edats
## BMI   1.00000000  0.6979141  0.07316517
## Chol  0.69791406  1.0000000 -0.33145274
## Edats 0.07316517 -0.3314527  1.00000000

9.2.3 Estimació

Les covariàncies de dos vectors obtinguts mesurant dues variables $X,Y$ sobre una mostra aleatòria simple de subjectes d’una població estimen la covariància poblacional de les variables $X,Y$ que han produït els vectors:

La covariància mostral $\widetilde{S}_{X,Y}$ sempre és un estimador no esbiaixat de la covariància poblacional $\sigma_{X,Y}$
La covariància ${S}_{X,Y}=\frac{n-1}{n}\widetilde{S}_{X,Y}$ és un estimador esbiaixat de la covariància poblacional $\sigma_{X,Y}$, amb biaix que tendeix a 0, i és més eficient que $\widetilde{S}_{X,Y}$
La covariància $S_{X,Y}$ és l’estimador màxim versemblant de $\sigma_{X,Y}$ quan la distribució conjunta de les variables $X,Y$ és el que s’anomena normal bivariant.

La correlació de Pearson de dos vectors obtinguts mesurant dues variables contínues $X,Y$ sobre una mostra aleatòria simple de subjectes d’una població estima la correlació poblacional de les variables $X,Y$. En concret:

$R_{X,Y}$ és un estimador màxim versemblant de $\rho_{X,Y}$ quan la distribució conjunta de $X,Y$ és normal bivariant. N’és un estimador esbiaixat, però el seu biaix tendeix a 0.

9.2.4 Correlació de Spearman

La correlació de Pearson mesura específicament la tendència de dues variables contínues a dependre linealment l’una de l’altra. Si no esperam que aquesta dependència lineal existeixi, o si les nostres variables són discretes o simplement ordinals, emprar la correlació de Pearson per a analitzar la relació entre dues variables no és el més adequat. Entre les propostes alternatives, la més popular és la correlació de Spearman.

Intuïtivament, la correlació de Spearman mesura la tendència que si $x_i>x_j$, passi que $y_i>y_j$. El seu valor és 1 si, per a tots $i,j$, \[ x_i>x_j\Longleftrightarrow y_i>y_j \] i el seu valor és -1 si, per a tots $i,j$, \[ x_i>x_j\Longleftrightarrow y_i<y_j \] Com més s’acosta la correlació de Spearman a valer 1 (o -1), per a més parelles d’índexs $(i,j)$ tals que $x_i>x_j$ es té que $y_i>y_j$ ($y_i<y_j$, si s’acosta a -1).

Formalment, la correlació de Spearman de dos vectors $X$ i $Y$ se defineix com la correlació de Pearson dels vectors de rangs de $X$ i $Y$. El vector de rangs d’un vector $X$ s’obté substituint cada valor de $X$ per la seva posició en el vector ordenat de menor a major, i en cas d’empats assignant a grups de valors empatats la mitjana de les posicions que ocuparien (aquests rangs ja han sortit, al test de Wilcoxon i al test de bondat d’ajust de Kolmogorov-Smirnov). Per exemple, el vector de rangs de \[ x=(4,5,1,5,1,3,4,4) \] és \[ (5,7.5,1.5,7.5,1.5,3,5,5) \] Com hem calculat aquest vector?

Primer assignam a cada valor del vector la seva posició si estiguessin ordenats de menor a major, i en cas d’empat per ara els ordenarem d’esquerra a dreta: \[ \begin{array}{r|cccccccc} x & 4& 5 & 1 & 5 & 1 & 3 & 4 & 4\\ \hline \text{Posició} & 4 & 7 & 1 & 8 & 2 & 3 & 5 & 6\\ \end{array} \]
Ara, per assignar els rangs finals:
- El rang dels dos elements 1 de $x$ és la mitjana de les posicions 1, 2 del vector ordenat: 1.5.
- Com que només hi ha un 3 a $x$, el seu rang és la seva posició en el vector ordenat: 3.
- El rang dels tres elements 4 és la mitjana de les posicions 4, 5 i 6 del vector ordenat: 5.
- Finalment, el rang dels dos elements 5 és la mitjana de les posicions 7, 8 del vector ordenat: 7.5.

\[ \begin{array}{r|cccccccc} x & 4& 5 & 1 & 5 & 1 & 3 & 4 & 4\\ \hline \text{Posició} & 4 & 7 & 1 & 8 & 2 & 3 & 5 & 6\\ \hline \text{Rang} & 5 & 7.5 & 1.5 & 7.5 & 1.5 & 3 & 5 & 5 \end{array} \]

Per cert, amb R el vector de rangs es calcula amb la funció rank:

rank(c(4,5,1,5,1,3,4,4))

## [1] 5.0 7.5 1.5 7.5 1.5 3.0 5.0 5.0

Amb R, la correlació de Spearman es calcula directament amb la funció cor entrant-li el paràmetre method="spearman". (El valor per defecte del paràmetre method és "pearson" i per això no l’indicam quan calculam la correlació de Pearson.)

Exemple 9.7 Considerem els vectors BMI i Chol de l’Exemple 9.4. El primer que farem serà calcular els seus vectors de rangs:

\[ \begin{array}{|c|c||c|c|} \hline BMI & \text{Rangs} & Chol& \text{Rangs} \\\hline\hline 18.3& 1 & 170& 1 \\ 24.4&4.5 & 202 & 2\\ 24.6&6 & 215& 5 \\ 24.4&4.5 & 218& 6\\ 22.2&3 & 210& 3.5\\ 19.5&2 & 210& 3.5\\\hline \end{array} \]

Per tant, la correlació de Spearman de \[ \mathit{BMI}=(18.3, 24.4, 24.6, 24.4, 22.2, 19.5)\mbox{ i }\mathit{Chol}=(170, 202, 215, 218, 210, 210) \] és la correlació de Pearson de \[ (1, 4.5, 6, 4.5, 3, 2)\mbox{ i }(1, 2, 5, 6, 3.5, 3.5) \]

Comprovem-ho:

cor(BMI,Chol,method="spearman")

## [1] 0.6470588

cor(c(1,4.5,6,4.5,3,2),c(1,2,5,6,3.5,3.5))

## [1] 0.6470588

9.2.5 Contrastos de correlació

En un contrast de correlació de dues variables poblacionals contínues $X$ i $Y$, la hipòtesi nul·la és que no hi ha correlació entre les dues variables, la qual cosa tradueix que no hi ha cap relació entre elles. \[ \left\{ \begin{array}{ll} H_0: & \rho_{XY}=0\\ H_1: & \rho_{XY}> 0\text{ o }\rho_{XY}< 0\text{ o }\rho_{XY}\neq 0 \end{array}\right. \]

Si en un contrast de correlació rebutjam la hipòtesi nul·la, en particular concloem que les variables $X$ i $Y$ són dependents (perquè si fossin independents, la seva correlació seria 0).

No explicarem com es fa a mà aquest contrast ni quines hipòtesis han de satisfer les variables poblacionals per que el resultat sigui fiable. Si estau interessats en el detall, podeu consultar la corresponent entrada de la Wikipedia. Simplement heu de saber que s’efectua amb la funció cor.test. La seva sintaxi és similar a la de les altres funcions que efectuen contrastos.

Exemple 9.8 Volem contrastar si hi ha correlació positiva entre el BMI i el nivell de colesterol d’un adult sa, amb un nivell de significació del 5%.

Variables poblacionals d’interès:

$\mathit{BMI}$: “Prenem un adult sa i anotam el seu BMI”
$\mathit{Chol}$: “Prenem un adult sa i anotam el nivell de colesterol en mg/dl”

Contrast: \[ \left\{ \begin{array}{ll} H_0: & \rho_{\textit{BMI,Chol}}=0\\ H_1: & \rho_{\textit{BMI,Chol}}>0 \end{array}\right. \]

Emprarem les mostres BMI i Chol de l’Exemple9.4.

cor.test(BMI,Chol,alternative="greater")

## 
##  Pearson's product-moment correlation
## 
## data:  BMI and Chol
## t = 1.949, df = 4, p-value = 0.06155
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
##  -0.08621998  1.00000000
## sample estimates:
##       cor 
## 0.6979141

Conclusió: No hem obtingut evidència estadísticament significativa que el BMI i el nivell de colesterol d’un adult sa tenguin correlació positiva (test de correlació, p-valor 0.06, IC 95% per a $\rho$ de -0.086 a 1).

La conclusió és que no hem obtingut evidència que el BMI i el nivell de colesterol tenguin correlació positiva a la població dels adults sans. No a la nostra mostra, que sí que ha donat correlació positiva. Recordau que els contrastos sempre refereixen a la població.

9.3 Test de la lliçó 9

(1) La covariància de dues variables aleatòries (marcau totes les continuacions correctes)

És sempre més gran o igual que 0
Mesura la tendència general de les dues variables a créixer (o decréixer) conjuntament
Mesura la tendència de les dues variables a créixer (o decréixer) conjuntament segons una funció lineal
Si val 0, les dues variables són independents
És el quocient de les variàncies de les dues variables aleatòries
Si les dues variables són independents, val 0
Totes les altres respostes són incorrectes

(2) La correlació de Pearson de dues variables aleatòries (marcau totes les continuacions correctes)

Mesura la tendència general de les dues variables a créixer (o decréixer) conjuntament
Mesura la tendència de les dues variables a créixer (o decréixer) conjuntament segons una funció lineal
És l’arrel quadrada de la covariància
Si val 0, les dues variables són independents
Si les dues variables són independents, val 0
Totes les altres respostes són incorrectes

(3) Quins valors pot prendre el coeficient de correlació de Pearson de dues variables quantitatives?

Qualsevol valor real
Qualsevol valor real més gran o igual que 0
Qualsevol valor real més gran o igual que 0, i també $\infty$
Qualsevol valor real entre -1 i 1
Qualsevol valor real entre 0 i 1
Els valors 0, -1 i 1
Totes les altres respostes són falses

(4) Quina, o quines, de les mesures següents serveix per quantificar la dispersió d’una variable aleatòria?

La covariància amb una variable constant
El p-valor d’un test khi quadrat
La variància mostral
La mitjana
La desviació típica
La variància
La correlació de Pearson amb una variable constant

(5) Una covariància -0.7 entre dues variables $X$ i $Y$ indica (marcau una sola resposta):

Que un augment de $X$ sol anar associat a un augment de $Y$
Que un augment de $X$ sol causar un augment de $Y$
Que un augment de $X$ sol anar associat a una disminució de $Y$
Que un augment de $X$ sol causar una disminució de $Y$
Que les variables $X$ i $Y$ són independents

(6) La covariància mostral de dos vectors (marcau totes les continuacions correctes):

Només està definida per a vectors de la mateixa longitud
Pot prendre qualsevol valor real
Només pot prendre valors entre -1 i 1
És la correlació de Pearson dividida pel producte de les desviacions típiques mostrals dels vectors
Si els vectors són $(x_1,\ldots ,x_n)$ i $(y_1,\ldots ,y_n)$, mesura la tendència dels punts $(x_i,y_i)$ a estar sobre una recta
S’obté multiplicant per $n-1$ i dividint per $n$ la covariància “a seques” dels vectors
Estima la covariància de les variables aleatòries que han produït els vectors
Totes les altres respostes són incorrectes

(7) La correlació de Pearson de dos vectors (marcau totes les continuacions correctes):

Només està definida per a vectors de la mateixa longitud
Pot prendre qualsevol valor real
Només pot prendre valors entre -1 i 1
És la covariància mostral dividida pel producte de les desviacions típiques dels vectors
Si els vectors són $(x_1,\ldots ,x_n)$ i $(y_1,\ldots ,y_n)$, mesura la tendència dels punts $(x_i,y_i)$ a estar sobre una recta
S’obté multiplicant per $n$ i dividint per $n-1$ la correlació mostral de Pearson dels vectors
Estima la correlació de les variables aleatòries que han produït els vectors
Totes les altres respostes són incorrectes

(8) Quines de les matrius següents són matrius de correlacions de Pearson d’alguna parella de vectors? \[ \begin{array}{ccccc} \left(\begin{array}{ccc} 1 & 1\cr 1 & 1 \end{array}\right) & \left(\begin{array}{ccc} 1 & 1.2 \cr 1.2 & 1 \end{array}\right) & \left(\begin{array}{ccc} 1 & 0.8\cr -0.8 & 1 \end{array}\right) & \left(\begin{array}{ccc} 0.6 & 0.8\cr 0.8 & 0.6 \end{array}\right) & \left(\begin{array}{ccc} 1 & 0\cr 0 & 1 \end{array}\right)\\ \text{(a)} & \text{(b)} & \text{(c)} & \text{(d)} & \text{(e)} \end{array} \] Marcau totes les respostes correctes:

La (a)
La (b)
La (c)
La (d)
La (e)
Cap

(9) La correlació de Pearson de dos vectors (marcau totes les continuacions correctes, haureu de pensar un poc):

No varia si sumam a un dels vectors una constant
No varia si multiplicam un dels vectors per una constant $>0$
No varia si multiplicam un dels vectors per una constant diferent de 0
No varia si multiplicam els dos vectors per la mateixa constant diferent de 0
Totes les altres respostes són incorrectes

(10) Un contrast de correlació de Pearson (marcau totes les continuacions correctes):

Té sempre com a hipòtesi nul·la que les dues variables tenen correlació de Pearson 0
Té sempre com a hipòtesi nul·la que les dues variables tenen correlació de Pearson positiva
Té sempre com a hipòtesi alternativa que els dos vectors tenen correlació de Pearson 0
Té sempre com a hipòtesi alternativa que els dos vectors tenen correlació de Pearson positiva
També es pot usar per comparar amb 0 la covariància poblacional
Totes les altres respostes són incorrectes

(11) Volem contrastar si el nivell mitjà de colesterol en sang (mesurat en mg/dl) és igual, o no, en els pacients que presenten accidents cardiovasculars que en els pacients que no en presenten a partir de dues mostres independents de 100 individus cadascuna. Quina prova estadística és la més apropiada? Marcau una sola resposta.

Un contrast de correlació de Spearman
Un test t
Un test khi quadrat
Un contrast de correlació de Pearson
Un test exacte de Fisher

(12) En un contrast de correlació entre xifres de colesterol lligat a lipoproteïnes de baixa densitat i la reducció del diàmetre de les artèries coronàries s’ha observat una $R$ de 0.14, amb un p-valor menor de 0.01. Quina és la interpretació més correcta?

Existeix una correlació forta entre els dos vectors, però no és estadísticament significativa
Existeix una correlació feble positiva entre els dos vectors, però és estadísticament significativa
Existeix una correlació forta entre els dos vectors i és estadísticament significativa
L’augment de les xifres de colesterol lligat a proteïnes de baixa densitat provoca l’augment del diàmetre de les artèries coronàries
L’augment del diàmetre de les artèries coronàries causa l’augment de les xifres de colesterol lligat a proteïnes de baixa densitat

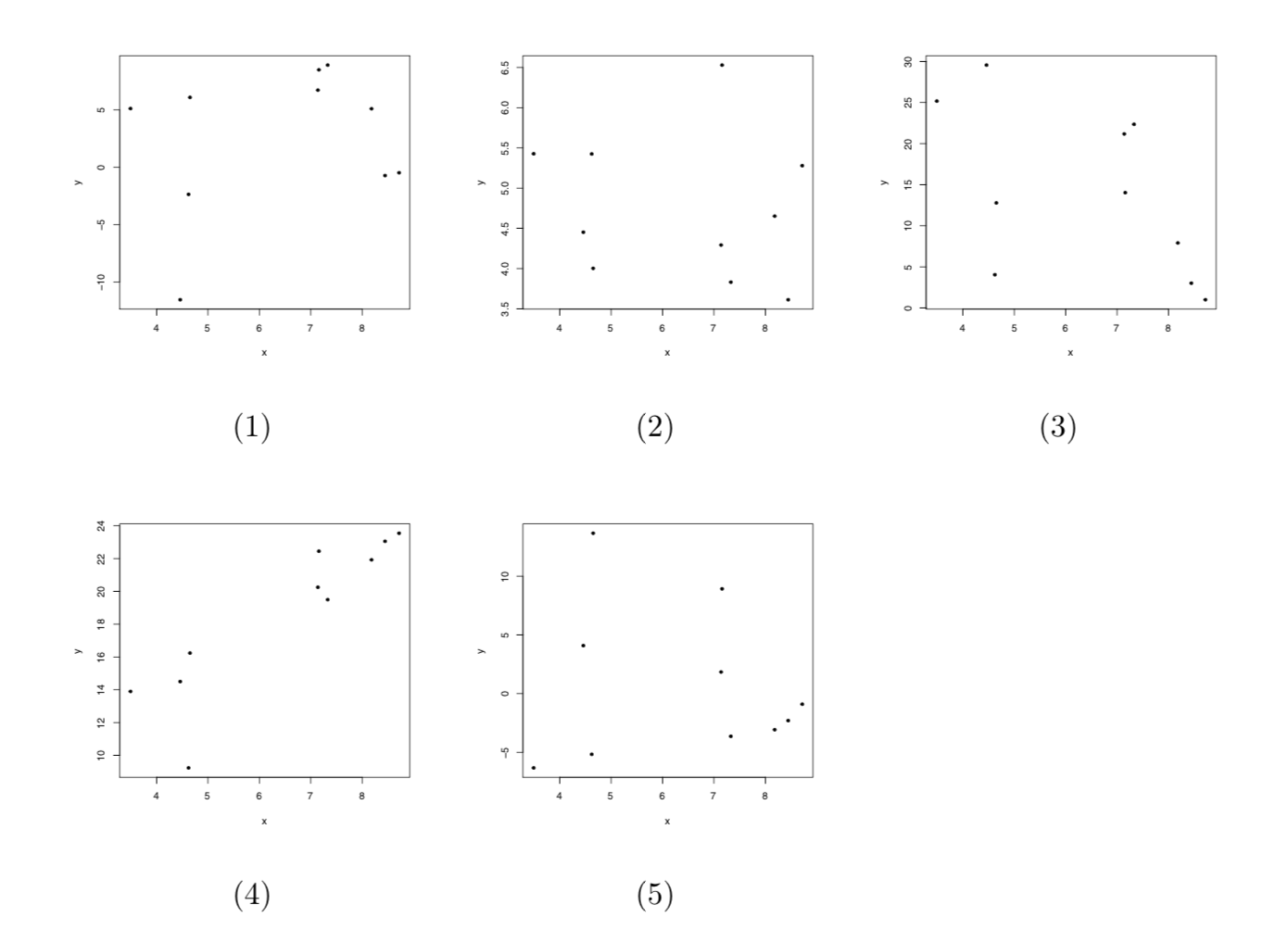
Figura 9.3: Gràfics de dispersió de les preguntes (14) a (18)

(13) Dels gràfics de dispersió de la figura, quin correspon a $R=-0.5$?

El (a)
El (b)
El (c)
El (d)
El (e)

(14) Dels gràfics de dispersió de la figura, quin correspon a $R=-0.1$?

El (a)
El (b)
El (c)
El (d)
El (e)

(15) Dels gràfics de dispersió de la figura, quin correspon a $R=0.1$?

El (a)
El (b)
El (c)
El (d)
El (e)

(16) Dels gràfics de dispersió de la figura, quin correspon a $R=0.5$?

El (a)
El (b)
El (c)
El (d)
El (e)

(17) Dels gràfics de dispersió de la figura, quin correspon a $R=0.9$?

El (a)
El (b)
El (c)
El (d)
El (e)

(18) Quin és el rang dels valors 2 al vector $(-1, -1, 1, -2, -1, 1, 3, 1, 1, 2, 1, 2, 1, 3)$?

4
11
11.5
12
11 i 12
Cap dels anteriors