Tema 3 Intervals de confiança

L’estimació puntual ens dóna el valor d’una característica d’una població, però no ens indica l’error que es comet amb aquesta estimació. A la pràctica, el que se sol fer és complementar una estimació puntual amb un interval que mesuri la precisió de l’estimació. Aquesta precisió depèn:

  • De la variabilitat de la variable aleatòria d’interès: \(\sigma_X\)

  • De la mida de la mostra: \(n\)

  • De la variabilitat de l’estimador (que segurament depèn de les dues anteriors): \(\sigma_{\overline{X}}\), \(\sigma_{\widehat{p}_X}\)…

  • Del nivell de confiança, o seguretat, de l’estimació: com de segurs volem estar que l’estimació és correcta

3.1 Definicions bàsiques

Un interval de confiança del Q% (abreviadament, un IC Q%) d’un paràmetre poblacional és un interval obtingut aplicant a una mostra aleatòria simple de mida \(n\) una fórmula que satisfà la propietat següent:

L’interval obtingut conté el valor del paràmetre poblacional el Q% de les vegades que l’aplicam sobre mostres aleatòries simples de mida \(n\) preses a l’atzar

Tenir una confiança del Q% significa doncs que empram una fórmula que encerta el Q% de les vegades; o, per ser precisos, el Q% de les vegades que l’aplicam bé. Però assumim que un (100-Q)% de les vegades que l’aplicam ens equivocam, i no sabem quin és el nostre cas.

Exemple 3.1 En un experiment hem mesurat el percentatge d’augment d’alcohol en sang a 40 persones després de prendre 4 canyes de cervesa. La mitjana i la desviació típica mostral d’aquests percentatges d’increment han estat \(\overline{x}=41.2\) i \(\widetilde{s}=2.1\). Com veurem a l’Exemple 3.3, un IC 95% per al percentatge d’augment mitjà d’alcohol en sang d’una persona després de beure 4 canyes de cervesa és [40.53, 41.87].

Això significa que estam segurs al 95% que l’augment mitjà d’alcohol en sang d’una persona després de beure 4 canyes de cervesa està entre el 40.53% i el 41.87%, perquè aquest interval l’haurem calculat amb una fórmula que el 95% de les vegades que l’aplicam (bé) sobre mostres aleatòries de 40 persones dóna un interval que conté la mitjana poblacional que volem estimar. Nosaltres som optimistes i “confiam” estar dins aquest 95% d’encerts.

No confongueu:

  • Interval de referència del Q% per a una variable aleatòria: Interval que conté el valor de la variable aleatòria en un individu amb probabilitat Q%.

  • Interval de confiança del Q% per a un paràmetre: Interval que conté el valor poblacional del paràmetre de la variable aleatòria “amb probabilitat” Q%, en el sentit que l’hem calculat amb una fórmula que dóna un interval que conté el paràmetre el Q% de les vegades que l’aplicam a una mostra aleatòria.

  • Interval de referència del Q% per a un estimador: Interval que conté el valor de l’estimador sobre una mostra aleatòria amb probabilitat Q%.

Per exemple:

  • Si diem que un interval de referència del 95% per a la concentració d’una proteïna en sèrum en individus sans mesurada en g/dl és [11,16], això significa significa que un 95% dels individus sans tenen una concentració d’aquesta proteïna en sèrum entre 11 i 16 g/dl, o, equivalentment, que un individu sa escollit a l’atzar té, amb un 95% de probabilitat, una concentració d’aquesta proteïna en sèrum entre 11 i 16 g/dl

  • Si diem que un interval de confiança del 95% per a la concentració mitjana d’una proteïna en sèrum en individus sans mesurada en g/dl és [11,16], això significa que hem pres una mostra aleatòria de concentracions d’aquesta proteïna en sèrum en individus sans i a partir d’aquesta mostra hem estimat que, amb un 95% de confiança, la concentració mitjana d’aquesta proteïna en sèrum en individus sans està entre 11 i 16 g/dl (i tenim un 95% de confiança en aquest interval perquè l’hem calculat amb una fórmula que dóna un interval que conté la mitjana poblacional un 95% de les vegades que l’empram sobre mostres aleatòries de la mateixa mida que la nostra).

  • Si diem que el 95% de les mostres de 100 concentracions d’una determinada proteïna en sèrum en individus sans tenen la mitjana mostral entre 11 i 16, això és un interval de referència del 95% per a la mitjana mostral de mostres de mida 100, no un interval de confiança per a la concentració mitjana poblacional ni un interval de referència per al valor de la concentració en un individu.

Que un IC Q% per a un paràmetre \(\theta\) sigui \([a,b]\) serveix:

  • Per estimar \(\theta\) amb aquest marge de confiança: Estam bastant segurs que el valor poblacional de \(\theta\) està entre \(a\) i \(b\) (la fórmula emprada encerta sovint)

  • Per poder comparar el valor poblacional de \(\theta\) amb un valor concret amb aquest marge de confiança: Estam bastant segurs que el valor real de \(\theta\) no està ni per sota de \(a\) ni per sobre de \(b\) i per tant que és diferent de tots aquests valors

Per exemple: si un IC 95% per a la prevalència \(p\) d’una determinada característica en una població (la fracció d’individus que tenen aquesta característica) va de 0.025 a 0.047:

  • Estam molt (“un 95%”) segurs que \(p\in [0.025,0.047]\) (perquè la fórmula emprada per calcular aquest interval encerta en un 95% de les vegades)

  • Estam molt segurs que \(p>0.02\) (perquè tot l’interval on estam molt segurs que cau el valor real de \(p\) està a la dreta de 0.02)

  • Estam molt segurs que \(p\neq 0.05\) (perquè 0.05 no pertany a l’interval on estam molt segurs que cau el valor real de \(p\))

  • Però no estam molt segurs que \(p=0.03\), per molt que \(0.03\in [0.025,0.047]\): estam molt segurs que \(p\) està entre 0.025 i 0.047, però no tenim cap seguretat que valgui un valor concret entre aquests límits, només que està entre aquests límits.

Hi ha dos tipus de mètodes bàsics de càlcul d’intervals de confiança a partir d’una mostra aleatòria:

  • Paramètrics: Usant alguna fórmula basada en la distribució mostral de l’estimador

    • Es basen en teoremes

    • Només serveixen si la variable aleatòria \(X\) i la mostra aleatòria satisfan (aproximadament) les hipòtesis del teorema

  • No paramètrics: El més emprat és el bootstrap:

    • De la mostra, es prenen a l’atzar moltes (milers) mostres aleatòries simples de la mateixa mida que la mostra, es calcula l’estimador amb cada una d’aquestes mostres i s’usa el vector de resultats per estimar un interval de confiança (per exemple, podríem prendre com a IC 95% l’interval entre els quantils 0.025 i 0.975 d’aquest vector)

    • Es pot usar sempre (si la mostra és aleatòria)

    • Empra un procés aleatori: en cada execució sobre les mateixes dades pot donar un interval diferent

El bootstrap és una eina molt poderosa per calcular intervals de confiança i, en general, per estimar la distribució mostral d’un estadístic. Tant, que a la pràctica ja comença a substituir els mètodes paramètrics. Emperò no fa miracles: si la mostra és petita o molt poc representativa de la població, un IC calculat amb el bootstrap servei de tan poc com un de calculat amb un mètode paramètric.

3.2 Exemple: Interval de confiança del 95% per a la mitjana d’una variable aleatòria normal

Una de les fórmules més conegudes per a intervals de confiança és la següent:

Si \(X\sim N(\mu,\sigma)\) i en tenim una mostra aleatòria simple de mida \(n\), mitjana mostral \(\overline{X}\) i variància mostral \(\widetilde{S}^2_X\), un IC 95% per a \(\mu\) és \[ \Bigg[\overline{X}-t_{n-1,0.975}\cdot \frac{\widetilde{S}_X}{\sqrt{n}},\ \overline{X}+t_{n-1,0.975}\cdot\frac{\widetilde{S}_X}{\sqrt{n}}\Bigg] \] on \(t_{n-1,0.975}\) indica el 0.975-quantil de la distribució \(t_{n-1}\).
A alguns de vosaltres us hauran explicat a Batxillerat, o trobareu a llibres que consulteu, una fórmula per a l’IC 95% per a \(\mu\) similar a aquesta, però canviant-hi la \(\widetilde{S}_X\) per \(\sigma\) i el \(t_{n-1,0.975}\) per \(z_{0.975}\). Aquesta altra fórmula només es pot fer servir si coneixeu la desviació típica poblacional \(\sigma\), que a la pràctica, mai serà el cas. Per tant, per favor, oblidau-la.

Anem a explicar d’on surt aquesta fórmula, ja que és un paradigma de com s’obtenen la majoria de les fórmules paramètriques per a intervals de confiança.

Suposem doncs que \(X\sim N(\mu,\sigma)\) i que en tenim una mostra aleatòria simple de mida \(n\), mitjana mostral \(\overline{X}\) i variància mostral \(\widetilde{S}^2_X\). En aquesta situació, sabem que \[ T=\frac{\overline{X}-\mu}{\widetilde{S}_{X}/\sqrt{n}} \] té distribució t de Student amb \(n-1\) graus de llibertat, \(t_{n-1}\).

Si podem trobar \(A,B\in \mathbb{R}\) tals que \[ P(A\leqslant T\leqslant B)=0.95, \] llavors: \[ \begin{array}{rl} 0.95 & =P\Bigg(A\leqslant\dfrac{\overline{X}-\mu}{\widetilde{S}_{X}/\sqrt{n}}\leqslant B\Bigg)\\[2ex] & =P\Bigg(A\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\leqslant\overline{X}-\mu \leqslant B\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\Bigg)\\[2ex] & =P\Bigg(-\overline{X}+A\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\leqslant-\mu \leqslant-\overline{X}+B\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\Bigg)\\[2ex] & =P\Bigg(\overline{X}-B\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\leqslant\mu \leqslant\overline{X}-A\cdot \dfrac{\widetilde{S}_X}{\sqrt{n}}\Bigg) \end{array} \]

Com que \(P(A\leqslant T\leqslant B)=0.95\) significa que per al 95% de les mostres aleatòries simples de mida \(n\) el valor de \(T\) està entre \(A\) i \(B\), \[ P\Bigg(\overline{X}-B\cdot \frac{\widetilde{S}_X}{\sqrt{n}}\leqslant\mu \leqslant\overline{X}-A\cdot \frac{\widetilde{S}_X}{\sqrt{n}}\Bigg)=0.95 \] significa que per al 95% de les mostres aleatòries simples de mida \(n\) la \(\mu\) cau dins l’interval \[ \Bigg[\overline{X}-B\cdot \frac{\widetilde{S}_X}{\sqrt{n}},\ \overline{X}-A\cdot \frac{\widetilde{S}_X}{\sqrt{n}}\Bigg] \] Per tant, això serà un IC 95% per a \(\mu\).

Ens falta trobar els \(A,B\) tals que \(P(A\leqslant T\leqslant B)=0.95\). Per trobar-los, emprarem quantils de la distribució de \(T\). Recordem que si indicam amb \(t_{n-1,0.975}\) el 0.975-quantil d’una \(t_{n-1}\), per definició tenim que \[ P(T\leqslant t_{n-1,0.975})=0.975 \] i per la simetria de la \(t\), \[ P(T\leqslant-t_{n-1,0.975})=P(T\geqslant t_{n-1,0.975})=0.025 \] Per tant: \[ \begin{array}{l} P(-t_{n-1,0.975}\leqslant T\leqslant t_{n-1,0.975})\\ \quad =P(T\leqslant t_{n-1,0.975})-P(T\leqslant-t_{n-1,0.975})\\ \quad =0.975-0.025=0.95 \end{array} \]

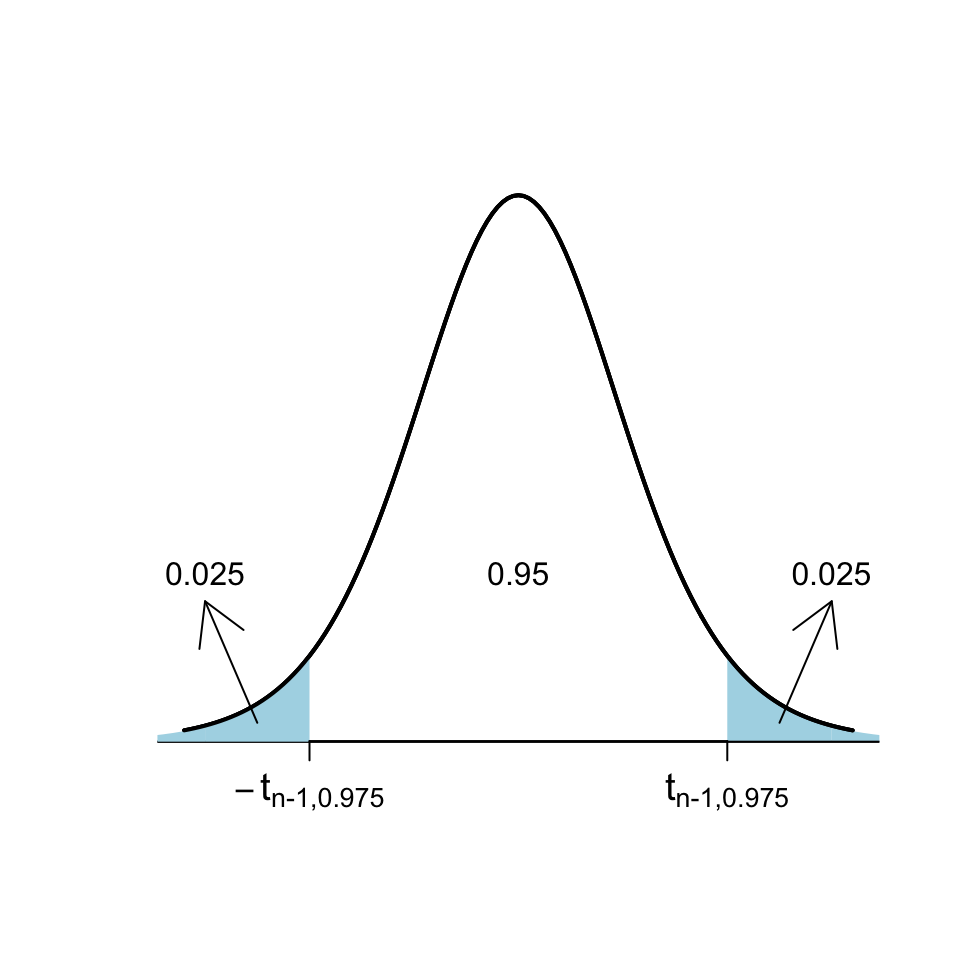
Així doncs, podem prendre \[ A=-t_{n-1,0.975},\quad B=t_{n-1,0.975} \] i obtenim l’IC 95% per a \(\mu\) anunciat: \[ \Bigg[\overline{X}-t_{n-1,0.975}\cdot \frac{\widetilde{S}_X}{\sqrt{n}},\ \overline{X}+t_{n-1,0.975}\cdot\frac{\widetilde{S}_X}{\sqrt{n}}\Bigg] \]

L’escriurem \[ \overline{X}\pm t_{n-1,0.975}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \]

Exemple 3.2 Fem un experiment per veure que, efectivament, aquesta fórmula “encerta”, en el sentit que conté la \(\mu\), al voltant del 95% de les vegades. Al bloc de codi següent: generam una Població de 107 “individus” que segueixen una llei normal estàndard i en calculam la mitjana mu; definim una funció IC que calcula l’IC 95% per a la mitjana \(\mu\) amb la fórmula anterior; prenem 200 mostres aleatòries simples de mida 50 de la nostra població i les aplicam aquesta funció, obtenint una matriu M de 200 columnes formades pels dos extrems dels intervals (l’inferior a la primera filera i el superior a la segona filera); finalment, miram quantes vegades hem encertat, és a dir, a quantes columnes de M la mitjana poblacional mu està entre l’entrada de la primera filera i la de la segona.

## [1] 189

Hem encertat 189 vegades, és a dir, un 94.5% de les vegades. És aproximadament el que esperàvem. Si ho provau amb altres llavors d’aleatorietat obtendreu altres resultats, de vegades millors, de vegades pitjors.

Per veure millor els encerts, dibuixam els intervals en un gràfic, on apareixeran en gris els que encerten i en vermell els que no encerten.

Atenció! De mitjana, un IC Q% NO conté el valor real del paràmetre en un (100-Q)% de les ocasions.

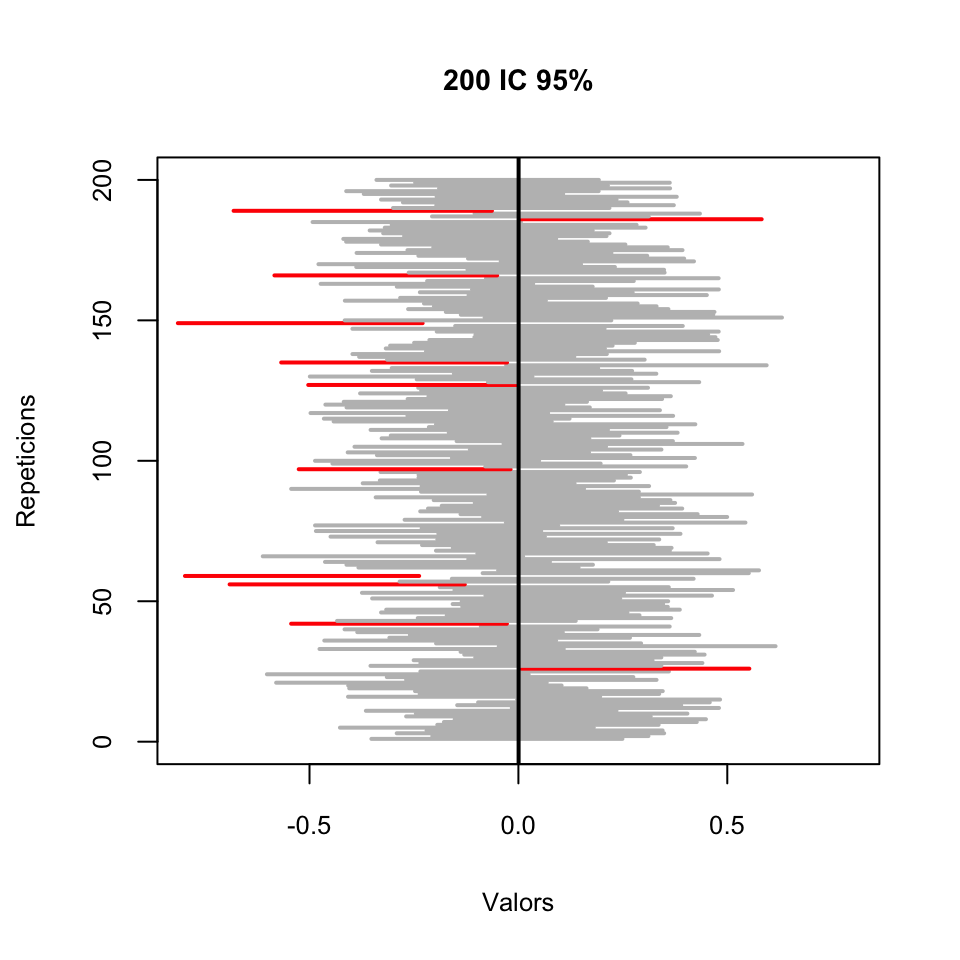
Per exemple, de mitjana, un 5% de les vegades que calculam un IC 95%, el paràmetre poblacional no pertany a l’interval obtingut. Per tant, si calculam \(n\) IC 95% sobre mostres aleatòries simples independents, el nombre de vegades que l’interval resultant no contendrà el paràmetre poblacional seguirà una distribució binomial \(B(n,0.05)\). El gràfic següent dóna el valor de \(P(X\geqslant 1)\) per a una variable aleatòria \(X\) de tipus \(B(n,0.05)\), per a \(n=0,...,100\), i per tant la probabilitat que si calculam \(n\) IC 95% sobre mostres aleatòries simples independents, almenys un d’ells no contengui el paràmetre poblacional desitjat.

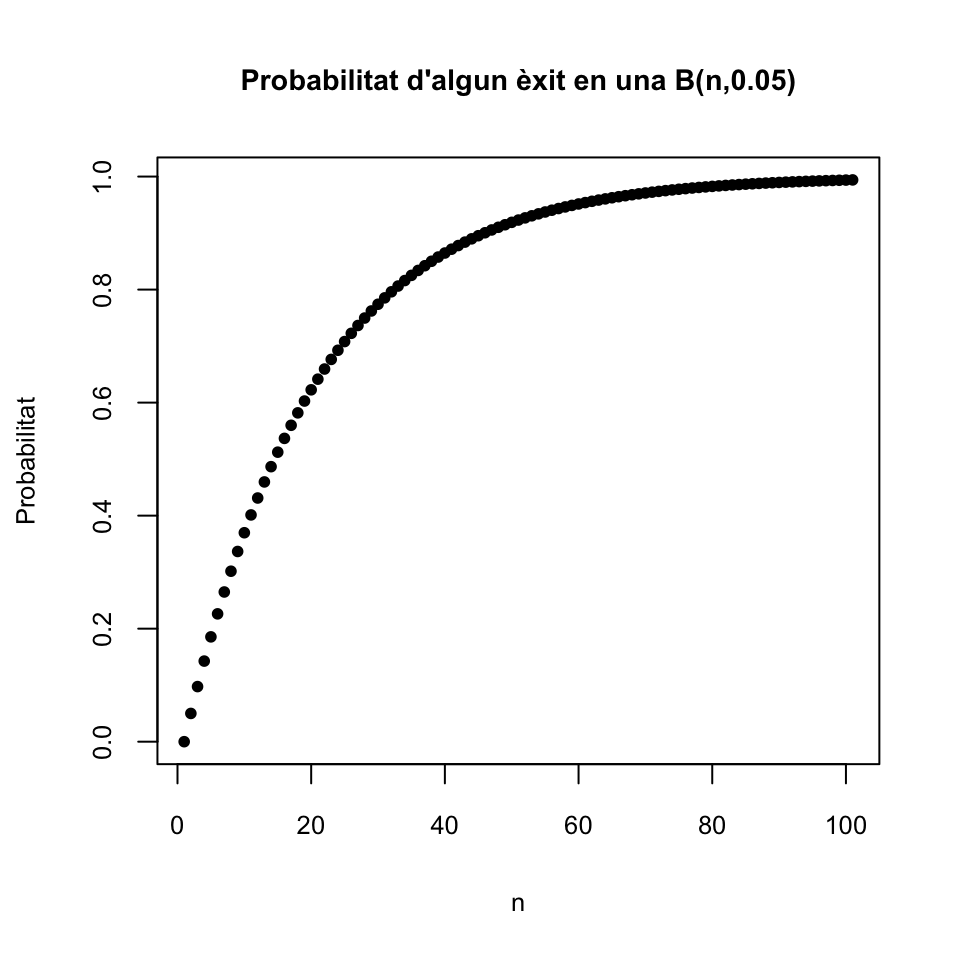
Tornant a l’IC 95% per a \(\mu\) d’una variable normal donat per la fórmula \[ \overline{X}\pm t_{n-1,0.975}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \] fixau-vos que:

  • Està centrat en \(\overline{X}\), per tant en cada càlcul estarà centrat en la mitjana mostral

  • Tal i com l’hem calculat, la probabilitat que \(\mu\) caigui fora d’aquest interval es reparteix per igual als dos costats: un 2.5% de les vegades la \(\mu\) poblacional estarà a l’esquerra de l’extrem inferior i un 2.5% de les vegades estarà a la dreta de l’extrem superior

Exemple 3.3 En un experiment hem mesurat el percentatge d’augment d’alcohol en sang a 40 persones després de prendre 4 canyes de cervesa. La mitjana i la desviació típica mostral d’aquests percentatges d’increment han estat \[ \overline{x}=41.2,\quad \widetilde{s}=2.1 \]

Per calcular un IC 95% per al percentatge mitjà d’augment, suposarem que la variable aleatòria d’interès (de la que volem estimar la mitjana)

  • \(X\): “Prenem una persona i li mesuram el percentatge d’augment d’alcohol en sang després de prendre 4 canyes de cervesa”

és normal i que la mostra que hem pres d’aquesta variable és aleatòria simple.

Llavors, com que \(t_{n-1,0.975}\)=qt(0.975,39)=2.0227, un IC 95% és \[ 41.2\pm 2.0227\cdot \frac{2.1}{\sqrt{40}}\Rightarrow 41.2\pm 0.67\Rightarrow [40.53, 41.87] \]

Per tant, estimam amb un 95% de confiança que el percentatge mitjà d’augment d’alcohol en sang després de prendre 4 canyes de cervesa està entre el 40.53% i el 41.87%.

Per calcular l’interval anterior hem suposat que la variable poblacional “Percentatge d’augment d’alcohol en sang després de prendre 4 canyes de cervesa” segueix una distribució normal. I si no fos normal?

  • En aquest cas, com que \(n=40\), és gran pel Teorema 3.2 de la propera secció l’interval obtingut segueix essent (aproximadament) un interval de confiança del 95% per a \(\mu\)

  • Si \(n\) fos petit i \(X\) molt diferent d’una normal, no es pot usar aquesta fórmula i cal buscar-se la vida (per exemple, emprar el mètode de bootstrap)

També hem suposat que era una mostra aleatòria simple. I si no ho és?

  • Si és aleatòria, com que el nombre de persones que poden prendre 4 canyes de cervesa és pràcticament la població mundial, molt gran, a efectes pràctics la podem considerar simple.

  • Però segur que no és aleatòria, sinó oportunista. No hem tret per sorteig de la llista de tota la població mundial, ni tan sols de la de Mallorca, 40 persones i les hem fetes prendre 4 cerveses, sinó que hem cercat voluntaris. En aquest cas no podem fer res per salvar la fórmula, i la seva validesa depèn de si la mostra de persones presa pot passar per aleatòria o no.

3.3 Interval de confiança per a la mitjana basat en la t de Student

A partir d’ara, per tal d’evitar ambigüitats, a les fórmules hi expressarem el nivell de confiança dels intervals en tant per u, no en tant per cent; és a dir, com una proporció en comptes de com un percentatge. Per tant, parlarem d’intervals de confiança de nivell de confiança \(q\), amb \(q\) entre 0 i 1, en lloc d’intervals de confiança del \(Q\%\) amb \(Q=100q\). Amb aquestes notacions, per exemple, els intervals de confiança del 95% seran intervals de confiança de nivell de confiança 0.95.

La fórmula

El mateix argument que abans, canviant 0.95 per \(q\) dóna:

Teorema 3.1 Si \(X\sim N(\mu,\sigma)\) i en prenem una mostra aleatòria simple de mida \(n\), un interval de confiança de nivell de confiança \(q\) (en tant per u) per a \(\mu\) és \[ \overline{X}\pm t_{n-1,(1+q)/2}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \]

Fixau-vos que als IC 95%, \(q=0.95\) i per tant \((1+q)/2=1.95/2=0.975\).

Usant el Teorema Central del Límit i algunes aproximacions, tenim el següent resultat:

Teorema 3.2 Sigui \(X\) una variable aleatòria qualsevol de mitjana poblacional \(\mu\). Suposem que prenem una mostra aleatòria simple de \(X\) de mida \(n\) gran (diguem, de 40 o més elements). Llavors, un interval de confiança de nivell de confiança \(q\) per a \(\mu\) és aproximadament \[ \overline{X}\pm t_{n-1,(1+q)/2}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \]

L’aproximació del teorema anterior és millor com més gran sigui \(n\) o com més propera a una normal sigui la variable poblacional \(X\).

En resum:
Podem emprar la fórmula per a l’interval de confiança de nivell de confiança \(q\) per a la mitjana poblacional basada en la t de Student \[ \overline{X}\pm t_{n-1,(1+q)/2}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \] quan la variable poblacional és normal o quan la mostra aleatòria simple és gran.

Exemple 3.4 L’empresa RX-print ofereix una impressora de radiografies d’altíssima qualitat. En la seva publicitat afirma que els seus cartutxos imprimeixen una mitjana de 500 radiografies amb l’especificació:

Dades tècniques: Mostra de mida \(n=25\), població suposada normal, nivell de confiança del 90%

Uns radiòlegs desitgen comprovar aquestes afirmacions i prenen una mostra de cartutxos a l’atzar de mida \(n=25\), obtenint una mitjana de \(\overline{x}=518\) radiografies i una desviació típica mostral \(\widetilde{s}=39.9\).

Amb aquesta mostra, la mitjana poblacional anunciada pel fabricant cau dins l’interval de confiança del 90%?

La variable aleatòria d’interès és \(X\) és “Prenem un cartutxo d’aquesta empresa i miram el nombre de radiografies que permet imprimir”, de mitjana \(\mu\) per a la qual volem calcular un IC 90%. Suposarem que la variable \(X\) és normal, perquè l’empresa ho suposa a les dades tècniques. Per tant podem emprar la fórmula \[ \overline{x}\pm t_{n-1,(q+1)/2} \frac{\widetilde{s}}{\sqrt{n}} \] on \(n=25\), \(\overline{x}=518\), \(\widetilde{s}=39.9\), \(q=0.9\), \((q+1)/2=0.95\) i \(t_{24,0.95}\)=qt(0.95,24)\(=1.71\).

Operant: \[ 518\pm 1.71\times \frac{39.9}{\sqrt{25}}\Rightarrow 518\pm 13.65\Rightarrow [504.35,531.65] \] Tenim, doncs, un 95% de confiança que el nombre mitjà de radiografies per cartutxo està entre 504.35 i 531.65, i en particular que no és 500 (però en benefici del consumidor: estam molt segurs que és més gran que 500).

Exemple 3.5 A l’exemple anterior hem suposat que la variable aleatòria era normal. Què passaria si fos molt diferent d’una normal?

Com que \(n=25\) no és prou gran, en principi no podríem aplicar la fórmula de l’interval de confiança basada en la t de Student. Emprarem el mètode del bootstrap, per a la qual cosa necessitam tenir les dades originals, i no només els seus estadístics. Tenim aquestes dades en el vector Radios següent:

## [1] 518
## [1] 39.89987

Prenem 5000 mostres aleatòries simples de mida 25 (la mateixa mida que el conjunt de dades original) de les dades i calculam la mitjana de cada mostra; fixam la llavor d’aleatorietat per que el càlcul sigui reproduïble:

Ara prenem com a IC 90% l’interval que tanca el 90% de valors centrals d’aquest vector de mitjanes mostrals, és a dir, l’interval que va del quantil 0.05 al quantil 0.95 d’aquest vector de mitjanes:

##     5%    95% 
## 504.96 530.92

Obtenim l’interval [504.96,530.92]: amb la fórmula basada en la t de Student, havíem obtingut l’interval [504.35,531.65].

Algunes consideracions

Observau que l’estructura de l’interval de confiança de nivell de confiança \(q\) per a \(\mu\) donat al Teorema 3.2 és \[\begin{align} & \text{estimador}\nonumber\\ & \qquad \pm \frac{1+q}{2}\text{-quantil de la distr. mostral}\times \text{error típic de l'estimació} \tag{3.1} \end{align}\]

Aquesta estructura és molt típica (tot i que, com veurem, no tots els intervals de confiança paramètrics tenen aquesta forma) i satisfà que:

  • L’interval de confiança està centrat en el valor de l’estimador

  • La “probabilitat d’equivocar-nos” es reparteix per igual als dos costats de l’interval: una fracció \(q/2\) de les vegades el paràmetre estarà a l’esquerra de l’extrem inferior i una fracció \(q/2\) de les vegades estarà a la dreta de l’extrem superior

A més, tenim que:

  • Per a una mateixa mostra i una mateixa fórmula (paramètrica) per calcular l’interval de confiança, si el nivell de confiança creix, l’interval s’eixampla

    Això és general, per a tots els intervals de confiança paramètrics. La idea intuitiva és que, per estar més segurs que un interval conté un valor, l’interval ha de ser més ample. A un interval de confiança amb l’estructura (3.1), el motiu matemàtic és que si \(q\) creix, el quantil d’ordre (1+\(q\))/2 de la distribució mostral creix.

    Per exemple, a l’Exemple 3.3, teníem \(n=40\), \(\overline{x}=41.2\) i \(\widetilde{s}=2.1\):

    • L’IC 95% té \(q=0.95\), per tant \(t_{n-1,(1+q)/2}=t_{39,0.975}=2.02\), i donava \[ 41.2\pm 2.02\cdot \frac{2.1}{\sqrt{40}}\Rightarrow 41.2\pm 0.67 \]

    • L’IC 99% té \(q=0.99\), per tant \(t_{n-1,(1+q)/2}=t_{39,0.995}=2.71\), i dóna \[ 41.2\pm 2.71\cdot \frac{2.1}{\sqrt{40}}\Rightarrow 41.2\pm 0.9 \] més ample

  • Però si canviam de mostra (o de fórmula, si n’hi ha més d’una) per calcular l’interval de confiança, pot passar qualsevol cosa.

Amb R

La funció

calcula l’interval de confiança basat en la t de Student per a la \(\mu\) de la variable aleatòria de la que el vector X n’és una mostra. El paràmetre conf.level permet especificar el nivell de confiança (en tant per u). El seu valor per defecte és 0.95, així que per calcular un IC 95% no cal especificar-lo.

Per exemple, l’IC 90% per al nombre mitjà de radiografies per cartutxo de l’Exemple 3.4 es calcularia amb

## [1] 504.3472 531.6528
## attr(,"conf.level")
## [1] 0.9

Càlcul de la mida de la mostra per fixar l’error

Recordem que l’interval de confiança de nivell de confiança \(q\) per a \(\mu\) basat en la t de Student \[ \overline{X}\pm t_{n-1,(1+q)/2}\cdot \frac{\widetilde{S}_X}{\sqrt{n}} \] és simètric i centrat en \(\overline{X}\). La seva amplada és la diferència entre els seus extrems \[ 2t_{n-1,(1+q)/2}\times \frac{\widetilde{S}_X}{\sqrt{n}} \]

El marge d’error (error, precisió) \(M\) en l’estimació de \(\mu\) per mitjà d’aquest interval de confiança és el que sumam i restam a \(\overline{X}\) per obtenir l’interval, és a dir, la meitat de la seva amplada: \[ M=t_{n-1,(1+q)/2}\times \frac{\widetilde{S}_X}{\sqrt{n}} \]

Fixau-vos que si estimam que el valor de \(\mu\) és \(\overline{X}\), l’error que cometem és \(|\overline{X}-\mu|\). Aleshores, si el nostre interval de confiança per a \(\mu\) és \(\overline{X}\pm M\) i l’encertam (és a dir, aquest interval conté el valor real de \(\mu\)), aleshores l’error que cometem quan diem que el valor de \(\mu\) és \(\overline{X}\) és com a màxim \(M\), perquè si \(\mu\in [\overline{X}-M,\overline{X}+M]\), aleshores \(|\overline{X}-\mu|\leqslant M\).

Una pregunta típica a l’hora de planejar un experiment és quina ha de ser la mida de la mostra que hem de prendre per que el marge d’error en estimar \(\mu\) amb un nivell de confiança donat sigui com a màxim un cert valor desitjat \(M_{max}\). És a dir, volem trobar la \(n\) més petita tal que \[ t_{n-1,(1+q)/2}\times \frac{\widetilde{S}_X}{\sqrt{n}}\leqslant M_{max}. \] Però fixau-vos que en aquesta desigualtat la \(n\) hi apareix al quantil i a l’error típic, i a més la \(\widetilde{S}_X\) depèn de la mostra. El que farem per respondre la pregunta serà fer algunes trampes:

  • Aproximarem la t de Student per una normal estàndard (ja que segurament la \(n\) haurà de ser gran): \[ t_{n-1,(1+q)/2}\rightsquigarrow z_{(1+q)/2} \]

  • Estimarem el valor de \(\widetilde{S}_X\) mitjançant la desviació típica mostral \(\widetilde{S}_0\) d’una prova pilot (un experiment anterior, realitzat per nosaltres o publicat per qualcú altre a qualque lloc de confiança)

  • D’aquesta manera, aproximam l’error \(M\) per mitjà de \[ M\approx z_{(1+q)/2}\times \frac{\widetilde{S}_0}{\sqrt{n}} \]

  • I ara si imposam que \(M\leqslant M_{max}\), ja podem aïllar la \(n\):

\[ z_{(1+q)/2}\times \frac{\widetilde{S}_0}{\sqrt{n}}\leqslant M_{max}\Longrightarrow n\geqslant\left(\frac{ z_{(1+q)/2}\cdot \widetilde{S}_0}{M_{max}} \right)^2 \]

En resum:

Teorema 3.3 Per estimar la \(\mu\) amb nivell de confiança \(q\) amb un marge d’error com a màxim \(M_{max}\) mitjançant la fórmula basada en la t de Student, prendrem una mostra de mida \[ n\geqslant\left(\frac{ z_{(1+q)/2}\cdot \widetilde{S}_0}{M_{max}} \right)^2, \] on \(\widetilde{S}_0\) és la desviació típica mostral obtinguda en una estimació anterior de \(\mu\) (en una prova pilot).

Naturalment, quan després prenguem una mostra de mida \(n\) que satisfaci aquesta condició, pot passar qualsevol cosa, ja que hem emprat els resultats d’una mostra per estimar la desviació típica d’una altra mostra i a més hem aproximat els quantils de la t de Student per els d’una normal estàndard, que són més petits. Però almenys haurem fet tot el que haurem pogut per fitar l’error dins el marge desitjat.

Exemple 3.6 A l’Exemple 3.3, hem emprat una mostra de \(n=40\) persones, amb \(\overline{x}=41.2\) i \(\widetilde{s}=2.1\), i l’error ha estat \[ t_{0.975,39}\cdot \frac{2.1}{\sqrt{40}}=0.67 \] Quin és el nombre mínim de persones que hauríem hagut d’emprar per estimar la mitjana amb un nivell de confiança del 95% i un error de (com a màxim) 0.5? És a dir, quin el nombre mínim de persones que hauríem hagut d’emprar per obtenir un IC 95% d’amplada (com a màxim) 1?

Empram l’exemple com a prova pilot: \[ n\geqslant\left(\frac{ z_{(1+q)/2}\cdot \widetilde{s}}{M_{max}} \right)^2= \left(\frac{1.96\cdot 2.1}{0.5} \right)^2=67.77 \]

El valor de \(n\) més petit que satisfà aquesta condició és 68, per tant aquest és el nombre mínim de persones que hauríem hagut d’emprar per esperar obtenir un IC 95% d’amplada (com a màxim) 1.

3.4 Intervals de confiança per a proporcions

Suposem que tenim una variable Bernoulli \(X\) amb probabilitat d’èxit \(p_X\) desconeguda. Volem calcular un interval de confiança per a \(p_X\). Per fer-ho, prenem una mostra aleatòria simple de \(X\) de mida \(n\), amb nombre d’èxits \(S\) i per tant proporció mostral d’èxits \(\widehat{p}_{X}=S/n\)

Explicarem tres mètodes per calcular aquest interval de confiança:

  • El mètode exacte de Clopper-Pearson, que es pot aplicar sempre però sol donar intervals de confiança més amples del necessari.

  • El mètode aproximat de Wilson, que es pot emprar quan la mostra és gran, posem de mida 40 o més, i es basa en el fet que, pel Teorema Central del Límit, la proporció mostral de mostres aleatòries simples segueix una distribució aproximadament normal.

  • El mètode aproximat de Laplace, que és una simplificació del mètode de Wilson, però només es pot emprar quan la mostra és bastant més gran, posem de mida 100 o més, i la proporció mostral \(\widehat{p}_{X}\) no és molt propera a 0 o a 1. És el mètode més clàssic i conegut.

Mètode “exacte” de Clopper-Pearson

Aquest mètode es basa en el fet que el nombre d’èxits \(S\) en mostres aleatòries simples de mida \(n\) de \(X\) segueix una distribució binomial \(B(n,p_X)\). Raonant de manera similar a com obteníem l’interval per a \(\mu\) basat en la t de Student (us estalviarem els detalls) arribam a la fórmula següent:

Teorema 3.4 Un interval de confiança de nivell de confiança \(q\) per a \(p_X\) és \([p_0,p_1]\), on (recordau que \(n\) indica la mida de la mostra i \(S\) el nombre d’èxits)

  • \(p_0\) és la solució de l’equació \[ \sum_{k=S}^n\binom{n}{k}p_0^k(1-p_0)^{n-k}= \frac{1-q}{2} \]

  • \(p_1\) és la solució de l’equació \[ \sum_{k=0}^S\binom{n}{k}p_1^k(1-p_1)^{n-k}= \frac{1-q}{2} \]

Calcular a mà aquest interval és intractable, i en general dóna més ample del necessari (degut a la natura discreta de la distribució binomial, que només pren valors nombres naturals), però es pot emprar amb mostres aleatòries simples de qualsevol mida ja que empra que el nombre d’èxits \(S\) en mostres aleatòries simples de mida \(n\) de \(X\) segueix una distribució binomial i això sempre és veritat.

Per calcular-lo amb R, podeu emprar la funció del paquet epitools

on Sés el nombre d’èxits, n la mida de la mostra, i conf.level el nivell de confiança en tant per u, que per defecte val 0.95.

Exemple 3.7 De 10 pacients tractats amb un medicament, 2 s’han curat. Quin seria un IC 95% per a la proporció p de pacients que aquest medicament cura?

Emprarem el mètode de Clopper-Pearson:

##   x  n proportion lower upper conf.level
## 1 2 10        0.2 0.025 0.556       0.95

Dóna l’interval [0.025,0.556]. Estimam per tant amb una confiança del 95% que aquest medicament cura entre el 2.5% i el 55.6% dels pacients.

Sí, aquest interval és molt ample. La culpa no és del mètode de Clopper-Pearson, és de la mida petita de la mostra.

L’interval de Clopper-Pearson té l’inconvenient que, en general, no està centrat en \(\widehat{p}_{X}\). Per exemple, el centre de l’interval anterior és \((0.025+0.556)/2= 0.29\), diferent de \(\widehat{p}_X=0.2\)

Mètode de Wilson

Suposem ara que prenem una mostra aleatòria simple de \(X\) de mida \(n\) gran (posem, de 40 o més subjectes) i proporció mostral d’èxits \(\widehat{p}_{X}\). En aquestes condicions, pel Teorema Central del Límit, \[ Z=\dfrac{\widehat{p}_{X}-p_X} {\sqrt{\frac{p_X(1-p_X)}{n}}}\approx N(0,1) \] Per tant \[ P\Big(-z_{(1+q)/2}\leqslant\dfrac{\widehat{p}_{X}-p_X} {\sqrt{\frac{p_X(1-p_X)}{n}}}\leqslant z_{(1+q)/2}\Big)=q \]

Aïllant \(p_X\) obtenim:

Teorema 3.5 Si la mida \(n\) de la mostra és gran, un interval de confiança de nivell de confiança \(q\) per a \(p_X\) és (aproximadament): \[ \frac{\widehat{p}_{X}+\frac{z_{(1+q)/{2}}^2}{2n}\pm z_{(1+q)/{2}}\sqrt{\frac{\widehat{p}_{X}(1-\widehat{p}_{X})}{n}+\frac{z_{(1+q)/{2}}^2}{4n^2}}}{1+\frac{z_{(1+q)/{2}}^2}{n}} \]

Amb R es calcula amb la funció

del paquet epitools, amb la mateixa sintaxi que binom.exact. Aquest interval també té l’inconvenient que, si us hi fixau, no està centrat en \(\widehat{p}_{X}\): el seu centre és \[ \frac{\widehat{p}_{X}+\frac{z_{(1+q)/{2}}^2}{2n}}{1+\frac{z_{(1+q)/{2}}^2}{n}} \]

Mètode de Laplace

Suposem finalment que prenem una mostra aleatòria simple de \(X\) de mida \(n\) encara més gran i \(\widehat{p}_{X}\) enfora de 0 i 1. Per fixar idees, suposem que \[ n\geqslant 100,\ n\widehat{p}_{X}\geqslant 10,\ n(1-\widehat{p}_{X})\geqslant 10 \] En aquest cas, a la fórmula de l’interval de Wilson podem suposar que els termes \(z_{(1+q)/{2}}^2/n\) són (aproximadament) 0 i obtenim la fórmula següent:

Teorema 3.6 En les condicions explicades, un interval de confiança de nivell de confiança \(q\) per a \(p_X\) és (aproximadament): \[ \widehat{p}_{X}\pm z_{(q+1)/2}\sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}} \]

Amb R es calcula amb la funció

del paquet epitools, amb la mateixa sintaxi que binom.exact. Aquesta fórmula és la més popular, amb més de 200 anys de rodatge.

Us heu de saber la fórmula de Laplace, no cal saber les fórmules dels altres dos intervals.

Més exemples

Exemple 3.8 En una mostra aleatòria de 500 famílies amb nins en edat escolar es va trobar que 340 introduïen fruita diàriament en la dieta dels seus fills. A partir d’aquestes dades, volem calcular un interval de confiança del 95% per a la proporció real de famílies d’aquesta ciutat amb nins en edat escolar que incorporen fruita fresca cada dia en la dieta dels seus fills.

Diguem \(X\) a la variable aleatòria “Prenem una família amb nins en edat escolar i miram si inclou diàriament fruita a la dieta dels fills”. És Bernoulli, diguem \(p_X\) a la seva probabilitat d’èxit: la probabilitat que una família amb nins en edat escolar inclogui diàriament fruita a la dieta dels fills. Cercam un interval de confiança del 95% per a \(p_X\).

Com que \(n=500\geqslant 100\), \(n\widehat{p}_X=340\geqslant 10\) i \(n(1-\widehat{p}_X)=160\geqslant 10\), podem emprar la fórmula de Laplace \[ \widehat{p}_{X}\pm z_{(q+1)/2}\sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}} \] amb \(n=500\), \(\widehat{p}_{X}=340/500=0.68\) i \(z_{(q+1)/2}=z_{0.975}=1.96\). Dóna \[ 0.68\pm 1.96\sqrt{\frac{0.68(1-0.68)}{500}}\Rightarrow [0.639,0.721] \]

Amb R:

##     x   n proportion lower upper conf.level
## 1 340 500       0.68 0.639 0.721       0.95

Amb els altres mètodes, que també podríem aplicar en aquest cas, obtenim els intervals:

##     x   n proportion lower upper conf.level
## 1 340 500       0.68 0.637 0.721       0.95
##     x   n proportion lower upper conf.level
## 1 340 500       0.68 0.638 0.719       0.95

En resum, estimam que entre aproximadament un 64% i un 72% de les famílies d’aquesta ciutat amb nins en edat escolar inclouen diàriament fruita fresca en la dieta dels seus fills.

Quan podem calcular més d’un interval per a \(p_X\), quin calculam?

D’entrada cal dir que si podem calcular més d’un interval, segurament donaran molt parescuts, com heu pogut comprovar a l’exemple anterior. A més, recordau que les tres fórmules només ens donen “un nivell de confiança q” si s’apliquen a mostres aleatòries simples, i les nostres mostres gairebé sempre seran oportunistes, cas en el qual, si ens posam perepunyetes, no en podem aplicar cap.

Però en tot cas, si no filam molt prim i podem triar, hem de tenir en compte que:

  • L’interval de Clopper-Pearson és exacte, no empra cap aproximació, però:
    • Tendeix a donar un interval més ample del necessari
    • No està centrat en la proporció mostral
    • Només és un interval “exacte” si la mostra és aleatòria simple, cosa que gairebé sempre serà fals (com a molt, serà “aproximadament” aleatòria simple)
    • Com que no es pot calcular “a mà”, no és molt popular

  • L’interval de Wilson és aproximat, fa servir l’aproximació a la normal donada pel Teorema Central del Límit. Això no és un gran emperò, pequè tanmateix segurament la mostra serà com a molt “aproximadament” aleatòria simple. Ara bé, tampoc no està centrat en la proporció mostral, i ens agrada poder donar els intervals en la forma “tal més menys qual” perquè d’aquesta manera donam l’estimació puntual i el marge d’error.

  • L’interval de Laplace és molt aproximat, però:
    • Forma part de la cultura general del científic, tothom el coneix
    • És l’únic centrat en la proporció mostral

Exemple 3.9 En un assaig d’un nou tractament de quimioteràpia, en una mostra de \(n\) malalts tractats, cap desenvolupà càncer testicular com a efecte secundari. Quin seria un interval de confiança al 95% per a la proporció de malalts tractats amb aquesta quimio que desenvolupen càncer testicular?

Per calcular-lo podem emprar el mètode de Clopper-Pearson i, si \(n\) és gran, el de Wilson. No podem emprar la fórmula de Laplace, perquè \(\widehat{p}_X=0\).

Pel que fa a Clopper-Pearson, aquest és un dels pocs casos que admeten solució analítica senzilla: dóna l’interval \[ \Big[0,1-\Big(\frac{1-q}{2}\Big)^{1/n}\Big] \] que, si \(q=0.95\), queda \[ [0,1-0.025^{1/n}]. \] Per exemple, si \(n=40\)

##   x  n proportion lower     upper conf.level
## 1 0 40          0     0 0.0880973       0.95
## [1] 0.0880973

Si podem emprar el mètode de Wilson, la fórmula \[ \frac{\widehat{p}_{X}+\frac{z_{(q+1)/2}^2}{2n}\pm z_{(q+1)/2}\sqrt{\frac{\widehat{p}_{X}(1-\widehat{p}_{X})}{n}+\frac{z_{(q+1)/2}^2}{4n^2}}}{1+\frac{z_{(q+1)/2}^2}{n}} \] amb \(\widehat{p}_{X}=0\) i \(z_{(1+q)/2}=1.96\) dóna \[ \frac{\frac{1.96^2}{2n}\pm 1.96\sqrt{\frac{1.96^2}{4n^2}}}{1+\frac{1.96^2}{n}}\Longrightarrow \Big[0,\frac{1.96^2}{n+1.96^2}\Big] \] Per exemple, un altre cop amb \(n=40\)

##   x  n proportion        lower     upper conf.level
## 1 0 40          0 6.330897e-18 0.0876216       0.95
## [1] 0.0876216

Quan s’ha de calcular “a ull” un interval de confiança del 95% per a una probabilitat \(p_X\) a partir d’una mostra aleatòria simple on no hi ha hagut cap èxit, sovint es fa servir la regla següent:

Regla del 3: Quan en una mostra aleatòria simple de mida \(n\) d’una variable aleatòria de Bernoulli de paràmetre \(p_X\) no hi trobam cap èxit, un IC 95% per a \(p_X\) va, aproximadament, de 0 a \(3/n\).

Amb aquesta regla, en el nostre exemple amb \(n=40\) obtendríem l’interval [0,3/40]=[0,0.075], no molt enfora del [0,0.088] que hem obtingut amb els altres dos mètodes.

Per veure com la regla del 3 aproxima l’interval de Clopper-Pearson, el gràfic següent mostra els valors \(3/n\) i l’extrem superior de l’IC 95% de Clopper-Pearson a partir d’una mostra de mida \(n\) amb 0 èxits:

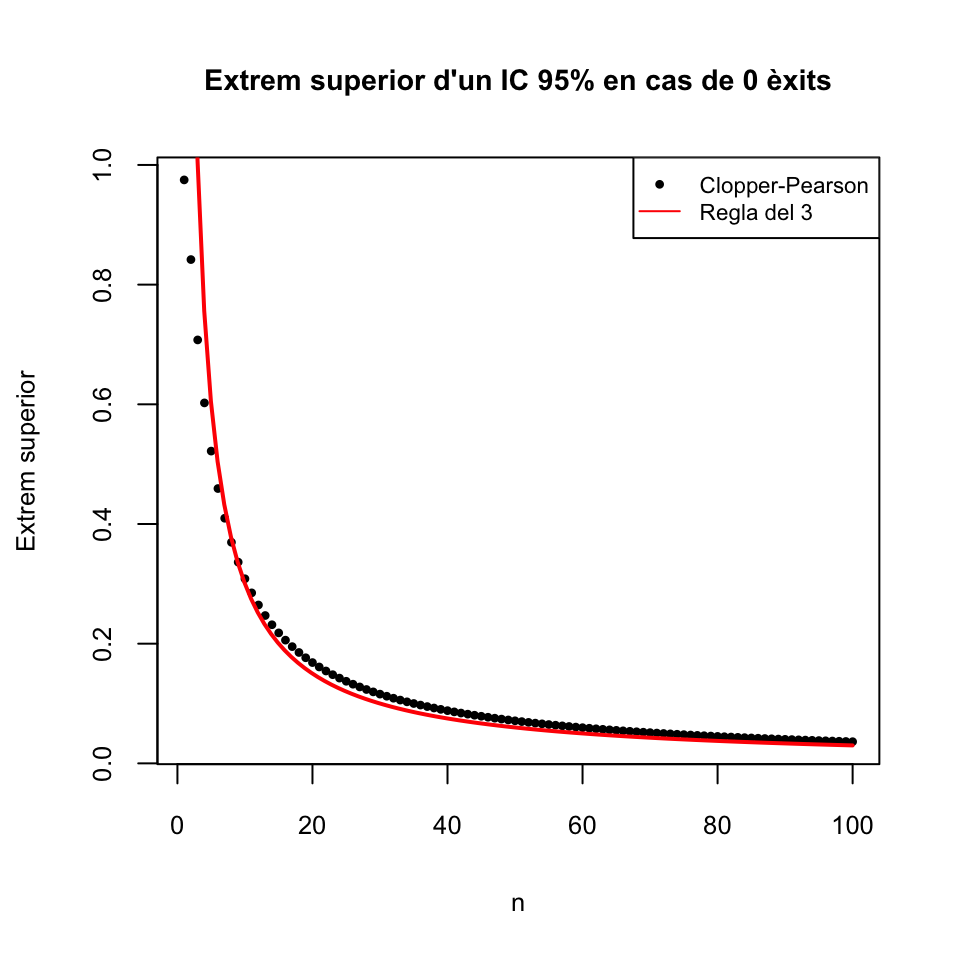
El gràfic següent mostra els valors \(3/n\) i els extrems superiors dels IC 95% de Clopper-Pearson i de Wilson a partir d’una mostra de mida \(n\) (\(n\geqslant 40\) per als intervals de confiança de Wilson) amb 0 èxits:

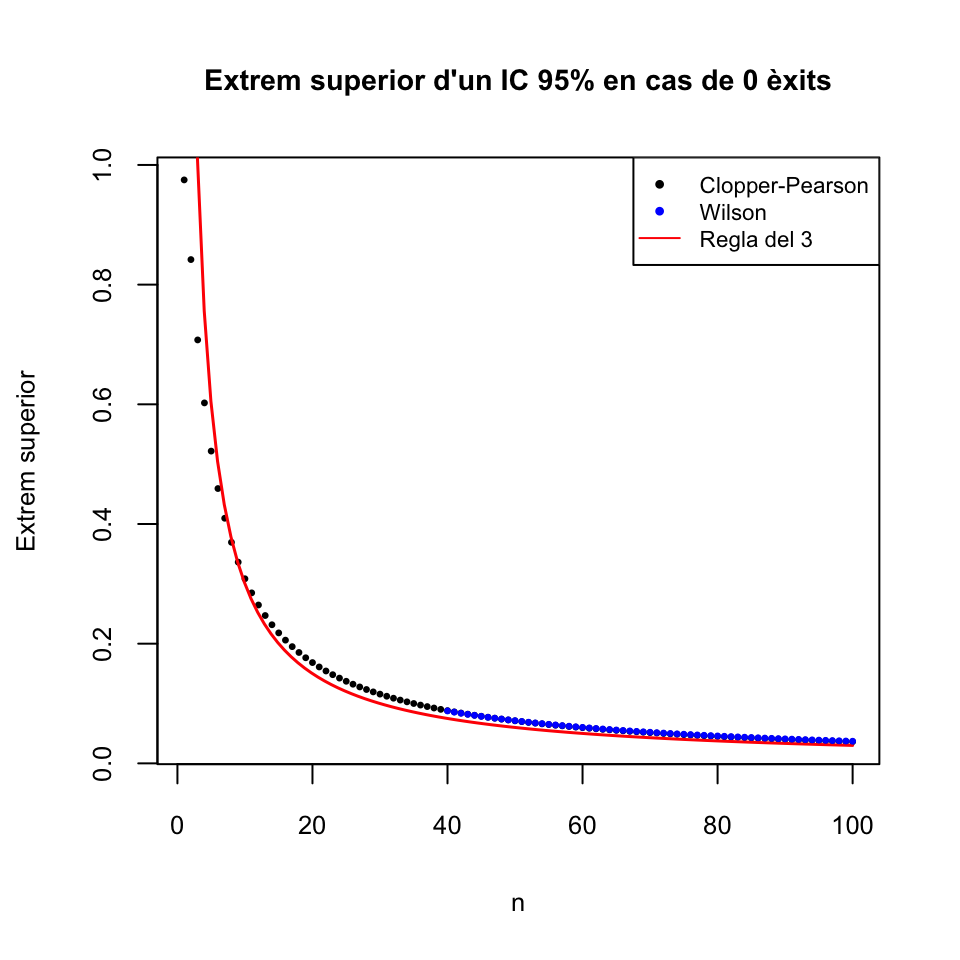
Els extrems superiors dels intervals de Clopper-Pearson i Wilson se superposen en aquest darrer gràfic.

Exemple 3.10 En un assaig d’un tractament de quimioteràpia, en una mostra de 100 pacients tractats, 25 desenvoluparen càncer testicular secundari. Volem calcular un IC 95% per a la proporció de pacients tractats amb aquesta quimioteràpia que desenvolupen càncer testicular.

En aquest cas podem emprar els tres mètodes:

##    x   n proportion  lower  upper conf.level
## 1 25 100       0.25 0.1688 0.3466       0.95
##    x   n proportion  lower upper conf.level
## 1 25 100       0.25 0.1755 0.343       0.95
##    x   n proportion  lower  upper conf.level
## 1 25 100       0.25 0.1651 0.3349       0.95

Concloem, amb un nivell de confiança del 95%, que entre aproximadament un 17% i un 34% dels pacients tractats amb aquesta quimioteràpia desenvolupen càncer testicular.

Càlcul de la mida de la mostra per a fixar l’error

L’error de l’interval de confiança de Laplace és \[ M= z_{(q+1)/2} \sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}} \] perquè l’interval de confiança de Laplace és \(\widehat{p}_X\pm M\) i per tant, si conté el valor real de \(p_X\), l’error \(|\widehat{p}_X-p_X|\) que cometem quan diem que el valor de \(p_X\) és \(\widehat{p}_X\) és com a màxim \(M\).

No podem determinar la mida de la mostra a fi que l’interval de confiança tingui un error màxim sense conèixer \(\widehat{p}_{X}\), que no coneixem sense una mostra.

Però en el cas de l’interval de Laplace per a una proporció, podem donar un \(n\) que garanteixi una amplada màxima donada valgui el que valgui \(\widehat{p}_{X}\in [0,1]\).

Fixau-vos que la funció \(y=p (1-p)\), amb \(p\in [0,1]\), és una paràbola còncava amb vèrtex al punt \(p=0.5\)

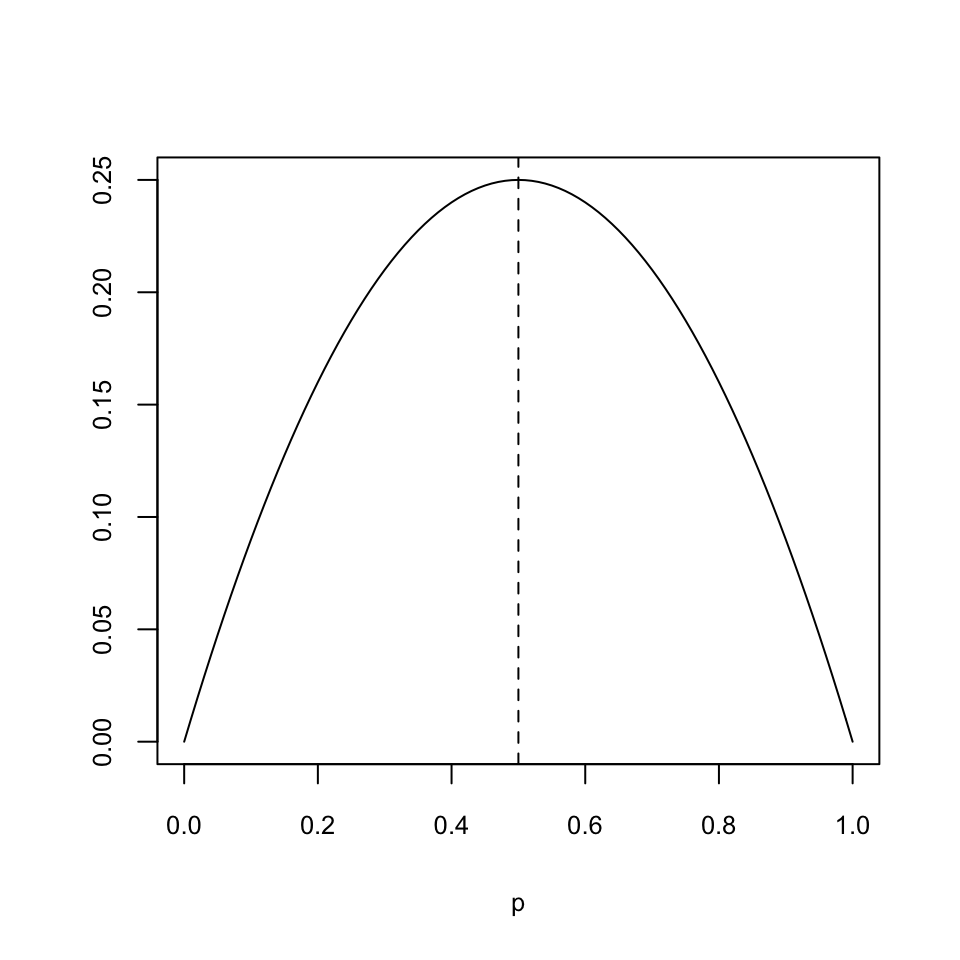Per tant, el seu màxim s’assoleix a \(p=0.5\). Així, doncs \[ \widehat{p}_{X} (1-\widehat{p}_{X})\leqslant 0.5(1-0.5)=0.5^2\text{ per a tot $\widehat{p}_X\in[0,1]$} \] i per tant \[ \begin{array}{l} \displaystyle M=z_{(q+1)/2} \sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}}\\ \qquad\displaystyle \leqslant z_{(q+1)/2}\sqrt{\frac{0.5^2}{n}}=\frac{0.5z_{(q+1)/2}}{\sqrt{n}}=\frac{z_{(q+1)/2}}{2\sqrt{n}} \end{array} \]

D’aquesta manera, si prenem \(n\) tal que \[ \frac{z_{(q+1)/2}}{2\sqrt{n}}\leqslant M_{max} \] aleshores segur que \(M\leqslant M_{max}\), valgui el que valgui \(\widehat{p}_{X}\).

Per tant, el que farem serà calcular la \(n\) per obtenir un error com a màxim \(M_{max}\) en el cas més desfavorable: quan l’interval és el més ample possible, és a dir, suposant que \(\widehat{p}_{X}=0.5\): \[ M_{max}\geqslant\frac{z_{(q+1)/2}}{2\sqrt{n}} \Rightarrow n\geqslant\left(\frac{z_{(q+1)/2}}{2\cdot M_{max}}\right)^2 \]

En resum:

Teorema 3.7 Si \[ n\geqslant\left(\frac{z_{(q+1)/2}}{2\cdot M_{max}}\right)^2, \] l’error de l’interval de Laplace calculat amb una mostra de mida \(n\) sempre serà com a molt \(M_{max}\).

Exemple 3.11 Quina és la mida més petita d’una mostra que ens garanteix un error de com a màxim 0.05 en estimar una proporció \(p_X\) emprant un interval de confiança de Laplace del 95%?

Pel teorema anterior, per garantir un error de 0.05 en calcular un IC 95% per una proporció \(p_X\) emprant la fórmula de Laplace, hem d’emprar una mostra de mida \(n\) tal que \[ n\geqslant\Bigg(\frac{z_{(1+q)/2}}{2M_{max}}\Bigg)^2=\Bigg(\frac{1.96}{0.1}\Bigg)^2=384.16 \]

La mida més petita que satisfà aquesta condició és \(n=385\).

La resposta correcta no és 384, per molt que 384.16 s’arrodoneixi a 384. Fixau-vos que 384 no és més gran que 384.16.

Observau tres coses:

  • El valor de \(n\) només depèn de la precisió i del nivell de confiança, no de la natura de l’estudi ni de proves pilot

  • Tal i com hem trobat la \(n\), estam segurs que si prenem una mostra com a mínim d’aquesta mida, el marge d’error de l’interval de confiança de Laplace serà com a màxim \(M_{max}\) (la seva amplada serà com a màxim \(2M_{max}\)), sigui quina sigui la mostra. És de les poques vegades que podem estar segurs de qualque cosa en estadística.

  • El teorema anterior és per l’amplada de l’interval de Laplace, però la \(n\) segurament us sortirà molt gran i en aquest cas l’interval de Laplace aproxima molt bé els altres dos intervals.

3.5 Intervals de confiança per a la variància d’una variable normal

Suposem que tenim una variable normal \(X\sim N(\mu,\sigma)\). Volem trobar un IC 95% per a la seva variància \(\sigma^2\) (o la seva desviació típica \(\sigma\)). Per calcular-lo, prenem una mostra aleatòria simple de mida \(n\), de variància mostral \(\widetilde{S}^2_X\).

Recordau que, en aquestes condicions, \[ \frac{(n-1) \widetilde{S}_{X}^2}{\sigma^2} \] té distribució \(\chi^2_{n-1}\)

Podem aprofitar aquest fet per obtenir intervals de confiança per a \(\sigma^2\):

Teorema 3.8 Si la variable \(X\) és normal, un interval de confiança de nivell de confiança \(q\) per a \(\sigma^2\) és
\[ \left[ \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1+q)/2}^2}, \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1-q)/2}^2} \right], \] on \(\chi_{n-1,r}^2\) és el \(r\)-quantil de la distribució \(\chi_{n-1}^2\)
La justificació d’aquesta fórmula és la usual: com que \[ \begin{array}{l} \displaystyle P(\chi_{n-1}^2\leqslant\chi_{n-1,(1-q)/2}^2)=\frac{1-q}{2}\\ \displaystyle P(\chi_{n-1}^2\geqslant\chi_{n-1,(1+q)/2}^2)=1-\frac{1+q}{2}=\frac{1-q}{2}, \end{array} \] tenim que \[ \begin{array}{l} q=P\left(\chi_{n-1,(1-q)/2}^2\leqslant\chi_{n-1}^2\leqslant \chi_{n-1,(1+q)/2}^2\right)\\[2ex] \quad\displaystyle =P\left(\chi_{n-1,(1-q)/2}^2\leqslant\frac{(n-1) \widetilde{S}_{X}^2}{\sigma^2}\leqslant \chi_{n-1,(1+q)/2}^2 \right)\\[2ex] \quad\displaystyle = P\left(\frac{(n-1) \widetilde{S}_{X}^2}{\chi_{n-1,(1+q)/2}^2}\leqslant\sigma^2\leqslant\frac{ (n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1-q)/2}^2} \right) \end{array} \]
Fixau-vos que aquest interval de confiança per \(\sigma^2\) no està centrat en \(\widetilde{S}_{X}^2\) ni en \({S}_{X}^2\). A més, com que \(\chi_{n-1}^2\) no és simètrica, s’han de calcular els dos quantils \(\chi_{n-1,(1-q)/2}^2\) i \(\chi_{n-1,(1+q)/2}^2\), perquè no hi ha cap relació entre ells que doni el valor d’un d’ells a partir del de l’altre.

Exemple 3.12 Un índex de qualitat d’un reactiu químic és la variabilitat en el temps que triga a actuar: es demana que aquest temps sigui aproximadament constant, és a dir, que tengui una desviació típica petita.

Hem realitzat 30 proves en les quals hem mesurat el temps d’actuació d’un determinat reactiu, i a partir dels resultats volem calcular un IC 95% per a la desviació típica del seu temps d’actuació. Tenim els resultats guardats en el vector següent:

Per ara suposarem que la distribució del temps d’actuació d’aquest reactiu és (aproximadament) normal. Més endavant estudiarem tècniques per determinar (amb un cert nivell de confiança) si podem acceptar que una mostra prové d’una variable normal.

Continuem. Com que la variable que ens dóna el temps és (aproximadament) normal, podem emprar la fórmula per a l’IC 95% per a \(\sigma^2\) anterior: \[ \left[ \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1+q)/2}^2}, \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1-q)/2}^2} \right] \]

on:

  • \(n=\)length(Temps)\(=30\)
  • \(\widetilde{S}_X^2=\)var(Temps)\(=301.55\)
  • \(q=0.95\), per tant \(\chi_{n-1,(1+q)/2}^2=\)qchisq(0.975,29)\(=45.72\) i \(\chi_{n-1,(1-q)/2}^2=\)qchisq(0.025,29)\(=16.05\)

Obtenim l’interval: \[ \left[ \frac{29\cdot 301.55}{45.72}, \frac{29\cdot 301.55}{16.05}\right]= [191.26, 544.96] \]

Aquest interval és per a la variància!

Per obtenir un interval de confiança per a la desviació típica, prenem arrels quadrades dels extrems: \[ [\sqrt{191.26}, \sqrt{544.96}]=[13.83,23.34] \]

Per tant la variabilitat dels temps d’actuació d’aquest reactiu és molt gran. Comparau aquest interval amb l’IC 95% per al seu temps mitjà d’actuació:

## [1] 21.88 34.85
## attr(,"conf.level")
## [1] 0.95

L’extrem superior de l’IC 95% per a la desviació típica és més gran que l’extrem inferior d’aquest IC 95% per a la mitjana.

Amb R, aquest interval de confiança amb nivell de confiança \(q\) per a la variància es pot calcular amb la funció

del paquete EnvStats, on X és el vector que conté la mostra i conf.level indica el nivell de confiança en tant per u, que per defecte és igual a 0.95.

Així, l’interval de confiança que ens demanàvem a l’exemple anterior es calcularia amb

##      LCL      UCL 
## 191.2627 544.9572 
## attr(,"conf.level")
## [1] 0.95
Que no, que aquest és el de la variància!

L’IC 95% per a la desviació típica és:

##      LCL      UCL 
## 13.82977 23.34432 
## attr(,"conf.level")
## [1] 0.95
L’interval per a la variància basat en la distribució \(\chi^2\) només és vàlid si la variable poblacional és (aproximadament) normal. En cas que no poguem acceptar que ho és, el millor és emprar un mètode no paramètric, com per exemple el bootstrap.

Exemple 3.13 Anem a calcular un IC 95% per a la desviació típica del temps de reacció de l’Exemple anterior amb el mètode del bootstrap.

Prenem 5000 mostres aleatòries simples de mida 30 del vector Temps i calculam la desviació típica mostral de cada mostra:

Ara prenem com a IC 95% l’interval que va del quantil 0.025 al quantil 0.975 d’aquest vector de desviacions típiques:

##     2.5%    97.5% 
## 11.00926 22.69609

No ha sortit molt diferent de l’obtingut amb la fórmula basada en la distribució \(\chi^2\).

3.6 “Poblacions finites”

Fins ara hem emprat mostres aleatòries simples. Què passa si prenem mostres aleatòries sense reposició?

Si la mida \(N\) de la població és molt més gran que la mida \(n\) de la mostra (posem \(N\geqslant 1000n\)), les fórmules donades fins ara funcionen (aproximadament) bé.

Quan la mida \(N\) de la població no és molt més gran que la mida \(n\) de la mostra, el que es fa és, a les fórmules que hem donat per als intervals de confiança per a \(\mu\) o \(p_X\), multiplicar-hi l’error estàndard pel factor de població finita \[ \sqrt{\frac{N-n}{N-1}} \]

Així:

  • Si \(X\) és una població de mida \(N\) amb mitjana poblacional \(\mu\) i prenem una mostra aleatòria sense reposició de \(X\), amb mitjana \(\overline{X}\) i desviació típica mostral \(\widetilde{S}_X\), i si \(X\) normal o si \(n\) és gran, es recomana prendre com a interval de confiança de nivell de confiança \(q\) per a \(\mu\) \[ \overline{X}\pm t_{n,(q+1)/2}\frac{\widetilde{S}_X}{\sqrt{n}}\sqrt{\frac{\vphantom{(}N-n}{N-1}} \]

  • Si \(X\) una població de mida \(N\) que segueix una distribució Bernoulli amb probabilitat d’èxit \(p_X\) i prenem una mostra aleatòria sense reposició de \(X\), amb \(n\) molt gran i nombres d’èxits i fracassos com a mínim 10, es recomana prendre com a interval de confiança de nivell de confiança \(q\) per a \(p_X\) \[ \widehat{p}_{X}\pm z_{(q+1)/2}\sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}}\sqrt{\frac{\vphantom{(}N-n}{N-1}} \]

  • En les condicions del punt anterior, per obtenir un interval de confiança de nivell de confiança \(q\) per a \(p_X\) amb un marge d’error \(M_{max}\) en el cas més desfavorable (\(\widehat{p}_X=0.5\)) caldrà prendre una mostra de mida \[ n\geqslant\frac{Nz_{(q+1)/2}^2}{4M_{max}^2(N-1)+z_{(q+1)/2}^2} \]

Exemple 3.14 En una mostra aleatòria de 727 estudiants (diferents) de la UIB (\(N=12000\)), 557 afirmàrem haver comès plagi en algun treball durant els seus estudis. Quin seria un interval de confiança del 95% per a la proporció \(p_X\) d’estudiants de la UIB que han comès plagi en algun treball?

Una mostra de 727 estudiants diferents és molt gran respecte del total d’estudiants de la UIB, per la qual cosa convé emprar la fórmula de Laplace amb el factor de població finita \[ \widehat{p}_{X}\pm z_{(q+1)/2}\sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}}\sqrt{\frac{\vphantom{(}N-n}{N-1}} \] on \(\widehat{p}_{X}=557/727=0.766\), \(z_{(q+1)/2}=1.96\), \(n=727\) i \(N=12000\): dóna \[ 0.766\pm \sqrt{\frac{0.766(1-0.766)}{727}}\sqrt{\frac{\vphantom{(}12000-727}{12000-1}}\Rightarrow [0.751,0.781] \] Estimam amb un nivell de confiança del 95% que entre un 75.1 i un 78.1 dels estudiants de la UIB han comès plagi en algun treball.

Exemple 3.15 De quina mida hem de prendre una mostra aleatòria sense reposició d’estudiants de la UIB per estimar una proporció amb nivell de confiança del 95% i un marge d’error màxim de 0.05?

Per la fórmula anterior (prenent \(N=12000\) i \(z_{(1+q)/2}=1.96\)), per garantir un marge d’error màxim de 0.05 cal prendre una mostra de mida \[ n\geqslant\frac{12000\cdot 1.96^2}{4\cdot 0.05^2(12000-1)+1.96^2}=372.3 \] Per tant, ens calen 373 estudiants.