Tema 1 Repàs de la distribució normal

1.1 Propietats de la distribució normal

Una variable aleatòria contínua $X$ és normal de paràmetres $\mu$ i $\sigma$, i ho indicarem escrivint $X\sim N(\mu,\sigma)$, quan la seva funció de densitat és

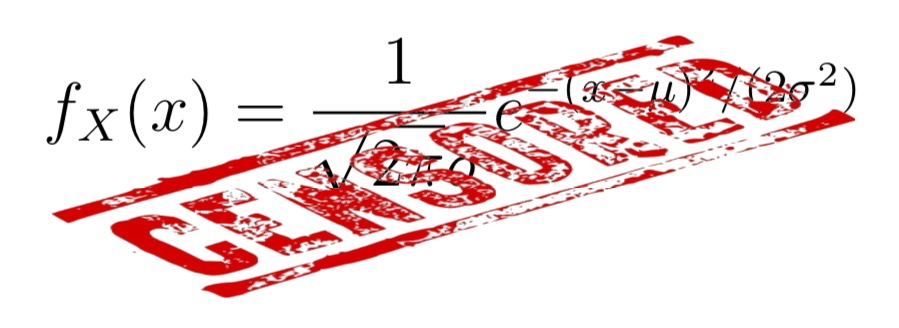
Naturalment, no cal saber aquesta fórmula. El que cal saber és que:

Una variable aleatòria normal $X$ és contínua, i per tant $P(X=x)=0$, $P(X\leqslant x)=P(X<x)$ etc.
Si $X\sim N(\mu,\sigma)$, aleshores el seu valor esperat és $E(X)=\mu$ i la seva desviació típica és $\sigma_X=\sigma$

Una variable aleatòria normal és típica (o estàndard) quan $\mu=0$ i $\sigma=1$; la indicarem usualment amb $Z$. Per tant, si $Z\sim N(0,1)$, $E(Z)=0$ i $\sigma_Z=1$.

La gràfica de la densitat d’una variable aleatòria normal és la famosa campana de Gauss:

La gràfica de la densitat d’una variable aleatòria normal és també la menys famosa gràfica del capell del gendarme:

La distribució normal és una distribució teòrica, no la trobareu exacta en la pràctica. I malgrat el seu nom, no és més “normal” que les altres distribucions que estudiarem.

La distribució normal és important perquè aproxima bé moltes distribucions reals, perquè:

Moltes variables aleatòries que consisteixen a prendre $n$ observacions independents d’una o diverses variables aleatòries i sumar-les, tenen distribució aproximadament normal quan $n$ és gran, encara que les variables aleatòries de partida no ho siguin.

Per exemple:

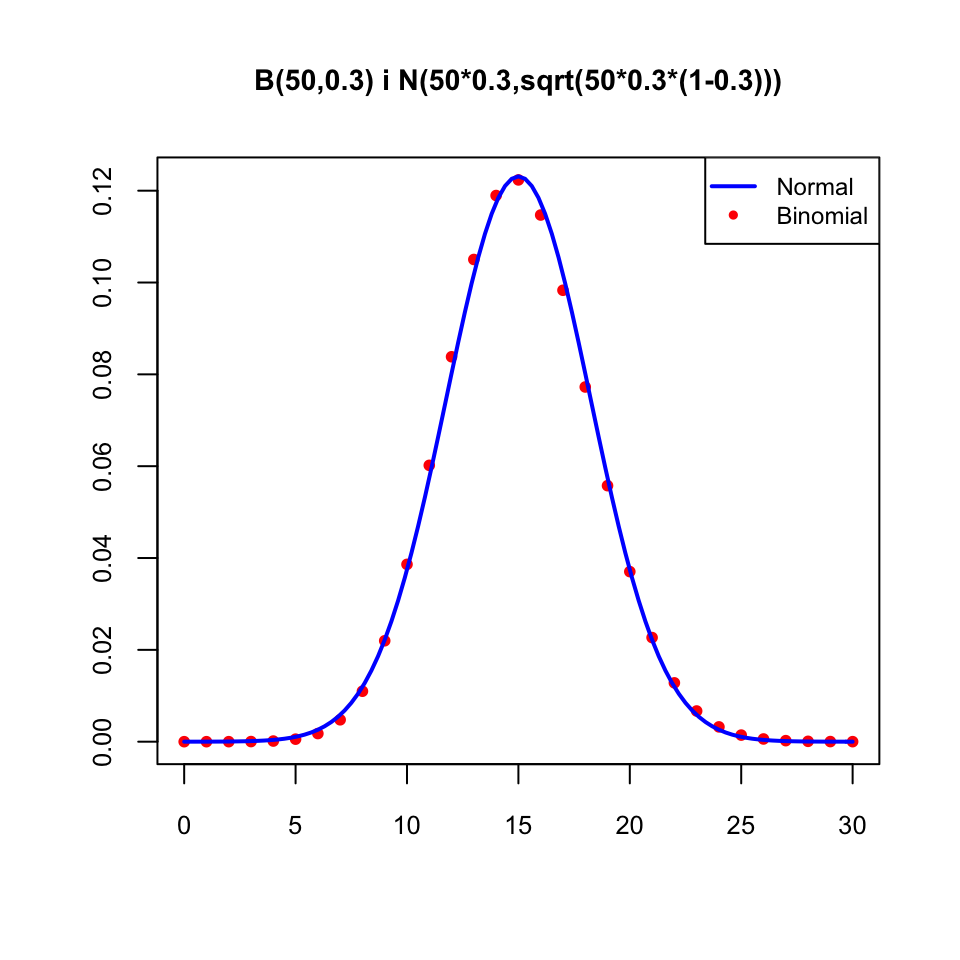
Si $X$ és una variable aleatòria binomial B(n,p), amb $n$ gran, alehores $X$ és aproximadament $N(np,\sqrt{np(1-p)})$, en el sentit que les dues funcions de densitat (salvant la diferència pel fet que la binomial és discreta i la normal contínua) són semblants:

Si $X$ és una variable aleatòria de Poisson $Po(\lambda)$ i $\lambda$ és gran, aleshores $X$ és aproximadament $N(\lambda,\sqrt{\lambda})$

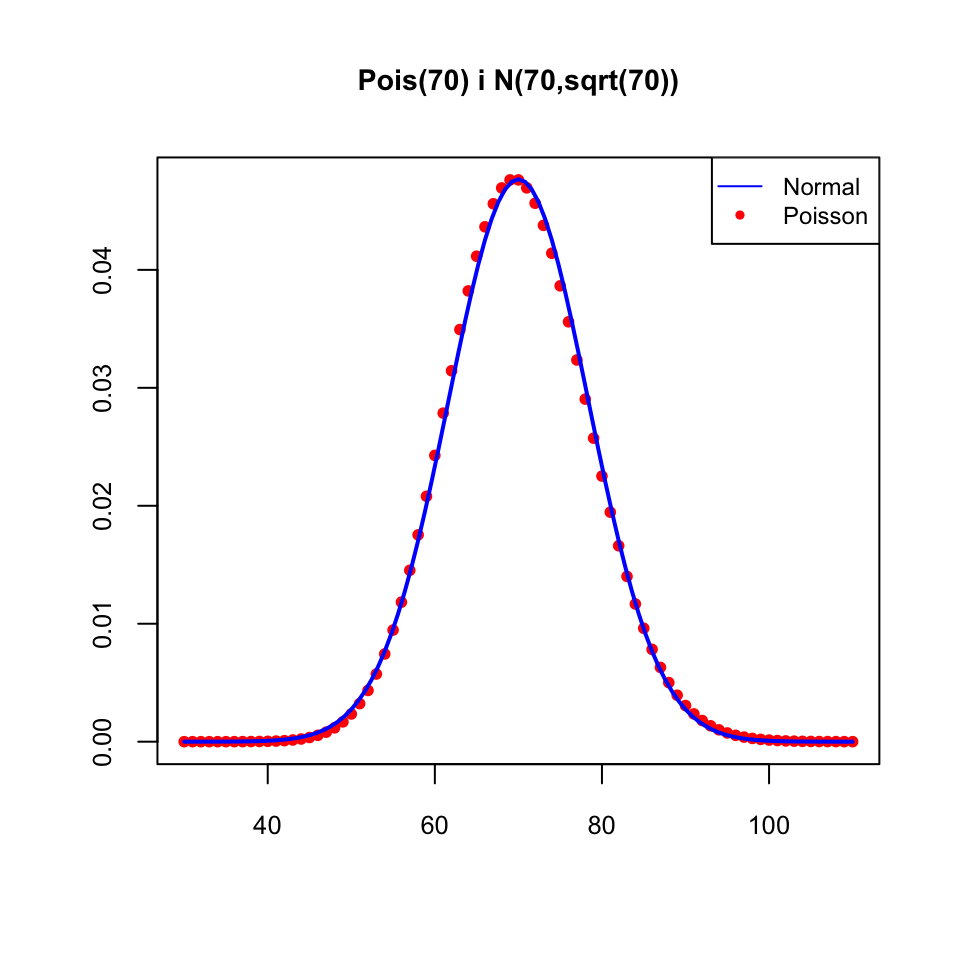
Quan s’aproxima una variable binomial o Poisson $X$ per mitjà d’una variable normal $Y$, és convenient aplicar l’anomenada correcció de continuïtat: per a cada $n\in \mathbb{N}$, interpretar $P(X\leqslant n)$ com $P(X< n+1/2)$ i aleshores aproximar:

$P(X\leqslant n)$ per mitjà de $P(Y< n+1/2)$
$P(X=n)$ per mitjà de $P(n-1/2< Y< n+1/2)$

Vegeu l’Exemple 1.1 a la propera secció.

Una de les propietats clau de la distribució normal és la seva simetria:

Si $X\sim N(\mu,\sigma)$, la seva densitat $f_X$ és simètrica respecte de $x=\mu$, és a dir, \[ f_{X}(\mu-x)=f_{X}(\mu+x), \] i té el màxim en $x=\mu$.

Diem aleshores que $\mu$ és la moda de $X$.

Recordem que no té sentit definir la moda d’una variable contínua $X$ com el valor $x_0$ tal que $P(X=x_0)$ sigui màxim, perquè $P(X=x)=0$ per a tot $x\in \mathbb{R}$. Es defineix llavors la moda d’una variable contínua $X$ com el valor (o els valors) $x_0$ tal(s) que $f_X(x_0)$ és màxim.

En particular, si $Z\sim N(0,1)$, llavors $f_{Z}$ és simètrica al voltant de $x=0$, és a dir, $f_{Z}(-x)=f_{Z}(x)$, i la moda de $Z$ és 0.

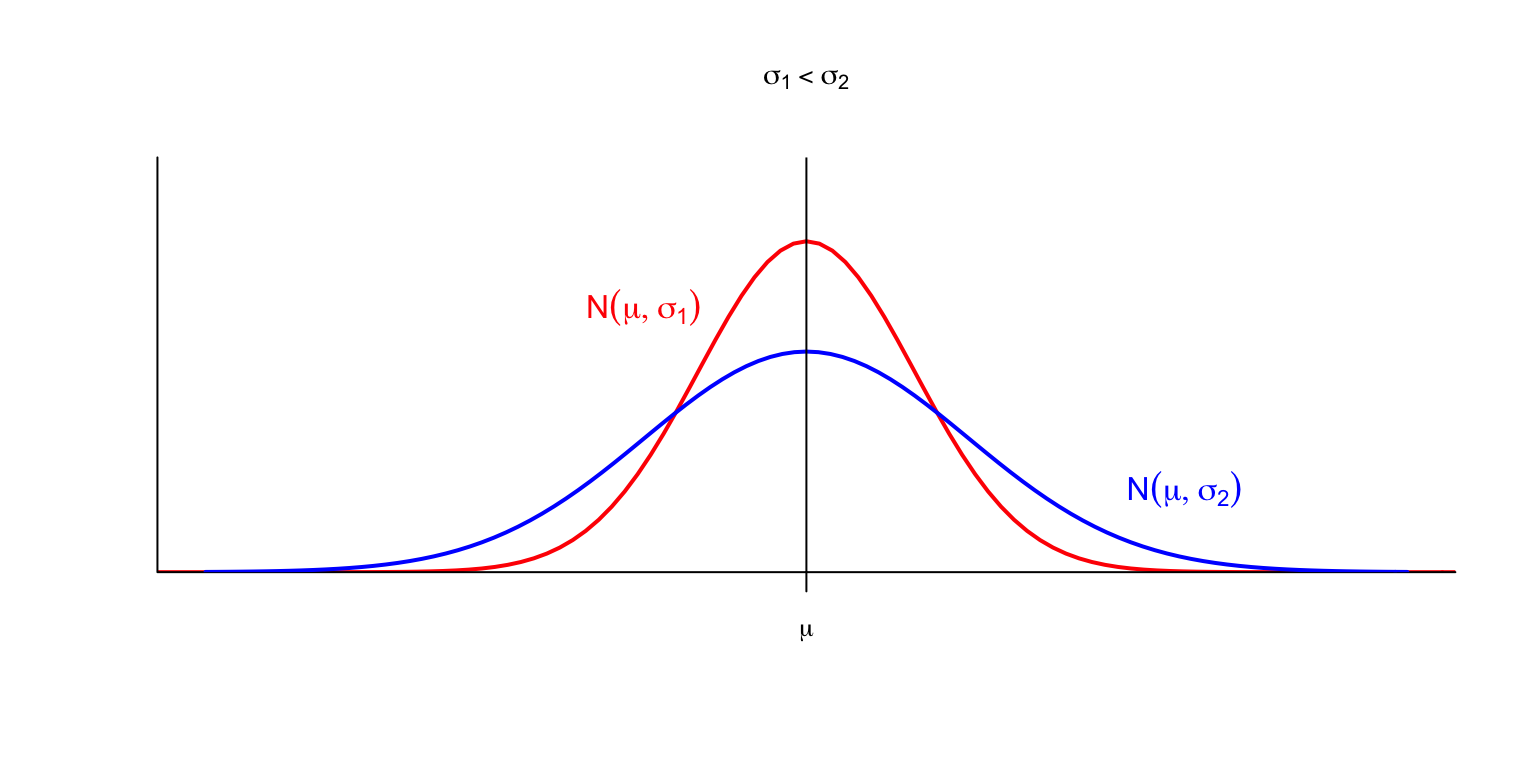
Si la $\mu$ creix, el màxim es desplaça a la dreta, i amb ell tota la corba de manera rígida.

Si la $\sigma$ creix, la corba s’aplata: en augmentar la desviació típica, els valors s’allunyen més del valor mitjà.

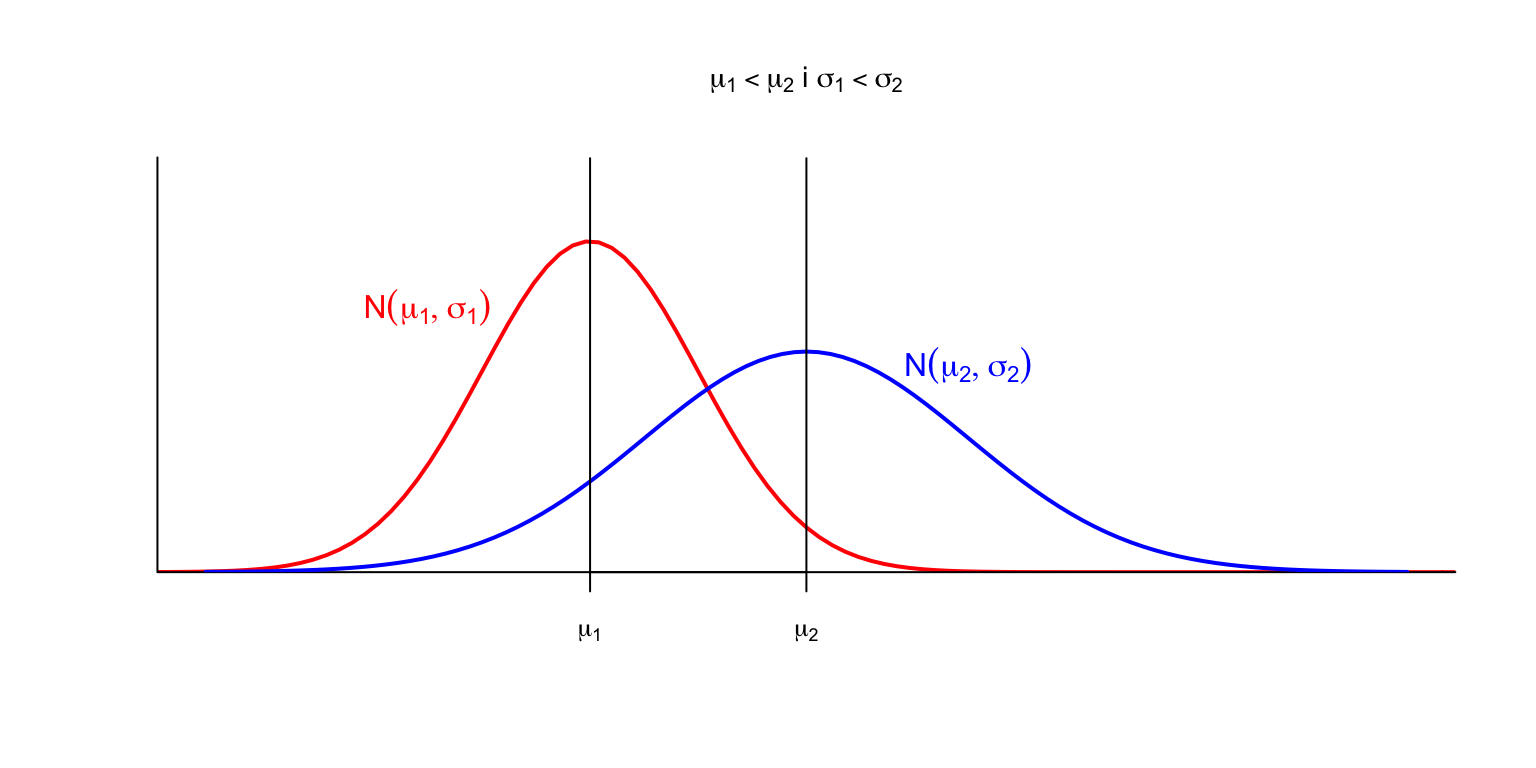
Vegem l’efecte combinat:

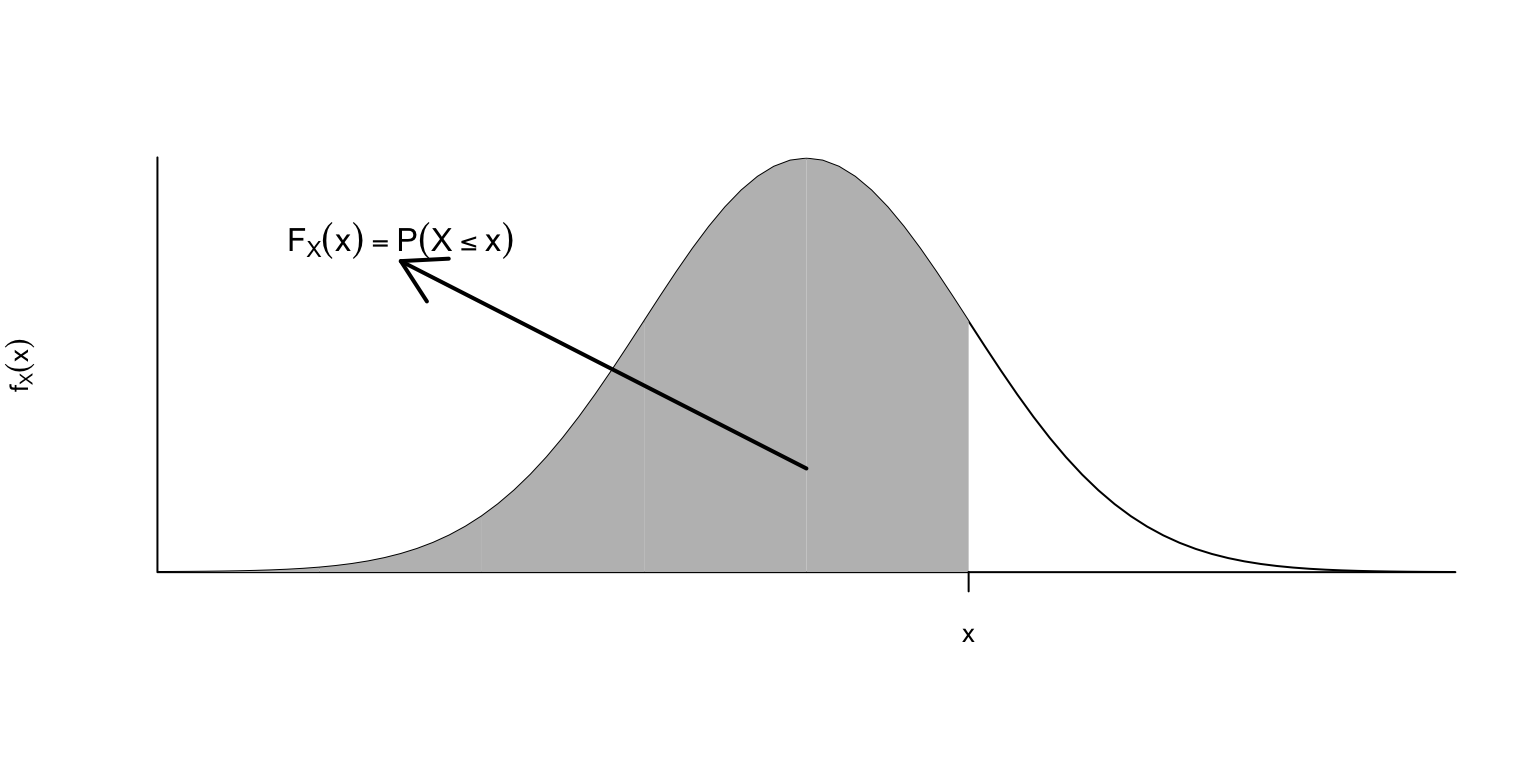
Recordem que la funció de distribució d’una variable aleatòria contínua $X$ \[ F_X(x)=P(X\leqslant x) \] és l’àrea compresa entre la corba definida per la densitat $y=f_X(x)$ i l’eix d’abscisses a l’esquerra de $x$.

La simetria de $f_X$ fa que les àrees a l’esquerra de $\mu-x$ i a la dreta de $\mu+x$ siguin iguals.

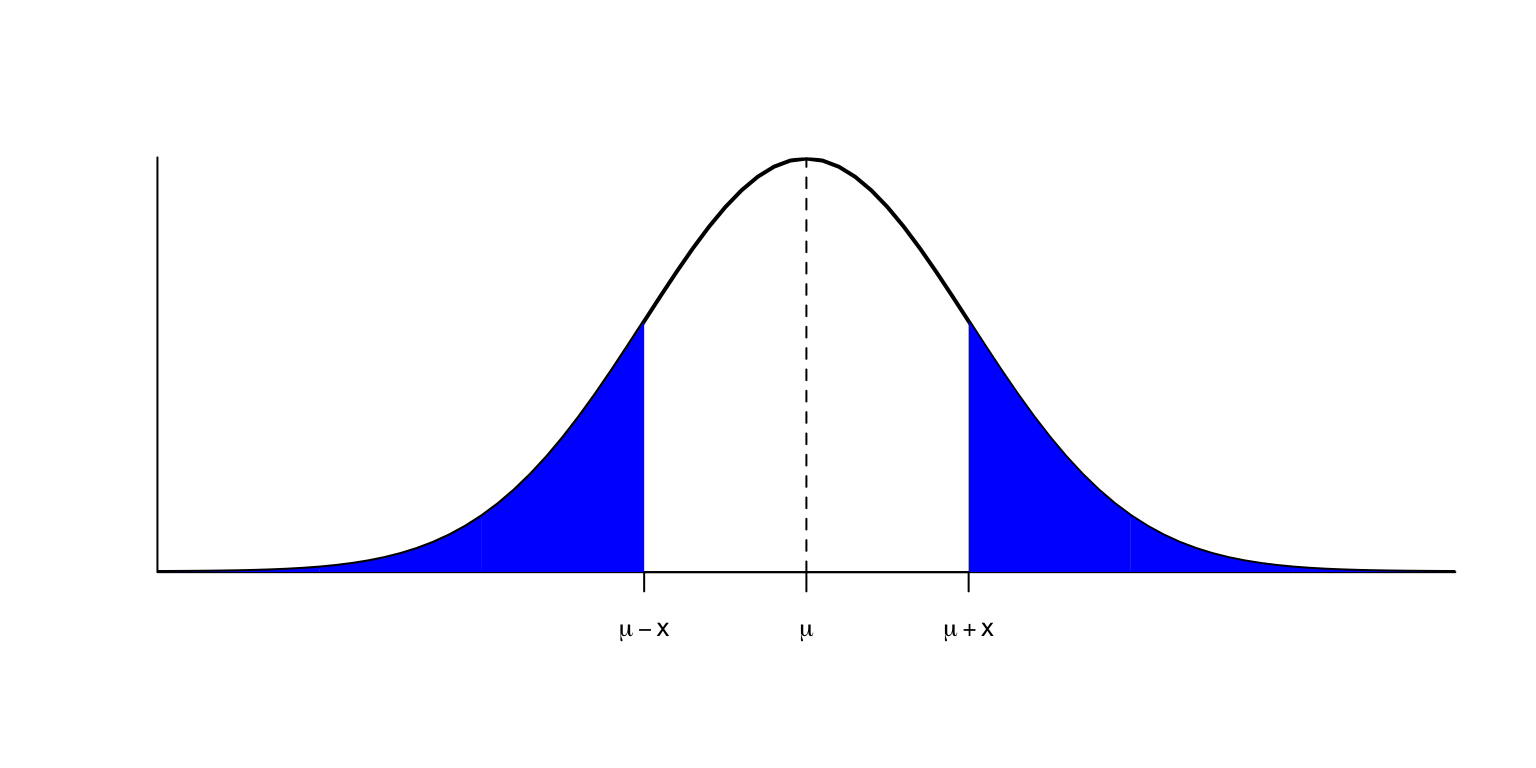
És a dir, \[ P(X\leqslant\mu-x) = P(X\geqslant\mu+x)=1-P(X\leqslant\mu+x) \] En particular (prenent $x=0$) \[ P(X\leqslant\mu)=1-P(X\leqslant\mu)\Rightarrow P(X\leqslant\mu)=0.5, \] i per tant $\mu$ és també la mediana de $X$.

Si $X\sim N(\mu,\sigma)$, $\mu$ és la moda, la mitjana, o esperança, i la mediana de $X$.

En particular, si $Z\sim N(0,1)$, les àrees a l’esquerra de $-z$ i a la dreta de $z$ són iguals, \[ P(Z\leqslant-z)=P(Z\geqslant z)=1-P(Z\leqslant z), \] i la mediana de $Z$ és 0.

Indicarem amb $z_q$ el $q$-quantil d’una variable normal estàndard $Z$. És a dir, $z_q$ és el valor tal que $P(Z\leqslant z_q)=q$.

A banda del fet que $z_{0.5}=0$ (la mediana de $Z$ és 0), hi ha dos quantils més de la normal estándard que heu de saber “de memòria”:

$z_{0.95}=1.64$; és a dir, $P(Z\leqslant 1.64)=0.95$ i per tant $P(Z\leqslant-1.64)=P(Z\geqslant 1.64)=0.05$.
$z_{0.975}=1.96$; és a dir, $P(Z\leqslant 1.96)=0.975$ i per tant $P(Z\leqslant-1.96)=P(Z\leqslant 1.96)=0.025$

Molt sovint el valor 1.96 de $z_{0.975}$ s’aproxima per 2. Teniu permís per fer-ho quan no disposeu de mitjans (R, aplis de mòbil) per calcular quantils.

1.2 Amb R

Per calcular probabilitats d’una variable normal emprant R, heu de recordar que la normal és norm. Per tant, si $X\sim N(\mu,\sigma)$:

dnorm(x,mu,sigma) dóna el valor de la densitat $f_X(x)$
pnorm(x,mu,sigma) dóna el valor de la distribució $F_X(x)=P(X\leqslant x)$; afegint-hi el paràmetre lower.tail=FALSE dóna el valor de $P(X>x)$
qnorm(q,mu,sigma) dóna el $q$-quantil de $X$
rnorm(N,mu,sigma) dóna un vector de $n$ nombres aleatoris generats amb aquesta distribució

A la normal estàndard no és necessari entrar-hi $\mu=0$ i $\sigma=1$, són els valors per defecte d’aquests paràmetres.

Vegem-ne alguns exemples:

Si $X\sim N(3,0.5)$, què val $P(X\leqslant 2)$?

pnorm(2,3,0.5)

## [1] 0.02275013

Si $X\sim N(-2,0.3)$, què val $P(X\geqslant-1.8)$?

1-pnorm(-1.8,-2,0.3)

## [1] 0.2524925

pnorm(-1.8,-2,0.3,lower.tail=FALSE)

## [1] 0.2524925

Si $X\sim N(0,1)$, què val $P(-1\leqslant X\leqslant 1)$?

Com que $P(-1\leqslant X\leqslant 1)=P(X\leqslant 1)-P(X\leqslant-1)$,

pnorm(1)-pnorm(-1)

## [1] 0.6826895

Què val el primer quartil d’una variable $N(3,0.5)$?

qnorm(0.25,3,0.5)

## [1] 2.662755

Comprovau els valors de $z_{0.95}$ i $z_{0.975}$ donats al final de la secció anterior.

Exemple 1.1 A la secció anterior, us hem dit que una variable binomial $B(n,p)$ amb $n$ gran s’aproxima per mitjà d’una variable normal $N(np,\sqrt{np(1-p)})$. Així, per exemple, una variable $X\sim B(400,0.2)$ s’aproxima per mitjà d’una variable $Y\sim N(400\cdot 0.2,\sqrt{400\cdot 0.2\cdot 0.8})=N(80,8)$. Vegem amb alguns exemples que aquesta aproximació és millor aplicant-hi la correcció de continuïtat:

$P(X\leqslant 70)$:

pbinom(70,400,0.2)

## [1] 0.1163917

$P(Y< 70+1/2)$:

pnorm(70.5,80,8)

## [1] 0.1175152

$P(Y\leqslant 70)$:

pnorm(70,80,8)

## [1] 0.1056498

$P(X=70)$:

dbinom(70,400,0.2)

## [1] 0.02338443

$P(70-1/2< Y< 70+1/2)$:

pnorm(70.5,80,8)-pnorm(69.5,80,8)

## [1] 0.02283949

$P(Y=70)$:

dnorm(70,80,8)

## [1] 0.02283114

NO! dnorm(70,80,8) és la funció de densitat de $Y$ (la fórmula que hem censurat al començament d’aquest tema) aplicada a 70, i no és igual a la probabilitat que $Y$ valgui 70. Recordau que $P(Y=70)=0$ perquè $Y$ és contínua.

1.3 Combinacions lineals

El resultat següent descriu el comportament de la mitjana i la variància d’una combinació lineal de variables aleatòries:

Teorema 1.1 Siguin $Y_1,\ldots,Y_n$ variables aleatòries, cada $Y_i$ de mitjana $\mu_i$ i variància $\sigma_i^2$, i siguin $a_1,\ldots,a_n,b\in \mathbb{R}$. Sigui $Y$ la variable aleatòria \[ Y=a_1Y_1+\cdots+a_nY_n+b. \] Aleshores

La mitjana de $Y$ és \[ \mu_Y=a_1\mu_1+\cdots+a_n\mu_n+b. \]
Si $Y_1,\ldots,Y_n$ són independents, aleshores la variància de $Y$ és \[ \sigma_Y^2=a_1^2\sigma_1^2+\cdots+a_n^2\sigma_n^2 \] i per tant la seva desviació típica és \[ \sigma_Y=\sqrt{a_1^2\sigma_1^2+\cdots+a_n^2\sigma_n^2}. \]

Una altra propietat destacada de la distribució normal és que tota combinació lineal de variables aleatòries normals independents torna a ser normal:

Teorema 1.2 Si $Y_1,\ldots,Y_n$ son variables aleatòries normals independents, cada $Y_i\sim N(\mu_i,\sigma_i)$, i $a_1,\ldots,a_n,b\in \mathbb{R}$, aleshores \[ Y=a_1Y_1+\cdots+a_nY_n+b \] és una variable aleatòria $N(\mu,\sigma)$ amb $\mu$ i $\sigma$ els que toquin pel teorema anterior:

$\mu=a_1\mu_1+\cdots+a_n\mu_n+b$
$\sigma=\sqrt{a_1^2\sigma_1^2+\cdots+a_n^2\sigma_n^2}$

Com a cas particular, obtenim que una transformació afí d’una variable aleatòria normal torna a ser normal:

Teorema 1.3 Si $X\sim N(\mu,\sigma)$ i $a,b\in \mathbb{R}$, llavors $aX+b$ també és normal, i en concret és $N(a\mu+b,|a|\cdot\sigma)$.

En particular, si $X\sim N(\mu,\sigma)$, llavors la seva tipificada \[ Z=\dfrac{X-\mu}{\sigma} \] és $N(0,1)$.

Les probabilitats de la normal tipificada determinen les de la normal original, perquè si $X\sim N(\mu,\sigma)$, \[ \begin{array}{rl} P(a\leqslant X\leqslant b) & \displaystyle =P\Big( \frac{a-\mu}{\sigma}\leqslant\frac{X-\mu}{\sigma}\leqslant\frac{b-\mu}{\sigma}\Big)\\ & \displaystyle =P\Big(\frac{a-\mu}{\sigma}\leqslant Z\leqslant\frac{b-\mu}{\sigma}\Big) \end{array} \]

Que tota combinació lineal de variables normals torni a ser del mateix tipus, és a dir, normal, és una propietat molt útil de les variables normals que pocs altres tipus de variables aleatòries tenen. Per exemple, si $X$ és una variable binomial $B(n,p)$ amb $p\neq 0$, $2X$ no és cap variable binomial, perquè només pren valors parells i una variable binomial $B(m,q)$ pot prendre tots els valors entre 0 i $m$.

1.4 Intervals de referència

Un interval de referència del $100q\%$ per a una variable aleatòria $X$ és un interval $[a,b]$ tal que \[ P(a\leqslant X\leqslant b)=q. \] És a dir, un interval de referència del $100q\%$ per a $X$ és un interval que conté els valors de $X$ del $100q\%$ de subjectes de la població on està definida.

Els més comuns són els intervals de referència del 95% ($q=0.95$), que satisfan que \[ P(a\leqslant X\leqslant b)=0.95 \] i són els, que per exemple, us donen com a valors de referència a les analítiques:

Quan es parla d’un interval de referència sense donar-ne la probabilitat, se sobreentén sempre que és l’interval de referència del 95%.

Quan $X\sim N(\mu,\sigma)$, aquests intervals de referència es prenen sempre centrats en la mitjana $\mu$, és a dir, de la forma $[\mu-x,\mu+x]$. Per calcular-los fàcilment, podem emprar el resultat següent:

Teorema 1.4 Si $X\sim N(\mu,\sigma)$, un interval de referència del $100q\%$ és \[ [\mu- z_{(1+q)/2}\cdot \sigma, \mu+ z_{(1+q)/2}\cdot \sigma] \] on $z_{(1+q)/2}$ indica el $(1+q)/2$-quantil de $Z\sim N(0,1)$. L’escriurem \[ \mu\pm z_{(1+q)/2}\cdot \sigma. \]

En efecte: \[ \begin{array}{l} P(\mu-x\leqslant X\leqslant\mu+x)=q\\ \qquad \Longleftrightarrow \displaystyle P\Big(\frac{\mu-x-\mu}{\sigma}\leqslant\frac{X-\mu}{\sigma}\leqslant\frac{\mu+x-\mu}{\sigma}\Big)=q\\ \qquad \Longleftrightarrow \displaystyle P(-x/{\sigma}\leqslant Z\leqslant{x}/{\sigma})=q\\ \qquad \Longleftrightarrow \displaystyle P(Z\leqslant{x}/{\sigma})-P(Z\leqslant-{x}/{\sigma})=q\\ \qquad \Longleftrightarrow \displaystyle P(Z\leqslant{x}/{\sigma})-(1-P(Z\leqslant{x}/{\sigma}))=q\\ \qquad \mbox{(per la simetria de $f_Z$ al voltant de 0)}\\ \qquad \Longleftrightarrow \displaystyle 2P(Z\leqslant{x}/{\sigma})=q+1\\ \qquad \Longleftrightarrow P(Z\leqslant{x}/{\sigma})=(1+q)/2\\ \qquad \Longleftrightarrow x/\sigma= z_{(1+q)/2}\\ \qquad \Longleftrightarrow x=z_{(1+q)/2}\cdot \sigma \end{array} \]

En particular, com que si $q=0.95$, aleshores $(1+q)/2=0.975$ i llavors $z_{0.975}=1.96$, i això sovint s’aproxima per 2, l’interval de referència del 95% per a $X\sim N(\mu,\sigma)$ és \[ \mu\pm 1.96\sigma \] o simplement, per simplificar, \[ \mu\pm 2\sigma. \] Això diu, bàsicament, que

si una població segueix una distribució normal $N(\mu,\sigma)$, un 95% dels seus individus tenen el seu valor de $X$ a distància como a màxim $2\sigma$ (“a dues sigmes”) de $\mu$.

Exemple 1.2 Segons l’OMS, les alçades de les dones europees de 18 anys segueixen una llei $N(163.1,18.53)$. Vull trobar un interval d’alçades centrat en la mitjana que contengui les de la meitat de les europees de 18 anys. És, a dir, vull trobar l’interval de referència del 50% per a la variable aleatòria $X$ definida per les alçades de les dones europees de 18 anys.

Com que $X\sim N(163.1,18.53)$ i si $q=0.5$, aleshores $(1+q)/2=0.75$, aquest interval és

163.1+qnorm(0.75)*18.53*c(-1,1)

## [1] 150.6017 175.5983

Arrodonint a cm, és l’interval [151, 176]. Per tant, la meitat de les dones europees de 18 anys fan entre 1.51 m i 1.76 m d’alçada.

Exemple 1.3 Quin és l’interval de referència per a les alçades de les dones europees de 18 anys?

Com que sobreentenem que es tracta de l’interval de referència del 95%, és \[ 163.1\pm 1.96\times 18.53\Longrightarrow [127, 199] \]

1.5 El z-score

El z-score (o valor z, puntuació z) d’un valor $x_0$ respecte d’una distribució $N(\mu,\sigma)$ és \[ \frac{x_0-\mu}{\sigma}. \] És a dir, el z-score de $x_0$ és el resultat de “tipificar” $x_0$ en el sentit del Teorema 1.3.

Si la variable poblacional és normal, com més gran és el valor absolut del z-score de $x_0$, més “rar” és $x_0$; el signe ens diu si és més gran o més petit que el valor esperat $\mu$.

Exemple 1.4 Recordau que, segons l’OMS, les altures de les dones europees de 18 anys segueixen una llei $N(163.1,18.53)$. Quin és el z-score d’una jugadora de bàsket de 18 anys que faci 191 cm?

Serà: \[ \frac{191-163.1}{18.53}=1.5 \] Això normalment es llegeix dient que aquesta alçada “està a 1.5 sigmes de l’alçada mitjana.”