Tema 9 ANOVA

L’objectiu d’aquest tema és generalitzar el contrast bilateral de dues mitjanes emprant un test t a més de dues mitjanes, de tal manera que amb un sol test poguem decidir si hi ha evidència que alguna parella d’aquestes mitjanes siguin diferents o si pel contrari podem acceptar que totes les mitjanes són iguals.

9.1 Nocions bàsiques

Comencem considerant un problema concret.

Exemple 9.1 Es realitzà un estudi per investigar l’efecte del CO2 sobre la taxa de creixement de Pseudomonas fragi, un corruptor d’aliments. Per contrastar si el seu creixement es veu afectat per la quantitat de CO2 en l’aire, s’administrà CO2 a 5 pressions atmosfèriques diferents a 10 cultius diferents per cada nivell de pressió de CO2 i s’anotà el percentatge d’increment de la massa cel·lular de cada cultiu al cap d’una hora.

Les dades obtingudes varen ser: \[ \begin{array}{c} \text{Pressió de CO${}_2$ (en atmosferes)}\\ \begin{array}{rrrrr} 0.0 & 0.08 & 0.29 & 0.50 & 0.86 \\\hline 62.6 & 50.9 & 45.5 & 29.5 & 24.9 \\ 59.6 & 44.3 & 41.1 & 22.8 & 17.2 \\ 64.5 & 47.5 & 29.8 & 19.2 & 7.8 \\ 59.3 & 49.5 & 38.3 & 20.6 & 10.5 \\ 58.6 & 48.5 & 40.2 & 29.2 & 17.8 \\ 64.6 & 50.4 & 38.5 & 24.1 & 22.1 \\ 50.9 & 35.2 & 30.2 & 22.6 & 22.6 \\ 56.2 & 49.9 & 27.0 & 32.7 & 16.8 \\ 52.3 & 42.6 & 40.0 & 24.4 & 15.9 \\ 62.8 & 41.6 & 33.9 & 29.6 & 8.8 \end{array} \end{array} \]

El contrast que es volia realitzar era:

  • \(H_0\): El percentatge mitjà d’increment del volum cel·lular d’un cultiu de P. fragi al cap d’una hora és el mateix per a totes les pressions de CO2 considerades.

  • \(H_1\): El percentatge mitjà d’increment del volum cel·lular d’un cultiu de P. fragi al cap d’una hora depèn de la pressió de CO2

    que en el nostre experiment traduïm en:

    \(H_1\): No és veritat que el percentatge mitjà d’increment del volum cel·lular d’un cultiu de P. fragi al cap d’una hora sigui el mateix per a totes les pressions de CO2 considerades

    És a dir:

    \(H_1\): Hi ha almenys dues d’aquestes pressions de CO2 sota les quals els percentatges mitjans d’increment del volum cel·lular d’un cultiu de P. fragi al cap d’una hora són diferents

La hipòtesi alternativa en un contrast d’hipòtesis ha de ser complementària a la nul·la, sense que hi hagi cap opció intermèdia entre la nul·la i l’alternativa. D’aquesta manera, si no s’obté evidència de la hipòtesi alternativa, hem d’acceptar la nul·la. Amb aquesta idea al cap, observau que si la hipòtesi nul·la és “totes les mitjanes són iguals”, l’alternativa no pot ser “totes les mitjanes són diferents”, sinó hi ha almenys dues mitjanes que són diferents.

Aquest experiment és un cas particulat del problema següent:

Tenim \(k>2\) poblacions. Volem decidir si la mitjana d’una certa variable aleatòria és la mateixa a totes aquestes poblacions, o no.

Usualment, aquestes \(k\) poblacions seran subpoblacions d’una única població, definides per nivells d’un o diversos factors. Per exemple, a l’estudi del creixement del P. fragi, les poblacions que consideram estan totes formades per cultius d’aquest bacteri, i es diferencien en la pressió de CO2.

En el context d’aquest tipus d’estudis, a aquests nivells els anomenam tractaments. És a dir, tornant a l’exemple anterior, els nivells de pressió de CO2 serien els tractaments que analitzam en aquest estudi.

Per simplificar el llenguatge, sovint cometrem l’abús d’identificar una subpoblació d’aquestes amb el nivell, o tractament, que la defineix. D’aquesta manera, parlarem per exemple de

la mitjana poblacional del tractament “0.29 atmosferes”

per referir-nos a la mitjana de la població definida pel tractament “0.29 atmosferes”, és a dir, al percentatge mitjà d’increment del volum cel·lular en una hora d’un cultiu de P. fragi a 0.29 atmosferes de pressió de CO2. I de

la mitjana mostral del tractament “0.29 atmosferes”

per referir-nos a la mitjana de la nostra mostra de la població definida pel tractament “0.29 atmosferes”, és a dir, a la mitjana dels percentatges d’increment del volum cel·lular dels cultius de P. fragi a 0.29 atmosferes obtinguts en aquest experiment.

Si diem \(\mu_1,\ldots,\mu_k\) a les mitjanes d’aquesta variable en aquestes \(k\) poblacions, aquesta pregunta correspon al contrast: \[ \left\{ \begin{array}{l} H_0 : \mu_1 =\mu_2 =\cdots =\mu_k \\ H_1 : \text{Hi ha }i,j\text{ tals que } \mu_i \neq\mu_j \end{array} \right. \]

Aleshores, prendrem una mostra aleatòria de cada població (una mostra estratificada de la població total, recordau?), i a partir d’aquestes mostres decidirem aquest contrast.

Exemple 9.2 Continuem amb el nostre Exemple 9.1. Per a cada \(\ell=0,0.08,0.29,0.50,0.86\), consideram la variable aleatòria

  • \(X_\ell\): “Percentatge de creixement del volum cel·lular en una hora d’un cultiu de P. fragi a \(\ell\) atmòsferes de CO2”, de mitjana \(\mu_\ell\)

Volem realitzar el contrast \[ \left\{ \begin{array}{l} H_0 : \mu_0=\mu_{0.08}=\mu_{0.29}=\mu_{0.50}=\mu_{0.86} \\ H_1 : \text{No totes aquestes mitjanes són iguals} \end{array} \right. \]

En temes anteriors, per comparar les mitjanes d’una variable sobre dues poblacions, calculàvem les mitjanes de dues mostres i les comparàvem. Per comparar les mitjanes de \(k\geqslant 3\) poblacions, podríem fer-ho per parelles, però hauríem de fer \(\binom{k}{2}\) contrastos i això augmenta la probabilitat d’error. A més, les hem de comparar totes amb totes, perquè podria passar que no poguéssim rebutjar que \(\mu_1= \mu_2\) ni que \(\mu_2= \mu_3\) però en canvi sí que poguéssim rebutjar que \(\mu_1= \mu_3\).

El que volem és un test que ens digui en un sol pas si totes les mitjanes són iguals o no; si concloem que no, després ja cercarem quines mitjanes són diferents si volem.

La tècnica més usual per efectuar aquest tipus de contrast és l’Anàlisi de la Variància o ANOVA (de l’anglès ANalysis Of VAriance; en llibres en castellà o català de vegades hi trobareu el terme ANDEVA, d’ANàlisi DE la VAriància, però no el farem servir, perquè trobam que sona més a marca de producte d’higiene íntima femenina que a tècnica estadística seriosa). L’ANOVA és tot un món, i té moltes variants segons el disseny de l’experiment que ha produït les dades:

  • Segons quants factors emprem per separar la població en subpoblacions

  • Segons com triem els nivells dels factors

  • Segons com prenguem les mostres

En aquest curs veurem els tres dissenys més bàsics:

  • L’ANOVA d’1 via, que generalitza el test t de dues mitjanes a partir de dues mostres independents a \(k\) mitjanes de poblacions definides pels nivells d’un únic factor, a partir de \(k\) mostres independents

  • L’ANOVA de blocs, que generalitza el test t de dues mitjanes a partir de dues mostres aparellades a \(k\) mitjanes de poblacions definides pels nivells d’un únic factor, a partir de \(k\) mostres aparellades

  • L’ANOVA de 2 vies, que generalitza el test t de dues mitjanes a partir de dues mostres independents a més de dues mitjanes de poblacions definides per les combinacions de nivells de dos factors, a partir de mostres independents

Recordau que en català “Anàlisi” és femení, mentre que en castellà “Análisis” és masculí. Per tant en català diem “una ANOVA” i en castellà “un ANOVA”. Expressau-vos bé, per favor.
ANO…VA? Que no volíem comparar mitjanes? Idò com és que analitzam variàncies?

L’estratègia per comparar les mitjanes de 3 o més poblacions serà fixar-nos en tres fonts de variabilitat, o dispersió, de les dades:

  • La variabilitat total de les dades (respecte de la mitjana mostral global)

  • La variabilitat dins cada mostra (respecte de la mitjana mostral corresponent)

  • La variabilitat de les mitjanes mostrals (respecte de la mitjana mostral global)

La idea és que si les mitjanes mostrals tenen molta variabilitat, ho prendrem com a senyal que les mitjanes poblacionals no poden ser totes iguals. Com ho mesurarem?

Amb definicions adients de les “variabilitats”, resultarà que

La variabilitat total de les dades és igual a la suma de la variabilitat de les mitjanes mostrals més la suma de les variabilitats dins les mostres.

Aleshores, la idea bàsica anterior es tradueix en:

Si la variabilitat total de les dades és molt més gran que la suma de les variabilitats dins les mostres, hi haurà una gran variabilitat de les mitjanes mostrals, i ho prendrem com a senyal que les mitjanes poblacionals no són iguals.

Per exemple, si teniu molta variabilitat global

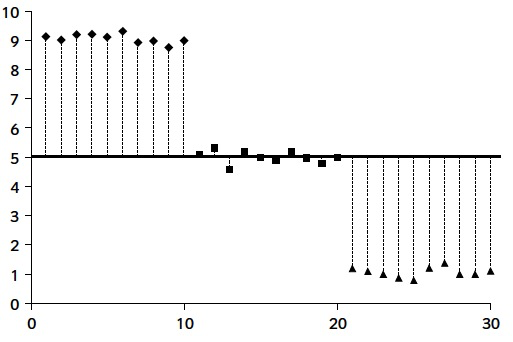
i molt poca dins cada tractament

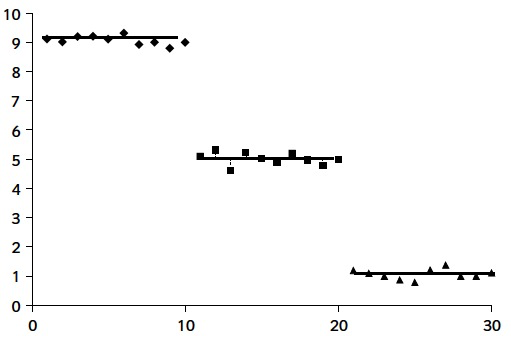
serà evidència que les mitjanes poblacionals són diferents

Si en canvi teniu molta variabilitat global

però també molta dins cada tractament

no podrem concloure que les mitjanes poblacionals siguin diferents.

La pregunta és ara com quantificam aquestes variabilitats i com definim què significa “molt més gran”. Es tractarà de trobar un estadístic de contrast del qual en coneguem la distribució mostral si la hipòtesi nul·la és vertadera i que esperem que prengui un valor petit si la hipòtesi nul·la és vertadera.

9.2 ANOVA d’1 via

9.2.1 Contrast bàsic

La situació és la següent. Tenim una variable aleatòria \(X\) i un (únic) factor, els \(k\) nivells (o tractaments) del qual classifiquen la població en \(k\) subpoblacions. Diguem \(\mu_i\) a la mitjana de \(X\) en els individus del nivell \(i\)-èsim. Volem comparar aquestes mitjanes \(\mu_1\),…,\(\mu_k\) i en concret decidir si són totes iguals o no.

En un experiment de disseny d’ANOVA d’1 via (en anglès, 1 way; el motiu d’aquest nom és que empram una única “manera” de classificar la població, en anglès one way que també es tradueix per “una via”, i així ha quedat el nom en les nostres llengües):

  • S’empra un factor amb \(k>2\) nivells per classificar una població en subpoblacions

  • Es pren una m.a.s. de cada subpoblació, de manera independent les unes de les altres, i es mesura sobre tots els subjectes de les mostres la variable d’interès \(X\)

Per exemple, l’experiment del nostre Exemple 9.1 té disseny d’ANOVA d’1 via:

  • La variable \(X\) és el percentatge d’increment cel·lular en una hora d’un cultiu de P. fragi

  • El factor emprat per classificar la població és la pressió de CO2: es consideren 5 nivells diferents, sota els quals es realitzen els cultius

  • S’hi ha pres una m.a.s. per a cada nivell de pressió, i de manera independent les unes de les altres

Ja que hi som, anam a organitzar les dades d’aquest experiment de manera adient. Les emmagatzemarem en un dataframe que anomenarem CO2 amb dues variables:

  • Inc: Percentatge d’increment de la massa cel·lular (al cap d’una hora); una variable numèrica
  • Pre: Nivell de pressió, com a factor
De cara a fer-ho amb R, és important que recordeu que la variable que defineix les subpoblacions, en aquest cas la que dóna el nivell de pressió de CO2, sigui un factor.

Les dades eren:

\[ \begin{array}{c} \text{Pressió de CO${}_2$ (en atmosferes)}\\ \begin{array}{rrrrr} 0.0 & 0.08 & 0.29 & 0.50 & 0.86 \\\hline 62.6 & 50.9 & 45.5 & 29.5 & 24.9 \\ 59.6 & 44.3 & 41.1 & 22.8 & 17.2 \\ 64.5 & 47.5 & 29.8 & 19.2 & 7.8 \\ 59.3 & 49.5 & 38.3 & 20.6 & 10.5 \\ 58.6 & 48.5 & 40.2 & 29.2 & 17.8 \\ 64.6 & 50.4 & 38.5 & 24.1 & 22.1 \\ 50.9 & 35.2 & 30.2 & 22.6 & 22.6 \\ 56.2 & 49.9 & 27.0 & 32.7 & 16.8 \\ 52.3 & 42.6 & 40.0 & 24.4 & 15.9 \\ 62.8 & 41.6 & 33.9 & 29.6 & 8.8 \end{array} \end{array} \]

Entrarem els increments per fileres (és més fàcil de copiar i aferrar), per tant el factor Pre ha d’estar format per 10 còpies consecutives del vector (0.0,0.08,0.29,0.50,0.86).

## 'data.frame':    50 obs. of  2 variables:
##  $ Inc: num  62.6 50.9 45.5 29.5 24.9 59.6 44.3 41.1 22.8 17.2 ...
##  $ Pre: Factor w/ 5 levels "0.0","0.08","0.29",..: 1 2 3 4 5 1 2 3 4 5 ...
##    Inc  Pre
## 1 62.6  0.0
## 2 50.9 0.08
## 3 45.5 0.29
## 4 29.5 0.50
## 5 24.9 0.86
## 6 59.6  0.0
## 7 44.3 0.08

Veiem que hem definit del dataframe com toca. Donem ara una ullada a les dades. Primer un diagrama de punts de cada nivell de CO2 (amb només 10 valors per nivell, és més adient dibuixar-los tots que resumir-los en diagrames de caixes):

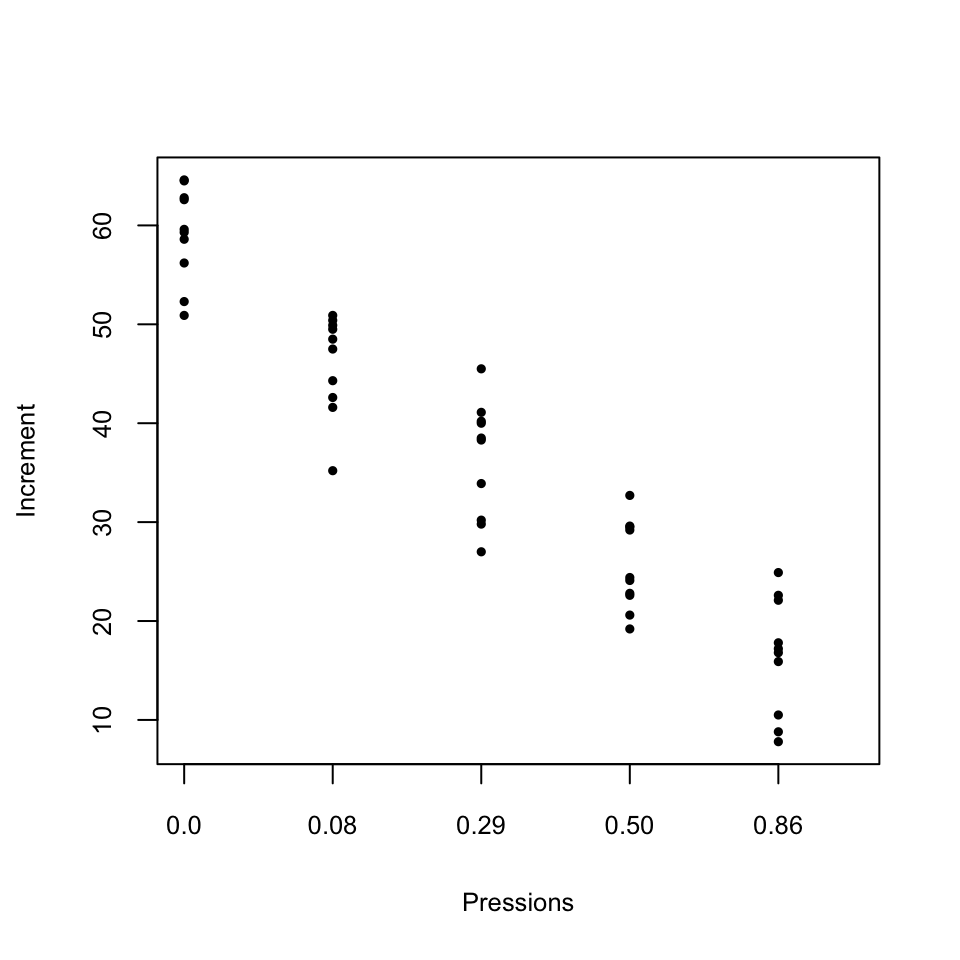
I ara un que mostri la variabilitat de les dades i les mitjanes com els del final de la secció anterior. Aquest gràfic normalment no el dibuixarem, simplement és per comparar-lo amb aquells gràfics.

# Els paràmetres generals
plot(1:50,c(CO2$Inc[CO2$Pre=="0.0"],CO2$Inc[CO2$Pre=="0.08"],CO2$Inc[CO2$Pre=="0.29"],CO2$Inc[CO2$Pre=="0.50"],CO2$Inc[CO2$Pre=="0.86"]),type="n",xlab="Número del cultiu",ylab="Increment")
# Els punts
points(1:10,CO2$Inc[CO2$Pre=="0.0"],pch=16,col="red")
points(11:20,CO2$Inc[CO2$Pre=="0.08"],pch=15,col="blue")
points(21:30,CO2$Inc[CO2$Pre=="0.29"],pch=17,col="green")
points(31:40,CO2$Inc[CO2$Pre=="0.50"],pch=19,col="brown2")
points(41:50,CO2$Inc[CO2$Pre=="0.86"],pch=18,col="brown")
# La mitjana mostral global
lines(c(0,50),c(mean(CO2$Inc),mean(CO2$Inc)),lwd=2)
text(5,34,"Mitjana global",cex=0.75)
# Les mitjanes mostrals de les mostres
lines(c(0,10),c(mean(CO2$Inc[CO2$Pre=="0.0"]),mean(CO2$Inc[CO2$Pre=="0.0"])),lwd=2,col="red")
lines(c(10,20),c(mean(CO2$Inc[CO2$Pre=="0.08"]),mean(CO2$Inc[CO2$Pre=="0.08"])),lwd=2,col="blue")
lines(c(20,30),c(mean(CO2$Inc[CO2$Pre=="0.29"]),mean(CO2$Inc[CO2$Pre=="0.29"])),lwd=2,col="green")
lines(c(30,40),c(mean(CO2$Inc[CO2$Pre=="0.50"]),mean(CO2$Inc[CO2$Pre=="0.50"])),lwd=2,col="brown2")
lines(c(40,50),c(mean(CO2$Inc[CO2$Pre=="0.86"]),mean(CO2$Inc[CO2$Pre=="0.86"])),lwd=2,col="brown")
text(20,mean(CO2$Inc[CO2$Pre=="0.0"]),"Mitjana del nivell 0.0",col="red",cex=0.75)
text(30,mean(CO2$Inc[CO2$Pre=="0.08"]),"Mitjana del nivell 0.083",col="blue",cex=0.75)
text(40,mean(CO2$Inc[CO2$Pre=="0.29"]+2),"Mitjana del nivell 0.29",col="green",cex=0.75)
text(20,mean(CO2$Inc[CO2$Pre=="0.50"]),"Mitjana del nivell 0.50",col="brown2",cex=0.75)
text(30,mean(CO2$Inc[CO2$Pre=="0.86"]),"Mitjana del nivell 0.86",col="brown",cex=0.75)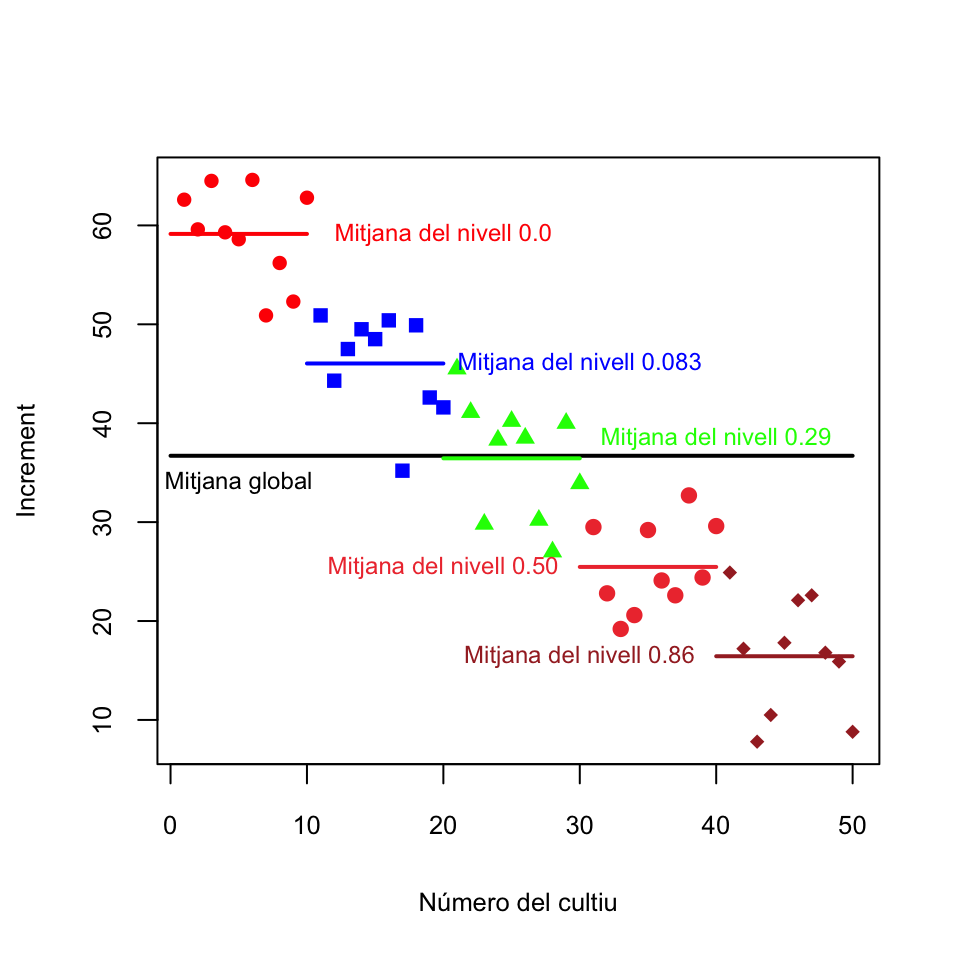

Veiem que hi ha una gran dispersió dins la mostra completa, no massa dispersió dins cada mostra per nivell, i les mitjanes mostrals per nivells són bastant diferents. Naturalment, fins que no fem una anàlisi estadística no sabrem si aquestes variabilitats i diferències són estadísticament significatives o no.

En un experiment amb disseny d’ANOVA d’1 via, disposarem les dades en una taula com la de l’Exemple anterior, amb les columnes representant els tractaments: \[ \begin{array}{c} \text{Tractaments}\\ \begin{array}{cccc} 1 & 2 &\ldots & k \\\hline X_{11} & X_{21} & \cdots & X_{k1} \\ X_{12} & X_{22} & \cdots & X_{k2} \\ \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & X_{kn_k} \\ X_{1n_1} & \vdots & \vdots & \\ & X_{2n_2} & & \\\hline \end{array} \end{array} \]

on

  • Cada \(n_i\) és la mida de la mostra del tractament \(i\); com hem intentat representar a la taula, aquests \(n_i\) no tenen perquè ser tots iguals (però millor si ho són, perquè la potència d’un contrast ANOVA depèn del mínim d’aquests \(n_i\))

  • \(X_{ij}\) és el valor de la variable sota estudi al subjecte \(j\) del tractament \(i\)

  • \(N=n_1+\cdots+n_k\) és la mida total de la mostra

ALERTA! Les notacions són diferents que les usuals a les matrius o a les taules de dades. A \(X_{ij}\), \(i\) hi indica la columna i \(j\) la filera.

Fixau-vos que aquí no és veritat que cada filera representi un individu: en realitat cada columna pot tenir una alçada diferent. En aquesta taula cada \(X_{ij}\) representa un individu diferent.

Perquè es pugui realitzar un contrast ANOVA d’1 via, s’han de satisfer les condicions següents:

  • Les \(k\) mostres han de ser m.a.s. independents extretes de \(k\) poblacions específiques, amb mitjanes \(\mu_1,\ldots,\mu_k\)

  • \(N\geqslant k+1\) (alguna mostra ha de tenir més d’un subjecte)

  • Cadascuna de les \(k\) poblacions ha de seguir una llei normal

  • Homogeneïtat de les variàncies, o homocedasticitat: Totes aquestes poblacions han de tenir la mateixa variància, que indicarem amb \(\sigma^2\)

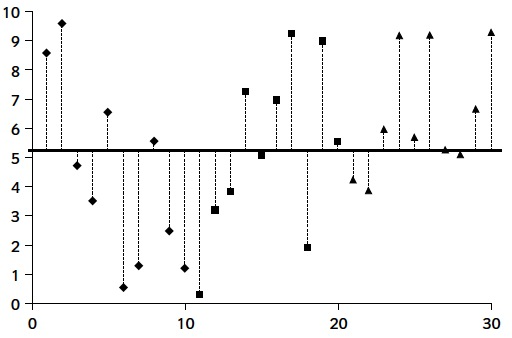
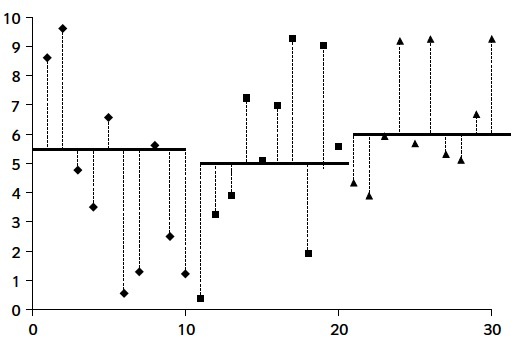
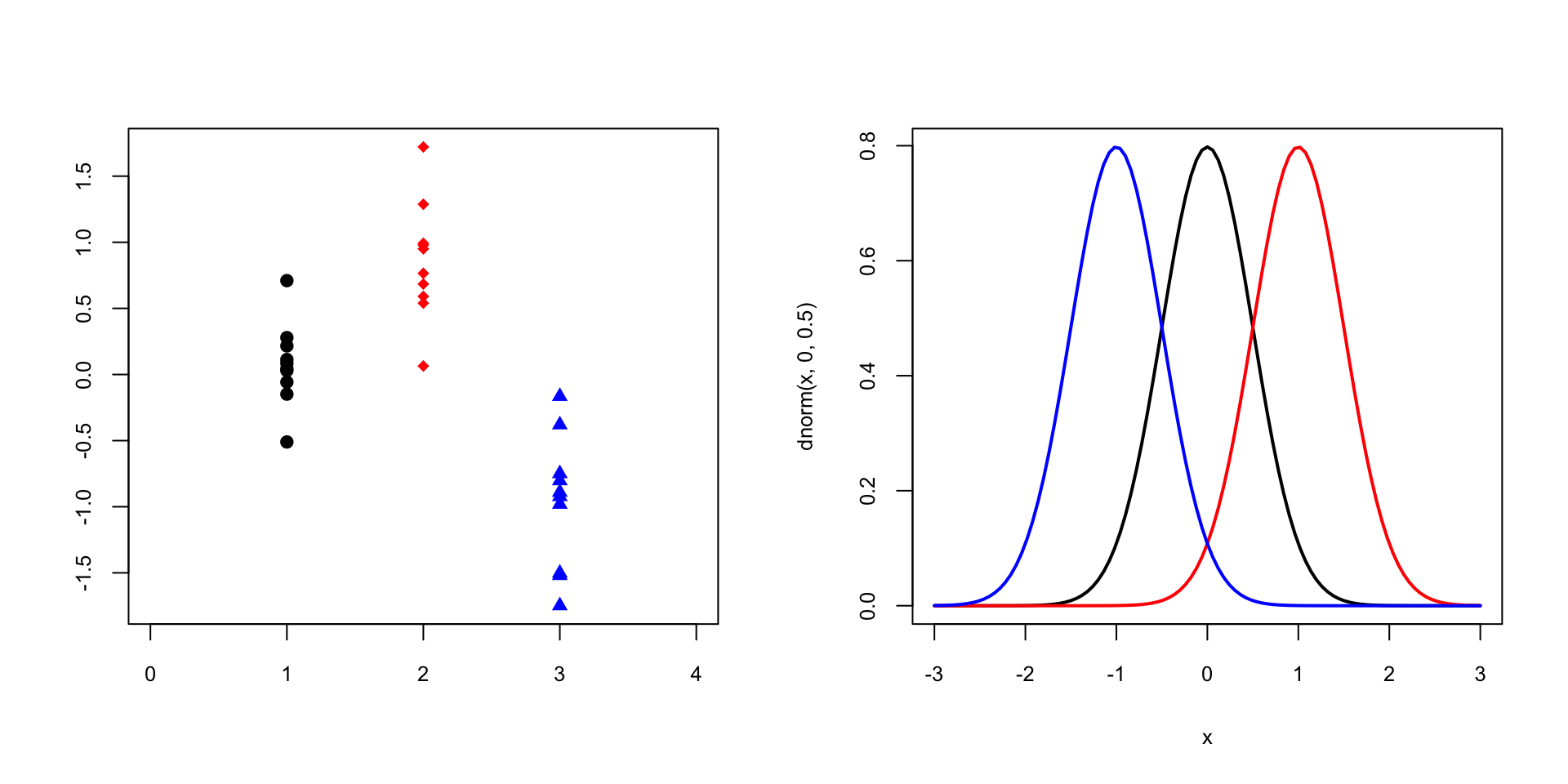
No basten mostres grans. Aquí no hi juga cap paper el Teorema Central del Límit. Però, per sort, les conclusions d’una ANOVA són bastant robustes encara que falli la condició de normalitat de les subpoblacions. En canvi són molt sensibles a l’heterocedasticitat (el contrari d’homocedasticitat; “hetero” indica el contrari de “homo”).

Donades diverses variables, hi tenim homocedasticitat quan totes tenen la mateixa variància, i heterocedasticitat quan no totes tenen la mateixa variància. Fixau-vos que ens referim a les variàncies de les poblacions, no de les mostres. Per exemple, les tres mostres del gràfic de l’esquerra següent provenen de variables normals amb la mateixa variància, representades al gràfic de la dreta: hi ha homocedasticitat:

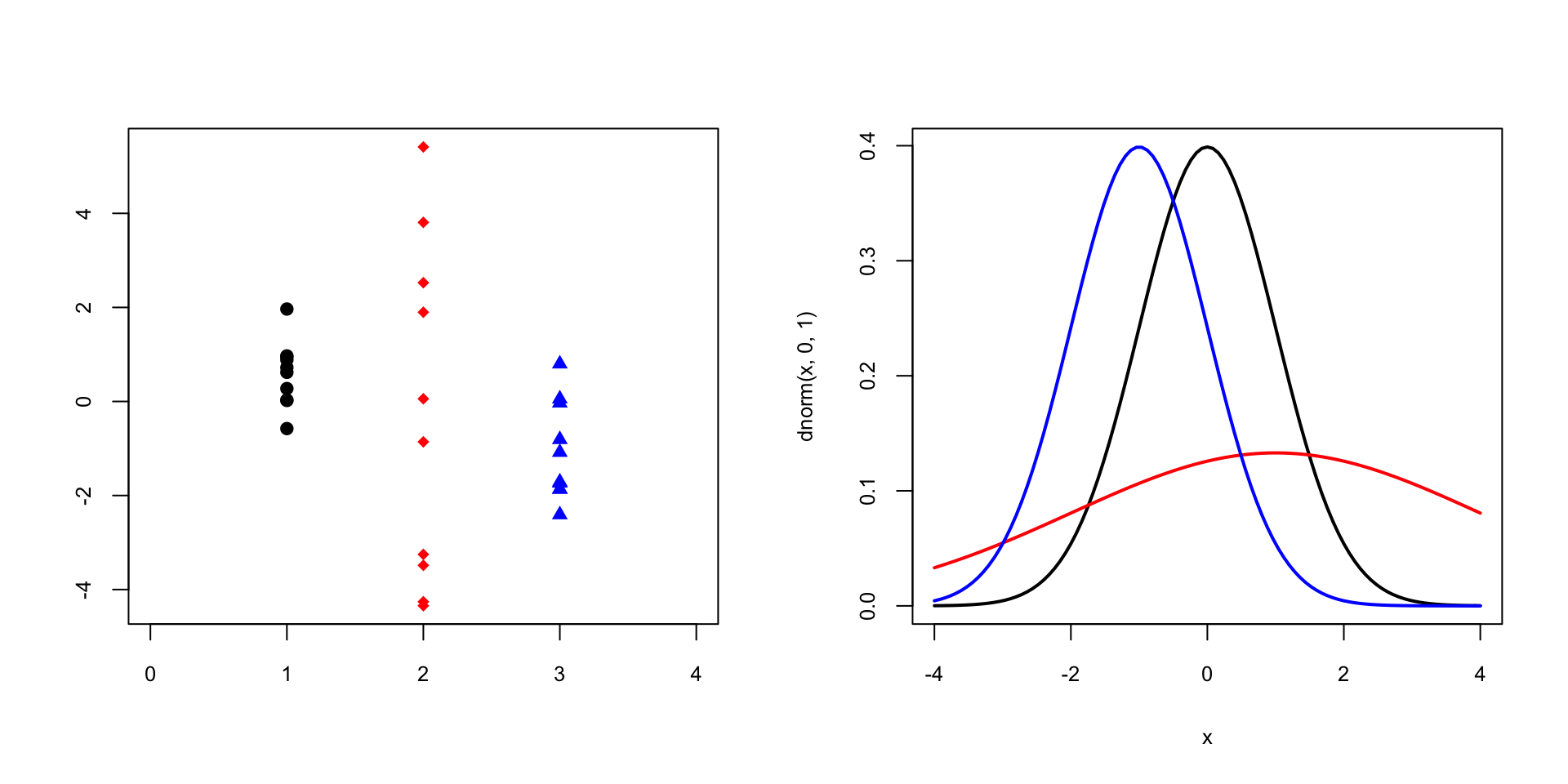
En canvi, al gràfic següent dues mostres provenen de variables normals amb la mateixa variància, però la tercera prové d’una normal amb una variància molt més gran: hi ha heterocedasticitat:

L’homocedasticitat no és que les mostres dels tractaments tenguin la mateixa variància, sinó que els tractaments tenguin la mateixa variància poblacional.

Diguem \(\mu\) a la mitjana poblacional de la població global (sense tenir en compte la classificació donada pels tractaments). Recordau que la hipòtesi nul·la del contrast que volem realitzar és \[ H_0: \mu_1=\cdots=\mu_k \] Si és vertadera, aleshores en realitat passarà que \[ \mu_1=\cdots=\mu_k=\mu \] perquè si totes les subpoblacions tenen la mateixa mitjana, aquesta mitjana comuna serà la mitjana de tota la població.

En aquest tema és el primer cop que tenim ocasió de parlar de models estadístics. Informalment, un model no és res més que una descripció matemàtica del comportament d’una o vàries variables aleatòries sobre una població. Aquests models inclouen assumpcions sobre la població que poden ser veritat o no, i que si no ho són aleshores les conclusions de l’anàlisi estadística que fem basant-nos en aquest model no tendran cap sentit.

En concret, l’ANOVA d’1 via es basa en el model següent: per a cada \(i=1,\ldots,k\), \[ X_i=\mu+(\mu_i-\mu)+(X_i-\mu_i) \] on:

  • \(X_i\) representa el valor de la variable \(X\) sobre un individu del nivell \(i\)-èsim

  • \(\mu_i-\mu\) representa la desviació de la mitjana de \(X\) en el nivell \(i\)-èsim respecte de la mitjana global \(\mu\); en direm l’efecte del tractament \(i\)-èsim i representa la contribució al valor de \(X\) sobre un individu del nivell \(i\)-èsim del fet de pertànyer a aquest nivell

  • \(X_i-\mu_i\), la desviació de la variable \(X\) sobre un individu del nivell \(i\)-èsim respecte de la mitjana d’aquest nivell, \(\mu_i\), representa el component aleatori en una medició concreta de \(X\) sobre un individu del nivell \(i\)-èsim, és a dir, “la part de la diferència entre \(X_{i}\) i \(\mu\) que no explica el tractament”; en diem l’error aleatori, o el residu.

Fixau-vos que la fórmula que descriu aquest model és sempre veritat (podeu simplificar les \(\mu_i\) i les \(\mu\) de la dreta), i bàsicament diu que el valor de \(X\) sobre un individu és la suma de tres components:

  • La mitjana global
  • L’efecte del tractament
  • L’error aleatori

i en particular que res més no influeix en el valor de \(X\) sobre un individu. Per tant, si això no és veritat, és a dir, si aquest valor pot dependre d’altres efectes que no tinguem en compte, el model no és vàlid, i les conclusions de l’ANOVA tampoc.

Passem ara a la mostra amb la que volem realitzar el contrast. Siguin:

  • \(\overline{X}_{i}\): Mitjana mostral de la mostra del tractament \(i\)-èsim: \[ \overline{X}_{i} = \frac{\sum_{j=1}^{n_i} X_{ij}}{n_i} \] Estima la mitjana \(\mu_i\) de la subpoblació definida pel tractament \(i\)-èsim

  • \(\overline{X}\): Mitjana mostral de tota la mostra: \[ \overline{X}=\frac{\sum_{i=1}^k \sum_{j=1}^{n_i} X_{ij}}{N} \] Estima la mitjana \(\mu\) de la població global

Es té la identitat següent:

Teorema 9.1 (Identitat de les sumes de quadrats) \[ SS_{Total}=SS_{Tr}+SS_E \] on

  • \(SS_{Total}=\displaystyle\sum_{i=1}^k\sum_{j=1}^{n_i} (X_{ij}-\overline{X})^2\); és la Suma Total de Quadrats

  • \(SS_{Tr}=\displaystyle\sum_{i=1}^k n_i(\overline{X}_{i}-\overline{X})^2\); és la Suma de Quadrats dels Tractaments

  • \(SS_E=\displaystyle\sum_{i=1}^k\sum_{j=1}^{n_i} (X_{ij}-\overline{X}_{i})^2\); és la Suma de Quadrats dels Residus o dels Errors

Fixau-vos que

  • \(SS_{Total}\) representa la variabilitat total de les dades: de fet, és el numerador de la variància de la mostra total

  • \(SS_{Tr}\) representa la variabilitat de les mitjanes: és molt semblant al que seria el numerador de la variància d’un vector format per \(n_1\) còpies de \(\overline{X}_1\), \(n_2\) còpies de \(\overline{X}_2\), …, \(n_k\) còpies de \(\overline{X}_k\) (i seria aquest numerador si \(n_1=\cdots=n_k\))

  • \(SS_E\) representa la suma de les variabilitats de les dades de la mostra de cada tractament: de fet, és la suma dels numeradors de les variàncies de les \(k\) mostres dels diferents tractaments

  • \(SS_{Total}=SS_{Tr}+SS_E\) diu que la variabilitat total de la mostra descompon en la suma de la variabilitat de les mitjanes i la suma de les variabilitats de les mostres de cada tractament

Fixau-vos que, amb la terminologia introduïda quan explicàvem el model de l’ANOVA d’1 via, cada \(X_{ij}-\mu_i\) estima el residu, o error, sobre l’individu \(j\)-èsim del nivell \(i\)-èsim. Per això a \(\displaystyle\sum_{i=1}^k\sum_{j=1}^{n_i} (X_{ij}-\overline{X}_{i})^2\) li diem la Suma de Quadrats dels Residus o dels Errors.
Exemple 9.3 Tornem al nostre Exemple 9.1. Tenim les dades guardades en el dataframe CO2 
## 'data.frame':    50 obs. of  2 variables:
##  $ Inc: num  62.6 50.9 45.5 29.5 24.9 59.6 44.3 41.1 22.8 17.2 ...
##  $ Pre: Factor w/ 5 levels "0.0","0.08","0.29",..: 1 2 3 4 5 1 2 3 4 5 ...

Aleshores:

  • Les mitjanes mostrals dels tractaments, \(\overline{X}_{i}\), es calculen amb
##    Pre   Inc
## 1  0.0 59.14
## 2 0.08 46.04
## 3 0.29 36.45
## 4 0.50 25.47
## 5 0.86 16.44
  • La mitjana mostral global, \(\overline{X}\), és:
## [1] 36.708
  • La \(SS_{Total}=\displaystyle\sum_{i=1}^k\sum_{j=1}^{n_i} (X_{ij}-\overline{X})^2\) és
## [1] 12522.36
  • Per calcular \[ SS_{Tr}=\displaystyle\sum_{i=1}^k n_i(\overline{X}_{i}-\overline{X})^2 \] hem d’observar que les mitjanes \(\overline{X}_{i}\) formen la variable Inc del dataframe mitjanes.tracts i els \(n_i\) són les freqüències absolutes de cada nivell dins la variable CO2$Pre.
## [1] 11274.32
  • Per calcular \[ SS_E=\displaystyle\sum_{i=1}^k\sum_{j=1}^{n_i} (X_{ij}-\overline{X}_{i})^2 \] podem fixar-nos que, tal i com hem construït el dataframe CO2, les entrades de CO2$Inc que difereixen en un múltiple de 5 són del mateix tractament; per exemple, les entrades que corresponen a pressió 0 són la 1a, la 6a, la 11a etc.; les entrades que corresponen a pressió 0.83 són la 2a, la 7a, la 12a etc.; i així successivament. Per tant, si fem CO2$Inc-mitjanes.tracts$Inc, com que la longitud de CO2$Inc és 10 vegades la de mitjanes.tracts$Inc, el que estarem dient és que a CO2$Inc se li resti un vector format per 10 còpies consecutives de mitjanes.tracts$Inc, i d’aquesta manera justament a cada entrada de CO2$Inc se li restarà l’entrada de mitjanes.tracts$Inc que és la mitjana del seu tractament. Per tant, \(SS_E\) es pot calcular amb
## [1] 1248.038

Comprovem la identitat de les sumes de quadrats:

## [1] 12522.36
## [1] 12522.36

La idea del contrast ANOVA és que

Rebutjam la hipòtesi nul·la si \(SS_{Tr}\) és prou gran

Per la identitat de les sumes de quadrats \(SS_{Total}=SS_{Tr}+SS_E\), això ho podem traduir en

Rebutjam la hipòtesi nul·la si \(SS_{Total}\) és molt més gran que \(SS_E\)

I això en realitat ho traduïm en

Rebutjam la hipòtesi nul·la si \(SS_{Tr}\) és prou més gran que \(SS_E\)

Per mesurar-ho emprarem els estadístics següents:

  • Quadrat mitjà dels tractaments: \[ MS_{Tr}=\frac{SS_{Tr}}{k-1} \]
  • Quadrat mitjà residual: \[ MS_E=\frac{SS_E}{N-k} \]

Aquests estadístics són variables aleatòries, i sota les condicions necessàries per poder fer una ANOVA (mostres aleatòries simples independents, variable poblacional normal per a cada tractament, homocedasticitat), satisfan que

  • \(E(MS_{Tr})=\displaystyle\sigma^2 + \sum_{i=1}^k \frac{n_i (\mu_i-\mu)^2}{k-1}\)

  • \(E(MS_E)=\sigma^2\)

En particular, es pot usar \(MS_E\) per estimar la variància poblacional comuna \(\sigma^2\) de tots els tractaments.

Ara, si \(H_0:\mu_1=\cdots=\mu_k (=\mu)\) és certa, \[ \sum_{i=1}^k \frac{n_i (\mu_i -\mu)^2}{k-1}=0, \] i si \(H_0\) no és certa, aquesta quantitat és \(>0\)

Per tant

  • Si \(H_0\) és certa, \(E(MS_E)=E(MS_{Tr})\) i per tant hauríem d’esperar que aquests dos estadístics tinguessin valors propers, és a dir, hauríem d’esperar que \[ \frac{MS_{Tr}}{MS_E}\approx 1 \]

  • Si \(H_0\) és falsa, \(E(MS_E)<E(MS_{Tr})\) i hauríem d’esperar que \(MS_{Tr}\) donàs valors més grans que \(MS_E\), és a dir, hauríem d’esperar que \[ \frac{MS_{Tr}}{MS_E}> 1 \]

Aleshores, prenem com a estadístic de contrast el quocient \[ F=\frac{MS_{Tr}}{MS_E} \] el qual satisfà la propietat següent.

Teorema 9.2 Sota les condicions necessàries per poder realitzar una ANOVA i si \(H_0:\mu_1=\cdots=\mu_k\) és certa,

  • La distribució de \(F\) és una F de Fisher amb \(k-1\) i \(N-k\) graus de llibertat, \(F_{k-1,N-k}\)

  • El seu valor és proper a 1

Per tant, en una ANOVA rebutjarem la hipòtesi nul·la si el valor \(F_0\) de \(F\) obtingut sobre la nostra mostra és molt gran. Això ho traduirem en que rebutjarem la hipòtesi nul·la si la probabilitat que \(F\) sigui més gran que \(F_0\) és petita, i aquesta probabilitat serà el p-valor del contrast.

Si \(k=2\), aquesta \(F\) és igual al quadrat de l’estadístic del test t de 2 mostres independents i variàncies iguals. Per tant, efectuar una ANOVA d’1 via amb només 2 tractaments és equivalent a efectuar un test t amb mostres independents i mateixa variància poblacional.
Per si qualcú necessita una dosi d’àlgebra, recordau que el quadrat de l’estadístic del test t de 2 mostres independents i variàncies iguals és \[ T^2=\frac{(\overline{X}_1-\overline{X}_2)^2}{(\frac{1}{n_1}+\frac{1}{n_2})\cdot \frac{(n_1-1)\widetilde{S}_1^2+(n_2-1)\widetilde{S}_2^2}{n_1+n_2-2}} \] i que el nostre \(F\) és \(MS_{Tr}/MS_E\). Ara, en el cas \(k=2\), \[ MS_E=\frac{\sum_{j=1}^{n_1}(X_{1j}-\overline{X}_1)^2+\sum_{j=1}^{n_2}(X_{2j}-\overline{X}_2)}{N-2}= \frac{(n_1-1)\widetilde{S}_{X_1}+(n_2-1)\widetilde{S}_{X_2}}{n_1+n_2-2} \] que surt al denominador de \(T^2\). Per tant ens queda veure que \(MS_{Tr}\) és igual a \[ \frac{(\overline{X}_1-\overline{X}_2)^2}{\frac{1}{n_1}+\frac{1}{n_2}} \] Per simplificar, diguem \(S_1=n_1\overline{X}_1=\sum_{j=1}^{n_1} X_{1j}\), \(S_2=n_2\overline{X}_2=\sum_{j=1}^{n_2} X_{2j}\) i \[ S=(n_1+n_2)\overline{X}=\sum_{i=1}^2\sum_{j=1}^{n_i} X_{ij}=S_1+S_2=n_1\overline{X}_1+n_2\overline{X}_2. \] Doncs va, desenvolupem \(MS_{Tr}\) en aquest cas \(k=2\): \[ \begin{array}{rl} MS_{Tr} & \displaystyle = \frac{n_1(\overline{X}_1-\overline{X})^2+n_2(\overline{X}_2-\overline{X})^2}{1}\\ & \displaystyle = n_1\overline{X}_1^2-2n_1\overline{X}_1\overline{X}+n_1\overline{X}^2+ n_2\overline{X}_2^2-2n_2\overline{X}_2\overline{X}+n_2\overline{X}^2\\ & \displaystyle = S_1\overline{X}_1+S_2\overline{X}_2-2S_1\overline{X}-2S_2\overline{X}+(n_1+n_2)\overline{X}^2\\ & \displaystyle =S_1\overline{X}_1+S_2\overline{X}_2-2(S_1+S_2)\overline{X}+(S_1+S_2)\overline{X}\\ & \displaystyle =S_1\overline{X}_1+S_2\overline{X}_2-(S_1+S_2)\overline{X}\\ & \displaystyle = S_1\overline{X}_1+S_2\overline{X}_2 -\frac{(S_1+S_2)(n_1\overline{X}_1+n_2\overline{X}_2)}{n_1+n_2}\\ & \displaystyle =\frac{(n_1+n_2)S_1\overline{X}_1+(n_1+n_2)S_2\overline{X}_2-n_1S_1\overline{X}_1-n_1S_2\overline{X}_1-n_2S_1\overline{X}_2-n_2S_2\overline{X}_2}{n_1+n_2}\\ & \displaystyle =\frac{n_2S_1\overline{X}_1+n_1S_2\overline{X}_2-n_1S_2\overline{X}_1-n_2S_1\overline{X}_2}{n_1+n_2}\\ & \displaystyle =\frac{n_2n_1\overline{X}_1^2+n_1n_2\overline{X}_2^2-n_1n_2\overline{X}_2\overline{X}_1-n_2n_1\overline{X}_1\overline{X}_2}{n_1+n_2}\\ & \displaystyle =\frac{n_1n_2(\overline{X}_1^2+\overline{X}_2^2-2\overline{X}_1\overline{X}_2)}{n_1+n_2}\\ & \displaystyle =\frac{n_1n_2(\overline{X}_1-\overline{X}_2^2}{n_1+n_2}\\ & \displaystyle =\frac{(\overline{X}_1-\overline{X}_2)^2}{\frac{n_1+n_2}{n_1n_2}}\\ & \displaystyle =\frac{(\overline{X}_1-\overline{X}_2)^2}{\frac{1}{n_1}+\frac{1}{n_2}} \end{array} \]

En resum, per realitzar una ANOVA d’1 via a partir d’una mostra:

  • Calculam les sumes de quadrats \[ SS_{Tr},\ SS_E \]

  • Calculam els quadrats mitjans \[ MS_{Tr}=\frac{SS_{Tr}}{k-1},\ MS_E=\frac{SS_E}{N-k} \]

  • Calculam l’estadístic de contrast sobre la nostra mostra \[ F_0=\frac{MS_{Tr}}{MS_E} \]

  • Calculam el p-valor \[ P(F_{k-1,N-k}\geqslant F_0) \]

  • Si el p-valor és més petit que el nivell de significació \(\alpha\), rebutjam \(H_0\) i concloem que no totes les mitjanes són iguals. En cas contrari, acceptam que totes les mitjanes són iguals.

Exemple 9.4 Continuem amb el nostre Exemple 9.1.

  • Ja sabem que \(N=50\), \(k=5\), \(SS_{Total}=12522.36\), \(SS_{Tr}=11274.32\) i \(SS_E=1248.038\).

  • Els quadrats mitjans són:

## [1] 2818.58
## [1] 27.73418
  • L’estadístic de contrast val:
## [1] 101.6284
  • El p-valor \(P(F_{k-1,N-k}\geqslant F_0)\) val
## [1] 0

Conclusió: Hem trobat evidència estadística que el nivell de pressió de CO2 influeix en el creixement mitjà del microorganisme Pseudomonas fragi (ANOVA, p-valor 0).

Per ara només concloem que no totes les mitjanes (dels percentatges d’increment de volum cel·lular) són iguals: no concloem que totes aquestes mitjanes siguin diferents. No és el mateix!

Un contrast ANOVA d’1 via se sol resumir en la taula ANOVA següent: \[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & k-1 & SS_{Tr}& MS_{Tr} & F & \text{p-valor} \\ \text{Residus} & N-k & SS_E & MS_E & \\\hline \end{array} \]

Així, la taula de l’ANOVA de l’Exemple 9.1 és \[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & 4 & 11274.32& 2818.58 & 101.63 & 0 \\ \text{Residus} & 45 & 1248.04 & 27.73 & \\\hline \end{array} \]

En aquesta taula, a banda de l’estadístic de contrast i el p-valor, ens pot interessar el valor del \(MS_E\), que estima la variància comuna de tots els tractaments. En el nostre exemple, (si se satisfan les condicions per poder efectuar una ANOVA d’1 via) estimam que les variables que ens donen els percentatges d’increment en 1 hora de les poblacions de P. fragi sota les diferents pressions de CO2 considerades tenen totes variància (poblacional) 27.73.

Vegem un altre exemple.

Exemple 9.5 Disposam de quatre tractaments genètics diferents, numerats de l’1 al 4, per corregir un cert gen defectuós responsable d’una malaltia. Els investigadors volen saber si els quatre tractaments tenen una eficàcia similar o no. Per contrastar-ho, en un assaig clínic es varen prendre 20 pacients amb aquesta malaltia, els repartiren aleatòriament en 4 grups de 5 malalts cadascun, i assignaren de forma aleatòria un dels quatre tractaments a cada grup. Després d’aplicar el tractament, es va mesurar a cada pacient l’expressió del gen defectuós sota estudi.

Les dades obtingudes varen ser

\[ \begin{array}{c} \text{Tractament}\\ \begin{array}{llll} 1 & 2 & 3 & 4 \\ \hline 96 & 93 & 70 & 78 \\ 99 & 90 & 90 & 87 \\ 100 & 75 & 84 & 57 \\ 104 & 80 & 76 & 66 \\ 84 & 90 & 78 & 76 \end{array} \end{array} \]

Aquest experiment té disseny d’ANOVA d’1 via:

  • La variable \(X\) és l’expressió del gen defectuós

  • El factor emprat per classificar les expressions té per nivells els 4 tractaments objecte d’estudi

  • S’hi ha pres una m.a.s. per a cada tractament, i de manera independent les unes de les altres

Efectuau a mà l’ANOVA d’1 via d’aquestes dades.

Els resultats parcials us haurien de donar:

  • \(N=20\), \(k=4\),

  • Les mitjanes: \(\overline{X}_{1}=96.6\), \(\overline{X}_{2}=85.6\), \(\overline{X}_{3}=79.6\), \(\overline{X}_{4}=72.8\), \(\overline{X}=83.65\)

  • Les sumes de quadrats: \(SS_{Total}=2766.55\), \(SS_{Tr}=1528.15\), \(SS_E=1238.4\)

  • Els quadrats mitjans: \(MS_{Tr}=509.4\), \(MS_{E}=77.4\)

  • L’estadístic de contrast, \(F_0=6.6\)

  • El p-valor: \(P(F_{3,16}>6.6)=\texttt{1-pf(6.6,3,16)}=0.004\)

  • La taula de l’ANOVA \[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & 3& 1528.15 & 509.4 & 6.6 & 0.004 \\ \text{Residus} & 16 & 1238.4 & 77.4 & \\\hline \end{array} \]

Conclusió: Hem trobat evidència estadísticament significativa que les quatre teràpies no tenen totes la mateixa eficàcia mitjana (ANOVA, p-valor 0.004).

9.2.2 Amb R

Per realitzar una ANOVA, s’aplica la funció

a la fórmula que separa les dades numèriques segons els nivells del factor (ha de ser un factor o, a partir de la versió 4.0 de R, un vector de paraules). Si la fórmula només especifica els noms de les variables, s’hi ha d’indicar el nom del dataframe amb el paràmetre data.

Per exemple, l’ANOVA de l’Exemple 9.1 s’obté amb

##             Df Sum Sq Mean Sq F value Pr(>F)    
## CO2$Pre      4  11274  2818.6   101.6 <2e-16 ***
## Residuals   45   1248    27.7                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

o, equivalentment, amb

##             Df Sum Sq Mean Sq F value Pr(>F)    
## Pre          4  11274  2818.6   101.6 <2e-16 ***
## Residuals   45   1248    27.7                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

D’aquesta manera obtenim la taula de l’ANOVA que hem explicat fa una estona. La primera filera, Pre, correspon als tractaments, que són els nivells del factor Pre de CO2. El valor de Pr(> F) és el p-valor del contrast.

Exemple 9.6 Per realitzar l’ANOVA de l’Exemple 9.5, primer hem d’entrar les dades en un dataframe. Un altre cop, entrarem les dades per fileres i per tant els indicadors dels tractaments s’han d’entrar com el vector (1,2,3,4) repetit 5 vegades.

## 'data.frame':    20 obs. of  2 variables:
##  $ Expr : num  96 93 70 78 99 90 90 87 100 75 ...
##  $ Tract: int  1 2 3 4 1 2 3 4 1 2 ...
##             Df Sum Sq Mean Sq F value   Pr(>F)    
## Tract        1   1498  1497.7   21.25 0.000218 ***
## Residuals   18   1269    70.5                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

No ha donat el mateix p-valor que quan l’hem fet a mà!

No hem entrat els tractaments com un factor. Fixau-vos que el nombre de graus de llibertat a la filera dels tractaments en aquesta taula és 1 i no 3, que és el que tocaria.

Va, fem-ho bé:

## 'data.frame':    20 obs. of  2 variables:
##  $ Expr : num  96 93 70 78 99 90 90 87 100 75 ...
##  $ Tract: Factor w/ 4 levels "1","2","3","4": 1 2 3 4 1 2 3 4 1 2 ...
##   Expr Tract
## 1   96     1
## 2   93     2
## 3   70     3
## 4   78     4
## 5   99     1
## 6   90     2
##             Df Sum Sq Mean Sq F value  Pr(>F)   
## Tract        3   1528   509.4   6.581 0.00417 **
## Residuals   16   1238    77.4                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ara sí que hem obtingut el mateix.

9.2.3 Comparacions posteriors per parelles

Si hem rebutjat la hipòtesi nul·la \(H_0:\mu_1=\cdots =\mu_k\), podem demanar-nos quins són els tractaments que donen mitjanes diferents. Això es pot fer de diverses maneres, aquí veurem la més “òbvia”: comparar totes les parelles de mitjanes per mitjà de tests t. És a dir, per a cada parell de tractaments, realitzar el contrast \[ \left\{ \begin{array}{l} H_0 : \mu_i=\mu_j \\ H_1 : \mu_i\neq\mu_j \end{array} \right. \] L’estadístic que fem servir en cada un d’aquests contrastos és ara \[ T=\frac{\overline{X}_{i} - \overline{X}_{j}}{\sqrt{{MS_E}\cdot (\frac{1}{n_i} +\frac{1}{n_j})}} \] que, si la hipòtesi nul·la d’aquest contrast és vertadera, segueix una distribució \(t\) de Student amb \(N-k\) graus de llibertat, \(t_{N-k}\).

Tots aquests contrastos per parelles serien tests t amb mostres independents i la mateixa variància. Per ventura alguns recordeu que la fórmula que us hem explicat al tema de Contrastos paramètrics per a aquests tests no és aquesta, sinó \[ T=\frac{\overline{X}_i-\overline{X}_j}{\sqrt{ \frac{(n_i-1)\widetilde{S}_i^2+(n_j-1)\widetilde{S}_j^2}{n_i+n_j-2}\cdot \Big(\frac{1}{n_i}+\frac{1}{n_j}\Big)}} \] que, si \(\mu_i=\mu_j\) és vertadera, té distribució \(t_{n_i+n_j-2}\). En aquesta fórmula, el factor \[ \frac{(n_i-1)\widetilde{S}_i^2+(n_j-1)\widetilde{S}_j^2}{n_i+n_j-2} \] dins l’arrel quadrada del denominador estima la variància comuna de \(X_i\) i \(X_j\).

Però en una ANOVA tenim més dades (les mostres de tots els tractaments, no només d’una parella) i les podem emprar totes per estimar la variància comuna de tots els tractaments. Com ja hem dit quan parlàvem de la distribució dels Quadrats Mitjans, aquesta estimació és \(MS_E\), que és el que apareix ara dins l’arrel quadrada del denominador. I com que hem emprat totes les dades que tenim per estimar aquesta variància, i no només les de dues mostres, també canvia el nombre de graus de llibertat.

El p-valor de cada contrast serà \(2P(t_{N-k}\geqslant|t_{i,j}|)\), on \(t_{i,j}\) és el valor que hi pren aquest estadístic \(T\).

Ara bé, observau que d’aquesta manera realitzam \(\binom{k}{2}\) contrastos. Com més contrastos fem, més probabilitat tenim d’equivocar-nos.

Si es realitzen \(c\) contrastos amb nivell de significació \(\alpha\), la probabilitat d’Error de Tipus I a qualcun és més gran que \(\alpha\): de fet, és \(1-(1-\alpha)^c\).

Per exemple, a l’Exemple 9.1, si realitzam els \(c=\binom{5}{2}=10\) contrastos (totes les pressions contra totes les pressions) amb nivell de significació \(\alpha =0.05\), la probabilitat de cometre almenys un Error de Tipus I a qualcun (si totes les mitjanes fossin iguales en la realitat) és \(1-(1-0.05)^{10} \approx 0.4\).

Per tant, haurem de reduir el nivell de significació de cada contrast per que la probabilitat global de cometre qualque Error de Tipus I sigui \(\alpha\). O, equivalentement, augmentar (s’en diu ajustar) el p-valor de cada contrast abans de comparar-lo amb l’\(\alpha\) global fixat.

Tot seguit explicam dos d’aquests mètodes d’ajust de p-valors.

9.2.3.1 Mètode de Bonferroni

El mètode d’ajust de p-valors més popular és el de Bonferroni. Emprant que \(1-(1-x)^c \leqslant c\cdot x\), si volem efectuar \(c\) contrastos amb nivell de significació (global) \(\alpha\),

realitzam cada contrast amb nivell de significació \(\alpha/c\)

i així el nivell de significació global segur que serà menor o igual que \(c\cdot \alpha/c=\alpha\). O, equivalentment

multiplicam el p-valor de cada contrast per \(c\) abans de comparar-lo amb el nivell de significació \(\alpha\)

Les dues accions són equivalents, perquè \[ p<\alpha/c \Longleftrightarrow c\cdot p<\alpha \]

Bé, gairebé equivalents. Si quan multiplicau un dels p-valors per \(c\) us dóna un valor més gran que 1, heu de donar com a p-valor ajustat 1. Pensau que, ajustats o no, els p-valors representen probabilitats, i per tant no poden ser més grans que 1.

Exemple 9.7 A l’Exemple 9.1, si realitzam els 10 contrastos per parelles, per obtenir un nivell de significació global \(\alpha =0.05\) amb el mètode de Bonferroni,

  • Hem de efectuar cada contrast amb nivell de significació 0.05/10=0.005

o equivalentment

  • Hem de multiplicar cada p-valor per 10 i comparar-los amb 0.05

A l’Exemple 2, si realitzam els 6 contrastos de totes les parelles possibles, per obtenir un nivell de significació global \(\alpha =0.05\),

  • Hem de efectuar cada contrast amb nivell de significació 0.05/6=0.0083

o equivalentment

  • Hem de multiplicar cada p-valor per 6

Amb R,

  • Per calcular tots els p-valors de cop (sense ajustar) podem emprar la funció
  • Per calcular tots els p-valors ajustats amb qualque mètode, s’ha d’especificar al paràmetre p.adjust.method. Per exemple, per ajustar-los amb el mètode de Bonferroni, s’hauria d’entrar p.adjust.method="bonferroni" (fixau-vos que bonferroni hi va entre cometes i començant amb minúscula).

Exemple 9.8 Tornem a l’Exemple 9.5.

  • Per obtenir tots els p-valors, que després nosaltres haurem de comparar amb \(\alpha/6\), executam
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  EG$Expr and EG$Tract 
## 
##   1       2       3      
## 2 0.06554 -       -      
## 3 0.00756 0.29688 -      
## 4 0.00058 0.03522 0.23937
## 
## P value adjustment method: none
  • Per obtenir tots els p-valors ajustats segons Bonferroni, que després nosaltres haurem de comparar amb \(\alpha\), entram
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  EG$Expr and EG$Tract 
## 
##   1      2      3     
## 2 0.3933 -      -     
## 3 0.0453 1.0000 -     
## 4 0.0035 0.2113 1.0000
## 
## P value adjustment method: bonferroni

Podeu comprovar que els p-valors d’aquest segon resultat són els del primer resultat multiplicats per 6 (llevat d’arrodoniments i dels 1 que poden representar resultats més grans que 1).

Suposem que fixam el nivell de significació global usual \(\alpha=0.05\). En la primera execució de pairwise.t.test, els únics p-valors per davall de \(0.05/6=0.0083\) han estat els dels parells (1,3) i (1,4). En la segona, els únics p-valors per davall de 0.05 han estat també els dels parells (1,3) i (1,4). Casualitat? No, havien de coincidir les conclusions, perquè les dues tècniques són equivalents.

Conclusió: Hem trobat evidència estadísticament significativa que la teràpia 1 té una eficàcia mitjana diferent de la de les teràpies 3 i 4 (ANOVA d’1 via, test posterior de Bonferroni, p-valors 0.0453 i 0.0035, respectivament), i no trobam evidència estadísticament significativa de cap altra diferència en les eficàcies mitjanes.

9.2.3.2 Mètode de Holm

Un altre mètode popular d’ajust de p-valors, més potent que el de Bonferroni, i que de fet és el mètode que empra R per defecte és el mètode de Holm, que funciona bàsicament de la forma següent:

  1. Siguin \(C_{1},\ldots ,C_{c}\) els contrastos per parelles que es volen realitzar i \(p_{1},\ldots ,p_{c}\) els p-valors corresponents

  2. Ordenam aquests p-valors en ordre creixent \(p_{(1)}< \cdots< p_{(c)}\) i reenumeram consistentment els contrastos \(C_{(1)},\ldots, C_{(c)}\)

  3. Per a cada \(j=1,\ldots,c\), calculam el p-valor ajustat \(\widetilde{p}_{(j)}=(c+1-j)\cdot p_{(j)}\)

  4. Aleshores rebutjam la hipòtesi nul·la als contrastos \(C_{(j)}\) on \(\widetilde{p}_{(j)}<\alpha\)

Exemple 9.9 Anem a fer a mà l’ajust dels p-valors segons Holm a l’Exemple 9.5.

  1. Taula amb els p-valors dels contrastos \[ \begin{array}{c|c} \text{Contrast} & \text{p-valor} \\ \hline \text{1-2} & 0.06554\\ \text{1-3} & 0.00756\\ \text{1-4} & 0.00058\\ \text{2-3} &0.29688\\ \text{2-4} & 0.03522\\ \text{3-4} & 0.23937 \end{array} \]

  2. Ordenam en ordre creixent del p-valor

\[ \begin{array}{c|c} \text{Contrast} & \text{p-valor} \\ \hline \text{1-4} & 0.00058\\ \text{2-3} & 0.00756\\ \text{2-4} & 0.03522\\ \text{1-2} & 0.06554\\ \text{3-4} & 0.23937\\ \text{2-3} &0.29688\\ \end{array} \]

  1. Ajustam: per a cada \(j\), multiplicam el \(j\)-èsim p-valor (en ordre decreixent) per \(6+1-j\)

\[ \begin{array}{c|cc} \text{Contrast} & \text{p-valor} & \text{p-valor ajustat}\\ \hline \text{1-4} & 0.00058 & 6\times 0.00058 = 0.00348\\ \text{1-3} & 0.00756 & 5\times 0.00756 = 0.03780\\ \text{2-4} & 0.03522 & 4\times 0.03522 = 0.14088\\ \text{1-2} & 0.06554 & 3\times 0.06554 = 0.19662\\ \text{3-4} & 0.23937 & 2\times 0.23937 = 0.47874\\ \text{2-3} & 0.29688 & 1\times 0.29688 = 0.29688\\ \end{array} \]

  1. Comparam els p-valors ajustats amb \(\alpha\). En aquest cas, amb \(\alpha=0.05\) arribam a la mateixa conclusió que amb el mètode de Bonferroni: concloem que \(\mu_1\neq \mu_4\) i \(\mu_1\neq \mu_3\) i que no podem rebutjar que les altres parelles de mitjanes siguin iguals

Amb R, s’ha d’especificar a la funció pairwise.t.test el paràmetre p.adjust.method="holm", o no especificar aquest paràmetre perquè “holm” és el valor per defecte de p.adjust.method.

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  EG$Expr and EG$Tract 
## 
##   1      2      3     
## 2 0.1966 -      -     
## 3 0.0378 0.4787 -     
## 4 0.0035 0.1409 0.4787
## 
## P value adjustment method: holm

Exemple 9.10 Els tests posteriors per parelles de l’Exemple 9.1 amb el mètode de Bonferroni i de Holm són:

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  CO2$Inc and CO2$Pre 
## 
##      0.0     0.08    0.29    0.50   
## 0.08 1.4e-05 -       -       -      
## 0.29 1.6e-11 0.00186 -       -      
## 0.50 < 2e-16 3.0e-10 0.00028 -      
## 0.86 < 2e-16 2.5e-15 6.6e-10 0.00389
## 
## P value adjustment method: bonferroni
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  CO2$Inc and CO2$Pre 
## 
##      0.0     0.08    0.29    0.50   
## 0.08 5.6e-06 -       -       -      
## 0.29 1.2e-11 0.00037 -       -      
## 0.50 < 2e-16 1.8e-10 8.4e-05 -      
## 0.86 < 2e-16 2.0e-15 3.3e-10 0.00039
## 
## P value adjustment method: holm

Conclusió: Hem trobat evidència estadísticament significativa que cada una de les diferents pressions de CO2 considerades dona lloc a un increments mitjà diferent del volum cel·lular de P. fragi al cap d’una hora (ANOVA d’1 via, test posterior de Holm, p-valors ajustats tots més petits que 0.0004).

Ara sí que hem trobat evidència que totes les mitjanes són diferents. Amb l’ANOVA, només podíem concloure que algunes mitjanes són diferents, però no quines.

9.2.4 Verificació de les condicions

Recordau que per a que la conclusió d’una ANOVA d’1 via tengui sentit:

  1. Les mostres de cada tractament han de ser aleatòries simples i independents i almenys una ha de tenir més d’un element.

  2. La població definida per cada tractament ha de ser normal.

  3. Totes aquestes poblacions han de tenir la mateixa variància (homocedasticitat).

El punt (1) és responsabilitat de l’investigador, però (2) i (3) s’han de contrastar. Si fallen, sobretot si falla (3), no es pot usar una ANOVA: convé emprar un test no paramètric.

La normalitat de les mostres s’ha de contrastar amb algun test de normalitat. A la corresponent lliçó de R explicam com automatitzar el procés per fer-ho per totes les mostres de cop (spoiler: emprant la funció aggregate). Aquí ho farem de manera planera, variable a variable. Per exemple, emprarem el test de Shapiro-Wilkis per contrastar la normalitat dels nostres dos exemples:

  • A l’exemple del CO2:
## [1] 0.320568
## [1] 0.1023687
## [1] 0.5197501
## [1] 0.465208
## [1] 0.4840276
  • A l’exemple de l’expressió de gens:
## [1] 0.306206
## [1] 0.2722278
## [1] 0.9611411
## [1] 0.9065984

En tots dos casos podem acceptar que totes les mostres provenen de variables normals.

Si efectuam \(k\) contrastos de normalitat amb nivell de significació \(\alpha\), tenim una probabilitat de cometre algun error de tipus I de \(1-(1-\alpha)^k\). Per tant, com als contrastos posteriors per parelles, convé ajustar els p-valors a fi que el nivell de significació global sigui \(\alpha\). En aquests dos exemple això no afecta les conclusions.

Pel que fa a contrastar l’homocedasticitat, els dos tests més populars són:

  • Si acceptam que les mostres provenen de distribucions normals, el test de Bartlett, implementat en R en la funció bartlett.test.
  • Si no acceptam que les mostres provenen de distribucions normals, el test de Fligner-Killeen, implementat en R en la funció fligner.test.

En tots dos casos, la funció s’aplica a una fórmula, exactament igual que aov. Per exemple, per contrastar l’homocedasticitat dels increments de volum cel·lular sota diferents pressions de CO2 de l’Exemple 9.1 amb un test de Bartlett, entraríem:

## 
##  Bartlett test of homogeneity of variances
## 
## data:  CO2$Inc by CO2$Pre
## Bartlett's K-squared = 1.0701, df = 4, p-value = 0.899

Podem acceptar que les variàncies de les subpoblacions definides pels percentatges d’increment del volum cel·lular sota les diferents pressions de CO2 considerades són totes iguals.

Ja que hi som, comprovem l’homocedasticitat de l’Exemple 9.5, ara amb el test de Fligner-Killeen i emprant l’altra sintaxi possible per que la vegeu

## 
##  Fligner-Killeen test of homogeneity of variances
## 
## data:  Expr by Tract
## Fligner-Killeen:med chi-squared = 0.89109, df = 3, p-value = 0.8276

9.2.5 Test no paramètric

Si en un experiment de disseny d’ANOVA d’1 via no podem emprar una ANOVA perquè no se satisfaci la normalitat de les poblacions o, sobretot, l’homocedasticitat, cal emprar un test no paramètric. El més popular es el test de Kruskal-Wallis, que generalitza el test de Mann-Whitney a més de 2 poblacions igual que l’ANOVA generalitza el test t; es fa amb la funció kruskal.test.

Per exemple, per aplicar-lo a les dades de l’Exemple 9.1:

## 
##  Kruskal-Wallis rank sum test
## 
## data:  CO2$Inc by CO2$Pre
## Kruskal-Wallis chi-squared = 44.716, df = 4, p-value = 4.555e-09

Seguim concloent que no totes les mitjanes (en realitat, les medianes) són iguals.

Si el test de Kruskal-Wallis permet rebutjar la igualtat de mitjanes, i voleu determinar quins parells són diferents, disposau de la funció pairwise.wilcox.test que efectua contrastos per parelles de Mann-Whitney (amb el paràmetre paired=FALSE). Té la mateixa sintaxi que pairwise.t.test i com en aquella funció, el mètode d’ajust dels p-valors s’hi entra amb el paràmetre p.adjust.method, el valor per defecte del qual és el mètode de Holm.

Per exemple, per realitzar tots els contrastos de Mann-Whitney en l’exemple del CO2 emprant el mètode d’ajust de Bonferroni, entram:

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  CO2$Inc and CO2$Pre 
## 
##      0.0     0.08    0.29    0.50   
## 0.08 0.00211 -       -       -      
## 0.29 0.00011 0.01050 -       -      
## 0.50 0.00011 0.00011 0.00325 -      
## 0.86 0.00011 0.00011 0.00011 0.03186
## 
## P value adjustment method: bonferroni

Tornam a concloure que els percentatges mitjans d’increment són tots diferents.

9.3 ANOVA de blocs

De la mateixa manera que l’ANOVA d’1 via generalitza a més de dues mitjanes el contrast d’igualtat de dues mitjanes emprant mostres independents, l’ANOVA de blocs generalitza a més de dues mitjanes el contrast d’igualtat de dues mitjanes emprant mostres aparellades.

9.3.1 Contrast bàsic

Comencem amb un exemple

Exemple 9.11 Volem determinar si l’energia que es requereix per dur a terme tres activitats físiques (córrer, caminar i muntar amb bicicleta) és la mateixa o no. Quantificam aquesta energia amb el nombre de Kcal consumides per Km recorregut.

Les diferències metabòliques entre els individus poden afectar l’energia requerida per dur a terme una determinada activitat. Per tant, no és aconsellable triar tres grups d’individus i a cada grup fer-li fer una de les tres activitats físiques: les diferències metabòliques entre els individus triats podrien afectar els resultats i amagar l’efecte real.

Ens decidim per un disseny experimental en paral·lel: Seleccionam alguns individus i demanam a cadascun que corri, camini i recorri amb bicicleta una distància fixada en tres moments diferents, seleccionant l’ordre de les activitats de cada individu a l’atzar, i mesuram per a cada individu i cada activitat el consum de Kca/Km.

Si a tots els individus els féssim fer les tres activitats en el mateix ordre, podria ser que qualque factor extern que no controlàssim influís en el resultat. Per exemple, si tots caminen al mateix temps, després corren al mateix temps i després pedalen al mateix temps, i hi ha grans diferències de temperatura ambient entre els tres moments, això podria influir en el resultat final. Si, en canvi, aleatoritzam l’ordre de les activitats, en principi aquestes diferències es compensen.

Aquests són els resultats obtinguts per a 8 individus:

\[ \begin{array}{c} \hphantom{Individu}\text{Activitat}\\ \begin{array}{c|ccc} \text{Individu} &\text{1 (corrent)} &\text{2 (caminant)}&\text{3 (pedalant)}\\ \hline 1&1.4&1.1&0.7\\ 2&1.5&1.2&0.8\\ 3&1.8&1.3&0.7\\ 4&1.7&1.3&0.8\\ 5&1.6&0.7&0.1\\ 6&1.5&1.2&0.7\\ 7&1.7&1.1&0.4\\ 8&2.0&1.3&0.6\\ \end{array} \end{array} \]

En aquest estudi, fixau-vos que empram els nivells d’un factor (tipus de desplaçament) per classificar la població (els consums energètics) en tres subpoblacions, però ara les mostres que hem pres no són independents sinó aparellades: hem mesurat els consums energètics dels tres esports sobre els mateixos individus. Per tant no podem realitzar una ANOVA d’1 via per analitzar els resultats.

L’ANOVA de blocs (complets aleatoris, però ometrem aquests adjectius perquè és l’únic que veurem) generalitza el contrast de 2 mitjanes amb mostres aparellades a \(k\) mitjanes amb mostres aparellades.

La situació general és la següent. Tenim una variable aleatòria \(X\) i un factor de \(k\) nivells, o tractaments, que classifica la població en \(k\) subpoblacions (a les que, recordau, identificam amb els tractaments). Diguem \(\mu_i\) a la mitjana de \(X\) en els individus del nivell \(i\)-èsim. Volem comparar aquestes mitjanes \(\mu_1\),…,\(\mu_k\) i en concret decidir si són totes iguals o no. És a dir, el contrast és \[ \left\{ \begin{array}{l} H_0 : \mu_{1} =\mu_{2} =\cdots =\mu_{k} \\ H_1 : \text{Hi ha } i,j \text{ tals que } \mu_{i} \not=\mu_{j} \end{array} \right. \]

En un experiment de disseny d’ANOVA de blocs:

  1. Escollim una mostra aleatòria de \(b\) blocs: conjunts de \(k\) subjectes aparellats (per exemple, escollim \(b\) subjectes i entenem cada bloc com a format per \(k\) còpies del mateix subjecte), on fixau-vos que \(k\) és el nombre de tractaments.

  2. Dins cada bloc, assignam aleatòriament a cada subjecte un tractament, de manera que cada tractament s’empri exactament un cop dins cada bloc.

Així, el disseny de l’Exemple 9.11 és d’una ANOVA de blocs:

  • La variable aleatòria és l’energia consumida (en Kcal) per una persona en recórrer un km

  • Els tractaments són els tres tipus de desplaçament

  • Prenem 8 persones de manera raonablement aleatòria i interpretam cada una com un bloc

  • Assignam a cada persona el tres tractaments en un ordre escollit a l’atzar per a cada una d’elles

La filosofia del contrast serà similar a la de l’ANOVA d’1 via, comparant variabilitats: si la variabilitat de les mitjanes de les mostres és molt més gran que la variabilitat dels “errors”, rebutjarem la igualtat de totes les mitjanes poblacionals.

En una ANOVA de blocs, les dades se solen representar en forma d’una taula com la següent \[ \begin{array}{c} \hphantom{Bloc}\text{Tractament}\\ \begin{array}{ccccc} \text{Bloc} &\text{Tract. 1} &\text{Tract. 2}&\ldots & \text{Tract. $k$}\\ \hline 1 & X_{11} & X_{21} & \ldots & X_{k1} \\ 2 & X_{12} & X_{22} & \ldots & X_{k2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b & X_{1b} & X_{2b} & \ldots & X_{kb} \\ \hline \end{array} \end{array} \]

on cada \(X_{ij}\) és el valor del tractament \(i\)-èsim en l’individu corresponent del bloc \(j\)-èsim. Com en les taules emprades en l’ANOVA d’1 via, observau que no és la notació usual de les taules de dades, sinó la transposada: a \(X_{{i}{j}}\), \(i\) hi indica la columna, el tractament, i \(j\) hi indica la filera, és a dir, el bloc. D’aquesta manera, cada filera \((X_{1j},\ldots,X_{kj})\) representa un bloc.

Exemple 9.12 Tornant al nostre Exemple 9.11 inicial, els blocs són els 8 individus (\(b=8\)) i els tractaments, les diferents activitats (\(k=3\)). Si

  • \(\mu_{1}\) representa el nombre mitjà de Kcal que es consumeixen corrent 1 km
  • \(\mu_{2}\) representa el nombre mitjà de Kcal que es consumeixen caminant 1 km
  • \(\mu_{3}\) representa el nombre mitjà de Kcal que es consumeixen pedalant 1 km

el contrast que volem realitzar és \[ \left\{ \begin{array}{l} H_0 : \mu_{1} = \mu_{2} = \mu_{3} \\ H_1 : \mu_{1} \neq \mu_{2}\text{ o } \mu_{1} \neq \mu_{3}\text{ o } \mu_{2} \neq \mu_{3} \end{array} \right. \]

Per que les conclusions d’una ANOVA de blocs tenguin sentit cal que:

  • Les \(k\cdot b\) observacions constitueixin mostres aleatòries, cadascuna de mida 1, de les \(k\cdot b\) poblacions definides per les parelles (tractament,bloc)

  • Aquestes \(k\cdot b\) poblacions són totes normals, cada una amb mitjana \(\mu_{ij}\), on \(i\) indica el tractament i \(j\) indica el bloc, i totes amb la mateixa variància \(\sigma^2\)

  • No hi ha interacció entre els blocs i els tractaments. Això significa que l’efecte dels blocs i els tractaments és additiu: la diferència entre les mitjanes poblacionals de cada parella concreta de tractaments és la mateixa a cada bloc \[ \mu_{i_1j_1}-\mu_{i_2j_1}=\mu_{i_1j_2}-\mu_{i_2j_2} \]

    Per exemple, que no hi hagi interacció entre els blocs i els tractaments a l’Exemple 9.11 significa que:

    • La diferència entre el consum energètic mitjà en córrer i en caminar és la mateixa a cada individu de la mostra
    • La diferència entre el consum energètic mitjà en córrer i en pedalar és la mateixa a cada individu de la mostra
    • La diferència entre el consum energètic mitjà en caminar i en pedalar és la mateixa a cada individu de la mostra

En canvi, hi hauria interacció si, per exemple, la diferència entre el consum energètic mitjà en córrer i en caminar depengués de l’individu: si en uns la diferència fos més gran que en d’altres.

Amb un sol valor per cada parell (tractament,bloc), cap d’aquestes condicions necessàries per poder realitzar una ANOVA de blocs no es pot contrastar i per tant l’experimentador ha de decidir si se satisfan o no segons la seva experiència.

Què significa això de la interacció entre dues variables?

Imaginau que podem administrar dos analgèsics, A i B, a dones i homes, i mesuram el temps que triguen en fer efecte. Diguem

  • \(\mu_{AD}\): temps mitjà que triga en fer efecte l’analgèsic A sobre les dones
  • \(\mu_{BD}\): temps mitjà que triga en fer efecte l’analgèsic B sobre les dones
  • \(\mu_{AH}\): temps mitjà que triga en fer efecte l’analgèsic A sobre els homes
  • \(\mu_{BH}\): temps mitjà que triga en fer efecte l’analgèsic B sobre els homes

Aleshores:

  • No hi ha interacció entre els analgèsics i el sexe si la diferència en el temps mitjà en fer efecte A i B és la mateixa en les dones que en els homes: \[ \mu_{AD}-\mu_{BD}= \mu_{AH}-\mu_{BH} \]

  • En canvi, sí que hi ha interacció entre els analgèsics i el sexe quan aquestes dues diferències són diferents, la qual cosa significaria que la diferència d’efectivitat entre els dos analgèsics no és la mateixa en els homes que en les dones: \[ \mu_{AD}-\mu_{BD}\neq \mu_{AH}-\mu_{BH} \]

Fixau-vos que això no és exactament equivalent al fet que un analgèsic sigui més efectiu en un sexe que en l’altre, per exemple més en les dones que en els homes: si l’altre analgèsic també és més efectiu en les dones que en els homes, pot ser que la diferència entre les mitjanes se mantengui i no hi hagi interacció.

Recordarem algunes notacions, i n’introduïm algunes altres. Pel que fa a la població:

  • Direm \(\mu_i\) a la mitjana de la variable d’interès sobre la població definida pel tractament \(i\)-èsim
  • Direm \(\mu\) a la mitjana de la variable d’interès sobre el total de la població, sense distingir tractaments
  • Direm \(\mu_{\bullet j}\) a la mitjana de la variable d’interès sobre el bloc \(j\)-èsim

L’ANOVA de blocs se basa en el model següent: per a tots \(i=1,\ldots,k\) i \(j=1,\ldots,b\) \[ X_{ij}=\mu+ (\mu_{i}-\mu) +(\mu_{\bullet j}-\mu) + E_{ij} \] on:

  • \(X_{ij}\) indica el valor de la variable \(X\) per al tractament \(i\)-èsim en el bloc \(j\)-èsim

  • \(\mu_i-\mu\) representa la desviació de la mitjana de \(X\) en el nivell \(i\)-èsim respecte de la mitjana global \(\mu\) (l’efecte del tractament \(i\)-èsim)

  • \(\mu_{\bullet j}-\mu\) representa la desviació de la mitjana de \(X\) en el bloc \(j\)-èsim respecte de la mitjana global \(\mu\) (l’efecte del bloc \(j\)-èsim)

  • \(E_{ij}\) representa la part de la diferència entre \(X_{ij}\) i \(\mu\) que no expliquen ni el tractament ni el bloc; en diem l’error aleatori, o el residu.

Aquest model diu bàsicament que el valor de \(X\) sobre un individu és la suma de quatre components:

  • La mitjana global \(\mu\) de \(X\) sobre tota la població
  • L’efecte del tractament
  • L’efecte del bloc
  • L’error aleatori

i per tant hi pressuposam que res més no influeix en el valor de \(X\), i en particular que l’efecte del bloc i el del tractament se sumen, sense que hi hagi interacció entre ells. Si això no és veritat, és a dir, si aquest valor pot dependre d’altres efectes que no tinguem en compte o si hi ha interacció entre els blocs i els tractaments, el model no és vàlid, i les conclusions de l’ANOVA tampoc.

Pel que fa a la nostra mostra:

  • \(\overline{X}_{i}\) és la mitjana mostral de la mostra del tractament \(i\)-èsim \[ \overline{X}_{i}=\dfrac{\sum_{j=1}^b X_{ij}}{b} \]

  • \(\overline{X}_{\bullet j}\) és la mitjana mostral de les mesures preses sobre el bloc \(j\)-èsim \[ \overline{X}_{\bullet j}=\dfrac{\sum_{i=1}^k X_{ij}}{k} \]

  • \(\overline{X}\) és la mitjana mostral de tota la mostra \[ \overline{X}=\dfrac{\sum_{i=1}^k\sum_{j=1}^b X_{ij}}{k\cdot b} \]

Exemple 9.13 Tornem a l’Exemple 9.11. Recordem que les dades eren

\[ \begin{array}{c} \hphantom{Individu}\text{Tractament}\\ \begin{array}{c|ccc} \text{Individu} &\text{1 (corrent)} &\text{2 (caminant)}&\text{3 (pedalant)}\\ \hline 1&1.4&1.1&0.7\\ 2&1.5&1.2&0.8\\ 3&1.8&1.3&0.7\\ 4&1.7&1.3&0.8\\ 5&1.6&0.7&0.1\\ 6&1.5&1.2&0.7\\ 7&1.7&1.1&0.4\\ 8&2.0&1.3&0.6\\ \end{array} \end{array} \]

Per tant les mitjanes serien, amb aquestes notacions

\[ \begin{array}{c} \text{Tractament}\\ \begin{array}{c|ccc|c} \text{Individu} &\text{1 (corrent)} &\text{2 (caminant)}&\text{3 (pedalant)} & \text{Mitjanes}\\ \hline 1&1.4&1.1&0.7 & \overline{X}_{\bullet1}\\ 2&1.5&1.2&0.8 & \overline{X}_{\bullet2}\\ 3&1.8&1.3&0.7 & \overline{X}_{\bullet3}\\ 4&1.7&1.3&0.8 & \overline{X}_{\bullet4}\\ 5&1.6&0.7&0.1 & \overline{X}_{\bullet5}\\ 6&1.5&1.2&0.7 & \overline{X}_{\bullet6}\\ 7&1.7&1.1&0.4 & \overline{X}_{\bullet7}\\ 8&2.0&1.3&0.6 & \overline{X}_{\bullet8}\\ \hline \text{Mitjanes} & \overline{X}_{1} & \overline{X}_{2} & \overline{X}_{3} & \overline{X} \end{array} \end{array} \]

Anem a calcular-les. Emmagatzemarem les dades en un dataframe Dades de tres variables:

  • kilocal: les Kcal/Km consumides
  • blocs: l’individu
  • tracts: l’activitat

Per poder després fer l’ANOVA, aquests dos darrers han de ser factors. Com que entrarem les dades de la taula per fileres:

  • el factor tracts ha d’estar format per 8 còpies del vector (1,2,3), on 1 representa córrer, 2, caminar i 3, pedalar
  • el factor blocs ha de tenir la forma (1,1,1,2,2,2,3,3,3,…)
##  [1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8
## Levels: 1 2 3 4 5 6 7 8
##  [1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
## Levels: 1 2 3
## 'data.frame':    24 obs. of  3 variables:
##  $ kilocal: num  1.4 1.1 0.7 1.5 1.2 0.8 1.8 1.3 0.7 1.7 ...
##  $ tracts : Factor w/ 3 levels "1","2","3": 1 2 3 1 2 3 1 2 3 1 ...
##  $ blocs  : Factor w/ 8 levels "1","2","3","4",..: 1 1 1 2 2 2 3 3 3 4 ...
##   kilocal tracts blocs
## 1     1.4      1     1
## 2     1.1      2     1
## 3     0.7      3     1
## 4     1.5      1     2
## 5     1.2      2     2
## 6     0.8      3     2
  • Calculem les mitjanes mostrals dels tractaments, \(\overline{X}_i\):
##   tracts kilocal
## 1      1    1.65
## 2      2    1.15
## 3      3    0.60
  • Calculem les mitjanes mostrals dels blocs, \(\overline{X}_{\bullet j}\):
##   blocs  kilocal
## 1     1 1.066667
## 2     2 1.166667
## 3     3 1.266667
## 4     4 1.266667
## 5     5 0.800000
## 6     6 1.133333
## 7     7 1.066667
## 8     8 1.300000
  • Calculem la mitjana mostral global \(\overline{X}\):
## [1] 1.133333

A l’ANOVA de blocs s’hi té la identitat següent:

Teorema 9.3 (Identitat de les sumes de quadrats) \[ SS_{Total}=SS_{Tr}+SS_{Blocs}+SS_E \] on

  • \(SS_{Total}=\displaystyle\sum\limits_{i=1}^k\sum\limits_{j=1}^b (X_{ij}- \overline{X})^2\); és la Suma Total de Quadrats

  • \(SS_{Tr}=\displaystyle b\sum\limits_{i=1}^k (\overline{X}_{i}-\overline{X})^2\); és la Suma de Quadrats dels Tractaments

  • \(SS_{Blocs}=\displaystyle k\sum\limits_{j=1}^b (\overline{X}_{\bullet j}-\overline{X})^2\); és la Suma de Quadrats dels Blocs

  • \(SS_E=\displaystyle\sum\limits_{i=1}^k\sum\limits_{j=1}^b (X_{ij} - \overline{X}_{i}- \overline{X}_{\bullet j}+\overline{X})^2\); és la Suma de Quadrats dels Residus o dels Errors

En aquesta identitat

  • \(SS_{Total}\) representa la variabilitat total de les dades: és el numerador de la variància de la mostra total

  • \(SS_{Tr}\) representa la variabilitat de les mitjanes dels tractaments: és \(b\) vegades el numerador de la variància de \((\overline{X}_1,\overline{X}_2,\ldots,\overline{X}_k)\)

  • \(SS_{Tr}\) representa la variabilitat de les mitjanes dels blocs: és \(k\) vegades el numerador de la variància de \((\overline{X}_{\bullet 1},\overline{X}_{\bullet 2},\ldots,\overline{X}_{\bullet b})\)

  • \(SS_E\) representa la “resta de la variabilitat”

Per a que el model de l’ANOVA de blocs \[ X_{ij}=\mu+ (\mu_{i}-\mu) +(\mu_{\bullet j}-\mu) + E_{ij} \] ha de passar (aïllant) que \[ E_{ij}=X_{ij}-\mu_{i}-\mu_{\bullet j}+\mu \] i aleshores \(SS_E\) és la suma dels quadrats de les estimacions d’aquests errors aleatoris per als individus de la nostra mostra.

Per tant \[ SS_{Total}=SS_{Tr}+SS_{Blocs}+SS_E \] bàsicament diu que en una ANOVA de blocs

la variabilitat total descompon en la suma de la variabilitat de les mitjanes dels tractaments més la variabilitat de les mitjanes dels blocs més la variabilitat “residual”.

Exemple 9.14 Tornem a l’Exemple 9.11

Recordem les dades que ja tenim

## 'data.frame':    24 obs. of  3 variables:
##  $ kilocal: num  1.4 1.1 0.7 1.5 1.2 0.8 1.8 1.3 0.7 1.7 ...
##  $ tracts : Factor w/ 3 levels "1","2","3": 1 2 3 1 2 3 1 2 3 1 ...
##  $ blocs  : Factor w/ 8 levels "1","2","3","4",..: 1 1 1 2 2 2 3 3 3 4 ...
##   tracts kilocal
## 1      1    1.65
## 2      2    1.15
## 3      3    0.60
##   blocs  kilocal
## 1     1 1.066667
## 2     2 1.166667
## 3     3 1.266667
## 4     4 1.266667
## 5     5 0.800000
## 6     6 1.133333
## 7     7 1.066667
## 8     8 1.300000
## [1] 1.133333
  • Calculem la suma total de quadrats \[ SS_{Total}=\sum\limits_{i=1}^k\sum\limits_{j=1}^b (X_{ij}- \overline{X})^2 \]
## [1] 5.353333
  • Calculem la suma de quadrats dels tractaments \[ SS_{Tr}=b\sum\limits_{i=1}^k (\overline{X}_{i}-\overline{X})^2 \] Fixau-vos que el vector \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\) és la variable kilocal de mean.tracts.
## [1] 4.413333
  • Calculem la suma de quadrats dels blocs \[ SS_{Blocs}=k\sum\limits_{j=1}^b (\overline{X}_{\bullet j}-\overline{X})^2 \] Fixau-vos que el vector \((\overline{X}_{\bullet 1},\ldots,\overline{X}_{\bullet b})\) és la variable kilocal de mean.blocs.
## [1] 0.5533333

  • Calculem la suma de quadrats dels residus \[ SS_E=\sum\limits_{i=1}^k\sum\limits_{j=1}^b (X_{ij} - \overline{X}_{i}- \overline{X}_{\bullet j}+\overline{X})^2 \] Per calcular aquesta suma, actuarem com al càlcul de la \(SS_E\) de l’ANOVA d’1 via, tenint en compte que

    • Les entrades de Dades$kilocal que difereixen en un múltiple de 3 són del mateix tractament: per exemple, la 1a, la 4a, la 7a etc. corresponen al tractament 1 (córrer). Si a Dades$kilocal li restam el vector de les mitjanes del tractaments, mean.tracts$kilocal, en realitat estam dient a R que li resti 8 còpies consecutives d’aquest vector, i per tant a cada entrada de Dades$kilocal li restam la mitjana del seu tractament.

    • Cada grup de 3 entrades consecutives de Dades$kilocal corresponen a un bloc: les tres primeres al bloc 1, les tres següents al bloc 2 etc. Per tant, per restar a cada entrada de Dades$kilocal la mitjana del bloc corresponent, li hem de restar rep(mean.blocs$kilocal,each=3).

## [1] 0.3866667

Comprovem la identitat de les sumes de quadrats:

## [1] 5.353333
## [1] 5.353333

A partir d’aquí, tot funciona com a l’ANOVA d’1 via. Al contrast \[ \left\{ \begin{array}{l} H_0 : \mu_{1}=\cdots =\mu_{k} \\ H_1 : \text{Hi ha } i,j=1,\ldots ,k \text{ tals que } \mu_{i}\neq \mu_{j} \end{array} \right. \] rebutjarem la hipòtesi nul·la si \(SS_{Tr}\) és prou més gran que \(SS_{E}\). Per mesurar-ho, emprarem els estadístics següents:

  • Quadrat mitjà dels tractaments: \[ MS_{Tr}=\dfrac{SS_{Tr}}{k-1} \]

  • Quadrat mitjà dels errors: \[ MS_E = \dfrac{SS_E}{(b-1) (k-1)} \] Fixau-vos que el denominador és diferent que al \(MS_E\) de l’ANOVA d’1 via

  • A més, R calcula el Quadrat mitjà dels blocs, que nosaltres no farem servir però que donam per si de cas: \[ MS_{Blocs}=\dfrac{SS_{Blocs}}{b-1} \]

Si se satisfan les condicions necessàries que hem esmentat per que l’ANOVA es pugui realitzar, es té que \[ \begin{array}{l} E(MS_{Tr})=\sigma^2 + \dfrac{b}{k-1}\sum\limits_{i=1}^k (\mu_{i}-\mu)^2 \\ E(MS_E)=\sigma^2 \end{array} \]

I \(MS_E\) torna a estimar la variància comuna de totes les poblacions definides per les parelles (tractament,bloc).

Aleshores, com a l’ANOVA d’1 via, si \(H_0:\mu_{1}=\cdots =\mu_{k}(=\mu)\) és certa, \[ \sum\limits_{i=1}^k (\mu_{i}-\mu)^2 = 0, \] i per tant \(E(MS_{Tr})=E(MS_E)\), mentre que si \(H_0\) no és certa \[ \sum\limits_{i=1}^k (\mu_{i}-\mu)^2 > 0 \] cas en el qual \(E(MS_{Tr})>E(MS_E)\).

Aleshores prendrem com a estadístic de contrast el quocient \[ F=\frac{MS_{Tr}}{MS_E} \] Si \(H_0\) és certa:

  • La seva distribució és de tipus F de Fisher amb \(k-1\) i \((k-1)(b-1)\) graus de llibertat, \(F_{k-1,(k-1)(b-1)}\)
En general, els graus de llibertat de l’estadístic F d’una ANOVA, sigui del tipus que sigui, són els denominadors emprats en les definicions dels quadrats mitjans del numerador i el denominador.
  • El seu valor és proper a 1

I per tant rebutjarem la hipòtesi nul·la si el valor \(F_0\) de \(F\) sobre la nostra mostra és prou més gran que 1, la qual cosa decidirem comparant el p-valor \(P(F_{k-1,(k-1)(b-1)}\geqslant F_0)\) amb el nivell de significació \(\alpha\).

En resum, per realitzar una ANOVA de blocs a partir d’una mostra:

  • Calculam \(SS_{Tr},SS_E\)

  • Calculam \(MS_{Tr},MS_E\)

  • Calculam el valor \(F_0\) de l’estadístic de contrast \[ F=\frac{MS_{Tr}}{MS_E} \]

  • Calculam el p-valor \[ P(F_{k-1,(k-1)(b-1)}\geqslant F_0) \]

  • Si aquest p-valor és més petit que el nivell de significació \(\alpha\), rebutjam \(H_0\) i concloem que no totes les mitjanes són iguals. En cas contrari, acceptam que totes les mitjanes són iguals.

Totes aquestes dades se solen recollir en la taula ANOVA següent: \[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & k-1 & SS_{Tr}& MS_{Tr} & F & \text{p-valor} \\ \text{Blocs} & b-1 & SS_{Blocs} & MS_{Blocs} & \\ \text{Residus} & (k-1)(b-1) & SS_E & MS_E & \\\hline \end{array} \]

Exemple 9.15 Tornem al nostre Exemple 9.11. Ja hem calculat:

\[ \begin{array}{cccccc} k & b & SS_{Total} & SS_{Tr} & SS_{Blocs} & SS_E\\ \hline 3 & 8 & 5.3533 & 4.4133 & 0.5533 & 0.3867 \end{array} \] Aleshores:

  • \(MS_{Tr}=\dfrac{SS_{Tr}}{k-1}=2.2066\)

  • \(MS_{Blocs}=\dfrac{SS_{Blocs}}{b-1}=0.079\)

  • \(MS_E = \dfrac{SS_E}{(b-1) (k-1)}=0.0276\)

  • \(F=\dfrac{MS_{Tr}}{MS_E}=79.949\)

  • p-valor: \(P(F_{2,14}\geqslant 79.949)=2\cdot 10^{-8}\)

  • Conclusió: Hem obtingut evidència estadística que no és veritat que les tres activitats tenguin el mateix consum energètic mitjà per km (ANOVA de blocs, p-valor 2·10-8)

La taula ANOVA d’aquest exemple és

\[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & 2 & 4.4133&2.2067&79.949 & 2\cdot 10^{-8} \\ \text{Blocs} & 7 & 0.5533&0.079& & \\ \text{Residus} & 14 & 0.3867&0.0276& & \\\hline \end{array} \]

9.3.2 Amb R

L’ANOVA de blocs s’efectua amb R aplicant summary(aov( )) a la fórmula que separa la variable numèrica per la suma dels factors que representen els tractaments i els blocs. Així, l’ANOVA de blocs de l’Exemple 9.11 es fa amb

##              Df Sum Sq Mean Sq F value  Pr(>F)    
## Dades$tracts  2  4.413  2.2067  79.897 2.2e-08 ***
## Dades$blocs   7  0.553  0.0790   2.862  0.0446 *  
## Residuals    14  0.387  0.0276                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

o, equivalentment, amb

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## tracts       2  4.413  2.2067  79.897 2.2e-08 ***
## blocs        7  0.553  0.0790   2.862  0.0446 *  
## Residuals   14  0.387  0.0276                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Obtenim la taula d’abans (llevat d’una petita diferència en la \(F\) deguda a que als càlculs a mà anàvem arrodonint pel camí) amb dues entrades més: l’estadístic de contrast i el p-valor de la filera blocs, que corresponen al contrast sobre hi ha diferència o no entre les mitjanes dels blocs (en aquest exemple, els consums mitjans energètics per km dels individus de la mostra en desplaçar-se de qualsevol de les tres maneres).

9.3.3 Comparacions posteriors per parelles

Com en el cas d’1 via, si rebutjam la hipòtesi nul·la, podem demanar-nos quins són els tractaments que tenen mitjanes diferents. Ho podem respondre fent un test t per a cada parella de tractaments emprant mostres aparellades i aplicant un ajust del p-valor (Bonferroni, Holm…). No donarem els detalls de les fórmules, simplement heu de saber que amb R es fa com a l’ANOVA d’1 via: amb la funció pairwise.t.test, però ara indicant-hi que paired=TRUE.

Exemple 9.16 A l’experiment de l’Exemple 9.11 hem arribat a la conclusió que no totes les mitjanes són iguals. Emprem un contrast posterior per parelles amb l’ajust de Bonferroni per mirar quines són diferents.

## 
##  Pairwise comparisons using paired t tests 
## 
## data:  Dades$kilocal and Dades$tracts 
## 
##   1       2      
## 2 0.00108 -      
## 3 0.00011 1.1e-05
## 
## P value adjustment method: bonferroni

Conclusió: Hem obtingut evidència estadísticament significativa que les tres activitats tenen diferent consum energètic mitjà per km (ANOVA de blocs, test posterior de Bonferroni, p-valors ajustats inferiors a 0.0011)

9.3.4 Contrast no paramètric

Si en un experiment amb disseny d’ANOVA de blocs no podem aplicar l’ANOVA perquè sospitem que no se satisfan les condicions necessàries, cal emprar un test no paramètric. El més popular és el test de Friedman, que generalitza el test de Wilcoxon a més de 2 mostres. En R està implementat en la funció friedman.test que s’aplica a la mateixa fórmula que summary(aov( )) excepte que cal substituir-hi la suma “+” per una barra vertical “|”. Per exemple:

## 
##  Friedman rank sum test
## 
## data:  kilocal and tracts and blocs
## Friedman chi-squared = 16, df = 2, p-value = 0.0003355

La conclusió és la mateixa que abans: No tots els consums energètics mitjans són iguals (test de Friedman, p-valor 0.0003).

Si ara volem realitzar els tests posteriors per parelles, el més adient és emprar en tots ells el test de Wilcoxon, amb la funció pairwise.wilcox.test que ja empràvem a l’ANOVA d’1 via, però ara amb paired=TRUE:

## 
##  Pairwise comparisons using Wilcoxon signed rank test with continuity correction 
## 
## data:  Dades$kilocal and Dades$tracts 
## 
##   1     2    
## 2 0.042 -    
## 3 0.042 0.042
## 
## P value adjustment method: holm

Obtenim evidència estadísticament significativa que les tres activitats tenen consums energètics mitjans diferents (test de Friedman, test posterior per parelles de Wilcoxon amb ajust de Holm, p-valors ajustats 0.042).

9.4 ANOVA de 2 vies

Amb l’ANOVA d’1 via comparàvem les mitjanes de més de 2 subpoblacions definides pels nivells d’un únic factor. Ara ens interessa el cas en què aquestes subpoblacions estan definides combinant els nivells de més d’un factor. Es diu en aquest cas que el disseny de l’experiment és d’ANOVA factorial. Nosaltres aquí considerarem només el cas més senzill, quan s’empren només 2 factors (2 vies). A més, per simplificar, només estudiarem el cas en què totes les mostres de cada combinació de nivells d’un factor i de l’altre tenen la mateixa mida.

Per tant, en un experiment amb disseny d’ANOVA de 2 vies:

  • Tenim una variable aleatòria \(X\)

  • Classificam la població segons les combinacions dels nivells de dos factors

  • Prenem una m.a.s. de cada combinació de nivells, independents i totes de la mateixa mida, i hi mesuram la variable \(X\)

9.4.1 Contrast bàsic

Comencem amb un exemple.

Exemple 9.17 S’havien observat diferències estacionals en el desenvolupament de les gònades d’una espècie de peixos que viuen als llacs africans, i es volia saber si això era conseqüència de la diferència entre estacions en hores de llum o en temperatura. Per decidir-ho, en un experiment s’intentà determinar l’efecte de la llum i la temperatura sobre l’índex gonadosomàtic o GSI (una mesura de creixement de l’ovari) d’aquesta espècie de peixos. S’hi van utilitzar dos fotoperíodes (l’estival, 14 hores de llum i 10 hores de foscor; i l’hivernal, 9 hores de llum-15 hores de foscor) i dues temperatures (l’estival, 27o C, i l’hivernal, 16o C). En concret, com diem, es volia determinar si el GSI mitjà depèn del fotoperíode, o de la temperatura, o de la combinació dels dos tractaments, i si a més hi ha interacció entre ells, en el sentit que en alguna combinació de nivells dels dos tractaments els dos efectes no s’acumulin, sinó que l’efecte final sigui més gran, o més petit, que la suma dels dos efectes per separat.

L’experiment es va realitzar sobre 20 femelles. Es van dividir aleatòriament en 4 subgrups de 5 exemplars cadascun. Cada grup va rebre una combinació diferent de llum i temperatura. Als 3 mesos es mesuraren els seus GSI.

Els resultats obtinguts varen ser:

\[ \begin{array}{c} \hphantom{(temperatura)}\text{Factor A}\\ \hphantom{(temperatura)}\text{(hores de llum)}\\ \begin{array}{c|cc} \text{Factor B} & \text{9 hores}& \text{14 hores}\\ \text{(temperatura)}& &\\\hline 16^\circ &1.30&1.01\\ &2.88&1.52\\ &2.42&1.02\\ &2.66&1.32\\ &2.94&1.63\\\hline 27^\circ &0.90&0.83\\ &1.06&0.67\\ &0.98&0.57\\ &1.29&0.47\\ &1.12&0.66\\ \end{array} \end{array} \]

El disseny experimental d’aquest estudi és d’ANOVA de 2 vies:

  • La variable aleatòria d’interés \(X\) és el GSI d’un peix (femella) als 3 mesos

  • Classificam la població (els peixos) segons les combinacions dels nivells de dos factors (A: el fotoperíode; B: la temperatura)

  • Prenem una m.a.s. de cada combinació de nivells, independents i totes de la mateixa mida, i mesuram el GSI dels individus seleccionats

La situació general en una ANOVA de 2 vies serà la següent:

  • Tenim en compte dos factors, A i B. El factor A té \(a\) nivells (o tractaments, recordau) i el factor B, \(b\) nivells.

    En el nostre exemple, \(a=b=2\)

  • Fem \(n\) observacions de cada combinació de tractaments, un de cada factor. El nombre total d’observacions serà per tant \(N=n\cdot a\cdot b\).

    En el nostre exemple, \(n=5\) i \(N=20\)

  • Indicarem amb \(X_{ijk}\), \(i=1,\ldots,a\), \(j=1,\ldots,b\), \(k=1,\ldots,n\), el valor de la variable \(X\) en el \(k\)-èsim subjecte de la mostra corresponent al nivell \(i\)-èsim del factor A i el nivell \(j\)-èsim del factor B

  • Donarem les dades en una taula d’aquest estil:

\[ \begin{array}{c} \hphantom{Factor B}\text{Factor A}\\ \begin{array}{c|cccc} \text{Factor B} & 1& 2 & \ldots & a\\ \hline 1&X_{111}&X_{211}&\cdots&X_{a11}\\ &X_{112}&X_{212}&\cdots&X_{a12}\\ &\cdots&\cdots&\cdots&\cdots\\ &X_{11n}&X_{21n}&\cdots&X_{a1n}\\\hline 2&X_{121}&X_{221}&\cdots&X_{a21}\\ &X_{122}&X_{222}&\cdots&X_{a22}\\ &\cdots&\cdots&\cdots&\cdots\\ &X_{12n}&X_{22n}&\cdots&X_{a2n}\\\hline \vdots&\vdots&\vdots&\vdots&\vdots\\ \vdots&\vdots&\vdots&\vdots&\vdots\\\hline b&X_{1b1}&X_{2b1}&\cdots&X_{ab1}\\ &X_{1b2}&X_{2b2}&\cdots&X_{ab2}\\ &\cdots&\cdots&\cdots&\cdots\\ &X_{1bn}&X_{2bn}&\cdots&X_{abn}\\\hline \end{array} \end{array} \]

Per que tengui sentit realitzar una ANOVA de 2 vies sobre aquestes dades, s’han de satisfer les condicions següents:

  • Les observacions per a cada combinació de nivells constitueixen mostres aleatòries simples independents, totes de la mateixa mida \(n\)

  • Cadascuna de les \(a\cdot b\) subpoblacions definides per les combinacions de tractaments, un de cada factor, és normal

  • Homocedasticitat: Totes aquestes subpoblacions tenen la mateixa variància, que indicarem amb \(\sigma^2\)

Els paràmetres que intervindran en el contrast són:

  • \(\mu\): la mitjana poblacional global

  • \(\mu_{i\bullet}\): la mitjana poblacional del nivell \(i\)-èsim del factor A

  • \(\mu_{\bullet j}\): mitjana poblacional del nivell \(j\)-èsim del factor B

  • \(\mu_{ij}\): mitjana poblacional de la combinació \((i,j)\) de nivells d’A i B

L’ANOVA de 2 vies se basa en el model següent: per a tots \(i=1,\ldots,a\) i \(j=1,\ldots,b\) \[ X_{ij}=\mu+ \alpha_i +\beta_j + (\alpha\beta)_{ij}+E_{ij} \] on:

  • \(X_{ij}\) indica el valor de la variable \(X\) sobre un individu que pertany al nivell \(i\)-èsim del factor A i al nivell \(j\)-èsim del factor B

  • \(\alpha_i=\mu_{i\bullet}-\mu\) representa la desviació de la mitjana de \(X\) en el nivell \(i\)-èsim del factor A respecte de la mitjana global \(\mu\) (l’efecte del tractament \(i\)-èsim del factor A)

  • \(\beta_j=\mu_{\bullet j}-\mu\) representa la desviació de la mitjana de \(X\) en el nivell \(j\)-èsim del factor B respecte de la mitjana global \(\mu\) (l’efecte del tractament \(j\)-èsim del factor B)

  • \((\alpha\beta)_{ij}=\mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu\) representa l’efecte de la interacció entre el nivell \(i\)-èsim del factor \(A\) i el nivell \(j\)-èsim del factor \(B\); si no hi hagués interacció, tendríem que \[ \mu_{ij}-\mu=(\mu_{i\bullet}-\mu)+(\mu_{\bullet j}-\mu) \] (l’efecte dels dos tractaments se sumaria; la demostració la donam en un bloc de corbes perilloses més a baix) i aquesta contribució de la interacció seria 0.

  • \(E_{ij}=X_{ij}-\mu_{ij}\) representa la part de la diferència entre \(X_{ij}\) i \(\mu\) que no expliquen ni el tractament ni el bloc ni la interacció; en diem l’error aleatori, o el residu.

Aquest model diu bàsicament que el valor de \(X\) sobre un individu és la suma de cinc components:

  • La mitjana global \(\mu\) de \(X\) sobre tota la població
  • L’efecte del tractament A
  • L’efecte del tractament B
  • L’efecte de la interacció
  • L’error aleatori

Passem ara a la mostra amb la que volem realitzar el contrast. Siguin:

  • \(\overline{X}_{ij}=\dfrac{\sum_{k=1}^n X_{ijk}}{n}\): la mitjana mostral de la combinació \((i,j)\) de nivells d’A i B; estima \(\mu_{ij}\)

  • \(\overline{X}_{i\bullet}=\dfrac{\sum_{j=1}^b\sum_{k=1}^n X_{ijk}}{bn}\): la mitjana mostral del nivell \(i\)-èsim del factor A; estima \(\mu_{i\bullet}\)

  • \(\overline{X}_{\bullet j}=\dfrac{\sum_{i=1}^a\sum_{k=1}^n X_{ijk}}{an}\): la mitjana mostral del nivell \(j\)-èsim del factor B estima \(\mu_{\bullet j}\)

  • \(\overline{X}=\dfrac{\sum_{i=1}^{a}\sum_{j=1}^b\sum_{k=1}^n X_{ijk}}{a b n}\): la mitjana mostral de tota la mostra; estima \(\mu\)

Exemple 9.18 Les mitjanes de la taula de l’Exemple 9.17 correspondrien a

\[ \begin{array}{c} \text{Factor A}\\ \begin{array}{c|cc|cc|c} \text{Factor B}&\text{9 hores} & &\text{14 hores} & & \\ \hline 16^\circ &1.30& & 1.01& &\\ &2.88& & 1.52& &\\ &2.42& \!\!\!\!\!\!\overline{X}_{11} & 1.02&\!\!\!\!\!\!\! \overline{X}_{21} &\overline{X}_{\bullet1}\\ &2.66& & 1.32& &\\ &2.94& & 1.63& &\\\hline 27^\circ &0.90& & 0.83& &\\ &1.06& & 0.67& &\\ &0.98&\!\!\!\!\!\! \overline{X}_{12} & 0.57&\!\!\!\!\!\!\! \overline{X}_{22} &\overline{X}_{\bullet2}\\ &1.29& & 0.47& &\\ &1.12& & 0.66& &\\\hline & \overline{X}_{1\bullet} & & \overline{X}_{2\bullet} & & \end{array} \end{array} \]

Anem a calcular-les. Organitzarem les dades en un dataframe peixos amb 3 variables:

  • GSI, quantitativa, contendrà el GSI de cada peix

  • llum, un factor que contendrà el valor del nivell del factor A (fotoperíode) per a cada peix

  • temp, un factor que contendrà el valor del nivell del factor B (temperatura) per a cada peix

Com a tots els ANOVA, els factors que s’empren per classificar la població convé que siguin això, factors (o, almenys, vectors de paraules, no vectors numèrics), al dataframe si volem després emprar la funció aov per fer l’ANOVA.

Entrarem les dades de la taula per fileres. Per tant el factor llum ha d’estar format per 10 còpies consecutives del vector (9,14) i el factor temp ha d’estar format per 10 còpies de “16” seguides de 10 còpies de “27”.

##  [1] 9  14 9  14 9  14 9  14 9  14 9  14 9  14 9  14 9  14 9  14
## Levels: 9 14
##  [1] 16 16 16 16 16 16 16 16 16 16 27 27 27 27 27 27 27 27 27 27
## Levels: 16 27
## 'data.frame':    20 obs. of  3 variables:
##  $ GSI : num  1.3 1.01 2.88 1.52 2.42 1.02 2.66 1.32 2.94 1.63 ...
##  $ llum: Factor w/ 2 levels "9","14": 1 2 1 2 1 2 1 2 1 2 ...
##  $ temp: Factor w/ 2 levels "16","27": 1 1 1 1 1 1 1 1 1 1 ...
##    GSI llum temp
## 1 1.30    9   16
## 2 1.01   14   16
## 3 2.88    9   16
## 4 1.52   14   16
## 5 2.42    9   16
## 6 1.02   14   16

Calculem les mitjanes:

  • Les \(\overline{X}_{ij}\):
##   llum temp  GSI
## 1    9   16 2.44
## 2   14   16 1.30
## 3    9   27 1.07
## 4   14   27 0.64

Hem obtingut aquesta taula: \[ \begin{array}{c|cc} \overline{X}_{ij} & 9 & 14\\ \hline 16 & 2.44 & 1.30\\ 27 & 1.07 & 0.64 \end{array} \]

  • Les \(\overline{X}_{i\bullet}\):
##   llum   GSI
## 1    9 1.755
## 2   14 0.970
  • Les \(\overline{X}_{\bullet j}\):
##   temp   GSI
## 1   16 1.870
## 2   27 0.855
  • La \(\overline{X}\):
## [1] 1.3625

Hem obtingut la taula següent: \[ \begin{array}{cc|cc|c} \overline{X}_{1\bullet} & \overline{X}_{2\bullet} & \overline{X}_{\bullet 1} & \overline{X}_{\bullet 2} & \overline{X} \\ \hline 1.755 & 0.970 & 1.870 & 0.855 & 1.3625 \end{array} \]

En l’ANOVA de 2 vies hi tenim les identitats següents:

Teorema 9.4 (Identitat de les sumes de quadrats) \[ \begin{array}{l} SS_{Total} = SS_{Tr}+SS_E\\[1ex] SS_{Tr} = SS_A+SS_B+SS_{AB} \end{array} \] on

  • \(SS_{Total}=\displaystyle\sum\limits_{i=1}^a\sum\limits_{j=1}^b\sum\limits_{k=1}^n (X_{ijk}-\overline{X})^2\); és la Suma Total de Quadrats

  • \(SS_{Tr}=\displaystyle n\sum\limits_{i=1}^a\sum\limits_{j=1}^b (\overline{X}_{ij}-\overline{X})^2\); és la Suma de Quadrats dels Tractaments

  • \(SS_{A}=\displaystyle b n\sum\limits_{i=1}^a (\overline{X}_{i\bullet}-\overline{X})^2\); és la Suma de Quadrats del Factor A

  • \(SS_{B}=\displaystyle a n\sum\limits_{i=1}^b (\overline{X}_{\bullet j}-\overline{X})^2\); és la Suma de Quadrats del Factor B

  • \({SS_{AB}}=n \sum\limits_{i=1}^a\sum\limits_{j=1}^b (\overline{X}_{ij}-\overline{X}_{i\bullet}-\overline{X}_{\bullet j}+\overline{X})^2\); és la Suma de Quadrats de la Interacció

  • \(SS_E=\displaystyle\sum\limits_{i=1}^a\sum\limits_{j=1}^b\sum\limits_{k=1}^n (X_{ijk}-\overline{X}_{ij})^2\); és la Suma de Quadrats dels Residus o dels Errors

Com als ANOVA anteriors, aquestes sumes de quadrats representen les diferents fonts de variabilitat de les dades:

  • \(SS_{Total}\) representa la variabilitat total de les dades

  • \(SS_{Tr}\) representa la variabilitat de les mitjanes de les combinacions de nivells

  • \(SS_{A}\) representa la variabilitat de les mitjanes dels nivells del factor A

  • \(SS_{B}\) representa la variabilitat de les mitjanes dels nivells del factor B

  • \(SS_E\) representa la suma de les variabilitats dins cada combinació de nivells

  • \(SS_{AB}\) representa la variabilitat deguda a la interacció

Recordau que, si no hi hagués interacció, per a cada parella de nivells \(j,j'\) de B, les diferències \[ \mu_{ij}-\mu_{ij'} \] serien totes la mateixa, independentment del nivell \(i\) de \(A\). Diguem a aquesta diferència \(\delta_{jj'}\). Si ara calculam la mitjana per a tots els nivells \(j'\) de B tenim \[ \mu_{ij}-\mu_{i\bullet}=\mu_{ij}-\frac{1}{b}\sum_{j'=1}^b \mu_{ij'}= \frac{1}{b} \sum_{j'=1}^b(\mu_{ij}-\mu_{ij'})= \frac{1}{b}\sum_{j'=1}^b \delta_{jj'} \] Aquest valor no depèn del nivell \(i\). Per tant, si ara calculam la mitjana per a tots els nivells \(i\) d’A \[ \mu_{\bullet j}-\mu=\frac{1}{a}\sum_{i=1}^a(\mu_{ij}-\mu_{i\bullet})=\frac{1}{b}\sum_{j'=1}^b \delta_{jj'} \] En resum, si no hi hagués interacció entre els dos factors, tendríem que \[ \begin{array}{l} \mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu=(\mu_{ij}-\mu_{i\bullet})-(\mu_{\bullet j}-\mu)\\ \qquad\displaystyle =\frac{1}{b}\sum_{j'=1}^b \delta_{jj'}-\frac{1}{b}\sum_{j'=1}^b \delta_{jj'}=0 \end{array} \] i per tant, sobre la nostra mostra, esperaríem que \[ \overline{X}_{ij}-\overline{X}_{i\bullet}-\overline{X}_{\bullet j}+\overline{X}=0 \] Aleshores, \(SS_{AB}\) és la suma dels quadrats de les divergències, per a cada parell \((i,j)\), d’aquests valors a la nostra mostra respecte del que esperaríem si no hi hagués interacció.

A més, de \(\mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu=0\) deduïm que \[ \mu_{ij}-\mu=\mu_{i\bullet}+\mu_{\bullet j}-2\mu=(\mu_{i\bullet}-\mu)+(\mu_{\bullet j}-\mu) \] com afirmàvem en parlar del model de l’ANOVA de 2 vies.

Observau que de \[ \begin{array}{l} SS_{Total} = SS_{Tr}+SS_E\\[1ex] SS_{Tr} = SS_A+SS_B+SS_{AB} \end{array} \] s’en dedueix que \[ SS_{Total} = SS_A+SS_B+SS_{AB}+SS_E \]

La variabilitat total descompon en la suma de la variabilitat de les mitjanes del factor A més la variabilitat de les mitjanes del factor B més la variabilitat deguda a la interacció més la variabilitat de les dades dins cada combinació de tractaments, un de cada factor.

Exemple 9.19 Comprovem aquestes identitats amb les dades de l’Exemple 9.17.

Procurau entendre com calculam les sumes de quadrats; hem donat els raonaments detallats als altres dos tipus d’ANOVA, aquí ja no els donarem.
  • La \(SS_{Total}\):
## [1] 11.13377
  • La \(SS_{A}\):
## [1] 3.081125
  • La \(SS_{B}\):
## [1] 5.151125
  • La \(SS_{AB}\):
## [1] 0.630125
  • La \(SS_{Tr}\):
## [1] 8.862375
  • La \(SS_{E}\):
## [1] 2.2714

Comprovem les igualtats de sumes de quadrats

## [1] 8.862375
## [1] 8.862375
## [1] 11.13377
## [1] 11.13377

Com als altres ANOVA, compararem la variabilitat de les mitjanes amb la variabilitat dels errors. Per això, emprarem els quadrats mitjans següents:

  • Quadrat mitjà del factor A: \[ MS_A =\dfrac{SS_A}{a-1} \]

  • Quadrat mitjà del factor B: \[ MS_B =\dfrac{SS_B}{b-1} \]

  • Quadrat mitjà de la interacció: \[ MS_{AB}=\dfrac{SS_{AB}}{(a-1)(b-1)} \]

  • Quadrat mitjà dels tractaments: \[ MS_{Tr}=\dfrac{SS_{Tr}}{ab-1} \]

  • Quadrat mitjà dels errors: \[ MS_E=\dfrac{SS_E}{ab (n-1)} \]

Fixau-vos que els denominadors són diferents dels dels quadrats mitjans homònims en les altres ANOVA.

Exemple 9.20 Al nostre Exemple 9.17, on \(n=5\) i \(a=b=2\), hem obtingut les sumes de quadrats següents:

\[ \begin{array}{cccccc} SS_{Total} & SS_A & SS_B & SS_{AB} &SS_{Tr} & SS_E\\ \hline 11.1338 & 3.0811 & 5.1511 & 0.6301 & 8.8624 & 2.2714 \end{array} \]

Per tant:

\[ \begin{array}{ccccc} MS_A & MS_B & MS_{AB} & MS_{Tr} & MS_E\\ \hline 3.0811 & 5.1511 & 0.6301 & 2.9541 & 0.142 \end{array} \]

En una ANOVA de 2 vies, ens poden interessar els quatre contrastos següents:

  • Contrast de mitjanes del factor A: Contrastam si hi ha diferències entre les mitjanes dels tractaments del factor A: \[ \left\{ \begin{array}{l} H_0 : \mu_{1\bullet}=\mu_{2\bullet}=\cdots =\mu_{a\bullet} \\ H_1 : \text{Hi ha } i,i'\text{ tals que } \mu_{i\bullet} \not = \mu_{i'\bullet} \end{array} \right. \] L’estadístic de contrast és \[ F_A=\frac{MS_A}{MS_E}, \] el qual, si \(H_0\) és certa, té distribució \(F\) de Fisher amb \(a-1\) i \(ab(n-1)\) graus de llibertat i valor proper a 1

  • Contrast de mitjanes del factor B: Contrastam si hi ha diferències entre les mitjanes dels tractaments del factor B: \[ \left\{ \begin{array}{l} H_0 : \mu_{\bullet 1}=\mu_{\bullet 2}=\cdots =\mu_{ \bullet b} \\ H_1 : \text{Hi ha } j,j'\text{ tals que } \mu_{\bullet j} \not = \mu_{\bullet j'} \end{array} \right. \] L’estadístic de contrast és \[ F_B=\frac{MS_B}{MS_E}, \] el qual, si \(H_0\) és certa, té distribució \(F\) de Fisher amb \(b-1\) i \(ab(n-1)\) graus de llibertat i valor proper a 1

  • Contrast dels tractaments: Contrastam si hi ha diferències entre les mitjanes de les parelles (nivell de A, nivell de B): \[ \left\{ \begin{array}{l} H_0 : \text{Per a tots }i,j,i',j',\ \mu_{ij}=\mu_{i'j'} \\ H_1 : \text{Hi ha } i,j,i',j'\text{ tals que } \mu_{ij}\neq \mu_{i'j'} \end{array} \right. \] L’estadístic de contrast és \[ F_{Tr}=\frac{MS_{Tr}}{MS_E}, \] el qual, si \(H_0\) és certa, té distribució \(F\) de Fisher amb \(ab-1\) i \(ab(n-1)\) graus de llibertat i valor proper a 1

  • Contrast de no interacció: Contrastam si hi ha interacció entre els factors A i B: \[ \left\{ \begin{array}{l} H_0 : \text{No hi ha interacció entre els nivells d'$A$ i $B$} \\ H_1 : \text{Hi ha interacció entre alguns nivells d'$A$ i $B$} \end{array} \right. \] L’estadístic de contrast és \[ F_{AB} = \frac{MS_{AB}}{MS_E}, \] el qual, si \(H_0\) és certa, té distribució \(F\) de Fisher amb \((a-1)(b-1)\) i \(ab(n-1)\) graus de llibertat i valor proper a 1

En els quatre contrastos, el p-valor és \[ P(F_{x,y}\geqslant\text{valor de l'estadístic sobre la mostra}) \] on \(F_{x,y}\) representa la distribució \(F\) de Fisher amb els graus de llibertat que pertoquin al contrast.

Com fins ara, els graus de llibertat de cada estadístic de contrast F són els denominadors emprats en les definicions dels quadrats mitjans del numerador i el denominados.

Tota aquesta informació se recull en la taula ANOVA següent:

\[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} & ab-1 & SS_{Tr}& MS_{Tr} & F_{Tr} & \text{p-valor}_{Tr} \\ \text{Factor A} & a-1 & SS_{A}& MS_{A} & F_A & \text{p-valor}_A \\ \text{Factor B} & b-1 & SS_{B}& MS_{B} & F_B & \text{p-valor}_B \\ \text{Interacció AB} & (a-1)(b-1) & SS_{AB}& MS_{AB} & F_{AB} & \text{p-valor}_{AB} \\ \text{Residus} & ab(n-1) & SS_E & MS_E & \\\hline \end{array} \]

Exemple 9.21 Tornant a l’Exemple 9.17, tenim que \(n=5\), \(a=b=2\) i ja hem calculat els quadrats mitjans següents:

\[ \begin{array}{ccccc} MS_A & MS_B & MS_{AB} & MS_{Tr} & MS_E\\ \hline 3.0811 & 5.1511 & 0.6301 & 2.9541 & 0.142 \end{array} \]

Realitzem els quatre contrastos:

  • Hi ha diferència en la mitjana del GSI segons el fotoperíode? \[ \begin{array}{l} F_A=\dfrac{MS_{A}}{MS_E}=21.7\\ \text{p-valor}_A=P(F_{1,16}\geqslant 21.7)=\texttt{1-pf(21.7,1,16)}=0.0003 \end{array} \] Conclusió: Hem trobat evidència estadística que el GSI mitjà és diferent segons el fotoperíode (ANOVA de blocs, p-valor 0.0003)

  • Hi ha diferència en la mitjana del GSI segons la temperatura? \[ \begin{array}{l} F_B=\dfrac{MS_{B}}{MS_E}=36.3\\ \text{p-valor}_B=P(F_{1,16}\geqslant 36.3)=\texttt{1-pf(36.3,1,16)}=2\cdot 10^{-5} \end{array} \] Conclusió: Hem trobat evidència estadística que el GSI mitjà és diferent segons la temperatura (ANOVA de blocs, p-valor 2·10-5)

  • Hi ha diferència en la mitjana del GSI segons les combinacions de fotoperíode i temperatura? \[ \begin{array}{l} F_{Tr}=\dfrac{MS_{Tr}}{MS_E}=20.8\\ \text{p-valor}_{Tr}=P(F_{3,16}\geqslant 20.8)=\texttt{1-pf(20.8,3,16)}=9\cdot 10^{-6} \end{array} \] Conclusió: Hem trobat evidència estadística que no tots els GSI mitjans per a les combinacions de fotoperíode i temperatura són iguals (ANOVA de blocs, p-valor 9·10-6)

  • Hi ha interacció entre el fotoperíode i la temperatura? \[ \begin{array}{l} F_{AB}=\dfrac{MS_{AB}}{MS_E}=4.437\\ \text{p-valor}_{AB}=P(F_{1,16}\geqslant 4.437)=\texttt{1-pf(4.437,1,16)}=0.051 \end{array} \] Conclusió: No hem trobat evidència estadística que hi hagi interacció entre el fotoperíode i la temperatura (ANOVA de blocs, p-valor 0.051)

La taula ANOVA és

\[ \begin{array}{llllll} \hline \text{Origen de la}&\text{Graus de}&\text{Sumes de}&\text{Quadrats} & \text{Estadístic de}&\text{p-valor}\\[-0.5ex] \text{variabilitat}&\text{llibertat}&\text{quadrats}&\text{mitjans}&\text{contrast} & \\\hline \text{Tractaments} &3&8.862&2.954&20.8 & 9\cdot 10^{-6} \\ \text{Factor A} &1&3.081&3.081&21.7 & 0.0003 \\ \text{Factor B} & 1&5.151&5.151&36.3 & 2\cdot 10^{-5} \\ \text{Interacció AB} & 1&0.630&0.630&4.44 & 0.051 \\ \text{Residus} & 19&11.134&& & \\\hline \end{array} \]

Hem fet quatre contrastos. No hauríem d’ajustar els p-valors?

No, perquè estam emprant les mateixes dades als quatre contrastos, no són contrastos independents. És a dir, o la mostra ens ha sortit representativa i totes les conclusions són més o menys fiables, o la mostra ens ha sortit rareta i totes les conclusions són poc fiables.

9.4.2 Amb R

A l’ANOVA de 2 vies:

  • Els contrastos de les mitjanes de cada un dels factors i de no interacció s’efectuen aplicant summary(aov( )) a la fórmula que separa la variable numèrica pel producte dels dos factors, indicat amb un asterisc *.

  • El contrast dels tractaments, és a dir, de les mitjanes de les subpoblacions definides per les combinacions de nivells, un de cada factor, s’efectua aplicant summary(aov( )) a la fórmula que separa la variable numèrica per la combinació dels dos factors, indicada amb dos punts :.

Així, l’ANOVA de blocs de l’Exemple 9.11 es fa amb

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## llum         1  3.081   3.081  21.704 0.000262 ***
## temp         1  5.151   5.151  36.285 1.77e-05 ***
## llum:temp    1  0.630   0.630   4.439 0.051268 .  
## Residuals   16  2.271   0.142                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##             Df Sum Sq Mean Sq F value   Pr(>F)    
## llum:temp    3  8.862   2.954   20.81 9.06e-06 ***
## Residuals   16  2.271   0.142                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La primera funció calcula les fileres “Factor A”, “Factor B”, “Interacció AB” i “Residus” de la taula ANOVA, i de la segona funció us heu de quedar amb la primera filera, que us dóna la filera “Tractaments” de la taula ANOVA. No confongueu les fileres llum:temp de la primera taula, que és la de les Interaccions, amb la de la segona, que és la dels Tractaments.