Lección 9 ANOVA básico

En esta lección explicamos cómo efectuar con R los ANOVA básicos que se estudian en cursos introductorios de estadística inferencial: de uno y dos factores y de bloques completos aleatorios. El tema central de la lección son los aspectos técnicos del ANOVA con R y los tests posteriores de comparación de pares de medias. Incluimos además una sección con algunas instrucciones que permiten contrastar las condiciones necesarias sobre los datos para que un contraste ANOVA tenga sentido y una sección con algunos contrastes no paramétricos alternativos al ANOVA que se puedan usar justamente cuando no tiene sentido realizar un ANOVA.

9.1 Los modelos del ANOVA en R

Los modelos a los que se aplica un ANOVA u otras muchas funciones, como por ejemplo la función lm para calcular la recta de regresión lineal, se especifican en R mediante fórmulas. El operador básico para construir una fórmula es la tilde, ~. Las fórmulas suelen tener la forma Y~modelo, donde la Y es un vector y el modelo es una combinación de vectores o factores que representa el modelo con el que queremos explicar el vector Y (en palabras técnicas, al que queremos ajustar los datos del vector Y). Por ejemplo, para calcular la recta de regresión por mínimos cuadrados de un vector Y respecto de un vector X, usamos lm(Y~X). Esto significa que aplicamos la función lm a la fórmula Y~X que indica que queremos explicar Y en función de X.

En los ANOVA que consideramos en esta lección se usan cuatro tipos de fórmulas. Concretamente, si X es una variable numérica y F1 y F2 son dos factores:

La fórmula X~F1 se usa para indicar el ANOVA de un factor, F1, de la variable X.
La fórmula X~F1+F2 se usa para indicar el ANOVA de dos factores, F1 y F2, de la variable X, sin tener en cuenta la interacción entre los factores; es decir, suponiendo que sus efectos se suman, sin que haya interacción entre los mismos. Es el tipo de fórmula que se usa en los ANOVA de bloques.
La fórmula X~F1*F2 se usa para indicar el ANOVA de dos factores, F1 y F2, de la variable X, teniendo en cuenta además la posible interacción entre estos factores.
La fórmula X~F1:F2 se usa para indicar el ANOVA de un factor que tiene como niveles los pares ordenados de niveles de F1 y F2.

La función básica de R para realizar un ANOVA es aov. Su sintaxis genérica es

aov(fórmula, data=...)

con los argumentos siguientes:

fórmula: Una fórmula que especifique un modelo de ANOVA.
data: Opcional, sirve para especificar, si es necesario, el data frame al que pertenecen las variables utilizadas en la fórmula.

Así, por ejemplo, si tenemos un data frame llamado DF, con una variable numérica X y un factor Fact, para realizar el ANOVA de la variable X respecto del factor Fact con la función aov podríamos entrar

aov(X~Fact, data=DF)

aov(DF$X~DF$Fact)

Otra posibilidad, que por ahora no usaremos pero sí más adelante, es aplicar la función anova (no la confundáis con aov) al resultado de lm. La sintaxis sería entonces

anova(lm(fórmula, data=...))

9.2 ANOVA de un factor

Para ilustrar el ANOVA de un factor con R utilizaremos un experimento en el que se quiso determinar si cuatro dietas concretas tenían alguna influencia en el tiempo de coagulación de la sangre en mamíferos: véase Statistics for Experimenters (2a edición), de G. P. Box, W. G. Hunter y J. S. Hunte (Wiley, 2005), p. 133. Para ello se escogieron 24 animales, se repartieron de manera aleatoria en 4 grupos de 6 ejemplares cada uno, y a cada grupo se le asignó de manera aleatoria una de las 4 dietas objeto de estudio, que indicaremos con A, B, C y D. Al cabo de un cierto tiempo se midió el tiempo de coagulación de la sangre en estos animales. Los resultados (redondeados a enteros) se muestran en la Tabla 9.1. Observad que estamos ante un diseño experimental de un solo factor: la dieta.

Tabla 9.1: Tiempos de coagulación bajo diferentes dietas.
A	B	C	D
62	63	68	56
60	67	66	62
63	71	71	60
59	64	67	61
63	65	68	63
59	66	68	64

Para contrastar si los tiempos medios de coagulación son los mismos para las cuatro dietas o no, vamos a realizar un ANOVA de estos datos. Para ello, lo primero que tenemos que hacer es recoger los datos en un data frame, formado por una variable numérica con los valores de la tabla y un factor cuyos niveles sean las diferentes dietas, de manera que a cada valor en la variable numérica le corresponda la dieta con la que se obtuvo. Nosotros entraremos los datos de la tabla anterior por filas, y entonces el factor tendrá que ser

A, B, C, D, A, B, C, D, A...

Otra opción sería entrar los datos por columnas, y entonces entraríamos como factor

A, A, A, A, A, A, B, B, B,...

Entramos pues los datos de la tabla, por filas:

coag=c(62,63,68,56,60,67,66,62,63,71,71,60,59,64,67,61,63,65,68,63,59,66,68,64)

Definimos de manera adecuada el factor de las dietas, como 6 copias de la fila A,B,C,D:

diet=rep(c("A","B","C","D"), times=6)

Finalmente, definimos el data frame y comprobamos que es correcto:

coagulacion=data.frame(coag,diet)
str(coagulacion)

## 'data.frame':	24 obs. of  2 variables:
##  $ coag: num  62 63 68 56 60 67 66 62 63 71 ...
##  $ diet: Factor w/ 4 levels "A","B","C","D": 1 2 3 4 1 2 3 4 1 2 ...

head(coagulacion)

##   coag diet
## 1   62    A
## 2   63    B
## 3   68    C
## 4   56    D
## 5   60    A
## 6   67    B

Para analizar la igualdad de los tiempos medios de coagulación bajo las cuatro dietas, realizaremos un ANOVA de la variable coag separándola según (ajustándola a) el factor diet. Antes de empezar, es conveniente visualizar los datos para hacernos una idea de su distribución; por ejemplo, por medio de un diagrama de cajas con una caja por cada nivel:

boxplot(coag~diet, data=coagulacion)

Observad que también hemos empleado una fórmula para indicar que queremos los diagramas de cajas de la variable coag separada por la variable diet del data frame coagulacion. Obtenemos la Figura 9.1, donde podemos ver que las medias muestrales para las dietas A y C son muy diferentes, y que en cambio seguramente no podríamos rechazar que las medias poblacionales de las dietas A y D sean iguales. Por lo tanto, el resultado que esperamos del ANOVA es que nos permita rechazar la hipótesis nula de que los cuatro tiempos medios de coagulación son iguales. Ahora bien, hasta que no realicemos el ANOVA no sabremos si las diferencias que observamos en este diagrama son estadísticamente significativas o no.

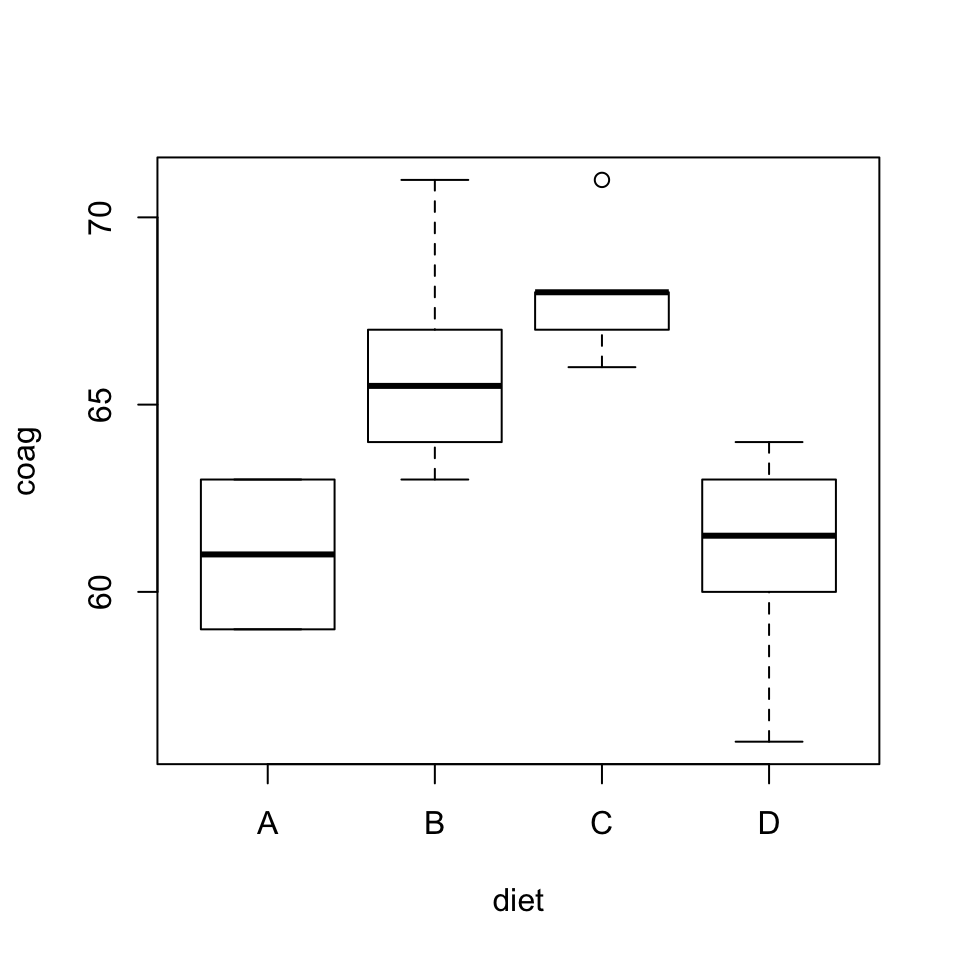
Figura 9.1: Diagrama de cajas de los tiempos de coagulación según las diferentes dietas.

Como hemos comentado, para realizar el ANOVA deseado, entramos:

aov(coag~diet, data=coagulacion)

## Call:
##    aov(formula = coag ~ diet, data = coagulacion)
## 
## Terms:
##                 diet Residuals
## Sum of Squares   228       112
## Deg. of Freedom    3        20
## 
## Residual standard error: 2.366432
## Estimated effects may be unbalanced

El resultado no es la tabla del ANOVA. Para obtenerla, hay que aplicar summary al resultado de aov:

summary(aov(coag~diet, data=coagulacion))

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## diet         3    228    76.0   13.57 4.66e-05 ***
## Residuals   20    112     5.6                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

El resultado de esta función summary es la tabla ANOVA usual:

En la primera columna, dos etiquetas: el nombre del factor, en este caso diet, y Residuals, que representa los errores o residuos del ANOVA.
La segunda columna, etiquetada Df, nos da los grados de libertad correspondientes al factor (su número de niveles menos 1) y a los residuos (el número de individuos en la tabla, menos el número de niveles del factor).
La tercera columna, Sum Sq, nos muestra las sumas de los cuadrados del factor, $SS_{Tr}$, y de los residuos, $SS_E$.
La cuarta columna, Mean Sq, contiene las medias de los cuadrados del factor, $MS_{Tr}$, y de los residuos, $MS_E$.
La quinta columna, F value, nos da el valor del estadístico de contraste.
En la sexta columna, Pr(>F), aparece el p-valor del contraste.
La séptima columna, sin etiqueta, indica el nivel de significación del p-valor según el código usual, explicado en la última línea del resultado. A mayor número de asteriscos, más significativo es el p-valor y por lo tanto es más fuerte la evidencia de que las medias comparadas no son todas iguales.

En nuestro caso, hemos obtenido un p-valor del orden de $4.7\times 10^{-5}$. Esto nos permite rechazar la hipótesis nula y concluir que no todos los tiempos medios de coagulación para las diferentes dietas consideradas son iguales, como intuíamos. Recordad que esto no significa que hayamos obtenido evidencia de que todos los tiempos medios de coagulación son diferentes, solo de que hay al menos un par de dietas que dan tiempos medios diferentes. Si ahora queremos determinar de qué pares de dietas se trata, tendremos que realizar algún test de comparaciones de pares de medias: véase la Sección 9.6.

Para ahorrar espacio vertical, en lo que queda de lección vamos a eliminar los símbolos que marcan los niveles de significación de los p-valores. Para ello entramos la siguiente instrucción:

options(show.signif.stars=FALSE)

A partir de ahora, y mientras no cerremos la sesión, estos símbolos no aparecerán más en las tablas ANOVA.

summary(aov(coag~diet, data=coagulacion))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## diet         3    228    76.0   13.57 4.66e-05
## Residuals   20    112     5.6

Si en algún momento de la sesión queréis volver a ver los códigos de significación, basta que entréis

options(show.signif.stars=TRUE)

Como hemos comentado, una manera alternativa de realizar un ANOVA es mediante anova(lm(...)). Con esta construcción obtenemos directamente la tabla, sin necesidad de aplicarle summary.

anova(lm(coag~diet, data=coagulacion))

## Analysis of Variance Table
## 
## Response: coag
##           Df Sum Sq Mean Sq F value    Pr(>F)
## diet       3    228    76.0  13.571 4.658e-05
## Residuals 20    112     5.6

Para extraer los datos de la tabla ANOVA obtenida con la función summary(aov(...)), y así poder operar directamente con ellos, hay que añadirle los sufijos adecuados. Consultemos su estructura.

tabla=summary(aov(coag~diet, data=coagulacion)) 
str(tabla)

## List of 1
##  $ :Classes 'anova' and 'data.frame':	2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 3 20
##   ..$ Sum Sq : num [1:2] 228 112
##   ..$ Mean Sq: num [1:2] 76 5.6
##   ..$ F value: num [1:2] 13.6 NA
##   ..$ Pr(>F) : num [1:2] 4.66e-05 NA
##  - attr(*, "class")= chr [1:2] "summary.aov" "listof"

Vemos que la tabla ANOVA obtenida con summary(aov(...)) es una list formada por un solo objeto (List of 1), que a su vez es un data frame cuyas variables son las columnas numéricas de la tabla. Por lo tanto, para obtener una columna de estas, primero hemos de añadir el sufijo [[1]], que extrae el data frame de la list, y a continuación el sufijo $columna correspondiente a la columna de la tabla ANOVA que nos interesa. Por ejemplo, la columna de las sumas de los cuadrados es:

tabla[[1]]$"Sum Sq"

## [1] 228 112

De manera similar, como el p-valor es el primer elemento de la columna Pr(>F), lo obtenemos con:

tabla[[1]]$"Pr(>F)"[1]

## [1] 4.658471e-05

Fijaos en que, como los nombres de estas columnas contienen espacios en blanco u otros símbolos no aceptados en los nombres de objetos de R (recordad la Lección 4 de la primera parte), hay que especificarlos entre comillas.

El resultado de anova(lm(...)) ya es directamente un data frame, por lo que para extraer los valores de la tabla ANOVA que produce podemos usar la sintaxis usual de los data frames.

tabla2=anova(lm(coag~diet, data=coagulacion))
str(tabla2)

## Classes 'anova' and 'data.frame':	2 obs. of  5 variables:
##  $ Df     : int  3 20
##  $ Sum Sq : num  228 112
##  $ Mean Sq: num  76 5.6
##  $ F value: num  13.6 NA
##  $ Pr(>F) : num  4.66e-05 NA
##  - attr(*, "heading")= chr  "Analysis of Variance Table\n" "Response: coag"

tabla2$"Sum Sq"

## [1] 228 112

tabla2$"Pr(>F)"[1]

## [1] 4.658471e-05

Veamos otro ejemplo de ANOVA de un factor.

Ejemplo 9.1 En un experimento, se estudió el efecto de seis dietas sobre el crecimiento de crías de conejo doméstico: véase Experimental Design and Analysis, de M. Lentner y T. Bishop (Valley Book Co. 1986), p. 428. Los datos obtenidos están recogidos en la tabla de datos rabbit del paquete faraway.

library(faraway)
str(rabbit)

## 'data.frame':	30 obs. of  3 variables:
##  $ treat: Factor w/ 6 levels "a","b","c","d",..: 6 2 3 3 1 2 3 6 4 1 ...
##  $ gain : num  42.2 32.6 35.2 40.9 40.1 38.1 34.6 34.3 37.5 44.9 ...
##  $ block: Factor w/ 10 levels "b1","b10","b2",..: 1 1 1 3 3 3 4 4 4 5 ...

Consultando la Ayuda de rabbit nos enteramos de que el factor treat indica la dieta, con niveles a,b,c,d,e,f, y de que la variable gain indica el aumento de peso; la variable block, que indica la camada, es irrelevante en este análisis concreto.

Si dibujamos el diagrama de cajas de los crecimientos para cada dieta, obtenemos la Figura 9.2, donde no observamos grandes diferencias en los crecimientos medios.

boxplot(gain~treat, data=rabbit)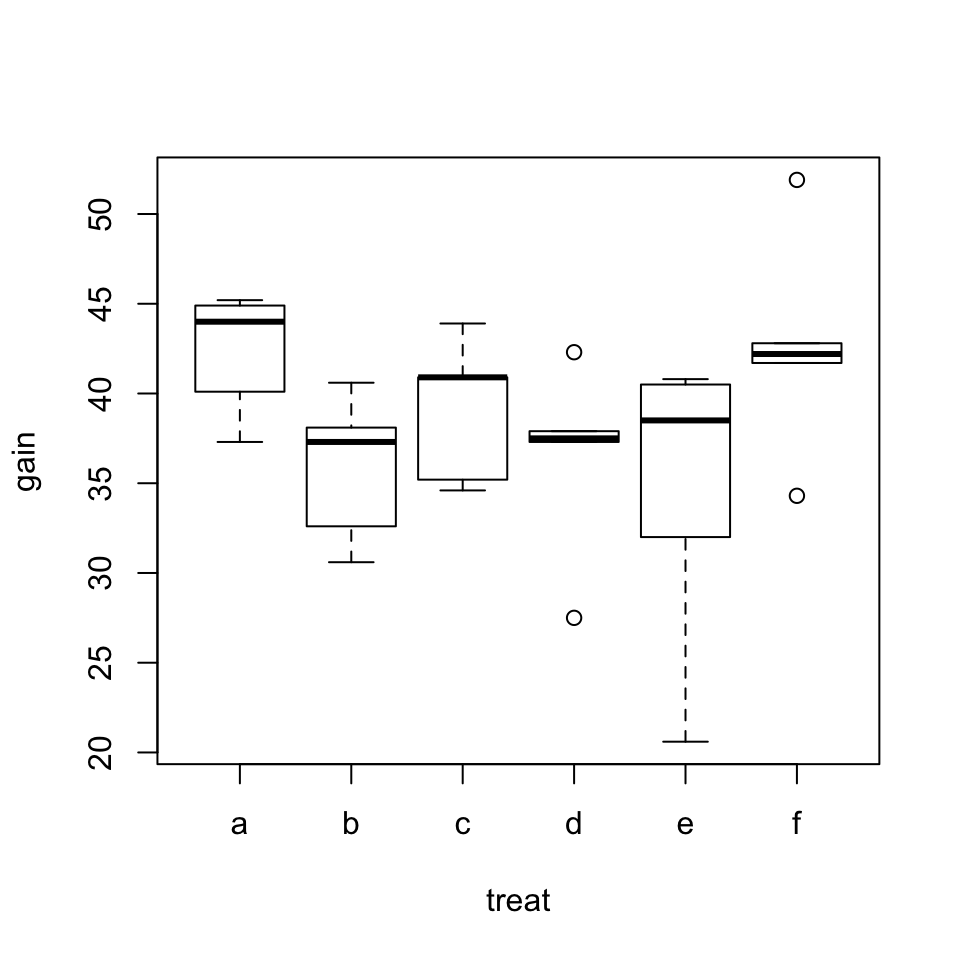

Figura 9.2: Diagrama de cajas de los crecimientos de crías de conejo según las diferentes dietas.

Para determinar si hay diferencia en los aumentos medios de peso bajo las seis dietas, realizaremos un ANOVA de la variable gain ajustándola al factor treat.

summary(aov(gain~treat, data=rabbit))

##             Df Sum Sq Mean Sq F value Pr(>F)
## treat        5  293.4   58.68   1.886  0.134
## Residuals   24  746.5   31.10

El p-valor es 0.134, lo que indica que, efectivamente, no hay evidencia de que las dietas den lugar a crecimientos medios diferentes. Si hubiéramos querido obtener solo el p-valor, podríamos haber entrado:

summary(aov(gain~treat, data=rabbit))[[1]]$"Pr(>F)"[1]

## [1] 0.1342124

Es muy importante tener presente que, al usar las instrucciones aov o anova(lm(...)) para realizar un ANOVA, se tiene que emplear un factor (o varios, en las próximas secciones) para separar la variable numérica en subpoblaciones. Veamos un ejemplo de lo que pasa si nos descuidamos en este punto.

Ejemplo 9.2 En un experimento se estudió el efecto de la vitamina C en el crecimiento de los dientes: véase The Statistics of Bioassay de C. I. Bliss (Academic Press, 1952), p. 499-501. Se tomaron 60 cobayas y se trató cada uno de ellos con una combinación diferente de dosis de vitamina C (0.5, 1 o 2 mg) y método de suministro de la misma (mediante zumo de naranja o como ácido ascórbico) durante 6 semanas, y se cuantificó el crecimiento de sus dientes durante dicho período (más en concreto, se midió la longitud media de sus odontoblastos al final del mismo). El resultado es una tabla de 60 datos, que aparecen recogidos en el fichero ToothGrowth del paquete UsingR.

library(UsingR)
str(ToothGrowth)

## 'data.frame':	60 obs. of  3 variables:
##  $ len : num  4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
##  $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
##  $ dose: num  0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...

La Ayuda de ToothGrowth nos dice que la variable len contiene la longitud media final de los odontoblastos del animal, la variable supp el método de suministro (OJ indica zumo de naranja, orange juice, y VC indica ácido ascórbico puro, vitamine C), y la variable dose la dosis.

Nos vamos a olvidar por el momento de la variable supp, y vamos a contrastar si la dosis de vitamina C tiene influencia en el crecimiento de los dientes. Para ello realizamos un ANOVA de un factor.

summary(aov(len~dose, data=ToothGrowth))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## dose         1   2224  2224.3   105.1 1.23e-14
## Residuals   58   1228    21.2

¿Veis algo raro? Hemos comentado que se usaron tres dosis diferentes, por lo que el número de grados de libertad en la fila del factor, dose, tendría que ser 2, y no 1. ¿Qué ha pasado? Muy sencillo: dose es una variable numérica, y para usar aov el factor ha de ser eso, un factor. Así que lo primero que tenemos que hacer es convertir esta variable en un factor. Los haremos sobre un duplicado de la tabla ToothGrowth original, a la que llamaremos ToothGrowth2.

ToothGrowth2=ToothGrowth
ToothGrowth2$dose=as.factor(ToothGrowth2$dose)
str(ToothGrowth2)

## 'data.frame':	60 obs. of  3 variables:
##  $ len : num  4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
##  $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
##  $ dose: Factor w/ 3 levels "0.5","1","2": 1 1 1 1 1 1 1 1 1 1 ...

summary(aov(len~dose, data=ToothGrowth2))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## dose         2   2426    1213   67.42 9.53e-16
## Residuals   57   1026      18

Ahora está bien. El p-valor prácticamente 0 nos permite rechazar la hipótesis nula y concluir que hay dosis de vitamina C que dan lugar a diferentes crecimientos medios de los odontoblastos.

9.3 ANOVA de bloques completos aleatorios

Para ilustrar este tipo de ANOVA, analizaremos un experimento sobre producción de penicilina: vVéase Practical Regression and Anova using R, de J. Faraway, p. 186 (este texto se puede descargar de la página web https://cran.r-project.org/doc/contrib/Faraway-PRA.pdf). En dicho experimento, se evaluaron cuatro procesos diferentes para determinar si había diferencias en su efectividad. Los cuatro procesos usaban una técnica de cultivo sumergido y empleaban agua de macerado de maíz como fuente de nitrógeno orgánico. Como la composición de este líquido puede afectar la producción final de penicilina, para evaluar los cuatro procesos se prepararon 5 mezclas diferentes de agua de macerado de maíz, de cada mezcla se tomaron 4 muestras y se asignaron de manera aleatoria a los cuatro procesos de producción. Los resultados obtenidos son los de la Tabla 9.2, y aparecen recogidos en la tabla de datos penicillin del paquete faraway.

Tabla 9.2: Producción de penicilina bajo diferentes procesos de producción y mezclas.
Mezcla	A	B	C	D
1	89	88	97	94
2	84	77	92	79
3	81	87	87	85
4	87	92	89	84
5	79	81	80	88

Observad que estamos ante un diseño experimental de bloques completos aleatorios. Los bloques son las mezclas de agua de macerado de maíz y los tratamientos (los procesos de producción) se han asignado de manera aleatoria a las unidades experimentales (las muestras) de cada bloque, de tal manera que cada bloque contiene exactamente una unidad experimental para cada tratamiento. Este es un ejemplo paradigmático de uso de bloques: para evitar la influencia de la variable “extraña” dada por la composición del agua de macerado de maíz, que puede influir en la producción, se escogen al azar unas mezclas y se prueban todos los procesos de manera independiente sobre cada mezcla.

Demos un vistazo a esta tabla de datos.

str(penicillin)

## 'data.frame':	20 obs. of  3 variables:
##  $ treat: Factor w/ 4 levels "A","B","C","D": 1 2 3 4 1 2 3 4 1 2 ...
##  $ blend: Factor w/ 5 levels "Blend1","Blend2",..: 1 1 1 1 2 2 2 2 3 3 ...
##  $ yield: num  89 88 97 94 84 77 92 79 81 87 ...

head(penicillin)

##   treat  blend yield
## 1     A Blend1    89
## 2     B Blend1    88
## 3     C Blend1    97
## 4     D Blend1    94
## 5     A Blend2    84
## 6     B Blend2    77

Según la Ayuda de penicillin, la variable treat es el proceso de producción, con valores A, B, C y D; la variable blend es la mezcla usada (los bloques), con valores Blend1 a Blend5; y la variable numérica yield es un valor que cuantifica la producción de penicilina.

Veamos cómo son los diagramas de cajas de la producción de penicilina separada por procesos de producción y por mezclas:

boxplot(yield~treat, data=penicillin)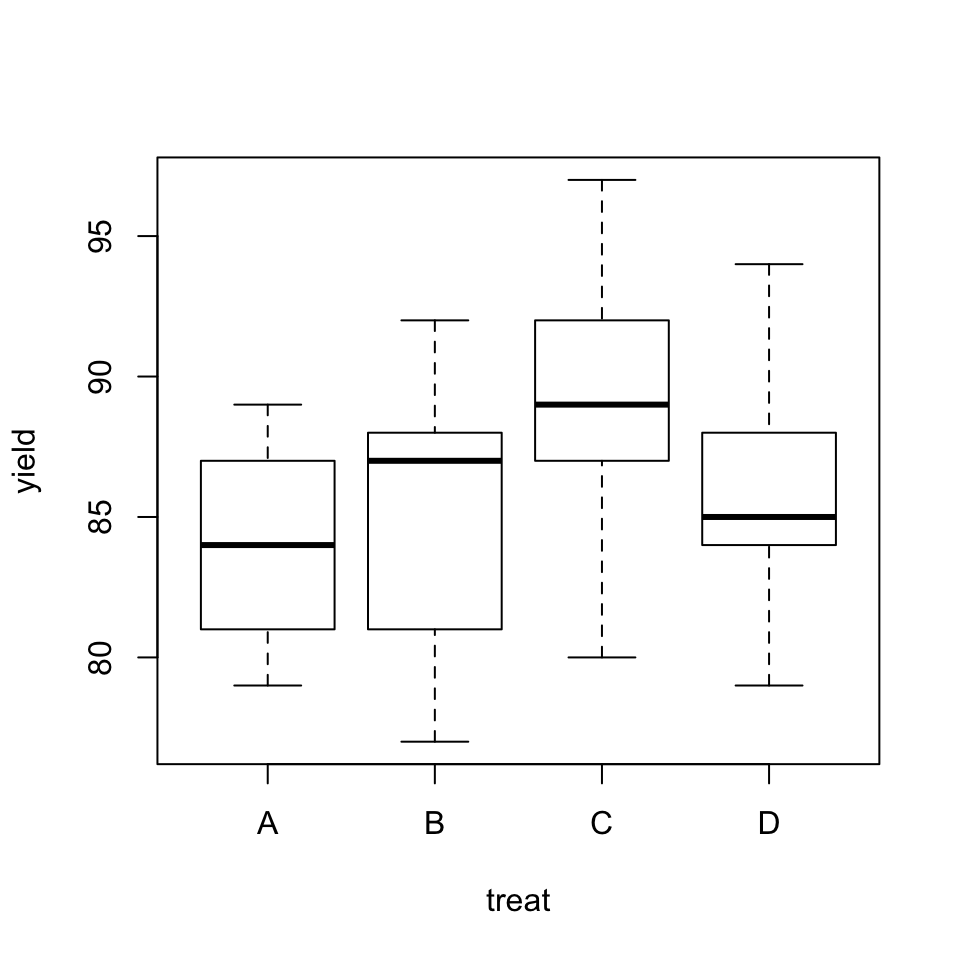

Figura 9.3: Diagrama de cajas de la producción de penicilina bajo los diferentes procesos de producción.

boxplot(yield~blend, data=penicillin)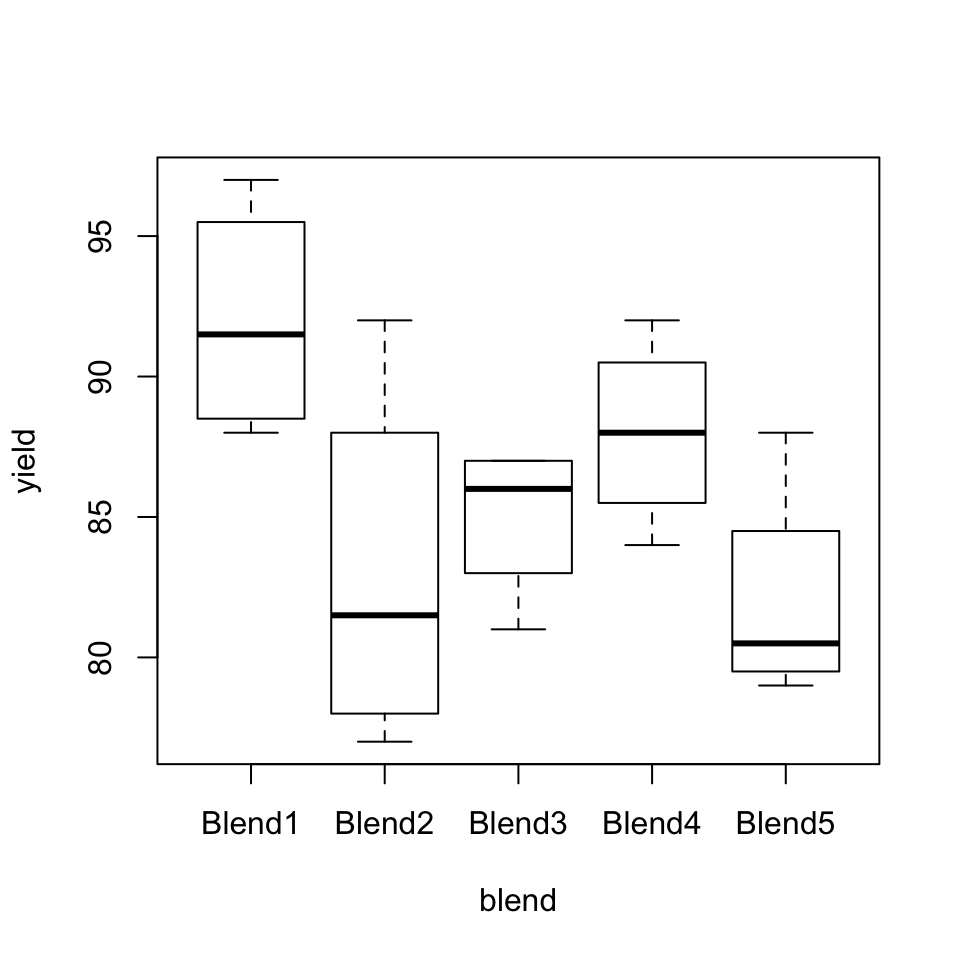

Figura 9.4: Diagrama de cajas de la producción de penicilina según las diferentes mezclas.

Vemos que no hay mucha diferencia entre las producciones para los diferentes procesos (sin tener en cuenta los bloques), y que sí que hay algunas diferencias en las producciones según la composición del agua de macerado de maíz; ya hemos comentado que es bien sabido que su composición influye en la producción.

Si realizamos un ANOVA de un factor para cada uno de estos dos factores por separado, obtenemos resultados consistentes con esta observación visual:

summary(aov(yield~treat, data=penicillin))

##             Df Sum Sq Mean Sq F value Pr(>F)
## treat        3     70   23.33   0.762  0.532
## Residuals   16    490   30.62

summary(aov(yield~blend, data=penicillin))

##             Df Sum Sq Mean Sq F value Pr(>F)
## blend        4    264   66.00   3.345  0.038
## Residuals   15    296   19.73

El p-valor del ANOVA separando por procesos de producción es 0.532, lo que indica que no podemos rechazar la hipótesis nula de que los procesos de producción tengan igual productividad media (sin tener en cuenta las mezclas), y el p-valor del ANOVA separando por mezclas es 0.038, lo que, con un nivel de significación del 5%, nos permite rechazar que todas las mezclas produzcan la misma cantidad media de penicilina. Pero precisamente, el hecho de que la mezcla influya en la producción es lo que hace que el primer ANOVA no sea fiable: a lo mejor el efecto de las mezclas enmascara las diferencias en las productividades de los procesos bajo estudio. Para determinarlo, vamos a realizar un ANOVA de bloques, es decir, de dos factores y efectos acumulados.

summary(aov(yield~treat+blend, data=penicillin))

##             Df Sum Sq Mean Sq F value Pr(>F)
## treat        3     70   23.33   1.239 0.3387
## blend        4    264   66.00   3.504 0.0407
## Residuals   12    226   18.83

El p-valor que nos interesa en esta tabla es el de la fila treat: es 0.34, por lo que si tenemos en cuenta los bloques tampoco detectamos evidencia de que haya diferencias en la productividad media de los procesos estudiados. El segundo p-valor de la tabla, 0.0407, es el del ANOVA de bloques que resulta de intercambiar los bloques y el tratamiento, tomando las mezclas como el factor a analizar y los procesos de producción como los bloques:

summary(aov(yield~blend+treat, data=penicillin))

##             Df Sum Sq Mean Sq F value Pr(>F)
## blend        4    264   66.00   3.504 0.0407
## treat        3     70   23.33   1.239 0.3387
## Residuals   12    226   18.83

Podemos extraer los resultados de una tabla de un ANOVA de bloques generada por summary(aov(...)) añadiendo los mismos sufijos que en el caso de un factor. Así, por ejemplo, los p-valores son:

tabla=summary(aov(yield~treat+blend, data=penicillin))
tabla[[1]]$"Pr(>F)"

## [1] 0.33865812 0.04074617         NA

y si solo nos interesa el del factor treat:

tabla[[1]]$"Pr(>F)"[1]

## [1] 0.3386581

Veamos otro ejemplo de ANOVA de bloques completos aleatorios.

Ejemplo 9.3 Para estudiar si las diferentes actividades de evaluación llevadas a cabo en la asignatura de Matemáticas I tienen una dificultad similar (o mejor dicho, para mirar de confirmar nuestras sospechas de que no es así), escogimos una muestra aleatoria de 15 estudiantes de Biología o Bioquímica que se hubieran presentado al control 2 de dicha asignatura en el curso 2012-2013, y anotamos las notas obtenidas por estos estudiantes en los apartados de Tests, Talleres, Ejercicios de Casa, Control 1 y Control 2. Si obtenemos evidencia de que no todas las medias de las notas de las diferentes actividades fueron iguales, podremos concluir que no todas las actividades tienen la misma dificultad. Los datos obtenidos son los de la tabla 9.3.

Tabla 9.3: Notas obtenidas por 15 estudiantes en diferentes actividades de evaluación.
Estudiante	Tests	Casa	Talleres	Control.1	Control.2
1	48	42	85	31	20
2	94	86	100	52	48
3	98	94	93	93	90
4	60	58	71	66	46
5	52	56	79	64	24
6	78	73	84	80	95
7	84	84	94	83	70
8	83	76	99	51	55
9	75	55	70	85	48
10	24	49	57	19	55
11	47	47	64	44	35
12	53	42	78	50	8
13	82	93	92	66	30
14	66	62	74	24	56
15	49	40	74	35	21

Como podemos observar, se trata de un experimento de bloques completos aleatorios: hemos escogido de manera aleatoria unos bloques (los estudiantes) y para cada estudiante hemos apuntado el valor de cada uno de los niveles del factor a estudiar (las notas en las diferentes actividades). Este diseño es el adecuado para este problema, puesto que hay una gran variabilidad en las notas obtenidas por estudiantes diferentes, desde matrículas a suspensos. Al tomar bloques, es decir, al considerar todas las notas de un conjunto aleatorio fijo de estudiantes, eliminamos el efecto de esta variabilidad.

Vamos a construir un data frame con estos datos. Este data frame tendrá tres variables: notas, con las notas obtenidas por los estudiantes; acts, con los tipos de actividades de evaluación realizados; y bloques, con el indicador de cada estudiante. Entraremos las notas siguiendo las filas de la tabla anterior, y por lo tanto tenemos que construir estos dos factores entrando sus niveles en el orden adecuado: el factor acts ha de estar formado por 15 copias de la fila de actividades, y el factor bloques ha de estar formado por 5 copias de 1, 5 copias de 2, y así hasta 5 copias de 15. Y recordad que bloques ha de ser un factor, puesto que queremos usarlo en un ANOVA.

notas=c(48,42,85,31,20,94,86,100,52,48,98,94,93,93,90,60,58,
   71,66,46,52,56,79,64,24,78,73,84,80,95,84,84,94,83,70,83,76,
   99,51,55,75,55,70,85,48,24,49,57,19,55,47,47,64,44,35,53,42,
   78,50,8,82,93,92,66,30,66,62,74,24,56,49,40,74,35,21)
acts=rep(c("Tests","Casa","Talleres","Control 1","Control 2"), times=15)
bloques=as.factor(rep(1:15,each=5)) 
notas.bloques=data.frame(notas,acts,bloques)
str(notas.bloques)

## 'data.frame':	75 obs. of  3 variables:
##  $ notas  : num  48 42 85 31 20 94 86 100 52 48 ...
##  $ acts   : Factor w/ 5 levels "Casa","Control 1",..: 5 1 4 2 3 5 1 4 2 3 ...
##  $ bloques: Factor w/ 15 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ...

head(notas.bloques)

##   notas      acts bloques
## 1    48     Tests       1
## 2    42      Casa       1
## 3    85  Talleres       1
## 4    31 Control 1       1
## 5    20 Control 2       1
## 6    94     Tests       2

Vamos a dibujar los diagramas de cajas de las notas de las diferentes actividades y de los diferentes estudiantes:

boxplot(notas.bloques$notas~notas.bloques$acts)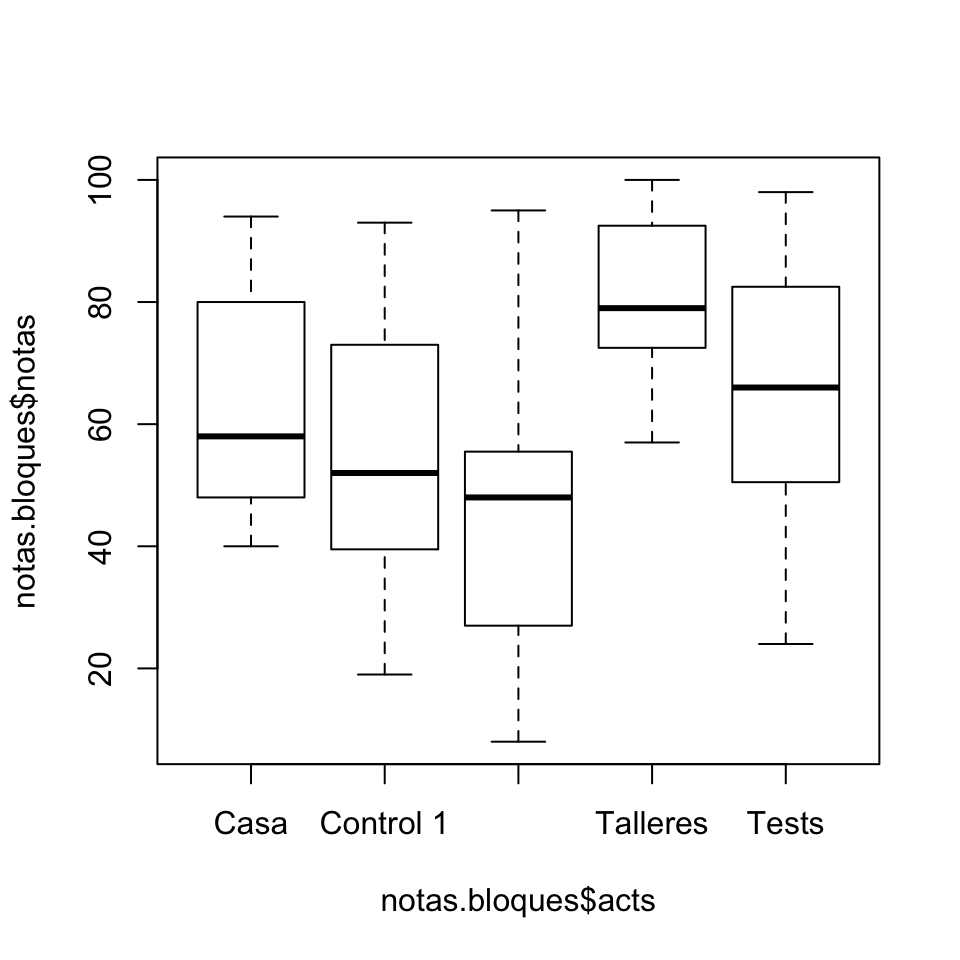

Figura 9.5: Diagrama de cajas de las notas en las diferentes actividades.

boxplot(notas.bloques$notas~notas.bloques$bloques)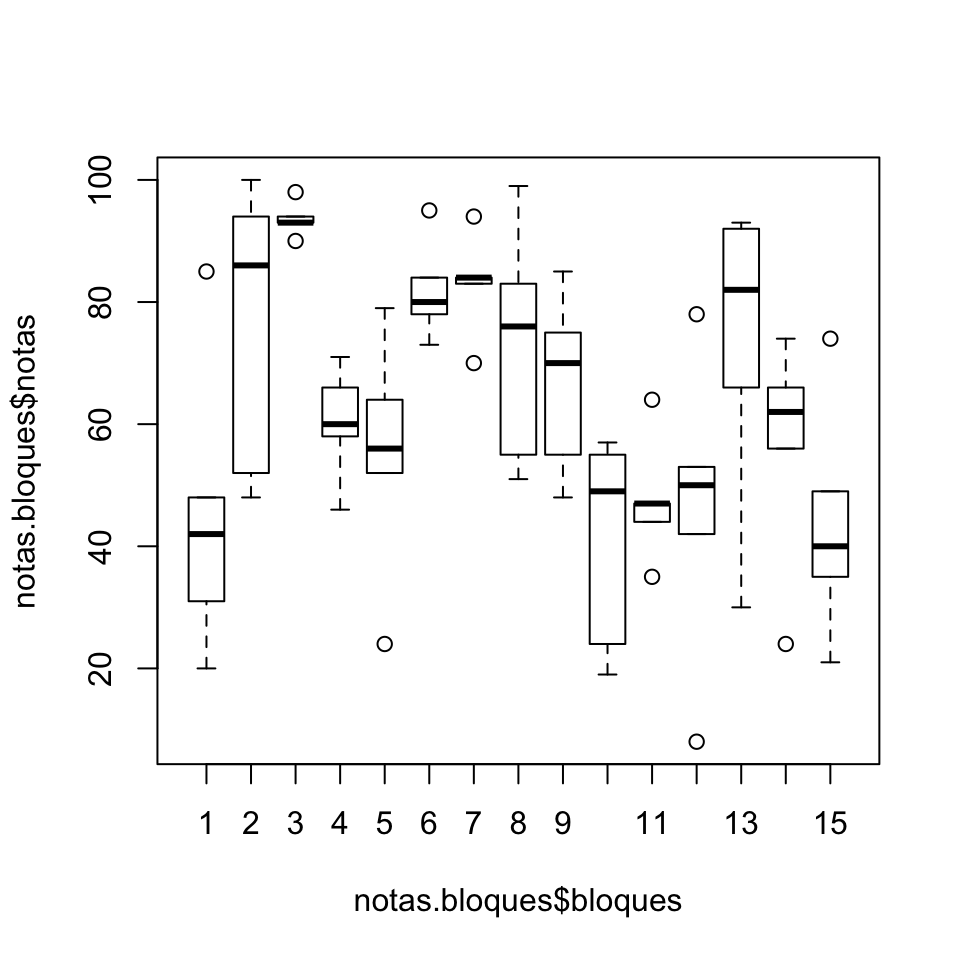

Figura 9.6: Diagrama de cajas de las notas de los estudiantes.

Podemos observar diferencias en las notas de algunas actividades: por ejemplo, las notas del control 2 son muy inferiores a las de los talleres. Asimismo, como nos temíamos, vemos una gran variabilidad en las notas de los estudiantes.

Realicemos ahora el ANOVA.

summary(aov(notas~acts+bloques, data=notas.bloques))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## acts         4   9646  2411.5  13.133 1.31e-07
## bloques     14  19430  1387.9   7.558 1.47e-08
## Residuals   56  10283   183.6

El p-valor que nos interesa es el de la primera fila, etiquetada con el factor cuyos niveles queremos comparar, en este caso acts. Este p-valor es muy pequeño, del orden de $10^{-7}$, lo que es evidencia de que, como nos temíamos, no todas las notas medias de las actividades de evaluación son iguales.

9.4 ANOVA de dos vías

Para ilustrar el ANOVA de dos vías, es decir, de dos factores que pueden interacccionar, analizaremos en primer lugar los resultados de un experimento sobre el efecto de venenos y antídotos: véase “An analysis of transformations”, de G. Box y D. Cox, J. Roy. Stat. Soc. Series B 26 (1964), pp. 211-252; véase también Practical Regression and Anova using R, de J. Faraway, p. 182. En este experimento se usaron tres venenos y cuatro antídotos, y cada combinación de veneno y antídoto se administró a cuatro ratas elegidas de manera aleatoria e independiente. A continuación, se anotó el tiempo de supervivencia de cada animal, en unidades de 10 horas. Se trata, pues, de un diseño experimental de dos factores, en el que cada individuo ha sido asignado al azar a cada nivel de los dos factores. Por otro lado, no podemos descartar a priori que haya interacción entre venenos y antídotos, puesto que un antídoto puede ser más efectivo para un veneno que para otro.

El objetivo del experimento era contrastar la igualdad de los tiempos medios de supervivencia según el veneno, según el antídoto, y según la combinación veneno-antídoto. Los datos obtenidos en este experimento se han recogido en la tabla rats del paquete faraway.

Pero ahora tenemos un problema con este data frame. Si cargamos en una misma sesión varios paquetes que contengan objetos con el mismo nombre, R entiende en cada momento que ese nombre refiere al objeto del paquete que se haya cargado más recientemente. Como en esta lección hemos cargado el paquete UsingR después del paquete faraway, en estos momentos rats refiere a una tabla de datos del paquete survival que se ha cargado con UsingR y que no tiene nada que ver con los datos de este experimento. Una solución posible sería en este punto volver a cargar el paquete faraway. Otra opción más rápida es definir rats como el objeto rats de faraway por medio de la instrucción rats=faraway::rats. La construcción paquete::objeto invoca el objeto (una función, una tabla de datos,…) del paquete y sirve para eliminar ambigüedades como la que nos encontramos aquí. Además, tiene la ventaja de que no es necesario cargar el paquete, basta que esté instalado

Vamos a cargar y explorar estos datos.

rats=faraway::rats
str(rats)

## 'data.frame':	48 obs. of  3 variables:
##  $ time  : num  0.31 0.82 0.43 0.45 0.45 1.1 0.45 0.71 0.46 0.88 ...
##  $ poison: Factor w/ 3 levels "I","II","III": 1 1 1 1 1 1 1 1 1 1 ...
##  $ treat : Factor w/ 4 levels "A","B","C","D": 1 2 3 4 1 2 3 4 1 2 ...

head(rats)

##   time poison treat
## 1 0.31      I     A
## 2 0.82      I     B
## 3 0.43      I     C
## 4 0.45      I     D
## 5 0.45      I     A
## 6 1.10      I     B

En la Ayuda de rats nos enteramos de que el factor treat contiene el antídoto, con niveles A, B, C y D; el factor poison contiene el veneno, con niveles I, II y III; y la variable numérica time contiene el tiempo de supervivencia de las ratas. Veamos cómo son los diagramas de cajas de estos tiempos, separados por venenos y por antídotos.

boxplot(time~poison, data=rats)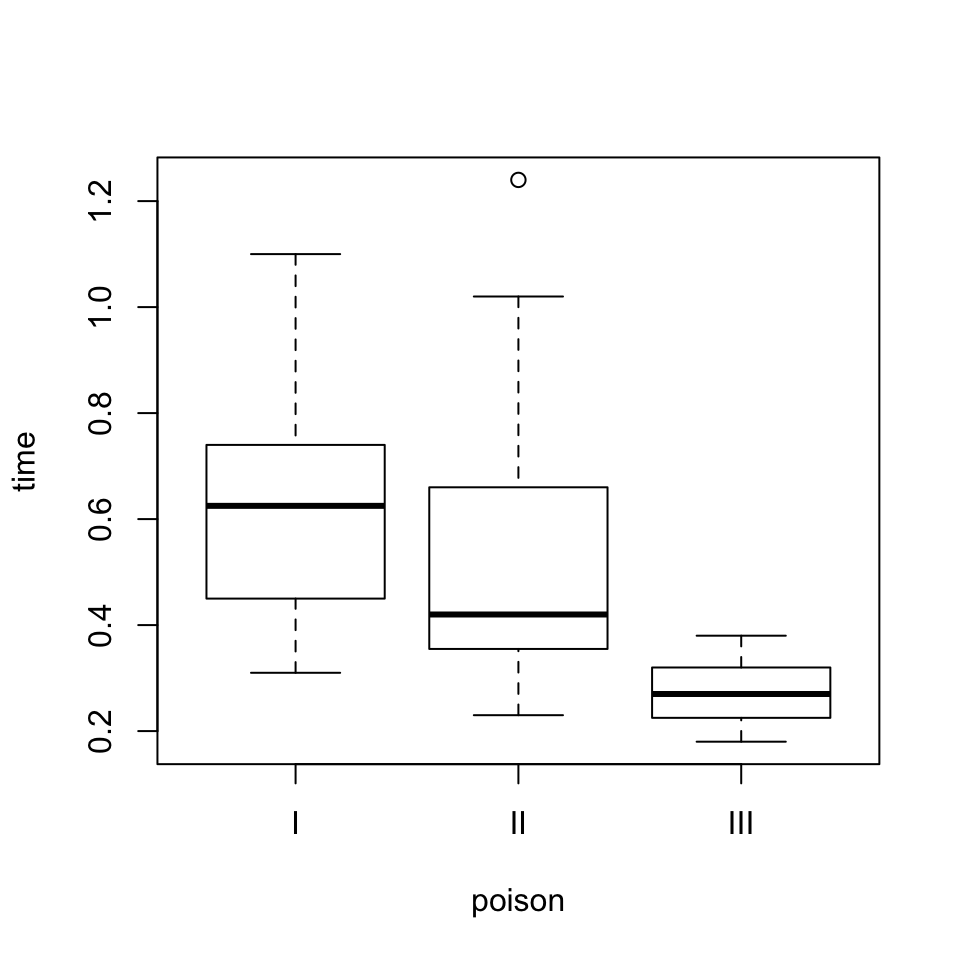

Figura 9.7: Diagrama de cajas de los tiempos de supervivencia según los venenos.

boxplot(time~treat, data=rats)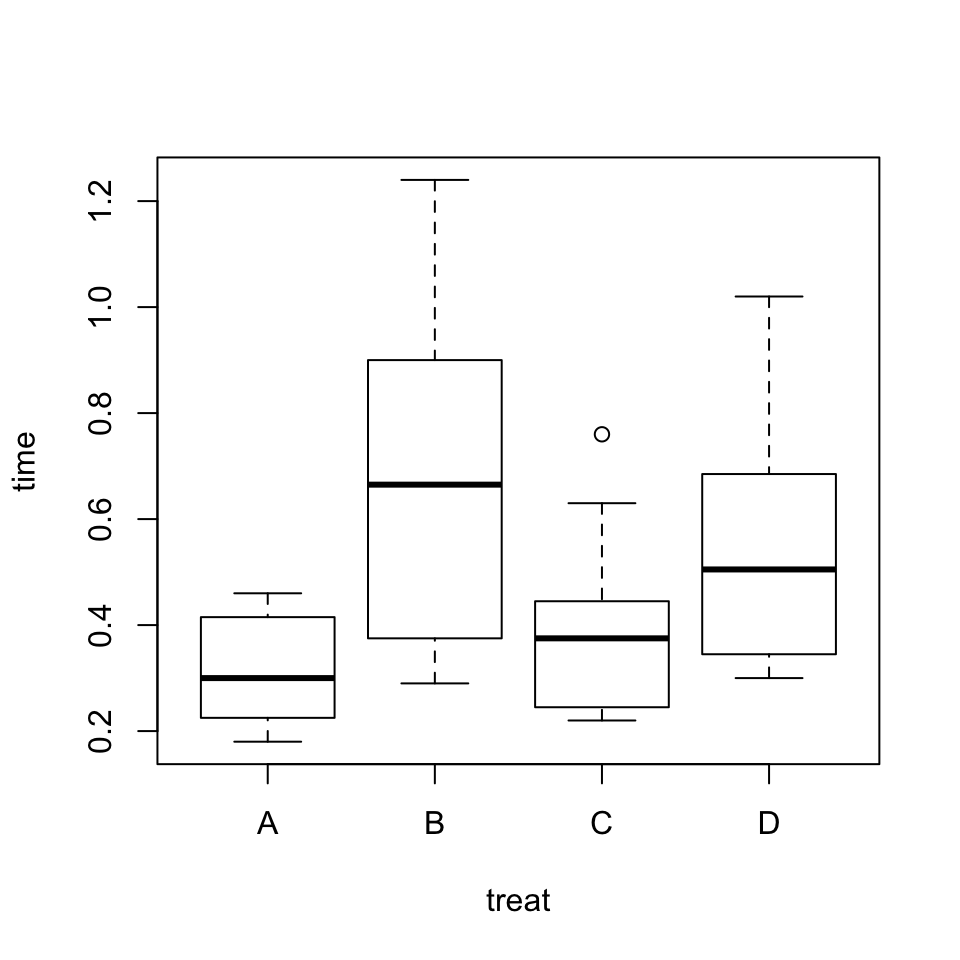

Figura 9.8: Diagrama de cajas de los tiempos de supervivencia según los antídotos

Parece que hay diferencias en los tiempos medios de supervivencia tanto para los diferentes venenos como para los diferentes antídotos. Podemos también dibujar un diagrama de cajas de los tiempos de supervivencia separándolos por combinaciones de veneno y antídoto. La instrucción para hacerlo es la siguiente (observad la fórmula del argumento):

boxplot(time~poison:treat, data=rats)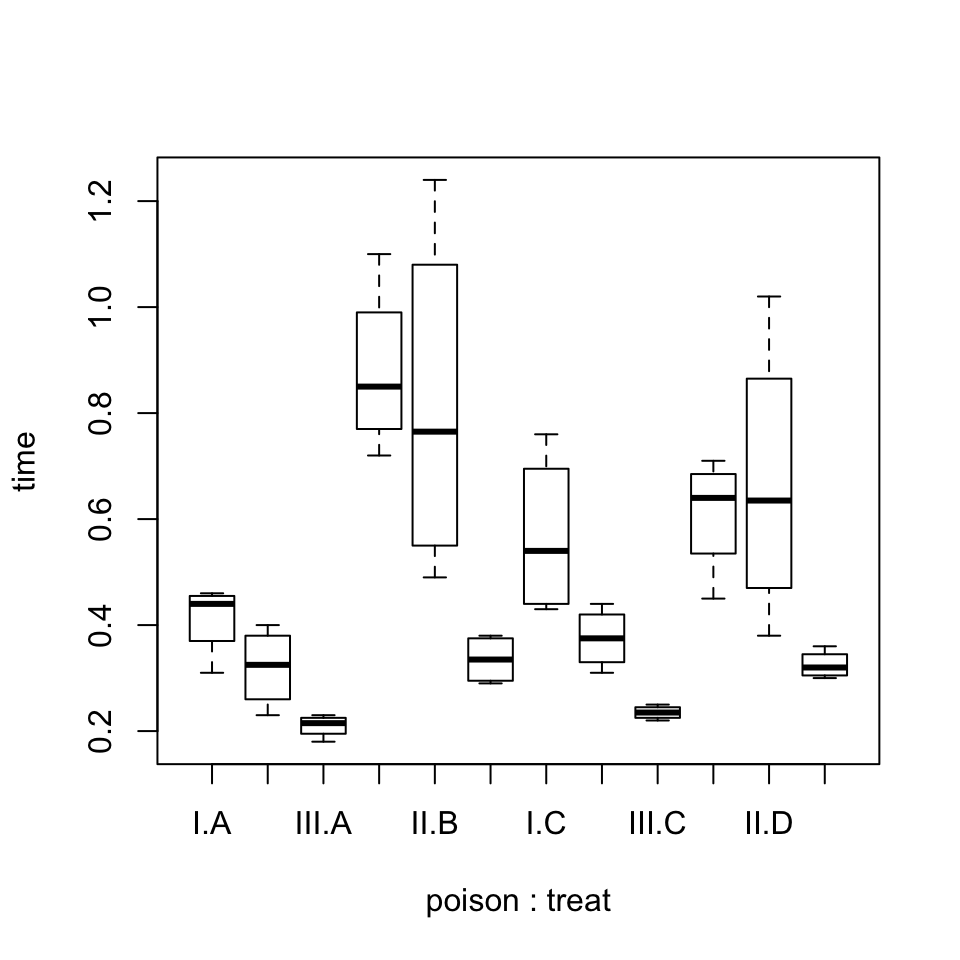

Figura 9.9: Diagrama de cajas de los tiempos de supervivencia según las combinaciones de veneno y antídoto.

El código para efectuar el ANOVA de dos vías del tiempo de supervivencia de las ratas bajo los efectos combinados de los venenos y los antídotos es el siguiente:

summary(aov(time~poison*treat, data=rats))

##              Df Sum Sq Mean Sq F value   Pr(>F)
## poison        2 1.0330  0.5165  23.222 3.33e-07
## treat         3 0.9212  0.3071  13.806 3.78e-06
## poison:treat  6 0.2501  0.0417   1.874    0.112
## Residuals    36 0.8007  0.0222

En la última columna de la tabla que obtenemos, el primer p-valor es el del contraste de la igualdad de tiempos medios de supervivencia según el veneno (poison): su valor, $3.3\times 10^{-7}$, nos permite concluir que estos tiempos medios no son todos iguales. El segundo p-valor es el del contraste de la igualdad de tiempos medios de supervivencia según el antídoto (treat): que valga $3.8\times 10^{-6}$ indica que estos tiempos medios tampoco son todos iguales. Finalmente, el tercer p-valor es el del contraste de interacción entre veneno y antídoto (poison:treat). Recordad que existe dicha interacción cuando los cambios en la variable de respuesta (en este ejemplo, el tiempo de supervivencia) originados por uno de los factores no son los mismos para diferentes niveles del otro factor: es decir, en el contexto de este experimento, si algún antídoto es más (o menos) efectivo contra algún veneno que contra otro. Como aquí este p-valor vale 0.112, no obtenemos evidencia estadísticamente significativa de dicha interacción: aceptamos que cada uno de los antídotos tiene un efecto similar sobre cada veneno (pero no todos los antídotos son igual de efectivos).

Observaréis que la tabla del ANOVA que produce R con esta fórmula no contiene la fila que permite contrastar si hay diferencia entre las medias de las poblaciones definidas por combinaciones de niveles, uno por cada factor: en este ejemplo, por las combinaciones de veneno y antídoto. Si se desea obtener esta fila, basta realizar un ANOVA de un factor que combine los dos factores del experimento.

summary(aov(time~poison:treat, data=rats))

##              Df Sum Sq Mean Sq F value   Pr(>F)
## poison:treat 11 2.2044 0.20040    9.01 1.99e-07
## Residuals    36 0.8007 0.02224

Vemos que también hay diferencias estadísticamente significativas entre las combinaciones veneno–antídoto.

En el caso del ANOVA de dos vías, es interesante dibujar el gráfico de interacción entre factores. En un gráfico de interacción del factor $F_1$ respecto del factor $F_2$ en el ANOVA de una variable numérica $X$ respecto de estos factores, se dibuja una línea quebrada para cada nivel de $F_1$. Esta línea une, mediante segmentos, los valores medios que toma la variable $X$ en nuestra muestra para cada nivel de $F_2$ en el nivel de $F_1$ correspondiente. Si no hay ninguna interacción entre estos factores, las líneas resultantes serán paralelas. Cuanto más se alejen de ser paralelas, más evidencia de interacción habrá entre estos dos factores.

Estos gráficos de interacción se dibujan en R con la instrucción interaction.plot aplicada, por este orden, a los dos factores y la variable numérica. Así, pues, para obtener el gráfico de interacción de la variable antídoto respecto de la variable veneno en el ANOVA anterior, entraríamos la siguiente instrucción:

interaction.plot(rats$treat, rats$poison, rats$time)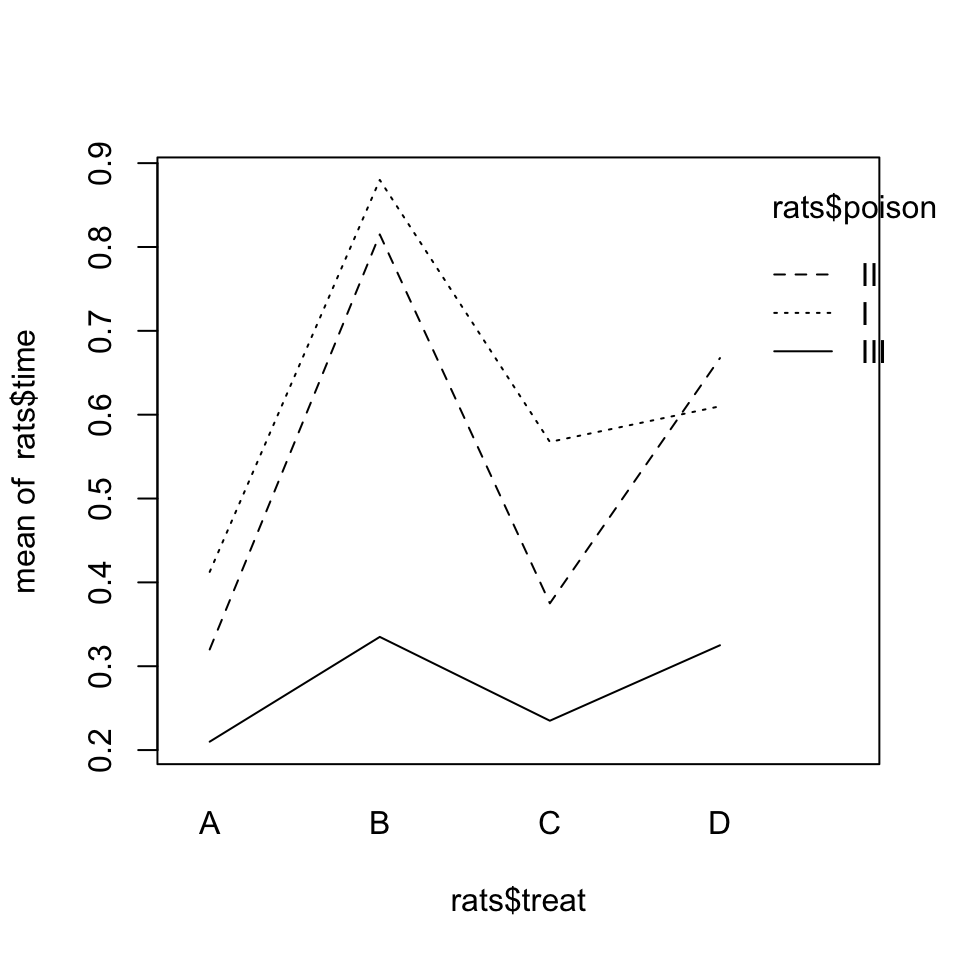

Figura 9.10: Gráfico de interacción del veneno y el antídoto.

En el gráfico resultante observamos que los tres niveles del veneno producen líneas casi paralelas, aunque se observa una ligera interacción: la pendiente de la recta correspondiente al veneno II entre los valores medios de C y D es mucho mayor que la de las rectas correspondientes a los otros dos venenos, lo que indica que en el experimento el antídoto D ha sido menos efectivo contra el veneno II que contra los otros dos. No obstante, la diferencia no ha sido estadísticamente significativa.

Este diagrama no ha quedado muy bonito, ya que las variables aparecen en él con sus nombres completos, y los factores no aparecen en la leyenda ordenados alfabéticamente. Una posibilidad para mejorarlo es cambiar las etiquetas de los ejes y la leyenda (eliminándola con legend=FALSE y añadiéndola a nuestro gusto con la función legend). Ya que estamos, dibujaremos algo más gruesas las líneas. En general, la instrucción interaction.plot admite todos los parámetros de plot más algunos de específicos que podéis conocer consultando su Ayuda.

interaction.plot(rats$treat, rats$poison, rats$time, legend=FALSE,
  xlab="Antídoto", ylab="Tiempo medio de supervivencia", lwd=c(2,2,2))
legend("topright", lty=1:3, cex=0.6, title="Venenos", legend=c("I","II","III"))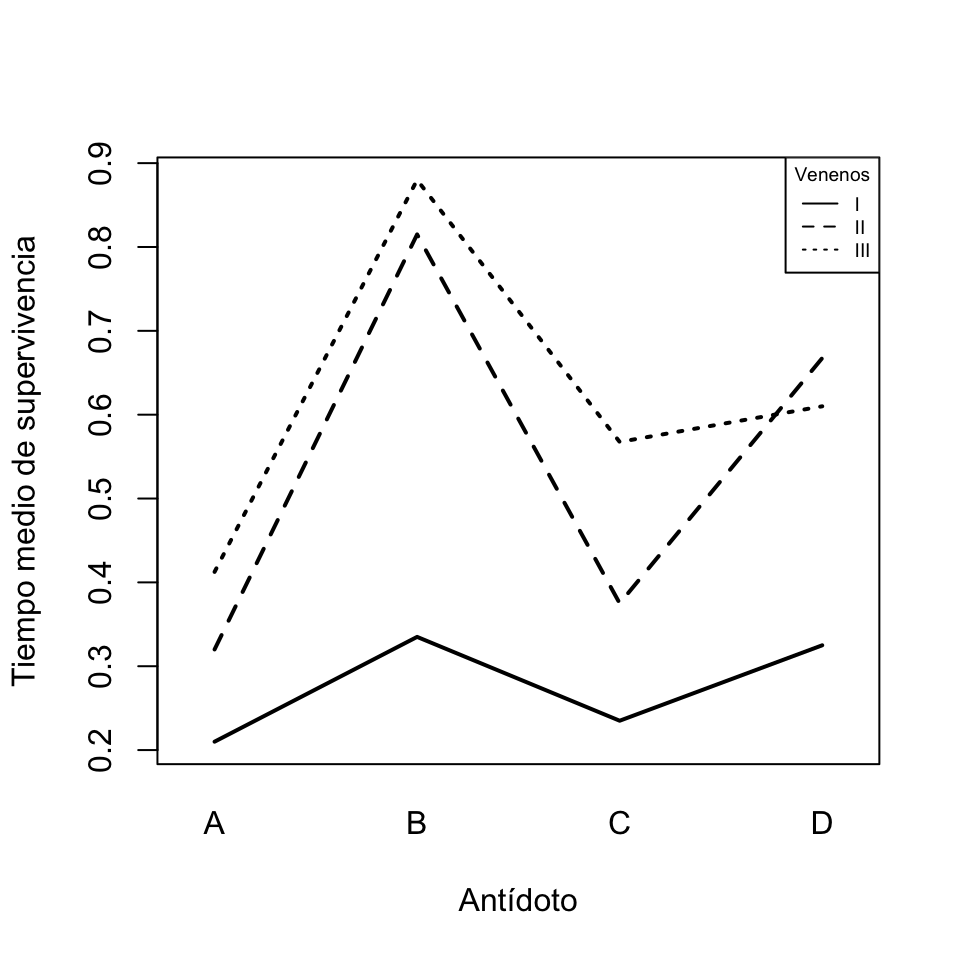

Figura 9.11: Gráfico de interacción del veneno y el antídoto.

Veamos otro ejemplo de ANOVA de dos vías.

Ejemplo 9.4 En el Ejemplo 9.2 hablábamos de un cierto experimento sobre el efecto de la vitamina C en el crecimiento de los dientes, y de la tabla de datos ToothGrowth del paquete UsingR que recoge los datos obtenidos en ese experimento. Ahora vamos a realizar un ANOVA de dos factores sobre esta tabla de datos para contrastar la influencia en dicho crecimiento de la dosis de vitamina C y del método de suministrarla, teniendo en cuenta que sus efectos pueden interaccionar. Recordad de aquel ejemplo que, si queremos llevar a cabo un ANOVA sobre esta tabla que involucre la variable dose que contiene la dosis, primero hay que convertir esta variable en un factor. Volveremos a copiar la tabla ToothGrowth en una nueva tabla ToothGrowth2 y modificaremos en esta tabla dicha variable.

ToothGrowth2=ToothGrowth 
ToothGrowth2$dose=as.factor(ToothGrowth2$dose)
str(ToothGrowth2)

## 'data.frame':	60 obs. of  3 variables:
##  $ len : num  4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
##  $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
##  $ dose: Factor w/ 3 levels "0.5","1","2": 1 1 1 1 1 1 1 1 1 1 ...

Demos ahora una ojeada a los diagramas de cajas de esta tabla, separando las longitudes de los odontoblastos por dosis, por suministro y por ambos.

boxplot(len~dose, data=ToothGrowth2)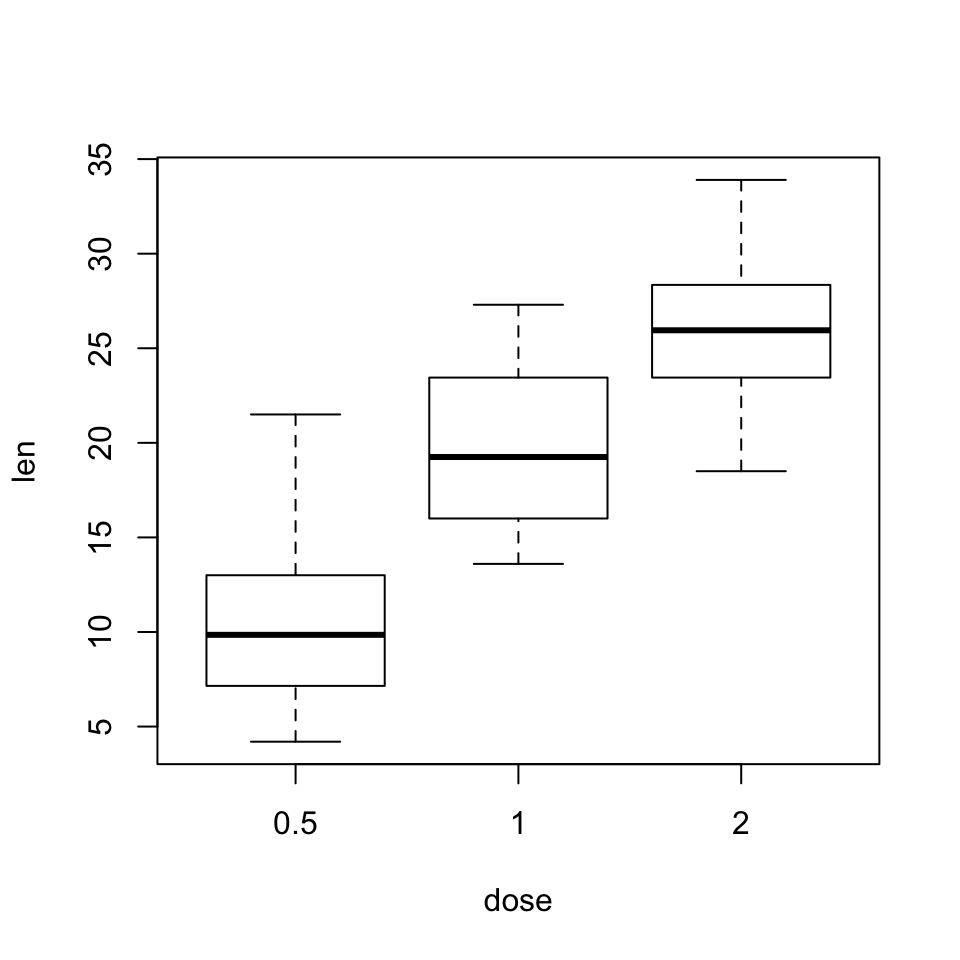

Figura 9.12: Diagrama de cajas de las longitudes de los odontoblastos según la dosis de vitamina C.

boxplot(len~supp, data=ToothGrowth2)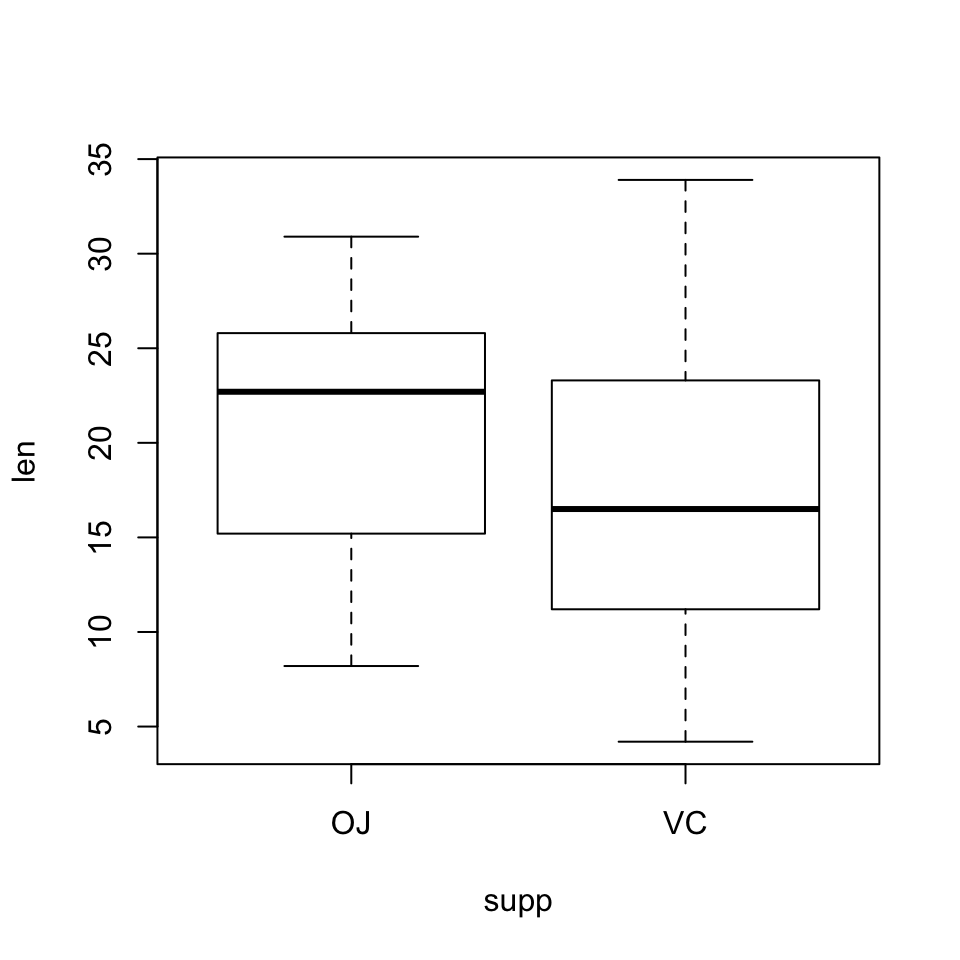

Figura 9.13: Diagrama de cajas de las longitudes de los odontoblastos según el método de suministro de vitamina C.

boxplot(len~dose:supp, data=ToothGrowth2)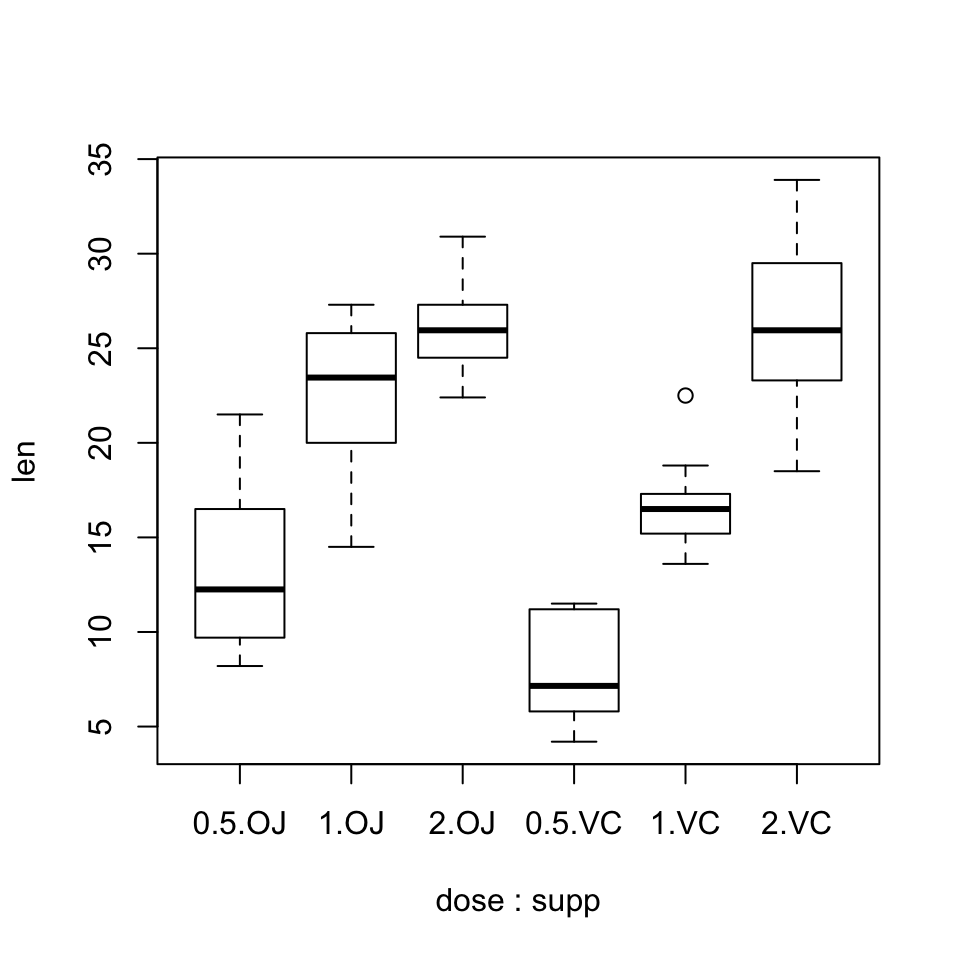

Figura 9.14: Diagrama de cajas de las longitudes de los odontoblastos según la dosis y el método de suministro.

Podemos observar diferencias tanto según la dosis como según el método de suministro. ¿Serán significativas?

summary(aov(len~supp*dose, data=ToothGrowth2))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## supp         1  205.4   205.4  15.572 0.000231
## dose         2 2426.4  1213.2  92.000  < 2e-16
## supp:dose    2  108.3    54.2   4.107 0.021860
## Residuals   54  712.1    13.2

summary(aov(len~supp:dose, data=ToothGrowth2))

##             Df Sum Sq Mean Sq F value Pr(>F)
## supp:dose    5 2740.1   548.0   41.56 <2e-16
## Residuals   54  712.1    13.2

El resultado muestra que, efectivamente, hay diferencias significativas en el crecimiento de los dientes tanto según la dosis (p-valor prácticamente 0) como según el método de suministro (p-valor $2\times 10^{-4}$) o la combinación de ambos (p-valor prácticamente 0), y también que hay evidencia estadística de interacción entre los dos factores (p-valor 0.022). El gráfico de interacción entre las dosis y el método de suministro que produce la instrucción siguiente refleja esta interacción: la línea correspondiente a la dosis de 2 mg no es paralela a las otras.

interaction.plot(ToothGrowth2$supp, ToothGrowth2$dose, ToothGrowth2$len,  legend=FALSE,
 xlab="Método de suministro", ylab="Crecimiento medio", lwd=c(2,2,2))
legend("topright",lty=1:3,cex=0.6,title="Dosis",legend=c("0.5","1","2"))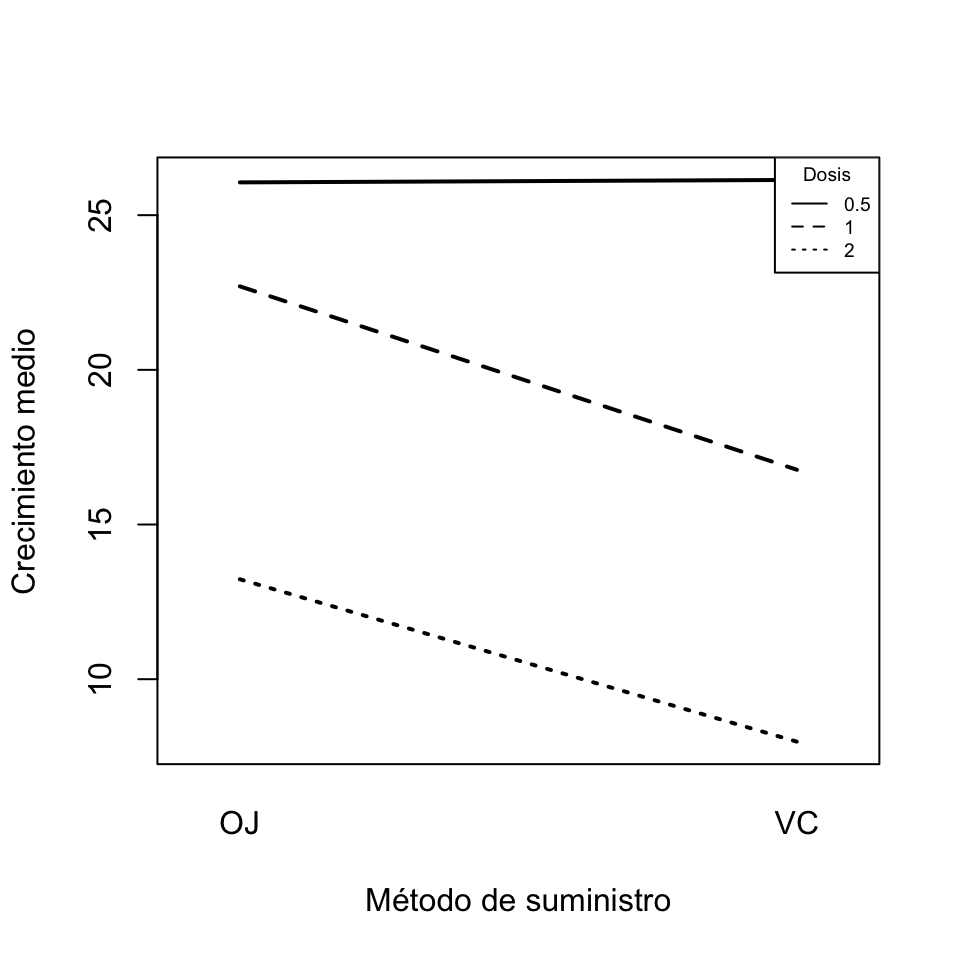

Figura 9.15: Gráfico de interacción de la dosis de vitamina C y el método de suministro.

El hecho de haber detectado interacción entre los dos factores hace que nos interese estudiar el efecto de los niveles de un factor en el otro. Esto se puede llevar a cabo mediante varios ANOVA de un factor.

En primer lugar, vamos estudiar, para cada método de suministro de vitamina C, si hay diferencias entre los crecimientos medios de los odontoblastos según la dosis cuando la vitamina C se suministra mediante ese método. Para ello vamos a realizar dos ANOVA de un factor, la dosis, sobre dos data frames extraídos de ToothGrowth2, uno con las filas donde supp toma el valor OJ y otro con las filas donde supp toma el valor VC. Vamos extraer estas subtablas de datos usando la instrucción subset. Recordad que la construcción

subset(df, condición)

define un data frame con las filas del data frame df que cumplen la condición.

TG.OJ=subset(ToothGrowth2, supp=="OJ")
TG.VC=subset(ToothGrowth2, supp=="VC")

Ahora realizamos los dos ANOVA:

summary(aov(len~dose, data=TG.OJ))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## dose         2  885.3   442.6   31.44 8.89e-08
## Residuals   27  380.1    14.1

summary(aov(len~dose, data=TG.VC))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## dose         2   1650   824.7   67.07 3.36e-11
## Residuals   27    332    12.3

En ambos casos el p-valor es muy pequeño, lo que indica que para cada tipo de suministro de vitamina C, el crecimiento medio de los dientes varía con la dosis.

En este tipo de análisis, hay que tener en cuenta que si realizamos $N$ contrastes independientes en un mismo experimento, cada uno de ellos con un nivel de significación $\alpha$, la probabilidad de rechazar en alguno de ellos la hipótesis nula si en todos es verdadera es \[ 1-(1-\alpha)^N\approx N\alpha. \] Por lo tanto, si queremos garantizar un nivel de significación global $\alpha$, hay que realizar cada contraste con nivel de significación $\alpha/N$. (Para ser exactos, si llamamos $\alpha_c$ al nivel de significación de cada contraste necesario para obtener un nivel de significación global $\alpha$, se cumple que $1-(1-\alpha_c)^N=\alpha$, de donde podemos despejar $\alpha_c$ y obtenemos $\alpha_c=1-\sqrt[N]{1-\alpha}$, que es un poco mayor que $\alpha/N$. Por ejemplo, para $\alpha=0.05$ y $N=20$ tenemos que $\alpha_c=0.0341$ mientras que $\alpha/N=0.025$.) En este ejemplo concreto, si hubiéramos deseado un nivel de significación global 0.05, deberíamos haber realizado cada uno de los ANOVA con un nivel de significación 0.025, lo que no afecta a las conclusiones, ya que los p-valores han sido realmente muy pequeños.

También podemos estudiar, para cada dosis, si hay diferencias entre las medias de crecimiento según el método de suministro. Como solo hay dos métodos de suministro, para cada dosis tanto da realizar un ANOVA o un simple test t suponiendo que las varianzas son iguales (ya que es una de las condiciones para poder realizar el ANOVA).

TG.0.5=subset(ToothGrowth2, dose==0.5)
summary(aov(len~supp, data=TG.0.5))

##             Df Sum Sq Mean Sq F value Pr(>F)
## supp         1  137.8  137.81   10.05 0.0053
## Residuals   18  246.9   13.72

TG.1=subset(ToothGrowth2, dose==1)
summary(aov(len~supp, data=TG.1))

##             Df Sum Sq Mean Sq F value   Pr(>F)
## supp         1  175.8  175.82   16.26 0.000781
## Residuals   18  194.6   10.81

TG.2=subset(ToothGrowth2, dose==2)
summary(aov(len~supp, data=TG.2))

##             Df Sum Sq Mean Sq F value Pr(>F)
## supp         1   0.03   0.032   0.002  0.964
## Residuals   18 270.61  15.034

En este caso, para garantizar un nivel de significación global de 0.05, hay que realizar cada contraste con un nivel de significación de 0.05/3=0.017. Obtenemos evidencia de que hay diferencia en el crecimiento medio de los odontoblastos según el tipo de suministro solo para las dosis de 0.5 y 1 mg, que es donde hemos obtenido p-valores inferiores al nivel de significación.

Si la variable dose hubiera tenido, pongamos, 20 niveles en vez de 3, definir una subtabla para cada nivel y efectuar el ANOVA correspondiente hubiera sido muy largo. Para automatizar cálculos como estos, lo mejor es definir una función que calcule el p-valor del ANOVA de una variable respecto de un factor sobre la subtabla definida por un nivel variable $x$ de un segundo factor, y luego aplicar esta función al vector de los niveles de este segundo factor. En este ejemplo concreto usaríamos el código siguiente.

Anova_dosis=function(x){
  summary(aov(len~supp, 
       data=subset(ToothGrowth2, dose==x)))[[1]]$"Pr(>F)"[1]
   }
round(sapply(levels(ToothGrowth2$dose), FUN=Anova_dosis),4)

##    0.5      1      2 
## 0.0053 0.0008 0.9637

9.5 Condiciones del ANOVA

Los resultados de un ANOVA nos permiten extraer conclusiones solo si las poblaciones a las que se aplica cumplen una serie de condiciones; las dos básicas son la normalidad y la igualdad de varianzas. La condición de normalidad requiere que cada nivel de cada factor defina una distribución normal, es decir, que cada muestra aleatoria simple de un tratamiento provenga de una población normal. La condición de igualdad de varianzas requiere que todas estas distribuciones tengan la misma varianza.

En la Lección 6 ya estudiamos algunos tests específicos de normalidad: los tests de Kolmogorov-Smirnov-Lillliefors, de Anderson-Darling, de Shapiro-Wilk y de D’Agostino-Pearson. Cada uno tiene sus ventajas y sus inconvenientes: el primero es muy popular, por ser una variante del test de Kolmogorov-Smirnov; el segundo, detecta mejor las discrepancias en los extremos; el test de Shapiro-Wilk es más potente para muestras grandes y menos sensible a repeticiones que los dos anteriores; y el test de D’Agostino-Pearson permite repeticiones de datos, pero no se puede usar con muestras de tamaño inferior a 20.

Veamos algunos ejemplos de aplicación de tests de normalidad en el contexto de un ANOVA.

Ejemplo 9.5 Queremos contrastar si los tiempos de coagulación bajo cuatro dietas dados en la Tabla 9.1 provienen de distribuciones normales. Como hay algunas repeticiones de valores en las columnas de la tabla y no llegan a los 20 valores cada una, usaremos el test de Shapiro-Wilk que, recordemos, está implementado en la función shapiro.test. Teníamos los datos guardados en un data frame llamado coagulacion.

str(coagulacion)

## 'data.frame':	24 obs. of  2 variables:
##  $ coag: num  62 63 68 56 60 67 66 62 63 71 ...
##  $ diet: Factor w/ 4 levels "A","B","C","D": 1 2 3 4 1 2 3 4 1 2 ...

Apliquemos la función shapiro.test a los tiempos de coagulación para cada dieta:

coagA=coagulacion[coagulacion$diet=="A",]$coag
shapiro.test(coagA)$p.value

## [1] 0.1130298

coagB=coagulacion[coagulacion$diet=="B",]$coag
shapiro.test(coagB)$p.value

## [1] 0.5227052

coagC=coagulacion[coagulacion$diet=="C",]$coag
shapiro.test(coagC)$p.value

## [1] 0.2375366

coagD=coagulacion[coagulacion$diet=="D",]$coag
shapiro.test(coagD)$p.value

## [1] 0.5227052

Los cuatro p-valores que obtenemos son grandes, mayores que 0.05, lo que quiere decir que en ninguno de los cuatro tests podemos rechazar la hipótesis nula: no hay evidencia de que los tiempos de coagulación bajo alguna de las cuatro dietas no sigan leyes normales, por lo que aceptamos que sí las siguen. Recordad además que, como hemos efectuado cuatro contrastes, para garantizar un nivel de significación global de 0.05 hemos de realizar cada uno con un nivel de significación de 0.05/4=0.0125: es decir, que con p-valores por encima de este nivel de significación no podríamos rechazar ninguna hipótesis nula.

¿Cómo podríamos haber automatizado el cálculo de estos p-valores, para no tener que definir “a mano” cada vector de tiempos de coagulación? Con el código siguiente, donde definimos una función Test.SW que calcula el p-valor del test de Shapiro-Wilk y la aplicamos con un aggregate a los tiempos de coagulación del data frame coagulacion separados según la dieta. De esta manera obtenemos un data frame cuya columna coag contiene, para cada nivel de diet, el p-valor del test de Shapiro-Wilk para los tiempos de coagulación de la dieta correspondiente.

Test.SW=function(x){shapiro.test(x)$p.value}
aggregate(coag~diet, data=coagulacion,FUN=Test.SW)

##   diet      coag
## 1    A 0.1130298
## 2    B 0.5227052
## 3    C 0.2375366
## 4    D 0.5227052

Ejemplo 9.6 Vamos a contrastar si en el ANOVA de dos vías del ejemplo de venenos y antídotos explicado en la Sección 9.4 se satisface que cada combinación de veneno y antídoto define una población normal. Para ello, en principio deberíamos repetir 12 veces, una para cada combinación de veneno y antídoto, un par de instrucciones como las siguientes:

time.I.A=rats[rats$poison=="I" & rats$treat=="A", ]$time
shapiro.test(time.I.A)$p.value

## [1] 0.07414486

Para evitarnos trabajo, vamos a usar la estrategia explicada al final del ejemplo anterior: aplicaremos la función Test.SW que hemos definido en dicho ejemplo a la variable numérica time del data frame rats separándola por las combinaciones de veneno y antídoto.

aggregate(time~poison:treat, data=rats, FUN=Test.SW)

##    poison treat       time
## 1       I     A 0.07414486
## 2      II     A 0.84756406
## 3     III     A 0.57735490
## 4       I     B 0.69983383
## 5      II     B 0.70083721
## 6     III     B 0.17057001
## 7       I     C 0.40503490
## 8      II     C 0.92091109
## 9     III     C 0.97187706
## 10      I     D 0.42739119
## 11     II     D 0.90650963
## 12    III     D 0.68893644

Todos los p-valores que obtenemos son mayores que 0.05 (y de hecho, para garantizar un nivel de significación global de 0.05, deberíamos realizar cada test de Shapiro-Wilk con un nivel de significación 0.05/12=0.0042), por lo que no podemos rechazar que todas las combinaciones de veneno y antídoto definan unos tiempos de supervivencia que sigan leyes normales.

Pasemos al contraste de igualdad de varianzas (su nombre técnico es contraste de homocedasticidad), en el que usaremos el llamado test de Bartlett. Supongamos, para fijar ideas, que tenemos $k$ vectores numéricos \[ x_i=(x_{i1},x_{i2},\ldots,x_{in_i}),\quad i=1,\ldots, k, \] cada uno de los cuales es una muestra aleatoria simple de una variable aleatoria normal (se supone que lo hemos contrastado previamente) de varianza $\sigma_i^2$. El contraste que queremos realizar es: \[ \left\{ \begin{array}{ll} H_0: & \sigma_1^2 = \cdots = \sigma_k^2\\ H_1: & \mbox{$\sigma_i^2 \neq \sigma_j^2$ para algunos $i, j$} \end{array} \right. \] Para realizar este contraste, se usa el estadístico de Bartlett: \[ K^2 = \frac{ (N-k)\ln (\widetilde{s}_p^2)-\sum_{i=1}^k (n_i -1)\ln (\widetilde{s}_i^2)}{ 1+\frac{1}{3(k-1)}\left(\sum_{i=1}^k \left(\frac{1}{n_i -1}\right)-\frac{1}{N-k}\right)}, \] donde \[ N=\sum_{i=1}^k n_i,\quad \widetilde{s}_p^2 = \frac{\sum_{i=1}^k (n_i -1) \widetilde{s}_i^2}{N-k},\quad \widetilde{s}_i^2 =\frac{\sum_{j=1}^{n_i} (x_{ij}-\overline{x}_{i})^2}{n_i -1},\ i=1,\ldots,k. \] Si las variables poblacionales son normales, este estadístico sigue aproximadamente una distribución $\chi^2_{k-1}$, y si la hipótesis nula es verdadera, su valor esperado es pequeño (puesto que, en este caso, los valores esperados de $\widetilde{s}_1^2,\ldots, \widetilde{s}_k^2$ y $\widetilde{s}_p^2$ son todos iguales). El p-valor del contraste es entonces $P(\chi^2_{k-1} > K^2)$.

R tiene una función que efectúa este test, bartlett.test, y puede aplicarse a una fórmula. Por ejemplo, para contrastar si las tres dietas en el ejemplo de la coagulación de la Sección 9.2 definen poblaciones con la misma varianza, podemos entrar

bartlett.test(coag~diet, data=coagulacion)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  coag by diet
## Bartlett's K-squared = 1.946, df = 3, p-value = 0.5837

Como el p-valor es alto, concluimos que las varianzas de los tiempos de coagulación bajo las tres dietas son la misma.

En los ANOVA de dos vías, se ha de comprobar la igualdad de varianzas para las combinaciones de niveles de los dos factores. En la fórmula que se entra al bartlett.test esta combinación no se puede especificar con :, como hemos hecho hasta ahora, sino con interaction. Por ejemplo, para contrastar por medio del test de Bartlett si las 12 combinaciones veneno-dieta en el ejemplo de venenos y antídotos explicado en la Sección 9.4 tienen la misma varianza, tenemos que entrar:

bartlett.test(time~interaction(poison,treat), data=rats)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  time by interaction(poison, treat)
## Bartlett's K-squared = 45.137, df = 11, p-value = 4.59e-06

Obtenemos un p-valor de $4.6\times 10^{-6}$, por lo tanto, hemos de rechazar la igualdad de varianzas: las conclusiones de ese ANOVA de dos vías no tienen en principio ninguna validez, puesto que hay evidencia de que no se cumple una de las condiciones para realizarlo.

Otros tests de igualdad de varianzas son el de Fligner-Killeen, implementado en la función fligner.test (y que tiene la misma particularidad que bartlett.test a la hora de especificar combinaciones de factores) y el test de Levene, implementado en la función leveneTest del paquete car (donde las combinaciones de factores sí que se pueden especificar con :). En cada caso, el test produce un p-valor con el significado usual. El test de Levene es muy popular, porque no requiere que las poblaciones sean normales, pero en el contexto del ANOVA esta propiedad no tiene ningún interés; además, cuando las poblaciones son normales, el test de Bartlett es más potente que el de Levene.

9.6 Comparaciones de pares de medias

Si en un ANOVA hemos rechazado la hipótesis nula de la igualdad de todas las medias, es posible que nos interese determinar qué medias son diferentes. Para ello podemos llevar a cabo algunos tests. En esta sección explicamos las instrucciones de R para tres de ellos.

9.6.1 Tests t por parejas

En los tests t por parejas, realizamos un contraste de medias para cada par de niveles del factor, teniendo en cuenta que, para garantizar un nivel de significación global $\alpha$, se ha de ajustar el nivel de significación de cada test. Hay diversos métodos para llevar a cabo este ajuste: los más populares son el método de Bonferroni, el de Holm, que es más potente, y el de Hochberg, que, para contrastes ANOVA que no sean de bloques, aún tiene mayor potencia.

La función que efectúa tests t por parejas es pairwise.t.test. Su sintaxis es

pairwise.t.test(var.numérica, factor, paired=..., p.adjust.method=...)

El valor de p.adjust.method es el método de ajuste de p-valores que deseamos usar, y se ha de entrar entrecomillado. El valor por defecto es el de Holm, indicado por "holm" aunque no es necesario especificarlo. Para usar el de Bonferroni, hay que especificar p.adjust.method="bonferroni", y para usar el de Hochberg, p.adjust.method="hochberg". Si no queréis ningún ajuste, tenéis que usar p.adjust.method="none". Para conocer qué otros métodos se pueden usar, sus ventajas e inconvenientes, consultad la Ayuda de p.adjust.

Por lo que refiere al parámetro paired, sirve para indicar si las muestras son independientes (igualándolo a FALSE, que es su valor por defecto) o emparejadas (igualándolo a TRUE); cuando el ANOVA es de bloques, las muestras son emparejadas, y por lo tanto se ha de especificar paired=TRUE.

Veamos algunos ejemplos de su uso.

Ejemplo 9.7 Para determinar cuáles de las tres dietas en el ejemplo de la coagulación de la Sección 9.2 dan tiempos medios de coagulación diferentes, vamos a efectuar un test t por parejas de Bonferroni.

pairwise.t.test(coagulacion$coag,coagulacion$diet,p.adjust.method="bonferroni")

## 
## 	Pairwise comparisons using t tests with pooled SD 
## 
## data:  coagulacion$coag and coagulacion$diet 
## 
##   A       B       C      
## B 0.00934 -       -      
## C 0.00031 0.95266 -      
## D 1.00000 0.00934 0.00031
## 
## P value adjustment method: bonferroni

Los p-valores del resultado ya han sido ajustados, y por lo tanto se han de comparar directamente con el nivel de significación $\alpha$ global. Por ejemplo, con un nivel de significación $\alpha=0.05$, obtenemos evidencia de que los tiempos medios para los pares de dietas (A,B), (A,C), (B,D), (C,D) son diferentes, y en cambio no hay evidencia de que los tiempos medios para los pares (A,D) y (B,C) sean diferentes.

Ejemplo 9.8 Para determinar qué actividades de evaluación de las consideradas en el Ejemplo 9.3 dan notas medias diferentes, vamos a realizar un test t por parejas de Holm. Primero vamos a comprobar que dichas actividades de evaluación definen poblaciones normales, condición necesaria para que los tests t por parejas tengan sentido.

Contrastaremos la normalidad de las notas para cada actividad de evaluación con el test de Shapiro-Wilk, y para no trabajar más de la cuenta, usaremos la técnica explicada en el Ejemplo 9.5.

Test.SW=function(x){round(shapiro.test(x)$p.value,4)}
aggregate(notas~acts, data=notas.bloques, FUN=Test.SW)

##        acts  notas
## 1      Casa 0.1384
## 2 Control 1 0.7054
## 3 Control 2 0.5515
## 4  Talleres 0.7612
## 5     Tests 0.5984

Todos los p-valores son altos, los que nos permite aceptar que las notas de cada actividad provienen de una distribución normal.

Así pues, podemos realizar el test t de Holm. En este caso tenemos que usar paired=TRUE, puesto que se trata de un ANOVA de bloques.

pairwise.t.test(notas.bloques$notas, notas.bloques$acts, paired=TRUE)

## 
## 	Pairwise comparisons using paired t tests 
## 
## data:  notas.bloques$notas and notas.bloques$acts 
## 
##           Casa   Control 1 Control 2 Talleres
## Control 1 0.4562 -         -         -       
## Control 2 0.0271 0.4562    -         -       
## Talleres  0.0012 0.0038    0.0012    -       
## Tests     0.4562 0.1640    0.0271    0.0038  
## 
## P value adjustment method: holm

Los p-valores superiores a 0.05 son los de los pares de actividades “Ejercicios de casa”-“Control 1”, “Control 1”-“Control 2”, “Ejercicios de casa”-“Tests” y “Control 1”-“Tests”. Por lo tanto, a un nivel de significación global de 0.05, no podemos rechazar que las notas medias de estos pares de actividades sean iguales, mientras que en los otros tenemos evidencia de que son diferentes.

9.6.2 Test de Duncan

Otro método popular para comparar los pares de medias es el test de Duncan. Con R se puede efectuar con la instrucción duncan.test del paquete agricolae. Su sintaxis básica es

duncan.test(aov, "factor", alpha=..., group=...)$sufijo

donde

aov es el resultado de la función aov (sin summary) con la que hemos calculado el ANOVA de partida.
El factor es el factor del ANOVA, y se ha de entrar entrecomillado y con el mismo nombre que se ha usado en la fórmula del aov.
El parámetro alpha sirve para entrar el nivel de significación $\alpha$: por defecto vale 0.05.
group puede valer TRUE o FALSE, y hace que el resultado se presente de forma diferente.
El sufijo tiene que ser groups si group=TRUE y comparison si group=FALSE.

Este test no se puede usar en el ANOVA de bloques, puesto que supone que las muestras de los tratamientos son independientes.

Ejemplo 9.9 Vamos a usar el test de Duncan para determinar qué pares de dietas en el ejemplo de la coagulación de la Sección 9.2 tienen tiempos medios de coagulación diferentes, con un nivel de significación global del 5%. En primer lugar, guardamos en un objeto el ANOVA calculado con aov, y luego aplicamos la función duncan.test a este objeto. Aquí lo haremos dos veces, una para cada posible valor del parámetro group, para poder comparar y comentar cómo se muestran los resultados. No entraremos el parámetro alpha, puesto que usamos su valor por defecto.

library(agricolae)
anova.coag=aov(coag~diet, data=coagulacion)
duncan.test(anova.coag, "diet", group=FALSE)$comparison

##       difference pvalue signif.       LCL        UCL
## A - B         -5 0.0016      ** -7.849968 -2.1500315
## A - C         -7 0.0001     *** -9.991509 -4.0084906
## A - D          0 1.0000         -2.849968  2.8499685
## B - C         -2 0.1588         -4.849968  0.8499685
## B - D          5 0.0021      **  2.008491  7.9915094
## C - D          7 0.0001     ***  3.918538 10.0814618

duncan.test(anova.coag, "diet", group=TRUE)$groups

##   coag groups
## C   68      a
## B   66      a
## A   61      b
## D   61      b

Observemos los resultados:

Con group=FALSE y sufijo comparison, obtenemos una tabla donde, para cada pareja de niveles del factor, se da, entre otros datos, un p-valor (la columna p value). Estos p-valores tienen el significado usual. En este ejemplo, de los p-valores se desprende que no podemos rechazar que las medias para los pares A-D y B-C sean iguales (los p-valores son grandes), mientras que, en cambio, hay evidencia significativa de que el resto de los pares de dietas tienen medias diferentes (los p-valores son pequeños). Las dos últimas columnas de la tabla definen intervalos de confianza (del nivel de confianza correspondiente al nivel de significación que hayamos entrado con alpha) para las diferencias de la medias en el orden especificado en la primera columna.
Con group=TRUE y sufijo groups, obtenemos una tabla donde se agrupan los niveles según la igualdad de medias. En este caso, asigna las dietas B y C al grupo a y las dietas A y D al grupo b: dietas en el mismo grupo hemos de aceptar que tienen medias iguales, dietas en grupos diferentes podemos concluir que tienen medias diferentes.

9.6.3 Método de Tukey

El método HSD de Tukey (las siglas HSD refieren a Honestly Significant Difference) es el método más preciso de comparación de parejas de medias para contrastes ANOVA de un factor en los que cada nivel tenga el mismo número de observaciones. Es un test similar al test t, pero usa otro estadístico con una distribución diferente, no vamos a entrar en detalles. Con R se efectúa aplicando la función TukeyHSD al resultado de aov.

Para explicar qué información obtenemos con esta función, vamos a aplicar el método de Tukey al ANOVA del ejemplo sobre tiempos de coagulación de la Sección 9.2.

anova.coag=aov(coag~diet, data=coagulacion)
TukeyHSD(anova.coag)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = coag ~ diet, data = coagulacion)
## 
## $diet
##              diff        lwr       upr     p adj
## B-A  5.000000e+00   1.175925  8.824075 0.0077978
## C-A  7.000000e+00   3.175925 10.824075 0.0002804
## D-A  1.421085e-14  -3.824075  3.824075 1.0000000
## C-B  2.000000e+00  -1.824075  5.824075 0.4766005
## D-B -5.000000e+00  -8.824075 -1.175925 0.0077978
## D-C -7.000000e+00 -10.824075 -3.175925 0.0002804

De esta manera, para cada par de niveles obtenemos, entre otra información:

La diferencia de sus medias muestrales, en la columna diff.
Los extremos inferior y superior de un intervalo de confianza del 95% para la diferencia de medias poblacionales en el orden dado en la primera columna, en las columnas lwr y upr, respectivamente. El nivel de confianza se puede ajustar con el parámetro conf.level dentro de la función.
El p-valor del contraste de igualdad de medias correspondiente, en la columna p adj.

En nuestro ejemplo, los intervalos de confianza para las diferencias de medias de los pares A-B, A-C, B-D y C-D no contienen el valor 0 (y los p-valores correspondientes son pequeños), lo que indica que podemos rechazar que estas medias sean iguales. En cambio, los intervalos de confianza para las diferencias de medias de los pares A-D y B-C sí que contienen el 0 (y los p-valores correspondientes son grandes), lo que indica que podemos aceptar que estas medias son iguales. En este caso obtenemos, por lo tanto, la misma conclusión que con el test t de Bonferroni.

9.7 Métodos no paramétricos

Cuando no se satisfacen las condiciones para poder aplicar un ANOVA, hay que usar algún otro método que no las requiera.

En el caso del ANOVA de una vía, el método alternativo no paramétrico recomendado es el test de Kruskal-Wallis, que generaliza a más de dos muestras el test de Mann-Whitney-Wilcoxon para dos muestras independientes en el mismo sentido que el ANOVA generaliza el test t; en particular, un test de Kruskal-Wallis para un factor con solo dos niveles es equivalente al test de Mann-Whitney. Con R, el test de Kruskal-Wallis se lleva a cabo con la función kruskal.test, con la misma sintaxis que aov. Naturalmente, el resultado no es una tabla ANOVA, porque no estamos haciendo un ANOVA, pero da un p-valor que indica si podemos rechazar o no que las medias por niveles sean todas iguales.

Por ejemplo, para efectuar el test de Kruskal-Wallis sobre la tabla de tiempos de coagulación del principio de la Sección 9.2, entraríamos:

kruskal.test(coag~diet, data=coagulacion)

## 
## 	Kruskal-Wallis rank sum test
## 
## data:  coag by diet
## Kruskal-Wallis chi-squared = 17.027, df = 3, p-value = 0.0006977

El p-valor nos da evidencia estadísticamente significativa de que no todos los tiempos medios de coagulación son iguales. Para determinar entonces qué pares de dietas dan tiempos medios diferentes, podríamos llevar a cabo un contraste por parejas. En principio no podremos usar un test t por parejas, ya que este presupone las condiciones de normalidad de las poblaciones e igualdad de las varianzas que son necesarias para el ANOVA y que suponemos que no se satisfacen (o habríamos hecho un ANOVA en vez de un test de Kruskal-Wallis). En su lugar, podemos usar un test de Mann-Whitney por parejas, con la función pairwise.wilcox.test. Su sintaxis es la misma que la de pairwise.t.test. En particular, hay que indicar con p.adjust.method el método de ajuste de los p-valores, siendo de nuevo "holm" su valor por defecto. Así, por ejemplo, para realizar un test de Mann-Whitney por parejas con ajuste de Bonferroni, entraríamos:

pairwise.wilcox.test(coagulacion$coag,coagulacion$diet,p.adjust.method="bonferroni")

## 
## 	Pairwise comparisons using Wilcoxon rank sum test 
## 
## data:  coagulacion$coag and coagulacion$diet 
## 
##   A     B     C    
## B 0.046 -     -    
## C 0.028 0.630 -    
## D 1.000 0.076 0.029
## 
## P value adjustment method: bonferroni

Con un nivel de significación de 0.05, obtenemos evidencia de que los pares de dietas (A,B), (A,C) y (C,D) dan tiempos medios de coagulación diferentes, y no podemos rechazar que los otros pares de dietas den el mismo tiempo de coagulación. El resultado ha sido ligeramente diferente del test t por parejas, donde también obteníamos evidencia de diferencia de medias entre las dietas B y D. Recordad que, en general, los métodos no paramétricos tienen potencia menor y por lo tanto les cuesta más detectar diferencias.

Por lo que refiere al ANOVA de bloques completos aleatorios, el método no paramétrico alternativo más popular es el test de Friedman, que generaliza a más de dos muestras el test de Wilcoxon para muestras emparejadas. Está implementado en la función friedman.test, cuya sintaxis es de nuevo la misma que la de aov excepto que la suma de los tratamientos y los bloques no se indica en la fórmula con un signo de suma sino con una barra vertical.

Por ejemplo, para efectuar el test de Friedman sobre la tabla de datos de notas en actividades de evaluación del Ejemplo 9.3, entraríamos:

friedman.test(notas~acts|bloques, data=notas.bloques)

## 
## 	Friedman rank sum test
## 
## data:  notas and acts and bloques
## Friedman chi-squared = 30.047, df = 4, p-value = 4.787e-06

El p-valor nos indica que hay evidencia estadísticamente significativa de que algunas notas medias fueron diferentes. Para determinar cuáles, podemos llevar a cabo un test de Wilcoxon por parejas, usando la función pairwise.wilcox.test con paired=TRUE. Por ejemplo, usando de nuevo el ajuste de Bonferroni:

pairwise.wilcox.test(notas.bloques$notas, notas.bloques$acts, 
   paired=TRUE, p.adjust.method="bonferroni")

## 
## 	Pairwise comparisons using Wilcoxon signed rank test 
## 
## data:  notas.bloques$notas and notas.bloques$acts 
## 
##           Casa   Control 1 Control 2 Talleres
## Control 1 1.0000 -         -         -       
## Control 2 0.0823 1.0000    -         -       
## Talleres  0.0133 0.0285    0.0031    -       
## Tests     1.0000 0.5693    0.1816    0.0132  
## 
## P value adjustment method: bonferroni

Encontramos evidencia de que las notas medias de los Talleres fueron diferentes de las del resto de actividades, y no podemos rechazar que las notas medias de las otras actividades fueran todas iguales.

Finalmente, en el caso de experimentos con dos o más factores, no hay una solución simple cuando no se satisfacen las condiciones necesarias para poder hacer un ANOVA. Una posible salida es usar un método adecuado de bootstrap. Sin entrar en detalles, una buena opción en un experimento de dos factores es usar la función pbad2way del paquete WRS2. Su sintaxis básica es

pbad2way(fórmula, est="median", nboot=...)

En el parámetro nboot se ha de entrar el número de muestras que se han de tomar; tened en cuenta que cuántas más toméis, mas tardará la ejecución. El parámetro est indica qué parámetro se quiere comparar, la media no está entre los valores disponibles así que aquí usaremos la mediana. Consultad la Ayuda de la función (y las referencias que se citan) para saber qué otros estadísticos podéis usar.

Por ejemplo, para llevar a cabo por medio de un bootstrap el contraste del Ejemplo 9.4 sobre el efecto de la vitamina C en el crecimiento de los dientes (y recordando que la tabla ToothGrowth2 contiene los datos con los tratamientos codificados como factores) podríamos entrar:

library(WRS2)
set.seed(42) #Fijamos la semilla de aleatoriedad, para que sea reproducible
pbad2way(len~supp*dose, data=ToothGrowth2, est="median", nboot=500)

## Call:
## pbad2way(formula = len ~ supp * dose, data = ToothGrowth2, est = "median", 
##     nboot = 500)
## 
##           p.value
## supp        0.002
## dose        0.000
## supp:dose   0.034

Grosso modo, los p-valores obtenidos tienen el significado usual en un bootstrap: la fracción de muestras en las que obtenemos un valor de un cierto estadístico tan o más extremo que el de la muestra global. Un p-valor pequeño nos da evidencia de que podemos rechazar la hipótesis nula. Los p-valores de las filas con los nombres de los factores son los de los contrastes de los mismos y el p-valor de la última fila es el del contraste de interacción. Por lo tanto, con este contraste concluimos que hay evidencia de que tanto la dosis de vitamina C como el método de suministrarla influyen en el crecimiento de los odontoblastos (en concreto, en su mediana) y que hay interacción entre ambos factores.

Como en el ANOVA, el contraste de la combinación de factores se ha de efectuar aparte: en este caso (ya que no podemos llevar a cabo un ANOVA, o no nos estaríamos complicando tanto la vida) una buena opción es usar un test de Kruskal-Wallis tomando como factor la combinación de factores (entrada en la fórmula por medio de interaction).

kruskal.test(len~interaction(supp,dose),data=ToothGrowth2)

## 
## 	Kruskal-Wallis rank sum test
## 
## data:  len by interaction(supp, dose)
## Kruskal-Wallis chi-squared = 45.806, df = 5, p-value = 9.948e-09

Concluimos que también hay evidencia de que la combinación de la dosis de vitamina C y el método de suministrarla influye en el crecimiento de los odontoblastos.

Para terminar, una advertencia sobre pbad2way: a veces da un error numérico, como en la siguiente ejecución en el otro ejemplo de experimento de 2 vías de la Sección 9.4:

pbad2way(time~poison*treat, data=rats, est="median", nboot=500)

## Error in solve.default(cov, ...): system is computationally singular: reciprocal condition number = 5.31267e-19

En este caso, el inventor del método recomienda emplear el parámetro pro.dis=TRUE, que modifica el método de cálculo de los estadísticos que se usan en el bootstrap y evita el error.

set.seed(42)
pbad2way(time~poison*treat, data=rats, est="median",nboot=500,pro.dis=TRUE)

## Call:
## pbad2way(formula = time ~ poison * treat, data = rats, est = "median", 
##     nboot = 500, pro.dis = TRUE)
## 
##              p.value
## poison         0.000
## treat          0.000
## poison:treat   0.174

9.8 Guía rápida

Fórmulas:
- X~F1 ajusta la variable X al factor F1.
- X~F1+F2 ajusta la variable X a los factores F1 y F2 sin tener en cuenta la interacción entre los factores.
- X~F1*F2 ajusta la variable X a los factores F1 y F2 teniendo en cuenta además la interacción entre los factores.
- X~F1:F2 ajusta la variable X a un factor que tiene como niveles los pares de niveles de F1 y F2.
options(show.signif.stars=...) sirve para desactivar (usando FALSE) o activar (con TRUE) los códigos de significación por medio de estrellitas.
aov(fórmula) efectúa el ANOVA indicado por la fórmula. El parámetro adicional data sirve para indicar el data frame del que se extraen los vectores y factores de la fórmula.
summary(aov(...)) muestra la tabla del ANOVA efectuado con la función aov. Añadiendo el sufijo [[1]]$"Pr(>F)" nos da directamente la columna de p-valores de la tabla.
anova(lm(fórmula, data=...)) también produce la tabla del ANOVA indicado por la fórmula. Con el sufijo $"Pr(>F)", nos da directamente la columna de p-valores de la tabla.
interaction.plot(factor1,factor2,vector) produce el gráfico de interacción del vector respecto de los dos factores.
subset(dataframe,condición) define un data frame con las filas del dataframe que cumplen la condición.
shapiro.test(x) realiza el test de normalidad de Shapiro-Wilk sobre el vector numérico x.
aggregate sirve para aplicar una función a una o varias variables de un data frame agrupando sus entradas por los niveles de uno o varios factores.
bartlett.test, con la misma sintaxis que aov, efectúa el test de Bartlett de homocedasticidad.
pairwise.t.test(x,factor) efectúa un test t por parejas de la variable x separada por los niveles del factor. Dos parámetros importantes:
- paired: se ha de igualar a TRUE en los ANOVA de bloques.
- p.adjust.method: sirve para indicar el método de ajuste de los p-valores.
duncan.test(aov,factor)$sufijo del paquete agricolae, efectúa el test de Duncan del ANOVA aov. Sus dos parámetros más importantes para nosotros son alpha, que sirve para indicar el nivel de significación y group, que sirve para indicar cómo queremos que muestre el resultado. El sufijo ha de ser ser groups si group=TRUE y comparison si group=FALSE.
TukeyHSD(aov) efectúa el test HSD de Tukey del ANOVA aov.
kruskal.test efectúa el test de Kruskal-Wallis. Su sintaxis es la misma que la de aov.
pairwise.wilcox.test efectúa un test de Wilcoxon (con paired=TRUE) o de Mann-Whitney-Wilcoxon (con paired=FALSE, el valor por defecto de este parámetro) por parejas. Su sintaxis es la misma que la de pairwise.t.test.
friedman.test efectúa el test de Friedman. Su sintaxis es la misma que la de aov.
pbad2way(fórmula, data=..., est="median") del paquete WRS2 lleva a cabo un contraste bootstrap de medianas de los datos de un experimento factorial de 2 vías. El parámetro nboot sirve para indicar el número de muestras a usar.

9.9 Ejercicios

Test

(1) En un experimento queremos comparar el valor medio de una cierta variable en cuatro poblaciones, A, B, C y D. Hemos tomado una muestra de 5 individuos de cada población y hemos medido en ellos la variable en cuestión. Los resultados para cada población han sido los siguientes: A=(23.1,17.2,20.1,19.5,18.8), B=(22.6,15.5,19.3,18.5,16.2), C=(21.1,26.4,24.7,21.4,20.9) y D=(20.4,24,23.4,24.9,21.5). Realizad un ANOVA de 1 vía sobre estos datos. Tenéis que dar el p-valor del contraste de la igualdad de las medias redondeado a 3 cifras decimales (sin ceros innecesarios a la derecha) y decir si podéis rechazar (con un SI) o no (con un NO), con un nivel de significación del 5%, la igualdad de todas las medias. Dad el p-valor y la conclusión en este orden, separados por un único espacio en blanco.

(2) En un experimento queremos comparar la influencia de cuatro tratamientos, A, B, C y D, sobre una determinada variable fisiológica. Para ello hemos aplicado cada tratamiento a los mismos 5 individuos, pero en órdenes y momentos escogidos al azar, y hemos medido en ellos la variable en cuestión tras cada tratamiento. Los resultados para cada tratamiento (ordenados en cada uno en el mismo orden, correspondiente a los individuos) han sido los siguientes: A=(23.1,17.2,20.1,19.5,18.8), B=(22.6,15.5,19.3,18.5,16.2), C=(21.1,26.4,24.7,21.4,20.9) y D=(20.4,24,23.4,24.9,21.5). Realizad un ANOVA de bloques sobre estos datos. Tenéis que dar el p-valor del contraste de la igualdad de las medias de los tratamientos redondeado a 3 cifras decimales (sin ceros innecesarios a la derecha) y decir si podéis rechazar (con un SI) o no (con un NO), con un nivel de significación del 5%, la igualdad de todas las medias de los tratamientos. Dad el p-valor y la conclusión en este orden, separados por un único espacio en blanco.

(3) En un experimento queremos comparar el valor medio de una cierta variable en cuatro poblaciones, A, B, C y D; los individuos de cada población además pueden clasificarse en dos tipos, X e Y, según una determinada característica que creemos que será relevante en nuestro estudio. Hemos tomado una muestra de 5 individuos de cada combinación población-característica y hemos medido en ellos la variable en cuestión. Los resultados para cada combinación población-característica han sido los siguientes: A-X=(29.2,30.9,31.3,30.0,30.0), B-X=(29.1,31.3,31.4,34.3,32.3), C-X=(31.3,40.7,32.6,34.8, 38.3), D-X=(32.2,36.0,31.6,31.8,32.6), A-Y=(26.3,25.9,25.6,25.3,24.9), B-Y=(30.7,29.8, 27.9,28.8,28.1), C-Y=(26.2,26.7,27.2,29.3,28.4), y D-Y=(20.5,26.2,27.9,23.3,27.8). Realizad un ANOVA de 2 vías sobre estos datos. Dad el p-valor del contraste de interacción entre el tratamiento y la característica redondeado a 3 cifras decimales (sin ceros innecesarios a la derecha) y decid si podéis concluir (con un SI) o no (con un NO), con un nivel de significación del 5%, que hay interacción entre el tratamiento y la característica. Dad el p-valor y la conclusión en este orden, separados por un único espacio en blanco.

(4) En un experimento queremos comparar el valor medio de una cierta variable en cuatro poblaciones, A, B, C y D. Hemos tomado una muestra de 5 individuos de cada población y hemos medido en ellos la variable en cuestión. Los resultados para cada población han sido los siguientes: A=(23.1,17.2,20.1,19.5,18.8), B=(22.6,15.5,19.3,18.5,16.2), C=(21.1,26.4,24.7,21.4,20.9) y D=(20.4,24,23.4,24.9,21.5). Realizad un test de Bartlett de homocedasticidad sobre estos datos, para saber si las varianzas poblacionales de las cuatro poblaciones son todas iguales o no. Tenéis que dar el p-valor del contraste de la igualdad de las varianzas redondeado a 3 cifras decimales (sin ceros innecesarios a la derecha) y decir si podéis rechazar (con un SI) o no (con un NO), con un nivel de significación del 5%, la igualdad de todas las varianzas. Dad el p-valor y la conclusión en este orden, separados por un único espacio en blanco.

(5) En un experimento hemos comparado el valor medio de una cierta variable en cuatro poblaciones, A, B, C y D. Hemos tomado una muestra de 5 individuos de cada población y hemos medido en ellos la variable en cuestión. Los resultados para cada población han sido los siguientes: A=(23.1,17.2,20.1,19.5,18.8), B=(22.6,15.5,19.3,18.5,16.2), C=(21.1,26.4,24.7,21.4,20.9) y D=(20.4,24,23.4,24.9,21.5). Realizad un test t por parejas de Bonferroni sobre estos datos con un nivel de significación del 5%, para determinar qué pares de poblaciones podemos concluir que tienen medias diferentes con este nivel de significación. Tenéis que decir si podéis rechazar (con un SI) o no (con un NO), con un nivel de significación del 5%, la igualdad de las medias de las poblaciones B y C.

9.9.1 Ejercicio

(1) La tabla de datos butterfat del paquete faraway contiene los porcentajes de contenido de grasa en la leche en muestras aleatorias de 5 razas. Para cada raza hay 20 vacas en la muestra: 10 vacas de dos años, 2year, y 10 de más de 4 años, Mature. Las variables de la tabla de datos son:

Butterfat: Porcentaje de contenido de grasa en la leche.
Breed: un factor que indica la raza de la vaca. Los niveles son: Ayrshire, Canadian, Guernsey, Holstein-Fresian y Jersey.
Age: una variable factor con los valores ya comentados: 2year y Mature.

Queremos usar estos datos para contrastar si el porcentaje medio de contenido de grasa en la leche depende de la raza o de la edad de la vaca.

(a) Dibujad sendos gráficos con los diagrama de cajas de los porcentajes de contenido de grasa en la leche de las vacas de la muestra separados por la raza de la vaca y separados por su edad, respectivamente. Comentadlos.

(b) Contrastad si cada muestra de una combinación de niveles (raza,edad) proviene de una distribución normal usando el test de Shapiro-Wilks con un nivel de significación $\alpha =0.05$.

(c) Contrastad si todas las muestras de combinaciones de niveles (raza,edad) tienen la misma varianza, con un nivel de significación $\alpha =0.05$.

(d) Se satisfacen las hipótesis para poder usar un ANOVA de 2 vías para comprobar si el porcentaje medio de grasa en la leche depende de la raza o de la edad de la vaca?

(e) Sea cual sea vuestra respuesta a la pregunta anterior, realizad un test ANOVA de 2 vías para contrastar con un nivel de significación $\alpha =0.05$ si el porcentaje medio de grasa en la leche depende de la raza o de la edad de la vaca (no hace falta contrastar las combinaciones (raza,edad)). Hay interacción entre la raza de la vaca y la edad de la misma?

(f) Sea cual sea vuestra respuesta a la pregunta (d), realizad también los contrastes de (e) mediante un test no paramétrico adecuado con un nivel de significación $\alpha =0.05$. Coinciden las conclusiones?

Respuestas al test

(1) 0.013 SI

Fijaos en que en el enunciado nos dan la tabla de datos siguiente por columnas:

A	B	C	D
23.1	22.6	21.1	20.4
17.2	15.5	26.4	24.0
20.1	19.3	24.7	23.4
19.5	18.5	21.4	24.9
18.8	16.2	21.9	21.5

Por lo tanto para entrarla de manera correcta como un data frame copiando los datos del enunciado hay que usar:

x=c(23.1,17.2,20.1,19.5,18.8,
    22.6,15.5,19.3,18.5,16.2,
    21.1,26.4,24.7,21.4,21.9,
    20.4,24.0,23.4,24.9,21.5)
pobl=rep(c("A","B","C","D"),each=5) 
X=data.frame(x,pobl)

A partir de aquí, la respuesta la obtenemos con

summary(aov(x~pobl,data=X))[[1]]$"Pr(>F)"

## [1] 0.01257876         NA

(2) 0.026 NO

Nosotros lo hemos resuelto con

x=c(23.1,17.2,20.1,19.5,18.8,
    22.6,15.5,19.3,18.5,16.2,
    21.1,26.4,24.7,21.4,21.9,
    20.4,24.0,23.4,24.9,21.5)
pobl=rep(c("A","B","C","D"), each=5)
bloques=as.factor(rep(1:5,4))
X.b=data.frame(x,pobl,bloques)
summary(aov(x~pobl+bloques,data=X.b))[[1]]$"Pr(>F)"[1]

## [1] 0.02561791

(3) 0.0234 SI

Nosotros lo hemos resuelto con

AX=c(29.2,30.9,31.3,30.0,30.0)
BX=c(29.1,31.3,31.4,34.3,32.3)
CX=c(31.3,40.7,32.6,34.8,38.3)
DX=c(32.2,36.0,31.6,31.8,32.6)
AY=c(26.3,25.9,25.6,25.3,24.9)
BY=c(30.7,29.8,27.9,28.8,28.1)
CY=c(26.2,26.7,27.2,29.3,28.4)
DY=c(20.5,26.2,27.9,23.3,27.8)
y=c(AX,BX,CX,DX,AY,BY,CY,DY)
fact.A=rep(rep(c("A","B","C","D"),each=5),2)
fact.X=rep(c("X","Y"),each=20)
DF=data.frame(y,fact.A,fact.X)
summary(aov(y~fact.A*fact.X))

##               Df Sum Sq Mean Sq F value   Pr(>F)
## fact.A         3   74.7    24.9   5.487  0.00371
## fact.X         1  330.1   330.1  72.700 9.62e-10
## fact.A:fact.X  3   49.3    16.4   3.619  0.02344
## Residuals     32  145.3     4.5

(4) 0.881 NO

Nosotros lo hemos resuelto con

bartlett.test(x~pobl,data=X)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  x by pobl
## Bartlett's K-squared = 0.6667, df = 3, p-value = 0.881

(5) SI

Nosotros lo hemos resuelto con

pairwise.t.test(X$x,X$pobl,p.adjust.method="holm")

## 
## 	Pairwise comparisons using t tests with pooled SD 
## 
## data:  X$x and X$pobl 
## 
##   A     B     C    
## B 0.762 -     -    
## C 0.143 0.034 -    
## D 0.151 0.041 0.861
## 
## P value adjustment method: holm

9.9.2 Soluciones sucintas del ejercicio

library(faraway)
BF=butterfat
str(BF)

## 'data.frame':	100 obs. of  3 variables:
##  $ Butterfat: num  3.74 4.01 3.77 3.78 4.1 4.06 4.27 3.94 4.11 4.25 ...
##  $ Breed    : Factor w/ 5 levels "Ayrshire","Canadian",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ Age      : Factor w/ 2 levels "2year","Mature": 2 1 2 1 2 1 2 1 2 1 ...

(a)

boxplot(Butterfat~Breed, data=BF)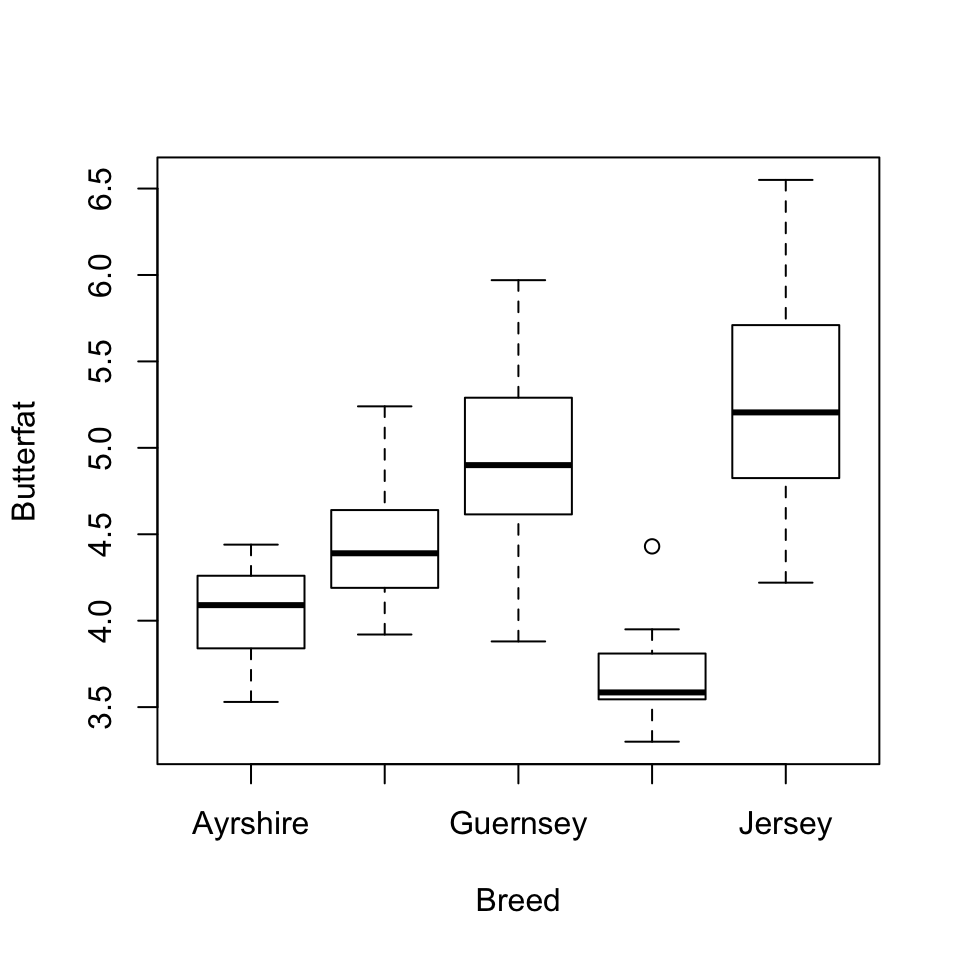

boxplot(Butterfat~Age, data=BF)

(b)

Test.SW=function(x){shapiro.test(x)$p.value}
aggregate(Butterfat~Breed:Age, data=BF,FUN=Test.SW)

##               Breed    Age  Butterfat
## 1          Ayrshire  2year 0.99921213
## 2          Canadian  2year 0.20778457
## 3          Guernsey  2year 0.95640414
## 4  Holstein-Fresian  2year 0.16320779
## 5            Jersey  2year 0.69510564
## 6          Ayrshire Mature 0.21757333
## 7          Canadian Mature 0.73627123
## 8          Guernsey Mature 0.33518154
## 9  Holstein-Fresian Mature 0.05739251
## 10           Jersey Mature 0.10347415

Podemos concluir con un nivel de significación del 5% que todas las muestras provienen de variables normales.

(c)

bartlett.test(Butterfat~interaction(Breed,Age), data=BF)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  Butterfat by interaction(Breed, Age)
## Bartlett's K-squared = 24.356, df = 9, p-value = 0.003772

No podemos aceptar que se dé homocedasticidad.

(d) No.

(e)

summary(aov(Butterfat~Breed*Age,data=BF))

##             Df Sum Sq Mean Sq F value Pr(>F)    
## Breed        4  34.32   8.580  49.565 <2e-16 ***
## Age          1   0.27   0.274   1.580  0.212    
## Breed:Age    4   0.51   0.128   0.742  0.566    
## Residuals   90  15.58   0.173                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(f)

library(WRS2)
pbad2way(Butterfat~Breed*Age,data=BF, est="median", nboot=500)

## Error in solve.default(cov, ...): system is computationally singular: reciprocal condition number = 4.97982e-19

¡Ups!

pbad2way(Butterfat~Breed*Age,data=BF, est="median", nboot=500,pro.dis=TRUE)

## Call:
## pbad2way(formula = Butterfat ~ Breed * Age, data = BF, est = "median", 
##     nboot = 500, pro.dis = TRUE)
## 
##           p.value
## Breed        0.00
## Age          0.28
## Breed:Age    0.83

Estudiante	Tests	Casa	Talleres	Control.1	Control.2
1	48	42	85	31	20
2	94	86	100	52	48
3	98	94	93	93	90
4	60	58	71	66	46
5	52	56	79	64	24
6	78	73	84	80	95
7	84	84	94	83	70
8	83	76	99	51	55
9	75	55	70	85	48
10	24	49	57	19	55
11	47	47	64	44	35
12	53	42	78	50	8
13	82	93	92	66	30
14	66	62	74	24	56
15	49	40	74	35	21

Estudiante	Tests	Casa	Talleres	Control.1	Control.2
1	48	42	85	31	20
2	94	86	100	52	48
3	98	94	93	93	90
4	60	58	71	66	46
5	52	56	79	64	24
6	78	73	84	80	95
7	84	84	94	83	70
8	83	76	99	51	55
9	75	55	70	85	48
10	24	49	57	19	55
11	47	47	64	44	35
12	53	42	78	50	8
13	82	93	92	66	30
14	66	62	74	24	56
15	49	40	74	35	21

Estudiante	Tests	Casa	Talleres	Control.1	Control.2
1	48	42	85	31	20
2	94	86	100	52	48
3	98	94	93	93	90
4	60	58	71	66	46
5	52	56	79	64	24
6	78	73	84	80	95
7	84	84	94	83	70
8	83	76	99	51	55
9	75	55	70	85	48
10	24	49	57	19	55
11	47	47	64	44	35
12	53	42	78	50	8
13	82	93	92	66	30
14	66	62	74	24	56
15	49	40	74	35	21