Lección 4 Intervalos de confianza
En esta lección explicamos cómo calcular con R algunos intervalos de confianza básicos. Recordad que un intervalo de confianza del \(q\times 100\%\) (con \(q\) entre 0 y 1) para un parámetro poblacional (la media, la desviación típica, la probabilidad de éxito de una variable Bernoulli, …) es un intervalo obtenido aplicando a una muestra aleatoria simple una fórmula que garantiza (si se cumplen una serie de condiciones sobre la distribución de la variable aleatoria poblacional que en cada caso dependen del parámetro y de la fórmula) que el \(q\times 100\%\) de las veces que la aplicáramos a una muestra aleatoria simple de la misma población, el intervalo resultante contendría el parámetro poblacional que queremos estimar. Esto es lo que significa lo de “confianza del \(q\times 100\%\)”: que confiamos en que nuestra muestra pertenece al \(q\times 100\%\) de las muestras (aleatorias simples) en las que la fórmula acierta y da un intervalo que contiene el parámetro deseado.
Algunas de las funciones que aparecen en esta lección volverán a salir en la próxima, ya que aunque calculan intervalos de confianza, su función principal es en realidad efectuar contrastes de hipótesis.
4.1 Intervalo de confianza para la media basado en la t de Student
Supongamos que queremos estimar a partir de una m.a.s. la media \(\mu\) de una variable \(X\) que sigue una distribución normal o de una variable cualquiera pero tomando una muestra grande (por fijar una cota, de tamaño 40 o mayor). En esta situación, si \(\overline{X}\), \(\widetilde{S}_{X}\) y \(n\) son, respectivamente, la media muestral, la desviación típica muestral y el tamaño de la muestra, un intervalo de confianza del \(q\times 100\%\) para \(\mu\) es
\[\begin{equation} \overline{X}\pm t_{n-1,(1+q)/2} \cdot \frac{\widetilde{S}_{X}}{\sqrt{n}} \tag{4.1} \end{equation}\]
donde \(t_{n-1,(1+q)/2}\) es el cuantil de orden \((1+q)/2\) de una variable aleatoria con distribución t de Student con \(n-1\) grados de libertad. Fijaos en que \(\widetilde{S}_{X}/\sqrt{n}\) es el error típico de la estimación de la media.
A la hora de calcular este intervalo de confianza, tenemos dos posibles situaciones. Una, típica de ejercicios, es cuando de la muestra sólo conocemos su media muestral \(\overline{X}\), su desviación típica muestral \(\widetilde{S}_X\) y su tamaño \(n\). Si los denotamos por x.b, sdm y n, respectivamente, y denotamos el nivel de confianza en tanto por uno \(q\) por q, podemos calcular los extremos de este intervalo de confianza con la expresión siguiente:
x.b+(qt((1+q)/2,n-1)*sdm/sqrt(n))*c(-1,1)Ahora bien, “en la vida real” lo usual es disponer de un vector numérico X con los valores de la muestra. En este caso, podemos usar la función t.test de R, que, entre otra información, calcula estos intervalos de confianza para \(\mu\). Si solo nos interesa el intervalo de confianza, podemos usar la sintaxis siguiente:
t.test(X,conf.level=...)$conf.intdonde tenemos que igualar el parámetro conf.level al nivel de confianza \(q\) en tanto por uno. Si \(q=0.95\), no hace falta entrarlo, porque es su valor por defecto.
pesos=c(2466,3941,2807,3118,3175,3515,3317,3742,3062,3033,2353,3515,3260,2892,
4423,3572,2750,3459,3374,3062,3205,2608,3118,2637,3438,2722,2863,3513)Vamos a suponer que nuestra muestra es aleatoria simple y que los pesos al nacer de los bebés con esta patología siguen una distribución normal. A partir de esta muestra, queremos calcular un intervalo de confianza del 95% para el peso medio de un recién nacido con luxación severa de cadera, y ver si contiene el peso medio de la población global de recién nacidos, que es de unos 3400 g.
Como suponemos que la variable aleatoria poblacional es normal, para calcular un intervalo de confianza del 95% para su valor medio vamos a usar la fórmula basada en la distribución t de Student, y por lo tanto la función t.test:
t.test(pesos)$conf.int## [1] 2997.849 3355.008
## attr(,"conf.level")
## [1] 0.95El intervalo que obtenemos es [2997.8, 3355] y está completamente a la izquierda del peso medio global de 3400 g, por lo que tenemos evidencia (a un 95% de confianza) de que los niños con luxación severa de cadera pesan de media al nacer por debajo de la media global. La apostilla entre paréntesis “a un 95% de confianza” aquí significa que hemos basado esta conclusión en un intervalo obtenido con una fórmula que acierta con una probabilidad del 95%, en el sentido de que el 95% de las ocasiones que aplicamos esta fórmula a una m.a.s. de una variable aleatoria normal, produce un intervalo que contiene la media de esta variable.
Observad que el resultado de t.test(pesos)$conf.int tiene un atributo, conf.level, que indica su nivel de confianza. En principio este atributo no molesta para nada en cálculos posteriores con los extremos de este intervalo de confianza, pero si os molesta, lo podéis quitar igualándolo a NULL.
IC.lux=t.test(pesos)$conf.int
attr(IC.lux,"conf.level")=NULL
IC.lux## [1] 2997.849 3355.008Veamos cómo podríamos haber obtenido este intervalo directamente con la fórmula (4.1):
x.b=mean(pesos)
sdm=sd(pesos)
n=length(pesos)
q=0.95
x.b+(qt((1+q)/2,n-1)*sdm/sqrt(n))*c(-1,1)## [1] 2997.849 3355.008Como podéis ver, coincide con el intervalo obtenido con la función t.test.
Ejemplo 4.2 Vamos a comprobar con un experimento esto de la “confianza” de los intervalos de confianza, y en concreto de la fórmula (4.1). Vamos a generar al azar una Población de 10,000,000 “individuos” con distribución normal estándard. Vamos a tomar 200 muestras aleatorias simples de tamaño 50 de esta población y calcularemos el intervalo de confianza para la media poblacional usando dicha fórmula. Finalmente, contaremos cuántos de estos intervalos de confianza contienen la media de la Población. Fijaremos la semilla de aleatoriedad para que el experimento sea reproducible y podáis comprobar que no hacemos trampa. En otras simulaciones habríamos obtenido resultados mejores o peores, es lo que tienen las simulaciones aleatorias.
set.seed(42)
Poblacion=rnorm(10^7) #La población
mu=mean(Poblacion) # La media poblacional
M=replicate(200, sample(Poblacion,50,replace=TRUE)) # Las muestras
dim(M)## [1] 50 200Tenemos una matriz M de 200 columnas y 50 filas, donde cada columna es una m.a.s. de nuestra población. Vamos a aplicar a cada una de estas muestras la función t.test para calcular un intervalo de confianza del 95% y luego contaremos los aciertos, es decir, cuántos de ellos contienen la media poblacional
IC.t=function(X){t.test(X)$conf.int}
ICs=apply(M,FUN=IC.t,MARGIN=2)
Aciertos=length(which((mu>=ICs[1,]) & (mu<=ICs[2,])))
Aciertos## [1] 189Hemos acertado 189 veces, es decir, un 94.5% de los intervalos obtenidos contienen la media poblacional. No hemos quedado muy lejos del 95% esperado.
Para visualizar mejor los aciertos, vamos a dibujar los intervalos apilados en un gráfico, donde aparecerán en azul claro los que aciertan y en rojo los que no aciertan.
plot(1,type="n",xlim=c(-0.8,0.8),ylim=c(0,200),xlab="Valores",ylab="Repeticiones",main="")
seg.int=function(i){
color="light blue";
if((mu<ICs[1,i]) | (mu>ICs[2,i])){color = "red"}
segments(ICs[1,i],i,ICs[2,i],i,col=color,lwd=2)
}
sapply(1:200,FUN=seg.int)
abline(v=mu,lwd=2)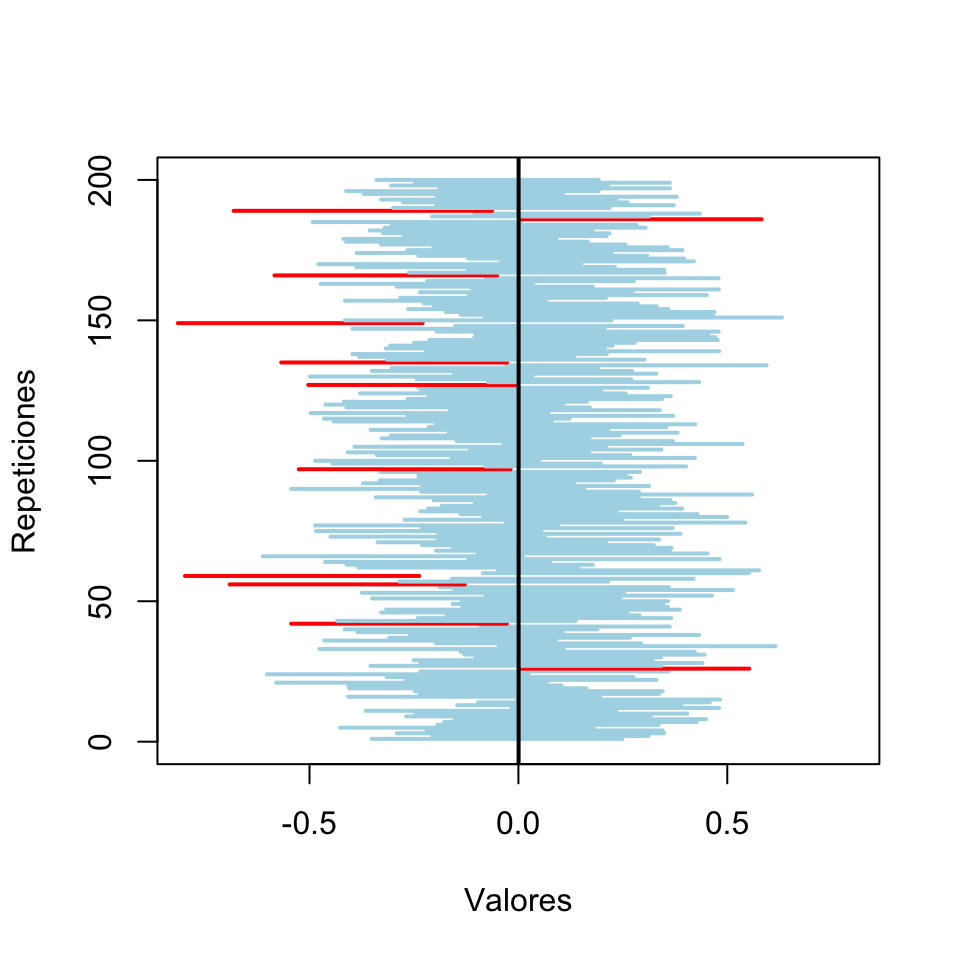
Figura 4.1: Aciertos y errores en 200 Intervalos de confianza al 95%
Fijaos en que los errores no se distribuyen por igual a los dos lados, hay muchos más intervalos que dejan la media poblacional a su izquierda que a su derecha, mientras que, en teoría, tendríamos que esperar que en la mitad de los errores la media poblacional estuviera a la izquierda del intervalo calculado y en la otra mitad a la derecha. Cosas de la aleatoriedad.
4.2 Intervalos de confianza para la proporción poblacional
En esta sección consideramos el caso en que la población objeto de estudio sigue una distribución Bernoulli y queremos estimar su probabilidad de éxito (o proporción poblacional) \(p\). Para ello, tomamos una muestra aleatoria simple de tamaño \(n\) y número de éxitos \(x\), y, por lo tanto, de proporción muestral de éxitos \(\widehat{p}_X=x/n\).
El método “exacto” de Clopper-Pearson para calcular un intervalo de confianza del \(q\times 100\%\) para \(p\) se basa en el hecho de que, en estas condiciones, el valor de \(x\) sigue una distribución binomial \(B(n,p)\). Este método se puede usar siempre, sin ninguna restricción sobre la muestra, y consiste básicamente en encontrar los valores \(p_0\) y \(p_1\) tales que
\[ \begin{array}{l} \displaystyle \sum_{k=x}^n\binom{n}{k}p_0^k(1-p_0)^{n-k}=(1-q)/2\\ \displaystyle\sum_{k=0}^x\binom{n}{k}p_1^k(1-p_1)^{n-k}=(1-q)/2 \end{array} \]
y dar el intervalo \([p_0,p_1]\). Para calcular este intervalo se puede usar la función binom.exact del paquete epitools. Su sintaxis es
binom.exact(x,n,conf.level)donde x y n representan, respectivamente, el número de éxitos y el tamaño de la muestra, y conf.level es \(q\), el nivel de confianza en tanto por uno. El valor por defecto de conf.level es 0.95.
Ejemplo 4.3 Supongamos que, de una muestra de 15 enfermos tratados con un cierto medicamento, solo 1 ha desarrollado taquicardia. Queremos conocer un intervalo de confianza del 95% para la proporción de enfermos tratados con este medicamento que presentan este efecto adverso.
Tenemos una población Bernoulli, formada por los enfermos tratados con el medicamento en cuestión, donde los éxitos son los enfermos que desarrollan taquicardia. La fracción de éstos es la fracción poblacional \(p\) para la que queremos calcular el intervalo de confianza del 95%. Para ello cargamos el paquete epitools y usamos binom.exact:
library(epitools)
binom.exact(1,15)## x n proportion lower upper conf.level
## 1 1 15 0.06666667 0.00168643 0.3194846 0.95El resultado de la función binom.exact es un data frame; el intervalo de confianza deseado está formado por los números en las columnas lower (extremo inferior) y upper (extremo superior):
binom.exact(1,15)$lower## [1] 0.00168643binom.exact(1,15)$upper## [1] 0.3194846Hemos obtenido el intervalo de confianza [0.002,0.319]: podemos afirmar con un nivel de confianza del 95% que el porcentaje de enfermos tratados con este medicamento que presentan este efecto adverso está entre el 0.2% y el 31.9%.
Supongamos ahora que el tamaño \(n\) de la muestra aleatoria simple es grande; de nuevo, digamos que \(n\geq 40\). En esta situación, podemos usar el Método de Wilson para aproximar, a partir del Teorema Central del Límite, un intervalo de confianza para el parámetro \(p\) al nivel de confianza \(q\times 100\%\), mediante la fórmula \[ \frac{\widehat{p}_{X}+\frac{z_{(1+q)/2}^2}{2n}\pm z_{(1+q)/2}\sqrt{\frac{\widehat{p}_{X}(1-\widehat{p}_{X})}{n}+\frac{z_{(1+q)/2}^2}{4n^2}}}{1+\frac{z_{(1+q)/2}^2}{n}} \] donde \(z_{(1+q)/2}\) es el cuantil de orden \((1+q)/2\) de una variable aleatoria normal estándar.
Para calcular este intervalo se puede usar la función binom.wilson del paquete epitools. Su sintaxis es
binom.wilson(x,n,conf.level)con los mismos parámetros que binom.exact.
Ejemplo 4.4 Supongamos que tratamos 45 ratones con un agente químico, y 10 de ellos desarrollan un determinado cáncer de piel. Queremos calcular un intervalo de confianza al 90% para la proporción \(p\) de ratones que desarrollan este cáncer de piel al ser tratados con este agente químico.
Como 45 es relativamente grande, usaremos el método de Wilson. Para comparar los resultados, usaremos también el método exacto. Fijaos que, en este ejemplo, \(q=0.9\).
binom.wilson(10,45,0.9)## x n proportion lower upper conf.level
## 1 10 45 0.2222222 0.1377238 0.3382281 0.9binom.exact(10,45,0.9)## x n proportion lower upper conf.level
## 1 10 45 0.2222222 0.1258186 0.3477285 0.9Con el método de Wilson obtenemos el intervalo [0.138,0.338] y con el método de Clopper-Pearson, el intervalo [0.126,0.348], un poco más ancho: hay una diferencia en los extremos de alrededor de un punto porcentual.
Supongamos finalmente que la muestra aleatoria simple es considerablemente más grande que la usada en el método de Wilson y que, además, la proporción muestral de éxitos \(\widehat{p}_{X}\) está alejada de 0 y de 1. Una posible manera de formalizar estas condiciones es requerir que \(n\geq 100\) y que \(n\widehat{p}_{X}\geq 10\) y \(n(1-\widehat{p}_{X})\geq 10\); observad que estas dos últimas condiciones son equivalentes a que tanto el número de éxitos como el número de fracasos en la muestra sean como mínimo 10. En este caso, se puede usar la fórmula de Laplace, que simplifica la de Wilson (aunque, en realidad, la precede en más de 100 años) suponiendo que, si n es grande y \(\widehat{p}_{X}(1-\widehat{p}_{X})/n\) no es muy cercano a 0, podemos igualar \(z_{(1+q)/2}^2/(2n)\) a 0: un intervalo de confianza del parámetro \(p\) al nivel de confianza \(q\times 100\%\) viene dado aproximadamente por la fórmula
\[
\widehat{p}_{X}\pm z_{(1+q)/2}\sqrt{\frac{\widehat{p}_{X}
(1-\widehat{p}_{X})}{n}}
\]
Esta fórmula está implementada en la función binom.approx del paquete epitools, de uso similar al de las dos funciones anteriores.
Ejemplo 4.5 En una muestra aleatoria de 500 familias con niños en edad escolar de una determinada ciudad se ha observado que 340 introducen fruta de forma diaria en la dieta de sus hijos. A partir de este dato, queremos encontrar un intervalo de confianza del 95% para la proporción real de familias de esta ciudad con niños en edad escolar que incorporan fruta fresca de forma diaria en la dieta de sus hijos.
Tenemos una población Bernoulli donde los éxitos son las familias que aportan fruta de forma diaria a la dieta de sus hijos, y la fracción de estas familias en el total de la población es la proporción poblacional \(p\) para la que queremos calcular el intervalo de confianza. Como \(n\) es muy grande y los números de éxitos y fracasos también lo son, podemos emplear el método de Laplace.
binom.approx(340,500)## x n proportion lower upper conf.level
## 1 340 500 0.68 0.6391123 0.7208877 0.95Por lo tanto, según la fórmula de Laplace, un intervalo de confianza al 95% para la proporción poblacional es [0.639,0.721]. ¿Qué hubiéramos obtenido con los otros dos métodos?
binom.wilson(340,500)## x n proportion lower upper conf.level
## 1 340 500 0.68 0.637873 0.7193822 0.95binom.exact(340,500)## x n proportion lower upper conf.level
## 1 340 500 0.68 0.6371369 0.7207188 0.95Como podéis ver, los resultados son muy parecidos, con diferencias de unas pocas milésimas.
4.3 Intervalo de confianza para la varianza de una población normal
Supongamos ahora que queremos estimar la varianza \(\sigma^2\), o la desviación típica \(\sigma\), de una población que sigue una distribución normal. Tomamos una muestra aleatoria simple de tamaño \(n\), y sea \(\widetilde{S}_{X}\) su desviación típica muestral. En esta situación, un intervalo de confianza del \(q\times 100\%\) para la varianza \(\sigma^2\) es \[ \left[ \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1+q)/2}^2},\ \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,(1-q)/2}^2}\right], \] donde \(\chi_{n-1,(1-q)/2}^2\) y \(\chi_{n-1,(1+q)/2}^2\) son, respectivamente, los cuantiles de orden \((1-q)/2\) y \((1+q)/2\) de una variable aleatoria que sigue una distribución \(\chi^2\) con \(n-1\) grados de libertad.
Si conocéis la varianza muestral \(\widetilde{S}_{X}^2\), que denotaremos por varm, podéis calcular este intervalo de confianza para la varianza con la fórmula siguiente (donde qindica el nivel de confianza en tanto por uno \(q\)):
(n-1)*varm*c(1/qchisq((1+q)/2,n-1),1/qchisq((1-q)/2,n-1))Si, en cambio, disponéis de la muestra, podéis calcular este intervalo de confianza con la función varTest del paquete EnvStats. La sintaxis es similar a la usada con t.test:
varTest(X,conf.level)$conf.intdonde X es el vector que contiene la muestra y conf.level el nivel de confianza, que por defecto es igual a 0.95.
Ejemplo 4.6 Un índice de calidad de un reactivo químico es el tiempo que tarda en actuar. Se supone que la distribución de este tiempo de actuación del reactivo es aproximadamente normal. Se realizaron 30 pruebas independientes, que forman una muestra aleatoria simple, en las que se midió el tiempo de actuación del reactivo. Los tiempos obtenidos fueron
reactivo = c(12,13,13,14,14,14,15,15,16,17,17,18,18,19,19,25,25,26,27,30,33,34,35,
40,40,51,51,58,59,83)Queremos usar estos datos para calcular un intervalo de confianza del 95% para la desviación típica de este tiempo de actuación.
El siguiente código calcula un intervalo de confianza al 95% para la varianza a partir del vector reactivo:
library(EnvStats)
varTest(reactivo)$conf.int## LCL UCL
## 191.2627 544.9572
## attr(,"conf.level")
## [1] 0.95Este intervalo de confianza es para la varianza. Como la desviación típica es la raíz cuadrada de la varianza, para obtener un intervalo de confianza al 95% para la desviación típica, tenemos que tomar la raíz cuadrada de este intervalo para la varianza:
sqrt(varTest(reactivo)$conf.int)## LCL UCL
## 13.82977 23.34432
## attr(,"conf.level")
## [1] 0.95Por lo tanto un intervalo de confianza del 95% para la desviación típica poblacional es [13.83, 23.34]. De nuevo, si os molesta, podéis eliminar el atributo conf.level igualándolo a NULL.
4.4 Bootstrap
Cuando no tiene sentido usar un método paramétrico como los explicados en las secciones anteriores para calcular un intervalo de confianza porque no se satisfacen las condiciones teóricas que garantizan que el intervalo obtenido contiene el 95% de las veces el parámetro poblacional deseado, podemos recurrir a un método no paramétrico. El más utilizado es el bootstrap, que básicamente consiste en:
Remuestrear la muestra: tomar muchas muestras aleatorias simples de la muestra de la que disponemos, cada una de ellas del mismo tamaño que la muestra original (pero simples, es decir, con reposición).
Calcular el estimador sobre cada una de estas submuestras.
Organizar los resultados en un vector.
Usar este vector para calcular un intervalo de confianza.
La manera más sencilla de llevar a cabo el cálculo final del intervalo de confianza es el llamado método de los percentiles, en el que se toman como extremos del intervalo de confianza del \(q\times 100\%\) los cuantiles de orden \((1-q)/2\) y \((1+q)/2\) del vector de estimadores, pero hay muchos otros métodos; encontraréis algunos en esta entrada de la Wikipedia.
Ejemplo 4.7 Volvamos a la muestra de pesos del Ejemplo 4.1, pero supongamos ahora que la variable aleatoria poblacional de la que la hemos extraído no es normal (o que no queremos suponer que lo sea). Vamos a usar el método bootstrap de los percentiles para calcular un intervalo de confianza del 95% para el peso medio poblacional.
Para ello, vamos a general 1000 muestras aleatorias simples de la muestra, todas ellas del mismo tamaño que la muestra, calcularemos la media de cada una de estas muestras simples, construiremos un vector con estas medias muestrales, y daremos como extremos del intervalo de confianza los cuantiles de orden 0.025 y 0.975 del vector así obtenido.
set.seed(42)
n=length(pesos)
X=replicate(1000,mean(sample(pesos,n,replace=TRUE)))
IC.boot=c(quantile(X,0.025),quantile(X,0.975))
round(IC.boot,1)## 2.5% 97.5%
## 3027.3 3350.6El intervalo obtenido en este caso es [3027.3, 3350.6]; como se trata de un método basado en una simulación aleatoria, seguramente con otra semilla de aleatoriedad daría un intervalo diferente. Para comparar, recordad que el intervalo de confianza obtenido con la fórmula basada en la t de Student ha sido [2997.8, 3355].
El paquete boot dispone de la función boot para llevar a cabo simulaciones bootstrap. Aplicando luego la función boot.ci al resultado de la función boot obtenemos diversos intervalos de confianza basados en el enfoque bootstrap. La sintaxis básica de la función boot es
boot(X,estadístico,R)donde:
Xes el vector que forma la muestra de la que disponemosRes el número de muestras que queremos extraer de la muestra originalEl
estadísticoes la función que calcula el estadístico deseado de la submuestra, y tiene que tener dos parámetros: el primero representa la muestra originalXy el segundo representa el vector de índices de una m.a.s. deX. Por ejemplo, si vamos a usar la funciónbootpara efectuar una simulación bootstrap de medias muestrales, podemos tomar comoestadísticola función:
media.boot=function(X,índices){mean(X[índices])}Por otro lado, el nivel de confianza se especifica en la función boot.ci mediante el parámetro conf (no conf.level, como hasta ahora), cuyo valor por defecto es, eso sí, el de siempre: 0.95.
A modo de ejemplo, vamos a usar las funciones del paquete boot para calcular un intervalo de confianza del 95% para la media de la variable aleatoria que ha producido el vector pesos.
library(boot)
set.seed(42)
simulacion=boot(pesos,media.boot,1000)El resultado simulacion de esta última instrucción es una list que incluye, en su componente t, el vector de 1000 medias muestrales obtenido mediante la simulación; sus 10 primeros valores son:
simulacion$t[1:10]## [1] 3189.14 3237.11 3301.32 3103.00 3154.11 3294.11 3347.25 3239.93
## [9] 3304.07 3217.11Calculemos ahora el intervalo de confianza deseado:
boot.ci(simulacion)## Warning in boot.ci(simulacion): bootstrap variances needed for studentized
## intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = simulacion)
##
## Intervals :
## Level Normal Basic
## 95% (3010, 3341 ) (3011, 3345 )
##
## Level Percentile BCa
## 95% (3008, 3342 ) (3009, 3344 )
## Calculations and Intervals on Original ScaleObtenemos cuatro intervalos de confianza para \(\mu\), calculados con cuatro métodos a partir de la simulación realizada (y un aviso de que no ha podido calcular un quinto intervalo). Cada uno de estos intervalos es un objeto de una list y por lo tanto se puede obtener con el sufijo adecuado, que podréis deducir del resultado de aplicar str al resultado de una función boot.ci. El intervalo Percentile es el calculado con el método de los percentiles que hemos explicado antes, y se obtiene con el sufijo $percent[4:5] (no ha dado lo mismo que antes, pese a usar la misma semilla de aleatoriedad, porque el procedimiento usado por la función boot.ci par calcular el intervalo de confianza no es exactamente el que hemos explicado). No vamos a entrar en detalle sobre los métodos que usa para calcular el resto de intervalos, en realidad todos tienen ventajas e inconvenientes.
Ejemplo 4.8 ¿Realmente funciona el enfoque bootstrap? Vamos a retomar el experimento realizado en el Ejemplo 4.2, donde construimos una matriz M cuyas columnas son 200 muestras aleatorias simples de tamaño 50 de una población que sigue una distribución normal estándard.
En dicho ejemplo calculamos para cada una de estas muestras el intervalo de confianza del 95% para la media poblacional usando la fórmula (4.1), que es la recomendada por la teoría en este caso. De los 200 intervalos calculados, 189 contuvieron la media poblacional, lo que representa un 94.5% de aciertos.
Ahora vamos a calcular para cada una de estas muestras un intervalo de confianza del 95% por el método bootstrap de los percentiles y compararemos las tasas de aciertos. Para mayor seguridad, vamos a volver a generar en las mismas condiciones las 200 muestras de la población, no sea que a lo largo de la lección hayamos modificado inadvertidamente el contenido de la matriz M (y así de paso fijamos la semilla de aleatoriedad).
set.seed(42)
Poblacion=rnorm(10^7) #La población
mu=mean(Poblacion) # La media poblacional
M=replicate(200, sample(Poblacion,50,replace=TRUE)) # Las muestras
IC.b=function(X){boot.ci(boot(X,media.boot,1000))$percent[4:5]}
ICs.bootstrap=apply(M,FUN=IC.b,MARGIN=2)
Aciertos.bootstrap=length(which((mu>=ICs.bootstrap[1,]) & (mu<=ICs.bootstrap[2,])))
Aciertos.bootstrap## [1] 186Con el bootstrap, hemos acertado en 186 ocasiones, lo que supone un 93% de aciertos.
4.5 Guía rápida
t.test(X, conf.level=...)$conf.intcalcula el intervalo de confianza delconf.level\(\times 100\%\) para la media poblacional usando la fórmula basada en la t de Student aplicada a la muestraX.binom.exact(x,n,conf.level=...), del paquete epitools, calcula el intervalo de confianza delconf.level\(\times 100\%\) para la proporción poblacional aplicando el método de Clopper-Pearson a una muestra de tamañonconxéxitos.binom.wilson(x,n,conf.level=...), del paquete epitools, calcula el intervalo de confianza delconf.level\(\times 100\%\) para la proporción poblacional aplicando el método de Wilson a una muestra de tamañonconxéxitos.binom.approx(x,n,conf.level=...), del paquete epitools, calcula el intervalo de confianza delconf.level\(\times 100\%\) para la proporción poblacional aplicando la fórmula de Laplace a una muestra de tamañonconxéxitos.varTest(X,conf.level=...)$conf.int, del paquete EnvStats, calcula el intervalo de confianza delconf.level\(\times 100\%\) para la varianza poblacional usando la fórmula basada en la ji cuadrado aplicada a la muestraX.boot(X,E,R), del paquete boot, lleva a cabo una simulación bootstrap, tomandoRsubmuestras del vectorXy calculando sobre ellas el estadístico representado por la funciónE.boot.ci, del paquete boot, aplicado al resultado de una funciónboot, calcula diversos intervalos de confianza a partir del resultado de la simulación efectuada conboot. El nivel de confianza se especifica con el parámetroconf.
4.6 Ejercicios
Test
(1) Tomad la muestra de todas las longitudes de pétalos de flores Iris setosa contenida en la tabla de datos iris y usadla para calcular un intervalo de confianza del 95% para el valor medio de las longitudes de pétalos de esta especie de flores usando la fórmula basada en la t de Student. Tenéis que dar el extremo inferior y el extremo superior, en este orden, separados por una coma (sin paréntesis u otros delimitadores, ni espacios en blanco) y redondeados a 2 cifras decimales (sin ceros innecesarios a la derecha).
(2) Tenemos una población de media \(\mu\) desconocida. Tomamos una muestra aleatoria simple de tamaño 80 y obtenemos una media muestral de 6.2 y una desviación típica muestral de 1.2. Usad estos datos y la fórmula del intervalo de confianza para la media basado en la t de Student para calcular un intervalo de confianza al 95% para \(\mu\). Tenéis que dar el extremo inferior y el extremo superior, en este orden, separados por una coma (sin paréntesis u otros delimitadores, ni espacios en blanco) y redondeados a 2 cifras decimales (sin ceros innecesarios a la derecha).
(3) Tenemos una población Bernoulli de proporción poblacional \(p\) desconocida. Tomamos una muestra aleatoria simple de 80 individuos y obtenemos una proporción muestral de 35% de éxitos. Calculad un intervalo de confianza para \(p\) a un nivel de confianza del 95% usando el método de Wilson. Tenéis que dar el extremo inferior y el extremo superior, en este orden, separados por una coma (sin paréntesis u otros delimitadores, ni espacios en blanco) y redondeados a 3 cifras decimales (sin ceros innecesarios a la derecha).
(4) Tomad la muestra de todas las longitudes de pétalos de flores Iris setosa contenida en la tabla de datos iris y usadla para calcular un intervalo de confianza del 95% para la varianza de las longitudes de pétalos de esta especie de flores. Tenéis que dar el extremo inferior y el extremo superior, en este orden, separados por una coma (sin paréntesis u otros delimitadores, ni espacios en blanco) y redondeados a 3 cifras decimales (sin ceros innecesarios a la derecha).
Problemas
(1) En la tabla de datos que encontraréis en el url https://www.dropbox.com/s/qcok2f7u51teqr6/pacientes.txt?raw=1 se ha recogido información acerca de un conjunto de pacientes que se han sometido a una revisión médica voluntaria. Sus variables son:
- SEXO: el sexo
- EDAD: la edad, en años
- ALTURA: la altura, en cm
- PESO: el peso, en Kg
- HIPERT: si es hipertenso o no
- IMC: el índice de masa corporal
- CARDIOPA: si sufre alguna cardiopatía o no
A partir de estos datos:
(a) Calculad un intervalo de confianza del 95% para el IMC medio de las mujeres usando la fórmula basada en la t de Student.
(b) Calculad un intervalo de confianza del 95% para la desviación típica del IMC de las mujeres usando la fórmula basada en la \(\chi^2\).
(c) Calculad un intervalo de confianza del 95% para la proporción de hombres hipertensos que sufren cardiopatías. Usad todos los métodos que tenga sentido usar y comparad los resultados.
(d) Calculad un intervalo de confianza del 95% para la desviación típica del IMC de las mujeres de 50 años o más usando la técnica bootstrap de los percentiles y 1000 muestras.
Respuestas al test
(1) 1.41,1.51
Nosotros lo hemos calculado con
round(t.test(iris[iris$Species=="setosa","Petal.Length"])$conf.int,2)## [1] 1.41 1.51
## attr(,"conf.level")
## [1] 0.95(2) 5.933,6.467
Nosotros lo hemos calculado con
x=6.2
n=80
sdm=1.2
conf.level=0.95
round(x+(qt((1+conf.level)/2,n-1)*sdm/sqrt(n))*c(-1,1),3)## [1] 5.933 6.467(3) 0.255,0.459
Nosotros lo hemos calculado con
round(binom.wilson(0.35*80,80),3)## x n proportion lower upper conf.level
## 1 28 80 0.35 0.255 0.459 0.95(4) 0.021,0.047
Nosotros lo hemos calculado con
round(varTest(iris[iris$Species=="setosa","Petal.Length"])$conf.int,3)## LCL UCL
## 0.021 0.047
## attr(,"conf.level")
## [1] 0.95Soluciones sucintas de los problemas
(1) Cargamos la tabla de datos:
Datos=read.table("https://www.dropbox.com/s/qcok2f7u51teqr6/pacientes.txt?raw=1",
header=TRUE)
str(Datos)## 'data.frame': 81 obs. of 7 variables:
## $ SEXO : Factor w/ 2 levels "Hombre","Mujer": 1 1 2 1 1 2 1 1 1 1 ...
## $ EDAD : int 47 51 54 50 52 53 49 52 50 48 ...
## $ ALTURA : int 170 170 148 170 165 151 170 168 170 166 ...
## $ PESO : int 80 73 46 74 67 51 73 72 73 73 ...
## $ HIPERT : Factor w/ 2 levels "Hipertenso","Normotenso": 2 1 1 1 2 1 1 2 2 2 ...
## $ IMC : num 27.7 25.3 21 25.6 24.6 ...
## $ CARDIOPA: Factor w/ 2 levels "Con cardiopatia",..: 2 1 2 2 2 2 2 2 1 1 ...(a)
t.test(Datos[Datos$SEXO=="Mujer","IMC"])$conf.int## [1] 22.3313 22.9053
## attr(,"conf.level")
## [1] 0.95(b)
sqrt(varTest(Datos[Datos$SEXO=="Mujer","IMC"])$conf.int)## LCL UCL
## 0.687995 1.106481
## attr(,"conf.level")
## [1] 0.95(c) Veamos el tamaño de la muestra
HH=Datos[Datos$SEXO=="Hombre" & Datos$CARDIOPA=="Con cardiopatia", "HIPERT"]
length(HH)## [1] 12table(HH)## HH
## Hipertenso Normotenso
## 4 8Con un tamaño tan pequeño, solo tiene sentido calcular el intervalo de Clopper-Pearson:
binom.exact(table(HH)[1],length(HH))## x n proportion lower upper conf.level
## Hipertenso 4 12 0.333333 0.0992461 0.651124 0.95(d) “A mano”
Muestra=Datos[Datos$SEXO=="Mujer" & Datos$EDAD>=50, "IMC"]
n=length(Muestra)
X=replicate(1000,sd(sample(Muestra,n,replace=TRUE)))
c(quantile(X,0.025),quantile(X,0.975))## 2.5% 97.5%
## 0.618456 0.996212Usando las funciones del paquete boot:
sd.boot=function(X,índices){sd(X[índices])}
simulacion=boot(Muestra,sd.boot,1000)
boot.ci(simulacion)$percent[4:5]## [1] 0.6252360 0.9977014