Lección 11 Clustering básico

En esta lección explicamos cómo usar R para clasificar objetos (o individuos, observaciones, etc.). En la práctica, supondremos que estos objetos están representados por medio de las filas de una tabla de datos de variables cuantitativas. A partir de estas descripciones como vectores numéricos, calcularemos de alguna manera la diferencia o semejanza entre cada par de objetos y las usaremos para clasificarlos, de manera que cada clase agrupe objetos parecidos. De esta manera, reducimos el problema de describir muchos objetos al de describir unas pocas clases. En este contexto, a las clases resultantes se las llama clusters y a la clasificación, clustering.

Veremos dos tipos de procedimientos de clustering: el método de k-medias, o k-means, donde hay que especificar a priori el número de clusters que queremos formar, y los métodos jerárquicos aglomerativos, que producen un árbol que indica el orden en el que se van agrupando los objetos de manera jerárquica, empezando por los más cercanos.

11.1 Método de k-medias o k-means

El método de k-medias produce una partición de una serie de objetos, representados mediante puntos \(x_1,\ldots,x_n\) de un espacio \(\mathbb{R}^p\), en un número prefijado k de clusters. En su versión básica, que es de la que toma su nombre genérico, se usa la distancia euclídea para comparar estos puntos y se identifica cada cluster con su centro: el punto medio (mean) de sus elementos. El objetivo es conseguir una clasificación óptima en el sentido siguiente. Dado un clustering de un conjunto de puntos, llamaremos \(SSC\) a la suma de los cuadrados de las distancias de los puntos a los centros de los clusters a los que han sido asignados. En símbolos, si los clusters resultantes son \(C_1,\ldots,C_k\), de centros \(c_1,\ldots,c_k\) respectivamente, y, para cada \(i=1,\ldots,k\), el cluster \(C_i\) está formado por los puntos \(C_i=\{x_{i,1},\ldots,x_{i,n_i}\}\), entonces \[ SSC=\sum_{i=1}^k\sum_{l=1}^{n_i} \|x_{i,l}-c_i\|^2 \] donde \(\|x-y\|^2\) indica la distancia euclídea al cuadrado entre los vectores \(x\) e \(y\) (recordad que si \(x=(x_1,\ldots,x_p)\) e \(y=(y_1,\ldots,y_p)\), su distancia euclídea al cuadrado es \(\|x-y\|^2=\sum\limits_{i=1}^p (x_i-y_i)^2\)). Entonces, el objetivo es conseguir un clustering con \(SSC\) mínima. Ya que estamos, denotaremos por \(SSC_i\) el sumando de \(SSC\) correspondiente al cluster \(C_i\); es decir, \[ SSC_i=\sum_{l=1}^{n_i} \|x_{i,l}-c_i\|^2. \]

No hay ningún algoritmo que resuelva este problema de manera eficiente, por lo que se han propuesto varios métodos heurísticos que calculan rápidamente clusterings aproximadamente óptimos. A continuación explicamos las líneas básicas de algunos de ellos.

Algoritmo de Lloyd: Para empezar, se escogen k centros, se calculan las distancias euclídeas de cada punto a cada centro, y se asigna a cada centro el cluster formado por los puntos que están más cerca de él que de los otros centros. A continuación, en pasos sucesivos se itera el bucle (1)–(3) siguiente hasta que en una iteración los clusters no se modifican:

1. Se sustituye cada centro por el punto medio de los puntos que forman su cluster.

2. Se calculan las distancias euclídeas de cada punto a cada centro.

3. Se asigna a cada centro el cluster formado por los puntos que están más cerca de él que de los otros centros.

El clustering resultante está formado entonces por los últimos clusters construidos.

Algoritmo de Hartigan-Wong: Este algoritmo empieza igual que el de Lloyd: se escogen k centros, se calculan las distancias euclídeas de cada punto a cada centro, y se asigna a cada centro el cluster de puntos que están más cerca de él que de los otros centros. A continuación, en pasos sucesivos se itera el bucle (1)–(5) siguiente hasta que en una iteración del mismo los clusters no cambian:

1. Se sustituye cada centro por el punto medio de los puntos asignados a su cluster.

2. Se calculan las distancias euclídeas de cada punto a cada centro.

3. Se asigna (temporalmente) a cada centro el cluster formado por los puntos que están más cerca de él que de los otros centros.

4. Si en esta asignación algún punto ha cambiado de cluster, digamos que el punto \(x_i\) se ha incorporado al cluster \(C_j\) de centro \(c_j\), entonces:

   • Se calcula el valor \(SSE_j\) que se obtiene multiplicando \(SSC_j\) por \(n_j/(n_j-1)\) (donde \(n_j\) indica el número de elementos del cluster \(C_j\)).

   • Se calcula, para todo otro cluster \(C_k\), el correspondiente valor \(SSE_{i,k}\) como si \(x_i\) hubiera ido a parar a \(C_k\).

   • Si algún \(SSE_{i,k}\) resulta menor que \(SSE_j\), \(x_i\) se asigna definitivamente al cluster \(C_k\) que da valor mínimo de \(SSE_{i,k}\).

5. Una vez realizado el procedimiento anterior para todos los puntos que han cambiado de cluster, estos se asignan a sus clusters definitivos y se da el bucle por completado.

Como en el algoritmo de Lloyd, el clustering resultante está formado por los últimos clusters construidos.

Algoritmo de McQueen: Es el mismo método que el de Lloyd salvo por el hecho de que no se recalculan todos los clusters y sus centros de golpe, sino elemento a elemento. Es decir, se empieza igual que en los dos algoritmos anteriores: se escogen k centros, se calculan las distancias euclídeas de cada punto a cada centro, se asigna a cada centro el cluster de puntos que están más cerca de él que de los otros centros, y se sustituye cada centro por el punto medio de los puntos asignados a su cluster. A partir de aquí, en pasos sucesivos se itera el bucle siguiente (recordemos que los puntos a clasificar son \(x_1,\ldots,x_n\), y los supondremos ordenados por su fila en la tabla de datos):

• Para cada \(i=1,\ldots,n\), se mira si el punto \(x_i\) está más cerca del centro de otro cluster que del centro del cluster al que está asignado.

• Si no lo está, se mantiene en su cluster y se pasa al punto siguiente, \(x_{i+1}\). Si se llega al final de la lista de puntos y todos se mantienen en sus clusters, el algoritmo se para.

• Si \(x_i\) está más cerca de otro centro, se traslada al cluster definido por este centro, se recalculan los centros de los dos clusters afectados (el que ha abandonado \(x_i\) y aquél al que se ha incorporado), y se reinicia el bucle, empezando de nuevo con \(x_1\).

El clustering resultante está formado por los clusters existentes en el momento de parar.

Ninguno de estos algoritmos garantiza un clustering óptimo, en el que la \(SSC\) resultante sea mínima. Lo que se suele hacer entonces es repetir varias veces el algoritmo con distintos conjuntos iniciales de k centros, y cruzar los dedos para que la \(SSC\) más pequeña que se obtenga en alguna de estas repeticiones sea efectivamente mínima. En todo caso, se ha demostrado que el algoritmo de Hartigan-Wong es, en general, más rápido y también más eficiente, en el sentido de que con mayor probabilidad da un clustering óptimo.⁹

El método de k-medias está implementado en R en la función kmeans. Su sintaxis básica es la siguiente:

kmeans(x, centers=..., iter.max=..., algorithm =...)

donde:

• x es la matriz o el data frame cuyas filas representan los objetos; en ambos casos, todas las variables han de ser numéricas.

• centers sirve para especificar los centros iniciales, y se puede usar de dos maneras: igualado a un número k, R escoge aleatoriamente los k centros iniciales, mientras que igualado a una matriz de k filas y el mismo número de columnas que x, R toma las filas de esta matriz como centros de partida.

• iter.max permite especificar el número máximo de iteraciones a realizar; su valor por defecto es 10. Al llegar a este número máximo de iteraciones, si el algoritmo aún no ha acabado porque los clusters aún no hayan estabilizado, se para y da como resultado los clusters que se han obtenido en la última iteración.

• algorithm indica el algoritmo a usar. Puede tomar como valor cualquiera de los que hemos explicado, y se ha de entrar entrecomillado. El método por defecto, que usa si no especificamos ninguno, es el de Hartigan-Wong.

Otros parámetros se pueden consultar en la Ayuda de la función.

Para ilustrar el funcionamiento de esta función, usaremos la tabla de datos saving del paquete faraway, que nos da 5 indicadores económicos de 50 países en el período 1960–1970. Dichos indicadores son:

• sr: la tasa de ahorro de cada país.
• pop15: su porcentaje de población menor de 15 años.
• pop75: su porcentaje de población mayor de 75 años.
• dpi: su renta per cápita en dólares.
• ddpi: su tasa de crecimiento, como porcentaje de su renta per cápita.

Echemos un vistazo a la tabla de datos:

library(faraway)
str(savings) 

## 'data.frame':	50 obs. of  5 variables:
##  $ sr   : num  11.43 12.07 13.17 5.75 12.88 ...
##  $ pop15: num  29.4 23.3 23.8 41.9 42.2 ...
##  $ pop75: num  2.87 4.41 4.43 1.67 0.83 2.85 1.34 0.67 1.06 1.14 ...
##  $ dpi  : num  2330 1508 2108 189 728 ...
##  $ ddpi : num  2.87 3.93 3.82 0.22 4.56 2.43 2.67 6.51 3.08 2.8 ...

head(savings)

##              sr pop15 pop75     dpi ddpi
## Australia 11.43 29.35  2.87 2329.68 2.87
## Austria   12.07 23.32  4.41 1507.99 3.93
## Belgium   13.17 23.80  4.43 2108.47 3.82
## Bolivia    5.75 41.89  1.67  189.13 0.22
## Brazil    12.88 42.19  0.83  728.47 4.56
## Canada     8.79 31.72  2.85 2982.88 2.43

En este ejemplo, para poder representar gráficamente los resultados obtenidos, sólo usaremos los indicadores tasa de ahorro (sr) y renta per cápita (dpi) de los países.

savings2=savings[,c(1,4)]

Vamos a clasificar los 50 países en 4 clusters. Este número lo hemos elegido por ahora de manera arbitraria, en la próxima sección ya explicaremos cómo se puede hallar el número más adecuado de clusters en el que clasificar una determinada tabla de datos. Vamos a usar el método por defecto de R, y le dejaremos generar al azar los centros iniciales, pero fijaremos la semilla de aleatoriedad con la función set.seed para que el resultado sea reproducible.

set.seed(100)
estudio.paises=kmeans(savings2, centers=4) 
estudio.paises

## K-means clustering with 4 clusters of sizes 20, 9, 11, 10
## 
## Cluster means:
##          sr       dpi
## 1  7.830500  260.3405
## 2 11.806667 1654.1378
## 3  9.933636  741.0073
## 4 11.141000 2709.2790
## 
## Clustering vector:
##      Australia        Austria        Belgium        Bolivia         Brazil 
##              4              2              2              1              3 
##         Canada          Chile          China       Colombia     Costa Rica 
##              4              3              1              1              1 
##        Denmark        Ecuador        Finland         France        Germany 
##              4              1              2              4              4 
##         Greece      Guatamala       Honduras        Iceland          India 
##              3              1              1              2              1 
##        Ireland          Italy          Japan          Korea     Luxembourg 
##              3              2              2              1              4 
##          Malta         Norway    Netherlands    New Zealand      Nicaragua 
##              3              4              2              2              1 
##         Panama       Paraguay           Peru    Philippines       Portugal 
##              3              1              1              1              3 
##   South Africa South Rhodesia          Spain         Sweden    Switzerland 
##              3              1              3              4              4 
##         Turkey        Tunisia United Kingdom  United States      Venezuela 
##              1              1              2              4              3 
##         Zambia        Jamaica        Uruguay          Libya       Malaysia 
##              1              1              3              1              1 
## 
## Within cluster sum of squares by cluster:
## [1]  187921.7  577293.5  272602.3 2894953.3
##  (between_SS / total_SS =  91.8 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"    
## [5] "tot.withinss" "betweenss"    "size"         "iter"        
## [9] "ifault"

Veamos en detalle el contenido de estudio.paises. En primer lugar, R nos dice que los clusters están formados por 20, 9, 11 y 10 países, respectivamente. Seguidamente nos da la matriz Cluster means, cuyas filas son las coordenadas de los centros de los clusters, en el orden correspondiente. A continuación, el Clustering vector nos indica a qué cluster pertenece cada país: en este caso, Australia está en el cluster 4, Austria, en el 2, y así sucesivamente. Luego nos da las “sumas de cuadrados de los clusters”, Within cluster sum of squares by cluster; es decir, el vector de las \(SSC_i\).

A modo de ejemplo, comprobemos que efectivamente la primera entrada del vector Within cluster sum of squares by cluster es \(SSC_1\). Vamos a guardar en un data frame savings.1 la subtabla de datos de los países que pertenecen al primer cluster, llamaremos centro.1 al vector de coordenadas del centro del primer cluster, y finalmente sumaremos los cuadrados de las distancias euclídeas de las filas de savings.1 a centro.1. Para ello, vamos a usar que el resultado de kmeans es una list que contiene, por un lado, la componente cluster formada por el Clustering vector de las asignaciones de objetos a clusters (y por lo tanto, podemos especificar las filas que corresponden a países que pertenecen al primer cluster con estudio.paises$cluster==1) y, por otro lado, la componente centers formada por la matriz Cluster means de centros (y por lo tanto las coordenadas del centro del primer cluster se obtienen con estudio.paises$centers[1,]).

savings.1=savings2[estudio.paises$cluster==1, ]   #Miembros del primer cluster
centro.1=estudio.paises$centers[1,]   #Centro del primer cluster
dist.euclid2=function(x,y){sum((x-y)^2)} #Distancia euclídea al cuadrado
distancia_a_centro.1=function(x){dist.euclid2(x, centro.1)}  #Distancia de un punto al centro del primer cluster
sum(apply(savings.1, MARGIN=1, FUN=distancia_a_centro.1))  #SSC_1

## [1] 187921.7

Coincide con la primera entrada del vector Within cluster sum of squares by cluster. Como el resultado de kmeans contiene la componente withinss formada por el vector de las \(SSC_1\), el valor de \(SSC_1\) se puede obtener directamente con

estudio.paises$withinss[1]

## [1] 187921.7

Debajo del vector de las \(SSC_i\), R nos da el porcentaje between_SS / total_SS, en este caso, un 91.8%. Aquí, total_SS representa la suma \(SST\) de los cuadrados de las distancias de los puntos al centro \(M\) del conjunto de todos los puntos, y between_SS indica la suma \(SSB\) de los cuadrados de las distancias de los centros de los clusters a \(M\), contada cada una de ellas tantas veces como elementos tiene cluster. Es decir, si los puntos de partida son \(x_1,\ldots,x_n\) y cada cluster \(C_i\) tiene centro \(c_i\) y está formado por \(n_i\) puntos, entonces \[ SST=\sum_{i=1}^n \|x_i-M\|^2,\qquad SSB=\sum_{i=1}^k n_i\|c_i-M\|^2. \] Los valores de \(SST\), \(SSC\) y \(SSB\) son las componentes totss, tos.withinss y betwenss, respectivamente, del resultado de kmeans.

Resulta que se tiene la identidad de sumas de cuadrados \[ SST=SSC+SSB \] que representa que la variabilidad total de los datos es igual a la suma de las variabilidades dentro de los clusters (la suma \(SSC\)) más la variabilidad de los centros de los clusters (\(SSB\)). Por lo tanto, el porcentaje between_SS / total_SS indica la fracción de la variabilidad total que explica la variabilidad de los centros de los clusters. Como, dada una tabla de datos, el valor de \(SST\) es fijo, una mayor fracción \(SSB/SST\) es equivalente a una menor \(SSC\), y por lo tanto a un mejor clustering.

Comprobemos todas estas afirmaciones en nuestro ejemplo. Vamos a empezar calculando a mano \(SST\) y comprobando que coincide con estudio.paises$totss. Para ello, calculamos el punto medio de todo el conjunto de datos y a continuación la suma de las distancias al cuadrado de todos los puntos a este centro global. Usaremos la función dist.euclid2 que hemos definido hace un rato para calcular las distancias euclídeas al cuadrado.

centro.global=apply(savings2, MARGIN=2, FUN=mean)   #El punto medio global, M
centro.global

##       sr      dpi 
##    9.671 1106.758

dist_a_centro=function(x){dist.euclid2(x,centro.global)}
SST=sum(apply(savings2, MARGIN=1, FUN=dist_a_centro))
SST

## [1] 48110220

estudio.paises$totss  #La SST contenida en el resultado de la función kmeans

## [1] 48110220

El valor de \(SSC\) ha de ser la suma de las \(SSC_i\), que ya hemos visto que forman el vector estudio.paises$withinss.

SSC=sum(estudio.paises$withinss)
SSC

## [1] 3932771

estudio.paises$tot.withinss  #La SSC contenida en el resultado de la función kmeans

## [1] 3932771

Finalmente, vamos a calcular la \(SSB\). Recordemos que la matriz de los centros de los clusters es el objeto estudio.paises$centers y se tiene que los tamaños de los clusters forman el vector estudio.paises$size.

Centros=estudio.paises$centers #La matriz de centros
Distancias_centros_centroglobal=apply(Centros,MARGIN=1,FUN=dist_a_centro)  #Distancias de los centros a M
SSB=sum(Distancias_centros_centroglobal*estudio.paises$size)  
SSB

## [1] 44177450

estudio.paises$betweenss  #La SSB contenida en el resultado de la función kmeans

## [1] 44177450

Comprobemos finalmente la identidad \(SST=SSC+SSB\):

SST

## [1] 48110220

SSB+SSC

## [1] 48110220

y comprobemos que el cociente \(SSB/SST\) es el 91.8% que nos ha dado R:

SSB/SST

## [1] 0.918255

Así pues, el resultado de una aplicación de kmeans es una list. R nos da sus componentes al final del resultado de kmeans, bajo Available components:. A modo de resumen, vamos a recordar las componentes más interesantes para nuestros propósitos:

• size: vector de tamaños de los clusters.

• cluster: vector de enteros indicando a qué cluster pertenece cada fila de la tabla de datos.

• centers: matriz de filas los vectores de coordenadas de los centros de los clusters.

• totss: la \(SST\).

• withinss: el vector de las \(SSC_i\).

• tot.withinss: la \(SSC\), es decir, la suma del vector anterior.

• betweenss: la \(SSB\).

Antes de continuar, tenemos de hacer un inciso. Cuando usamos un algoritmo de k-means partiendo de una configuración aleatoria de los centros iniciales, los resultados no tienen por qué ser los mismos cada vez que se ejecuta el algoritmo, debido a que distintas configuraciones iniciales de centros pueden desembocar en clusterings diferentes. Por este motivo, en el ejemplo anterior hemos usado set.seed(100) para que fuera reproducible. Con otra semilla de aleatoriedad, podría haber dado un resultado diferente, o no. Por ejemplo, con set.seed(2000) obtenemos un clustering con porcentaje \(SSB/SST\) más alto, y por lo tanto mejor (lo confirmamos comprobando que su \(SSC\) es menor que la anterior).

set.seed(2000)
estudio.paises2=kmeans(savings2, centers=4)
estudio.paises2

## K-means clustering with 4 clusters of sizes 9, 3, 30, 8
## 
## Cluster means:
##          sr       dpi
## 1 11.603333 1546.5244
## 2  7.736667 3428.0867
## 3  8.484667  407.2647
## 4 12.671250 2364.6250
## 
## Clustering vector:
##      Australia        Austria        Belgium        Bolivia         Brazil 
##              4              1              4              3              3 
##         Canada          Chile          China       Colombia     Costa Rica 
##              2              3              3              3              3 
##        Denmark        Ecuador        Finland         France        Germany 
##              4              3              1              4              4 
##         Greece      Guatamala       Honduras        Iceland          India 
##              3              3              3              1              3 
##        Ireland          Italy          Japan          Korea     Luxembourg 
##              1              1              1              3              4 
##          Malta         Norway    Netherlands    New Zealand      Nicaragua 
##              3              4              1              1              3 
##         Panama       Paraguay           Peru    Philippines       Portugal 
##              3              3              3              3              3 
##   South Africa South Rhodesia          Spain         Sweden    Switzerland 
##              3              3              3              2              4 
##         Turkey        Tunisia United Kingdom  United States      Venezuela 
##              3              3              1              2              3 
##         Zambia        Jamaica        Uruguay          Libya       Malaysia 
##              3              3              3              3              3 
## 
## Within cluster sum of squares by cluster:
## [1]  531037.1  543998.3 1580679.3  211532.6
##  (between_SS / total_SS =  94.0 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"    
## [5] "tot.withinss" "betweenss"    "size"         "iter"        
## [9] "ifault"

estudio.paises2$tot.withinss  #Nueva SSC

## [1] 2867247

estudio.paises$tot.withinss  #Anterior SSC

## [1] 3932771

La moraleja es que conviene ejecutar unas cuantas veces la función kmeans con centros iniciales aleatorios y quedarnos con el mejor clustering que obtengamos. En nuestro caso, en el bloque de código siguiente realizamos 10000 ejecuciones aleatorias y no encontramos ningún clustering con \(SSC\) inferior a estudio.paises2$tot.withinss, por lo que consideraremos estudio.paises2 como una clasificación óptima de nuestros datos en 4 clases.

fun.SSC=function(x){
set.seed(x)  
kmeans(savings2, centers=4)$tot.withinss
}
X=sample(10^8,10000)   #10000 semillas aleatorias
min(sapply(X,FUN=fun.SSC))  #Ejecutamos 10000 kmeans aleatorios y calculamos su mínimo SSC

## [1] 2867247

Para visualizar gráficamente un clustering de datos bidimensionales, lo más sencillo es producir el gráfico de dispersión de los puntos coloreándolos según los clusters.

plot(savings2, col=estudio.paises2$cluster, xlab="Tasa de ahorro", ylab="Renta per cápita",pch=20)
text(savings2, rownames(savings2), col=estudio.paises2$cluster, cex=0.6, pos=1) #Añadimos los nombres de los países a los puntos

Obtenemos la Figura 11.1. Observamos que los países “cercanos” están coloreados con el mismo color. Así, por ejemplo, los países más desarrollados están coloreados de color rojo y están en la parte superior del gráfico, ya que tienen la renta per cápita más alta, mientras que los países menos desarrollados están coloreados de color verde y están en la parte inferior del gráfico al tener la renta per cápita más baja.

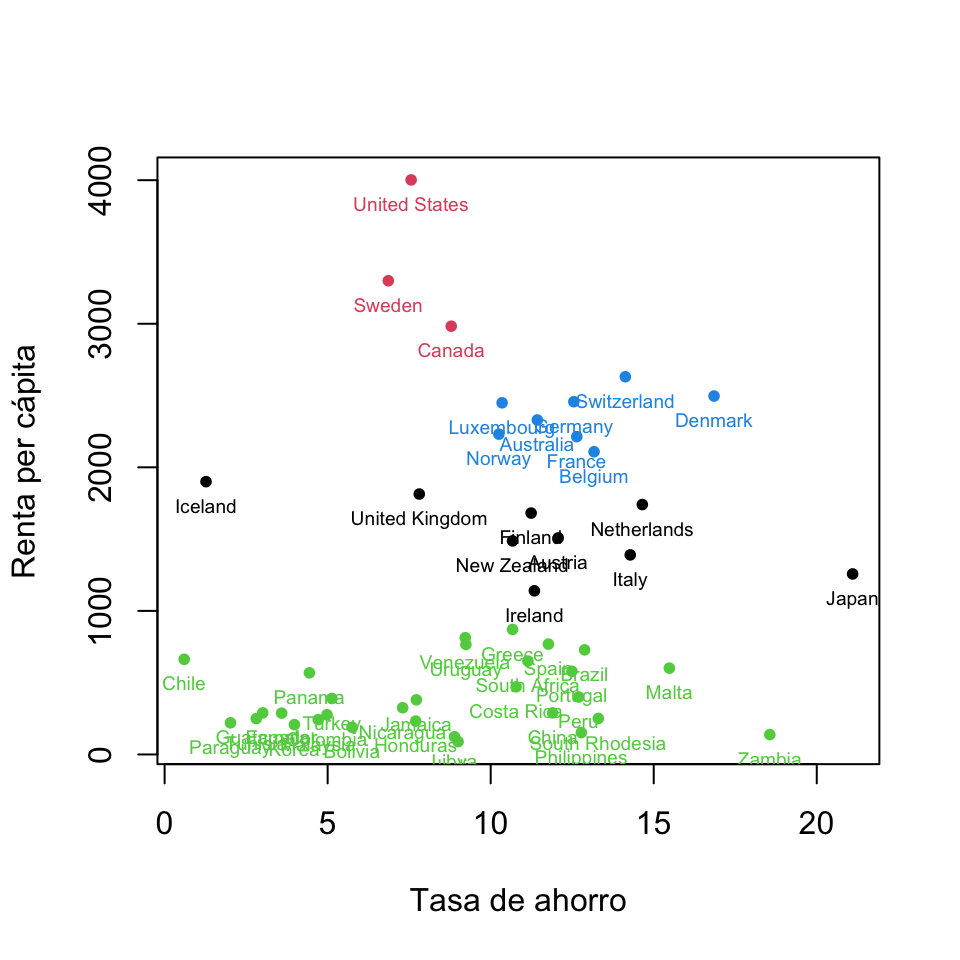
Figura 11.1: Representación gráfica de las variables “Tasa de ahorro” y “Renta per cápita” agrupadas según el clustering estudio.paises2.

Existen paquetes que aportan funciones para dibujar clusterings más informativos. Por ejemplo, la función clusplot del paquete cluster enmarca los clusters con elipses. Su sintaxis básica es

clusplot(x, vector, parámetros)

donde

• x es la matriz o la tabla de datos numéricos.

• El vector es la componente cluster del resultado de kmeans.

• Algunos otros parámetros útiles:

  • shade: un parámetro lógico que igualado a TRUE sombrea las elipses según su densidad (número de puntos dividido entre área de la elipse): más densamente cuanto más densas.

  • color: un parámetro lógico que igualado a TRUE colorea las elipses según su densidad, por defecto de azul a granate por orden creciente de intensidad.

  • labels, que puede tomar (entre otros) los valores siguientes: 0 (no añade ninguna etiqueta), 2 (etiqueta los puntos y las elipses), 3 (etiqueta solo los puntos), 4 (etiqueta solo las elipses).

  • col.clus: los colores de las elipses.

  • col.p: los colores de los puntos.

  • col.txt: los colores de las etiquetas.

  • lines, permite añadir líneas uniendo los clusters y puede tomar los valores siguientes: 0 (no añade ninguna línea), 1 (las líneas unen los centros) y 2 (las líneas unen las fronteras de las elipses). Estas líneas nos permiten hacernos una idea de las distancias entre los clusters.

  • cex y cex.text permiten modificar el tamaño de los puntos y de las etiquetas.

Esta función dispone de muchos más parámetros, que pueden consultarse en la Ayuda de clusplot.default. A modo de ejemplo, el código

library(cluster)
clustering=estudio.paises2$cluster
clusplot(savings2, clustering, shade=TRUE, lines=0, labels=3, color=TRUE,
          col.p="black", main="", sub="", cex.txt=0.75)

produce la Figura 11.2 (con main="" y sub="" hemos eliminado el título y subtítulo por defecto). Observaréis que los puntos de clusters diferentes se han representado por medio de símbolos diferentes, y que los ejes de coordenadas no se corresponden con las variables originales. En realidad, clusplot ha realizado un Análisis de Componentes Principales (ACP) de los datos, que para dos variables simplemente significa que ha centrado los datos y ha tomado como eje de abscisas la variable con mayor varianza. En este caso, tras centrar los datos, ha tomado como eje de abscisas (la Componente Principal 1) la “Renta per cápita” y como eje de ordenadas (la Componente Principal 2) la “Tasa de ahorro”; si no os gustan las etiquetas de los ejes por defecto, podéis modificarlas con los parámetros adecuados. Estudiaremos con detalle el Análisis de Componentes Principales en la siguiente lección.

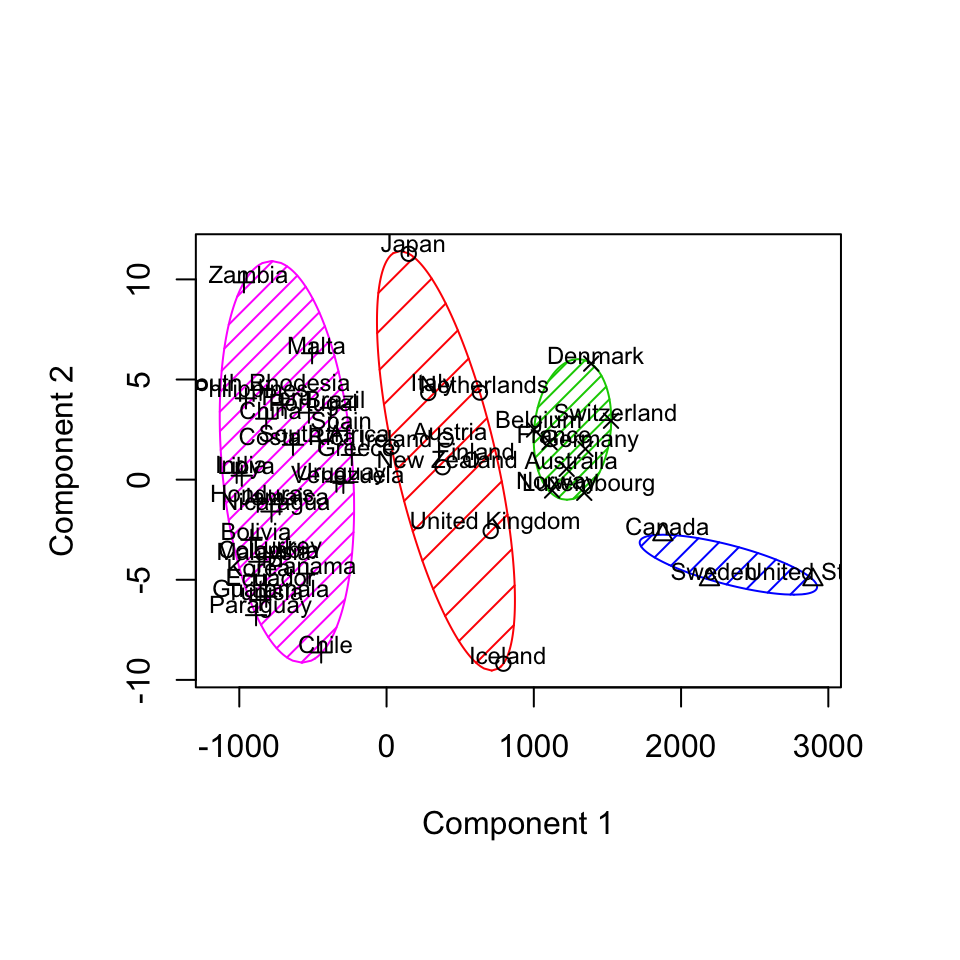
Figura 11.2: Representación gráfica del clustering “estudio.paises2” usando la función “clusplot”.

11.2 Elección del número de clusters

No se conoce ninguna manera de saber a priori el número correcto de clusters que tenemos que usar para clasificar un conjunto de datos. En cambio, sí que se dispone de algunos métodos más o menos aceptados para decidir a posteriori, una vez clasificados los datos en diversos números de clusters, cuál es el más adecuado.

El procedimiento general es el siguiente:

1. Tomamos una secuencia de valores consecutivos de k, usualmente de 2 hasta un tercio del número total de puntos (para que el número medio de puntos por cluster no sea inferior a 3).

2. Para cada k, ejecutamos varias veces la función kmeans con diferentes configuraciones iniciales de k centros, y nos quedamos con un clustering que tenga el menor valor de \(SSC\) de los obtenidos para esta k. Llamaremos \(SSC(k)\) al valor mínimo de las \(SSC\) obtenidas para k clusters.

3. A partir del vector de los \(SSC(k)\), medimos “algo” y a partir de esta medición decidimos la k.

Por ejemplo, una regla bastante extendida, y claramente arbitraria, es la regla del 90%: “se toma el valor de k mas pequeño para el que \((SST-SSC(k))/SST\geq 0.9\)” (observad que \(SST-SSC(k)\) es la \(SSB\) de un clustering que tenga \(SSC=SSC(k)\)).

Vamos a organizar la información necesaria para aplicar los métodos que vamos a explicar en esta sección a nuestra tabla de datos savings2. Como la tabla contiene información sobre 50 países, probaremos los valores para k de 2 a 17. Para cada valor de k, calcularemos 500 clusterings partiendo de k centros escogidos aleatoriamente con valores de set.seed tomados de un vector aleatorio de 500 entradas escogidas de manera equiprobable (con sample) entre 1 y 50000. De esta manera, los resultados serán bastante aleatorios, pero como hemos fijado el vector de semillas en un bloque de código anterior, serán reproducibles. Entonces, para cada k guardaremos la semilla del primer clustering que dé el valor mínimo de \(SSC\) entre las 500 repeticiones (para poder volver a calcularlo si es necesario) y su valor de \(SSC\). Finalmente, organizaremos la información en una matriz Resultados de 3 columnas: una para los valores de k, una para los primeros valores de las semillas de aleatoriedad que han dado, para cada k, la \(SSC\) mínima, y una tercera columna con los correspondientes valores mínimos \(SSC(k)\).

x=sample(50000,500,rep=FALSE) #Las 500 semillas aleatorias que usaremos
Resultados=c() 
for(k in 2:17){
  SSCs=c()	
  for (i in x){
    set.seed(i)
    SSCs=cbind(SSCs,c(i,kmeans(savings2,k)$tot.withinss))
    }	
  SSC.min=SSCs[,which.min(SSCs[2,])]
  Resultados=rbind(Resultados,c(k,SSC.min))}
dimnames(Resultados)=list(NULL, c("k", "semilla", "SSC"))
Resultados

##        k semilla         SSC
##  [1,]  2   48465 10550652.77
##  [2,]  3   48465  5290876.37
##  [3,]  4     763  2867247.28
##  [4,]  5   48465  1561126.26
##  [5,]  6   29454  1067250.81
##  [6,]  7   24564   672060.28
##  [7,]  8   24564   506455.05
##  [8,]  9   49964   385292.98
##  [9,] 10    9125   302132.14
## [10,] 11   45374   224846.04
## [11,] 12     430   176821.57
## [12,] 13    7115   130373.92
## [13,] 14   23066   108975.59
## [14,] 15    7115    97564.19
## [15,] 16   37528    80886.18
## [16,] 17   37528    75940.10

Si ahora, por ejemplo, quisiéramos aplicar la regla del 90%, calcularíamos para cada k el valor de \((SST-SS(k))/SST\) y tomaríamos el primer k para el que este cociente fuera mayor de 0.9

SST #Recordemos el valor de SST

## [1] 48110220

SSB=SST-Resultados[,3]
Resultados[min(which(SSB/SST>0.9)),1]

## k 
## 4

Con la regla del 90% hubiéramos escogido \(k=4\), que es justamente lo que hemos hecho en la sección anterior.

Un método muy popular para elegir el valor de k es el método del “codo”, que consiste en lo siguiente. Si representamos en un gráfico los puntos \((k,SS_C(k))\), la línea quebrada que se obtiene uniéndolos es más o menos cóncava. Si podemos detectar un valor de k a partir del cual \(SS_C(k)\) disminuya más lentamente que antes de él, ese k será el número recomendable de clusters a usar; si, en cambio, no existe ningún k con esta propiedad, es señal de que no existe ninguna clasificación natural de los objetos bajo estudio. Esta regla se llama el método del “codo” porque si superpusiésemos un brazo en la representación gráfica de los puntos \((k,SS_C(k))\), el punto correspondiente al k elegido sería dónde colocaríamos el codo.

Apliquemos este método a nuestra tabla de datos savings2. El código siguiente produce la Figura 11.3, que muestra que el número k adecuado de clusters parece ser 5:

plot(Resultados[,c(1,3)], xlab="k", ylab="SSC(k)", type="b", col="red")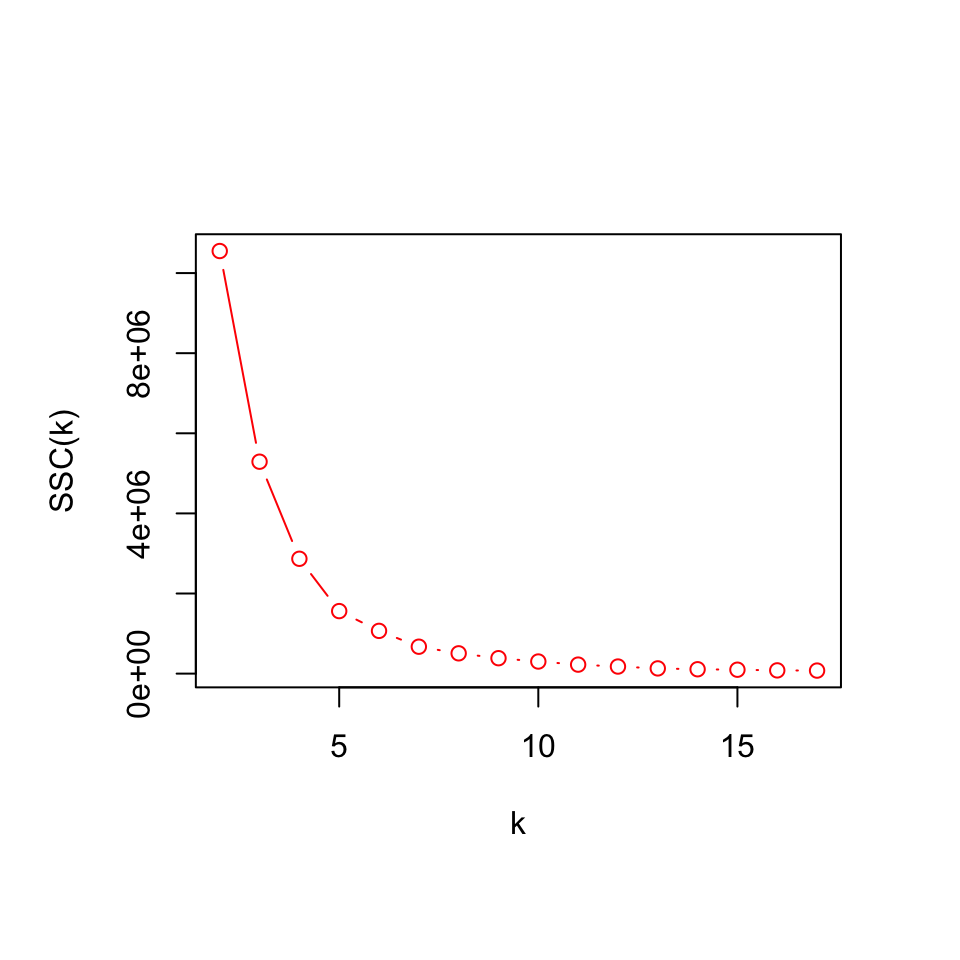 

Figura 11.3: Aplicación del método del codo para hallar el número óptimo de clusters en la tabla de datos “savings2”.

El último test del que queremos hablar para determinar el número adecuado de clusters es el llamado test F, el cual, aunque es un método muy usado, en nuestra opinión no tiene una justificación teórica suficiente. En este test, para cada k, se calcula el estadístico siguiente: \[ F_k=\frac{SS_C(k)-SS_C(k+1)}{SS_C(k+1)/(n-k-1)}, \] donde, recordemos, \(n\) es el número de filas de nuestra tabla de datos. Se toma entonces como p-valor del contraste, para cada k, la probabilidad de que una variable con distribución F de Fisher con \(p\) y \(p(n-k-1)\) grados de libertad (donde \(p\) es el número de variables de nuestra tabla de datos) tome un valor mayor que \(F_k\): \[ \mbox{p-valor}_k=P(F_{p,p(n-k-1)} > F_k). \] Una vez hallado este p-valor para cada k, escogemos como k adecuado aquel cuyo p-valor sea el más pequeño.

Vamos a aplicar este test F a nuestra tabla de datos. Recordemos que ya hemos calculado los valores \(SSC(k)\), en la tercera columna de la matriz Resultados.

k=2:16
n=dim(savings2)[1] 
p=dim(savings2)[2]
c(n,p)

## [1] 50  2

SSC=Resultados[ ,3]
F_k=(SSC[-16]-SSC[-1])/(SSC[-1]/(n-k-1))
p.valores=1-pf(F_k,p,p*(n-k-1))
F.test=cbind(k,F_k,p.valores)
F.test

##        k       F_k    p.valores
##  [1,]  2 46.723732 8.215650e-15
##  [2,]  3 38.882917 5.768719e-13
##  [3,]  4 37.649386 1.314504e-12
##  [4,]  5 20.361212 5.400730e-08
##  [5,]  6 25.285221 2.307249e-09
##  [6,]  7 13.733538 6.911503e-06
##  [7,]  8 12.893163 1.352875e-05
##  [8,]  9 11.009864 5.973559e-05
##  [9,] 10 13.405429 9.904776e-06
## [10,] 11 10.320742 1.083179e-04
## [11,] 12 13.181803 1.268388e-05
## [12,] 13  7.068920 1.573935e-03
## [13,] 14  4.093705 2.082776e-02
## [14,] 15  7.010500 1.705498e-03
## [15,] 16  2.149334 1.246509e-01

El p-valor más pequeño se obtiene para \(k=2\), por lo que éste sería el número adecuado de clusters según este test. Para terminar esta sección, vamos a dibujar los clusters que se obtienen para \(k=2\) y \(k=5\):

#k=2
set.seed(48465)
kmeans2=kmeans(savings2,centers=2)
plot(savings2, col=kmeans2$cluster, xlab="Tasa de ahorro", ylab="Renta per cápita",pch=20)
text(savings2, rownames(savings2), cex=0.6, pos=1, col=kmeans2$cluster)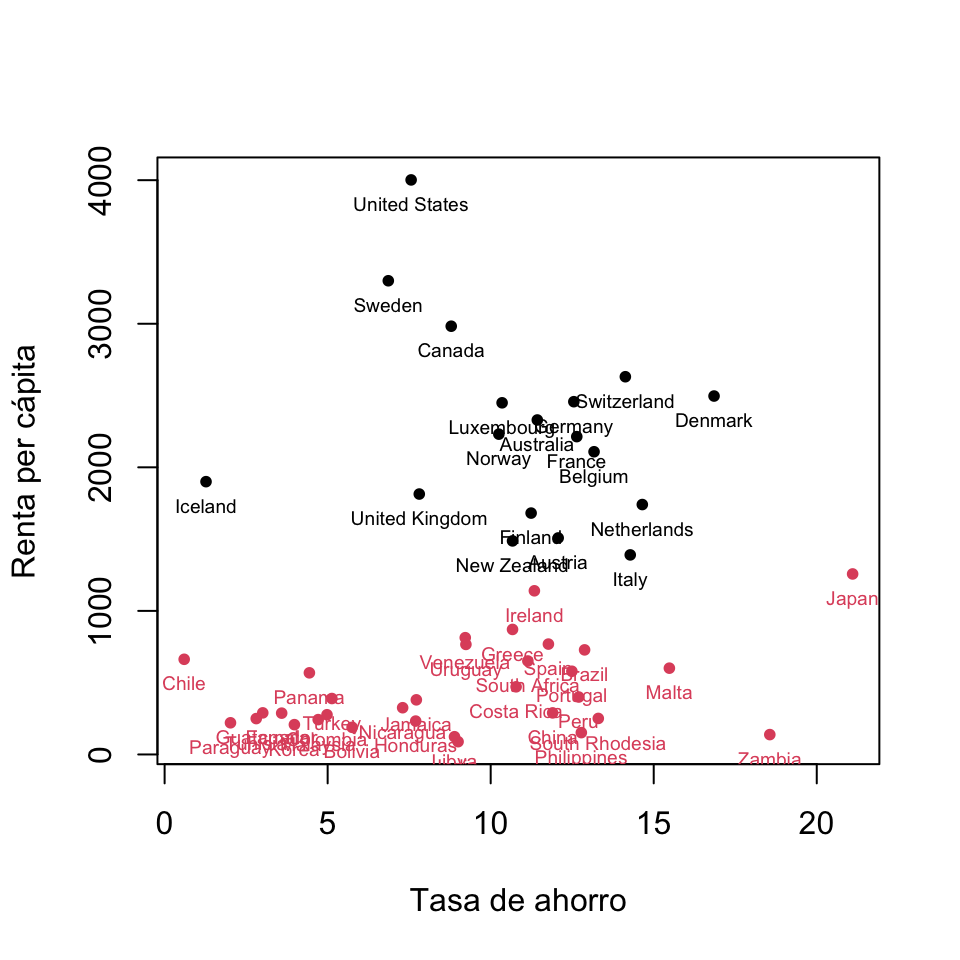 

Figura 11.4: Clustering óptimo de la tabla de datos “savings2” con 2 clusters.

#k=5
set.seed(48465)
kmeans5=kmeans(savings2,centers=5)
plot(savings2, col=kmeans5$cluster, xlab="Tasa de ahorro", ylab="Renta per cápita",pch=20)
text(savings2, rownames(savings2), cex=0.6, pos=1, col=kmeans5$cluster)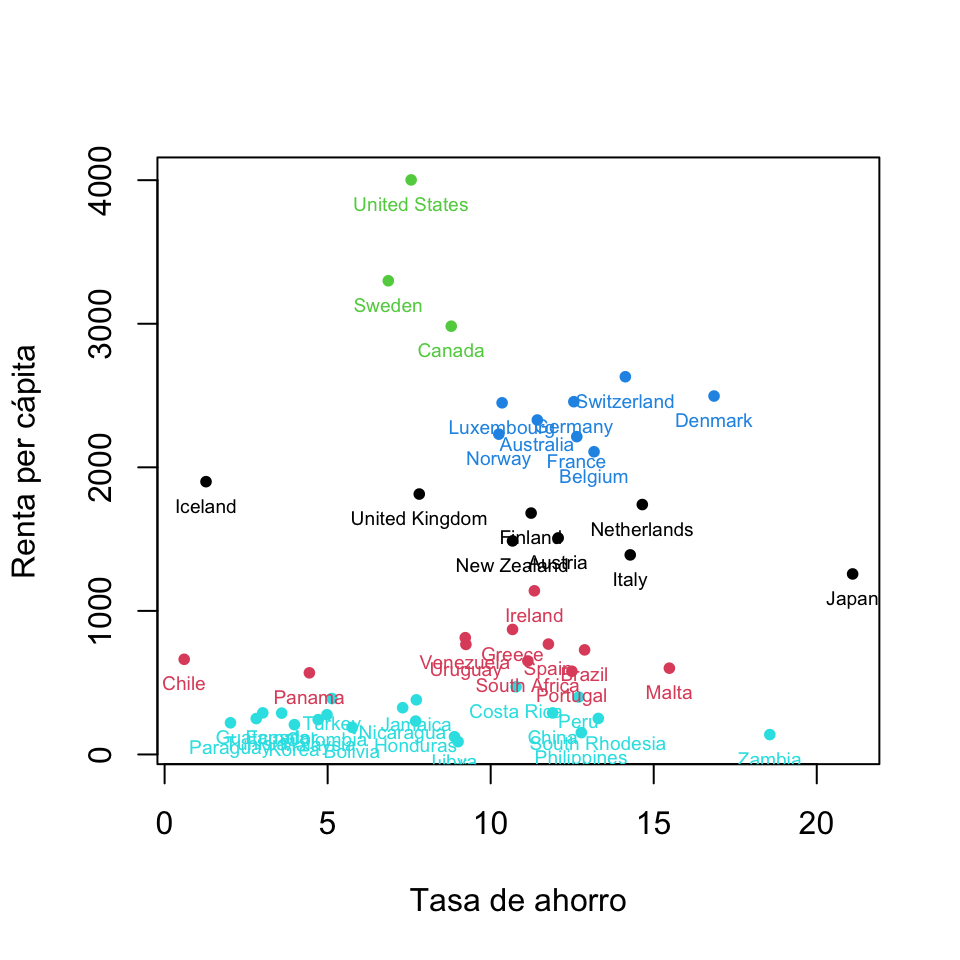 

Figura 11.5: Clustering óptimo de la tabla de datos “savings2” con 5 clusters.

11.3 Métodos jerárquicos aglomerativos

Dada una tabla de datos numéricos, un método de clustering jerárquico aglomerativo usa una matriz \(D\) de distancias entre las filas de la tabla de datos para ir agrupando secuencialmente los objetos que representan estas filas. El procedimiento básico es el siguiente:

1. Partimos de \(n\) objetos y de la matriz \(D\) de distancias entre ellos, de orden \(n\times n\).
2. Consideramos que, inicialmente, cada objeto forma un cluster de un solo elemento.
3. Hallamos los dos clusters \(C_1\) y \(C_2\) que están a distancia mínima.
4. Unimos estos clusters \(C_1\) y \(C_2\) en un nuevo cluster \(C_1+C_2\).
5. Eliminamos \(C_1\) y \(C_2\) de la lista de clusters.
6. Recalculamos la distancia de \(C_1+C_2\) a los demás clusters, con lo que obtendremos una matriz de distancias de un orden inferior a la que teníamos; la manera de recalcular estas distancias es la que da lugar a algoritmos diferentes.
7. Repetimos los pasos (3)–(6) hasta que sólo quede un único cluster.

La matriz de distancias \(D\) entre los objetos se puede calcular con la función dist, cuya sintaxis básica es

dist(x, method=...)

donde:

• x es nuestra tabla de datos (una matriz o un data frame de variables cuantitativas).

• method sirve para indicar la distancia que queremos usar, cuyo nombre se ha de entrar entrecomillado. La distancia por defecto es la euclídea que hemos venido usando hasta ahora. Otros posibles valores son (en lo que sigue, \(x=(x_1,\ldots,x_m)\) e \(y=(y_1,\ldots,y_m)\) son dos vectores de \(\mathbb{R}^m\)):

  • La distancia de Manhattan, "manhattan", que entre \(x\) e \(y\) vale \(\sum\limits_{i=1}^m |x_i-y_i|\).
  • La distancia del máximo, "maximum", que entre \(x\) e \(y\) vale \(\max_{i=1,\ldots,m} |x_i-y_i|\).
  • La distancia de Canberra, "canberra", que entre \(x\) e \(y\) vale \[ \sum_{i=1}^m \frac{|x_i-y_i|}{|x_i|+|y_i|}. \]
  • La distancia de Minkowski, "minkowski", que depende de un parámetro \(p>0\) (que se ha de especificar en la función dist con p igual a su valor), y que entre \(x\) e \(y\) vale \[ \sqrt[p]{\sum_{i=1}^m |x_i -y_i|^p} \] Observad que cuando \(p=1\) se obtiene la distancia de Manhattan y cuando \(p=2\) se obtiene la distancia euclídea usual.
  • La distancia binaria, "binary", que sirve básicamente para comparar vectores binarios (si los vectores no son binarios, R los entiende como binarios sustituyendo cada entrada diferente de 0 por 1). La distancia binaria entre \(x\) e \(y\) binarios es el número de posiciones en las que estos vectores tienen entradas diferentes, dividido por el número de posiciones en las que alguno de los dos vectores tiene un 1.

Una vez calculada la matriz de distancias, los diferentes métodos de clustering jerárquico aglomerativos están implementados en R en la función hclust, cuya sintaxis básica es la siguiente:

hclust(d, method=...)

donde:

• d es la matriz de distancias entre nuestros objetos calculada con la función dist.

• method sirve para especificar cómo se define la distancia de la unión de dos clusters al resto de los clusters en el paso (6) del algoritmo general. El nombre del método se ha de entrar entrecomillado. La función hclust dispone de muchos métodos en este sentido, los más populares son los siguientes:

  • El método de enlace completo, "complete", que es el método usado por hclust por defecto: dados tres clusters \(C_1,C_2,C\), la distancia de \(C_1+C_2\) a \(C\) es
    \[ d(C_1+C_2,C)=\max\{d(C,C_1),d(C,C_2)\} \] donde (en este método y en los que siguen) las distancias entre clusters \(d(C,C_1)\) y \(d(C,C_2)\) se conocen de pasos anteriores: o bien vienen dadas por la matriz de distancias \(D\), si son clusters individuales, o bien se han calculado por este mismo método al formarse por la unión de clusters más pequeños.

  • El método de enlace simple, "single": dados tres clusters \(C_1,C_2,C\), la distancia de \(C_1+C_2\) a \(C\) es
    \[ d(C_1+C_2,C)=\min\{d(C,C_1),d(C,C_2)\}. \]

  • El método de enlace promedio, "average", más conocido en filogenética como UPGMA (Unweighted Pair Group Method Using Arithmetic averages): dados tres clusters \(C_1,C_2,C\), la distancia de \(C_1+C_2\) a \(C\) es
    \[ d(C_1+C_2,C)=\frac{|C_1|}{|C_1|+|C_2|}d(C,C_1)+\frac{|C_2|}{|C_1|+|C_2|}d(C,C_2), \] donde \(|\ |\) denota el cardinal de cada cluster.

  • El método de Ward clásico, "ward.D": dados tres clusters \(C_1,C_2,C\), la distancia de \(C_1+C_2\) a \(C\) es
    \[ \begin{array}{rl} d(C_1+C_2,C)= & \displaystyle \frac{|C|+|C_1|}{|C|+|C_1|+|C_2|}d(C,C_1)+\frac{|C|+|C_2|}{|C|+|C_1|+|C_2|}d(C,C_2)\\[2ex] & \displaystyle -\frac{|C|}{ (|C|+|C_1|+|C_2|)^2}d(C_1,C_2). \end{array} \]

Para ilustrar cómo usar los métodos aglomerativos con R usaremos la famosa tabla de datos iris que reúne las longitudes y amplitudes de los sépalos y pétalos de \(150\) flores de tres especies de iris diferentes: Setosa, Versicolor y Virginica. Vamos a escoger al azar (pero fijando la semilla de aleatoriedad, para que sea reproducible) 5 flores de cada especie, calcularemos las distancias euclídeas entre los vectores numéricos de sus longitudes y amplitudes de sépalos y pétalos, y usaremos estas distancias para calcular algunos clusterings jerárquicos aglomerativos de estas flores, con diversos métodos.

set.seed(100) 
iris.setosa=iris[iris$Species=="setosa",] #Subtabla de flores setosa
iris.versicolor=iris[iris$Species=="versicolor",] #Subtabla de flores versicolor
iris.virginica=iris[iris$Species=="virginica",] #Subtabla de flores virginica
flores.setosa=iris.setosa[sample(1:50,5),] #Muestra de 5 flores setosa
flores.versicolor=iris.versicolor[sample(1:50,5),] #Muestra de 5 flores versicolor
flores.virginica=iris.virginica[sample(1:50,5),] #Muestra de 5 flores virginica
flores=rbind(flores.setosa,flores.versicolor,flores.virginica) #Tabla de datos con las 15 flores

En el data frame flores, las filas han heredado sus números de la tabla iris original, como podemos comprobar:

head(flores)

##    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 10          4.9         3.1          1.5         0.1     setosa
## 38          4.9         3.6          1.4         0.1     setosa
## 48          4.6         3.2          1.4         0.2     setosa
## 25          4.8         3.4          1.9         0.2     setosa
## 14          4.3         3.0          1.1         0.1     setosa
## 94          5.0         2.3          3.3         1.0 versicolor

Renumeremos las filas del 1 al 15:

rownames(flores)=1:15
head(flores)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 1          4.9         3.1          1.5         0.1     setosa
## 2          4.9         3.6          1.4         0.1     setosa
## 3          4.6         3.2          1.4         0.2     setosa
## 4          4.8         3.4          1.9         0.2     setosa
## 5          4.3         3.0          1.1         0.1     setosa
## 6          5.0         2.3          3.3         1.0 versicolor

Vamos a guardar en una matriz llamada distancias.iris las distancias euclídeas entre los vectores de longitudes y amplitudes de pares de miembros de la tabla flores.

distancias.iris=dist(flores[ ,1:4])

Calculamos finalmente el clustering jerárquico de estas 15 flores usando el método del enlace completo, y lo llamamos estudio.flores para poder referirnos a él en lo sucesivo:

estudio.flores=hclust(distancias.iris)

Para poder comprender un clustering jerárquico, lo mejor es dibujarlo en forma de árbol binario o, en este contexto, de dendrograma, con los objetos que clasificamos en las hojas. Para ello le aplicamos simplemente la función plot. Al usar esta función para representar gráficamente un clustering jerárquico, hay dos parámetros que hay que tener en cuenta (aparte de los usuales):

• hang, que controla la situación de las hojas del dendrograma respecto del margen inferior.

• labels, que permite poner nombres a los objetos; por defecto, se identifican en la representación gráfica por medio de sus números de fila en la matriz o el data frame que contiene los datos.

Demos una ojeada al clustering estudio.flores; usaremos primero el valor de hang por defecto (que es hang=0.1) y luego hang=-1 para que veáis la diferencia. Pondremos además nombres a las flores para identificar su especie, etiquetas adecuadas en los ejes, y con main=""y sub="" eliminaremos el título y el subtítulo que añade R por defecto.

nombres.flores=c(paste("Set",1:5,sep=""), paste("Vers",1:5,sep=""), paste("Vir",1:5,sep=""))
nombres.flores

##  [1] "Set1"  "Set2"  "Set3"  "Set4"  "Set5"  "Vers1" "Vers2" "Vers3"
##  [9] "Vers4" "Vers5" "Vir1"  "Vir2"  "Vir3"  "Vir4"  "Vir5"

plot(estudio.flores, labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="")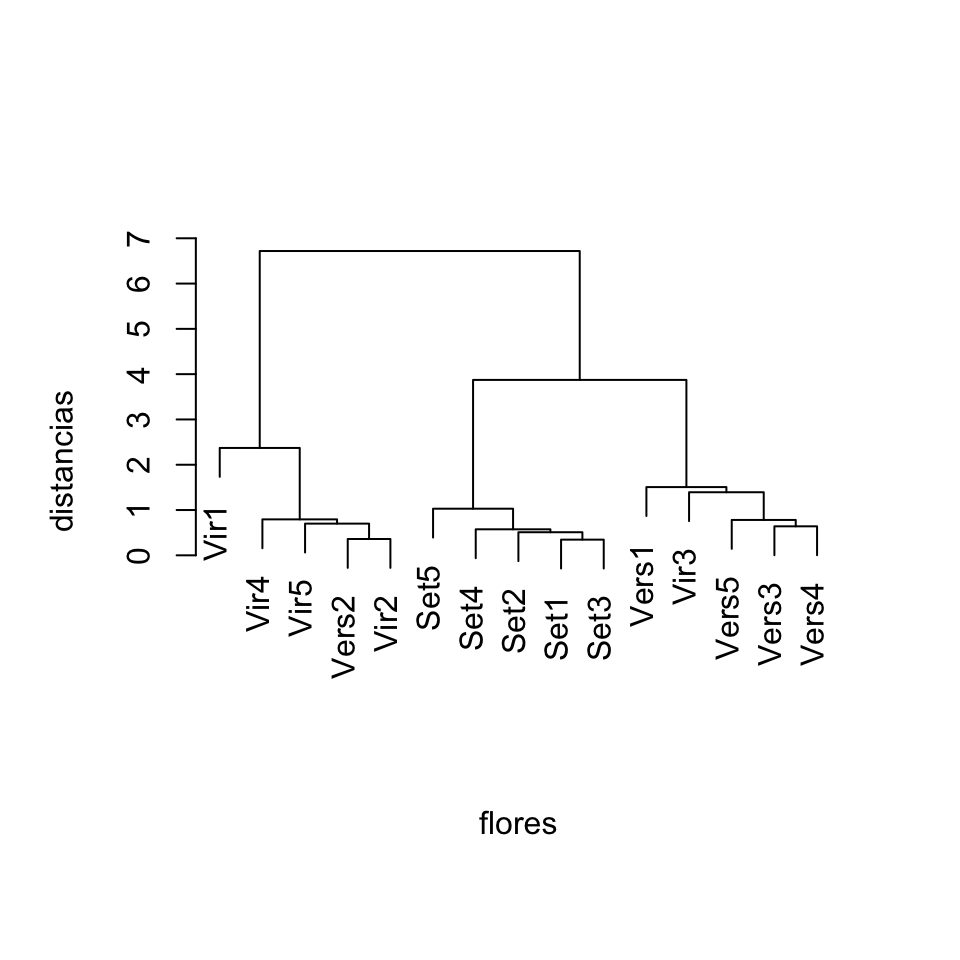

Figura 11.6: Dendrograma para 15 flores de iris producido con el método de enlace completo y dibujado con hang=0.1.

plot(estudio.flores, labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="", hang=-1)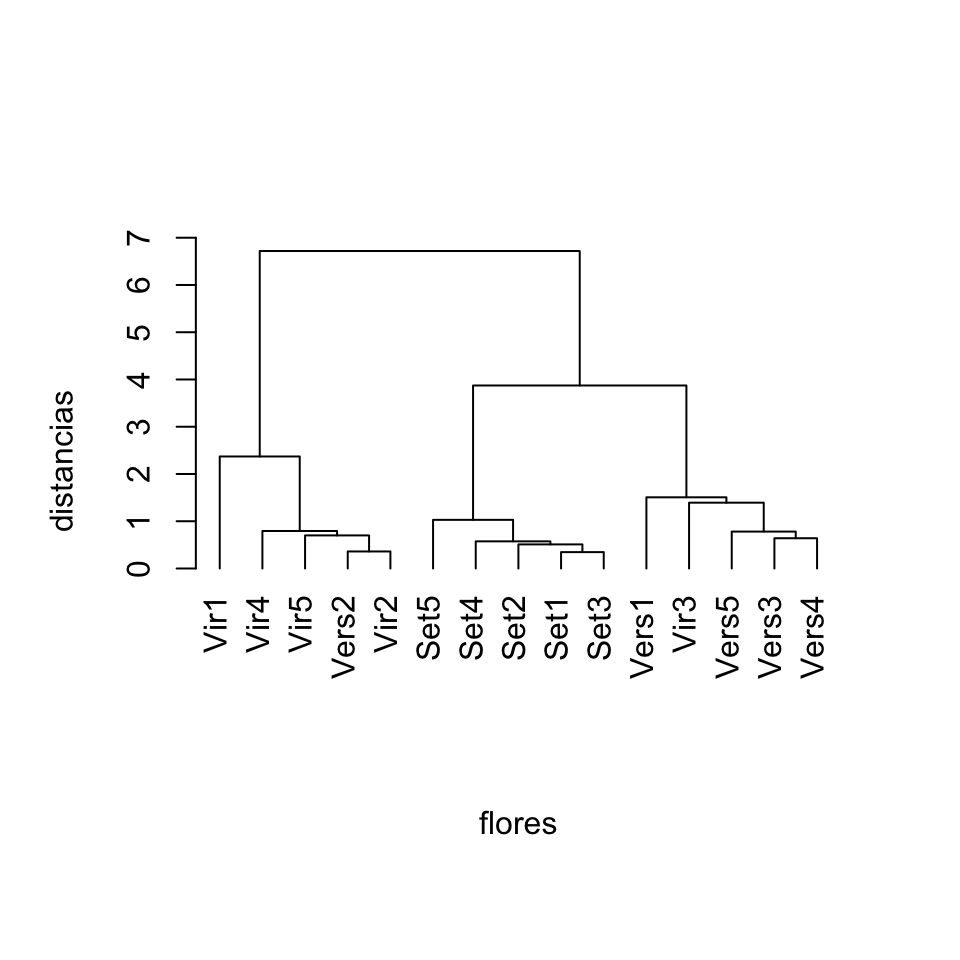

Figura 11.7: Dendrograma para 15 flores de iris producido con el método de enlace completo y dibujado con hang=-1.

Vemos cómo el clustering jerárquico separa, en nuestra muestra, las flores setosa del resto, mientras que las versicolor y las virginica aparecen algo mezcladas.

¿Cuál sería el resultado de usar otros métodos para calcular las distancias entre clusters? Veamos los resultados con los métodos de enlace simple, promedio y Ward.

plot(hclust(distancias.iris,method="single"), hang=-1, 
  labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="")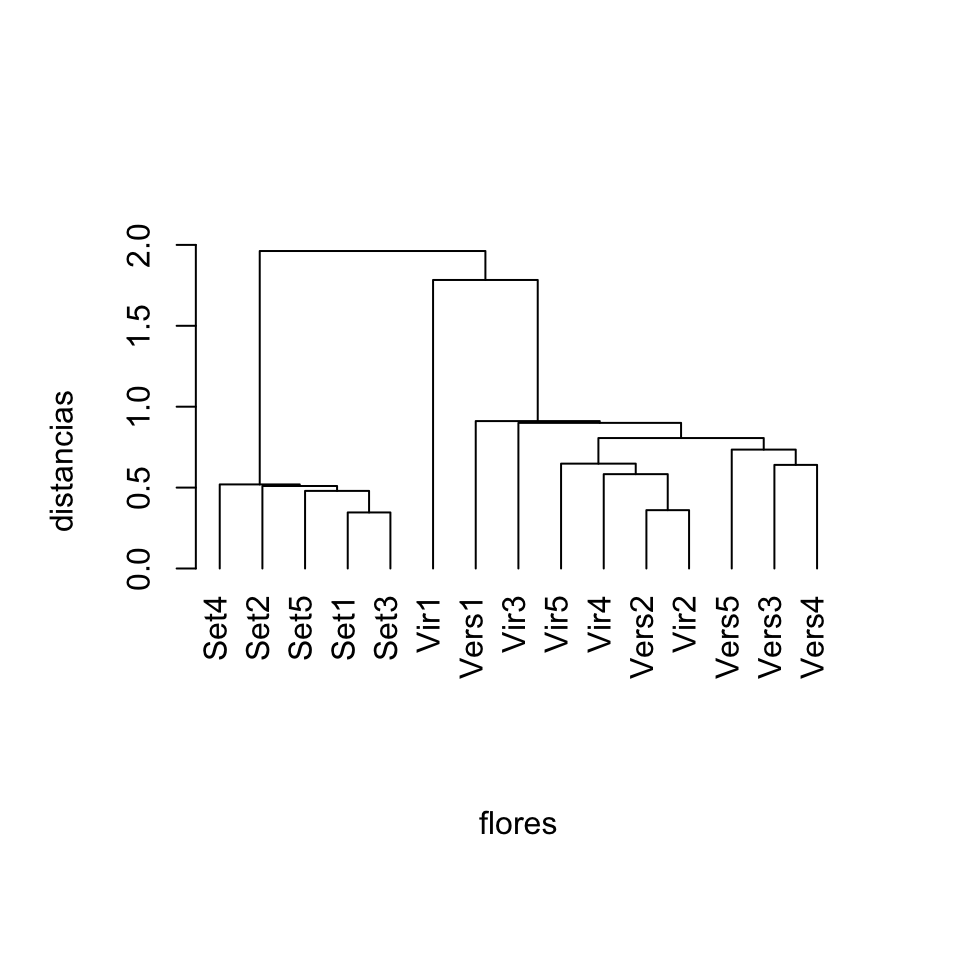 

Figura 11.8: Dendrograma para 15 flores de iris producido con el método de enlace simple.

plot(hclust(distancias.iris,method="average"), hang=-1, main="", sub="")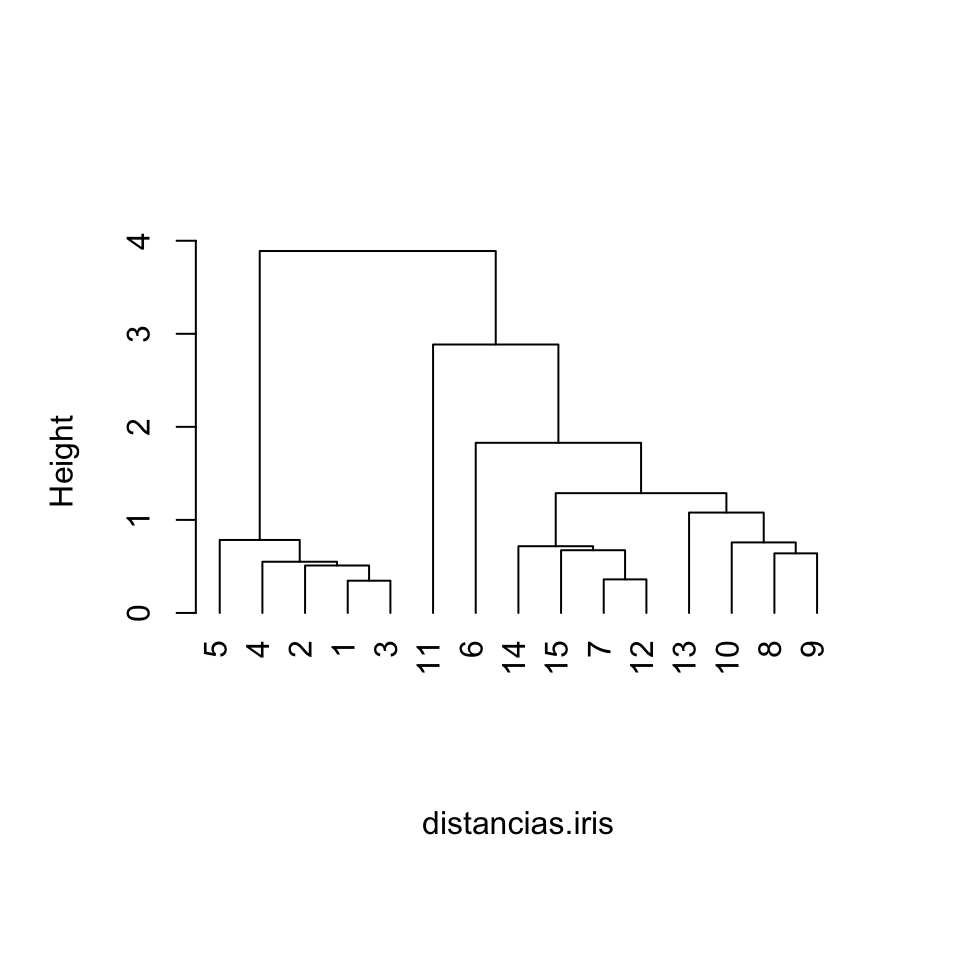

Figura 11.9: Dendrograma para 15 flores de iris producido con el método de enlace promedio.

plot(hclust(distancias.iris,method="ward.D"), hang=-1, 
  labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="")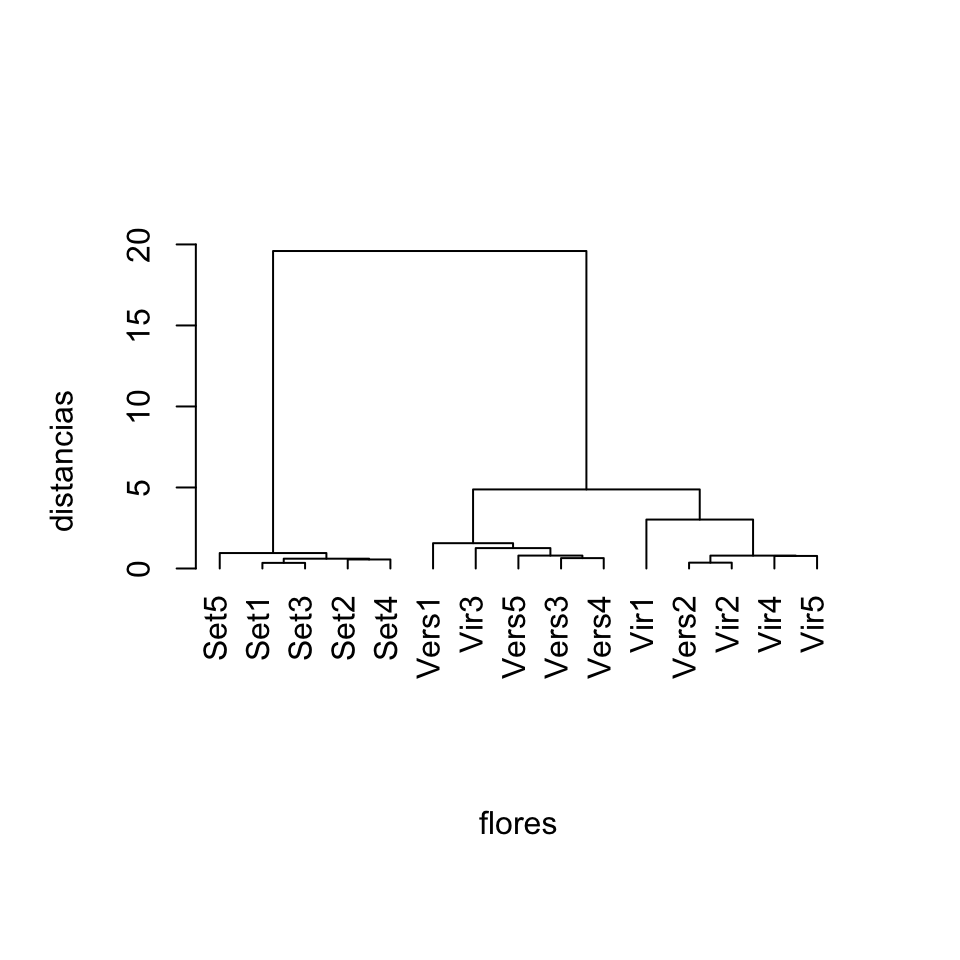

Figura 11.10: Dendrograma para 15 flores de iris producido con el método de Ward.

Observamos que cada método ha dado lugar a una jerarquía de clusters diferente.

Volviendo a la función hclust, veamos la estructura del clustering distancias.iris:

str(estudio.flores)

## List of 7
##  $ merge      : int [1:14, 1:2] -1 -7 -2 -4 -8 -15 -10 -14 -5 -13 ...
##  $ height     : num [1:14] 0.346 0.361 0.51 0.574 0.64 ...
##  $ order      : int [1:15] 11 14 15 7 12 5 4 2 1 3 ...
##  $ labels     : chr [1:15] "1" "2" "3" "4" ...
##  $ method     : chr "complete"
##  $ call       : language hclust(d = distancias.iris)
##  $ dist.method: chr "euclidean"
##  - attr(*, "class")= chr "hclust"

Como vemos, un clustering jerárquico producido con hclust es una list. Sus dos componentes más interesantes para nosotros son las siguientes.

Por un lado, la componente merge es una matriz de dos columnas que indica el orden en el que se han ido agrupando los objetos de dos en dos. En esta matriz, los objetos originales se representan con números negativos, y los nuevos clusters con números positivos que indican el paso en el que se han creado. En nuestro ejemplo:

estudio.flores$merge

##       [,1] [,2]
##  [1,]   -1   -3
##  [2,]   -7  -12
##  [3,]   -2    1
##  [4,]   -4    3
##  [5,]   -8   -9
##  [6,]  -15    2
##  [7,]  -10    5
##  [8,]  -14    6
##  [9,]   -5    4
## [10,]  -13    7
## [11,]   -6   10
## [12,]  -11    8
## [13,]    9   11
## [14,]   12   13

Este resultado nos dice que: en el primer paso del algoritmo, se han agrupado las flores 1 y 3; en el segundo paso del algoritmo, se han agrupado las flores 7 y 12; en el tercer paso del algoritmo, se han agrupado el cluster formado en el primer paso (flores 1 y 3) y la flor 2; en el cuarto paso, se han agrupado el cluster formado en el tercer paso (flores 1, 2 y 3) y la flor 4; y así sucesivamente. Es conveniente que dediquéis un rato a comparar esta matriz de emparejamientos con los dendrogramas que representan el clustering, como por ejemplo el de la Figura 11.7.

La otra componente que nos interesa es height, un vector que contiene las distancias a las que se han ido agrupando los pares de clusters, representadas como alturas en el eje de ordenadas en el dendrograma. Por ejemplo:

round(estudio.flores$height,4)

##  [1] 0.3464 0.3606 0.5099 0.5745 0.6403 0.7000 0.7810 0.7937 1.0296 1.3928
## [11] 1.5067 2.3707 3.8730 6.7186

indica que las dos flores agrupadas en el primer paso estaban a distancia 0.3464, las dos flores agrupadas en el segundo paso estaban a distancia 0.3606, el cluster y la flor agrupados en el tercer paso estaban a distancia 0.5099, etc. De nuevo, es conveniente comparar esta lista de alturas con el dendrograma de la Figura 11.7: las líneas horizontales que forman los clusters están a las alturas en los que se han unido sus componentes.

Un clustering jerárquico puede usarse para definir un clustering ordinario, es decir, una clasificación de los objetos bajo estudio. Esto se puede hacer de dos maneras: indicando cuántos clusters deseamos, o indicando a qué altura queremos cortar el dendrograma, de manera que clusters que se unan a una distancia mayor que dicha altura queden separados. Por ejemplo, en el dendrograma representado en la Figura 11.7, si cortamos a altura 3 obtenemos 3 clusters: de izquierda a derecha, uno formado por las cinco setosa, otro formado por cuatro virginica y una versicolor, y un tercero formado por la virginica y las cuatro versicolor restantes. Lo podéis comprobar imaginando una recta horizontal en el dendrograma a altura 3 y visualizando qué grupos forma.

Con R disponemos de dos funciones básicas para obtener agrupamientos a partir de un clustering jerárquico. La primera es la función cutree. Su sintaxis básica es

cutree(hclust, k=..., h=...)

donde hclust es el resultado de una función homónima, y se ha de especificar o bien el parámetro k que indica el número de clusters deseado o bien el parámetro h que indica la altura a la que queremos cortar. Veamos dos ejemplos. Para cortar a altura 3, usamos:

cutree(estudio.flores,h=3) 

##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 
##  1  1  1  1  1  2  3  2  2  2  3  3  2  3  3

Y para clasificar en 4 clusters, usamos:

cutree(estudio.flores,k=4) 

##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 
##  1  1  1  1  1  2  3  2  2  2  4  3  2  3  3

Como vemos, el resultado de cutree es un vector similar a la componente cluster de un kmeans.

Otra posibilidad es usar la función rect.hclust, que sobre el dendrograma dibujado en la instrucción inmediatamente anterior resalta los grupos enmarcándolos en rectángulos. La sintaxis es similar: se aplica al resultado de un hclust y al número k de grupos o a la altura h. Admite además un parámetro border que permite especificar los colores de los rectángulos (por defecto, todos rojos).

Veamos el resultado de su aplicación por defecto en los mismos casos que hemos aplicado cutree:

plot(estudio.flores, labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="", hang=-1)
rect.hclust(estudio.flores,h=3)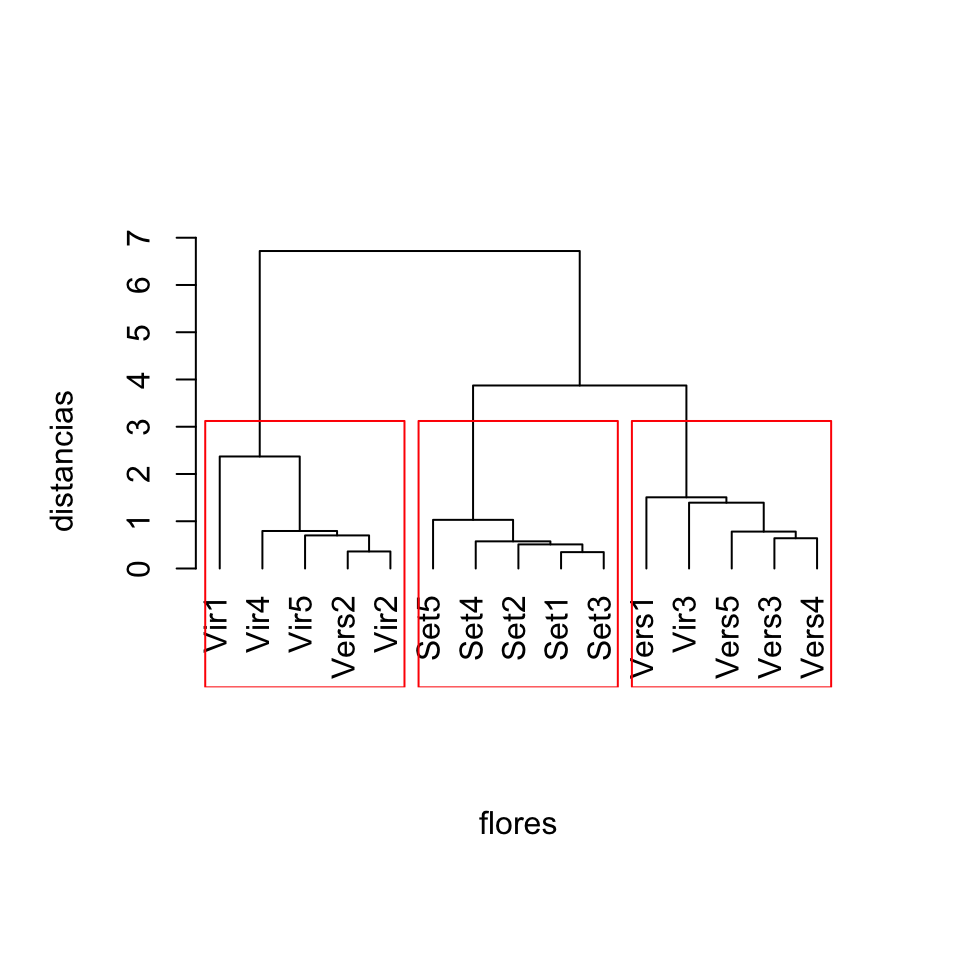

Figura 11.11: Clustering de 15 flores de iris a partir de su dendrograma calculado con el método de enlace completo, cortándolo a altura 3.

plot(estudio.flores, labels=nombres.flores, xlab="flores", ylab="distancias", main="", sub="", hang=-1)
rect.hclust(estudio.flores,k=4)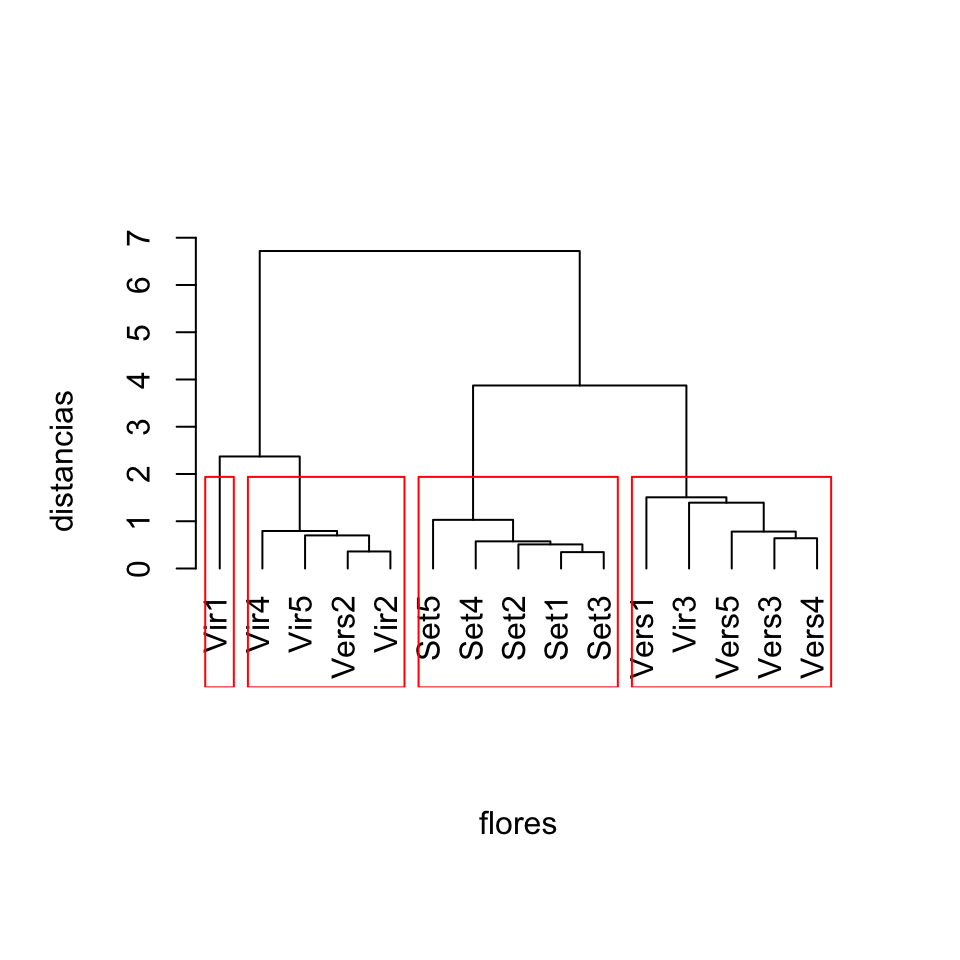  

Figura 11.12: Clustering de 15 flores de iris a partir de su dendrograma calculado con el método de enlace completo, usando 4 grupos.

11.4 Guía rápida

• kmeans aplica el algoritmo de k-means a una tabla de datos. Sus parámetros principales son:

  • centers, que sirve para especificar o bien el número de clusters o bien las coordenadas de los centros iniciales;
  • iter.max, que permite especificar el número máximo de iteraciones a realizar;
  • algorithm, que indica el algoritmo específico a usar.

  El resultado es una list cuyas componentes principales son:

  • cluster: vector que especifica a qué cluster pertenece cada individuo.
  • centers: matriz de los centros de los clusters.
  • totss: valor de \(SST\).
  • withinss: vector \((SSC_1,\ldots,SSC_k)\) .
  • tot.withinss: valor de \(SSC\).
  • betweenss: valor de \(SSB\).
  • size: vector de los tamaños de los clusters.

• clusplot del paquete cluster, permite representar gráficamente el resultado de un kmeans, enmarcando los clusters con elipses. Se aplica a la tabla de datos original y al componente cluster del kmeans, y dispone de muchos parámetros entre los que destacan, aparte de los usuales para plot:

  • shade: igualado a TRUE, sombrea las elipses según su densidad.
  • color: igualado a TRUE, colorea las elipses según su densidad.
  • labels: permite indicar qué queremos etiquetar en el gráfico.
  • col.clus: permite modificar los colores de las elipses.
  • col.p: permite modificar los colores de los puntos.
  • col.txt: permite modificar los colores de las etiquetas.
  • lines: permite añadir líneas uniendo los clusters.
  • cex: permite modificar el tamaño de los puntos.
  • cex.text: permite modificar el tamaño de las etiquetas.

• dist calcula la matriz de distancias entre las filas de una tabla de datos. Su parámetro principal es method, con el que se especifica la distancia concreta.

• hclust, aplicada a una matriz de distancias calculada con dist, produce un clustering jerárquico aglomerativo de los objetos representados en la tabla de datos original. Su parámetro principal es method, que permite especificar el algoritmo concreto que se desea usar. El resultado es una list, cuyas componentes principales son:

  • merge: una matriz que indica el orden en el que se han realizado los agrupamientos.

  • height: un vector que indica las distancias a las que se han realizado los agrupamientos.

• plot, aplicado al resultado de hclust, dibuja su dendrograma. Los parámetros específicos más importantes para esta aplicación de plot son:

  • hang: controla la situación de las hojas del dendrograma respecto del margen inferior.
  • labels: permite modificar las etiquetas de los objetos representados por las hojas del dendrograma.

• cutree permite obtener un clustering ordinario a partir del resultado de un hclust, bien sea especificando el número de clusters con el parámetro k, bien sea especificando la altura a la que deseamos cortar el clustering jerárquico con h.

• rect.hclust resalta, enmarcados en rectángulos sobre el dendrograma dibujado con plot en la instrucción inmediatamente anterior, los clusters que se producen al cortar el resultado de un hclust en k grupos o a la altura h.

11.5 Ejercicios

Test

(1) El data frame kanga del paquete faraway contiene diferentes medidas de los cráneos de 148 ejemplares de canguros de 3 especies. Considerad solo las medidas asociadas a su mandíbula (columnas 17 a 19), y como hay valores NA en estas variables, usad solo las filas que no contengan ningún NA. Vamos a llamar kanga.mand a la tabla resultante. Usad esta tabla de datos para realizar un clustering (de los canguros que queden en ella) con el método de k-means de Hartigan-Wong en \(k=3\) clases, usando como centros iniciales los puntos (1000,100,100), (1200,120,120) y (1500,150,150). Cuántos elementos tiene el cluster más grande que se obtiene de esta manera?

(2) Seguimos con la tabla kanga.mand. Realizad un clustering de sus canguros con el método de k-means de Hartigan-Wong en \(k=3\) clases usando 3 puntos iniciales escogidos al azar pero fijando la semilla de aleatoriedad en 314. Qué vale la \(SSC\) del cluster que contiene el quinto ejemplar de la tabla de datos (según el orden de las filas)? Dad el resultado redondeado a un entero.

(3) Seguimos con la tabla kanga.mand de las dos preguntas anteriores. Cuál de los dos clusterings calculados en las preguntas anteriores es mejor, el de la pregunta (1) o el de la pregunta (2)? La respuesta ha de ser 1 si es el de la pregunta (1), 2 si es el de la pregunta (2), o 0 si ninguno es mejor que el otro.

(4) Seguimos con la tabla kanga.mand de las preguntas anteriores. Realizad un clustering jerárquico de sus canguros usando la distancia euclídea y el método de enlace promedio. Si lo cortáis en 3 clases, cuántos elementos tiene el cluster más grande que obtenéis?

(5) Seguimos con la tabla kanga.mand de las preguntas anteriores. Realizad un clustering jerárquico de sus canguros usando la distancia euclídea y el método de Ward clásico. Si lo cortáis a altura 1000, cuántos clusters se forman?

Respuestas al test

(1) 62

Nosotros lo hemos calculado con

library(faraway)
kanga.mand=kanga[,17:19]
kanga.mand=na.omit(kanga.mand)
Centros=rbind(c(1000,100,100),c(1200,120,120),c(1500,150,150))
KM1=kmeans(kanga.mand,centers=Centros)
max(KM1$size)

## [1] 62

(2) 160802

Nosotros lo hemos calculado con

set.seed(314)
KM2=kmeans(kanga.mand,centers=3)
cluster.5=KM2$cluster[5]
round(KM2$withinss[cluster.5])

## [1] 160802

(3) 0

Nosotros lo hemos resuelto calculando los dos \(SSC\) y viendo que son iguales:

KM1$totss

## [1] 2938803

KM2$totss

## [1] 2938803

(4) 76

Nosotros lo hemos calculado con

D=dist(kanga.mand)
HC1=hclust(D,method="average")
table(cutree(HC1,k=3))

## 
##  1  2  3 
## 76  5 55

(5) 5

Nosotros lo hemos calculado con

HC2=hclust(D,method="ward.D")
table(cutree(HC2,h=1000))

## 
##  1  2  3  4  5 
## 26 50  5 35 20

---

9. Véase, por ejemplo, N. Slonim, E. Aharoni, K. Crammer, “Hartigan’s K-Means Versus Lloyd’s K-Means—Is It Time for a Change?”. Proceedings of the XXIII International Joint Conference on Artificial Intelligence (2013), pp. 1677-1684. Accesible (mayo 2019) en http://www.ijcai.org/Proceedings/13/Papers/249.pdf.↩︎