Lección 8 Introducción a la estadística descriptiva multidimensional
En general, los datos que se recogen en experimentos son multidimensionales: medimos varias variables aleatorias sobre una misma muestra de individuos, y organizamos esta información en tablas de datos en las que las filas representan los individuos observados y cada columna corresponde a una variable diferente. En las lecciones finales de la primera parte ya aparecieron datos cualitativos y ordinales multidimensionales, para los que calculamos y representamos gráficamente sus frecuencias globales y marginales; en esta lección estudiamos algunos estadísticos específicos para resumir y representar la relación existente entre diversas variables cuantitativas.
8.1 Matrices de datos cuantitativos
Supongamos que hemos medido los valores de \(p\) variables aleatorias \(X_1,\ldots,X_p\) sobre un conjunto de \(n\) individuos u objetos. Es decir, tenemos \(n\) observaciones de \(p\) variables. En cada observación, los valores que toman estas variables forman un vector que será una realización del vector aleatorio \(\underline{X}=(X_1,X_2,\ldots,X_p)\). Para trabajar con estas observaciones, las dispondremos en una tabla de datos donde cada fila corresponde a un individuo y cada columna, a una variable. En R, lo más conveniente es definir esta tabla en forma de data frame, pero, por conveniencia de lenguaje, en el texto de esta lección la representaremos como una matriz \[ {X}=\begin{pmatrix} x_{1 1} & x_{1 2} &\ldots & x_{1 p}\\ x_{2 1} & x_{2 2} &\ldots & x_{2 p}\\ \vdots & \vdots & \ddots &\vdots\\ x_{n 1} & x_{n 2} &\ldots & x_{n p} \end{pmatrix}. \] Utilizaremos las notaciones siguientes:
Denotaremos la \(i\)-ésima fila de \(X\) por \[ {x}_{i\bullet}=(x_{i 1}, x_{i 2}, \ldots, x_{i p}). \] Este vector está compuesto por las observaciones de las \(p\) variables sobre el \(i\)-ésimo individuo.
Denotaremos la \(j\)-ésima columna de \(X\) por \[ x_{\bullet j}=\begin{pmatrix}x_{1 j} \\ x_{2 j}\\ \vdots \\ x_{n j} \end{pmatrix}. \] Esta columna está formada por todos los valores de la \(j\)-ésima variable, es decir, es una muestra de \(X_j\).
Observad que, en cada caso, la bolita \(\bullet\) en el subíndice representa el índice “variable” de los elementos del vector o de la columna.
De esta manera, podremos expresar la matriz de datos \(X\) tanto por filas (individuos) como por columnas (muestras de variables): \[ {X}=\begin{pmatrix}{x}_{1\bullet}\\x_{2\bullet}\\\vdots \\ {x}_{n\bullet}\end{pmatrix}=({x}_{\bullet1}, {x}_{\bullet 2}, \ldots, {x}_{\bullet p}). \]
Con estas notaciones, podemos generalizar al caso multidimensional los estadísticos de una variable cuantitativa, definiéndolos como los vectores que se obtienen aplicando el estadístico concreto a cada columna de la tabla de datos. Así:
- El vector de medias de \(X\) es el vector formado por las medias aritméticas de sus columnas: \[ \overline{X}=(\overline{{{x}}}_{\bullet1}, \overline{{x}}_{\bullet 2}, \ldots, \overline{{x}}_{\bullet p}), \] donde, para cada \(j=1, \ldots, p\), \[ \overline{{x}}_{\bullet j}=\frac{1}{n}\sum\limits_{i=1}^n x_{i j}. \]
Observemos que \[ \begin{array}{rl} \overline{X} & \displaystyle = (\overline{{{x}}}_{\bullet1}, \overline{x}_{\bullet 2},\ldots,\overline{x}_{\bullet p}) = \frac{1}{n} \Big(\sum_{i=1}^n x_{i 1}, \sum_{i=1}^n x_{i 2},\ldots, \sum_{i=1}^n x_{i p}\Big)\\[1ex] & \displaystyle =\frac{1}{n} \sum_{i=1}^n (x_{i 1}, x_{i 2},\ldots,x_{i p} ) = \frac{1}{n} \sum_{i=1}^n {{x}_{i\bullet}} \end{array} \] Es decir, el vector de medias de \(X\) es la media aritmética de sus vectores fila.
El vector de varianzas de \(X\) es el vector formado por las varianzas de sus columnas: \[ s^2_{X}=(s^2_{1}, s^2_2, \ldots, s^2_p), \] donde \[ s_j^2=\frac{1}{n}\sum_{i=1}^n {(x_{ij}-\overline{{x}}_{\bullet j})^2}. \]
El vector de varianzas muestrales de \(X\) está formado por las varianzas muestrales de sus columnas: \[ \widetilde{s}^2_{X}=(\widetilde{s}^2_{1}, \widetilde{s}^2_2, \ldots, \widetilde{s}^2_p), \] donde \[ \widetilde{s}_j^2=\frac{1}{n-1}\sum_{i=1}^n {(x_{ij}-\overline{{x}}_{\bullet j})^2}=\frac{n}{n-1}s_j^2. \]
Los vectores de desviaciones típicas \(s_{X}\) y de desviaciones típicas muestrales \(\widetilde{s}_{X}\) de \(X\) son los formados por las desviaciones típicas y las desviaciones típicas muestrales de sus columnas, respectivamente: \[ \begin{array}{l} s_{X}=(s_{1}, s_2, \ldots, s_p)=(+\sqrt{\vphantom{s_p^2}{s}^2_{1}}, +\sqrt{\vphantom{s_p^2}{s}^2_2}, \ldots, +\sqrt{s_p^2})\\[1ex] \widetilde{s}_{X}=(\widetilde{s}_{1}, \widetilde{s}_2, \ldots, \widetilde{s}_p)=(+\sqrt{\vphantom{s_p^2}\widetilde{s}^2_{1}}, +\sqrt{\vphantom{s_p^2}\widetilde{s}^2_2}, \ldots, +\sqrt{\widetilde{s}^2_p}) \end{array} \]
Como en el caso unidimensional, \(\overline{X}\) es un estimador insesgado de la esperanza \(E(\underline{X})=\boldsymbol\mu\) del vector aleatorio \(\underline{X}\) del cual \(X\) es una muestra. Por lo que refiere a \({s}^2_{X}\) y \(\widetilde{s}^2_{X}\), ambas son estimadores del vector de varianzas de \(\underline{X}\): \(\widetilde{s}^2_{X}\) es insesgado y, cuando todas las variables aleatorias del vector son normales, \({s}^2_{X}\) es el máximo verosímil.
Estos vectores de estadísticos se pueden calcular con R aplicando la función correspondiente al estadístico a todas las columnas de la tabla de datos. La manera más sencilla de hacerlo en un solo paso es usando la función sapply, si tenemos guardada la tabla como un data frame, o apply con MARGIN=2, si la tenemos guardada en forma de matriz.
Ejemplo 8.1 Consideremos la tabla de datos \[ X=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \] formada por 4 observaciones de 3 variables; por lo tanto, \(n=4\) y \(p=3\). Vamos a guardarla en un data frame y a calcular sus estadísticos.
X=data.frame(V1=c(1,1,2,3),V2=c(-1,0,3,0),V3=c(3,3,0,1))
X## V1 V2 V3
## 1 1 -1 3
## 2 1 0 3
## 3 2 3 0
## 4 3 0 1- Su vector de medias es:
sapply(X, mean) ## V1 V2 V3
## 1.75 0.50 1.75- Su vector de varianzas muestrales es:
sapply(X, var) ## V1 V2 V3
## 0.9166667 3.0000000 2.2500000- Su vector de desviaciones típicas muestrales es:
sapply(X, sd) ## V1 V2 V3
## 0.9574271 1.7320508 1.5000000- Su vector de varianzas es:
var_ver=function(x){var(x)*(length(x)-1)/length(x)} #Varianza "verdadera"
sapply(X, var_ver) ## V1 V2 V3
## 0.6875 2.2500 1.6875- Su vector de desviaciones típicas es:
sd_ver=function(x){sqrt(var_ver(x))} #Desv. típica "verdadera"
sapply(X, sd_ver) ## V1 V2 V3
## 0.8291562 1.5000000 1.29903818.2 Transformaciones lineales
A veces es conveniente aplicar una transformación lineal a una tabla de datos \(X\), sumando a cada columna un valor y luego multiplicando cada columna resultante por otro valor. Los dos ejemplos más comunes de trasformación lineal son el centrado y la tipificación de datos.
Para centrar una matriz de datos \(X\), se resta a cada columna su media aritmética: \[ \widetilde{X}= \begin{pmatrix} x_{1 1}- \overline{x}_{\bullet 1}& x_{1 2}- \overline{x}_{\bullet 2} &\ldots & x_{1 p}- \overline{x}_{\bullet p}\\ x_{2 1} - \overline{x}_{\bullet 1}& x_{2 2}- \overline{x}_{\bullet 2} &\ldots & x_{2 p}- \overline{x}_{\bullet p}\\ \vdots & \vdots & \ddots &\vdots\\ x_{n 1} - \overline{x}_{\bullet 1}& x_{n 2}- \overline{x}_{\bullet 2} &\ldots & x_{n p}- \overline{x}_{\bullet p} \end{pmatrix}. \] Llamaremos a esta matriz la matriz de datos centrados de \(X\).
Ejemplo 8.2 Consideremos de nuevo la matriz de datos del Ejemplo 8.1, \[ {X}=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \]
Para centrarla, hemos de restar a cada columna su media. Ya hemos calculado estas medias hace un momento:
sapply(X, mean) ## V1 V2 V3
## 1.75 0.50 1.75Por lo tanto, su matriz de datos centrados es \[ \widetilde{X}=\left(\begin{array}{rrr} 1-1.75&-1-0.5&3-1.75\\ 1-1.75&0-0.5&3-1.75\\ 2-1.75&3-0.5&0-1.75 \\ 3-1.75&0-0.5&1-1.75 \end{array}\right)= \left(\begin{array}{rrr} -0.75&-1.5&1.25\\ -0.75&-0.5&1.25\\ 0.25&2.5&-1.75\\ 1.25&-0.5&-0.75 \end{array}\right). \]
Dado un vector de datos formado por una muestra de una variable cuantitativa, su vector de datos tipificados es el vector que se obtiene restando a cada entrada la media aritmética del vector y dividiendo el resultado por su desviación típica. De esta manera, se obtiene un vector de datos de media aritmética 0 y varianza 1. Tipificar un vector de datos es conveniente cuando se quiere trabajar con estos datos sin que influyan ni su media ni las unidades en los que están medidos: al dividir por su desviación típica, los valores resultantes son adimensionales. Por lo tanto, tipificar las variables de una tabla de datos permite compararlas dejando de lado las diferencias que pueda haber entre sus valores medios o sus varianzas.
La matriz tipificada de una matriz de datos \(X\) es la matriz \(Z\) que se obtiene tipificando cada columna; es decir, para tipificar una matriz de datos \(X\), restamos a cada columna su media y a continuación dividimos cada columna por la desviación típica de la columna original en \(X\) (que coincide con la desviación típica de la columna “centrada”, puesto que sumar o restar constantes no modifica la desviación típica): \[ Z=\begin{pmatrix} \frac{x_{1 1}- \overline{x}_{\bullet 1}}{s_1}& \frac{x_{1 2}- \overline{x}_{\bullet 2}}{s_2} &\ldots & \frac{x_{1 p}- \overline{x}_{\bullet p}}{s_p}\\[2ex] \frac{x_{2 1} - \overline{x}_{\bullet 1}}{s_1}& \frac{x_{2 2}- \overline{x}_{\bullet 2}}{s_2} &\ldots & \frac{x_{2 p}- \overline{x}_{\bullet p}}{s_p}\\[2ex] \vdots & \vdots & \ddots &\vdots\\ \frac{x_{n 1} - \overline{x}_{\bullet 1}}{s_1}& \frac{x_{n 2}- \overline{x}_{\bullet 2}}{s_2} &\ldots & \frac{x_{n p}- \overline{x}_{\bullet p}}{s_p} \end{pmatrix}. \]
Ejemplo 8.3 Vamos a tipificar a mano la tabla de datos \[ {X}=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \] del Ejemplo 8.1. Ya la hemos centrado en el Ejemplo 8.2. Para tipificarla, tenemos que dividir cada columna de esta matriz centrada por la desviación típica de la columna correspondiente en la matriz original. Hemos calculado estas desviaciones típicas en el Ejemplo 8.1:
sapply(X, sd_ver) ## V1 V2 V3
## 0.8291562 1.5000000 1.2990381Dividiendo cada columna de la matriz centrada \(\widetilde{X}\) por la correspondiente desviación típica obtenemos:
\[ \begin{array}{rl} Z & =\left(\begin{array}{rrr} -0.75/0.8291562&-1.5/1.5&1.25/1.2990381\\ -0.75/0.8291562&-0.5/1.5&1.25/1.2990381\\ 0.25/0.8291562&2.5/1.5&-1.75/1.2990381\\ 1.25/0.8291562&-0.5/1.5&-0.75/1.2990381 \end{array}\right)\\ & = \left(\begin{array}{rrr} -0.9045340&-1.0000000&0.9622504\\ -0.9045340&-0.3333333&0.9622504\\ 0.3015113&1.6666667&-1.3471506\\ 1.5075567&-0.3333333&-0.5773503 \end{array}\right) \end{array} \]
La manera más sencilla de aplicar con R una transformación lineal a una tabla de datos \(X\), y en particular de centrarla o tipificarla, es usando la instrucción
scale(X, center=..., scale=...)donde:
Xpuede ser tanto una matriz como un data frame; el resultado será siempre una matriz.El valor del parámetro
centeres el vector que restamos a sus columnas, en el sentido de que cada entrada de este vector se restará a todas las entradas de la columna correspondiente. Su valor por defecto (que no es necesario especificar, aunque también se puede especificar concenter=TRUE) es el vector \(\overline{X}\) de medias de \(X\); para indicar que no se reste nada, podemos usarcenter=FALSE.El valor del parámetro
scalees el vector por el que dividimos las columnas de \(X\): cada columna se divide por la entrada correspondiente de este vector. Su valor por defecto (que, de nuevo, se puede especificar igualando el parámetro aTRUE) es el vector \(\widetilde{s}_X\) de desviaciones típicas muestrales; para indicar que no se divida por nada, podemos usarscale=FALSE.
En particular, la instrucción scale(X) centra la tabla de datos \(X\) y divide sus columnas por sus desviaciones típicas muestrales; por lo tanto, no la tipifica según nuestra definición, ya que no las divide por sus desviaciones típicas “verdaderas”.
Ejemplo 8.4 Recordemos la tabla de datos \(X\) del Ejemplo 8.1.
X## V1 V2 V3
## 1 1 -1 3
## 2 1 0 3
## 3 2 3 0
## 4 3 0 1Su matriz centrada es:
X_centrada=scale(X, center=TRUE, scale=FALSE)
X_centrada## V1 V2 V3
## [1,] -0.75 -1.5 1.25
## [2,] -0.75 -0.5 1.25
## [3,] 0.25 2.5 -1.75
## [4,] 1.25 -0.5 -0.75
## attr(,"scaled:center")
## V1 V2 V3
## 1.75 0.50 1.75Coincide con la matriz obtenida en el Ejemplo 8.2.
Observad la estructura del resultado: en primer lugar nos da la matriz centrada, y a continuación nos dice que tiene un atributo llamado "scaled:center" cuyo valor es el vector usado para centrarla. Este atributo no interferirá para nada en las operaciones que realicéis con la matriz centrada, pero, si os molesta, recordad que se puede eliminar sustituyendo el resultado de centrar la matriz en los puntos suspensivos de la instrucción siguiente:
attr(... , "scaled:center")=NULLEn nuestro ejemplo:
attr(X_centrada, "scaled:center")=NULL
X_centrada## V1 V2 V3
## [1,] -0.75 -1.5 1.25
## [2,] -0.75 -0.5 1.25
## [3,] 0.25 2.5 -1.75
## [4,] 1.25 -0.5 -0.75Como ya hemos avisado, para tipificar esta tabla de datos no podemos hacer lo siguiente:
X_tip=scale(X)
X_tip## V1 V2 V3
## [1,] -0.7833495 -0.8660254 0.8333333
## [2,] -0.7833495 -0.2886751 0.8333333
## [3,] 0.2611165 1.4433757 -1.1666667
## [4,] 1.3055824 -0.2886751 -0.5000000
## attr(,"scaled:center")
## V1 V2 V3
## 1.75 0.50 1.75
## attr(,"scaled:scale")
## V1 V2 V3
## 0.9574271 1.7320508 1.5000000Para hacerlo bien según la definición que hemos dado, tenemos dos opciones. Una es multiplicar la matriz anterior por \(\sqrt{n/(n-1)}\), donde \(n\) es el número de filas de la tabla. (El motivo es que, como \(\widetilde{s}_X=\sqrt{\frac{n}{n-1}}\cdot s_X\), se tiene que \(\frac{1}{s_X}=\sqrt{\frac{n}{n-1}}\cdot \frac{1}{\widetilde{s}_X}\); por lo tanto, si queríamos dividir por \(s_X\) y scale(X) ha dividido por \(\widetilde{s}_X\), basta multiplicar su resultado por \(\sqrt{\frac{n}{n-1}}\) para obtener el efecto deseado.)
n=dim(X)[1] #Número de filas de X
X_tip=scale(X)*sqrt(n/(n-1))
X_tip| V1 | V2 | V3 |
|---|---|---|
| -0.9045340 | -1.0000000 | 0.9622504 |
| -0.9045340 | -0.3333333 | 0.9622504 |
| 0.3015113 | 1.6666667 | -1.3471506 |
| 1.5075567 | -0.3333333 | -0.5773503 |
Ahora sí que coincide con la matriz obtenida “a mano” en el Ejemplo 8.3.
Otra posibilidad es usar, como valor del parámetro scale, el vector \(s_X\) de desviaciones típicas de las columnas.
X_tip1=scale(X, scale=sapply(X, sd_ver))
X_tip1## V1 V2 V3
## [1,] -0.9045340 -1.0000000 0.9622504
## [2,] -0.9045340 -0.3333333 0.9622504
## [3,] 0.3015113 1.6666667 -1.3471506
## [4,] 1.5075567 -0.3333333 -0.5773503
## attr(,"scaled:center")
## V1 V2 V3
## 1.75 0.50 1.75
## attr(,"scaled:scale")
## V1 V2 V3
## 0.8291562 1.5000000 1.2990381Observaréis que la matriz resultante es la misma, pero el atributo que indica el vector por el que hemos dividido las columnas es diferente: en este caso, es el de desviaciones típicas.
Ahora, en ambos casos, podemos usar la función attr para eliminar los dos atributos, "scaled:center" y "scaled:scale", que se han añadido a la matriz tipificada. Por ejemplo:
attr(X_tip, "scaled:center")=NULL
attr(X_tip, "scaled:scale")=NULL
X_tip## V1 V2 V3
## [1,] -0.9045340 -1.0000000 0.9622504
## [2,] -0.9045340 -0.3333333 0.9622504
## [3,] 0.3015113 1.6666667 -1.3471506
## [4,] 1.5075567 -0.3333333 -0.57735038.3 Covarianzas y correlaciones
La covarianza entre dos variables es una medida de la tendencia que tienen ambas variables a variar conjuntamente. Cuando la covarianza es positiva, si una de las dos variables crece o decrece, la otra tiene el mismo comportamiento; en cambio, cuando la covarianza es negativa, esta tendencia se invierte: si una variable crece, la otra decrece y viceversa. Puesto que interpretar el valor de la covarianza más allá de su signo es difícil, se suele usar una versión “normalizada” de la misma, la correlación de Pearson, que mide de manera más precisa la relación lineal entre dos variables.
La covarianza generaliza la varianza, en el sentido de que la varianza de una variable es su covarianza consigo misma. Y como en el caso de la varianza, definiremos dos versiones de la covarianza: la “verdadera” y la muestral. La diferencia estará de nuevo en el denominador.
Formalmente, la covarianza de las variables \({x}_{\bullet i}\) y \({x}_{\bullet j}\) de una matriz de datos \(X\) es \[ s_{i j}=\frac{1}{n} \sum_{k =1}^n\big((x_{k i}-\overline{{x}}_{\bullet i})(x_{kj}-\overline{{x}}_{\bullet j})\big)= \frac{1}{n} \Big(\sum_{k =1}^n x_{k i} x_{k j}\Big) - \overline{{x}}_{\bullet i} \overline{{x}}_{\bullet j}, \] y su covarianza muestral es \[ \widetilde{s}_{ij} = \frac{1}{n-1} \sum_{k =1}^n\big((x_{k i}-\overline{{x}}_{\bullet i})(x_{kj}-\overline{{x}}_{\bullet j})\big)= \frac{n}{n-1} s_{ij}. \]
El estadístico \(\tilde{s}_{ij}\) es siempre un estimador insesgado de la covarianza \(\sigma_{i j}\) de las variables aleatorias \(X_i\) y \(X_j\) de las que \({x}_{\bullet i}\) y \({x}_{\bullet j}\) son muestras, mientras que \(s_{i j}\) es su estimador máximo verosímil cuando la distribución conjunta de \(X_i\) y \(X_j\) es normal bivariante.
Es inmediato comprobar a partir de sus definiciones que ambas covarianzas son simétricas, y que la covarianza de una variable consigo misma es su varianza: \[ s_{i j}= s_{j i}, \quad \widetilde{s}_{i j}= \widetilde{s}_{j i}, \quad s_{i i}=s_{i}^2, \quad \widetilde{s}_{ii}=\widetilde{s}_i^2. \]
Ejemplo 8.5 La covarianza de las dos primeras columnas de la matriz de datos \[ X=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \] del Ejemplo 8.1 se calcularía de la manera siguiente:
\[ s_{12}=\frac{1}{4}(1\cdot (-1)+1\cdot 0+2\cdot 3+3\cdot 0)-1.75\cdot 0.5= 1.25-0.875=0.375 \] Su covarianza muestral se obtendría multiplicando por \(4/3\) este valor: \[ \widetilde{s}_{12} = \frac{4}{3} s_{12}=0.5. \]
La covarianza muestral de dos vectores numéricos de la misma longitud \(n\) se puede calcular con R mediante la función cov.
Para obtener su covarianza “verdadera”, hay que multiplicar el resultado de cov por \((n-1)/n\).
Ejemplo 8.6 La covarianza muestral de las dos primeras columnas de la tabla de datos \(X\), que tenemos guardada en el data frame X, es:
cov(X$V1, X$V2)## [1] 0.5y su covarianza “verdadera” es:
n=dim(X)[1]
((n-1)/n)*cov(X$V1, X$V2) ## [1] 0.375Queremos recalcar que, como en el caso de la varianza con var, R calcula con cov la versión muestral de la covarianza.
Las matrices de covarianzas y de covarianzas muestrales de una tabla de datos \(X\) son, respectivamente, \[ {S}= \begin{pmatrix} s_{1 1} & s_{1 2} & \ldots & s_{1 p}\\ s_{2 1} & s_{2 2} & \ldots & s_{2 p}\\ \vdots & \vdots & \ddots & \vdots\\ s_{p 1} & s_{p 2} & \ldots & s_{p p} \end{pmatrix},\ \widetilde{{S}}= \begin{pmatrix} \widetilde{s}_{1 1} & \widetilde{s}_{1 2} & \ldots & \widetilde{s}_{1 p}\\ \widetilde{s}_{2 1} & \widetilde{s}_{2 2} & \ldots & \widetilde{s}_{2 p}\\ \vdots & \vdots & \ddots & \vdots\\ \widetilde{s}_{p 1} & \widetilde{s}_{p 2} & \ldots & \widetilde{s}_{p p} \end{pmatrix}, \] donde cada \(s_{i j}\) y cada \(\widetilde{s}_{i j}\) son, respectivamente, la covarianza y la covarianza muestral de las correspondientes columnas \({x}_{\bullet i}\) y \({x}_{\bullet j}\). Estas matrices de covarianzas miden la tendencia a la variabilidad conjunta de los datos de \(X\) y, si \(n\) es el número de filas de \(X\), se tiene que \[ S=\frac{n-1}{n}\widetilde{{S}}. \]
La matriz de covarianzas muestrales \(\widetilde{{S}}\) es un estimador insesgado de la matriz de covarianzas \(\Sigma\) del vector de variables aleatorias \(\underline{X}\), y si este tiene distribución normal multivariante, \(S\) es un estimador máximo verosímil de \(\Sigma\). Ambas matrices de covarianzas son simétricas, puesto que \(s_{i j}=s_{j i}\), y tienen todos sus valores propios \(\geq 0\).
La matriz de covarianzas muestrales de una tabla de datos se calcula aplicando la función cov al data frame o a la matriz que contenga dicha tabla. Para obtener su matriz de covarianzas “verdaderas”, es suficiente multiplicar el resultado de cov por \((n-1)/n\), donde \(n\) es el número de filas de la tabla de datos.
Ejemplo 8.7 Continuemos con la matriz \[ X=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \] del Ejemplo 8.1.
Su matriz de covarianzas muestrales es
cov(X) ## V1 V2 V3
## V1 0.9166667 0.500000 -1.083333
## V2 0.5000000 3.000000 -2.166667
## V3 -1.0833333 -2.166667 2.250000y su matriz de covarianzas es
n=dim(X)[1]
((n-1)/n)*cov(X) ## V1 V2 V3
## V1 0.6875 0.375 -0.8125
## V2 0.3750 2.250 -1.6250
## V3 -0.8125 -1.625 1.6875Como la matriz de covarianzas es difícil de interpretar como medida de variabilidad de una tabla de datos, debido a que no es una única cantidad sino toda una matriz, interesa cuantificar esta variabilidad mediante un único índice. No hay consenso sobre este índice, y entre los que se usan destacamos:
La varianza total de \(X\): la suma de las varianzas de sus columnas.
La varianza media de \(X\): la media de las varianzas de sus columnas, es decir, la varianza total partida por el número de columnas.
La varianza generalizada de \(X\): el determinante de su matriz de covarianzas.
La desviación típica generalizada de \(X\): la raíz cuadrada positiva de su varianza generalizada.
De cada uno de estos índices se definen, naturalmente, una versión muestral y una “verdadera”, según el tipo de varianzas o covarianzas que se usen en su cálculo.
Pasemos ahora a la correlación lineal de Pearson (o, de ahora en adelante, simplemente correlación de Pearson) de dos variables \({x}_{\bullet i}\) y \({x}_{\bullet j}\) de \(X\), que se define como \[ r_{i j}=\frac{s_{i j}}{s_i\cdot s_j}. \] Observad que \[ \frac{\widetilde{s}_{i j}}{\widetilde{s}_i\cdot \widetilde{s}_j}= \frac{\frac{n}{n-1}\cdot {s}_{i j}}{\sqrt{\frac{n}{n-1}}\cdot {s}_i \cdot\sqrt{\frac{n}{n-1}}\cdot{s}_j}= \frac{s_{i j}}{s_i \cdot s_j}=r_{i j}, \] y, por lo tanto, esta correlación se puede calcular también a partir de las versiones muestrales de la covarianza y las desviaciones típicas por medio de la misma fórmula.
El estadístico \(r_{ij}\) es un estimador máximo verosímil de la correlación de Pearson \(\rho_{i j}=Cor(X_i,X_j)\) de las variables aleatorias \(X_i\) y \(X_j\) cuando su distribución conjunta es normal bivariante, y aunque es sesgado, su sesgo tiende a 0 cuando \(n\) tiende a \(\infty\). Las propiedades más importantes de \(r_{i,j}\) son las siguientes:
Es simétrica: \(r_{i j}=r_{j i}\).
\(-1\leq r_{i j}\leq 1\).
\(r_{i i}=1\).
\(r_{i j}\) tiene el mismo signo que \(s_{i j}\).
\(r_{i j}=\pm 1\) si y, sólo si, existe una relación lineal perfecta entre las variables \({x}_{\bullet i}\) y \({x}_{\bullet j}\): es decir, si, y sólo si, existen valores \(a, b\in \mathbb{R}\) tales que \[ \left(\begin{array}{c} x_{1j}\\ \vdots \\ x_{nj}\end{array}\right)= a\cdot \left(\begin{array}{c} x_{1i}\\ \vdots \\ x_{ni}\end{array}\right) +b. \] La pendiente \(a\) de esta relación lineal tiene el mismo signo que \(r_{i j}\).
El coeficiente de determinación \(R^2\) de la regresión lineal por mínimos cuadrados de \({x}_{\bullet j}\) respecto de \({x}_{\bullet i}\) es igual al cuadrado de su correlación de Pearson, \(r_{i j}^2\); por lo tanto, cuánto más se aproxime el valor absoluto de \(r_{ij}\) a 1, más se acercan las variables \({x}_{\bullet i}\) y \({x}_{\bullet j}\) a depender linealmente la una de la otra.
Así pues, la correlación de Pearson entre dos variables viene a ser una covarianza “normalizada”, ya que, como vemos, su valor está entre -1 y 1, y mide la tendencia de las variables a estar relacionadas según una función lineal. En concreto, cuanto más se acerca dicha correlación a 1 (respectivamente, a -1), más se acerca una (cualquiera) de las variables a ser función lineal creciente (respectivamente, decreciente) de la otra.
Con R, la correlación de Pearson de dos vectores se puede calcular aplicándoles la función cor.
Ejemplo 8.8 En ejemplos anteriores hemos calculado la covarianza y las varianzas de las dos primeras columnas de la matriz de datos \[ {X}=\left(\begin{array}{rrr} 1&-1&3\\ 1&0&3\\ 2&3&0\\ 3&0&1 \end{array}\right) \]
Hemos obtenido los valores siguientes \[ s_{12}=0.375,\quad s_1=0.8291562,\quad s_2=1.5. \] Por lo tanto, su correlación de Pearson es \[ r_{1 2}=\frac{0.375}{0.8291562\cdot 1.5}=0.3015113. \]
Ahora vamos a calcularla con R, y aprovecharemos para confirmar su relación con el valor de \(R^2\) de la regresión lineal de la segunda columna respecto de la primera. Recordemos que esta tabla de datos sigue guardada en el data frame X.
X## V1 V2 V3
## 1 1 -1 3
## 2 1 0 3
## 3 2 3 0
## 4 3 0 1La correlación de sus dos primeras columnas es:
cor(X$V1, X$V2)## [1] 0.3015113que coincide con el valor obtenido “a mano”. Comprobemos ahora que su cuadrado es igual al valor de \(R^2\) de la regresión lineal:
cor(X$V1, X$V2)^2## [1] 0.09090909summary(lm(X$V2~X$V1))$r.squared## [1] 0.09090909La matriz de correlaciones de Pearson de \(X\) es
\[
{R}=
\begin{pmatrix}
1 & r_{1 2} & \ldots & r_{1 p}\\
r_{2 1} & 1 & \ldots & r_{2 p}\\
\vdots & \vdots & \ddots & \vdots\\
r_{p 1} & r_{p 2} & \ldots & 1
\end{pmatrix},
\]
donde cada \(r_{i j}\) es la correlación de Pearson de las columnas correspondientes de \(X\). Esta matriz de correlaciones tiene siempre determinante entre 0 y 1 (ambos extremos incluidos) y todos sus valores propios son mayores o iguales que 0, y con R se puede calcular aplicando la misma instrucción cor a la tabla de datos, sea en forma de matriz o de data frame.
Así, la matriz de correlaciones de nuestra tabla de datos \(X\) es:
cor(X)## V1 V2 V3
## V1 1.0000000 0.3015113 -0.7543365
## V2 0.3015113 1.0000000 -0.8339504
## V3 -0.7543365 -0.8339504 1.0000000Se tiene el teorema siguiente, que se puede demostrar mediante un simple, aunque farragoso, cálculo algebraico:
Teorema 8.1 La matriz de correlaciones de Pearson de \(X\) es igual a:
La matriz de covarianzas de su matriz tipificada.
La matriz de covarianzas muestrales de su matriz tipificada obtenida dividiendo por las desviaciones típicas muestrales en vez de por las “verdaderas”.
La importancia de este resultado es que, si la tabla de datos es muy grande, suele ser más eficiente calcular la matriz de covarianzas de su matriz tipificada que la matriz de correlaciones de Pearson de la tabla original.
Observad, por otro lado, que las dos matrices de covarianzas mencionadas en el enunciado coinciden, puesto que la matriz tipificada se obtiene multiplicando por \(\sqrt{n/(n-1)}\) la matriz tipificada obtenida dividiendo por las desviaciones típicas muestrales. Esto implica que la matriz de covarianzas muestrales de la matriz tipificada se obtiene multiplicando por \(n/(n-1)\) la matriz de covarianzas muestrales de la matriz tipificada obtenida dividiendo por las desviaciones típicas muestrales. Finalmente, la matriz de covarianzas se obtiene a partir de la de covarianzas muestrales multiplicándola por \((n-1)/n\). Entonces, los factores \(n/(n-1)\) y \((n-1)/n\) se compensan y resulta que la matriz de covarianzas de la matriz tipificada coincide con la matriz de covarianzas muestrales de la matriz tipificada obtenida dividiendo por las desviaciones típicas muestrales.
Recordemos que si aplicamos la función scale a una tabla de datos \(X\), la tipifica dividiendo por las desviaciones típicas muestrales. Por lo tanto, otra manera de reformular el teorema anterior es decir que
cor(X) da lo mismo que cov(scale(X)).
Comprobemos esta igualdad para nuestra matriz de datos \(X\).
cor(X)## V1 V2 V3
## V1 1.0000000 0.3015113 -0.7543365
## V2 0.3015113 1.0000000 -0.8339504
## V3 -0.7543365 -0.8339504 1.0000000cov(scale(X))## V1 V2 V3
## V1 1.0000000 0.3015113 -0.7543365
## V2 0.3015113 1.0000000 -0.8339504
## V3 -0.7543365 -0.8339504 1.0000000Cuando se calcula la covarianza o la correlación de Pearson de dos vectores que contienen valores NA, lo usual es no tenerlos en cuenta: es decir, si un vector contiene un NA en una posición, se eliminan de los dos vectores sus entradas en dicha posición. De esta manera, se tomaría como covarianza de \[ \left(\begin{array}{c} 1\\ 2\\ NA\\ 4\\ 6\\ 2\end{array}\right)\mbox{ y } \left(\begin{array}{c} 2\\ 4\\ -3\\ 5\\ 7\\ NA \end{array}\right) \] la de \[ \left(\begin{array}{c}1\\ 2\\ 4\\ 6\end{array}\right)\mbox{ y } \left(\begin{array}{c} 2\\ 4\\ 5\\ 7\end{array}\right). \]
Como ya nos pasaba con las funciones de estadística descriptiva univariante com mean o var, cuando aplicamos cov o cor a un par de vectores que contengan entradas NA, obtenemos por defecto NA. En las funciones univariantes usábamos na.rm=TRUE para pedir a R que obviara los NA, pero esta solución ahora no es posible, porque las posiciones de los NA también cuentan, y si los borramos tal cual se desmonta el emparejamiento de los datos. Así que, si se quiere que R calcule el valor de cov o cor sin tener en cuenta los NA, se ha de especificar añadiendo el parámetro use="complete.obs", que le indica que ha de usar las observaciones completas, es decir, las posiciones que no tienen NA en ninguno de los dos vectores.
Veamos el efecto sobre los dos vectores anteriores. Llamémosles \(x\) e \(y\), y sean \(x_1\) e \(y_1\) los vectores que se obtienen eliminando las entradas que contienen un NA en alguno de los dos vectores.
x=c(1,2,NA,4,6,2)
y=c(2,4,-3,5,7,NA)
x1=x[is.na(x)!=TRUE & is.na(y)!=TRUE]
y1=y[is.na(x)!=TRUE & is.na(y)!=TRUE]
x1## [1] 1 2 4 6y1## [1] 2 4 5 7Si calculamos la covarianza de \(x\) e \(y\) tal cual con la función cov, da NA:
cov(x, y)## [1] NAUsando use="complete.obs", obtenemos la covarianza de \(x_1\) e \(y_1\):
cov(x, y, use="complete.obs")## [1] 4.5cov(x1, y1)## [1] 4.5Lo mismo sucede con la función cor:
cor(x, y)## [1] NAcor(x, y, use="complete.obs")## [1] 0.9749135cor(x1, y1)## [1] 0.9749135Al calcular las matrices de covarianzas o correlaciones de una tabla de datos que contenga valores NA, se suele seguir una de las dos estrategias siguientes, según lo que interese al usuario:
Para cada par de columnas, se calcula su covarianza o su correlación con la estrategia explicada más arriba para dos vectores, obviando el hecho de que forman parte de una tabla de datos mayor; es decir, al efectuar el cálculo para cada par de columnas concreto, se eliminan de cada una de ellas solo las entradas de las filas en las que alguna de las dos tiene un NA, sin tener en cuenta para nada las otras columnas. Esta opción se especifica dentro de la función
covocorcon el parámetrouse="pairwise.complete.obs".Antes de nada, se eliminan las filas de la tabla que contienen algún NA en alguna columna, dejando solo en la tabla las filas “completas”, las que no contienen ningún NA. Luego se calcula la matriz de covarianzas o de correlaciones de la tabla resultante. Esta opción se especifica con el parámetro
use="complete.obs".
Veamos un ejemplo. Consideremos la matriz de datos \(Y\) siguiente, cuyas dos primeras columnas son los vectores \(x\) e \(y\) anteriores:
Y=cbind(c(1,2,NA,4,6,2), c(2,4,-3,5,7,NA), c(-2,1,0,2,NA,0))
Y## [,1] [,2] [,3]
## [1,] 1 2 -2
## [2,] 2 4 1
## [3,] NA -3 0
## [4,] 4 5 2
## [5,] 6 7 NA
## [6,] 2 NA 0Supongamos que queremos calcular su matriz de correlaciones de Pearson. Como todas las filas de \(Y\) tienen entradas NA, todas las correlaciones fuera de la diagonal dan NA (R sabe que la correlación de un columna consigo misma siempre es 1, y ya no la calcula):
cor(Y)## [,1] [,2] [,3]
## [1,] 1 NA NA
## [2,] NA 1 NA
## [3,] NA NA 1Una opción es calcular las correlaciones de Pearson de cada par de variables eliminando sus valores NA pero sin tener en cuenta los posibles valores NA de la otra variable:
cor(Y, use="pairwise.complete.obs")## [,1] [,2] [,3]
## [1,] 1.0000000 0.9749135 0.8919017
## [2,] 0.9749135 1.0000000 0.4387268
## [3,] 0.8919017 0.4387268 1.0000000Observad que la entrada (1,2) de esta matriz es la correlación de los vectores \(x\) e \(y\) calculada con use="complete.obs".
Calculemos ahora la matriz de correlaciones de Pearson de la matriz con filas completas:
cor(Y, use="complete.obs")## [,1] [,2] [,3]
## [1,] 1.0000000 0.9285714 0.8910421
## [2,] 0.9285714 1.0000000 0.9958706
## [3,] 0.8910421 0.9958706 1.0000000Veamos que efectivamente coincide con la matriz de correlaciones de Pearson de la matriz que se obtiene eliminando las filas que contienen algún NA. Esta matriz es:
noNAs=is.na(Y[,1])!=TRUE & is.na(Y[,2])!=TRUE & is.na(Y[,3])!=TRUE
Y1=Y[noNAs,]
Y1## [,1] [,2] [,3]
## [1,] 1 2 -2
## [2,] 2 4 1
## [3,] 4 5 2y su matriz de correlaciones de Pearson es:
cor(Y1)## [,1] [,2] [,3]
## [1,] 1.0000000 0.9285714 0.8910421
## [2,] 0.9285714 1.0000000 0.9958706
## [3,] 0.8910421 0.9958706 1.00000008.4 Correlación de Spearman
La correlación de Pearson mide específicamente la tendencia de dos variables cuantitativas continuas a depender linealmente una de otra. En circunstancias en las que no esperemos esta dependencia lineal, o en las que nuestras variables sean cuantitativas discretas o simplemente cualitativas, usar la correlación de Pearson para analizar la relación entre dos variables no es lo más adecuado. Entre las propuestas alternativas, la más popular es la correlación de Spearman. Este índice asigna a cada valor de cada vector su rango (su posición en el vector ordenado de menor a mayor, y en caso de empates la media de las posiciones que ocuparían todos los empates) y calcula la correlación de Pearson de estos rangos. Con R, la correlación de Spearman se calcula directamente con la función cor entrándole el parámetro method="spearman". (El valor por defecto del parámetro method es "pearson" y por eso no lo indicamos cuando calculamos la correlación de Pearson.)
Ejemplo 8.9 Vamos a calcular la correlación de Spearman de las dos primeras columnas de la matriz de datos \(X\) que hemos venido usando en nuestros ejemplos. En la tabla siguiente calculamos los rangos de sus entradas:
\[ \begin{array}{|c|c|c|c|} \hline {x}_{\bullet 1}& rango & {x}_{\bullet 2}& rango \\\hline\hline 1& 1.5 & -1& 1 \\ 1&1.5 & 0 & 2.5\\ 2&3 & 3& 4 \\ 3&4 & 0& 2.5\\\hline \end{array} \] ¿Cómo hemos obtenido los rangos? Fijaos por ejemplo en la primera columna: los dos 1 ocuparían la posición 1 y 2, les asignamos a ambos como rango la media de estas posiciones, 1.5; el 2 ocuparía la posición 3 y el 3 ocuparía la posición 4, y estos son también sus rangos. Dejamos como ejercicio que comprobéis los rangos de los elementos de \(x_{\bullet 2}\).
Con R estos rangos se calculan con la función rank. Así, los rangos de los elementos de \(x_{\bullet 1}\) son
rank(X$V1)## [1] 1.5 1.5 3.0 4.0y los de los elementos de \(x_{\bullet 2}\) son
rank(X$V2)## [1] 1.0 2.5 4.0 2.5Por lo tanto, la correlación de Spearman de \[ (1,1,2,3)\mbox{ y }(-1,0,3,0) \] es la correlación de Pearson de \[ (1.5, 1.5, 3, 4)\mbox{ y }(1, 2.5, 4, 2.5) \]
Veámoslo:
cor(X$V1,X$V2,method="spearman")## [1] 0.5cor(rank(X$V1),rank(X$V2))## [1] 0.58.5 Contrastes de correlación
Como ya hemos comentado, podemos usar la correlación de Pearson \(r_{xy}\) de dos vectores \(x\) e \(y\), formados por los valores de dos variables cuantitativas \(X,Y\) medidos sobre una misma muestra de individuos, para estimar la correlación \(\rho_{XY}\) de estas variables poblacionales. Cuando además el vector aleatorio \((X,Y)\) tiene distribución normal bivariante, disponemos de una fórmula para calcular intervalos de confianza para la correlación poblacional y de un método para efectuar contrastes de hipótesis con hipótesis nula \(H_0: \rho_{XY}=0\) (“no hay correlación entre \(X\) e \(Y\)”). No vamos a entrar en los detalles de las fórmulas ni de los teoremas en que se basan, pero es importante que recordéis que la función de R que lleva a cabo dichos contrastes “de correlación” es la función cor.test. En particular, esta función calcula el intervalo de confianza asociado a un contraste de estos: si el contraste es bilateral, es decir, con hipótesis alternativa \(H_1: \rho_{XY}\neq 0\), el intervalo que produce esta función es el intervalo de confianza usual para \(\rho_{XY}\) con nivel de confianza correspondiente al nivel de significación del contraste.
La sintaxis de cor.test es la misma que la del resto de funciones para realizar contrastes de hipótesis básicos:
cor.test(x, y, alternative=..., conf.level=...)donde x e y son los dos vectores de datos, que también se pueden especificar mediante una fórmula. Estos dos vectores han de tener la misma longitud, puesto que se entiende que son mediciones sobre el mismo conjunto de individuos. El parámetro alternative puede tomar los tres valores usuales y su valor por defecto es, como siempre, "two.sided", que corresponde al contraste bilateral, con hipótesis alternativa \(H_1: \rho_{XY}\neq 0\). Los valores alternative="greater" y alternative="less" permiten contrastar si \(X\) e \(Y\) tienen correlación mayor o menor que 0, respectivamente.
Como en el resto de funciones de contrastes, el resultado es una list que, entre otros objetos, contiene:
p.value: El p-valor del test.conf.int: Un intervalo de confianza del nivel de confianza especificado.estimate: El valor de la correlación de Pearson (calculado conuse="complete.obs"si algún vector contiene valores NA).
Ejemplo 8.10 Queremos contrastar si hay correlación positiva entre el peso de una madre en el momento de la concepción del hijo y el peso de su hijo en el momento de nacer. Para ello vamos a usar la tabla de datos birthwt incluida en el paquete MASS que ya usamos en una lección anterior, que contiene información sobre recién nacidos y sus madres, y que en particular dispone de las variables bwt, que da el peso del recién nacido en gramos, y lwt, que da el peso de la madre en libras en el momento de su última menstruación. Vamos a suponer que ambos pesos siguen distribuciones normales. Si denotamos por \(X\) e \(Y\) las correspondientes variables poblacionales, queremos realizar el contraste
\[
\left\{\begin{array}{l}
H_0: \rho_{XY}=0\\
H_1: \rho_{XY}>0
\end{array}\right.
\]
Vamos a usar la función cor.test.
library(MASS)
cor.test(birthwt$bwt, birthwt$lwt, alternative="greater")##
## Pearson's product-moment correlation
##
## data: birthwt$bwt and birthwt$lwt
## t = 2.5848, df = 187, p-value = 0.005252
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
## 0.06720637 1.00000000
## sample estimates:
## cor
## 0.1857333El p-valor 0.005 nos da evidencia estadísticamente significativa de que, en efecto, hay una correlación positiva entre el peso de la madre y el peso del recién nacido. El último valor, el 0.1857333 bajo el cor, es la correlación de Pearson de los dos vectores de pesos, y el 95 percent confidence interval es el intervalo de confianza del 95% del contraste unilateral planteado y nos dice que tenemos un 95% de confianza en que la correlación entre el peso de la madre y el peso del recién nacido es superior a 0.067.
Podríamos haber obtenido el p-valor del contraste de correlación anterior directamente con la instrucción
cor.test(birthwt$bwt, birthwt$lwt, alternative="greater")$p.value## [1] 0.005252088Si hubiéramos querido calcular un intervalo de confianza del 95% para \(\rho_{XY}\) que repartiera por igual a ambos lados el 5% de probabilidad de no contener su valor real, hubiéramos podido usar el intervalo de confianza del contraste bilateral:
cor.test(birthwt$bwt, birthwt$lwt)$conf.int## [1] 0.04417405 0.31998094
## attr(,"conf.level")
## [1] 0.95La potencia de un contraste de correlación se calcula con la función pwr.r.test del paquete pwr. En este caso, el tamaño del efecto es simplemente la correlación de Pearson, que se entra en la función mediante el parámetro r. Apliquémosla para calcular la potencia del contraste de correlación anterior:
library(pwr)
dim(birthwt)## [1] 189 10round(cor(birthwt$bwt,birthwt$lwt),4)## [1] 0.1857pwr.r.test(n=189,r=0.1857,sig.level=0.05,alternative="greater")##
## approximate correlation power calculation (arctangh transformation)
##
## n = 189
## r = 0.1857
## sig.level = 0.05
## power = 0.8223733
## alternative = greaterLa probabilidad de error de tipo II en este contraste era de un poco menos del 18%.
Si quisiéramos realizar este contraste de correlación con una potencia del 90% suponiendo que la magnitud del efecto va ser pequeña, usaríamos primero cohen.ES con test="r" para determinar qué magnitud del efecto se considera pequeña y a continuación pwr.r.test dejando sin especificar la n:
cohen.ES(test="r",size="small")##
## Conventional effect size from Cohen (1982)
##
## test = r
## size = small
## effect.size = 0.1pwr.r.test(power=0.9,r=0.1,sig.level=0.05,alternative="greater")##
## approximate correlation power calculation (arctangh transformation)
##
## n = 852.6473
## r = 0.1
## sig.level = 0.05
## power = 0.9
## alternative = greaterHubiéramos necesitado datos de al menos 853 recién nacidos.
8.6 Un ejemplo
Recordaréis el data frame iris, que tabulaba las longitudes y anchuras de los pétalos y los sépalos de una muestra de flores iris de tres especies. Vamos a extraer una subtabla con sus cuatro variables numéricas, que llamaremos iris_num, y calcularemos sus matrices de covarianzas y correlaciones.
str(iris)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...iris_num=iris[, 1:4]
n=dim(iris_num)[1] #Número de filasSu matriz de covarianzas muestrales es:
cov(iris_num) ## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 0.6856935 -0.0424340 1.2743154 0.5162707
## Sepal.Width -0.0424340 0.1899794 -0.3296564 -0.1216394
## Petal.Length 1.2743154 -0.3296564 3.1162779 1.2956094
## Petal.Width 0.5162707 -0.1216394 1.2956094 0.5810063Su matriz de covarianzas “verdaderas” es:
cov(iris_num)*(n-1)/n ## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 0.68112222 -0.04215111 1.2658200 0.5128289
## Sepal.Width -0.04215111 0.18871289 -0.3274587 -0.1208284
## Petal.Length 1.26582000 -0.32745867 3.0955027 1.2869720
## Petal.Width 0.51282889 -0.12082844 1.2869720 0.5771329Su matriz de correlaciones de Pearson es:
cor(iris_num) ## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
## Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
## Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
## Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000Observamos, por ejemplo, una gran correlación de Pearson positiva entre la longitud y la anchura de los pétalos, 0.963, lo que indica una estrecha relación lineal con pendiente positiva entre estas magnitudes. Valdría la pena, entonces, calcular la recta de regresión lineal de una de estas medidas en función de la otra.
lm(Petal.Length~Petal.Width, data=iris_num)##
## Call:
## lm(formula = Petal.Length ~ Petal.Width, data = iris_num)
##
## Coefficients:
## (Intercept) Petal.Width
## 1.084 2.230En cambio, la correlación de Pearson entre la longitud y la anchura de los sépalos es -0.1175698, muy cercana a cero, lo que es señal de que la variación conjunta de las longitudes y anchuras de los sépalos no tiene una tendencia clara.
Vamos a ordenar ahora los pares de variables numéricas de iris en orden decreciente de su correlación en valor absoluto, para saber cuáles están más correlacionadas (en positivo o negativo). Para ello, en primer lugar creamos un data frame cuyas filas están formadas por pares diferentes de variables numéricas de iris, su correlación de Pearson y el valor absoluto de esta última, y a continuación ordenamos las filas de este data frame en orden decreciente de estos valores absolutos. Todo esto lo llevamos a cabo en el siguiente bloque de código, que luego explicamos:
medidas=names(iris_num)
n=length(medidas) #En este caso, n=4
indices=upper.tri(diag(n))
medida1=matrix(rep(medidas, times=n), nrow=n, byrow=FALSE)[indices]
medida2=matrix(rep(medidas, times=n), nrow=n, byrow=TRUE)[indices]
corrs=as.vector(cor(iris_num))[indices]
corrs.abs=abs(corrs)
corrs_df=data.frame(medida1, medida2, corrs, corrs.abs)
corrs_df_sort=corrs_df[order(corrs_df$corrs.abs, decreasing=TRUE), ]
corrs_df_sort## medida1 medida2 corrs corrs.abs
## 6 Petal.Length Petal.Width 0.9628654 0.9628654
## 2 Sepal.Length Petal.Length 0.8717538 0.8717538
## 4 Sepal.Length Petal.Width 0.8179411 0.8179411
## 3 Sepal.Width Petal.Length -0.4284401 0.4284401
## 5 Sepal.Width Petal.Width -0.3661259 0.3661259
## 1 Sepal.Length Sepal.Width -0.1175698 0.1175698Vemos que el par de variables con mayor correlación de Pearson en valor absoluto son Petal.Length y Petal.Width, como ya habíamos observado, seguidos por Petal.Length y Sepal.Length.
Vamos a explicar el código. La función upper.tri, aplicada a una matriz cuadrada \(M\), produce la matriz triangular superior de valores lógicos del mismo orden que \(M\), cuyas entradas \((i,j)\) con \(i<j\) son todas TRUE y el resto todas FALSE. Existe una función similar, lower.tri, para producir matrices triangulares inferiores de valores lógicos.
upper.tri(diag(4))## [,1] [,2] [,3] [,4]
## [1,] FALSE TRUE TRUE TRUE
## [2,] FALSE FALSE TRUE TRUE
## [3,] FALSE FALSE FALSE TRUE
## [4,] FALSE FALSE FALSE FALSElower.tri(diag(4))## [,1] [,2] [,3] [,4]
## [1,] FALSE FALSE FALSE FALSE
## [2,] TRUE FALSE FALSE FALSE
## [3,] TRUE TRUE FALSE FALSE
## [4,] TRUE TRUE TRUE FALSEAmbas funciones disponen del parámetro diag que, igualado a TRUE, define también como TRUE las entradas de la diagonal principal.
upper.tri(diag(4), diag=TRUE)## [,1] [,2] [,3] [,4]
## [1,] TRUE TRUE TRUE TRUE
## [2,] FALSE TRUE TRUE TRUE
## [3,] FALSE FALSE TRUE TRUE
## [4,] FALSE FALSE FALSE TRUESi \(M\) es una matriz y \(L\) es una matriz de valores lógicos del mismo orden, M[L] produce el vector construido de la manera siguiente: de cada columna, se queda sólo con las entradas de \(M\) cuya entrada correspondiente en \(L\) es TRUE, y a continuación concatena estas columnas, de izquierda a derecha, en un vector. Así, por ejemplo, tomemos la matriz \(M\) siguiente:
M=matrix(1:16, nrow=4, byrow=T)
M## [,1] [,2] [,3] [,4]
## [1,] 1 2 3 4
## [2,] 5 6 7 8
## [3,] 9 10 11 12
## [4,] 13 14 15 16El vector formado por las entradas de su triángulo superior, concatenadas por columnas, se obtiene de la manera siguiente:
M[upper.tri(diag(4))]## [1] 2 3 7 4 8 12Ahora definimos las matrices siguientes, formadas por 4 copias (la primera por columnas, la segunda, por filas) del vector, al que hemos llamado medidas, de nombres de las variables numéricas de iris:
matrix(rep(medidas, times=4), nrow=4, byrow=FALSE)## [,1] [,2] [,3] [,4]
## [1,] "Sepal.Length" "Sepal.Length" "Sepal.Length" "Sepal.Length"
## [2,] "Sepal.Width" "Sepal.Width" "Sepal.Width" "Sepal.Width"
## [3,] "Petal.Length" "Petal.Length" "Petal.Length" "Petal.Length"
## [4,] "Petal.Width" "Petal.Width" "Petal.Width" "Petal.Width"matrix(rep(medidas, times=4), nrow=4, byrow=TRUE)## [,1] [,2] [,3] [,4]
## [1,] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"
## [2,] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"
## [3,] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"
## [4,] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"Al aplicar estas dos matrices a la matriz de valores lógicos upper.tri(diag(4)) obtenemos los nombres de las variables correspondientes a las filas y las columnas del triángulo superior, respectivamente, y al aplicar la matriz de correlaciones a esta matriz de valores lógicos, obtenemos sus entradas en este triángulo; en los tres vectores, las entradas siguen el mismo orden. Esto nos permite construir el data frame corrs_df cuyas filas están formadas por pares diferentes de variables numéricas de iris, su correlación de Pearson (columna corrs) y, aplicando abs a esta última variable, dicha correlación en valor absoluto (columna corrs.abs).
corrs_df## medida1 medida2 corrs corrs.abs
## 1 Sepal.Length Sepal.Width -0.1175698 0.1175698
## 2 Sepal.Length Petal.Length 0.8717538 0.8717538
## 3 Sepal.Width Petal.Length -0.4284401 0.4284401
## 4 Sepal.Length Petal.Width 0.8179411 0.8179411
## 5 Sepal.Width Petal.Width -0.3661259 0.3661259
## 6 Petal.Length Petal.Width 0.9628654 0.9628654Finalmente, la función order ordena los valores del vector al que se aplica, en orden decreciente si se especifica el parámetro decreasing=TRUE. Cuando aplicamos un data frame a una de sus variables reordenada de esta manera, reordena sus filas según el orden de esta variable. En este caso hubiéramos conseguido lo mismo con la función sort, pero la función order se puede aplicar a más de una variable del data frame: esto permite ordenar las filas del data frame en el orden de la primera variable de manera que, en caso de empate, queden ordenadas por la segunda variable, y así sucesivamente.
8.7 Representación gráfica de datos multidimensionales
La representación gráfica de tablas de datos multidimensionales tiene la dificultad de las dimensiones; para dos o tres variables es sencillo visualizar las relaciones entre las mismas, pero para más variables ya no nos bastan nuestras tres dimensiones espaciales y tenemos que usar algunos trucos, tales como representaciones gráficas conjuntas de pares de variables.
La manera más sencilla de representar gráficamente una tabla de datos formada por dos variables numéricas es aplicando la función plot a la matriz de datos o al data frame. Esta función produce el diagrama de dispersión (scatter plot) de los datos: el gráfico de los puntos del plano definidos por las filas de la tabla.
A modo de ejemplo, si extrajéramos de la tabla iris una subtabla conteniendo sólo las longitudes y anchuras de los pétalos y quisiéramos visualizar la relación entre estas dimensiones, podríamos dibujar su diagrama de dispersión con el código del bloque siguiente. El resultado es la Figura 8.1, que muestra una clara tendencia positiva: cuanto más largos son los pétalos, más anchos tienden a ser. Esto se corresponde con la correlación de Pearson de 0.963 que hemos obtenido en la sección anterior.
iris.pet=iris[ ,c("Petal.Length","Petal.Width")]
plot(iris.pet, pch=20, xlab="Largo", ylab="Ancho")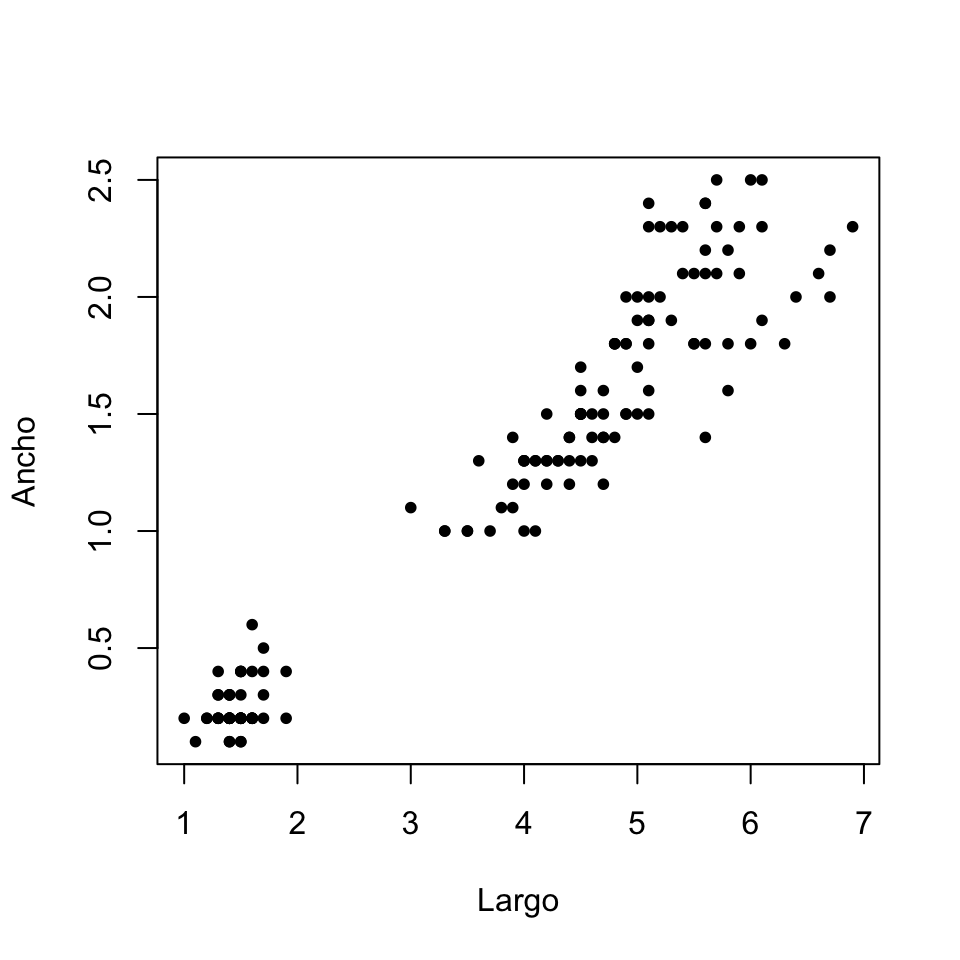
Figura 8.1: Diagrama de dispersión de las longitudes y anchuras de los pétalos de las flores de la tabla iris.
Para tablas de datos de tres columnas numéricas, podemos usar con un fin similar la instrucción scatterplot3d del paquete homónimo, que dibuja un diagrama de dispersión tridimensional. Como plot, se puede aplicar a un data frame o a una matriz; por ejemplo, para representar gráficamente las tres primeras variables numéricas de iris, podríamos usar el código siguiente y obtendríamos la Figura 8.2:
library(scatterplot3d)
scatterplot3d(iris[ , 1:3], pch=20)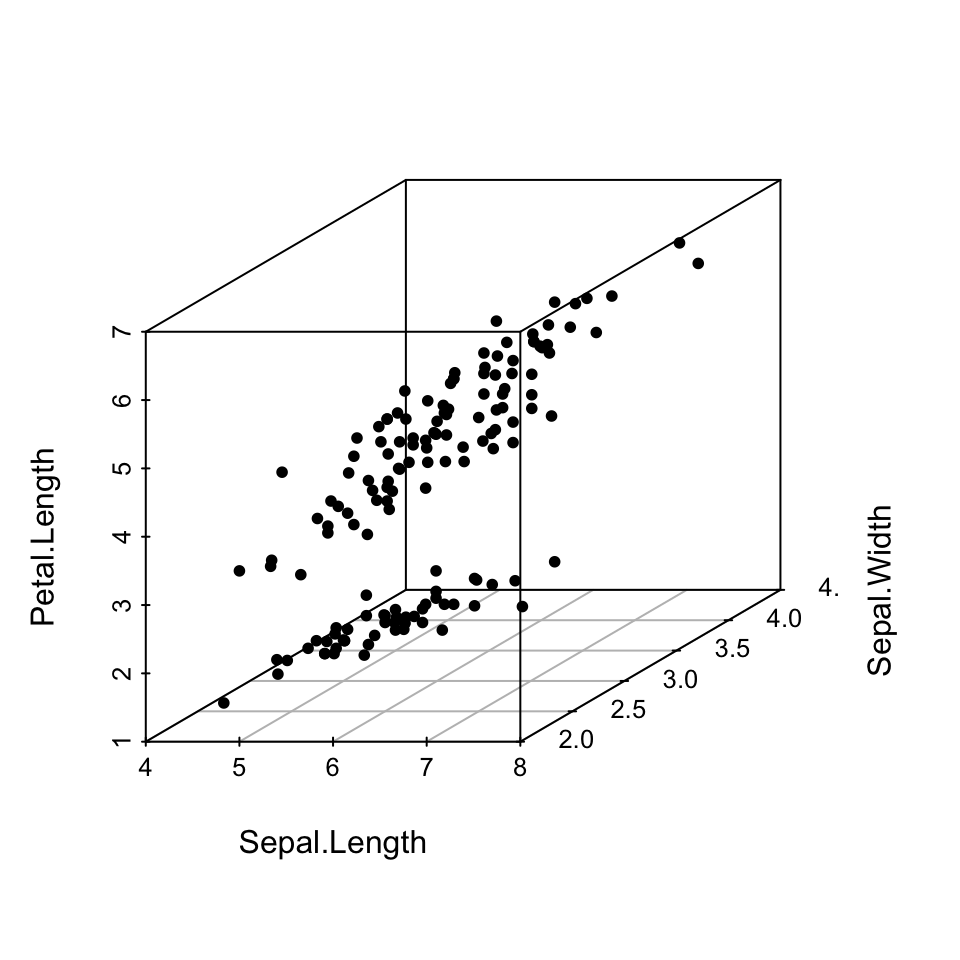
Figura 8.2: Diagrama de dispersión tridimensional de las tres primeras columnas de la tabla iris.
Podéis consultar la Ayuda de la instrucción para saber cómo modificar su apariencia: cómo ponerle un título, poner nombres adecuados a los ejes, usar colores, cambiar el estilo del gráfico, etc.
Una representación gráfica muy popular de las tablas de datos de tres o más columnas numéricas son las matrices formadas por los diagramas de dispersión de todos sus pares de columnas. Si la tabla de datos es un data frame, esta matriz de diagramas de dispersión se obtiene simplemente aplicando la función plot al data frame; por ejemplo, la instrucción
plot(iris[ , 1:4])produce el gráfico de la Figura 8.3. En este gráfico, los cuadrados en la diagonal indican a qué variables corresponden cada fila y cada columna, de manera que podamos identificar fácilmente qué variables compara cada diagrama de dispersión; así, en el diagrama de la primera fila y segunda columna de esta figura, las abscisas corresponden a anchuras de sépalos y las ordenadas a longitudes de sépalos. Observad que la nube de puntos no muestra una tendencia clara y en todo caso ligeramente negativa, lo que se corresponde con la correlación de Pearson entre estas variables de -0.118 que hemos obtenido en la sección anterior.
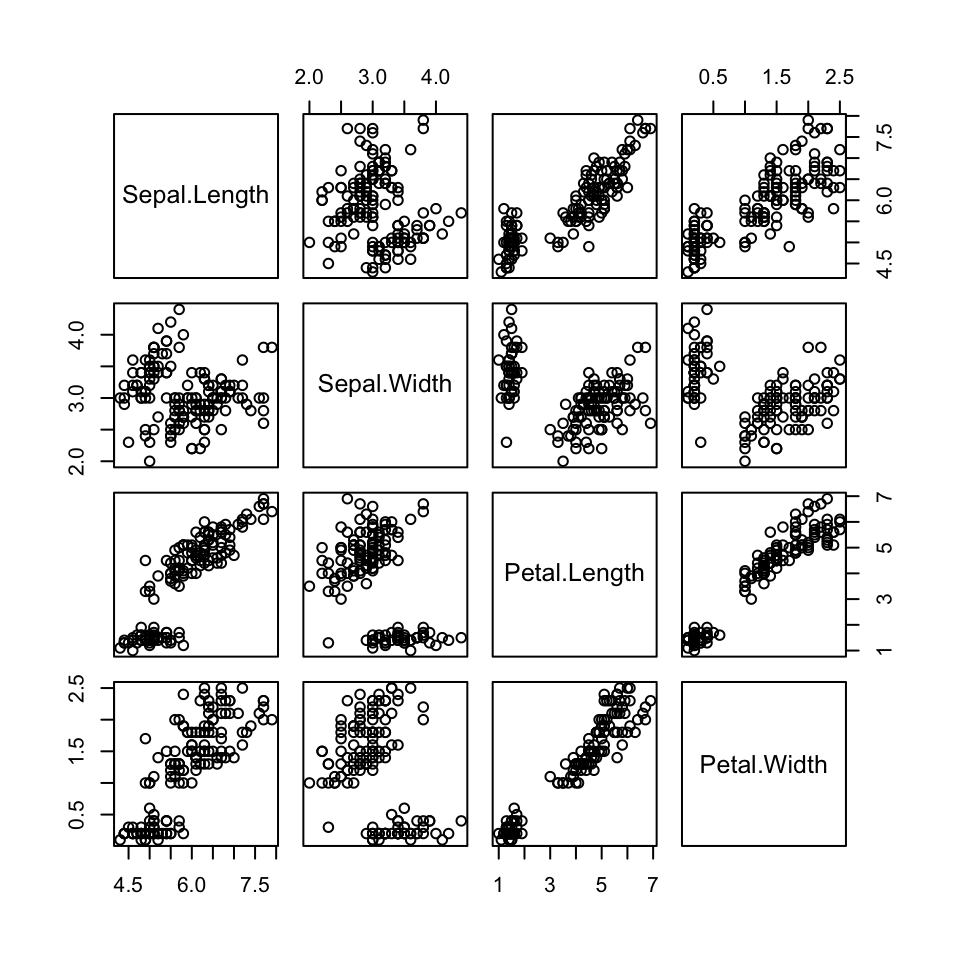
Figura 8.3: Matriz de diagramas de dispersión de la tabla iris.
Podemos usar los parámetros usuales de plot para mejorar el gráfico resultante; por ejemplo, podemos usar colores para distinguir las flores según su especie. Así, la instrucción siguiente produce el gráfico de la Figura 8.4.
plot(iris[ , 1:4], col=iris$Species, pch=20, cex=0.7)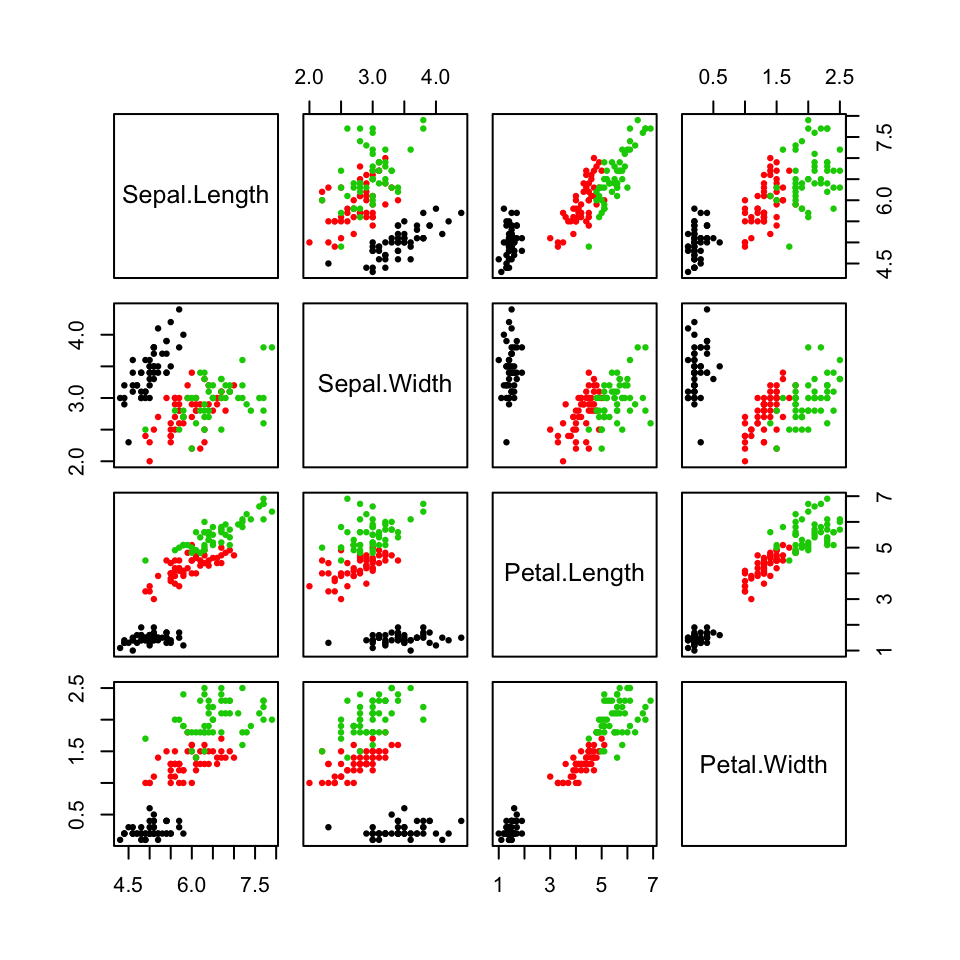
Figura 8.4: Matriz de diagramas de dispersión de la tabla iris, con las especies distinguidas por colores.
Para obtener la matriz de diagramas de dispersión de una tabla de datos multidimensional también se puede usar la función pairs: así, pairs(iris[, 1:4]) produce exactamente el mismo gráfico que plot(iris[, 1:4]). La ventaja principal de pairs es que se puede aplicar a una matriz para obtener la matriz de diagramas de dispersión de sus columnas, mientras que plot no.
El paquete car incorpora una función que permite dibujar matrices de diagramas de dispersión enriquecidos con información descriptiva extra de las variables de la tabla de datos y que además facilita el control del gráfico resultante, por lo que os recomendamos su uso frente a las funciones básicas plot y pairs. Se trata de la función spm (abreviatura de scatterplotMatrix); por ejemplo, el código siguiente produce el gráfico la Figura 8.5.
library(car)
spm(iris[ , 1:4], var.labels=c("Long. Sep.","Ancho Sep.","Long. Pet.","Ancho Pet."))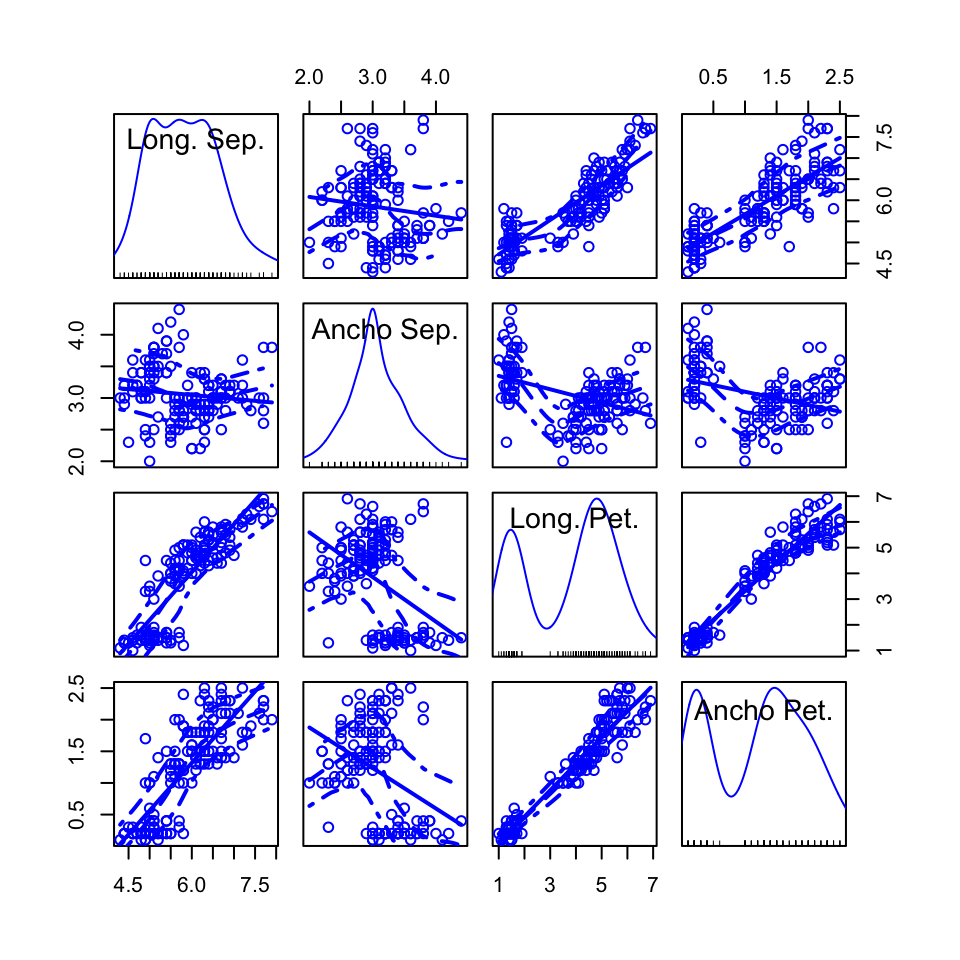
Figura 8.5: Una matriz de diagramas de dispersión de la tabla iris producida con la función spm.
Observad para empezar que hemos cambiado los nombres que identifican las variables en los cuadrados de la diagonal, con el parámetro var.labels, y que en dichos cuadrados aparecen además unas curvas: se trata de la curva de densidad estimada de la variable correspondiente de la que hablábamos en la Lección ?? de la primera parte del curso. La información gráfica contenida en estos cuadrados de la diagonal se puede modificar con el parámetro diagonal: podemos pedir, por ejemplo, que dibuje un histograma de cada variable (con diagonal=list(method ="histogram")) o su boxplot (con diagonal=list(method="boxplot")) o un normal-plot (con diagonal=list(method="qqplot")). Así, el código siguiente produce el gráfico la Figura 8.6.
spm(iris[ , 1:4], var.labels=c("Long. Sep.","Ancho Sep.","Long. Pet.","Ancho Pet."),
diagonal=list(method="boxplot"), pch=20,cex=0.75)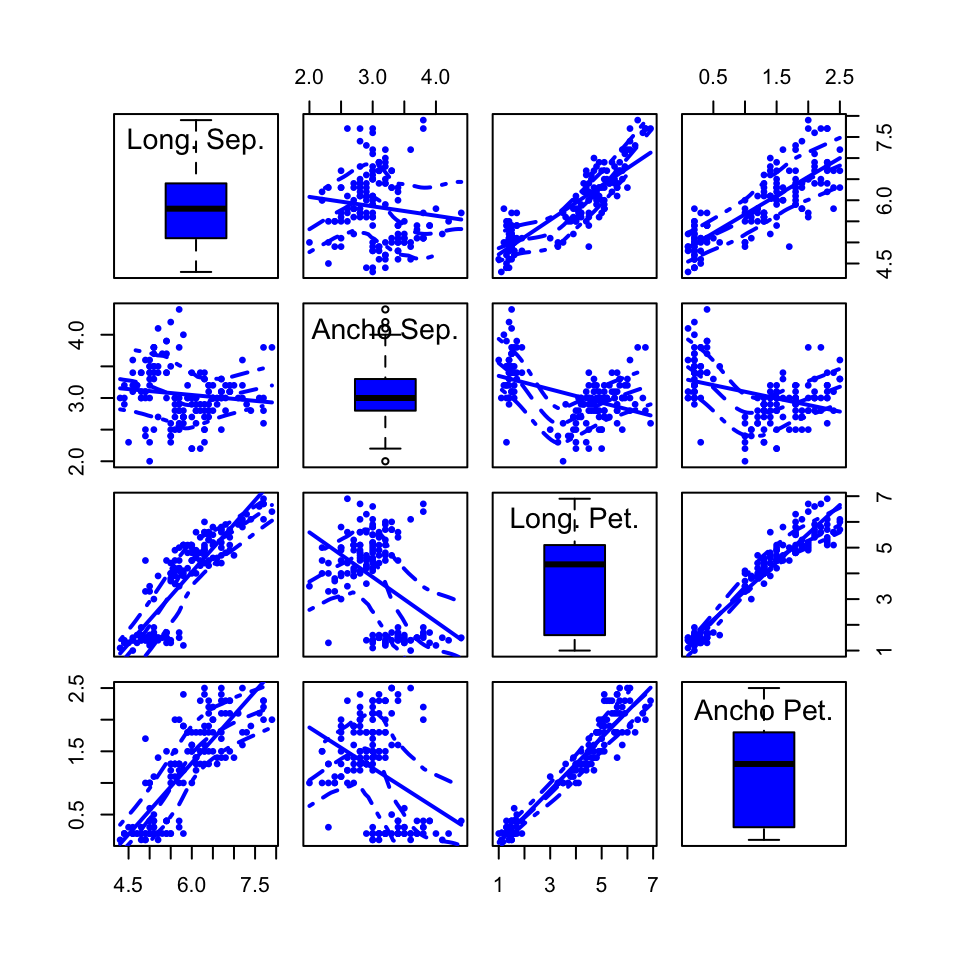
Figura 8.6: Matriz de diagramas de dispersión de la tabla iris con boxplots en la diagonal.
Observad también que los diagramas de dispersión de la matriz producida con spm contienen algunas líneas. La línea recta es la recta de regresión por mínimos cuadrados y, sin entrar en detalle sobre su significado exacto, las curvas discontinuas representan la tendencia de los datos. Podéis eliminar la recta de regresión con regLine=FALSE (no os lo recomendamos) y las curvas discontinuas con smooth=FALSE; si las queréis mantener, consultad la Ayuda de la función para saber cómo cambiar su estilo, color, etc.
A veces querremos agrupar los datos de las variables numéricas de una tabla de datos. Los motivos serán los mismos que cuando se trata de una sola variable: por ejemplo, si los datos son aproximaciones de valores reales, o si son muy heterogéneos. Cuando tenemos dos variables emparejadas agrupadas, se pueden representar gráficamente las frecuencias de sus pares de clases mediante un histograma bidimensional, que divide el conjunto de todos los pares de valores en rectángulos definidos por los pares de intervalos
e indica sobre cada rectángulo su frecuencia absoluta, por ejemplo mediante colores o intensidades de gris (dibujar barras verticales sobre las regiones es una mala idea, las de delante pueden ocultar las de detrás). Hay muchos paquetes de R que ofrecen funciones para dibujar histogramas bidimensionales; aquí explicaremos la función hist2d del paquete gplots. Su sintaxis básica es
hist2d(x,y, nbins=..., col=...)donde:
xeyson los vectores de primeras y segundas coordenadas de los puntos. Si son las dos columnas de un data frame de dos variables numéricas, lo podemos entrar en su lugar.nbinssirve para indicar los números de clases: podemos igualarlo a un único valor, y tomará ese número de clases sobre cada vector, o a un vector de dos entradas que indiquen el número de clases de cada vector.colsirve para especificar los colores a usar. Por defecto, los rectángulos vacíos aparecen de color negro, y el resto se colorean con tonalidades de rojo, de manera que los tonos más cálidos indican frecuencias mayores.
Además, podemos usar los parámetros usuales de plot para poner un título, etiquetar los ejes, etc.
A modo de ejemplo, vamos a dibujar el histograma bidimensional de las longitudes y anchuras de los pétalos de las flores iris, agrupando ambas dimensiones en los números de clases que da la regla de Freedman-Diaconis (y que calcula la función nclass.FD):
library(gplots)
hist2d(iris$Petal.Length, iris$Petal.Width,
nbins=c(nclass.FD(iris$Petal.Length),nclass.FD(iris$Petal.Width)))Obtenemos (junto con una serie de información en la consola que hemos omitido) la Figura 8.7, que podéis comparar con el diagrama de dispersión de los mismos datos de la Figura 8.1.
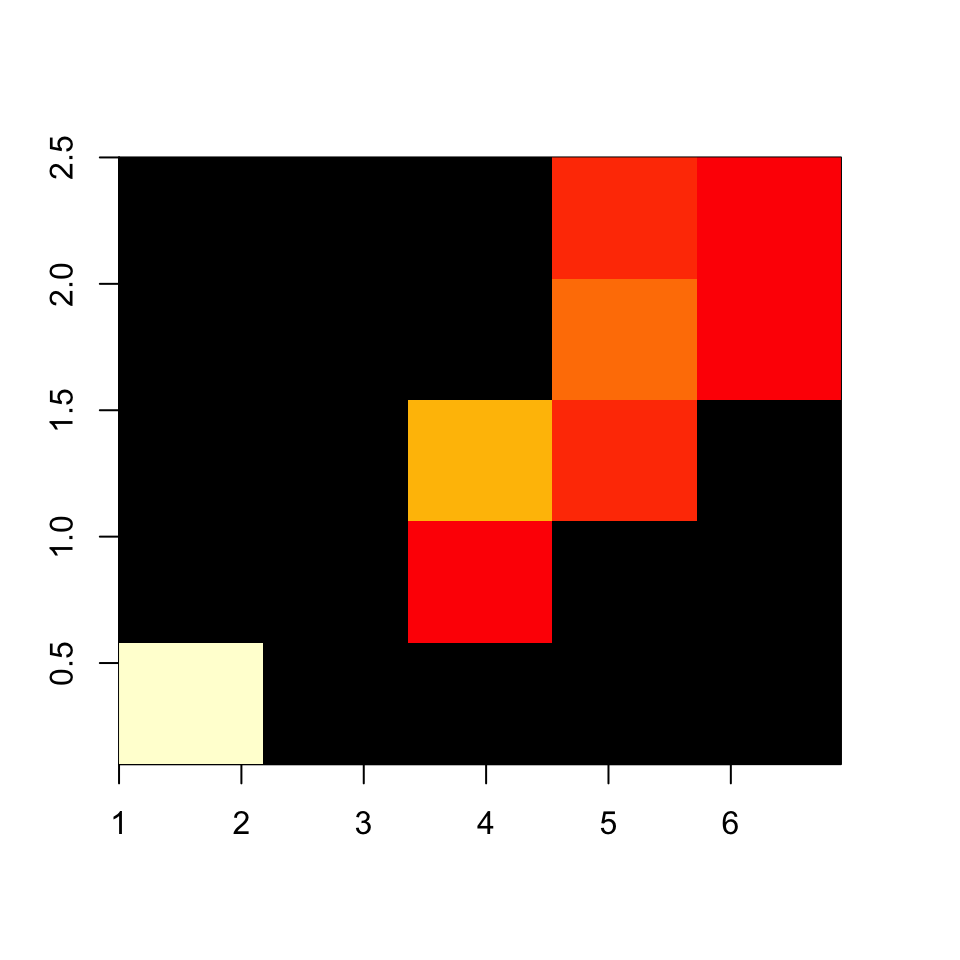
Figura 8.7: Histograma bidimensional de longitudes y anchuras de pétalos de flores iris.
En los histogramas bidimensionales con muchas regiones de diferentes frecuencias, es conveniente usar de manera adecuada los colores para representarlas. Una posibilidad es usar el paquete RColorBrewer, que permite elegir esquemas de colores bien diseñados. Las dos funciones básicas son:
brewer.pal(n,"paleta predefinida"), que carga en un vector de colores (una paleta) una secuencia de \(n\) colores de la paleta predefinida en el paquete. Los nombres y contenidos de todas las paletas predefinidas que se pueden usar en esta función se obtienen, en la ventana de gráficos, ejecutando la instruccióndisplay.brewer.all(). Por ejemplo, la paleta de colores de la Figura 8.8 se define con el código siguiente:
brewer.pal(11,"Spectral")
Figura 8.8: Paleta brewer.pal(11,“Spectral”)
colorRampPalette(brewer.pal(...))(m), produce una nueva paleta de \(m\) colores a partir del resultado debrewer.pal, interpolando nuevos colores. Luego se puede usar la funciónrevpara invertir el orden de los colores, lo que es conveniente en los histogramas bidimensionales si queremos que las frecuencias bajas correspondan a tonos azules y las frecuencias altas a tonos rojos. Así, la paleta de colores que se define con
rev(colorRampPalette(brewer.pal(11,"Spectral"))(50))es la de la Figura 8.9.
Figura 8.9: Paleta rev(colorRampPalette(brewer.pal(11,“Spectral”))(50))
Vamos a usar esta última paleta en un histograma bidimensional de la tabla de alturas de padres e hijos recogidas por Karl Pearson en 1903 y que tenemos guardada en el url https://raw.githubusercontent.com/AprendeR-UIB/Material/master/pearson.txt; el resultado es la Figura 8.10.
df_pearson=read.table("https://raw.githubusercontent.com/AprendeR-UIB/Material/master/pearson.txt",header=TRUE)
hist2d(df_pearson, nbins=30,
col=rev(colorRampPalette(brewer.pal(11,"Spectral"))(50)))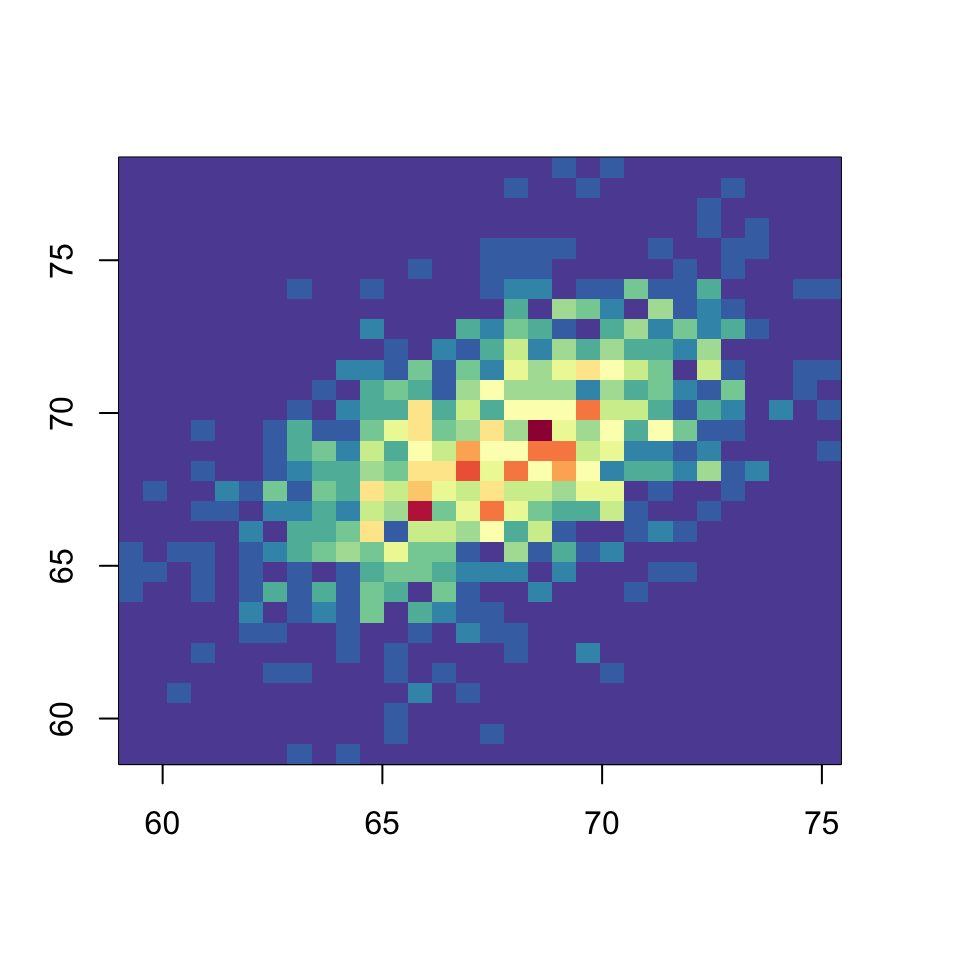
Figura 8.10: Histograma bidimensional de las alturas de padres e hijos recogidas por Karl Pearson.
Para terminar, veamos cómo producir un gráfico conjunto de un histograma bidimensional y los dos histogramas unidimensionales. Se trata de una modificación del gráfico similar explicado en http://www.everydayanalytics.ca/2014/09/5-ways-to-do-2d-histograms-in-r.html, el cual a su vez se inspira en un gráfico de la p. 62 de Computational Actuarial Science with R de Arthur Charpentier (Chapman and Hall/CRC, 2014). Considerad la función siguiente, cuyos parámetros son un data frame df de dos variables y un número n de clases, común para las dos variables:
hist.doble=function(df,n){
par.anterior=par()
h1=hist(df[,1], breaks=n, plot=F)
h2=hist(df[,2], breaks=n, plot=F)
m=max(h1$counts, h2$counts)
par(mar=c(3,3,1,1))
layout(matrix(c(2,0,1,3), nrow=2, byrow=T), heights=c(1,3), widths=c(3,1))
hist2d(df, nbins=n, col=rev(colorRampPalette(brewer.pal(11,"Spectral"))(50)))
par(mar=c(0,2,1,0))
barplot(h1$counts, axes=F, ylim=c(0, m), col="red")
par(mar=c(2,0,0.5,1))
barplot(h2$counts, axes=F, xlim=c(0, m), col="red", horiz=T)
par.anterior}Entonces, la instrucción
hist.doble(df_pearson,25)produce la Figura 8.11.
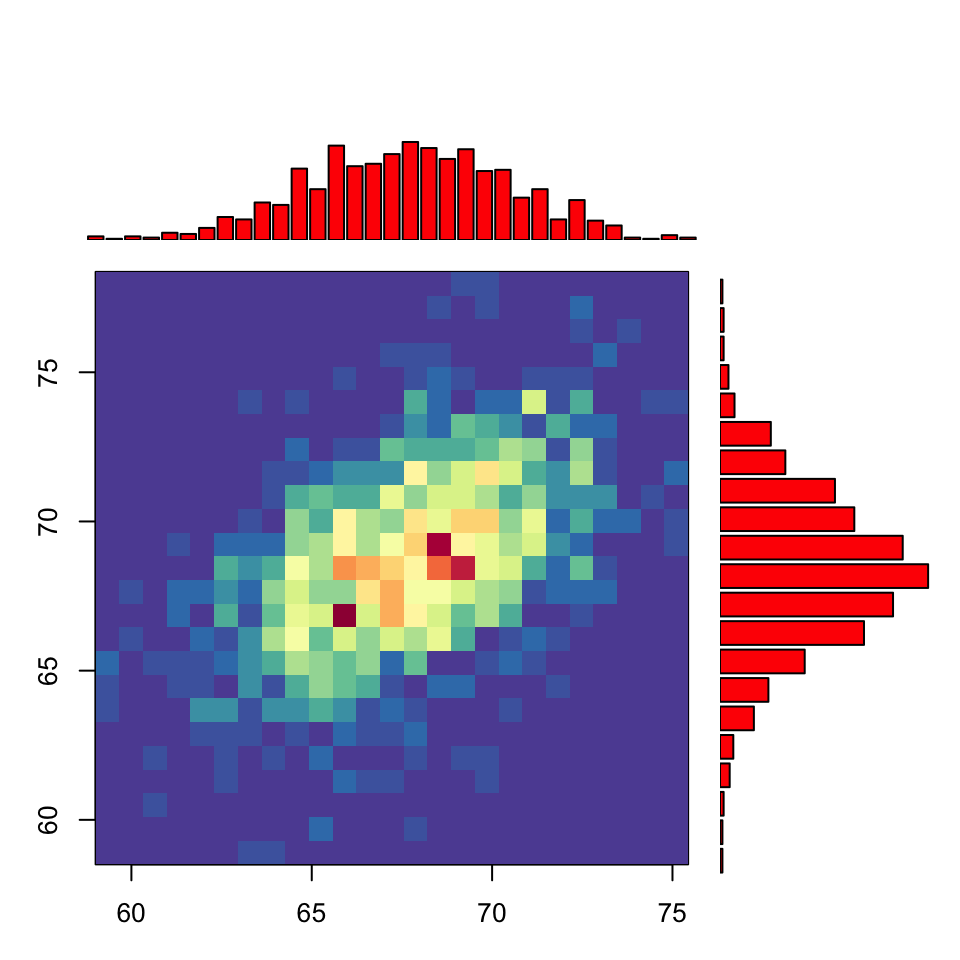
Figura 8.11: Histograma bidimensional con histogramas unidimensionales de las alturas de padres e hijos recogidas por Karl Pearson.
Algunas explicaciones sobre el código, por si lo queréis modificar:
Hemos “simulado” los histogramas mediante diagramas de barras de sus frecuencias absolutas, para poder dibujar horizontal el de la segunda variable.
El parámetro
axes=FALSEen losbarplotindica que no dibuje sus ejes de coordenadas.La función
parestablece los parámetros generales básicos de los gráficos. Como con esta función los modificamos, guardamos los parámetros anteriores enpar.anteriory al final los restauramos.El parámetro
marde la funciónparsirve para especificar, por este orden, los márgenes inferior, izquierdo, superior y derecho de la próxima figura, en números de líneas.La instrucción
layoutdivide la figura a producir en sectores con la misma estructura que la matriz de su primer argumento. Dentro de esta matriz, cada entrada indica qué figura de las próximas se ha de situar en ese sector. Las alturas y amplitudes relativas de los sectores se especifican con los parámetrosheightsywidths, respectivamente. Así, la instrucción
layout(matrix(c(2,0,1,3),nrow=2,byrow=T), heights=c(1,3),widths=c(3,1))divide la figura en 4 sectores. Los sectores de la izquierda serán el triple de anchos que los de la derecha (widths=c(3,1)), y los sectores inferiores serán el triple de altos que los superiores (heights=c(1,3)). En estos sectores, R dibujará los próximos gráficos según el esquema definido por la matriz del argumento:
\[
\left(\begin{array}{cc}
\mbox{segundo} & \mbox{ninguno}\\
\mbox{primero} & \mbox{tercero}
\end{array}\right).
\]
8.8 Guía rápida
sapply(data_frame,función)aplica lafuncióna las columnas deldata_frame.scalesirve para aplicar una transformación lineal a una matriz o a un data frame. Sus parámetros son:center: especifica el vector que restamos a sus columnas; por defecto, el vector de medias muestrales.scale: especifica el vector por el que dividimos sus columnas; por defecto, el vector de desviaciones típicas muestrales.
cov, aplicada a dos vectores, calcula su covarianza muestral; aplicada a un data frame o a una matriz, calcula su matriz de covarianzas muestrales. Dispone del parámetrouse, que:Para dos vectores:
* Igualado a `"complete.obs"`, calcula las covarianzas teniendo en cuenta sólo sus observaciones completas (las posiciones en las que ninguno de los dos vectores tiene un NA).Para más de dos vectores:
Igualado a
"pairwise.complete.obs", calcula la covarianza de cada par de columnas teniendo en cuenta sólo sus observaciones completas, independientemente del resto de la tabla; es decir, como si en el cálculo de la covarianza de cada par de columnas usáramosuse="complete.obs", sin tener en cuenta que forman parte de una tabla de datos con más columnas.Igualado a
"complete.obs", calcula las covarianzas de las columnas teniendo en cuenta sólo las filas completas de toda la matriz.
cor, aplicada a dos vectores, calcula su correlación de Pearson; aplicada a un data frame o a una matriz, calcula su matriz de correlaciones de Pearson. Se puede usar el parámetrousedecov. Usando el parámetromethod="spearman"calcula la correlación (o la matriz de correlaciones, si se aplica a un data frame o a una matriz) de Spearman.cor.testrealiza un contraste de correlación, con hipótesis nula que la correlación poblacional sea 0. Su sintaxis es la usual en funciones de contrastes.pwr.r.test, del paquete pwr, sirve para calcular la potencia de un contraste de correlación. Sus parámetros son:n, el tamaño de las muestras;r, su correlación de Pearson;sig.level, el nivel de significación;power, la potencia; yalternative, el tipo de contraste. Si se entran los valores de tres de los cuatro primeros parámetros, se obtiene el cuarto.upper.tri, aplicada a una matriz cuadrada M, produce la matriz triangular superior de valores lógicos del mismo orden que M. Con el parámetrodiag=TRUEse impone que el triángulo de valoresTRUEincluya la diagonal principal.lower.tri, aplicada a una matriz cuadrada M, produce la matriz triangular inferior de valores lógicos del mismo orden que M. Dispone del mismo parámetrodiag=TRUE.orderordena el primer vector al que se aplica, desempatando empates mediante el orden de los vectores subsiguientes a los que se aplica; el parámetrodecreasing=TRUEsirve para especificar que sea en orden decreciente.plot, aplicado a un data frame de dos variables numéricas, dibuja su diagrama de dispersión; aplicado a un data frame de más de dos variables numéricas, produce la matriz formada por los diagramas de dispersión de todos sus pares de variables.pairses equivalente aploten el sentido anterior, y se puede aplicar a matrices.spm, del paquete cars, produce matrices de dispersión más informativas y fáciles de modificar.scatterplot3d, del paquete scatterplot3d, dibuja diagramas de dispersión tridimensionales.hist2d, del paquete gplots, dibuja histogramas bidimensionales. Dispone de los parámetros específicos siguientes:nbins: indica los números de clases.col: especifica la paleta de colores que ha de usar para representar las frecuencias.
brewer.pal(n,"paleta predefinida"), del paquete RColorBrewer, carga en una paleta de colores una secuencia de n colores de la paleta predefinida en dicho paquete.colorRampPalette(brewer.pal(...))(m), del paquete RColorBrewer, genera una nueva paleta de \(m\) colores a partir del resultado debrewer.pal, interpolando nuevos colores.display.brewer.all(), del paquete RColorBrewer, muestra los nombres y contenidos de todas las paletas predefinidas en dicho paquete.parsirve para establecer los parámetros generales básicos de los gráficos.layoutdivide en sectores la figura a producir, para que pueda incluir varios gráficos independientes simultáneamente.
8.9 Ejercicios
Modelo de test
(1) Considerad la matriz de datos \[\left(\begin{array}{ccc} 10.6 & 2.4 & 7.5 \\ 7.4 & 3.7 & 10.9\\ 10.7 & 2.6 & 9.6 \\ 8.4 & 4.9 & 9.9\\16.7 & 6.2 & 13.2 \\ 11.3 & 4.3 & 7.7\end{array} \right).\] Calculad la entrada (4,2) de su matriz de datos tipificada, redondeada a 3 cifras decimales y sin ceros innecesarios a la derecha.
(2) Considerad la matriz de datos \[\left(\begin{array}{ccc} 10.6 & 2.4 & 7.5 \\ 7.4 & 3.7 & 10.9\\ 10.7 & 2.6 & 9.6 \\ 8.4 & 4.9 & 9.9\\16.7 & 6.2 & 13.2 \\ 11.3 & 4.3 & 7.7\end{array}\right).\] Calculad la covarianza muestral \(\widetilde{s}_{3,2}\), redondeada a 3 cifras decimales y sin ceros innecesarios a la derecha.
(3) Considerad la matriz de datos \[\left(\begin{array}{ccc} 10.6 & 2.4 & 7.5 \\ 7.4 & 3.7 & 10.9\\ 10.7 & 2.6 & 9.6 \\ 8.4 & 4.9 & 9.9\\16.7 & 6.2 & 13.2 \\ 11.3 & 4.3 & 7.7\end{array}\right).\] Calculad la correlación de Pearson \(r_{3,2}\), redondeada a 3 cifras decimales y sin ceros innecesarios a la derecha.
(4) Usando la función cor.test, realizad el contraste bilateral de correlación entre el perímetro del tronco y la altura de los cerezos negros americanos usando la muestra del dataframe trees que viene con la instalación básica de R. Dad el p-valor redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha, e indicad si la conclusión, con un nivel de significación del 5%, es que hay correlación o no entre estas dos variables, escribiendo SI o NO, según corresponda. Separad el p-valor de la conclusión con un único espacio en blanco.
(5) Calculad la correlación de Spearman de los vectores \(x=(4,8,6,9,5,9 ,4,7,10, 8)\) e \(y=(0,6,2,1,4,4,3,7,11,5)\). Dad el resultado redondeado a 3 cifras decimales sin ceros innecesarios a la derecha.
(6) ¿Cuál de las cuatro matrices siguientes es la matriz de covarianzas de una tabla de datos de 2 columnas y 5 filas? Solo hay una. \[ \begin{array}{l} A=\left(\begin{array}{cc} 0.7 & 3 \cr 3 & 1.2 \end{array}\right)\\ B=\left(\begin{array}{cc} 0.6 & 0.8\cr -0.8 & 0.6 \end{array}\right)\\ C=\left(\begin{array}{cc} 0.6 & 0.8\cr 0.8 & -0.6 \end{array}\right)\\ D=\left(\begin{array}{ccccc} 0.7 & 0.2 & 1.3 & 0.5& -0.1\cr 0.2 & 0.7 & -0.3 & -0.1 &-0.1\cr 1.3 & -0.3 & 3.1 & 1.3 & 0.4\cr 0.5& -0.1& 1.3 & 0.6 & 0.2\cr -0.1 & -0.1 & 0.4 & 0.2& 2.9\end{array}\right) \end{array} \]
Problemas
(1) El fichero https://raw.githubusercontent.com/AprendeR-UIB/Material/master/NotasMatesI14.csv recoge las notas medias (sobre 100) obtenidas en las diferentes actividades de evaluación de la asignatura Matemáticas I del grado de Biología, en el curso 2013/14, por parte de los estudiantes que fueron considerados “presentados” en la primera convocatoria. Estas actividades consistieron en:
- Dos controles (columnas
Control1yControl2). - Talleres de resolución de problemas (columna
Talleres). - Ejercicios para resolver en casa (columna
Casa). - Cuestionarios en línea sobre los contenidos de la asignatura y sobre R (columnas
TestsContyTestsR, respectivamente).
Cargad este fichero en un data frame.
(a) Calculad el vector de medias y el vector de desviaciones típicas de esta tabla de datos. ¿Cuáles son las actividades de evaluación cuyas notas presentan mayor y menor variabilidad?
(b) Calculad las matrices de covarianzas “verdaderas” y de correlaciones de Pearson de esta tabla de datos.
(c) ¿Qué par de variables tiene mayor correlación? ¿Qué par de variables tiene menor correlación?
(d) Comprobad en esta tabla de datos que su matriz de correlaciones es igual a la matriz de covarianzas de su tabla tipificada.
(e) Dibujad una matriz de diagramas de dispersión de estas notas añadiendo en cada uno la recta de regresión lineal por mínimos cuadrados (pero sin otras curvas que indiquen la tendencia de los datos). ¿Se pueden ver en este diagrama los pares de actividades de evaluación con mayor y menor correlación que habéis encontrado en el apartado (c)?
Respuestas al test
(1) 0.673
Nosotros lo hemos calculado con
X=matrix(c(10.6,2.4,7.5,7.4,3.7,10.9,10.7,2.6,9.6,8.4,4.9,9.9,16.7,6.2,13.2,11.3,4.3,7.7), nrow=6, byrow=TRUE)
n=dim(X)[1]
X.tip.Ex=scale(X)*sqrt(n/(n-1))
round(X.tip.Ex[4,2],3)## [1] 0.673(2) 2.114
Nosotros lo hemos calculado con
X=matrix(c(10.6,2.4,7.5,7.4,3.7,10.9,10.7,2.6,9.6,8.4,4.9,9.9,16.7,6.2,13.2,11.3,4.3,7.7), nrow=6, byrow=TRUE)
round(cov(X)[3,2],3)## [1] 2.114(3) 0.692
Nosotros lo hemos calculado con
X=matrix(c(10.6,2.4,7.5,7.4,3.7,10.9,10.7,2.6,9.6,8.4,4.9,9.9,16.7,6.2,13.2,11.3,4.3,7.7), nrow=6, byrow=TRUE)
round(cor(X)[3,2],3)## [1] 0.692(4) 0.003 SI
Nosotros lo hemos calculado con
round(cor.test(trees$Height,trees$Girth)$p.value,3)## [1] 0.003(5) 0.488
Nosotros lo hemos calculado con
x=c(4,8,6,9,5,9 ,4,7,10, 8)
y=c(0,6,2,1,4,4,3,7,11,5)
round(cor(x,y,method="spearman"),3)## [1] 0.488(6) A
Soluciones sucintas de los problemas
(1)
notas=read.table("https://raw.githubusercontent.com/AprendeR-UIB/Material/master/NotasMatesI14.csv",sep=",",header=TRUE)
str(notas)## 'data.frame': 107 obs. of 6 variables:
## $ Control1 : int 22 30 30 38 30 38 40 24 78 46 ...
## $ Control2 : int 0 0 0 0 3 4 5 6 7 7 ...
## $ Talleres : int 49 51 59 63 56 56 51 59 56 57 ...
## $ Casa : int 3 39 19 22 48 42 42 26 26 49 ...
## $ TestsR : int 2 24 48 45 59 68 38 34 37 66 ...
## $ TestsCont: int 14 31 33 38 59 58 26 18 39 47 ...(a)
Medias=round(sapply(notas,mean),1)
sd_ver=function(x){sqrt(var(x)*(length(x)-1)/length(x))}
Desv.Tip=round(sapply(notas,sd_ver),1)
Medias## Control1 Control2 Talleres Casa TestsR TestsCont
## 58.3 26.7 58.6 57.4 64.8 59.9Desv.Tip## Control1 Control2 Talleres Casa TestsR TestsCont
## 19.9 16.9 16.0 20.5 20.7 20.0Desv.Tip[which.max(Desv.Tip)]## TestsR
## 20.7Desv.Tip[which.min(Desv.Tip)]## Talleres
## 16(b)
n=dim(notas)[1]
Covariancias=((n-1)/n)*cov(notas)
Correlaciones=cor(notas)
Covariancias## Control1 Control2 Talleres Casa TestsR TestsCont
## Control1 394.8244 209.7321 168.6785 198.7234 225.4755 224.4155
## Control2 209.7321 285.7027 137.4756 225.4590 228.6795 247.2568
## Talleres 168.6785 137.4756 254.7333 170.6966 174.0035 182.4254
## Casa 198.7234 225.4590 170.6966 419.2941 284.8189 333.0139
## TestsR 225.4755 228.6795 174.0035 284.8189 426.6009 356.6300
## TestsCont 224.4155 247.2568 182.4254 333.0139 356.6300 401.8417Correlaciones## Control1 Control2 Talleres Casa TestsR TestsCont
## Control1 1.0000000 0.6244617 0.5318814 0.4884135 0.5493973 0.5634084
## Control2 0.6244617 1.0000000 0.5095954 0.6514049 0.6550271 0.7297323
## Talleres 0.5318814 0.5095954 1.0000000 0.5223030 0.5278423 0.5701837
## Casa 0.4884135 0.6514049 0.5223030 1.0000000 0.6734395 0.8112888
## TestsR 0.5493973 0.6550271 0.5278423 0.6734395 1.0000000 0.8613496
## TestsCont 0.5634084 0.7297323 0.5701837 0.8112888 0.8613496 1.0000000(c) ¿Qué par de variables tiene mayor correlación? ¿Qué par de variables tiene menor correlación?
which.max(Correlaciones[Correlaciones!=1])## [1] 25# La entrada 25 sin contar la diagonal es (TestsCont,TestsR)
Correlaciones[Correlaciones!=1][which.max(Correlaciones[Correlaciones!=1])]## [1] 0.8613496which.min(Correlaciones[Correlaciones!=1])## [1] 3# La entrada 3 sin contar la diagonal es (Casa,Control1)
Correlaciones[Correlaciones!=1][which.min(Correlaciones[Correlaciones!=1])]## [1] 0.4884135(d)
cov(scale(notas))## Control1 Control2 Talleres Casa TestsR TestsCont
## Control1 1.0000000 0.6244617 0.5318814 0.4884135 0.5493973 0.5634084
## Control2 0.6244617 1.0000000 0.5095954 0.6514049 0.6550271 0.7297323
## Talleres 0.5318814 0.5095954 1.0000000 0.5223030 0.5278423 0.5701837
## Casa 0.4884135 0.6514049 0.5223030 1.0000000 0.6734395 0.8112888
## TestsR 0.5493973 0.6550271 0.5278423 0.6734395 1.0000000 0.8613496
## TestsCont 0.5634084 0.7297323 0.5701837 0.8112888 0.8613496 1.0000000((n-1)/n)*cov(scale(notas,scale=sapply(notas,sd_ver)))## Control1 Control2 Talleres Casa TestsR TestsCont
## Control1 1.0000000 0.6244617 0.5318814 0.4884135 0.5493973 0.5634084
## Control2 0.6244617 1.0000000 0.5095954 0.6514049 0.6550271 0.7297323
## Talleres 0.5318814 0.5095954 1.0000000 0.5223030 0.5278423 0.5701837
## Casa 0.4884135 0.6514049 0.5223030 1.0000000 0.6734395 0.8112888
## TestsR 0.5493973 0.6550271 0.5278423 0.6734395 1.0000000 0.8613496
## TestsCont 0.5634084 0.7297323 0.5701837 0.8112888 0.8613496 1.0000000Correlaciones ## Control1 Control2 Talleres Casa TestsR TestsCont
## Control1 1.0000000 0.6244617 0.5318814 0.4884135 0.5493973 0.5634084
## Control2 0.6244617 1.0000000 0.5095954 0.6514049 0.6550271 0.7297323
## Talleres 0.5318814 0.5095954 1.0000000 0.5223030 0.5278423 0.5701837
## Casa 0.4884135 0.6514049 0.5223030 1.0000000 0.6734395 0.8112888
## TestsR 0.5493973 0.6550271 0.5278423 0.6734395 1.0000000 0.8613496
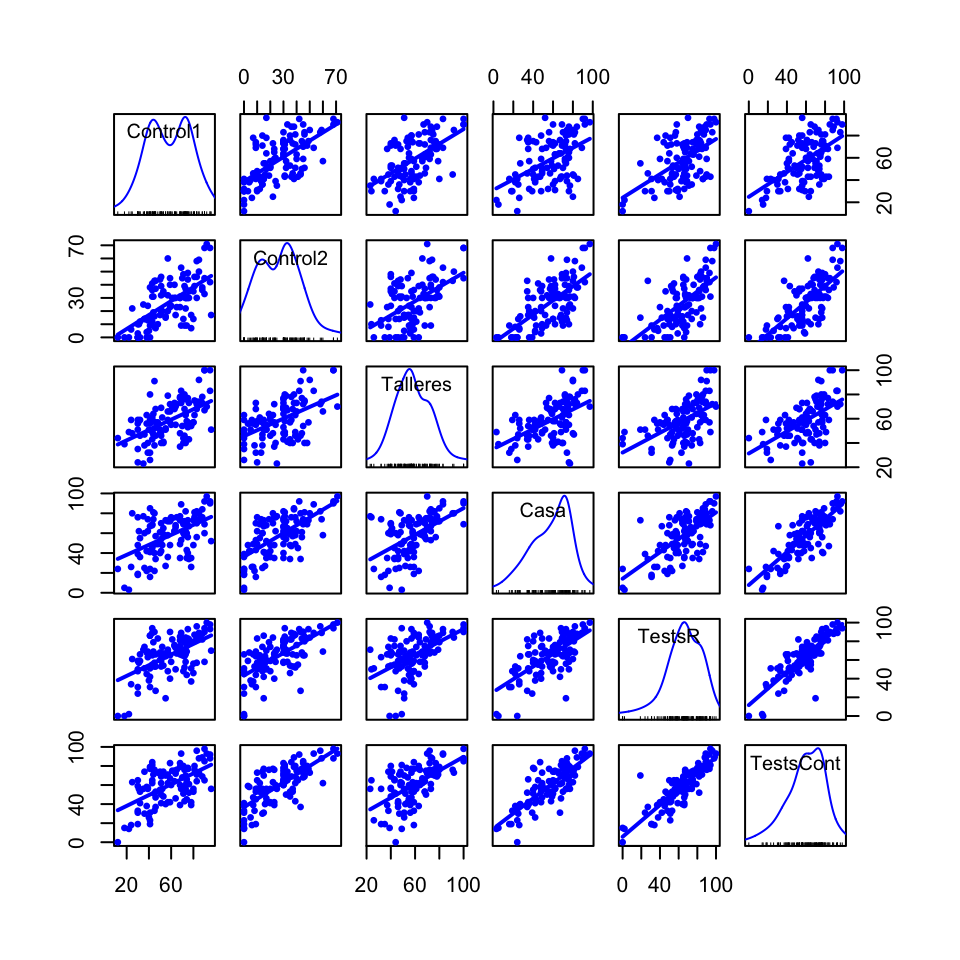
## TestsCont 0.5634084 0.7297323 0.5701837 0.8112888 0.8613496 1.0000000(e) Dibujad una matriz de diagramas de dispersión de estas notas añadiendo en cada uno la recta de regresión lineal por mínimos cuadrados (pero sin otras curvas que indiquen la tendencia de los datos). ¿Se pueden ver en este diagrama los pares de actividades de evaluación con mayor y menor correlación que habéis encontrado en el apartado (c)?
library(car)
spm(notas, smooth=FALSE,pch=20,cex=0.75)