Lección 6 Contrastes de bondad de ajuste
Una de las condiciones habituales que requerimos sobre una muestra, por ejemplo, al razonar sobre la distribución de sus estadísticos o al realizar contrastes de hipótesis, es que la población de la que la hemos extraído siga una determinada distribución. En la Lección ?? de la primera parte del curso comprobábamos gráficamente el ajuste de una muestra a una distribución normal mediante histogramas y dibujando las curvas de densidad muestral y de densidad de la normal. En esta lección presentamos algunas instrucciones que implementan contrastes de bondad de ajuste (goodness of fit), técnicas cuantitativas que permiten decidir si los datos de una muestra “se ajustan” a una determinada distribución de probabilidad, es decir, si la variable aleatoria que los ha generado sigue o no esta distribución de probabilidad.
Los contrastes de bondad de ajuste tienen el mismo significado que los explicados en la Lección 5. Se contrasta una hipótesis nula
- \(H_0\): La variable aleatoria poblacional tiene distribución \(X\)
contra la hipótesis alternativa
- \(H_1\): La variable aleatoria poblacional no tiene distribución \(X\)
Como siempre, para llevar a cabo el contraste tomamos una muestra aleatoria de la población. Entonces, obtenemos evidencia significativa de que la población no tiene distribución \(X\) cuando es muy raro obtener nuestra muestra si la población tiene esta distribución. En este caso, rechazamos la hipótesis nula en favor de la alternativa. Si, en cambio, no es del todo inverosímil que la muestra se haya generado con la distribución \(X\), aceptamos la hipótesis nula “por defecto” y concluimos que la población sí que tiene esta distribución. Pero que aceptemos la hipótesis nula no nos da evidencia de que la población tenga distribución \(X\): simplemente nos dice que no encontramos motivos para rechazarlo. Naturalmente, a efectos prácticos, si aceptamos la hipótesis nula de que la población tiene la distribución \(X\), actuaremos como si creyéramos que efectivamente esta hipótesis es verdadera, por ejemplo a la hora de decidir que fórmulas usar para calcular un intervalo de confianza o para efectuar un contraste de hipótesis. Pero no estaremos seguros de que podamos emplear estas fórmulas sobre nuestra muestra, simplemente no tendremos motivos para dudarlo.
Los pasos habituales para contrastar la bondad del ajuste de una muestra a una distribución son los siguientes:
Fijar la familia de distribuciones teóricas a la que queremos ajustar los datos. Esta familia estará parametrizada por uno o varios parámetros. Recordemos los ejemplos más comunes:
Si la familia es la Bernoulli, el parámetro es \(p\): la probabilidad poblacional de éxito.
Si la familia es la Poisson, el parámetro es \(\lambda\): la esperanza.
Si la familia es la binomial, los parámetros son \(n\) y \(p\): el tamaño de las muestras y la probabilidad de éxito, respectivamente.
Si la familia es la normal, los parámetros son \(\mu\) y \(\sigma\): la esperanza y la desviación típica, respectivamente.
Si la familia es la \(\chi^2\), el parámetro es el número de grados de libertad.
Si la familia es la t de Student, el parámetro es de nuevo el número de grados de libertad.
Otras familias de distribuciones tienen parámetros de localización (location), escala (scale) o forma (shape), por lo que no nos ha de extrañar si R nos pide que asignemos parámetros con estos nombres.
Si el diseño del experimento no fija sus valores, tendremos que estimar a partir de la muestra los valores de los parámetros que mejor se ajusten a nuestros datos. Ya hemos tratado la estimación de parámetros en la Lección 3.
Determinar qué tipo de contraste vamos a utilizar. En esta lección veremos dos tipos básicos de contrastes generales:
El test \(\chi^2\) de Pearson. Este test es válido tanto para variables discretas como para continuas, pero solo se puede aplicar a conjuntos grandes de datos (por fijar una cota concreta, de 30 o más elementos). Además, si el espacio muestral, es decir, el conjunto de resultados posibles, es infinito, es necesario agrupar estos resultados en un número finito de clases.
El test de Kolgomorov-Smirnov. Este test solo es válido para variables continuas, y compara la función de distribución acumulada muestral con la teórica. No requiere que la muestra sea grande, pero en cambio, en principio, no admite que los datos de la muestra se puedan repetir.4 Por desgracia, las repeticiones suelen ser habituales si la muestra es grande y la precisión de los datos es baja o la variabilidad de la población muestreada es pequeña.
Aparte, determinados tipos de distribuciones tienen sus contrastes de bondad de ajustes específicos. Este es el caso especialmente de la normal, para la que explicaremos algunos tests que permiten contrastar si una muestra proviene de alguna distribución normal.
Realizar el contraste y redactar las conclusiones. Es conveniente apoyar los resultados del contraste con gráficos. En esta lección explicaremos los gráficos cuantil-cuantil, o Q-Q-plots, que sirven para visualizar el ajuste de unos datos a una distribución conocida y son una buena alternativa a los histogramas con curvas de densidad.
6.1 Pruebas gráficas: Q-Q-plots
Para comparar la distribución de una muestra con una distribución poblacional teórica se pueden realizar diversas pruebas gráficas. En la Lección ?? de la primera parte del curso usábamos para ello histogramas con densidades estimadas y teóricas. En esta sección explicamos otro tipo de gráficos que pueden usarse con el mismo fin, los gráficos cuantil-cuantil, o, para abreviar, Q-Q-plots. Estos gráficos comparan los cuantiles observados de la muestra con los cuantiles teóricos de la distribución teórica.
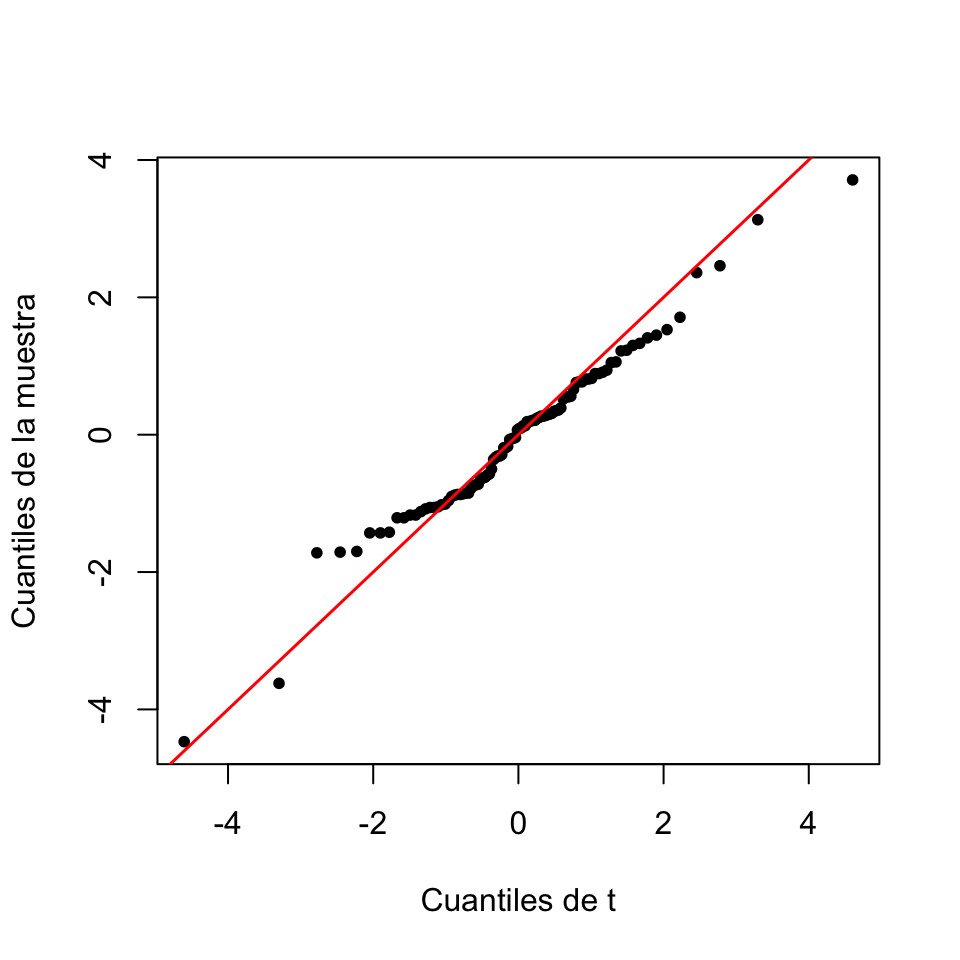
Figura 6.1: Q-Q-plot básico de la muestra del Ejemplo 6.1 contra una t de Student con 4 grados de libertad.
La Figura 6.1 muestra un Q-Q-plot. Cada punto corresponde a un cuantil: grosso modo, hay un punto para cada \(k/n\)-cuantil, siendo \(n\) la longitud de la muestra y \(k=1,\ldots,n\). Para cada uno de estos cuantiles, el punto correspondiente tiene abscisa el cuantil de la distribución teórica (en este caso, una t de Student con 4 grados de libertad) y ordenada el cuantil de la muestra. Por lo tanto, si el ajuste es bueno, para cada \(k/n\), el cuantil muestral y el cuantil teórico han de ser parecidos, de manera que los puntos del gráfico (les llamaremos Q-Q-puntos, para abreviar) han de estar cerca de la diagonal \(y=x\), que hemos añadido al gráfico. En general, se considera que un Q-Q-plot muestra un buen ajuste cuando no se observa una tendencia marcada de desviación respecto de la diagonal. Sin embargo, a menudo los Q-Q-plots son difíciles de interpretar, y es conveniente combinarlos con algún contraste de bondad de ajuste.
Hay varias maneras de producir Q-Q-plots con R. Aquí solo explicaremos una: la función qqPlot del paquete car. Su sintaxis básica es
qqPlot(x, distribution=..., parámetros, id=FALSE, ...)donde:
xes el vector con la muestra.El parámetro
distributionse ha de igualar al nombre de la familia de distribuciones entre comillas, y puede tomar como valor cualquier familia de distribuciones de la que R sepa calcular la densidad y los cuantiles: esto incluye las distribuciones que hemos estudiado hasta el momento:"norm","binom","poisson","t", etc.A continuación, se tienen que entrar los parámetros de la distribución, igualando su nombre habitual (
meanpara la media,sdpara la desviación típica,dfpara los grados de libertad, etc.) a su valor. En algunos casos, si no se especifican los parámetros,qqPlottoma sus valores por defecto: por ejemplo, si queremos realizar un Q-Q-plot contra una normal y no especificamos los valores de la media y la desviación típica de la distribución teórica,qqPlotlos toma iguales a 0 y 1, respectivamente.Por defecto, el gráfico obtenido con la función
qqPlotidentifica los dos Q-Q-puntos con ordenadas más extremas. Para omitirlos, usad el parámetroid=FALSE.
Otros parámetros a tener en cuenta:
qqPlotañade por defecto una rejilla al gráfico, que podéis eliminar congrid=FALSE.qqPlotañade por defecto una línea recta que une los Q-Q-puntos correspondientes al primer y tercer cuartil: se la llama recta cuartil-cuartil. Un buen ajuste de los Q-Q-puntos a esta recta significa que la muestra se ajusta a la distribución teórica, pero posiblemente con parámetros diferentes a los especificados. Os recomendamos mantenerla, pero si queréis eliminarla por ejemplo para substituirla por la diagonal \(y=x\), podéis usar el parámetroline="none".qqPlottambién añade dos curvas discontinuas que abrazan una “región de confianza del 95%” para el Q-Q-plot. Sin entrar en detalles, esta región contendría todos los Q-Q-puntos en un 95% de las ocasiones que tomáramos una muestra de la distribución teórica del mismo tamaño que la nuestra. Por lo tanto, si todos los Q-Q-puntos caen dentro de esta franja, no hay evidencia para rechazar que la muestra provenga de la distribución teórica. Esta franja de confianza es muy útil para interpretar el Q-Q-plot, pero la podéis eliminar conenvelope=FALSE.Se pueden usar los parámetros usuales de
plotpara poner nombres a los ejes, título, modificar el estilo de los puntos, etc., y otros parámetros específicos para modificar el aspecto del gráfico. Por ejemplo,col.linessirve para especificar el color de las líneas que añade. Consultad la Ayuda de la función.
Ejemplo 6.1 Consideremos la siguiente muestra:
muestra=c(0.27,0.81,-0.73,-0.96,1.33,0.91,-1.70,0.24,-0.19,0.29,1.41,0.13,-0.06,
-0.85,-0.59,-3.62,-1.02,2.36,0.34,-0.31,0.81,-0.88,0.27,0.52,1.05,0.20,0.76,0.25,
-1.43,3.71,-0.78,0.39,-1.01,1.53,-0.72,1.22,0.56,-1.17,-0.65,-0.33,-0.07,0.31,
-0.74,0.36,-1.72,-1.21,-0.05,-1.17,0.28,1.30,0.89,1.45,0.13,-1.12,3.13,-1.21,
-0.90,-0.31,-1.05,0.89,-1.06,0.21,-0.50,-0.36,-0.29,-0.19,-1.71,0.09,0.21,0.55,
-1.42,0.19,-0.62,2.46,-0.17,-0.63,0.77,0.94,0.55,0.35,-4.47,1.71,0.07,-0.57,
-1.43,-0.85,1.06,0.82,0.19,-1.08,0.30,-0.87,0.77,1.23,-0.04,0.66,-0.87,-0.86,
-1.06,0.10)Queremos comprobar gráficamente si sigue una distribución t de Student de 4 grados de libertad. Vamos a usar la función qqPlot con sus parámetros por defecto:
library(car)
qqPlot(muestra, distribution="t", df=4, id=FALSE)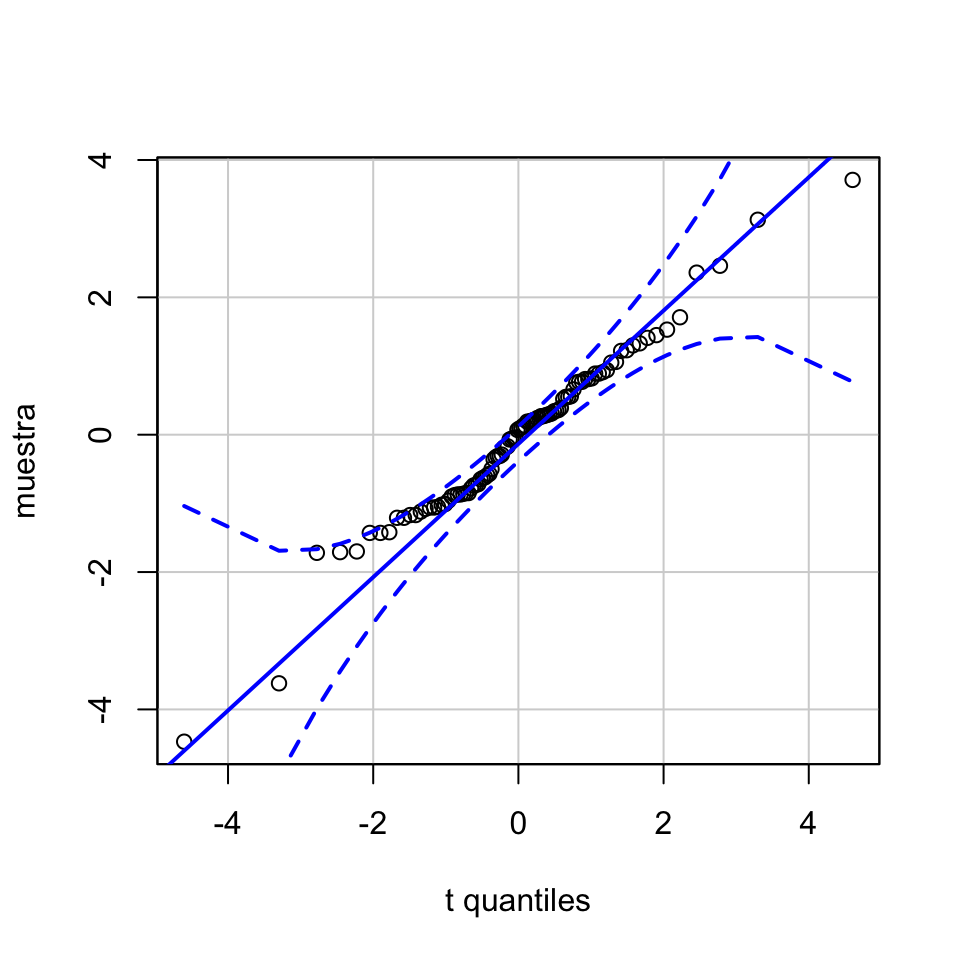
Figura 6.2: Q-Q-plot de la muestra del Ejemplo 6.1 contra una t de Student con 4 grados de libertad producido por defecto con qqPlot.
Como todos los Q-Q-puntos están dentro de la región de confianza del 95%, podemos aceptar que la muestra proviene de una t de Student.
El Q-Q-plot básico de la Figura 6.1 se ha obtenido con el código siguiente:
qqPlot(muestra, distribution="t", df=4, envelope=FALSE, xlab="Cuantiles de t",
ylab="Cuantiles de la muestra", line="none", pch=20, grid=FALSE, id=FALSE)
abline(0,1, col="red", lwd=1.5)Veamos otro ejemplo.
Ejemplo 6.2 Consideremos el data frame iris que contiene información sobre medidas relacionadas con las flores de una muestra de iris de tres especies. Vamos a producir un Q-Q-plot que ilustre si las longitudes de los sépalos de las plantas iris recogidas en esta tabla de datos siguen una distribución normal. A un Q-Q-plot que compara una muestra con una distribución normal se le suele llamar, para abreviar, un normal-plot.
En primer lugar, estimamos los parámetros máximo verosímiles de la distribución normal que podría haber generado nuestra muestra:
library(MASS)
iris.sl=iris$Sepal.Length
mu=fitdistr(iris.sl,"normal")$estimate[1]
sigma=fitdistr(iris.sl,"normal")$estimate[2]
round(c(mu,sigma),3)## mean sd
## 5.843 0.825y ahora generamos el Q-Q-plot usando estos parámetros
qqPlot(iris.sl, distribution="norm", mean=mu, sd=sigma, xlab="Cuantiles de la normal",
ylab="Cuantiles de la muestra", main="", pch=20, cex=0.7, id=FALSE)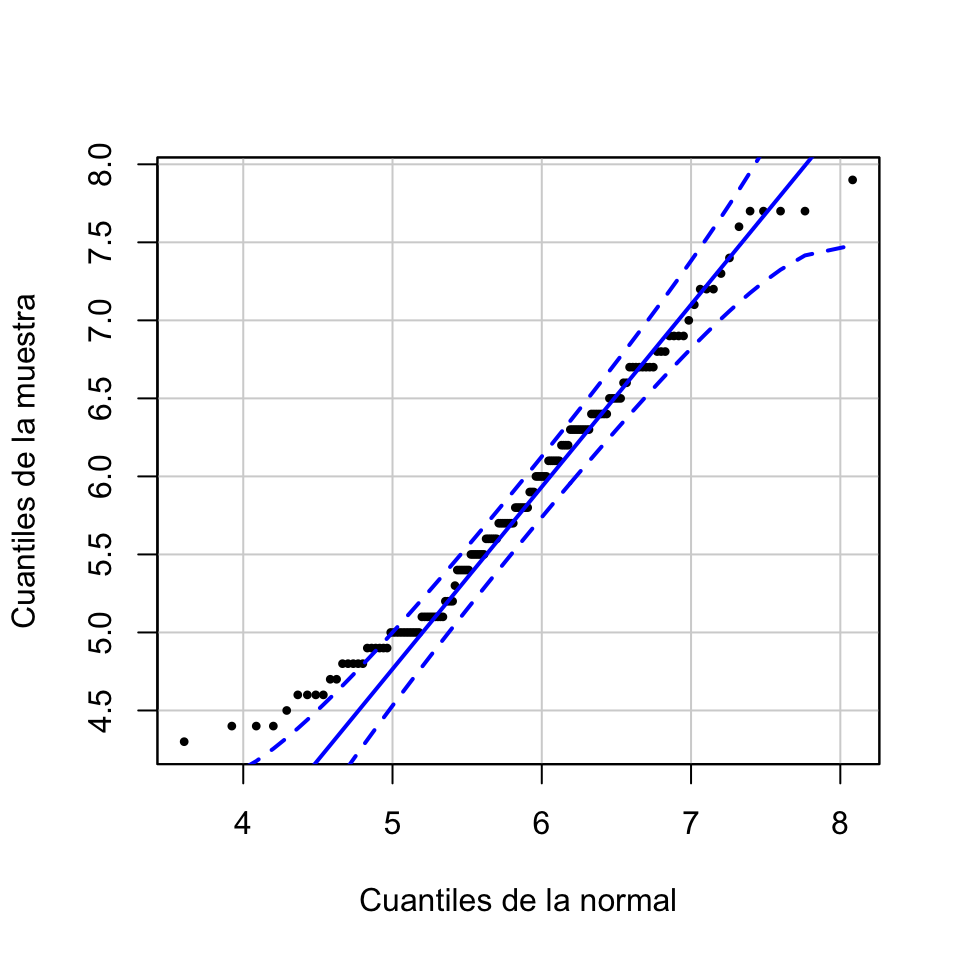
Figura 6.3: Normal-plot de longitudes de sépalos de flores iris.
Vemos cómo los primeros puntos salen de la región de confianza del 95% por encima. Esto significa que los valores más pequeños de la muestra son mayores de lo que sería de esperar si la muestra viniera de la variable normal. Interpretamos este Q-Q-plot como evidencia de que estas longitudes no siguen una distribución normal. Más adelante usaremos tests de normalidad específicos para contrastar la normalidad de estos datos.
6.2 El test \(\chi^2\) de Pearson
El test \(\chi^2\) de Pearson contrasta si una muestra ha sido generada o no con una cierta distribución, cuantificando si sus valores aparecen con una frecuencia cercana a la que sería de esperar si la muestra siguiera esa distribución. Esto se lleva a cabo por medio del estadístico de contraste
\[ X^2=\sum_{i=1}^k\frac{(\mbox{frec. observada}_i-\mbox{frec. esperada}_i)^2}{\mbox{frec. esperada}_i} \] donde k es el número de clases e i es el índice de las clases, de manera que “frec. observadai” y “frec. esperadai” denotan, respectivamente, la frecuencia observada de la clase i-ésima y su frecuencia esperada bajo la distribución que contrastamos. Si se satisfacen una serie de condiciones, este estadístico sigue aproximadamente una ley \(\chi^2\) con un número de grados de libertad igual al número de clases menos uno y menos el número de parámetros de la distribución teórica que hayamos estimado. Las condiciones que se han de satisfacer son:
La muestra ha de ser grande, digamos que de tamaño como mínimo 30;
Si los posibles valores son infinitos, hay que agruparlos en un número finito k de clases que cubran todos los posibles valores (recordad que en la Lección ?? de la primera parte del curso ya explicamos cómo agrupar variables aleatorias continuas con la función
cut);Las frecuencias esperadas de las clases en las que hemos agrupado el espacio muestral han de ser todas, o al menos una gran mayoría, mayores o iguales que 5.
La instrucción básica en R para realizar un test \(\chi^2\) es chisq.test. Su sintaxis básica es
chisq.test(x, p=..., rescale.p=..., simulate.p.value=...)donde:
xes el vector (o la tabla, calculada contable) de frecuencias absolutas observadas de las clases en la muestra.pes el vector de probabilidades teóricas de las clases para la distribución que queremos contrastar. Si no lo especificamos, se entiende que la probabilidad es la misma para todas las clases. Obviamente, estas probabilidades se tienen que especificar en el mismo orden que las frecuencias dexy, como son las probabilidades de todos los resultados posibles, en principio tienen que sumar 1; esta condición se puede relajar con el siguiente parámetro.rescale.pes un parámetro lógico que, si se iguala aTRUE, indica que los valores depno son probabilidades, sino solo proporcionales a las probabilidades; esto hace que R tome como probabilidades teóricas los valores deppartidos por su suma, para que sumen 1. Por defecto valeFALSE, es decir, se supone que el vector que se entra comopson probabilidades y por lo tanto debe sumar 1, y si esto no pasa se genera un mensaje de error indicándolo. Igualarlo aTRUEpuede ser útil, porque nos permite especificar las probabilidades mediante las frecuencias esperadas o mediante porcentajes. Pero también es peligroso, porque si nos hemos equivocado y hemos entrado un vector enpque no corresponda a una probabilidad, R no nos avisará.simulate.p.valuees un parámetro lógico que indica a la función si debe optar por una simulación para estimar el p-valor del contraste. Por defecto valeFALSE, en cuyo caso este p-valor no se estima sino que se calcula mediante la distribución \(\chi^2\) correspondiente. Si se especifica comoTRUE, R realiza una serie de replicaciones aleatorias de la situación teórica: por defecto, 2000, pero su número se puede especificar mediante el parámetroB. Es decir, genera un conjunto de vectores aleatorios de frecuencias con la distribución que queremos contrastar, cada uno de suma total la dex. A continuación, calcula la proporción de estas repeticiones en las que el estadístico de contraste es mayor o igual que el obtenido parax, y éste es el p-valor que da. Cuando no se satisfacen las condiciones para que \(X^2\) siga aproximadamente una distribución \(\chi^2\), estimar el p-valor mediante simulaciones es una buena alternativa.
Veamos un primer ejemplo sencillo.
Ejemplo 6.3 Tenemos un dado, y queremos contrastar si está equilibrado o trucado. Lo hemos lanzado 40 veces y hemos obtenido los resultados siguientes:
| Resultados | Frecuencias |
|---|---|
| 1 | 8 |
| 2 | 4 |
| 3 | 6 |
| 4 | 3 |
| 5 | 7 |
| 6 | 12 |
Si el dado está equilibrado, la probabilidad de cada resultado es 1/6 y por lo tanto la frecuencia esperada de cada resultado es 40/6=6.667. Como la muestra tiene más de 30 elementos y las frecuencias esperadas son todas mayores que 5, podemos realizar de manera segura un test \(\chi^2\). Por lo tanto, entraremos estas frecuencias en un vector y le aplicaremos la función chisq.test. Como contrastamos si todas las clases tienen la misma probabilidad, no hace falta especificar el valor del parámetro p.
freqs=c(8,4,6,3,7,12)
chisq.test(freqs)##
## Chi-squared test for given probabilities
##
## data: freqs
## X-squared = 7.7, df = 5, p-value = 0.174Observemos la estructura del resultado de un chisq.test. Nos da el valor del estadístico \(X^2\) (X-squared), el p-valor del contraste (p-value), y los grados de libertad de la distribución \(\chi^2\) que ha usado para calcularlo (df). En este caso, el p-valor es 0.174, y por lo tanto no podemos rechazar que el dado esté equilibrado: en más de 1 de cada 6 secuencias de 40 lanzamientos de un dado equilibrado obtenemos un valor de \(X^2\) tan grande como el de esta secuencia, o mayor.
Queremos remarcar que, como R no sabe si hemos estimado o no parámetros, el número de grados de libertad que usa chisq.test es simplemente el número de clases menos 1. Si no hemos estimado parámetros para calcular las probabilidades teóricas, ya va bien, pero si lo hemos hecho y por lo tanto el número de grados de libertad no es el adecuado, tendremos que calcular el p-valor correcto a partir del valor del estadístico. Veremos varios ejemplos más adelante.
El resultado de un chisq.test es una list, de la que podemos extraer directamente la información que deseemos con los sufijos adecuados. En concreto, podemos obtener el valor del estadístico \(X^2\) con el sufijo $statistic, los grados de libertad con el sufijo $parameter y el p-valor con el sufijo $p.value.
chisq.test(freqs)$statistic## X-squared
## 7.7chisq.test(freqs)$parameter## df
## 5chisq.test(freqs)$p.value## [1] 0.173563Imaginemos ahora que, en vez de lanzar el dado 40 veces, lo lanzamos 20 veces, y obtenemos los resultados siguientes:
| Resultados | Frecuencias |
|---|---|
| 1 | 4 |
| 2 | 2 |
| 3 | 3 |
| 4 | 2 |
| 5 | 3 |
| 6 | 6 |
¿Hay evidencia de que el dado esté trucado? Ahora la muestra no es grande y las frecuencias esperadas son todas 20/6=3.333, menores que 5. Por tanto, el p-valor del test \(\chi^2\) que se obtiene usando una distribución \(\chi^2_5\) no tiene por qué tener ningún significado. En una situación como ésta es cuando conviene usar el parámetro simulate.p.value. Vamos a pedir a R que simule 5000 veces el experimento de lanzar 20 veces un dado equilibrado, y que calcule como p-valor la proporción de simulaciones en las que el estadístico \(X^2\) haya dado un valor mayor o igual que el que se obtiene con nuestra muestra.
freqs2=c(4,2,3,2,3,6)
chisq.test(freqs2, simulate.p.value=TRUE, B=5000)##
## Chi-squared test for given probabilities with simulated p-value
## (based on 5000 replicates)
##
## data: freqs2
## X-squared = 3.4, df = NA, p-value = 0.7Resulta que en un 70% de las simulaciones el valor de \(X^2\) ha sido mayor o igual que el de nuestra muestra, 3.4. Por lo tanto, nuestra muestra entra dentro de lo normal para un dado equilibrado, por lo que no hay evidencia de que el dado esté trucado.
Como este p-valor se basa en simulaciones, en cada aplicación del test el p-valor puede dar resultados diferentes, pero en general la conclusión es robusta si se toma un número suficiente de simulaciones.
chisq.test(freqs2,simulate.p.value=TRUE,B=5000)$p.value## [1] 0.70126chisq.test(freqs2,simulate.p.value=TRUE,B=5000)$p.value## [1] 0.717656chisq.test(freqs2,simulate.p.value=TRUE,B=5000)$p.value## [1] 0.708858Como vemos, los p-valores son todos similares.
Por curiosidad, ¿qué p-valor da el test \(\chi^2\) usando la distribución de \(\chi^2_5\)?
chisq.test(freqs2)$p.value## Warning in chisq.test(freqs2): Chi-squared approximation may be incorrect## [1] 0.63857El p-valor no es muy diferente y la conclusión en este caso sería la misma, pero fijaos en el mensaje de advertencia: para la muestra dada, la aproximación de la distribución de \(X^2\) mediante una \(\chi^2\) no tiene por qué ser correcta.
Ejemplo 6.4 Vamos a estudiar las frecuencias de los nucleótidos en una cadena de ADN, y contrastar si aparecen los cuatro con la misma probabilidad o no. En este caso, el espacio muestral son los cuatro nucleótidos: adenina (A), citosina (C), guanina (G) y timina (T). Identificaremos una cadena de ADN con un vector de letras a, c, g y t. Si llamamos \(p_a\), \(p_c\), \(p_g\) y \(p_t\) a las probabilidades de aparición de estas letras, el contraste que queremos realizar es
\[
\left\{\begin{array}{l}
H_0 : p_a=p_c=p_g=p_t=0.25\\
H_1: \mbox{Algunos nucleótidos son más probables que otros}
\end{array}
\right.
\]
Vamos a analizar una cadena de ADN “de verdad”, extraída de la base de datos
GenBank. Para ello,
utilizaremos el paquete ape, que incorpora una función read.GenBank que permite leer secuencias de genes incluidas en esta base de datos y convertirlas en vectores de letras a, c, g y t. En concreto, si la aplicamos al número de acceso (accession number) de una secuencia (entrado entre comillas, ya que es una palabra) y usamos el parámetro as.character=TRUE, nos devuelve dicha secuencia como un vector de letras junto con otra información sobre la secuencia.
En este ejemplo, nos vamos a interesar por el gen que codifica la mioglobina humana, que es una proteína relativamente pequeña constituida por una sola cadena polipeptídica de 153 aminoácidos. Su número de acceso es AH002877.2. El código siguiente lee este gen y lo guarda en un objeto.
library(ape)
myoglobin=read.GenBank("AH002877.2", as.character=TRUE)Consultemos cómo es el objeto donde hemos guardado esta secuencia:
str(myoglobin)## List of 1
## $ AH002877.2: chr [1:6889] "g" "t" "a" "c" ...
## - attr(*, "species")= chr "Homo_sapiens"Vemos que se trata una list formada por una sola componente, el vector de bases, y un atributo. Vamos a extraer el vector, para poder trabajar con él. La manera más sencilla es añadiendo a la list el sufijo [[1]]:
myoglobin=myoglobin[[1]]
myoglobin[1:10]## [1] "g" "t" "a" "c" "t" "g" "t" "a" "t" "t"Nos preguntamos si podemos aceptar que en esta secuencia las cuatro bases aparecen de manera equiprobable. Para responder esta pregunta, calculamos las frecuencias de las letras con la función table y aplicamos el test \(\chi^2\) a los resultados.
table(myoglobin)## myoglobin
## a c g n t
## 1718 1453 2019 200 1499Aparecen valores n, que corresponden a bases no resueltas. Vamos borrarlas de la secuencia:
myoglobin=myoglobin[myoglobin!="n"]
table(myoglobin)## myoglobin
## a c g t
## 1718 1453 2019 1499Ahora ya estamos en condiciones de llevar a cabo el contraste deseado con la función chisq.test. Puesto que miramos si todos los resultados aparecen con la misma probabilidad, no hace falta especificar el vector p de probabilidades.
chisq.test(table(myoglobin))##
## Chi-squared test for given probabilities
##
## data: table(myoglobin)
## X-squared = 119.8, df = 3, p-value <2e-16El p-valor es prácticamente 0, podemos rechazar que las cuatro bases aparezcan con la misma probabilidad: las diferencias entre las frecuencias de los cuatro aminoácidos son lo suficientemente grandes como para hacer inverosímil que se hayan generado con la misma probabilidad.
Ejemplo 6.5 Siguiendo con el ejemplo anterior, vamos a contrastar ahora si las bases siguen una distribución en la que A y G aparecen un 25% de veces más que C y T. Usaremos p=c(1.25,1,1.25,1) para especificar estas proporciones.
chisq.test(table(myoglobin),p=c(1.25,1,1.25,1))## Error in chisq.test(table(myoglobin), p = c(1.25, 1, 1.25, 1)): probabilities must sum to 1.¡Vaya! Nos habíamos olvidado de especificar rescale.p=TRUE, para poder entrar como p un vector proporcional a las probabilidades.
chisq.test(table(myoglobin),p=c(1.25,1,1.25,1),rescale.p=TRUE)$p.value## [1] 1.30045e-05De nuevo, tenemos que rechazar la hipótesis nula.
Ejemplo 6.6 Vamos a realizar otro experimento con la cadena del gen de la mioglobina. Este gen consta de tres exones. El primero corresponde al número de acceso M10090.1. Vamos a comparar si la frecuencia de bases en este exón es similar a la de la cadena total, que hará de distribución teórica.
Para ello, leemos el exón y lo guardamos en una cadena
exon1=read.GenBank("M10090.1", as.character=TRUE)[[1]]Calculemos la tabla de frecuencias relativas de las bases en la cadena completa
probs.tot=prop.table(table(myoglobin))
round(probs.tot,3)## myoglobin
## a c g t
## 0.257 0.217 0.302 0.224Vamos a usar esta tabla como parámetro p de la función chisq.test:
chisq.test(table(exon1),p=probs.tot)$p.value## [1] 9.78458e-06El p-valor es muy pequeño, y por lo tanto podemos rechazar que en este exón las bases aparezcan con la misma probabilidad que en la cadena total.
Ejemplo 6.7 Ahora vamos a llevar a cabo el experimento siguiente. Queremos contrastar si la aparición de pares “cg” en la mioglobina humana es aleatoria, en el sentido de que se debe simplemente a las apariciones al azar de sus dos bases, o si por el contrario hay algún otro mecanismo que los produce.
Para ello, tomaremos la secuencia completa de la mioglobina humana, que tenemos almacenada en myoglobin, y repetiremos 100 veces el proceso siguiente: extraemos una muestra aleatoria simple de 20 posiciones de la secuencia y contamos cuántas de ellas contienen el par de bases “cg”. Luego contrastaremos si la muestra así obtenida proviene de una distribución binomial con la probabilidad de aparición de “cg” como si las dos bases fueran independientes.
Fijamos la semilla de aleatoriedad para que se pueda reproducir el experimento.5 El código, que luego explicamos, y el resultado son los siguientes:
cg.in.sample=function(x,S){#x un vector, S vector de índices
length(which(x[S]=="c" & x[S+1]=="g"))
}
set.seed(1700)
muestra=replicate(100, cg.in.sample(myoglobin,
sample(1:(length(myoglobin)-1), 20,replace=TRUE)))
muestra## [1] 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0
## [38] 0 0 0 0 0 0 0 1 1 0 0 2 0 2 0 0 0 1 0 1 0 1 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0
## [75] 0 0 2 0 1 2 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 1 1 1La función cg.in.sample que hemos definido toma un vector x y un vector de índices S y cuenta el número de índices s de S en los que x[s] es c y x[s+1] es g. Entonces, con el replicate, hemos repetido 100 veces el proceso de extraer una muestra aleatoria simple de 20 índices de myoglobin (excluyendo el último, para que sean posiciones donde empieza un par de letras) y aplicar la función cg.in.sample a myoglobin y a este vector de índices.
Queremos determinar si esta muestra sigue una distribución binomial. En concreto, vamos a plantear tres casos de esta pregunta:
Con probabilidad de aparición de la pareja “cg” 0.25·0.25=0.0625, que correspondería al hecho de que las dos bases aparecieran de manera equiprobable e independiente.
Con probabilidad de aparición de la pareja “cg” el producto de las frecuencias relativas de las bases en la secuencia global, que correspondería al hecho de que las dos bases aparecieran de manera independiente, pero no equiprobable sino con sus probabilidades dentro de la secuencia de la mioglobina.
Estimando el valor “real” de \(p\), lo que correspondería al hecho de que su probabilidad de aparición no tuviera nada que ver con las probabilidades individuales de sus dos bases.
Empezamos con el primer caso. Calculemos las frecuencias con las que aparecen los diferentes resultados en la muestra:
table(muestra)## muestra
## 0 1 2
## 76 19 5Y las frecuencias esperadas con las que deberían aparecer si siguieran una distribución B(20,0.0625):
round(dbinom(0:20,20,0.0625)*100,2)## [1] 27.51 36.67 23.23 9.29 2.63 0.56 0.09 0.01 0.00 0.00 0.00
## [12] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00Las frecuencias esperadas a partir de 4 son inferiores a 5 (recordad que la primera frecuencia corresponde al 0), y además su suma no llega a 5. Por lo tanto, vamos a agrupar en una sola clase los resultados mayores o iguales que 3. La nueva tabla de frecuencias esperadas es:
round(c(dbinom(0:2,20,0.0625),1-pbinom(2,20,0.0625))*100,2)## [1] 27.51 36.67 23.23 12.59Ahora tenemos dos opciones: o bien tomamos como resultados posibles “0”, “1”, “2” y “3 o más”, en cuyo caso contaríamos que hemos observado 0 veces este último resultado en nuestra muestra, o bien tomamos como resultados posibles “0”, “1”, y “2 o más”, que se corresponde con los valores observados. Como norma general, es recomendable usar el mayor número de clases posible. Por consiguiente, vamos a optar por la primera estrategia: 4 clases y no 3. Por lo tanto, hay que añadir a la tabla de frecuencias de la muestra un 0 en la columna correspondiente a 3 o más observaciones.
freq.obs=c(table(muestra),0)
prob.teor=c(dbinom(0:2,20,0.0625),1-pbinom(2,20,0.0625))
chisq.test(freq.obs,p=prob.teor)$p.value## [1] 4.91134e-26El p-valor es prácticamente 0, por lo que podemos concluir que la muestra no sigue una distribución B(20,0.0625): las apariciones de los pares “cg” no se explican por la aparición de sus dos bases de manera independiente y equiprobable.
¿Hubiera variado la conclusión si hubiéramos optado por solo considerar tres clases?
freq.obs=table(muestra)
prob.teor=c(dbinom(0:1,20,0.0625),1-pbinom(1,20,0.0625))
chisq.test(freq.obs,p=prob.teor)$p.value## [1] 6.70877e-27El p-valor es prácticamente el mismo, la conclusión es la misma.
Pasemos al segundo caso de nuestro problema. Vamos a calcular la frecuencia relativa de “c” y “g” en la secuencia completa de la mioglobina humana y tomaremos como probabilidad \(p\) el producto de ambas frecuencias relativas.
prop.table(table(myoglobin))## myoglobin
## a c g t
## 0.256840 0.217222 0.301839 0.224099p=prod(prop.table(table(myoglobin))[2:3])
p## [1] 0.0655661Calculemos ahora las frecuencias esperadas tomando esta \(p\):
round(dbinom(0:20,20,p)*100,2)## [1] 25.76 36.15 24.10 10.15 3.03 0.68 0.12 0.02 0.00 0.00 0.00
## [12] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00Vamos a tener que agrupar de nuevo en una sola clase los resultados mayores o iguales que 3.
freq.obs=c(table(muestra),0)
prob.teor=c(dbinom(0:2,20,p),1-pbinom(2,20,p))
chisq.test(freq.obs,p=prob.teor)$p.value## [1] 4.02804e-29Obtenemos de nuevo un valor prácticamente 0: las apariciones de los pares “cg” no se explican por la aparición de sus dos bases de manera independiente.
Finalmente, vamos a estimar el parámetro \(p\). La binomial es otra de las distribuciones no cubiertas por fitdistr, por lo que tendremos que apelar a lo que sabemos de teoría para hacerlo.
Como el valor esperado de una variable aleatoria \(X\sim B(n,p)\) es \(np\), estimaremos \(p\) mediante \(\overline{X}/n\). De hecho, éste es el estimador máximo verosímil de \(p\) cuando \(n\) es conocida.
p.estim=mean(muestra)/20
p.estim## [1] 0.0145Repetimos el proceso: calculemos las frecuencias teóricas
round(dbinom(0:20,20,p.estim)*100,2)## [1] 74.67 21.97 3.07 0.27 0.02 0.00 0.00 0.00 0.00 0.00 0.00
## [12] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00En este caso, hemos de agrupar los resultados en “0”, “1” y “2 o más”, para que las frecuencias teóricas sean mayores que 5. Coincide con los diferentes valores observados en la muestra.
freq.obs=table(muestra)
prob.teor=c(dbinom(0:1,20,p.estim),1-pbinom(1,20,p.estim))
chisq.test(freq.obs,p=prob.teor)##
## Chi-squared test for given probabilities
##
## data: freq.obs
## X-squared = 1.226, df = 2, p-value = 0.542¡Cuidado! Este p-valor no es el correcto. Hemos estimado un parámetro, pero R no lo sabe. Por lo tanto tenemos que bajar en 1 los grados de libertad y calcular el p-valor a mano, mediante \[ P(\chi_1^2\geq X^2)=1-P(\chi_1^2\leq 1.226) \]
1-pchisq(chisq.test(freq.obs,p=prob.teor)$statistic,1)## X-squared
## 0.268154El p-valor es grande. Por lo tanto, no podemos rechazar la hipótesis nula de que las apariciones de “cg” en muestras aleatorias de 20 posiciones sigan una ley binomial de parámetro \(p=0.0145\). Que es, por otro lado, lo que debería pasar si las “cg” estuvieran repartidas de manera aleatoria en la secuencia original, por lo que no podemos rechazar esto último.
La conclusión es, por lo tanto, que aceptamos que las “cg” aparecen distribuidas de manera aleatoria en la secuencia de la mioglobina humana, pero tenemos evidencia estadísticamente significativa de que las “c” y las “g” que las forman no aparecen de manera independiente.
6.3 El test \(\chi^2\) para distribuciones continuas
El procedimiento de contraste de bondad de ajuste mediante el test \(\chi^2\) para variables continuas tiene la particularidad de que es necesario un paso preliminar que consiste en definir los intervalos de clase para los que realizaremos el conteo de las frecuencias observadas. El proceso es similar al que estudiamos en la Lección ?? de la primera parte del curso para dibujar histogramas. Por lo tanto, necesitaremos definir unos intervalos de clase para el conteo de frecuencias absolutas observadas, y con las funciones cut y table obtendremos las frecuencias observadas de estas clases en la muestra de la variable continua.
Para obtener los intervalos podemos seguir dos estrategias razonables: reutilizar los generados por la función hist, o dividir el rango de la variable en un número prefijado \(k\) de intervalos de amplitud fija. Vamos a ver en detalle un ejemplo de cada tipo.
Ejemplo 6.8 Vamos a contrastar si las longitudes de los sépalos de las plantas iris recogidas en la tabla de datos iris siguen una distribución normal. Recordaréis que el Q-Q-plot de estas longitudes que mostrábamos en la Figura 6.3 mostraba evidencia de que no la siguen.
Primero vamos a estimar de nuevo la media y la desviación típica de la distribución de estas longitudes.
iris.sl=iris$Sepal.Length
mu=fitdistr(iris.sl,"normal")$estimate[1]
sigma=fitdistr(iris.sl,"normal")$estimate[2]
round(c(mu,sigma),3)## mean sd
## 5.843 0.825En este ejemplo, usaremos los intervalos en los que la función hist agrupa por defecto estos datos.
h=hist(iris.sl, plot=FALSE)
h$breaks## [1] 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0Ahora se nos presenta el problema de que los intervalos que definen estos puntos de corte (breaks) no cubren toda la recta real, que es el espacio muestral de una variable aleatoria normal. Así que tenemos que reemplazar los extremos de este vector de breaks por los límites del espacio muestral de la variable, que en este caso son \(-\infty\) e \(\infty\).
breaks2=h$breaks
breaks2[1]=-Inf #Cambiamos el primer elemento por -Infinito
breaks2[length(breaks2)]=Inf #Cambiamos el último elemento por Infinito
breaks2## [1] -Inf 4.5 5.0 5.5 6.0 6.5 7.0 7.5 InfAhora podemos calcular las frecuencias de la muestra en los intervalos definidos por estos puntos de corte:
freq.obs=table(cut(iris.sl,breaks=breaks2))
freq.obs##
## (-Inf,4.5] (4.5,5] (5,5.5] (5.5,6] (6,6.5] (6.5,7]
## 5 27 27 30 31 18
## (7,7.5] (7.5, Inf]
## 6 6Ahora calcularemos las probabilidades teóricas. Para cada intervalo \((x,y]\) en los que hemos cortado la recta real, tenemos que calcular \(P(x < X\leq y)= P(X\leq y)-P( X\leq x)\), para lo que usaremos expresiones de la forma pnorm(y,mu,sigma)-pnorm(x,mu,sigma).
Definimos dos vectores que nos den los extremos izquierdo y derecho de cada intervalo.
extremo.izq=breaks2[-length(breaks2)]
extremo.der=breaks2[-1]
extremo.izq## [1] -Inf 4.5 5.0 5.5 6.0 6.5 7.0 7.5extremo.der## [1] 4.5 5.0 5.5 6.0 6.5 7.0 7.5 InfAhora podemos calcular las probabilidades teóricas y las frecuencias esperadas de todos los intervalos de golpe. La probabilidades teóricas son:
probs.teor=pnorm(extremo.der,mu,sigma)-pnorm(extremo.izq,mu,sigma)
probs.teor## [1] 0.0517955 0.1016307 0.1852753 0.2365772 0.2116091 0.1325812 0.0581747
## [8] 0.0223563Las frecuencias esperadas son:
freq.esp=probs.teor*length(iris.sl)
round(freq.esp,3)## [1] 7.769 15.245 27.791 35.487 31.741 19.887 8.726 3.353La frecuencia esperada de la última clase es inferior a 5, así que vamos a fundirla con la penúltima y así la clase resultante tendrá una frecuencia esperada superior a 5.
k=length(probs.teor)
#Nuevas probabilidades teóricas:
probs.teor2=c(probs.teor[1:(k-2)],sum(probs.teor[(k-1):k]))
#Nuevas frecuencias observadas:
freq.obs2=c(freq.obs[1:(k-2)],sum(freq.obs[(k-1):k]))
chisq.test(freq.obs2,p=probs.teor2)##
## Chi-squared test for given probabilities
##
## data: freq.obs2
## X-squared = 11.12, df = 6, p-value = 0.08475Recordemos que el p-valor obtenido no es el correcto: como hemos estimado dos parámetros, lo tenemos que calcular con una \(\chi^2\) con 4 grados de libertad (dos menos de los que ha usado chisq.test):
test.iris=chisq.test(freq.obs2,p=probs.teor2)
1-pchisq(test.iris$statistic,test.iris$parameter-2)## X-squared
## 0.0252518El p-valor es inferior a 0.05, por tanto obtenemos evidencia de que la muestra no proviene de una población normal, es decir, de que las longitudes de los sépalos de las flores iris no siguen una ley normal.
Ejemplo 6.9 Vamos a repetir el estudio del ejemplo anterior, pero ahora calculando a mano los intervalos. En general, el número de intervalos debe ser suficiente para cubrir toda la forma de la distribución, pero tampoco conviene que haya muchos para evitar frecuencias esperadas pequeñas que obliguen a agrupar intervalos. Para una distribución normal se recomienda tomar entre 5 y 15 intervalos. Otra posibilidad es decidir el número de intervalos con alguna de las reglas explicadas en la Lección ?? de la primera parte del curso.
En nuestro ejemplo, vamos a usar 10 intervalos. Para calcularlos, tomamos el máximo y el mínimo de las observaciones, los restamos y dividimos por el número de intervalos (y, si fuera necesario, redondearíamos adecuadamente).
Ampl=(max(iris.sl)-min(iris.sl))/10
Ampl## [1] 0.36Los extremos de los intervalos en los que dividimos la muestra forman la secuencia que empieza en el mínimo y va sumando la amplitud hasta definir los \(k=10\) intervalos. Luego hay que adecuar los dos extremos para que cubran el dominio de la densidad de la distribución teórica, en nuestro caso toda la recta real.
breaks=min(iris.sl)+Ampl*(0:10)
breaks## [1] 4.30 4.66 5.02 5.38 5.74 6.10 6.46 6.82 7.18 7.54 7.90breaks2=breaks
breaks2[1]=-Inf
breaks2[length(breaks2)]=Inf
breaks2## [1] -Inf 4.66 5.02 5.38 5.74 6.10 6.46 6.82 7.18 7.54 InfCalculemos, como en el ejemplo anterior, las frecuencias observadas, las probabilidades teóricas y las frecuencias esperadas.
frec.obs=table(cut(iris.sl,breaks=breaks2))
frec.obs##
## (-Inf,4.66] (4.66,5.02] (5.02,5.38] (5.38,5.74] (5.74,6.1] (6.1,6.46]
## 9 23 14 27 22 20
## (6.46,6.82] (6.82,7.18] (7.18,7.54] (7.54, Inf]
## 18 6 5 6extremo.izq=breaks2[-length(breaks2)]
extremo.der=breaks2[-1]
prob.teor=pnorm(extremo.der,mu,sigma)-pnorm(extremo.izq,mu,sigma)
frec.esp=round(prob.teor*length(iris.sl),2)
frec.esp## [1] 11.37 12.51 19.20 24.44 25.79 22.56 16.37 9.85 4.91 2.99Agruparemos las frecuencias de los dos últimos intervalos y aplicaremos el test \(\chi^2\) con el número adecuado de grados de libertad:
frec.obs2=c(frec.obs[1:8], sum(frec.obs[9:10]))
prob.teor2=c(prob.teor[1:8], sum(prob.teor[9:10]))
test.iris.2=chisq.test(frec.obs2,p=prob.teor2)
1-pchisq(test.iris.2$statistic, test.iris.2$parameter-2)## X-squared
## 0.0227734El p-valor es de nuevo inferior a 0.05: volvemos a obtener evidencia significativa de que la muestra no proviene de una población normal.
6.4 El test de Kolgomorov-Smirnov
El test de Kolgomorov-Smirnov (K-S) es un test genérico para contrastar la bondad de ajuste a distribuciones continuas. Se puede usar con muestras pequeñas (se suele recomendar 5 elementos como el tamaño mínimo para que el resultado sea significativo), pero la muestra no puede contener valores repetidos: si los contiene, la distribución del estadístico de contraste bajo la hipótesis nula no es la que predice la teoría sino que solo se aproxima a ella, y por lo tanto los p-valores que se obtienen son aproximados.
Hay que tener en cuenta que el test K-S realiza un contraste en el que la hipótesis nula es que la muestra proviene de una distribución continua completamente especificada. Es decir, no sirve para contrastar si la muestra proviene, pongamos, de “alguna” distribución normal, sino solo para contrastar si proviene de una distribución normal con una media y una desviación típica concretas. Así pues, si queremos contrastar que la muestra proviene de alguna distribución de una familia concreta y estimamos sus parámetros a partir de la muestra, el test K-S solo nos permite rechazar o no la hipótesis de que la muestra proviene de la distribución de esa familia con exactamente esos parámetros. Por lo tanto, si el resultado es rechazar la hipótesis nula, esto no excluye que la muestra provenga de una distribución de la misma familia con otros parámetros. En la próxima sección veremos algunos tests que permiten contrastar, en general, si una muestra proviene de alguna distribución normal.
La función básica para realizar el test K-S es ks.test. Su sintaxis
básica para una muestra es
ks.test(x, y, parámetros)donde:
xes la muestra de una variable continua.ypuede ser un segundo vector, y entonces se contrasta si ambos vectores han sido generados por la misma distribución continua, o el nombre de la función de distribución (empezando conp) que queremos contrastar, entre comillas; por ejemplo"pnorm"para la distribución normal.Los
parámetrosde la función de distribución si se ha especificado una; por ejemplomean=0, sd=1para una distribución normal estándar.
Ejemplo 6.10 Efectuemos el test de Kolmogorov-Smirnov para contrastar si las longitudes de sépalos de flores iris siguen una distribución normal de media y desviación típica sus estimaciones máximo verosímiles a partir la muestra iris.sl. Recordemos que tenemos guardados de los dos últimos ejemplos los valores de estas estimaciones en las variables mu y sigma:
round(c(mu,sigma),3)## mean sd
## 5.843 0.825ks.test(iris.sl, "pnorm", mean=mu, sd=sigma)## Warning in ks.test(iris.sl, "pnorm", mean = mu, sd = sigma): ties should
## not be present for the Kolmogorov-Smirnov test##
## One-sample Kolmogorov-Smirnov test
##
## data: iris.sl
## D = 0.08945, p-value = 0.181
## alternative hypothesis: two-sidedObtenemos un p-valor de 0.181, que no nos permite rechazar la hipótesis de que siguen una ley N(5.843, 0.825). Pero R nos avisa de que hay empates. ¿Hay muchos? Vamos a calcular su frecuencia.
La función unique aplicada a un vector nos da el vector de sus elementos sin repeticiones. De esta manera podemos saber cuántos elementos diferentes hay en un vector, y por consiguiente también cuántas repeticiones.
length(unique(iris.sl))## [1] 351-length(unique(iris.sl))/length(iris.sl)## [1] 0.766667Por tanto, el vector (de 150 entradas) de longitudes de sépalos solo tiene 35 valores diferentes. El resto, un 76.67%, son valores repetidos. Hay muchos empates, y el resultado de este test en este caso es poco fiable
Como hemos comentado, el test K-S también se puede usar para contrastar si dos muestras se han obtenido de poblaciones con la misma distribución continua. Para hacerlo, se ha de aplicar la función ks.test a las dos muestras.
Ejemplo 6.11 La tabla de datos Salaries del paquete car contiene información sobre los sueldos de 397 profesores de una universidad norteamericana en el curso 2008-09. Démosle un vistazo.
library(car)
str(Salaries)## 'data.frame': 397 obs. of 6 variables:
## $ rank : Factor w/ 3 levels "AsstProf","AssocProf",..: 3 3 1 3 3 2 3 3 3 3 ...
## $ discipline : Factor w/ 2 levels "A","B": 2 2 2 2 2 2 2 2 2 2 ...
## $ yrs.since.phd: int 19 20 4 45 40 6 30 45 21 18 ...
## $ yrs.service : int 18 16 3 39 41 6 23 45 20 18 ...
## $ sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 1 ...
## $ salary : int 139750 173200 79750 115000 141500 97000 175000 147765 119250 129000 ...La variable sex nos da el sexo del profesor y la variable salary su sueldo anual en dólares. Queremos contrastar si los sueldos de hombres y mujeres siguen la misma distribución. Para ello, vamos a suponer que provienen de distribuciones continuas y usaremos el test K-S. Primero miraremos si hay muchos empates.
sal.female=Salaries[Salaries$sex=="Female",]$salary #Salarios de mujeres
sal.male=Salaries[Salaries$sex=="Male",]$salary #Salarios de hombres
1-length(unique(sal.female))/length(sal.female) #Proporción de salarios de mujeres repetidos## [1] 0.051282051-length(unique(sal.male))/length(sal.male) #Proporción de salarios de hombres repetidos## [1] 0.050279331-length(unique(Salaries$salary))/length(Salaries$salary) #Proporción global de salarios repetidos## [1] 0.06549118Las repeticiones en cada lista significan alrededor del 5% de los datos, y en total un 6.5%. No son muchas, así que vamos a arriesgarnos con el test K-S.
ks.test(sal.male,sal.female)##
## Two-sample Kolmogorov-Smirnov test
##
## data: sal.male and sal.female
## D = 0.2472, p-value = 0.0271
## alternative hypothesis: two-sidedEl p-valor pequeño nos permite rechazar que los salarios de hombres y mujeres sigan la misma distribución. Pero no nos paremos aquí.
Si dibujamos un boxplot (véase la Figura 6.4) de los salarios según el sexo, observaremos que los sueldos de los hombres tienen mayor mediana y variabilidad que los de las mujeres, incluyendo algunos valores atípicos grandes (¿el rector y otros altos cargos académicos?).
boxplot(salary~sex, data=Salaries, main="")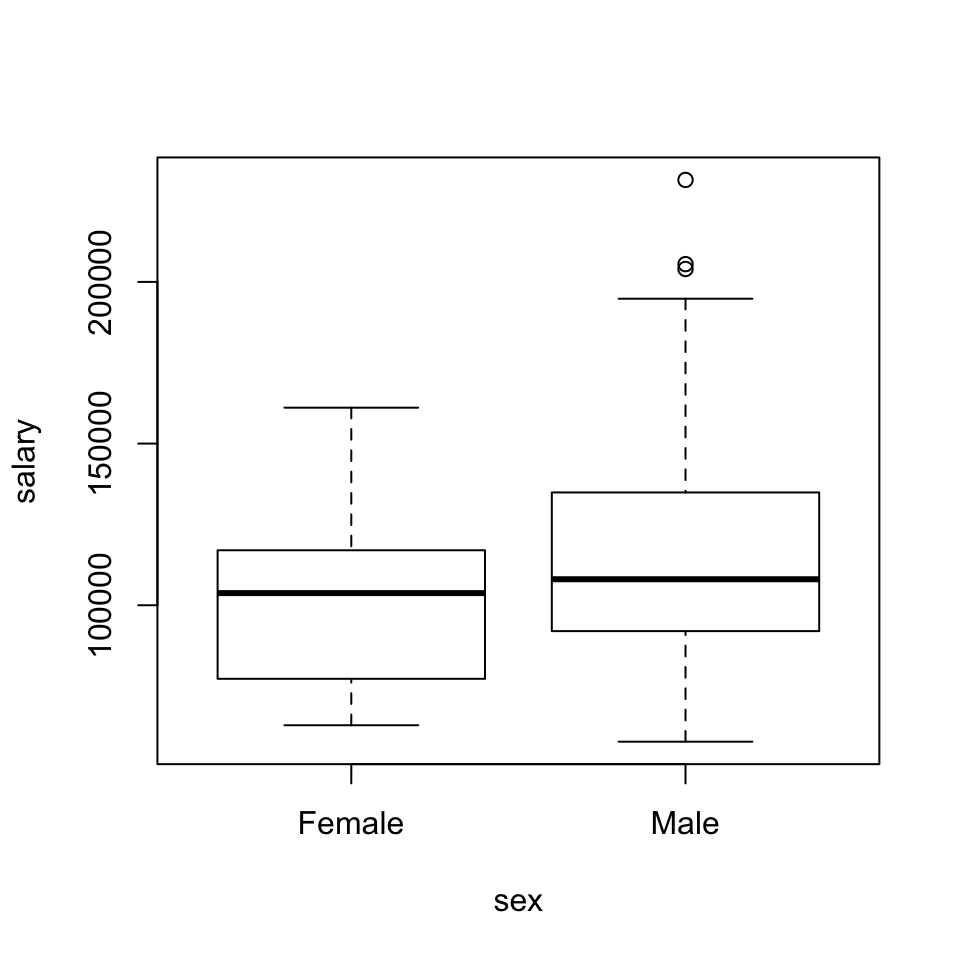
Figura 6.4: Boxplot de sueldos según el sexo en la tabla de datos Salaries
Si cancelamos este efecto, estandarizando las muestras, ¿siguen saliendo distribuciones diferentes? Para estandarizar las muestras usaremos la función scale, que explicaremos con más detalle en la Lección 8. Esta función, aplicada tal cual a un vector, le resta su media y divide el resultado por su desviación típica muestral.
ks.test(scale(sal.male),scale(sal.female))## Warning in ks.test(scale(sal.male), scale(sal.female)): p-value will be
## approximate in the presence of ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: scale(sal.male) and scale(sal.female)
## D = 0.139, p-value = 0.505
## alternative hypothesis: two-sidedAl estandarizar, ya no tenemos evidencia de que provengan de distribuciones diferentes. Es decir, podemos aceptar que sus valores tipificados siguen la misma distribución.
6.5 Tests de normalidad
Existen algunos tests específicos de normalidad que permiten contrastar si una muestra proviene de alguna distribución normal. El más conocido es el test de normalidad de Kolmogorov-Smirnov-Lilliefors (K-S-L). Se trata de una variante del test K-S, y se puede realizar aplicando a la muestra la función lillie.test del paquete nortest.
Vamos a usar el test K-S-L para contrastar si las longitudes de los sépalos de las iris siguen una ley normal.
library(nortest)
iris.sl=iris$Sepal.Length
lillie.test(iris.sl)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: iris.sl
## D = 0.08865, p-value = 0.00579El p-valor es muy pequeño, y nos permite rechazar que la muestra provenga de una población normal.
La ventaja del test K-S-L es que es muy conocido, ya que es una variante del K-S (incluso usa el mismo estadístico), pero tiene un inconveniente: aunque es muy sensible a las diferencias entre la muestra y la distribución teórica alrededor de sus valores medios, le cuesta detectar diferencias prominentes en un extremo u otro de la distribución. Esto afecta su potencia. Por ejemplo, sabemos que una t de Student se parece bastante a una normal estándar, pero su densidad es algo más aplanada y hace que en los dos extremos esté por encima de la de la normal. Al test K-S-L le cuesta detectar esta discrepancia, como podemos ver en el siguiente ejemplo:
set.seed(100)
x=rt(50,3) #Una muestra de una t de Student con 3 g.l.
lillie.test(x)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: x
## D = 0.1033, p-value = 0.201Este inconveniente del test K-S-L lo resuelve el test de normalidad de Anderson-Darling (A-D). Para realizarlo podemos usar la función ad.test del paquete nortest. Encontraréis los detalles del estadístico que usa en la Ayuda de la función.
ad.test(iris.sl)##
## Anderson-Darling normality test
##
## data: iris.sl
## A = 0.8892, p-value = 0.0225De nuevo obtenemos un p-valor muy pequeño. Veamos ahora que este test sí que detecta que la muestra anterior de una t de Student con 3 grados de libertad no proviene de una normal:
set.seed(100)
x=rt(50,3)
ad.test(x)##
## Anderson-Darling normality test
##
## data: x
## A = 1.166, p-value = 0.00433Un inconveniente común a los tests K-S-L y A-D es que, si bien pueden usarse con muestras pequeñas (pongamos de más de 5 elementos), se comportan mal con muestras grandes, de varios miles de elementos. En muestras de este tamaño, cualquier pequeña divergencia de la normalidad se magnifica y en estos dos tests aumenta la probabilidad de errores de tipo I. Un test que resuelve este problema es el de Shapiro-Wilk (S-W), implementado en la función shapiro.test de la instalación básica de R.
Este test es importante, porque un experimento reciente ha mostrado evidencia significativa de que su potencia es mayor que la de los tests anteriores.6
De nuevo, los detalles del estadístico que usa los encontraréis en la Ayuda de la función.
shapiro.test(iris.sl)##
## Shapiro-Wilk normality test
##
## data: iris.sl
## W = 0.9761, p-value = 0.0102set.seed(100)
x=rt(50,3)
shapiro.test(x)##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.8949, p-value = 0.000329Un último inconveniente que afecta a todos los tests explicados hasta ahora es el de los empates. Sus estadísticos tienen las distribuciones que se usan para calcular los p-valores cuando la muestra no tiene datos repetidos, y por lo tanto, si hay muchos, el p-valor puede no tener ningún significado. De los tres, el menos sensible a repeticiones es el S-W, pero si hay muchas es conveniente usar un test que no sea sensible a ellas, como por ejemplo el test omnibus de D’Agostino-Pearson. Este test se encuentra implementado en la función dagoTest del paquete fBasics, y lo que hace es cuantificar lo diferentes que son la asimetría y la curtosis de la muestra (dos parámetros estadísticos relacionados con la forma de la gráfica de la función de densidad muestral) respecto de los esperados en una distribución normal, y resume esta discrepancia en un p-valor con el significado usual.
library(fBasics)
dagoTest(iris.sl)##
## Title:
## D'Agostino Normality Test
##
## Test Results:
## STATISTIC:
## Chi2 | Omnibus: 5.7356
## Z3 | Skewness: 1.5963
## Z4 | Kurtosis: -1.7853
## P VALUE:
## Omnibus Test: 0.05682
## Skewness Test: 0.1104
## Kurtosis Test: 0.07421
##
## Description:
## Wed Mar 18 09:28:34 2020 by user:El p-valor relevante es el del “Omnibus test”, en este caso 0.0568 cae en la zona de penumbra.
Queremos hacer una última advertencia en esta sección. Aunque los tests que hemos explicado se pueden aplicar a muestras pequeñas, es muy difícil rechazar la normalidad de una muestra muy pequeña. Por ejemplo, una muestra de 10 valores escogidos con distribución uniforme entre 0 y 5 pasa holgadamente todos los tests de normalidad (salvo el de D’Agostino-Pearson, que requiere una muestra de al menos 20 elementos):
set.seed(100)
x=runif(10,0,5)
lillie.test(x)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: x
## D = 0.1459, p-value = 0.79ad.test(x)##
## Anderson-Darling normality test
##
## data: x
## A = 0.1663, p-value = 0.912shapiro.test(x)##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.9803, p-value = 0.967dagoTest(x)## Error in .omnibus.test(x): sample size must be at least 206.6 Guía rápida
qqPlot, del paquete car, sirve para dibujar un Q-Q-plot de una muestra contra una distribución teórica. Sus parámetros principales son:distribution: el nombre de la familia de distribuciones, entre comillas.- Los parámetros de la distribución:
meanpara la media,sdpara la desviación típica,dfpara los grados de libertad, etc. - Los parámetros usuales de
plot.
chisq.testsirve para realizar tests \(\chi^2\) de bondad de ajuste. Sus parámetros principales son:p: el vector de probabilidades teóricas.rescale.p: igualado aTRUE, indica que los valores depno son probabilidades, sino sólo proporcionales a las probabilidades.simulate.p.value: igualado aTRUE, R calcula el p-valor mediante simulaciones.B: en este último caso, permite especificar el número de simulaciones.
ks.testrealiza el test de Kolmogorov-Smirnov. Tiene dos tipos de uso:ks.test(x,y): contrasta si los vectoresxeyhan sido generados por la misma distribución continua.ks.test(x, "distribución", parámetros): contrasta si el vectorxha sido generado por la distribución especificada, que se ha de indicar con el nombre de la función de distribución de R (la que empieza con p).
lillie.test, del paquete nortest, realiza el test de normalidad de Kolmogorov-Smirnov-Lilliefors.ad.test, del paquete nortest, realiza el test de normalidad de Anderson-Darling.shapiro.testrealiza el test de normalidad de Shapiro-Wilk.dagoTest, del paquete fBasics, realiza el test ómnibus de D’Agostino-Pearson.
6.7 Ejercicios
Modelo de test
(1) Un determinado experimento tiene cinco resultados posibles: A, B, C, D, E. Lo repetimos un cierto número de veces y obtenemos 65 veces el resultado A, 95 veces el resultado B, 87 veces el resultado C, 70 veces el resultado D y 193 veces el resultado E. Realizad un test \(\chi^2\) para contrastar si los resultados A, B, C y D tienen la misma probabilidad y E tiene el doble de probabilidad que cada uno de los otros resultados. Dad el p-valor del contraste (redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha) y decid (contestando SI, en mayúsculas y sin acento, o NO) si tendríamos que rechazar la hipótesis nula con un nivel de significación \(\alpha=0.05\). Tenéis que dar las respuestas en este orden y separadas por un único espacio en blanco.
(2) Queremos contrastar si una determinada variable sigue una distribución de Poisson. Hemos efectuado algunas observaciones y hemos obtenido 10 veces el resultado 0, 32 veces el resultado 1, 18 veces el resultado 2, 19 veces el resultado 3 y 6 veces el resultado 4. Tenéis que calcular el estimador máximo verosímil del parámetro \(\lambda\) de una variable de Poisson que haya generado estas observaciones (redondeado a 3 cifras decimales, y sin ceros innecesarios a la derecha), calcular el p-valor (redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha) del test \(\chi^2\) para determinar si la muestra sigue alguna distribución de Poisson habiendo estimado como su parámetro \(\lambda\) este valor redondeado, y decir (contestando SI o NO) si, con un nivel de significación \(\alpha=0.1\), tendríamos que rechazar la hipótesis nula de que esta muestra proviene de una variable aleatoria de Poisson. Dad las tres respuestas en este orden y separadas por un único espacio en blanco.
(3) Queremos contrastar si una cierta variable sigue una distribución normal. Hemos efectuado 150 observaciones y hemos obtenido 9 veces un valor dentro de ]0,3], 27 veces un valor dentro de ]3,6], 51 veces un valor dentro de ]6,9], 46 veces un valor dentro de ]9,12] y 17 veces un valor dentro de ]12,15]. Tenéis que: calcular los estimadores máximo verosímiles del parámetro \(\mu\) y del parámetro \(\sigma\) de una variable normal que haya generado estas observaciones (ambos redondeados a 2 cifras decimales y sin ceros innecesarios a la derecha): calcular el p-valor (redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha) del test \(\chi^2\) para contrastar si la muestra sigue alguna distribución normal, empleando estos valores estimados redondeados de los parámetros que habéis dado para especificar la distribución teórica; y decir (contestando SI o NO) si, con un nivel de significación \(\alpha=0.05\), tendríamos que rechazar la hipótesis nula de que esta muestra proviene de una variable aleatoria normal. Dad las cuatro respuestas en este orden y separadas por un único espacio en blanco.
(4) Generad una muestra aleatoria x de 25 valores de una distribución \(\chi^2\) con 10 grados de libertad, fijando antes set.seed(2014), y aplicad el test de Kolmogorov-Smirnov para contrastar si x proviene de una distribución N(10,3.16). Dad el p-valor del test (redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha) y decid (contestando SI o NO) si, con un nivel de significación \(\alpha=0.05\), tendríamos que rechazar la hipótesis nula de que esta muestra proviene de esta distribución. Tenéis que dar las dos respuestas en este orden y separadas por un único espacio en blanco.
(5) Queremos contrastar si la muestra siguiente sigue una distribución normal: 4.6, 0.97, 0.3, 1.11, 2.16, 15.52, 1.13, 0.17, 0.64, 2.00. Dad el p-valor (redondeado a 3 cifras decimales y sin ceros innecesarios a la derecha) del test de Kolmogorov-Smirnov-Lilliefors para esta muestra y decid (contestando SI o NO) si, con un nivel de significación \(\alpha=0.05\), tendríamos que rechazar la hipótesis nula de que esta muestra sigue una distribución normal. Tenéis que dar las dos respuestas en este orden y separadas por un único espacio en blanco.
(6) Generad una muestra aleatoria x de 15 valores de una distribución normal con \(\mu=2\) y \(\sigma=0.8\) fijando antes set.seed(2014), y una muestra aleatoria y de 25 valores de una distribución exponencial de parámetro \(1/\lambda=0.5\) fijando antes set.seed(1007). Aplicad el test de Kolmogorov-Smirnov para contrastar si x e y provienen de una misma distribución continua. Tenéis que dar el p-valor del test (redondeado a 3 cifras decimales, sin ceros innecesarios a la derecha) y decir (contestando SI o NO) si, con un nivel de significación \(\alpha=0.05\), tendríamos que rechazar la hipótesis nula de que estas dos muestras provienen de la misma distribución continua. Dad las dos respuestas en este orden y separadas por un único espacio en blanco.
Problemas
(1) La tabla siguiente da, por cada Comunidad Autónoma, su población según el censo de 2013 y el número de defunciones durante el primer semestre de 2014:
| Comunidad | Población | Defunciones |
|---|---|---|
| Andalucía | 8440300 | 34810 |
| Aragón | 1347150 | 7196 |
| Asturias (Principado de) | 1068165 | 6623 |
| Balears (Illes) | 1111674 | 4088 |
| Canarias | 2118679 | 7593 |
| Cantabria | 591888 | 3031 |
| Castilla-La Mancha | 2100998 | 14532 |
| Castilla y León | 2519875 | 9765 |
| Cataluña | 7553650 | 32383 |
| Comunitat Valenciana | 5113815 | 21614 |
| Extremadura | 1104004 | 5751 |
| Galicia | 2765940 | 15888 |
| Madrid (Comunidad de) | 6495551 | 22446 |
| Murcia (Región de) | 1472049 | 5330 |
| Navarra (Comunidad Foral de) | 644477 | 2846 |
| País Vasco | 2191682 | 10639 |
| Rioja (La) | 322027 | 1489 |
| Ceuta | 84180 | 252 |
| Melilla | 83679 | 234 |
Tenéis esta tabla de datos en el url https://raw.githubusercontent.com/AprendeR-UIB/AprendeR2privat/master/INE.txt.
Efectuad un test \(\chi^2\) para contrastar si la población por comunidades autónomas y el número de defunciones por comunidad autónoma tienen la misma distribución.
(2) En los cursos introductorios de estadística se suele dar como ejemplo de variable aleatoria de Poisson los números de goles marcados en partidos de fútbol. Vamos a contrastarlo en un ejemplo concreto. La tabla siguiente da los números de partidos en los que se marcaron los diferentes números de goles en el Mundial de Sudáfrica del 2010:
| Goles | Partidos |
|---|---|
| 0 | 7 |
| 1 | 17 |
| 2 | 13 |
| 3 | 14 |
| 4 | 8 |
| 5 | 3 |
| 7 | 1 |
Usad un test \(\chi^2\) para contrastar si podemos aceptar que estos números de goles siguen una ley de Poisson.
(3) Considerad la tabla de datos que encontraréis en el url https://www.dropbox.com/s/qcok2f7u51teqr6/pacientes.txt?raw=1 y que ya usamos en un ejercicio de la Lección 4.
(a) Usad el test de Shapiro-Wilk para contrastar si los pesos de los hombres de esta tabla siguen una distribución normal
(b) Llevad a cabo el mismo contraste usando un test \(\chi^2\).
Respuestas al test
(1) 0.02 SI
Nosotros lo hemos calculado con
x=c(65,95,87,70,193)
round(chisq.test(x,p=c(1,1,1,1,2),rescale.p=T)$p.value,3)## [1] 0.02(2) 1.753 0.064 SI
Nosotros lo hemos calculado con
x=c(10,32,18,19,6)
lambda=round(fitdistr(rep(0:4,x),"poisson")$estimate,3) #Estimamos la lambda
c(dpois(0:3,lambda),1-ppois(3,lambda))*85 #Frecuencias esperadas## [1] 14.726539 25.815623 22.627394 13.221940 8.608503ChiT2=chisq.test(x,p=c(dpois(0:3,lambda),1-ppois(3,lambda))) #Test
p.valor2=1-pchisq(ChiT2$statistic,3) #p-valor correcto
c(lambda,round(p.valor2,3))## lambda X-squared
## 1.753 0.064(3) 8.2 3.18 0.692 NO
Nosotros lo hemos calculado con
x=c(9,27,51,46,17)
sum(x)## [1] 150muestra=rep(c(1.5,4.5,7.5,10.5,13.5),x)
fitdistr(muestra,"normal")## mean sd
## 8.2000000 3.1827661
## (0.2598718) (0.1837571)mu=round(fitdistr(muestra,"normal")$estimate[1],2)
sigma=round(fitdistr(muestra,"normal")$estimate[2],2)
left=c(-Inf,3,6,9,12)
right=c(3,6,9,12,Inf)
probs=pnorm(right,mu,sigma)-pnorm(left,mu, sigma)
ChiT3=chisq.test(x,p=probs)
p.valor3=1-pchisq(ChiT3$statistic,2)
c(mu,sigma,round(p.valor3,3))## mean sd X-squared
## 8.200 3.180 0.692(4) 0.313 NO
Nosotros lo hemos calculado con
set.seed(2014)
x=rchisq(25,10)
round(ks.test(x,"pnorm",mean=10,sd=3.16)$p.value,3)## [1] 0.313(5) 0.001 SI
Nosotros lo hemos calculado con
x=c(4.6, 0.97, 0.3, 1.11, 2.16, 15.52, 1.13, 0.17, 0.64, 2.00)
round(lillie.test(x)$p.value,3)## [1] 0.001(6) 0.117 NO
Nosotros lo hemos calculado con
set.seed(2014)
x=rnorm(15,2,0.8)
set.seed(1007)
y=rexp(25,0.5)
round(ks.test(x,y)$p.value,3)## [1] 0.117Soluciones sucintas de los problemas
(1) Para realizar el test \(\chi^2\) “exacto”:
INE=read.table("https://raw.githubusercontent.com/AprendeR-UIB/AprendeR2privat/master/INE.txt",
header=TRUE)
str(INE)## 'data.frame': 19 obs. of 3 variables:
## $ Comunidad : chr "Andalucía" "Aragón" "Asturias (Principado de)" "Balears (Illes)" ...
## $ Población : int 8440300 1347150 1068165 1111674 2118679 591888 2100998 2519875 7553650 5113815 ...
## $ Defunciones: int 34810 7196 6623 4088 7593 3031 14532 9765 32383 21614 ...Freq.Obs.INE=INE$Defunciones #Frecuencias observadas
Prob.Esp.INE=INE$Población/sum(INE$Población) #Probabilitades esperadas
chisq.test(Freq.Obs.INE, p=Prob.Esp.INE)##
## Chi-squared test for given probabilities
##
## data: Freq.Obs.INE
## X-squared = 8008.6, df = 18, p-value < 2.2e-16Como la muestra no es muy grande, es más conveniente efectuar un test \(\chi^2\) de Montecarlo
chisq.test(Freq.Obs.INE, p=Prob.Esp.INE, simulate.p.value=TRUE)##
## Chi-squared test for given probabilities with simulated p-value
## (based on 2000 replicates)
##
## data: Freq.Obs.INE
## X-squared = 8008.6, df = NA, p-value = 0.0004998La conclusión es la misma.
(2)
Goles=c(0,1,2,3,4,5,7)
Partidos=c(7,17,13,14,8,3,1)
N=sum(Partidos)
lambda=sum(Goles*Partidos)/N
probs=c(dpois(0:5,lambda),1-ppois(5,lambda)) #Probabilidades teóricas
probs*N #Frecuencias esperadas## [1] 6.936418 15.304161 16.883161 12.416717 6.848903 3.022214 1.588426Habrá que agrupar las tres últimas clases:
probs=c(dpois(0:3,lambda),1-ppois(3,lambda))
Partidos=c(Partidos[1:4],sum(Partidos[5:7]))
chisq.test(Partidos,p=probs)##
## Chi-squared test for given probabilities
##
## data: Partidos
## X-squared = 1.309, df = 4, p-value = 0.8598(3)
Datos=read.table("https://www.dropbox.com/s/qcok2f7u51teqr6/pacientes.txt?raw=1",
header=TRUE)
str(Datos)## 'data.frame': 81 obs. of 7 variables:
## $ SEXO : Factor w/ 2 levels "Hombre","Mujer": 1 1 2 1 1 2 1 1 1 1 ...
## $ EDAD : int 47 51 54 50 52 53 49 52 50 48 ...
## $ ALTURA : int 170 170 148 170 165 151 170 168 170 166 ...
## $ PESO : int 80 73 46 74 67 51 73 72 73 73 ...
## $ HIPERT : Factor w/ 2 levels "Hipertenso","Normotenso": 2 1 1 1 2 1 1 2 2 2 ...
## $ IMC : num 27.7 25.3 21 25.6 24.6 ...
## $ CARDIOPA: Factor w/ 2 levels "Con cardiopatia",..: 2 1 2 2 2 2 2 2 1 1 ...X=Datos$PESO[Datos$SEXO=="Hombre"](a)
library(nortest)
lillie.test(X)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: X
## D = 0.15413, p-value = 0.009027(b) Veamos cuántos datos tenemos
n=length(X)
n## [1] 45Como queremos que todas las clases tengan frecuencias esperadas al menos 5, no podemos usar muchas. Vamos a empezar con 7.
paso=round((max(X)-min(X))/7,1)
Límites=min(X)+paso*(0:7)
Límites[1]=-Inf
Límites[8]=Inf
Límites## [1] -Inf 69.1 71.2 73.3 75.4 77.5 79.6 Inftable(cut(X,breaks=Límites))| (-Inf,69.1] | (69.1,71.2] | (71.2,73.3] | (73.3,75.4] | (75.4,77.5] | (77.5,79.6] | (79.6, Inf] |
|---|---|---|---|---|---|---|
| 2 | 2 | 18 | 9 | 8 | 2 | 4 |
mu=mean(X)
dt=sd(X)
Límites.Izq=Límites[-8]
Límites.Der=Límites[-1]
probs=pnorm(Límites.Der,mu,dt)-pnorm(Límites.Izq,mu,dt)
Frecs.Esp=round(probs*n,2)
Frecs.Esp## [1] 1.93 4.96 9.83 12.23 9.57 4.70 1.77Habrá que agrupar las dos primeras clases y las dos últimas
Límites=Límites[-c(2,7)]
Límites## [1] -Inf 71.2 73.3 75.4 77.5 InfFrecs.Obs=table(cut(X,breaks=Límites))
Límites.Izq=Límites[-6]
Límites.Der=Límites[-1]
probs=pnorm(Límites.Der,mu,dt)-pnorm(Límites.Izq,mu,dt)
Frecs.Esp=round(probs*n,2)
Frecs.Esp## [1] 6.89 9.83 12.23 9.57 6.47test=chisq.test(Frecs.Obs,p=probs)
test##
## Chi-squared test for given probabilities
##
## data: Frecs.Obs
## X-squared = 9.1484, df = 4, p-value = 0.05749p.valor=1-pchisq(test$statistic,test$parameter-2)
p.valor## X-squared
## 0.01031437La conclusión usando el test S-W y el test \(\chi^2\) es la misma.
A las repeticiones se las suele llamar empates, ties en inglés, porque la función de distribución acumulada muestral ordena los datos y las repeticiones producen empates en las posiciones de valores sucesivos.↩︎
Lo confesamos, hemos elegido la semilla de aleatoriedad no porque seamos fans de Daniel Bernoulli sino para que la muestra obtenida solo contenga ceros, unos y doses, lo que, como veréis, motivará una pequeña discusión sobre qué clases tomar.↩︎
Véase N. M. Razali, Y. B. Wah, “Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests.” S. Stat. Model. Anal. 2 (2011), pp. 21–33.↩︎