Lección 12 Extras de R Markdown
Para la mayor parte de las necesidades de este curso en lo que se refiere a composición de ficheros R Markdown, el documento Markdown Quick Reference que encontraréis en el menú Help de RStudio es más que suficiente. En esta lección, vamos a ampliar diversos puntos:
- Cómo controlar el comportamiento de los bloques de código o chunks al compilar el fichero R Markdown, y su aspecto en el documento final.
- Cómo controlar el aspecto de los gráficos producidos en los chunks.
- Cómo incluir de manera sencilla tablas bien formateadas producidas con R.
- Cómo escribir fórmulas matemáticas bien formateadas.
12.1 Parámetros de los chunks de R
Los bloques de código de R, o chunks, se indican dentro de un documento R Markdown de la manera siguiente:
```{r}
# Y aquí el código de R
```Para crear un bloque de código, podemos usar el menú Insert de la barra superior de la ventana de ficheros. Si no queréis usar ese menú, tened en cuenta que cada signo ` se produce con un acento grave seguido de un espacio en blanco.
La parte entre llaves de la línea que abre el chunk puede contener una etiqueta (un nombre que sirva para identificar el chunk), separada de la r inicial por un espacio en blanco, y diversos parámetros. Estos parámetros se separan de la r (o de la etiqueta, si la hay) por una coma y entre ellos también con comas, y permiten determinar el comportamiento del bloque al compilar el documento pulsando el botón Knit. Los parámetros más útiles son:
echo: permite indicar si se ha de mostrar el código fuente de R en el documento final; su valor por defecto es
TRUE, y si lo igualáis aFALSE, no lo mostrará, dando sólo el resultado.eval: permite indicar si queremos que se evalúe el código; su valor por defecto es
TRUE, y si lo igualáis aFALSE, no lo evaluará.results: permite indicar cómo queremos ver el resultado de la ejecución del código en el documento final. Sus posibles valores son (y fijaos que hay que entrarlos entre comillas, porque son palabras):
"hide", hace que no se muestre el resultado en el documento final."markup", que es su valor por defecto, muestra los resultados en el documento final línea a línea, encabezados con dos marcas de comentario##, y literales, sin que el programa que abre el documento final los interprete como código."asis", devuelve los resultados en el documento final línea a línea y el programa con el que se abre el documento final los interpreta como texto y los formatea adecuadamente."hold", muestra todos los resultados de golpe al final del bloque de código.
Observad que no es lo mismo especificar que no se evalúe el código (
eval=FALSE) que hacer que se evalúe, pero no mostrar el resultado (results="hide"): en el segundo caso, el resultado del cálculo no aparecerá en el documento final, pero se podrá usar en bloques de código posteriores.message: permite indicar si se han de mostrar en el documento final los mensajes que R produce al ejecutar el código; su valor por defecto es
TRUE, y si lo igualáis aFALSEno los muestra.warning: permite indicar si se han de mostrar en el documento final los mensajes de advertencia que a veces producen algunas funciones al ejecutarse; como antes, su valor por defecto es
TRUE, y si lo igualáis aFALSEno los muestra.include: permite indicar si queremos “incluir” el chunk en el documento final: su valor por defecto es, naturalmente,
TRUE, pero igualado aFALSEno deja ninguna traza del chunk en el documento final (aunque sí que lo ejecuta, así que más adelante podemos usar sus resultados).
Para cada parámetro, el valor por defecto no tiene por qué especificarse.
Veamos a continuación algunos ejemplos:
- El bloque (con los valores por defecto para
echoyresults, así que no importaría especificarlos)
```{r,echo=TRUE,results="markup"}
x=1:10
x
sqrt(x)
```produce, en el documento final:
x=1:10
x## [1] 1 2 3 4 5 6 7 8 9 10sqrt(x)## [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751
## [8] 2.828427 3.000000 3.162278- El bloque
```{r,echo=TRUE,results="asis"}
x=1:10
x
sqrt(x)
```produce, en el documento final:
x=1:10
x[1] 1 2 3 4 5 6 7 8 9 10
sqrt(x)[1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751 [8] 2.828427 3.000000 3.162278
- El bloque
```{r,echo=TRUE,results="hold"}
x=1:10
x
sqrt(x)
```produce, en el documento final:
x=1:10
x
sqrt(x)## [1] 1 2 3 4 5 6 7 8 9 10
## [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751
## [8] 2.828427 3.000000 3.162278- El bloque
```{r,echo=FALSE}
x=1:10
x
sqrt(x)
```no aparece en el documento final, y sólo se muestra el resultado:
## [1] 1 2 3 4 5 6 7 8 9 10## [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751
## [8] 2.828427 3.000000 3.162278- El bloque
```{r,echo=TRUE,message=TRUE}
library(magic)
magic(5)
```produce, en el documento final:
library(magic)## Loading required package: abindmagic(5)## [,1] [,2] [,3] [,4] [,5]
## [1,] 9 2 25 18 11
## [2,] 3 21 19 12 10
## [3,] 22 20 13 6 4
## [4,] 16 14 7 5 23
## [5,] 15 8 1 24 17- El bloque
```{r,echo=TRUE,message=FALSE}
library(magic)
magic(5)
```produce, en el documento final:
library(magic)
magic(5)## [,1] [,2] [,3] [,4] [,5]
## [1,] 9 2 25 18 11
## [2,] 3 21 19 12 10
## [3,] 22 20 13 6 4
## [4,] 16 14 7 5 23
## [5,] 15 8 1 24 17Si queréis cambiar el valor de algún parámetro en todos los chunks de un documento, por ejemplo para esconderlos todos (con echo=FALSE) o para modificar las dimensiones de la figuras como explicaremos más adelante, lo más práctico es incluir al principio del fichero R Markdown un chunk de opciones globales, indicado con la etiqueta global_options. En este chunk las opcions globales se han de incluir en el argumento de la función
opts_chunk$set(...)del paquete knitr. También es una buena idea cargar en este chunk todos los paquetes que se van a usar en el documento. Y como seguramente no querréis que se note su existencia en el documento final, usad la opción include=FALSE. Así, por ejemplo, incluyendo al principio del fichero R Markdown el chunk
```{r global_options, include=FALSE}
library(knitr)
opts_chunk$set(
echo=FALSE,
message=FALSE,
warning=FALSE
)
```especificamos que, por defecto, en el documento final no aparezcan ni los bloques de código ni los mensajes que produce R al compilarlos.
Podéis encontrar la lista completa de parámetros que se pueden usar en chunks en la guía de knitr.
12.2 Los chunks en modo línea
Los bloques de código que hemos explicado en la sección anterior sirven para generar resultados en línea aparte. Si queremos introducir dentro de un párrafo un trozo de código de R que se ejecute al compilar el documento y muestre el resultado en el documento final, hay que hacerlo con `r código`.
Por ejemplo, si en el documento R Markdown escribimos
El cubo de dos es `r 2^3`, o lo que es lo mismo, 2^3^=`r 2^3`.
produce, al pulsar Knit, la salida
El cubo de dos es 8, o lo que es lo mismo, 23=8.
Veamos otro ejemplo más práctico. Supongamos que nos dan una muestra y queremos calcular su media, su varianza, su desviación típica y su tamaño muestral. Entonces, podemos cargar los datos y efectuar los cálculos en un bloque de código (que, si queremos, podemos ocultar completamente en el documento final con include=FALSE) y a continuación en un párrafo ir llamando los resultados mediante pequeños chunks Por ejemplo, podríamos usar el bloque
```{r,include=FALSE}
muestra=c(1,2,3,NA,2.8,3.1,4.9)
media=mean(muestra,na.rm=TRUE)
n=length(na.omit(muestra))
varianza=round(var(muestra,na.rm=TRUE)*(n-1)/n,3)
desv.tipica=round(sqrt(varianza),3)
```y a continuación escribir el párrafo
La muestra es de tamaño `r n`, su media es `r media`,
su varianza es `r varianza` y su desviación típica es `r desv.tipica`.
Entonces, en el documento final, el bloque con los cálculos permanecería oculto, y este párrafo produciría
La muestra es de tamaño 6, su media es 2.8, su varianza es 1.403 y su desviación típica es 1.184.
12.3 Figuras
En un fichero R Markdown, podemos controlar el tamaño, la posición etc. de los gráficos en el documento final (html, pdf o Word) por medio de opciones en el encabezamiento de los chunks que los producen. Veamos algunas de las opciones básicas más útiles:
fig.height y fig.width sirven para especificar la altura y la anchura, respectivamente, del gráfico “real”. Sus posibles valores son números enteros y se sobreentiende que están en pulgadas (no pueden usarse otras unidades); por defecto, ambos valen 7.
out.height y out.width sirven para especificar la altura y la anchura, respectivamente, del gráfico en el documento final. Estas opciones son útiles si se quieren indicar las dimensiones del gráfico en tamaños relativos respecto de las medidas de la caja de texto. Así, por ejemplo, al compilar con Knit PDF o Knit HTML, si se especifican fig.height y fig.width (o se dejan con sus valores por defecto) y se incluye la opción
out.width="60%"(entrecomillado), el gráfico aparecerá en el documento escalado de manera que su ancho sea un 60% del ancho del texto; cuando se compila con Knit Word,out.width="60%"no tiene ningún efecto.Como norma general, os recomendamos que uséis fig.height y fig.width para especificar las dimensiones del gráfico y lo incluyáis tal cual en el documento. Solo os recomendamos usar out.height o out.width cuando de trate de gráficos que se producen de manera diferente según sus dimensiones, como pueden ser las nubes de palabras. Para incorporar una nube de palabras a tamaño reducido en un documento R Markdown, lo mejor es dejar que R la produzca con su tamaño por defecto y luego reducirla con out.width; si reducís sus fig.height y fig.width, puede que algunas palabras no quepan en el gráfico o que queden muy apelmazadas.
fig.asp permite fijar la proporción altura/anchura de un gráfico si solo se especifica su fig.width.
fig.show sirve para controlar cómo se incluyen en el documento final los gráficos producidos en el chunk cuando hay más de uno. Su valor por defecto es
"as.is", que los va incluyendo a medida que se generan. Config.show="hold"se dibujan todos los gráficos de golpe al final del chunk.dev sirve para especificar el tipo de fichero gráfico que se genera. Solo hay un caso en que nos parece útil usar esta opción: si pensáis publicar vuestro documento html como una página web, os conviene usar
dev="svg"y el gráfico se creará en formato “Scalable Vector Graphics”, con lo que se escalará de manera correcta y sin perder calidad al aumentar o disminuir el ancho de la página web en el navegador.
Para más opciones, podéis consultar la Guía de Referencia de R Markdown.
Por otro lado, dentro de un chunk podemos usar las funciones par y layout, que también aparecen en algunas lecciones del curso. Estas funciones sirven para modificar el aspecto de los gráficos generados con R, y en particular pueden usarse para especificar el modo como se agrupan los gráficos producidos en un mismo chunk. Su efecto es el mismo al usarlas en la consola, salvo que allí los cambios introducidos con estas funciones son permanentes hasta que volvamos a cambiarlos, mientras que en un documento R Markdown solo afectan a su chunk.
Con la función
par(mfrow=c(x,y))organizaremos los gráficos producidos en el chunk formando una matriz de \(x\) filas e \(y\) columnas, llenando sus entradas por filas. A modo de ejemplo, si un chunk produce 3 gráficos y queremos mostrarlos juntos, con la opción fig.show="hold" aparecerán al final del chunk, uno debajo del otro. En cambio, si no especificamos la opción
fig.show y al principio del chunk incluimos par(mfrow=c(1,3)), se dibujarán uno al lado del otro formando un único gráfico (y entonces conviene ajustar con fig.height y fig.width o fig.asp sus dimensiones: por ejemplo, seguramente no querremos que este gráfico compuesto sea cuadrado).
Esta misma construcción se puede usar en la consola, pero entonces hay que tener en cuenta que a partir de la instrucción par(mfrow=c(x,y)) todos los gráficos se agruparán de esta manera. Para evitarlo, entrad par(mfrow=c(1,1)) cuando queráis volver al modo por defecto de los gráficos uno a uno. Veamos un ejemplo:
par(mfrow=c(2,2))
plot(iris[iris$Species=="setosa",1:2], main="Sépalos de setosa",
xlab="Longitud", ylab="Anchura", pch=20)
plot(iris[iris$Species=="versicolor",1:2], main="Sépalos de
versicolor", xlab="Longitud", ylab="Anchura", pch=20, col="red")
plot(iris[iris$Species=="virginica",1:2],main="Sépalos de virginica",
xlab="Longitud", ylab="Anchura", pch=20, col="blue")
plot(iris[ 1:2],main="Sépalos de iris",xlab="Longitud",
ylab="Anchura", pch=20, col="green")
par(mfrow=c(1,1))produce la Figura 12.1 y restaura el formato original.
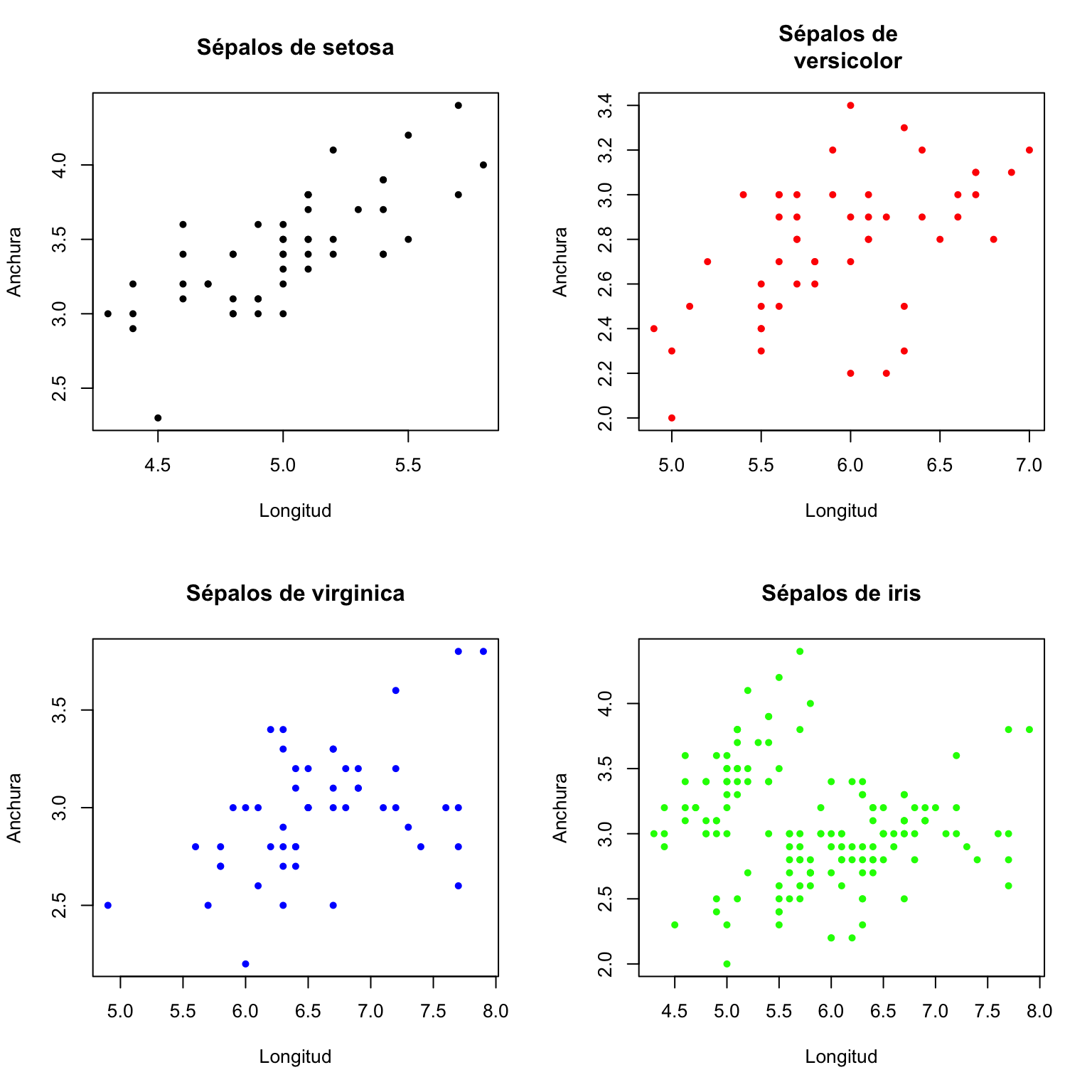
Figura 12.1: Cuatro gráficos en uno organizados con la instrucción par(mfrow=c(2,2))
En general, con la función par se pueden modificar “hasta nueva orden” muchos aspectos de los gráficos. Si lo hacéis, es conveniente que antes de modificarlos guardéis su valor actual con, por ejemplo, par.anterior=par(). A continuación, ya podéis modificar los parámetros de par que queráis; si en algún momento queréis volver al estilo original, bastará que entréis par(par.anterior).
Pasemos a la función layout. Su sintaxis básica es
layout(M, widths=..., heights=...)donde
M es una matriz que indica la composición en forma de cuadrícula de los gráficos que queremos agrupar en una misma figura. Sus entradas han de ser 0,1,2,…,n donde n el número de gráficos que queremos organizar (el 0 puede faltar, pero no podemos saltarnos ninguna entre 1 y n). Entonces, si la entrada (i,j) de la matriz M es el número k>0, el k-ésimo gráfico producido en el chunk se situará en la posición (i,j) de la cuadrícula; si la entrada (i,j) de la matriz es 0, la posición (i,j) de la cuadrícula quedará vacía. Si un valor se repite en diferentes entradas de M, el gráfico correspondiente se reparte entre estas entradas.
El parámetro
widthssirve para especificar las anchuras relativas de las diferentes columnas (por defecto, todas iguales): para ello, se iguala al vector de estas anchuras.El parámetro
heightssirve para especificar, de manera similar, las alturas relativas de las diferentes filas; por defecto, todas son iguales.
Así, el código
M=matrix(c(1,1,1,2,3,4),nrow=2,byrow=TRUE)
layout(M)
plot(iris[ 1:2], main="Sépalos de iris", xlab="Longitud",
ylab="Anchura", pch=20, col="green")
plot(iris[iris$Species=="setosa",1:2], main="Sépalos de setosa",
xlab="Longitud", ylab="Anchura", pch=20)
plot(iris[iris$Species=="versicolor",1:2],main="Sépalos de
versicolor", xlab="Longitud", ylab="Anchura", pch=20, col="red")
plot(iris[iris$Species=="virginica",1:2],main="Sépalos de virginica",
xlab="Longitud", ylab="Anchura", pch=20, col="blue")
layout(1)produce la Figura 12.2, que no es ninguna maravilla, pero sirve para observar cómo la matriz M organiza los gráficos: el primer plot ocupa toda la primera fila, y los otros tres, las tres posiciones de la segunda fila ordenados de izquierda a derecha. Como antes, el efecto de layout es permanente, por lo que si queréis volver al modo “gráficos de uno en uno” lo más práctico es que entréis al terminar vuestro gráfico compuesto la instrucción layout(1), como hemos hecho en el código anterior.
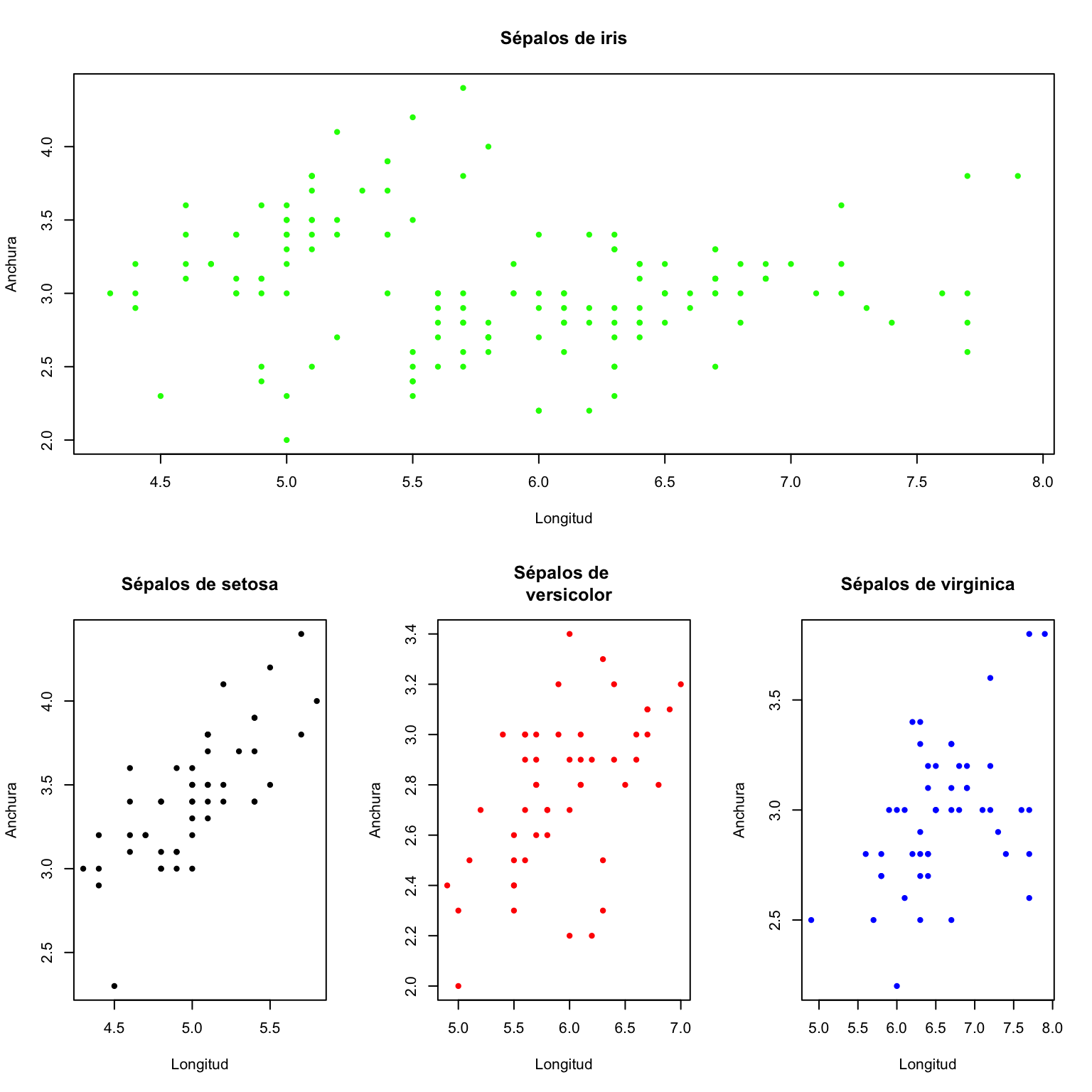
Figura 12.2: Tres gráficos en uno organizados con la instrucción layout(matrix(c(1,1,1,2,3,4),nrow=2,byrow=TRUE))
12.4 Tablas
La manera más sencilla de incluir tablas producidas con R en un fichero R Markdown es usando el paquete printr. Este paquete hace que las matrices, tablas de contingencia y dataframes se presenten como tablas de manera adecuada, que además dependerá del formato de salida elegido. Veamos algunos ejemplos de chunks y cómo se ven sus resultados. Para empezar, veamos como muestra los dataframes en el documento final. El chunk
library(printr)
head(iris)produce:
- En este documento html, la tabla siguiente:
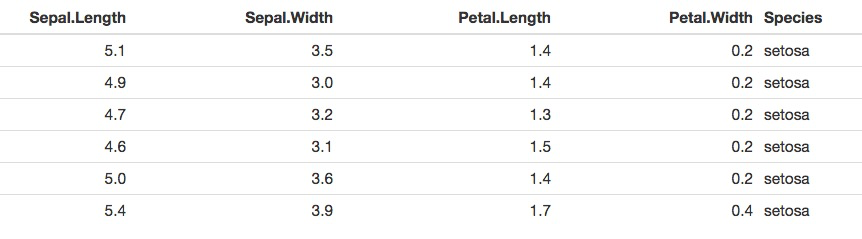
Figura 12.3: Una tabla en formato html producida con printr
- En un documento pdf, la tabla siguiente:
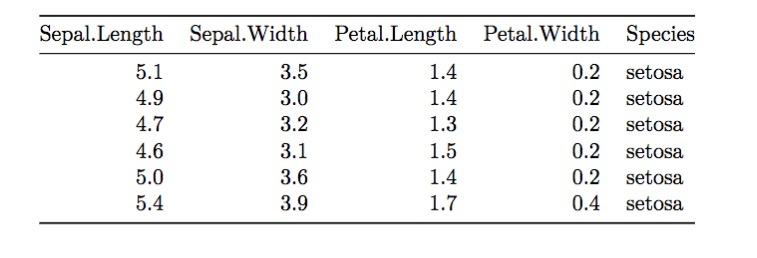
Figura 12.4: Una tabla en formato pdf producida con printr
- En un documento Word, la tabla siguiente:
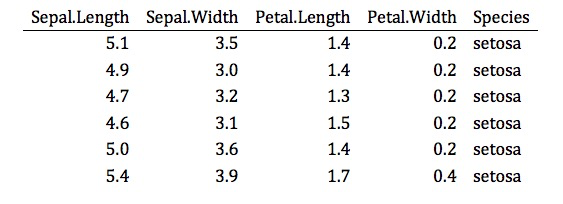
Figura 12.5: Una tabla en formato Word producida con printr
A partir de ahora, y en lo que queda de sección, sólo mostraremos los resultados en formato html.
Veamos como se ven los diferentes tipos de tabla de contingencia en el documento html final:
Sexo=c("M","H","H","H","H","M","M","H","M","H","H","M","M","H",
"H","M","H","M","H","H","H","M","H","M","H","H","H","H","H","M")
Respuesta=c("No","Si","Si","Si","No","No","Si","No","No","No",
"No","No","Si","No","No","Si","Si","Si","Si","Si","Si","No","Si",
"No","Si","Si","Si","No","Si","Si")
Edad=c("40-60","40-60",">60",">60","40-60","20-40","20-40",
"40-60","20-40","<20",">60","<20","40-60","40-60","<20",
"20-40","40-60","<20",">60","40-60","40-60","<20","20-40",
"20-40",">60","20-40","40-60","20-40","40-60","<20")
table(Edad)| <20 | >60 | 20-40 | 40-60 |
|---|---|---|---|
| 6 | 5 | 8 | 11 |
table(Respuesta,Edad)| Respuesta/Edad | <20 | >60 | 20-40 | 40-60 |
|---|---|---|---|---|
| No | 4 | 1 | 4 | 4 |
| Si | 2 | 4 | 4 | 7 |
table(Respuesta,Sexo,Edad)| Respuesta | Sexo | Edad | Freq |
|---|---|---|---|
| No | H | <20 | 2 |
| >60 | 1 | ||
| 20-40 | 1 | ||
| 40-60 | 3 | ||
| M | <20 | 2 | |
| >60 | 0 | ||
| 20-40 | 3 | ||
| 40-60 | 1 | ||
| Si | H | <20 | 0 |
| >60 | 4 | ||
| 20-40 | 2 | ||
| 40-60 | 6 | ||
| M | <20 | 2 | |
| >60 | 0 | ||
| 20-40 | 2 | ||
| 40-60 | 1 |
Veamos finalmente como se ven las matrices en el documento html final.
M=matrix(c(2,8,5,5,9,7,3,6,6,5,2,7,3,7,7,8,9,6,9,3,2,
3,3,10,8,10,2,10,8,7,3,3,2,6,3,2,1,9,8,5),nrow=8)
M| 2 | 6 | 9 | 8 | 2 |
| 8 | 5 | 6 | 10 | 6 |
| 5 | 2 | 9 | 2 | 3 |
| 5 | 7 | 3 | 10 | 2 |
| 9 | 3 | 2 | 8 | 1 |
| 7 | 7 | 3 | 7 | 9 |
| 3 | 7 | 3 | 3 | 8 |
| 6 | 8 | 10 | 3 | 5 |
dimnames(M)=list(NULL, paste("Col",1:5,sep="."))
M| Col.1 | Col.2 | Col.3 | Col.4 | Col.5 |
|---|---|---|---|---|
| 2 | 6 | 9 | 8 | 2 |
| 8 | 5 | 6 | 10 | 6 |
| 5 | 2 | 9 | 2 | 3 |
| 5 | 7 | 3 | 10 | 2 |
| 9 | 3 | 2 | 8 | 1 |
| 7 | 7 | 3 | 7 | 9 |
| 3 | 7 | 3 | 3 | 8 |
| 6 | 8 | 10 | 3 | 5 |
Si en algún momento queréis volver a la presentación usual de matrices, dataframes y tablas de contingencia, basta que descarguéis el paquete printr entrando en un chunk la instrucción
detach(package:printr, unload=TRUE)y luego ya lo volveréis a cargar si lo necesitáis de nuevo. Así, ahora que ya hemos descargado el paquete, la matriz M anterior se ve:
M| Col.1 | Col.2 | Col.3 | Col.4 | Col.5 |
|---|---|---|---|---|
| 2 | 6 | 9 | 8 | 2 |
| 8 | 5 | 6 | 10 | 6 |
| 5 | 2 | 9 | 2 | 3 |
| 5 | 7 | 3 | 10 | 2 |
| 9 | 3 | 2 | 8 | 1 |
| 7 | 7 | 3 | 7 | 9 |
| 3 | 7 | 3 | 3 | 8 |
| 6 | 8 | 10 | 3 | 5 |
12.5 Fórmulas matemáticas
La manera de incluir fórmulas matemáticas en R Markdown se basa en la sintaxis del sistema de composición de textos científicos LaTeX. Esta misma sintaxis, con pequeñas modificaciones, se usa para escribir fórmulas matemáticas bien formateadas en otros contextos: en los foros de Moodle, en las entradas y comentarios de blogs en Blogger o Wordpress, en la Wikipedia, etc.
Incluir fórmulas en un texto R Markdown no tiene ningún misterio. Solo hay que introducir el código que representa la fórmula de una de las dos formas siguientes:
Para las fórmulas o ecuaciones dentro del mismo párrafo, se escribe el código entre dos dólares:
$código$.Para las fórmulas o ecuaciones que queramos que aparezcan centradas en una línea aparte, se escribe el código entre dos dobles dólares:
$$código$$.
Al componer una fórmula a partir del código, RStudio ignora los espacios en blanco que hayamos escrito en ella, y añade los espacios en blanco a partir del significado lógico de sus elementos. Por ejemplo (y dejamos algunos espacios en blanco innecesarios para que veáis que no tienen ningún efecto en el resultado), el código siguiente:
Las raíces de la ecuación $x^2= 2$ son $x=\sqrt{ 2}$ y $x=-\sqrt{2} $;
en general, las raíces de $ax^2+b x+c=0$, con $a\neq 0$, vienen dadas
por la fórmula
$$
x=\frac{-b\pm\sqrt{b^2-4 a c}}{2a}.
$$produce el texto siguiente:
Las raíces de la ecuación \(x^2=2\) son \(x=\sqrt{2}\) y \(x=-\sqrt{2}\); en general, las raíces de \(ax^2+bx+c=0\), con \(a\neq 0\), vienen dadas por la fórmula \[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.\]
Observad el código:
Las potencias, y en general los superíndices, se indican con
^.La raíz cuadrada de algo se indica con
\sqrt{algo}(de square root).Una fracción se indica con
\frac{numerador}{denominador}(de fraction).Los signos \(\pm\) y \(\neq\) se indican con las marcas
\pm(de plus-minus) y\neq(de not equal), respectivamente.
Como podéis ver, las marcas de LaTeX que definen los diferentes elementos de las fórmulas matemáticas tienen nombres intuitivamente claros y (salvo las que corresponden a sígnos usuales como la suma o la resta) empiezan con el signo \.
A continuación damos algunas tablas con las marcas correspondientes a algunos de los signos matemáticos más usuales:
- Algunos operadores binarios
\[ \begin{array}{cl|cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline + & \texttt{+} &- & \texttt{-} & \pm & \texttt{\pm} & \times & \texttt{\times} \\ \cdot & \texttt{\cdot} & / & \texttt{/} & \cap & \texttt{\cap} & \cup & \texttt{\cup} & \end{array} \]
Algunos signos para relaciones \[ \begin{array}{cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline =& \texttt{=} & \neq & \texttt{\neq} &< & \texttt{<} \\> & \texttt{>} & \leq & \texttt{\leq} & \geq & \texttt{\geq} \\ \subseteq & \texttt{\subseteq} & \subsetneq & \texttt{\subsetneq} & \in & \texttt{\in} \\ \equiv & \texttt{\equiv } &\sim & \texttt{\sim} & \approx & \texttt{\approx} \end{array} \]
Algunos operadores
\[ \begin{array}{cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \sum& \texttt{\sum} &\prod& \texttt{\prod} & \bigcap& \texttt{ \bigcap} \\ \bigcup& \texttt{\bigcup} & \int& \texttt{\int} \end{array} \]
- Algunos delimitadores
\[ \begin{array}{cl|cl|cl} \text{Signos} & \text{Marcas} & \text{Signos} & \text{Marcas} &\text{Signos} & \text{Marcas} \\ \hline (\quad )& \texttt{( )} & [\quad ]& \texttt{[ ]} & \{\quad \} & \texttt{\\{ \\}} \\ \lfloor\quad\rfloor & \texttt{\lfloor \rfloor} &\lceil\quad \rceil& \texttt{\lceil \rceil} \end{array} \]
- Algunas letras griegas: la marca es simplemente su nombre (en inglés) precedido del signo
\
\[ \begin{array}{cl|cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \alpha& \texttt{\alpha} &\beta& \texttt{\beta} &\gamma& \texttt{\gamma} &\delta& \texttt{\delta} \\ \epsilon& \texttt{\epsilon} & \theta& \texttt{\theta} &\gamma& \texttt{\gamma} & \lambda& \texttt{\lambda} \\ \mu& \texttt{\mu} &\nu& \texttt{\nu} &\pi& \texttt{\pi} & \rho& \texttt{\rho}\\ \sigma& \texttt{\sigma} &\tau & \texttt{\tau } &\varphi& \texttt{\varphi} &\chi& \texttt{\chi} \\ \omega& \texttt{\omega} & \Gamma& \texttt{\Gamma} & \Sigma& \texttt{\Sigma} &\Omega& \texttt{\Omega} \end{array} \]
Algunos acentos en matemáticas \[ \begin{array}{cl|cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \hat{x}& \texttt{\hat x} &\bar{x}& \texttt{\bar x} &\dot{x}& \texttt{\dot x} & \tilde{x}& \texttt{\tilde x} \end{array} \]
Algunos acentos “expandibles”
\[ \begin{array}{cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} \\ \hline \widetilde{xyz} & \texttt{\widetilde{xyz}} &\widehat{xyz}& \texttt{\widehat{xyz}} \\ \overline{xyz}& \texttt{\overline{xyz}} & \overbrace{xyz}& \texttt{\overbrace{xyz}} \end{array} \]
Algunas flechas \[ \begin{array}{cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \leftarrow & \texttt{\leftarrow} & \Leftarrow & \texttt{\Leftarrow} &\rightarrow & \texttt{\rightarrow} \\ \Rightarrow & \texttt{\Rightarrow} & \leftrightarrow & \texttt{\leftrightarrow} & \Leftrightarrow & \texttt{\Leftrightarrow} \\ \mapsto & \texttt{\mapsto} \end{array} \]
Algunas funciones \[ \begin{array}{cl|cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \sin & \texttt{\sin} & \cos & \texttt{\cos} &\tan & \texttt{\tan} & \log & \texttt{\log} \\ \ln & \texttt{\ln} & \max & \texttt{\max} & \min & \texttt{\min} & \lim & \texttt{\lim}\\ \end{array} \]
Otros signos útiles \[ \begin{array}{cl|cl|cl} \text{Signo} & \text{Marca} & \text{Signo} & \text{Marca} &\text{Signo} & \text{Marca} \\ \hline \ldots & \texttt{\ldots} &\cdots & \texttt{\cdots} & \infty & \texttt{\infty} \\ \emptyset & \texttt{\emptyset} & \$ & \texttt{\$} \% & \texttt{\%} \end{array} \]
Algunos puntos que hay que tener en cuenta en la composición de fórmulas:
Los subíndices y superíndices se indican con los signos
_y^, respectivamente. Si el subíndice o superíndice está formado por dos o más caracteres, hay que entrarlo entre llaves. Por ejemplo,$x_i$produce \(x_i\) y$x^{25}$produce \(x^{25}\), pero, cuidado,$x^25$produce \(x^25\).Disponéis de diversos tipos de letra para usar en fórmulas matemáticas. Las dos más útiles son:
Negrita, que se indica con
\mathbf{...}; por ejemplo,\mathbf{X}y\mathbf{a}producen \(\mathbf{X}\) y \(\mathbf{a}\), respectivamente.La llamada Negrita de pizarra, que se usa en las notaciones de algunos conjuntos de números y se indica con
\mathbb{...}; por ejemplo,\mathbb{N}produce \(\mathbb{N}\) (el conjunto de los números naturales) y\mathbb{R}produce \(\mathbb{R}\) (los números reales).
\sqrtproduce raíces cuadradas o de orden superior:\sqrt{xyz}produce \(\sqrt{xyz}\) mientras que\sqrt[n]{xyz}produce \(\sqrt[n]{xyz}\).\frac{numerador}{denominador}produce fracciones; su tamaño y composición depende de si la fórmula ha de aparecer en el interior de un párrafo o ha de aparecer en línea aparte. Por ejemplo,$\frac{abc}{xyz}$produce \(\frac{abc}{xyz}\).Podemos especificar que los delimitadores se adapten a la altura de la expresión que envuelven, combinándolos con
\lefty\right. Comparad los tamaños de los paréntesis en$\left(X\right)$y$\left(\frac{abc}{xyz}\right)$, que producen \(\left(X\right)\) y \(\left(\frac{abc}{xyz}\right)\), respectivamente.Podemos incluir chunks en modo línea dentro de fórmulas matemáticas: por ejemplo,
$\sqrt{2}=`r round(sqrt(2),4)`$produce en el documento final \(\sqrt{2}=1.4142\).
Podemos incluir matrices, o, más en general, tablas, en las fórmulas matemáticas. Una tabla se define empezando con \begin{array}{formato} y acabando con \end{array}. El formato es una secuencia de letras l (de izquierda, left), r (de derecha, right) o c (de centrada): el número de letras indica el número de columnas, y cada letra indica el tipo de alineamiento de la columna correspondiente. Así, por ejemplo, \begin{array}{rccl} define una tabla de cuatro columnas: la primera alineada a la derecha, la segunda y la tercera centradas, y la cuarta alineada a la izquierda.
Entre el \begin{array}{formato} y el \end{array} se introducen por filas los valores de la tabla: los elementos de cada fila se separan con el signo & y el cambio de fila se indica con \\.
Para definir una matriz, hemos de envolver la tabla con los delimitadores \left( y \right). Por ejemplo,
$$
\left(\begin{array}{ccc}
a_{1,1} & a_{1,2} & a_{1,3}\\
a_{2,1} & a_{2,2} & a_{2,3}
\end{array}\right)
$$produce la matriz (en línea aparte)
\[
\left(\begin{array}{ccc}
a_{1,1} & a_{1,2} & a_{1,3}\\
a_{2,1} & a_{2,2} & a_{2,3}
\end{array}\right)
\]
De manera similar, para indicar el determinante de una matriz, hemos de usar los delimitadores \left | y \right |.
Dos cuestiones a tener en cuenta:
- Si sólo queremos usar un delimitador a un lado de la tabla, tenemos que incluir al otro lado
\left.o\right., según corresponda; las marcas\lefty\rightsiempre han de ir en parejas. Por ejemplo,
$$
\left.\begin{array}{l}
2x+3y=5\\
6x-2y=8
\end{array}\right\}
$$produce el sistema de ecuaciones \[ \left.\begin{array}{l} 2x+3y=5\\ 6x-2y=8 \end{array}\right\} \]
- Si en una entrada de una tabla en modo matemático queremos introducir texto, lo tenemos que incluir en una
caja de texto definida con la instrucción
\text{...}. Por ejemplo,
$$
f(x)=\left\{
\begin{array}{ll}
2x & \text{si }x\leq 0 \\
3x & \text{si }x\geq 0
\end{array}
\right.
$$produce
\[
f(x)=\left\{
\begin{array}{ll}
2x & \mbox{si }x\leq 0 \\
3x & \mbox{si }x\geq 0
\end{array}
\right.
\]
Observad que hemos dejado un espacio en blanco dentro de los \text{si } para separar los “si” de las fórmulas que los siguen:
el contenido de un \text{...} se transforma en texto, y por lo tanto se tienen en cuenta los espacios en blanco igual que en el texto normal.
Si necesitáis escribir expresiones matemáticas de manera regular en vuestros documentos R Markdown, os recomendamos que consultéis la sección de Matemáticas del Wikibook de LaTeX.