Lección 2 Conceptos básicos de muestreo
En todo estudio estadístico hemos de distinguir entre población, que es un conjunto de sujetos con una o varias características que podemos medir y deseamos estudiar, y muestra, un subconjunto de una población. Por ejemplo, si quisiéramos estudiar alguna característica de los estudiantes de grado de la UIB, entenderíamos que estos forman la población de interés, y si entonces escogiéramos al azar 10 estudiantes de cada grado, obtendríamos una muestra de esta población. Pero también podríamos considerar los estudiantes de grado de la UIB como una muestra de la población de los estudiantes universitarios españoles: depende del estudio que queramos realizar.
Recordad que, cuando disponemos de un conjunto de datos obtenidos midiendo una o varias características sobre los sujetos de una muestra, podemos llevar a cabo dos tipos de análisis estadístico:
Exploratorio o descriptivo: su objetivo es resumir, representar y explicar los datos de la muestra. Para llevarlo a cabo, se usan técnicas de estadística descriptiva como las que hemos descrito en lecciones anteriores.
Inferencial o confirmatorio: su objetivo es deducir (inferir), a partir de los datos de la muestra, información significativa sobre el total de la población. A menudo esta inferencia pasa por contrastar una hipótesis sobre alguna propiedad de la población. Las técnicas que se usan en los análisis inferenciales forman la estadística inferencial.
Por ejemplo, supongamos que hemos tomado una muestra de estudiantes de la UIB y sabemos sus calificaciones en un semestre concreto y sus números de hermanos. En un estudio exploratorio simplemente describiríamos estos datos mediante estadísticos y gráficos, mientras que usaríamos técnicas de estadística inferencial para deducir información sobre la población de todos los estudiantes de la UIB a partir de esta muestra: ¿Cuál estimamos que ha sido la nota media de los estudiantes de la UIB en el semestre en cuestión? La distribución de los números de hermanos en estudiantes de la UIB, ¿es similar a la del conjunto de la población española? ¿Es verdad que los estudiantes de la UIB con más hermanos tienen tendencia a tener mejores notas?
Un estudio inferencial suele desglosarse en los pasos siguientes:
Establecer la característica que se desea estimar o la hipótesis que se desea contrastar.
Determinar la información (los datos) que se necesita para hacerlo.
Diseñar un experimento que permita recoger estos datos; este paso incluye:
Decidir qué tipo de muestra se va a tomar y su tamaño.
Elegir las técnicas adecuadas para realizar las inferencias deseadas a partir de la muestra que se tomará.
Tomar una muestra y medir los datos deseados sobre los individuos que la forman.
Aplicar las técnicas de inferencia elegidas con el software adecuado.
Obtener conclusiones.
Si las conclusiones son fiables y suficientes, redactar un informe; en caso contrario, volver a empezar.
En la próxima sección nos centraremos en las técnicas de muestreo: los métodos generales para seleccionar muestras representativas de una población que tenemos a nuestra disposición en el tercer paso de la lista anterior.
2.1 Tipos de muestreo
Existen muchos tipos de muestreo, cada uno de los cuales proporciona una muestra representativa de la población en algún sentido. A continuación describimos de forma breve algunas de estas técnicas.
Muestreo aleatorio con y sin reposición
Un muestreo aleatorio consiste en seleccionar una muestra de la población de manera que todas las muestras del mismo tamaño sean equiprobables; es decir, que si fijamos el número de individuos de la muestra, cualquier conjunto de ese número de individuos tenga la misma probabilidad de ser seleccionado.
Hay dos tipos básicos de muestreo aleatorio que vale la pena distinguir. Para ilustrarlos, supongamos que disponemos de una urna con 100 bolas numeradas del 1 al 100, de la que queremos extraer una muestra de 15 bolas. La Figura 2.1 representa dicha urna.

Figura 2.1: Una urna de 100 bolas
Una manera de hacerlo sería repetir 15 veces el proceso de sacar una bola de la urna, anotar su número y devolverla a la urna. El tipo de muestra obtenida de esta manera recibe el nombre de muestra aleatoria con reposición, o simple (una m.a.s., para abreviar). Observad que con este procedimiento una misma bola puede aparecer varias veces en una muestra, y que todos los subconjuntos de 15 bolas “con posibles repeticiones” tienen la misma probabilidad de obtenerse. Un posible resultado serían las bolas azules de la Figura 2.2; la bola azul más oscuro ha sido escogida dos veces en la muestra.
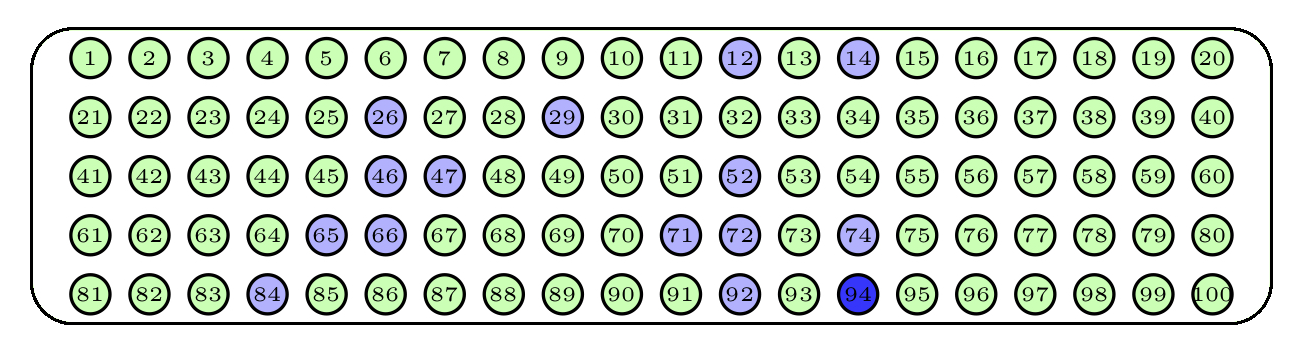
Figura 2.2: Una muestra aleatoria simple
Otra manera de extraer nuestra muestra sería repetir 15 veces el proceso de sacar una bola de la urna pero ahora sin devolverla. Esto es equivalente a extraer de golpe 15 bolas de la urna. Estas muestras no tienen bolas repetidas, y cualquier selección de 15 bolas diferentes tiene la misma probabilidad de ser la obtenida. En este caso se habla de una muestra aleatoria sin reposición. Un posible resultado serían las bolas azules de la Figura 2.3.
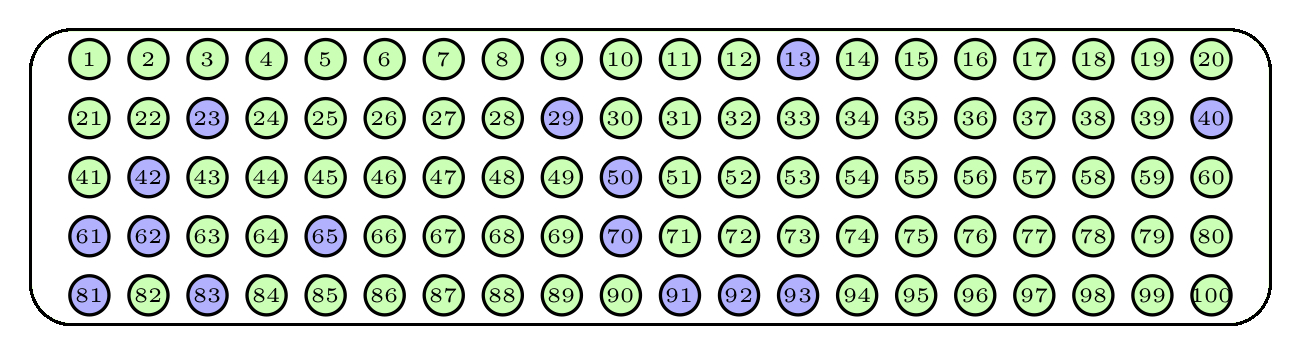
Figura 2.3: Una muestra aleatoria sin reposición
Cuando el tamaño de la población es muy grande en relación a la muestra, la probabilidad de que haya repeticiones en una muestra aleatoria simple es muy pequeña. Esto nos permite entender en este caso que los muestreos aleatorios con y sin reposición son equivalentes en el sentido siguiente: puesto que si la población es muy, muy grande, un muestreo con reposición daría muy probablemente una muestra con todos sus elementos diferentes, si tomamos directamente la muestra sin reposición podemos aceptar que permitíamos repeticiones, pero que no se han dado, y que por tanto es simple.
A modo de ejemplo, vamos a calcular la probabilidad de al menos una repetición en muestras aleatorias simples de diferentes tamaños de una población de 12,000 individuos (aproximadamente, el número de estudiantes de la UIB) y representar estas probabilidades en un gráfico. Recordad que la probabilidad de que los sujetos de una muestra aleatoria simple de tamaño n tomada de una población de N individuos no sean todos diferentes es
\[
1-\frac{N(N-1)(N-2)\cdots (N-n+1)}{N^n}.
\]
Esta probabilidad es la que calcula la función P.Rep(n,N) del bloque de código siguiente, y su gráfica es la de la Figura 2.4. La curva negra representa las probabilidades deseadas. Hemos añadido al gráfico una línea horizontal que marca la probabilidad 0.01 y que muestra que la probabilidad de alguna repetición en una m.a.s. de 16 o menos estudiantes de la UIB es inferior al 1%: en más de 99 de cada 100 veces que tomemos una m.a.s. de a lo sumo 16 estudiantes, nos saldrán todos diferentes
P.Rep=function(n,N){1-prod((N:(N-n+1))/N)}
prob=sapply(1:200,P.Rep,N=12000)
plot(1:200,prob,type="l",lwd=2,xlab="n",ylab="probabilidad",
main="",xaxp=c(0,200,20),yaxp=c(0,1,10))
abline(h=0.01,col="red")
text(160,0.04,labels="probabilidad 0.01",col="red",cex=0.7)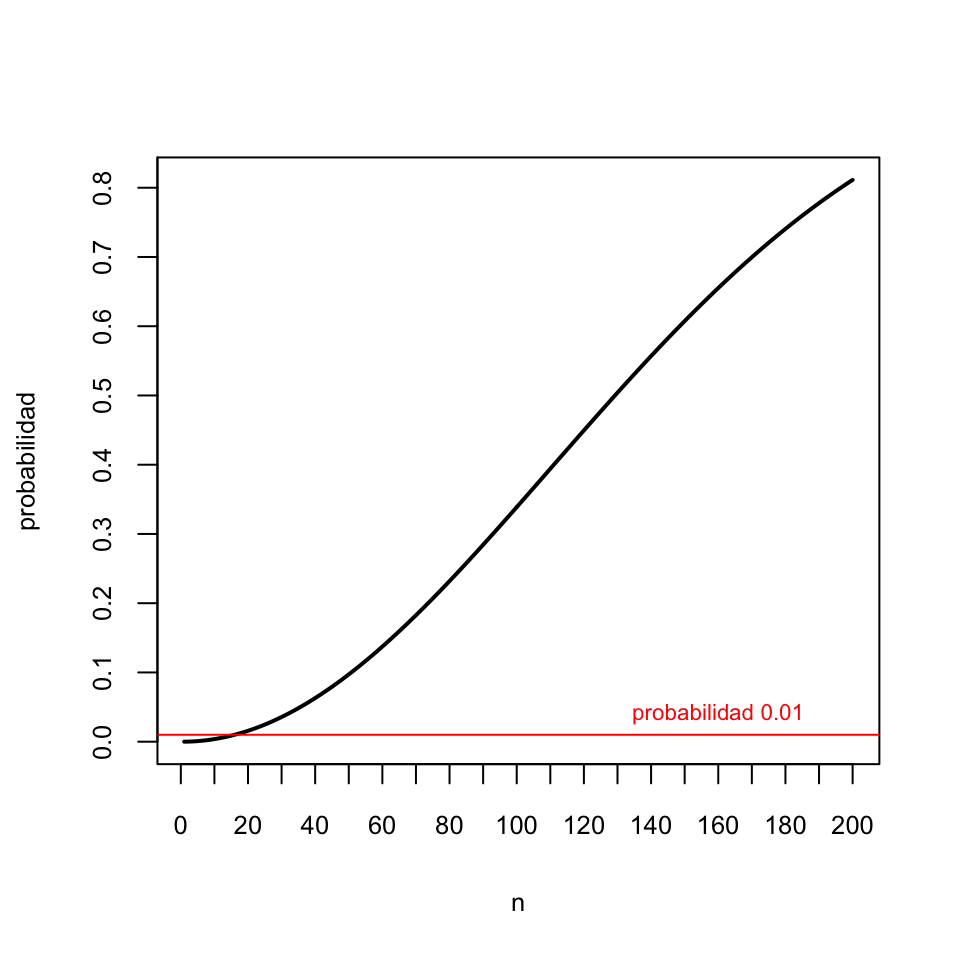
Figura 2.4: Probabilidad de repetición en una m.a.s. de n estudiantes de la UIB
Así, por ejemplo, una muestra aleatoria de 10 estudiantes diferentes de la UIB podría haberse obtenido perfectamente tomando los estudiantes con reposición, porque la probabilidad de alguna repetición en una m.a.s. como esta es muy pequeña: 0.004. En cambio, es difícil de creer que una muestra aleatoria de 200 estudiantes diferentes de la UIB sea simple, porque la probabilidad de alguna repetición en una m.a.s. como esta es grande: 0.811.
Por cierto, aunque en el bloque de código anterior hemos definido “a mano” la función P.Rep para recordar cómo se calculan estas probabilidades, R dispone de la distribución de probabilidad birthday relacionada con la probabilidad de repeticiones en muestras aleatorias simples. En concreto,
pbirthday(n,N)nos da la probabilidad de que se produzca al menos una repetición en una muestra aleatoria simple de tamaño n tomada de una población de N individuosqbirthday(p,N)nos da el tamaño mínimo que ha de tener una muestra aleatoria simple de una población de N individuos para que la probabilidad de una repetición sea como mínimo \(p\).
Veámoslo:
- La probabilidad de alguna repetición en una m.a.s. de 10 estudiantes de la UIB es:
pbirthday(10,12000)## [1] 0.003743964P.Rep(10,12000)## [1] 0.003743964- La probabilidad de alguna repetición en una m.a.s. de 200 estudiantes de la UIB es:
pbirthday(200,12000)## [1] 0.8113007P.Rep(200,12000)## [1] 0.8113007- El tamaño mínimo de una m.a.s. para que la probabilidad de alguna repetición sea al menos de 0.01 es:
qbirthday(0.01,12000)## [1] 17pbirthday(17,12000)## [1] 0.01127449pbirthday(16,12000)## [1] 0.009954432La mayoría de técnicas de estadística inferencial que se pueden usar para muestras aleatorias simples se pueden considerar igualmente válidas para muestras aleatorias sin reposición si el tamaño de la población es muy grande en relación al de la muestra (por dar una regla, digamos que, al menos, unas 1000 veces mayor). Si el tamaño de la población es relativamente pequeño por comparación a la muestra, algunas de estas técnicas se pueden salvar aplicando correcciones adecuadas para compensar la pequeñez de la población, y otras directamente pierden toda validez.
En todo caso, conviene ser consciente de que si queremos tomar una muestra aleatoria con o sin reposición de una población, es necesario disponer de una lista completa de todos sus individuos para poder sortear a quién vamos a seleccionar. Esto no siempre es posible. ¿Alguien tiene la lista completa de, pongamos, todos los diabéticos de España? ¿Que incluya los que no saben que lo son? Por lo tanto, en la vida real no siempre podemos tomar muestras aleatorias en el sentido que hemos explicado.
Muestreo sistemático
Una manera muy sencilla de obtener una muestra de una población cuando disponemos de una lista ordenada de sus individuos es tomarlos a intervalos constantes: cada quinto individuo, cada décimo individuo. Podemos añadir una componente aleatoria escogiendo al azar el primer individuo que elegimos, y a partir del cual empezamos a contar. Así, por ejemplo, si de una clase de 100 estudiantes quisiéramos escoger una muestra de 10, podríamos elegir un estudiante al azar, y a partir de él, por orden alfabético, elegir el décimo estudiante, el vigésimo, el trigésimo, etc.; si al llegar al final de la lista de clase no hubiéramos completado la muestra, volveríamos al principio de la misma. A esta técnica se la llama muestreo sistemático, aleatorio si además el primer sujeto se escoge de manera aleatoria. Por ejemplo, la Figura 2.5 describe una muestra aleatoria sistemática de 15 bolas de nuestra urna de 100 bolas: hemos empezado a escoger por la bola roja oscura, que ha sido elegida al azar, y a partir de ella hemos tomado 1 de cada 7 bolas, volviendo al principio cuando hemos llegado al final de la lista de bolas
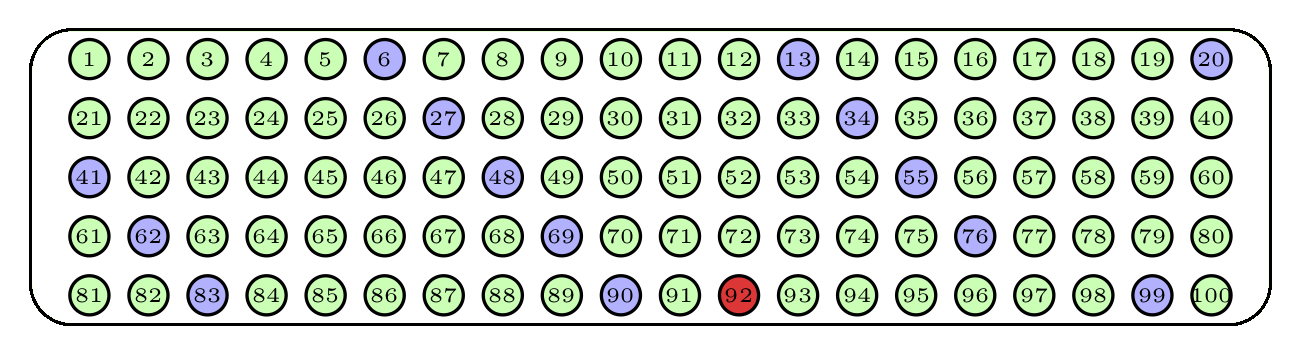
Figura 2.5: Una muestra aleatoria sistemática
Cuando no disponemos de una lista de toda la población pero sí que tenemos una manera de acceder de manera ordenada a sujetos de la misma (por ejemplo, enfermos que acuden a un hospital), podemos realizar un muestreo sistemático tomando los sujetos a intervalos constantes a medida que los encontramos y hasta completar el tamaño deseado de la muestra. Por ejemplo, para escoger una muestra de 10 estudiantes de la UIB, podríamos escoger cada décimo estudiante que entrase en un edificio del Campus por una puerta concreta hasta llegar a los 10.
Cuando el orden de los individuos de la población en la lista es aleatorio, el muestreo sistemático aleatorio es equivalente al muestreo aleatorio sin reposición. Pero en general este no es el caso, y se pueden producir sesgos. Por poner un caso extremo, si una clase de 100 estudiantes estuviera formada por 50 parejas de hermanos y tomáramos una muestra sistemática de 50 estudiantes, eligiéndolos por orden alfabético de los apellidos uno sí, uno no, es seguro que no aparecería ninguna pareja de hermanos en la muestra (porque dos hermanos son siempre consecutivos en la lista, y en nuestra muestra no habría ningún par de sujetos consecutivos). En cambio, la probabilidad de que una muestra aleatoria sin reposición del mismo tamaño contuviera una pareja de hermanos es prácticamente 1; en concreto esta probabilidad sería
\[ 1-\frac{100\times 98\times 96\times\cdots\times 2}{100\times 99\times 98\times\cdots\times 51}=1-\frac{2^{50}\cdot 50!^2}{100!}=1. \]
Muestreo aleatorio estratificado
Este tipo de muestreo se utiliza cuando la población está clasificada en estratos que son de interés para la propiedad estudiada. En este caso, se toma una muestra aleatoria de cada estrato y se unen en una muestra global. A este proceso se le llama muestreo aleatorio estratificado. Las muestras de cada estrato se toman de manera independiente las unas de las otras y de tamaños prefijados. Por lo que refiere a estos tamaños, la estrategia usual es imponer que la composición por estratos de la muestra global mantenga las proporciones de la población original, de manera que el tamaño de la muestra de cada estrato represente el mismo porcentaje del total de la muestra que el estrato correspondiente en la población completa. Pero a veces se usa una estrategia completamente diferente, y se toman los tamaños de manera que estratos que representan una fracción muy pequeña de la población (tan pequeña que no esperaríamos que tuvieran representación en una muestra aleatoria transversal de la población, es decir, tomada del total de la población sin tener en cuenta su composición en estratos) tengan una representación en la muestra mucho mayor que la que les tocaría.
Por ejemplo, los estratos podrían ser grupos de edad y podríamos tomar la muestra de cada grupo de edad de tamaño proporcional a la fracción que representa dicho grupo de edad en la población total. O podrían ser los sexos y procuraríamos que nuestra muestra estuviera formada por un 50% de hombres y un 50% de mujeres. O, en las Islas Baleares, los estratos podrían ser las islas, y entonces podríamos imponer que el número de representantes de cada isla en la muestra fuera proporcional a su población relativa dentro del conjunto total de la comunidad autónoma, o podríamos escoger la misma cantidad de individuos de cada isla, independientemente de su población.
Por continuar con nuestra urna de 100 bolas, supongamos que contiene 40 bolas de un color y 60 de otro color según muestra la Figura 2.6.
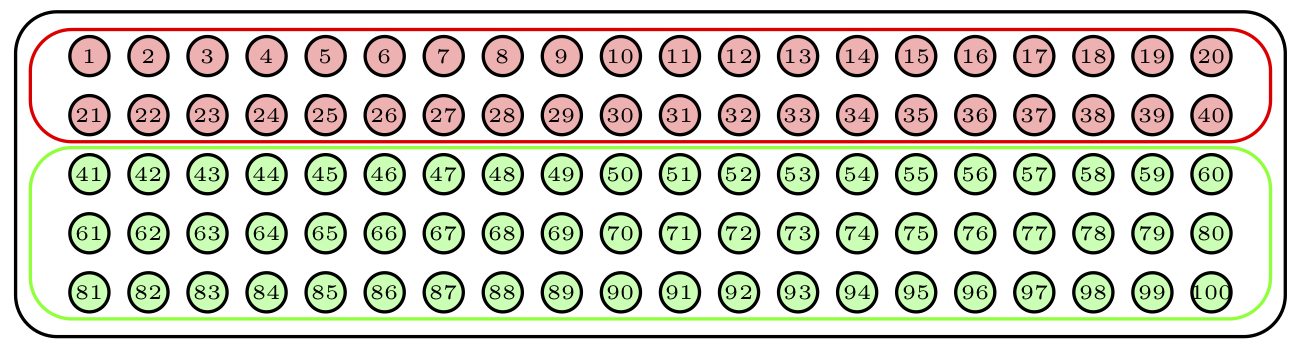
Figura 2.6: Nuestra urna ahora tiene 2 estratos
Para tomar una muestra aleatoria estratificada de 15 bolas, considerando como estratos los dos colores e imponiendo que la muestra refleje la composición de la urna, tomaríamos una muestra aleatoria de 6 bolas del primer color y una muestra aleatoria de 9 bolas del segundo color. De esta manera, los porcentajes de colores en la muestra serían los mismos que en la urna. La Figura 2.7 describe una muestra obtenida de esta manera.
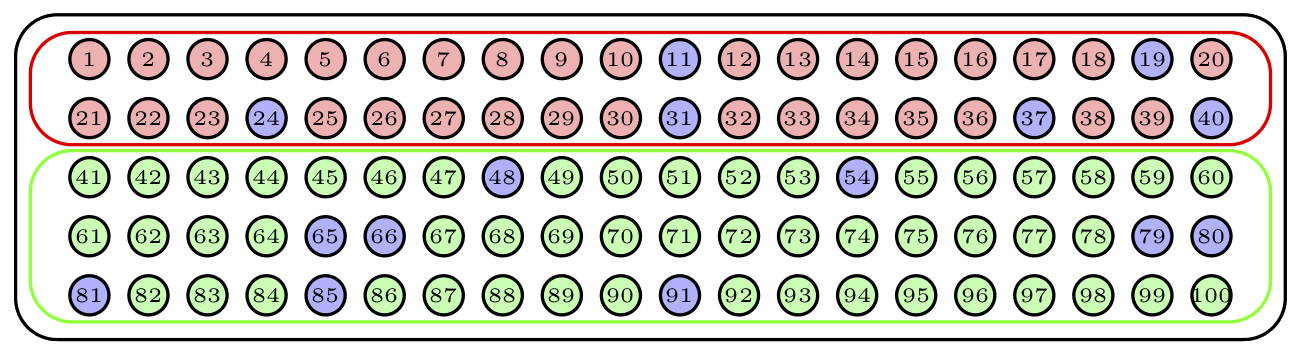
Figura 2.7: Una muestra aleatoria estratificada
En todo caso, el muestreo por estratos solo es necesario si esperamos que las características de la propiedad poblacional que queremos estudiar varíen según el estrato. Por ejemplo, si queremos tomar una muestra para estimar la altura media de los españoles adultos y no creemos que la altura de un español adulto dependa de su provincia de origen, no hay ninguna necesidad de esforzarse en tomar una muestra de cada provincia de manera que todas las provincias estén representadas adecuadamente en la muestra.
Muestreo por conglomerados
El proceso de obtener y estudiar una muestra aleatoria en algunos casos es caro o difícil, incluso aunque dispongamos de la lista completa de la población. Imaginemos que quisiéramos estudiar los hábitos de alimentación de los estudiantes de Primaria de Baleares. Para ello, previo permiso de la autoridad competente, tendríamos que seleccionar una muestra representativa de los escolares de Baleares. Seguramente podríamos disponer de su lista completa y por lo tanto podríamos tomar una muestra aleatoria, pero entonces acceder a las niñas y niños que la formasen seguramente significaría contactar con unos pocos alumnos de muchos centros de primaria, lo que volvería el proceso lento y costoso. Y eso si la Conselleria d’Educació nos facilitase la lista completa de alumnos.
Una alternativa posible sería, en vez de extraer una muestra aleatoria de todos los estudiantes de Primaria, escoger primero al azar unas pocas aulas de primaria de colegios de las Baleares, a las que llamamos en este contexto conglomerados (clusters), y formar entonces nuestra muestra con todos los alumnos de estas aulas. Y es que es mucho más sencillo poseer la lista completa de estudiantes de unas pocas aulas que conseguir la lista completa de todos los estudiantes de todos los colegios, y mucho más barato ir a unos pocos colegios concretos que ir a todos los colegios de las Islas a entrevistar a unos pocos estudiantes en cada centro.
Por poner otro ejemplo, efectuamos también un muestreo por conglomerados cuando para medir algunas características de los ejemplares de una planta en un bosque concreto, cuadriculamos la superficie del bosque, escogemos una muestra aleatoria de sectores de la cuadrícula (serían los conglomerados de este ejemplo) y estudiamos las plantas de interés contenidas en los sectores elegidas.
Volviendo de nuevo a nuestra urna, supongamos que sus 100 bolas se agrupan en 20 conglomerados de 5 bolas cada uno según las franjas verticales de la Figura 2.8 (donde mantenemos la clasificación en dos colores para poder comparar el resultado del muestreo por conglomerados con el estratificado).
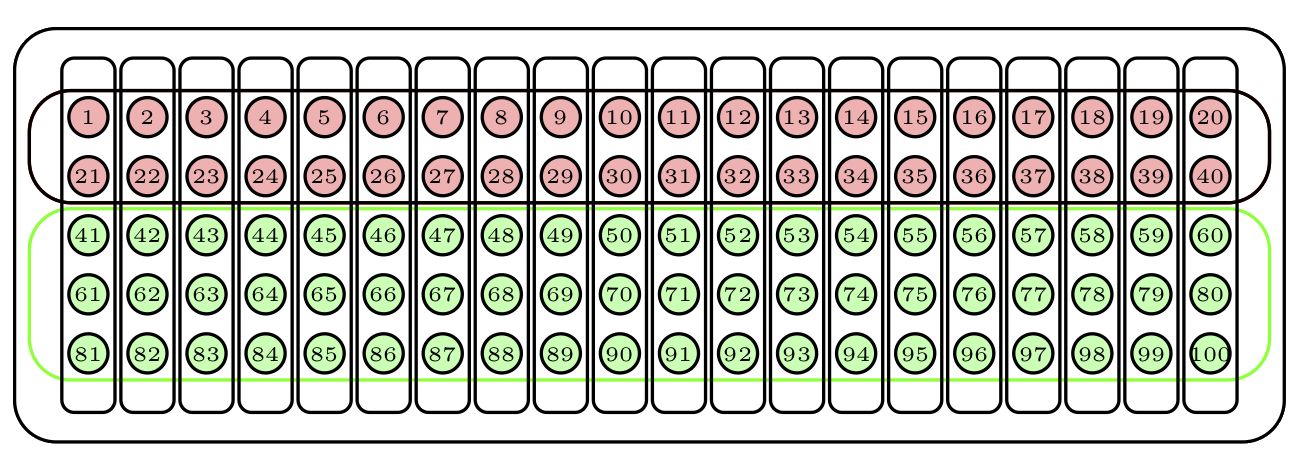
Figura 2.8: Nuestra urna ahora tiene 2 estratos y 20 conglomerados
Para obtener una muestra aleatoria por conglomerados de tamaño 15, escogeríamos al azar 3 conglomerados y la muestra estaría formada por sus bolas. La Figura 2.9 describe una muestra obtenida de esta manera: los conglomerados escogidos están marcados en azul.
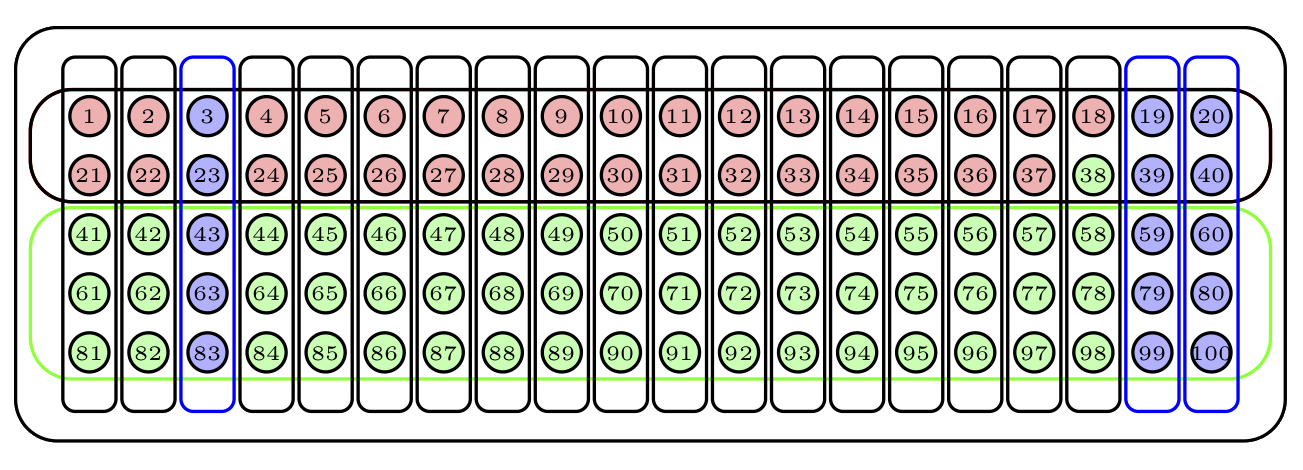
Figura 2.9: Una muestra aleatoria por conglomerados
Observad la diferencia entre el muestreo estratificado y el muestreo por conglomerados:
En una muestra estratificada se escoge una muestra aleatoria de cada estrato existente.
En una muestra por conglomerados se escogen algunos conglomerados al azar y se incluye en la muestra todos sus elementos.
Muestreos no aleatorios
Cuando la selección de la muestra no es aleatoria, se habla de muestreo no aleatorio. En realidad es el tipo más frecuente de muestreo porque casi siempre nos tenemos que conformar con los sujetos disponibles. Por ejemplo, en la UIB, para estimar la opinión que de un profesor tienen los alumnos de una clase, se consulta solo a los estudiantes que voluntariamente rellenan la encuesta de opinión, que de ninguna manera forman una muestra aleatoria: el perfil del estudiante que contesta voluntariamente una encuesta de este tipo está muy definido y no viene determinado por el azar. En este caso se trataría de una muestra auto-seleccionada.
Otro tipo de muestras no aleatorias son las oportunistas. Este es el caso, por ejemplo, si para estimar la opinión que de un profesor tienen los alumnos de una asignatura se visita un día la clase y se pasa la encuesta a los estudiantes que ese día asistieron a clase. De nuevo, puede que los alumnos presentes no sean representativos del alumnado de la asignatura (pueden ser los más aplicados, o los que no tienen la gripe, o a los que la asignatura no les coincide con otra). Veamos otros ejemplos de muestreo oportunista. Supongamos que queremos estudiar una característica de los animales de una determinada especie en un hábitat, y la medimos en los animales que capturamos. Estos ejemplares no tienen por qué ser representativos de la población: a lo mejor son los menos espabilados. O imaginad que tenéis una bolsa con bolas de diferentes tamaños. Si las removéis bien, las pequeñas tenderán a ir a parar al fondo y las grandes a quedar en la parte superior. Por lo tanto, si tomáis una muestra de la capa superior (que será lo más cómodo), no será representativa del total de la bolsa.
La Figura 2.10 describe una muestra oportunista de nuestra urna: sus 15 primeras bolas. Aunque toda muestra de un mismo tamaño tiene la misma probabilidad de obtenerse por medio de un muestreo aleatorio sin reposición, es difícil de creer que esta muestra sea aleatoria; basta que calculéis cuál es la probabilidad de que en una muestra aleatoria de 15 bolas de nuestra urna todas tengan el mismo color:
\[ \frac{40\times 39\times \cdots\times 26+60\times 59\times \cdots\times 46}{100\times 99\times \cdots\times 86}=2.1\times 10^{-4} \]
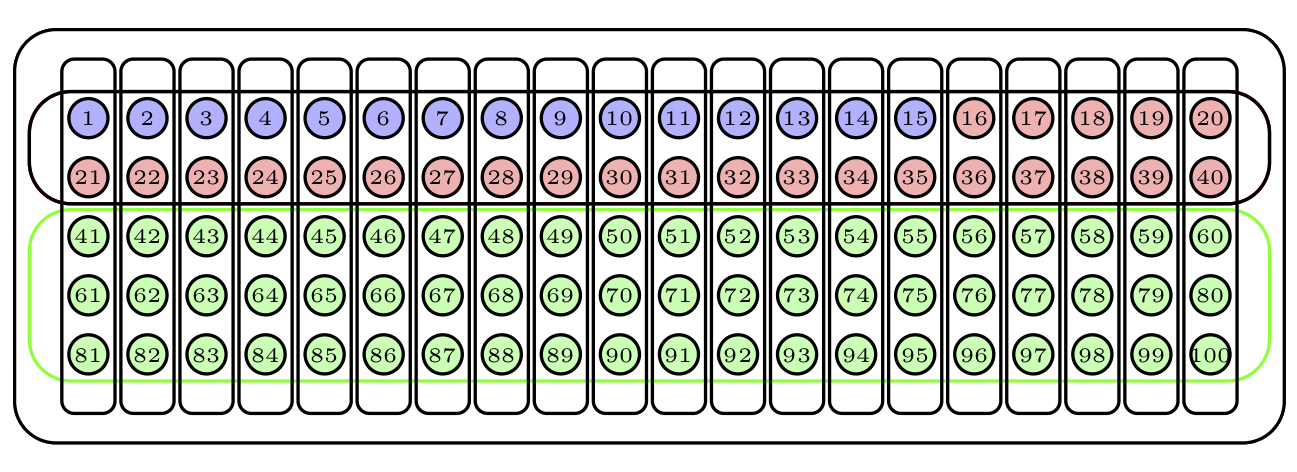
Figura 2.10: Una muestra oportunista
Las técnicas de estadística inferencial no se pueden aplicar a muestras no aleatorias, pero normalmente son las únicas que podemos conseguir. En este caso, lo que se suele hacer es describir en detalle las características de la muestra para justificar que, pese a no ser aleatoria, es representativa de la población y podría haber sido aleatoria. Por ejemplo, la muestra oportunista anterior de nuestra urna no es de ninguna manera representativa de su contenido por lo que refiere al color de las bolas.
Muestreo polietápico
En el ejemplo de los estudiantes de Primaria, la muestra final de estudiantes ha estado formada por todos los individuos de las aulas elegidas. Otra opción podría haber sido, tras seleccionar la muestra aleatoria de conglomerados, tomar de alguna manera una muestra aleatoria de cada uno de ellos. Por ejemplo, algunos estudios poblacionales a nivel estatal se realizan solamente en algunas provincias escogidas aleatoriamente, en las que luego se encuesta una muestra aleatoria de habitantes. Este sería un ejemplo de muestreo polietápico, en el que la muestra no se obtiene en un solo paso, sino mediante diversas elecciones sucesivas. La Figura 2.11 muestra un ejemplo sencillo de muestreo polietápico de nuestra urna: hemos elegido al azar 5 conglomerados (marcados en azul) y de cada uno de ellos hemos elegido 3 bolas al azar sin reposición.
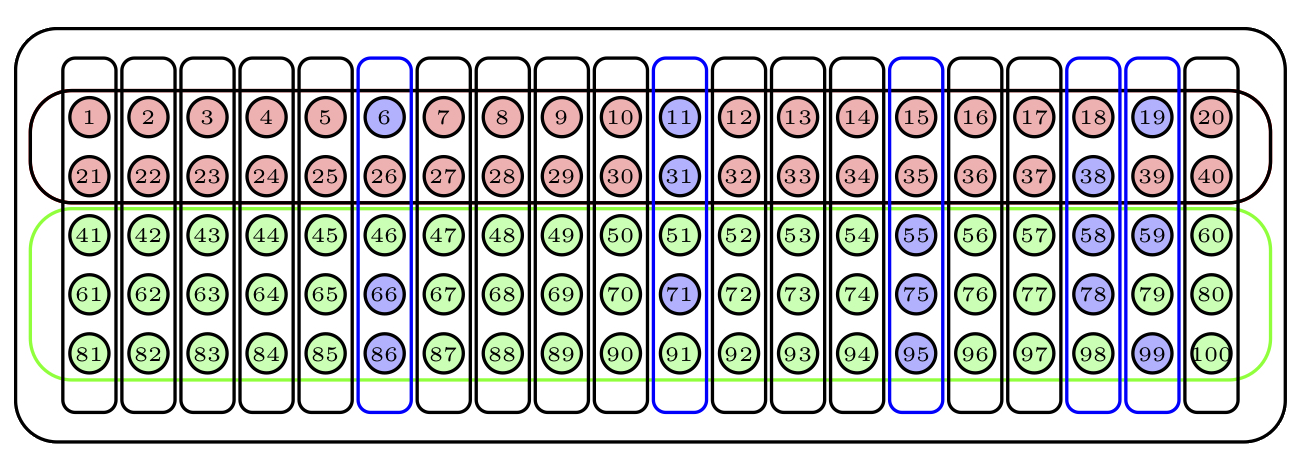
Figura 2.11: Una muestra polietápica
Otro ejemplo enrevesado (pero real) de muestreo polietápico sería, para elegir una muestra de adolescentes de una ciudad grande, escoger en primer lugar 4 secciones censales al azar; a continuación, escoger al azar 10 manzanas de cada una de estas secciones censales y una esquina de cada manzana; finalmente, recorrer cada manzana en sentido horario a partir de la esquina seleccionada y visitar un portal de cada tres, entrevistando todos los habitantes de 13 a 19 años en las casas o fincas visitadas. En este proceso, hemos realizado tres muestreos aleatorios sin reposición (de secciones censales, de manzanas y de esquinas) y un muestreo sistemático (los portales). Si además los adolescentes que estudiamos al final no son todos los que viven en los portales seleccionados sino solo los que encontramos en casa el día que los visitamos, este muestreo oportunista significaría un cuarto paso en la formación de la muestra.
Existen otros tipos de muestreo, solo hemos explicado los más comunes. En cualquier caso, lo importante es recordar que el estudio estadístico que se realice a posteriori deberá ser diferente según el tipo de muestreo usado. Por ejemplo, no se pueden usar las mismas técnicas para analizar una muestra aleatoria simple que una muestra por conglomerados. En este curso estudiaremos las propiedades de las diferentes técnicas de estimación solamente para el caso de muestreo aleatorio simple, es decir, al azar y con reposición, o al azar sin reposición si la población es muy, muy grande en comparación con la muestra.
2.2 Muestreo aleatorio con R
Recordemos que un método de selección al azar de muestras de tamaño n (es decir, formadas por n individuos) de una cierta población produce muestras aleatorias simples (m.a.s.) cuando todas las muestras posibles de n individuos (con posibles repeticiones) tienen la misma probabilidad de ser elegidas. El tener una m.a.s. de una población junto con un tamaño muestral adecuado n nos asegurará que la estimación que hagamos sea muy probablemente correcta.
La manera más sencilla de llevar a cabo un muestreo aleatorio simple es numerar todos los individuos de una población y sortearlos eligiendo números de uno en uno como si se tratase de una lotería, por ejemplo con algún generador de números aleatorios. Esto se puede llevar a cabo fácilmente con R.
R dispone de un generador de muestras aleatorias de un vector. La función básica es
sample(x, n, replace=...)donde:
xes un vector o un número natural \(x\), en cuyo caso R entiende que representa el vector 1,2,…,\(x\);nes el tamaño de la muestra que deseamos extraer;el parámetro
replacepuede igualarse aTRUE, y será una muestra aleatoria con reposición, es decir, simple, o aFALSE, y será una muestra aleatoria sin reposición. Este último es su valor por defecto, por lo que no es necesario especificarlo si se quiere obtener una muestra sin reposición.
Los dos primeros parámetros han de entrarse en este orden o igualados a los parámetros x y size, respectivamente.
Así, por ejemplo, para obtener una m.a.s. de 15 números entre 1 y 100, podemos entrar:
sample(100,15,replace=TRUE)## [1] 48 5 17 72 84 99 72 40 6 27 7 25 99 92 69Naturalmente, y como ya nos encontramos en la Lección 1 cuando generábamos vectores aleatorios con una distribución dada, cada ejecución de sample con los mismos parámetros puede dar lugar a muestras diferentes, y todas ellas tienen la misma probabilidad de aparecer:
sample(100,15,replace=TRUE)## [1] 7 84 46 43 15 95 95 53 63 18 41 33 4 62 57sample(100,15,replace=TRUE)## [1] 49 79 35 4 93 90 16 32 44 7 44 34 72 60 50sample(100,15,replace=TRUE)## [1] 55 9 45 96 55 13 32 68 67 2 35 85 52 57 3Veamos cómo extraer una m.a.s de una tabla de datos. Recordemos el dataframe iris, que recoge medidas de pétalos y sépalos de 150 flores de tres especies de iris.
str(iris)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...Si queremos extraer una m.a.s. de 15 ejemplares (filas) de esta tabla de datos, podemos generar con sample una m.a.s. de índices de filas de la tabla (recordad que dim aplicado a un dataframe nos da un vector con sus dimensiones, es decir, sus números de filas y de columnas, en este orden; por lo tanto, dim(iris)[1] es el número de filas de iris):
x=sample(dim(iris)[1],15,replace=TRUE) y a continuación crear un dataframe que contenga solo estas filas:
muestra_iris=iris[x,]
muestra_iris## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 46 4.8 3.0 1.4 0.3 setosa
## 133 6.4 2.8 5.6 2.2 virginica
## 85 5.4 3.0 4.5 1.5 versicolor
## 89 5.6 3.0 4.1 1.3 versicolor
## 91 5.5 2.6 4.4 1.2 versicolor
## 43 4.4 3.2 1.3 0.2 setosa
## 114 5.7 2.5 5.0 2.0 virginica
## 122 5.6 2.8 4.9 2.0 virginica
## 146 6.7 3.0 5.2 2.3 virginica
## 100 5.7 2.8 4.1 1.3 versicolor
## 102 5.8 2.7 5.1 1.9 virginica
## 32 5.4 3.4 1.5 0.4 setosa
## 107 4.9 2.5 4.5 1.7 virginica
## 115 5.8 2.8 5.1 2.4 virginica
## 66 6.7 3.1 4.4 1.4 versicolorSi solo quisiéramos una muestra aleatoria de longitudes de pétalos, podríamos aplicar directamente la función sample al vector correspondiente:
muestra_long_pet=sample(iris$Petal.Length,15,replace=TRUE)
muestra_long_pet## [1] 6.6 5.0 4.5 1.6 3.6 4.0 1.3 4.6 1.6 3.6 1.5 1.5 1.6 3.8 6.1El hecho de que funciones como sample o los generadores de vectores aleatorios con una cierta distribución de probabilidad fijada, como rnorm o rbinom, produzcan… pues eso, vectores aleatorios, puede tener inconvenientes a la hora de reproducir una simulación. R permite “fijar” el resultado de una función aleatoria con la instrucción set.seed. Sin entrar en detalles sobre cómo funcionan, los diferentes algoritmos que usa R para generar números aleatorios usan una semilla de aleatoriedad, que se modifica después de la ejecución del algoritmo, y por eso cada vez dan un resultado distinto. Pero, para una semilla fija, el algoritmo da el mismo resultado siempre. Lo que hace la función set.seed es igualar esta semilla al valor que le entramos. Si tras aplicar esta función a un número concreto ejecutamos una instrucción que genere un vector aleatorio de una longitud fija con una distribución fija, el resultado será siempre el mismo. Veamos un ejemplo de su efecto, generando muestras aleatorias simples de 10 longitudes de pétalos de flores iris con diferentes semillas de aleatoriedad:
sample(iris$Petal.Length,10,replace=TRUE)## [1] 6.7 5.1 3.3 1.6 4.0 1.5 1.5 1.5 1.4 1.6set.seed(20)
sample(iris$Petal.Length,10,replace=TRUE)## [1] 4.5 5.0 5.8 4.3 1.4 1.9 4.8 1.3 4.5 5.7set.seed(20)
sample(iris$Petal.Length,10,replace=TRUE)## [1] 4.5 5.0 5.8 4.3 1.4 1.9 4.8 1.3 4.5 5.7sample(iris$Petal.Length,10,replace=TRUE)## [1] 1.1 4.7 1.7 5.6 5.6 4.7 1.4 4.8 4.9 5.6set.seed(10)
sample(iris$Petal.Length,10,replace=TRUE)## [1] 5.6 4.7 5.3 4.0 4.4 1.2 5.1 4.7 1.7 1.4set.seed(10)
sample(iris$Petal.Length,10,replace=TRUE)## [1] 5.6 4.7 5.3 4.0 4.4 1.2 5.1 4.7 1.7 1.4Ejecutado inmediatamente después de set.seed(20), sample(iris$Petal.Length,10,replace=TRUE) siempre da lo mismo. Y ejecutado después de set.seed(10), sample(iris$Petal.Length,10,replace=TRUE) vuelve a dar siempre lo mismo, pero diferente de con set.seed(20).
La función set.seed no solo fija el resultado de la primera instrucción tras ella que genere un vector aleatorio, sino que, como fija la semilla de aleatoriedad y las funciones posteriores la modificarán de manera determinista, también fija los resultados de todas las instrucciones siguientes que generen vectores aleatorios.
set.seed(100)
sample(10,3)## [1] 10 7 6sample(10,3)## [1] 3 9 2sample(10,3)## [1] 7 6 9set.seed(100)
sample(10,3)## [1] 10 7 6sample(10,3)## [1] 3 9 2sample(10,3)## [1] 7 6 9Si queréis volver a “reiniciar” la semilla de la aleatoriedad tras haber usado un set.seed, podéis usar set.seed(NULL).
set.seed(100)
sample(10,3)## [1] 10 7 6set.seed(NULL)
sample(10,3)## [1] 7 10 8set.seed(100)
sample(10,3)## [1] 10 7 6set.seed(NULL)
sample(10,3)## [1] 9 2 10A veces querremos tomar diversas muestras aleatorias de una misma población y calcular algo sobre ellas. Para hacerlo podemos usar la función replicate. La sintaxis básica es
replicate(n, instrucción)donde n es el número de repeticiones de la instrucción. Por ejemplo, para tomar 10 muestras aleatorias simples de 15 longitudes de pétalos de flores iris, podemos hacer:
muestras=replicate(10, sample(iris$Petal.Length,15,replace=TRUE))
muestras## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 4.2 4.7 5.6 5.6 5.0 5.2 1.7 4.5 4.5 5.1
## [2,] 5.2 3.9 1.3 4.7 5.2 1.4 4.5 5.1 4.9 1.2
## [3,] 5.5 3.5 4.5 4.6 4.3 6.1 6.0 4.0 1.5 1.7
## [4,] 1.3 5.3 5.1 5.1 1.7 4.4 3.8 6.1 3.8 1.5
## [5,] 1.4 4.3 1.5 4.1 5.6 1.5 5.8 4.5 1.3 6.9
## [6,] 1.4 5.5 5.8 6.1 1.5 5.1 6.1 5.1 1.5 5.0
## [7,] 6.7 6.1 1.6 4.9 1.4 6.1 4.5 4.7 5.0 5.8
## [8,] 1.3 4.5 1.5 1.4 6.3 1.4 5.0 3.8 5.2 4.7
## [9,] 4.1 1.5 5.0 4.8 4.5 5.6 5.5 5.4 4.7 3.5
## [10,] 5.0 4.3 3.7 4.6 5.6 4.7 6.0 5.1 5.1 5.6
## [11,] 1.6 1.0 1.4 5.4 5.1 1.3 1.3 1.5 5.4 5.7
## [12,] 1.4 5.5 4.4 1.5 3.9 4.5 1.5 1.4 1.5 4.2
## [13,] 1.5 4.0 1.6 6.3 5.3 1.6 5.1 5.5 4.7 1.6
## [14,] 1.4 6.0 1.9 1.6 1.6 4.5 5.0 5.1 5.2 1.4
## [15,] 1.4 3.0 1.3 4.1 1.6 4.1 1.4 4.7 6.0 1.9Observad que R ha organizado los 10 vectores generados con el replicate como columnas de una matriz.
Si solo nos hubiera interesado calcular las medias, redondeadas a 2 cifras decimales, de 10 muestras aleatorias simples de 15 longitudes de pétalos de flores iris, podríamos haber hecho
medias=replicate(10,round(mean(sample(iris$Petal.Length,15,replace=TRUE)),2))
medias## [1] 3.42 3.85 4.00 4.17 3.91 4.11 3.08 3.69 3.67 3.76En este caso, como el resultado de la instrucción que iteramos es un solo número, los resultados del replicate forman un vector.
¿Y si quisiéramos la media y la desviación típica muestral de 10 muestras de estas? No podemos usar sin más dos replicate, como en
rbind(replicate(10,round(mean(sample(iris$Petal.Length,15,replace=TRUE)),2)),
replicate(10,round(sd(sample(iris$Petal.Length,15,replace=TRUE)),2)))## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 4.05 3.69 3.77 3.61 3.43 2.98 3.93 4.37 3.35 4.09
## [2,] 1.75 1.35 1.71 1.79 1.76 1.69 1.86 1.72 2.02 1.64porque es muy probable que el conjunto de muestras de las que hemos calculado la media en el primer replicate sea diferente del conjunto de muestras de las que hemos calculado la desviación típica en el segundo replicate. Lo más adecuado es definir una función que calcule un vector con estos dos valores (la función info del chunk siguiente), y luego usarla dentro de un único replicate:
info=function(x){round(c(mean(x),sd(x)),2)}
info_lp=replicate(10,info(sample(iris$Petal.Length,15,replace=TRUE)))
info_lp## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 3.45 3.52 3.79 3.82 4.21 4.35 3.69 3.56 3.62 2.89
## [2,] 1.71 1.83 1.72 1.64 1.63 1.93 1.93 1.85 1.72 1.85En este último caso, R ha organizado la información obtenida como columnas de una matriz: la primera fila son las medias y la segunda las desviaciones típicas.
Naturalmente, la función set.seed permite “fijar” el resultado de un replicate que incluya la generación de valores aleatorios:
set.seed(1000)
replicate(10,round(mean(sample(iris$Petal.Length,15,replace=TRUE)),2))## [1] 3.25 3.85 4.35 3.24 4.25 4.36 3.39 3.77 3.75 3.90set.seed(1000)
replicate(10,round(mean(sample(iris$Petal.Length,15,replace=TRUE)),2))## [1] 3.25 3.85 4.35 3.24 4.25 4.36 3.39 3.77 3.75 3.90Un último comentario sobre la función sample. Aunque aquí la vamos a usar principalmente para tomar muestras aleatorias en las que todos los sujetos de la población tengan la misma probabilidad de ser escogidos, también podemos emplearla para obtener muestras en las que diferentes sujetos puedan tener probabilidades diferentes de salir. Estas probabilidades se especifican con el parámetro prob igualado a un vector de probabilidades (o de pesos proporcionales a probabilidades) de la misma longitud que el vector x al cual apliquemos sample. De esta manera, la primera entrada de prob representa la probabilidad del primer elemento de x, la segunda entrada de prob representa la probabilidad del segundo elemento de x, etc.
Por ejemplo, si queremos tomar una muestra aleatoria de tamaño 10 del vector (1,2,3) de manera que cada elemento de este vector tenga probabilidad de ser escogido proporcional a su valor (es decir, el 2 tiene el doble de probabilidades de aparecer en la muestra que el 1, y el 3, el triple), podemos usar:
sample(1:3,10,prob=1:3)## Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'¡Ups! Para tomar una muestra de 10 elementos de una población de 3 sujetos, habrá que permitir repeticiones
sample(1:3,10,replace=TRUE,prob=1:3)## [1] 3 3 2 3 1 3 2 2 3 2Para terminar esta lección, damos una función sencilla para efectuar muestreos sistemáticos aleatorios. El objetivo es, dado un vector de longitud n, obtener una muestra de tamaño n. Lo que haremos será tomar el cociente por exceso \(k=\lceil N/n\rceil\) de n entre n para determinar el período con el que tenemos que tomar los elementos de manera que todos los elementos puedan ser escogidos. A continuación elegimos al azar un elemento del vector con sample y a partir de él generamos una progresión aritmética de n elementos y paso \(k\), volviendo al inicio del vector si llegamos al final sin haber completado la muestra (lo que especificamos tomando los valores de la progresión aritmética módulo n).
sist.sample=function(N,n){
k=ceiling(N/n)
x0=sample(N,1)
seq(x0,length.out=n,by=k)%%N
}Por ejemplo, una muestra sistemática de 10 flores iris se podría obtener de la manera siguiente:
x=sist.sample(dim(iris)[1],10) #Los índices de la muestra sistemática
muestra_sist_iris=iris[x,] #La muestra de la tabla iris
muestra_sist_iris| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 86 | 6.0 | 3.4 | 4.5 | 1.6 | versicolor |
| 101 | 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 116 | 6.4 | 3.2 | 5.3 | 2.3 | virginica |
| 131 | 7.4 | 2.8 | 6.1 | 1.9 | virginica |
| 146 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 11 | 5.4 | 3.7 | 1.5 | 0.2 | setosa |
| 26 | 5.0 | 3.0 | 1.6 | 0.2 | setosa |
| 41 | 5.0 | 3.5 | 1.3 | 0.3 | setosa |
| 56 | 5.7 | 2.8 | 4.5 | 1.3 | versicolor |
| 71 | 5.9 | 3.2 | 4.8 | 1.8 | versicolor |
Como 150/10=15, podemos observar que los índices avanzan de 15 en 15 a partir del que ha sido escogido al azar en primer lugar.
2.3 Guía rápida
pbirthday(n,N)calcula la probabilidad de que se produzca al menos una repetición en una m.a.s. de tamaño n tomada de una población de N individuos.qbirthday(p,N)calcula el tamaño mínimo que ha de tener una m.a.s. de una población de N individuos para que la probabilidad de una repetición sea como mínimo \(p\).sample(x, n)genera una muestra aleatoria de tamañondel vectorx. Sixes un número natural \(x\), representa el vector 1,2,…,\(x\). Dispone de los dos parámetros siguientes:replace, que igualado aTRUEproduce muestras con reposición e igualado aFALSE(su valor por defecto) produce muestras sin reposición.prob, que permite especificar las probabilidades de aparición de los diferentes elementos dex(por defecto, son todas la misma).
set.seedpermite fijar la semilla de aleatoriedad.replicate(n,expresión)evalúanveces laexpresión, y organiza los resultados como las columnas de una matriz (o un vector, si el resultado de cadaexpresiónes unidimensional).
2.4 Ejercicios
Test
(1) Queremos escoger 100 estudiantes de grado de la UIB para preguntarles cuántas horas semanales estudian. Como creemos que el tipo de estudio cursado influye en este dato, clasificamos los estudiantes según el centro (facultad o escuela) en el que están matriculados, y tomaremos una muestra al azar de cada centro, por sorteo a partir de la lista de todos los matriculados en ese centro y de manera que el tamaño de la muestra de cada centro sea proporcional al número de matriculados en el mismo. ¿De qué tipo de muestreo se tratará?
- Muestreo aleatorio simple
- Muestreo aleatorio estratificado
- Muestreo aleatorio sin reposición
- Muestreo aleatorio por conglomerados
- Muestreo aleatorio sistemático
- Ninguno de los anteriores
(2) Con una sola instrucción, calculad la media de una muestra aleatoria sin reposición de 15 elementos escogidos de un vector numérico llamado \(X\).
(3) Con una sola instrucción, extraed un subdataframe del dataframe iris formado por una muestra aleatoria sin reposición de 40 filas, y llamadlo muestra. Y antes de contestar, comprobad que funciona.
(4) Con una sola instrucción, calculad un vector formado por las medias de 100 muestras aleatorias sin reposición de 20 elementos cada una escogidos de un vector numérico llamado \(X\) y llamadlo medias.
Problemas
(1) El bloque de código siguiente carga en un dataframe llamado DCR la tabla de datos datacrab.txt que se encuentra en el url https://raw.githubusercontent.com/AprendeR-UIB/Material/master/datacrab.txt y que contiene información sobre una muestra de cangrejos.
library(RCurl)
datos=getURL("https://raw.githubusercontent.com/AprendeR-UIB/Material/master/datacrab.txt")
DCR=read.table(text=datos,header=TRUE)
str(DCR)## 'data.frame': 173 obs. of 5 variables:
## $ input : int 3 4 2 4 4 3 2 4 3 4 ...
## $ color.spine: int 3 3 1 3 3 3 1 2 1 3 ...
## $ width : num 28.3 22.5 26 24.8 26 23.8 26.5 24.7 23.7 25.6 ...
## $ satell : int 8 0 9 0 4 0 0 0 0 0 ...
## $ weight : int 3050 1550 2300 2100 2600 2100 2350 1900 1950 2150 ...(a) Definid una función de parámetros N, n y s que tome N muestras aleatorias simples de n filas de este dataframe usando como semilla de aleatoriedad el número \(s\); a continuación, calcule las medias de los pesos de los individuos de cada una de estas muestras; y finalmente calcule la media y la desviación típica muestral del vector formado por estas medias. Tenéis que usar set.seed y replicate para definir la función.
(b) Aplicadla a N=100, n=30 y tomando como \(s\) el número formado por las 5 primeras cifras de vuestro NIF o pasaporte.
(c) ¿Qué valores predice el Teorema Central del Límite que se deberían obtener? ¿Habéis obtenido resultados similares a los predichos por dicho teorema?
(2) Extraed una muestra aleatoria estratificada sin reposición de 15 flores de la tabla iris manteniendo en la muestra las proporciones de las diferentes especies en la tabla.
Respuestas al test
(1) b
(2) mean(sample(X,15))
(También sería correcto sum(sample(X,15))/15. Y en ambos casos también sería correcto añadiendo dentro de la función sample el parámetro replace=FALSE, que hemos omitido porque es el valor por defecto de replace.)
(3) muestra=iris[sample(dim(iris)[1],40),]
(También sería correcto consultar antes el número de filas con str o tail, ver que son 150, y responder muestra=iris[sample(150,40),]. Hay otras respuestas correctas, no las damos para no liaros. Además, y como antes, también sería correcto añadir replace=FALSE.)
(4) medias=replicate(100,mean(sample(X,20)))
(¿Ya os hemos dicho que también sería correcto incluyendo replace=FALSE en el argumento de sample?)
Soluciones sucintas de los problemas
(1) (a) Una posible función:
M=function(N,n,s){
set.seed(s)
Muestras=replicate(N,mean(sample(DCR$weight,n,replace=TRUE)))
Res=round(c(mean(Muestras),sd(Muestras)),2)
attr(Res,"names")=c("Media","Desv. Típica")
Res
}(b)
M(100,30,42)## Media Desv. Típica
## 2439.62 106.48(c) El Teorema Central del Límite predice como media la de la población (que en este caso es el vector DCR$weight)
round(mean(DCR$weight),2)## [1] 2437.19y como desviación típica la desviación típica de la población dividida por la raíz cuadrada del tamaño de las muestras
round((sd(DCR$weight)*sqrt(length(DCR$weight)-1)/sqrt(length(DCR$weight)))/sqrt(30),2)## [1] 105.04(2) Vamos a dar una función mucho más general de la que necesitamos en este ejercicio. Sus parámetros son un dataframe DF, el factor Fact con el que clasificamos sus filas, el tamaño n de la muestra, y rep, un valor lógico que indique si tomamos las muestras con o sin reposición y que por defecto valdrá FALSE, es decir, sin reposición, como la definición por defecto de sample:
Clust_sample=function(DF,Fact,n,rep=FALSE){
# Cargamos las variables del dataframe en el entorno global
attach(DF)
# Calculamos los tamaños de las muestras de cada estrato
Tamaños=round(prop.table(table(Fact))*n)
# Para cada nivel del factor, tomamos una muestra aleatoria
# sin reposición de las filas de ese nivel y del tamaño que
# hemos calculado
Muestra=c()
for(i in 1:length(levels(Fact))){
Muestra=c(Muestra,sample(which(Fact==levels(Fact)[i]),Tamaños[i],replace=rep))
}
# Borramos las variables del dataframe del entorno global
detach(DF)
# Si la muestra ha quedado "corta" debido a redondeos al calcular
# los tamaños de las submuestras, añadimos al azar tantas filas
# como hagan falta.
# Distinguimos si permitimos repeticiones o no
if (rep==FALSE){
# Las nuevas filas han de ser diferentes de las anteriores
Muestra=c(Muestra,sample((1:dim(DF)[1])[-Muestra],n-length(Muestra)))
}else{
# Las nuevas filas pueden ser iguales a las anteriores
Muestra=c(Muestra,sample((1:dim(DF)[1]),n-length(Muestra),replace=TRUE))
}
sort(Muestra)
}Apliquemos la función a la tabla iris:
iris[Clust_sample(iris,Species,15),]## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 13 4.8 3.0 1.4 0.1 setosa
## 15 5.8 4.0 1.2 0.2 setosa
## 18 5.1 3.5 1.4 0.3 setosa
## 23 4.6 3.6 1.0 0.2 setosa
## 28 5.2 3.5 1.5 0.2 setosa
## 56 5.7 2.8 4.5 1.3 versicolor
## 63 6.0 2.2 4.0 1.0 versicolor
## 65 5.6 2.9 3.6 1.3 versicolor
## 69 6.2 2.2 4.5 1.5 versicolor
## 78 6.7 3.0 5.0 1.7 versicolor
## 118 7.7 3.8 6.7 2.2 virginica
## 119 7.7 2.6 6.9 2.3 virginica
## 122 5.6 2.8 4.9 2.0 virginica
## 132 7.9 3.8 6.4 2.0 virginica
## 140 6.9 3.1 5.4 2.1 virginicaUna construcción equivalente, sin usar un bucle for
Clust_sample2=function(DF,Fact,n,rep=FALSE){
attach(DF)
M=length(levels(Fact))
Tamaños=round(prop.table(table(Fact))*n)
F=function(i){sample(which(Fact==levels(Fact)[i]),Tamaños[i],replace=rep)}
Muestra=unlist(sapply(1:M,FUN=F))
detach(DF)
if (rep==FALSE){
Muestra=c(Muestra,sample((1:dim(DF)[1])[-Muestra],n-length(Muestra)))
}else{
Muestra=c(Muestra,sample((1:dim(DF)[1]),n-length(Muestra),replace=TRUE))
}
sort(Muestra)
}
iris[Clust_sample2(iris,Species,15),]| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 13 | 4.8 | 3.0 | 1.4 | 0.1 | setosa |
| 18 | 5.1 | 3.5 | 1.4 | 0.3 | setosa |
| 25 | 4.8 | 3.4 | 1.9 | 0.2 | setosa |
| 29 | 5.2 | 3.4 | 1.4 | 0.2 | setosa |
| 44 | 5.0 | 3.5 | 1.6 | 0.6 | setosa |
| 51 | 7.0 | 3.2 | 4.7 | 1.4 | versicolor |
| 57 | 6.3 | 3.3 | 4.7 | 1.6 | versicolor |
| 77 | 6.8 | 2.8 | 4.8 | 1.4 | versicolor |
| 88 | 6.3 | 2.3 | 4.4 | 1.3 | versicolor |
| 100 | 5.7 | 2.8 | 4.1 | 1.3 | versicolor |
| 121 | 6.9 | 3.2 | 5.7 | 2.3 | virginica |
| 123 | 7.7 | 2.8 | 6.7 | 2.0 | virginica |
| 137 | 6.3 | 3.4 | 5.6 | 2.4 | virginica |
| 139 | 6.0 | 3.0 | 4.8 | 1.8 | virginica |
| 148 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
Por ejemplo, podríamos usar esta función para extraer una muestra aleatoria estratificada con reposición de 15 cangrejos de la tabla datacrab.txt usada en el problema anterior usando como estratos los valores de la variable color.spine.
prop.table(table(DCR$color.spine))##
## 1 2 3
## 0.2138728 0.0867052 0.6994220DCR$color.spine=as.factor(DCR$color.spine)
Muestra=DCR[Clust_sample(DCR,color.spine,15,TRUE),]
Muestra## input color.spine width satell weight
## 50 3 1 30.3 3 3600
## 62 4 3 24.5 5 2050
## 64 3 3 26.0 5 2150
## 67 3 3 29.0 10 3200
## 74 3 3 25.4 6 2250
## 81 4 2 24.5 0 2250
## 82 5 3 27.5 0 2900
## 116 5 3 23.7 0 1800
## 137 3 1 28.4 5 3100
## 147 3 1 31.7 4 3725
## 151 3 3 27.6 4 2850
## 152 3 3 26.2 0 2300
## 156 3 3 24.7 4 1950
## 162 3 3 26.0 3 2275
## 165 3 3 26.5 7 2750prop.table(table(Muestra$color.spine))##
## 1 2 3
## 0.20000000 0.06666667 0.73333333