Lección 2 La calculadora
Cuando se trabaja en modo interactivo en la consola de R, hay que escribir las instrucciones a la derecha de la marca de inicio > de la línea inferior (que omitimos en los bloques de código de este libro).
Para evaluar una instrucción al terminar de escribirla, se tiene que pulsar la tecla Entrar (\(\hookleftarrow\)); así, por ejemplo, si junto a la marca de inicio escribimos 2+3 y pulsamos Entrar, R escribirá en la línea siguiente el resultado, 5, y a continuación una nueva línea en blanco encabezada por la marca de inicio, donde podremos continuar entrando instrucciones.
2+3 #Y ahora aquí pulsamos Entrar
#> [1] 5Bueno, hemos hecho trampa. Como ya habíamos comentado en la lección anterior, se pueden escribir comentarios: R ignora todo lo que se escribe en la línea después de un signo #. También podéis observar que R ha dado el resultado en una línea que empieza con [1]; ya discutiremos en la Lección 4 qué significa este [1].
Si la expresión que entramos no está completa, R no la evaluará y en la línea siguiente esperará a que la acabemos, indicándolo con la marca de continuación, por defecto un signo +. (En estas notas, y excepto en el ejemplo que damos a continuación, no mostraremos este signo + para no confundirlo con una suma.) Además, si cometemos algún error de sintaxis, R nos avisará con un mensaje de error.
2*(3+5 #Pulsamos Entrar, pero no hemos acabado
+ ) #ahora sí#> [1] 16## Error: <text>:1:6: inesperado ')'
## 1: 2*3+5)
## ^Como podemos ver, al ejecutar la segunda instrucción, R nos avisa de que el paréntesis no está en su sitio.
Se puede agrupar más de una instrucción en una sola línea separándolas con signos de punto y coma. Al pulsar la tecla Entrar, R las ejecutará todas, una tras otra y en el orden en el que las hayamos escrito.
2+3; 2+4; 2+5
#> [1] 5
#> [1] 6
#> [1] 72.1 Números reales: operaciones y funciones básicas
La separación entre la parte entera y la parte decimal en los números reales se indica con un punto, no con una coma. Por consistencia, en el texto también seguiremos el convenio angloamericano de usar un punto en lugar de una coma como separador decimal.
2+2,5## Error: <text>:1:4: inesperado ','
## 1: 2+2,
## ^2+2.5
#> [1] 4.5Las operaciones usuales se indican en R con los signos que damos en la lista siguiente. Por lo que se refiere a los dos últimos operadores en esta lista, recordad que si \(a\) y \(b\) son dos números reales, con \(b>0\), la división entera de \(a\) por \(b\) da como cociente entero el mayor número entero \(q\) tal que \(q\cdot b\leqslant a\), y como resto la diferencia \(a-q\cdot b\). Por ejemplo, la división entera de 29.5 entre 6.3 es 29.5=4·6.3+4.3, con cociente entero 4 y resto 4.3. (Cuando \(b<0\), R da como cociente entero el menor número entero \(q\) tal que \(q\cdot b\geqslant a\), y como resto la diferencia \(a-q\cdot b\), que en este caso es negativa.)
- Suma:
+ - Resta: -
- Multiplicación:
* - División:
/ - Potencia:
^ - Cociente entero:
%/% - Resto de la división entera:
%%
A continuación, damos algunos ejemplos de manejo de estas operaciones. Observad el uso natural de los paréntesis para indicar la precedencia de las operaciones.
2*3+5/2
#> [1] 8.5
2*(3+5/2) #Aquí lo único que dividimos entre 2 es 5
#> [1] 11
2*((3+5)/2)
#> [1] 8
2/3+4 #Aquí el denominador de la fracción es 3
#> [1] 4.666667
2/(3+4)
#> [1] 0.2857143
2^3*5 #Aquí el exponente es 3
#> [1] 40
2^(3*5)
#> [1] 32768
2^-5 #En este caso no hacen falta paréntesis...
#> [1] 0.03125
2^(-5) #Pero queda más claro si se usan
#> [1] 0.03125
534%/%7 #¿Cuántas semanas completas caben en 534 días?
#> [1] 76
534%%7 #¿Y cuántos días sobran?
#> [1] 2
534-76*7
#> [1] 2El objeto pi representa el número real \(\pi\).
pi
#> [1] 3.141593¡Cuidado! No podemos omitir el signo * en las multiplicaciones.
2(3+5)## Error in eval(expr, envir, enclos): tentativa de aplicar una no-función2*(3+5)
#> [1] 162pi## Error: <text>:1:2: unexpected symbol
## 1: 2pi
## ^2*pi
#> [1] 6.283185Cuando un número es muy grande o muy pequeño, R emplea la llamada notación científica para dar una aproximación.
2^40
#> [1] 1.099512e+12
2^(-20)
#> [1] 9.536743e-07En este ejemplo, 1.099512e+12 representa el número 1.099512·1012, es decir, 1099512000000, y 9.536743e-07 representa el número 9.536743· 10-7, es decir,
0.0000009536743. Como muestra el ejemplo siguiente, no es necesario que un número sea especialmente grande o pequeño
para que R lo escriba en notación científica: basta que esté rodeado de otros números en esa notación.
c(2^40,2^(-20),17/3) #La función c sirve para definir vectores
#> [1] 1.099512e+12 9.536743e-07 5.666667e+00Este 5.666667e+00 representa el número 5.666667·100, es decir,
5.666667.
R dispone, entre muchas otras, de las funciones numéricas de la lista siguiente:
Valor absoluto, \(|x|\):
abs(x)Raíz cuadrada, \(\sqrt(x)\):
sqrt(x)Exponencial, \(e^x\):
exp(x)Logaritmo neperiano, \(\ln(x)\):
log(x)Logaritmo decimal, \(\log_{10}(x)\):
log10(x)Logaritmo binario, \(\log_2(x)\):
log2(x)Logaritmo en base \(a\), \(\log_a(x)\):
log(x,a)Factorial, \(n!\):
factorial(n)Número combinatorio, \(\binom{n}{m}\):
choose(n,m)Seno, \(\sin(x)\):
sin(x)Coseno, \(\cos(x)\):
cos(x)Tangente, \(\tan(x)\):
tan(x)Arcoseno, \(\arcsin(x)\):
asin(x)Arcocoseno, \(\arccos(x)\):
acos(x)Arcotangente, \(\arctan(x)\):
atan(x)
Recordad que el valor absoluto \(|x|\) de un número \(x\) se obtiene tomando \(x\) sin signo: \(|-8|=|8|=8\). Recordad también que el factorial \(n!\) de \(n\), es el producto \[ n!=n\cdot (n-1)\cdot (n-2) \cdots 3\cdot 2 \cdot 1 \] (con el convenio de que \(0!=1\)), y es igual al número de maneras posibles de ordenar una lista de \(n\) objetos diferentes (su número de permutaciones), y que el número combinatorio \(\binom{n}{m}\), con \(m\leqslant n\), es \[ \binom{n}{m}=\frac{n!}{m!\cdot (n-m)!}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m(m-1)(m-2)\cdots 2\cdot 1}, \] y es igual al número de maneras posibles de escoger un subconjunto de \(m\) elementos de un conjunto de \(n\) objetos diferentes.
Las funciones de R se aplican a sus argumentos introduciéndolos siempre entre paréntesis. Si la función se tiene que aplicar a más de un argumento, éstos se tienen que especificar en el orden que toque y separándolos mediante comas; R no tiene en cuenta los espacios en blanco alrededor de las comas. Veamos algunos ejemplos:
sqrt(4)
#> [1] 2
sqrt(8)-8^(1/2)
#> [1] 0
log10(8)
#> [1] 0.90309
log(8)/log(10)
#> [1] 0.90309
7^log(2,7) #7 elevado al logaritmo en base 7 de 2 es 2
#> [1] 210! #R no entiende esta expresión10! #R no entiende esta expresiónfactorial(10)
#> [1] 3628800
exp(sqrt(8))
#> [1] 16.91883
choose(5,3) #Núm. de subconjuntos de 3 elementos de un conjunto de 5
#> [1] 10
choose(3,5) #Núm. de subconjuntos de 5 elementos de un conjunto de 3
#> [1] 0R entiende que los argumentos de las funciones sin, cos y tan están en radianes. Si queremos aplicar una de estas funciones a un número de grados, podemos traducir los grados a radianes multiplicándolos por \(\pi/180\).
De manera similar, los resultados de asin, acos y atan también están en radianes, y se pueden traducir a grados
multiplicándolos por \(180/\pi\).
cos(60) #Coseno de 60 radianes
#> [1] -0.952413
cos(60*pi/180) #Coseno de 60 grados
#> [1] 0.5
acos(0.5) #Arcocoseno de 0.5 en radianes
#> [1] 1.047198
acos(0.5)*180/pi #Arcocoseno de 0.5 en grados
#> [1] 60
acos(2)
#> [1] NaNEste último NaN (acrónimo de Not a Number) significa que el resultado no existe; en efecto, \(\mathrm{arccos}(2)\) no existe como número real, ya que \(\cos(x)\) siempre pertenece al intervalo \([-1,1]\).
Ya hemos visto que R dispone del signo pi para representar el número real \(\pi\). En cambio,
no tiene ningún signo para indicar la constante de Euler \(e\), y hay que emplear exp(1).
2*exp(1) #2·e
#> [1] 5.436564
exp(pi)-pi^exp(1) #e^pi-pi^e
#> [1] 0.6815349Para terminar esta sección, observad el resultado siguiente:
sqrt(2)^2-2
#> [1] 4.440892e-16R opera numéricamente con \(\sqrt{2}\), no formalmente, y por eso no da como resultado de \((\sqrt{2})^2-2\) el valor 0 exacto, sino el número pequeñísimo 4.440892·10-16; de hecho, R trabaja internamente con una precisión de aproximadamente 16 cifras decimales, por lo que no siempre podemos esperar resultados exactos. Si necesitáis trabajar de manera exacta con más cifras significativas, os recomendamos usar las funciones del paquete Rmpfr.
2.2 Cifras significativas y redondeos
En cada momento, R decide cuántas cifras muestra de un número según el contexto. También podemos especificar este número de cifras para toda una sesión, entrándolo en lugar de los puntos suspensivos en options(digits=...). Hay que tener presente que ejecutar esta instrucción no cambiará la precisión de los cálculos, sólo cómo se muestran los resultados.
Si queremos conocer una cantidad específica n de cifras significativas de un número x, podemos emplear la función
print(x, n)Observad su efecto:
sqrt(2)
#> [1] 1.414214
print(sqrt(2), 20)
#> [1] 1.4142135623730951
print(sqrt(2), 2)
#> [1] 1.4
2^100
#> [1] 1.267651e+30
print(2^100, 15)
#> [1] 1.26765060022823e+30
print(2^100, 5)
#> [1] 1.2677e+30El número máximo de cifras que podemos pedir con print es 22; si pedimos más, R nos dará un mensaje de error.
print(sqrt(2), 22)
#> [1] 1.4142135623730951print(sqrt(2), 23)
#> Error in print.default(sqrt(2), 23): invalid printing digits 23Por otro lado, hay que tener en cuenta que, como ya hemos comentado, R trabaja con una precisión de unas 16 cifras decimales y por lo tanto los dígitos más allá de esta precisión pueden ser incorrectos. Por ejemplo, si le pedimos las 22 primeras cifras de \(\pi\), obtenemos el resultado siguiente:
print(pi, 22)
#> [1] 3.1415926535897931En cambio, \(\pi\) vale en realidad 3.141592653589793238462…, lo que significa que el valor que da R es erróneo a partir de la decimosexta cifra decimal.
La función print permite indicar las cifras que queremos leer, pero no sirve para especificar las cifras decimales con las que queremos trabajar.
Para redondearun número \(x\) a una cantidad específica n de cifras decimales, y trabajar solamente con esas cifras, hay que usar la función
round(x, n)La diferencia entre los efectos de print y round consiste en que print(sqrt(2), 4) es igual a \(\sqrt{2}\), pero R sólo muestra sus primeras 4 cifras, 1.414, mientras que round(sqrt(2), 3) es igual a 1.414. Veamos algunos ejemplos
print(sqrt(2), 4)
#> [1] 1.414
print(sqrt(2), 4)^2
#> [1] 1.414
#> [1] 2
1.414^2
#> [1] 1.999396
round(sqrt(2), 3)
#> [1] 1.414
round(sqrt(2), 3)^2
#> [1] 1.999396En caso de empate, R redondea al valor que termina en cifra par, siguiendo la regla de redondeo en caso de empate recomendada por el estándar IEEE 754 para aritmética en coma flotante.
round(2.25, 1)
#> [1] 2.2
round(2.35, 1)
#> [1] 2.4¿Qué pasa si no se indica el número de cifras en el argumento de round?
round(sqrt(2))
#> [1] 1
round(sqrt(2), 0)
#> [1] 1Al entrar round(sqrt(2)), R ha entendido que el número de cifras decimales al que queríamos redondear era 0. Esto significa que 0 es el valor por defecto de este parámetro. No es necesario especificar los valores por defecto de los parámetros de una función, y para saber cuáles son, hay que consultar su Ayuda. Así, por ejemplo, la Ayuda de round indica que su sintaxis es
round(x, digits=0)donde el valor de digits ha de ser un número entero que indique el número de cifras decimales. Esta sintaxis significa que el valor por defecto del parámetro digits es 0.
Escribir digits= en el argumento para especificar el número de cifras decimales es optativo, siempre que mantengamos el orden de los argumentos indicado en la Ayuda: en este caso, primero el número y luego las cifras. Este es el motivo por el que podemos escribir
round(sqrt(2), 1) en lugar de round(sqrt(2), digits=1). Si cambiamos el orden de los argumentos, entonces sí que hay que especificar el nombre del parámetro, como muestra el siguiente ejemplo:
round(digits=3, sqrt(2))
#> [1] 1.414
round(3, sqrt(2))
#> [1] 3En la lista de funciones ya vimos una función de dos argumentos que toma uno por defecto: log. Su sintaxis completa es log(x, base=...), y si no especificamos la base, toma su valor por defecto, \(e\), y calcula el logaritmo neperiano.
La función round(x) redondea \(x\) al valor entero más cercano (y en caso de empate, al que termina en cifra par). R también dispone de otras funciones que permiten redondear a números enteros en otros sentidos específicos:
floor(x)redondea \(x\) a un número entero por defecto, dando el mayor número entero menor o igual que \(x\), que denotamos por \(\lfloor x\rfloor\).ceiling(x)redondea \(x\) a un número entero por exceso, dando el menor número entero mayor o igual que \(x\), que denotamos por \(\lceil x\rceil\).trunc(x)da la parte entera de \(x\), eliminando la parte decimal: es lo que se llama truncar \(x\) a un entero.
floor(8.3) #El mayor entero menor o igual que 8.3
#> [1] 8
ceiling(8.3) #El menor entero mayor o igual que 8.3
#> [1] 9
trunc(8.3) #La parte entera de 8.3
#> [1] 8
round(8.3) #El entero más cercano a 8.3
#> [1] 8
floor(-3.7) #El mayor entero menor o igual que -3.7
#> [1] -4
ceiling(-3.7) #El menor entero mayor o igual que -3.7
#> [1] -3
trunc(-3.7) #La parte entera de -3.7
#> [1] -3
round(-3.7) #El entero más cercano a -3.7
#> [1] -42.3 Definición de variables
R funciona mediante objetos, estructuras de diferentes tipos que sirven para realizar diferentes tareas. Una variable es un tipo de objeto que sirve para guardar datos.
Por ejemplo, si queremos crear una variable x que contenga el valor \(\pi^2\), podemos escribir:
x=pi^2Al entrar esta instrucción, R creará el objeto x y le asignará el valor que hemos especificado.
En general, se puede crear una variable y asignarle un valor, o asignar un nuevo valor a una variable definida anteriormente, mediante
la construcción
nombre_de_la_variable=valorTambién se puede conectar el nombre de la variable con el valor por medio de una flecha -> o <-, compuesta de un guión y un signo de desigualdad, de manera que el sentido de la flecha vaya del valor a la variable; por ejemplo, las tres primeras instrucciones siguientes son equivalentes, y asignan el valor 2 a la variable \(x\), mientras que las dos últimas son incorrectas:
x=2
x<-2
2->x2=x## Error in 2 = x: lado izquierdo de la asignación inválida (do_set)2<-x## Error in 2 <- x: lado izquierdo de la asignación inválida (do_set)Nosotros usaremos sistemáticamente el signo = para hacer asignaciones.
Se puede usar como nombre de una variable cualquier palabra que combine letras mayúsculas y minúsculas (R las distingue), con acentos o sin (aunque os recomendamos que no uséis letras acentuadas, ya que se pueden importar mal de un ordenador a otro), dígitos (0,…, 9), puntos . y guiones bajos _, siempre que empiece con una letra o un punto. Aunque no esté prohibido, es muy mala idea redefinir nombres que ya sepáis que tienen significado para R, como por ejemplo pi o sqrt.
Como podéis ver en las instrucciones anteriores y en las que siguen, cuando asignamos un valor a una variable, R no da ningún resultado; después podemos usar el nombre de la variable para referirnos al valor que representa. Es posible asignar varios valores a una misma variable en una misma sesión: naturalmente, en cada momento R empleará el último valor asignado. Incluso se puede redefinir el valor de una variable usando en la nueva definición su valor actual.
x=5
x^2
#> [1] 25
x=x-2 #Redefinimos x como su valor actual menos 2
x
#> [1] 3
x^2
#> [1] 9
x=sqrt(x) #Redefinimos x como la raíz cuadrada de su valor actual
x
#> [1] 1.7320512.4 Definición de funciones
A menudo querremos definir alguna función. Para ello tenemos que usar, en vez de simplemente =, una construcción especial:
nombre_de_la_función=function(variables){definición}Una vez definida una función, la podemos aplicar a valores de la variable o variables.
Veamos un ejemplo. Vamos a llamar \(f\) a la función \(x^2-2^x\), usando \(x\) como variable, y a continuación la aplicamos a \(x=30\):
f=function(x){x^2-2^x}
f(30)
#> [1] -1073740924Conviene que os acostumbréis a escribir la fórmula que define la función entre llaves {...}. A veces es necesario y a veces no, pero no vale la pena discutir cuándo.
El nombre de la variable se indica dentro de los paréntesis que siguen al function. En el ejemplo anterior, la variable era \(x\), y por eso hemos escrito =function(x). Si hubiéramos querido definir la función con variable \(t\), habríamos usado =function(t) (y, naturalmente, habríamos escrito la fórmula que define la función con la variable \(t\)):
f=function(t){t^2-2^t}Se pueden definir funciones de dos o más variables con function, declarándolas todas. Por ejemplo, para definir la función \(f(x,y)=e^{(2x-y)^2}\), tenemos que entrar
f=function(x, y){exp((2*x-y)^2)}y ahora ya podemos aplicar esta función a pares de valores:
f(0, 1)
#> [1] 2.718282
f(1, 0)
#> [1] 54.59815Las funciones no tienen por qué tener como argumentos o resultados sólo números reales: pueden involucrar vectores, matrices, tablas de datos, etc. Y se pueden definir por medio de secuencias de instrucciones, no sólo mediante fórmulas numéricas directas; en este caso, hay que separar las diferentes instrucciones con signos de punto y coma o escribir cada instrucción en una nueva línea. Ya iremos viendo ejemplos a medida que avance el curso.
En cada momento se pueden saber los objetos (por ejemplo, variables y funciones) que se han definido en la sesión hasta ese momento entrando
la instrucción ls() o consultando la pestaña Environment.
Para borrar la definición de un objeto, hay que aplicarle la función rm.
Si se quiere hacer limpieza y borrar de golpe las definiciones de todos los objetos que se han definido hasta el momento,
se puede emplear la instrucción rm(list=ls()) o usar el botón con el icono de la escoba de la barra superior de la pestaña Environment.
rm(list=ls()) #Borramos todas las definiciones
f=function(t){t^2-2^t}
a=1
a
#> [1] 1
ls()
#> [1] "a" "f"
rm(a)
ls()
#> [1] "f"a
#> Error in eval(expr, envir, enclos): objeto 'a' no encontrado2.5 Números complejos (opcional)
Hasta aquí, hemos operado con números reales. Con R también podemos operar con números complejos. Los signos para las operaciones son los mismos que en el caso real.
(2+5i)*3
#> [1] 6+15i
(2+5i)*(3+7i)
#> [1] -29+29i
(2+5i)/(3+7i)
#> [1] 0.7068966+0.0172414iFijaos en que cuando entramos en R un número complejo escrito en forma binomial \(a+bi\), no escribimos un * entre la i y su coeficiente; de hecho, no hay que escribirlo :
2+5*i
#> Error in eval(expr, envir, enclos): objeto 'i' no encontradoPor otro lado, si el coeficiente de \(i\) es 1 o -1, hay que escribir el 1: por ejemplo, \(3-i\) se tiene que escribir 3-1i. Si no lo hacemos, R da un mensaje de error.
(3+i)*(2-i)
#> Error in eval(expr, envir, enclos): objeto 'i' no encontrado(3+1i)*(2-1i)
#> [1] 7-1iLos complejos que tienen como parte imaginaria un número entero o un racional escrito en forma decimal se pueden entrar directamente en forma binomial, como lo hemos hecho hasta ahora. Para definir números complejos más… complejos, se puede usar la función
complex(real=..., imaginary=...)Veamos un ejemplo:
1+2/3i #Esto en realidad es 1 más 2 partido por 3i
#> [1] 1-0.666667i1+(2/3)i ## Error in eval(expr, envir, enclos): objeto 'i' no encontradocomplex(real=1, imaginary=2/3)
#> [1] 1+0.666667iz=1+sqrt(2)i## Error in eval(expr, envir, enclos): objeto 'i' no encontrado
z=complex(real=1, imaginary=sqrt(2))
z
#> [1] 1+1.414214iComo sabéis, los números complejos se inventaron para poder trabajar con raíces cuadradas de números negativos. Ahora bien, por defecto, cuando calculamos la raíz cuadrada de un número negativo R no devuelve un número complejo, sino que se limita a avisarnos de que no existe.
sqrt(-3)
#> Warning in sqrt(-3): Se han producido NaNs
#> [1] NaNSi queremos que R produzca un número complejo al calcular la raíz cuadrada de un número negativo, tenemos que especificar que este número negativo es un número complejo. La mejor manera de hacerlo es declarándolo como complejo aplicándole la función as.complex
sqrt(as.complex(-3))
#> [1] 0+1.732051iLa mayoría de las funciones que hemos dado para los números reales admiten extensiones para números complejos, y con R se calculan con la misma función. Ahora no entraremos a explicar cómo se definen estas extensiones, sólo lo comentamos por si sabéis qué hacen y os interesa calcularlas.
sqrt(2+3i)
#> [1] 1.674149+0.895977i
exp(2+3i)
#> [1] -7.31511+1.042744i
sin(2+3i)
#> [1] 9.154499-4.168907i
acos(as.complex(2)) #El arcocoseno de 2 es un número complejo
#> [1] 0+1.316958iLa raíz cuadrada merece un comentario. Naturalmente, sqrt(2+3i) calcula un número complejo \(z\) tal que \(z^2=2+3i\). Como ocurre con los números reales, todo número complejo diferente de 0 tiene dos raíces cuadradas, y una se obtiene multiplicando la otra por -1.
R da como raíz cuadrada de un número real la positiva, y como raíz cuadrada de un complejo la que tiene parte real positiva, y si su parte real es 0, la que tiene parte imaginaria positiva.
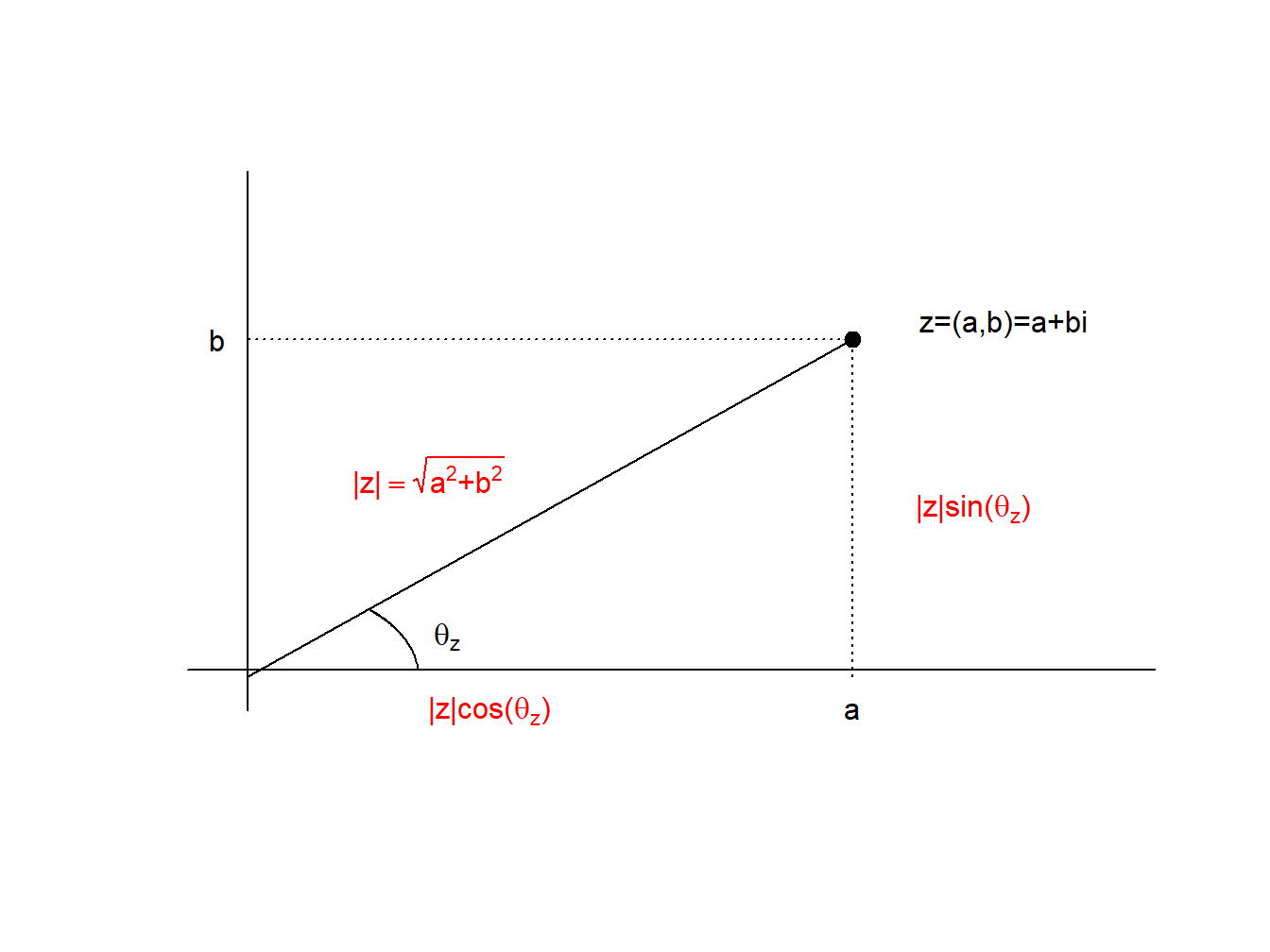
Figura 2.1: Interpretación geométrica de los números complejos.
Un número complejo \(z=a+bi\) se puede representar como el punto \((a,b)\) del plano cartesiano \(\mathbb{R}^2\). Esto permite asociarle dos magnitudes geométricas: véase la Figura 2.1
El módulo de \(z\), que denotaremos por \(|z|\), es la distancia euclídea de \((0,0)\) a \((a,b)\): \[ |z|=\sqrt{a^2+b^2}. \] Si \(z\in \mathbb{R}\), su módulo coincide con su valor absoluto; en particular, si \(z=0\), su módulo es \(0\), y es el único número complejo de módulo 0.
El argumento de \(z\) (para \(z\neq 0\)), que denotaremos por \(\theta_{z}\), es el ángulo que forman el semieje positivo de abscisas y el vector que va de \((0,0)\) a \((a,b)\). Este ángulo está determinado por las ecuaciones \[ \cos (\theta_{z})=\frac{a}{\sqrt{a^2+b^2}},\qquad \sin (\theta_{z})=\frac{b}{\sqrt{a^2+b^2}}. \]
R sabe calcular módulos y argumentos de números complejos. Los argumentos los da en radianes y dentro del intervalo \((-\pi,\pi]\). En general, R dispone de las funciones básicas específicas para números complejos de la lista siguiente:
- Parte real:
Re - Parte imaginaria:
Im - Módulo:
Mod - Argumento:
Arg - Conjugado:
Conj
Recordad que el conjugado de un número complejo \(z=a+bi\) es \(\overline{z}=a-bi\). Veamos algunos ejemplos de uso de estas funciones:
Re(4-7i)
#> [1] 4
Im(4-7i)
#> [1] -7
Mod(4-7i)
#> [1] 8.062258
Arg(4-7i)
#> [1] -1.05165
Conj(4-7i)
#> [1] 4+7iEl módulo y el argumento de un número complejo \(z\neq 0\) lo determinan de manera única, porque \[ z=|z|\big(\cos(\theta_z)+\sin(\theta_z)i\big). \] Si queremos definir un número complejo mediante su módulo y argumento, no hace falta utilizar esta igualdad: podemos usar la instrucción
complex(modulus=..., argument=...)Por ejemplo:
z=complex(modulus=3, argument=pi/5)
z
#> [1] 2.427051+1.763356i
Mod(z)
#> [1] 3
Arg(z)
#> [1] 0.6283185
pi/5
#> [1] 0.62831852.6 Guía rápida
- Signos de operaciones aritméticas:
- Suma:
+ - Resta:
- - Multiplicación:
* - División:
/ - Potencia:
^ - Cociente entero:
%/% - Resto de la división entera:
%%
- Suma:
- Funciones numéricas:
- Valor absoluto:
abs - Raíz cuadrada:
sqrt - Exponencial de base e:
exp - Logaritmo neperiano:
log - Logaritmo decimal:
log10 - Logaritmo binario:
log2 - Logaritmo en base \(a\):
log(...,base=a) - Factorial:
factorial - Número combinatorio:
choose - Seno:
sin - Coseno:
cos - Tangente:
tan - Arcoseno:
asin - Arcocoseno:
acos - Arcotangente:
atan
- Valor absoluto:
pies el número \(\pi\).print(x, n)muestra el valor de \(x\) con \(n\) cifras significativas.round(x, n)redondea el valor de \(x\) a \(n\) cifras decimales.floor(x)redondea \(x\) a un número entero por defecto.ceiling(x)redondea \(x\) a un número entero por exceso.trunc(x)da la parte entera de \(x\).variable=valorasigna elvalora lavariable. Otras construcciones equivalentes sonvariable<-valoryvalor->variable.función=function(variables){instrucciones}define lafunciónde variables las especificadas entre los paréntesis mediante las instrucciones especificadas entre las llaves.ls()nos da la lista de objetos actualmente definidos.rmborra la definición del objeto u objetos a los que se aplica.rm(list=ls())borra las definiciones de todos los objetos que hayamos definido.complexse usa para definir números complejos que no se puedan entrar directamente en forma binomial. Algunos parámetros importantes:realeimaginary: sirven para especificar su parte real y su parte imaginaria.modulusyargument: sirven para especificar su módulo y su argumento.
as.complexconvierte un número real en complejo.- Funciones específicas para números complejos:
- Parte real:
Re - Parte imaginaria:
Im - Módulo:
Mod - Argumento:
Arg - Conjugado:
Conj
- Parte real:
2.7 Ejercicios
Test
En los tests, tenéis que entrar las respuestas sin dejar ningún espacio en blanco excepto los que se pidan explícitamente. Cuando os pidan que deis una instrucción de R, no tenéis que incluir la marca de inicio >. Del mismo modo, cuando os pidan que copiéis un resultado dado por R, no tenéis que incluir el [1].
(1) Dad una expresión para calcular \((2+7)8+\frac{5}{2}-3^6+8!\), con las operaciones escritas exactamente en el orden dado y sin paréntesis innecesarios, y a continuación, separado por un único espacio en blanco, copiad exactamente el resultado que ha dado R al evaluarla.
(2) Dad una expresión para calcular \(|\sin(\sqrt{2})-e^{\sqrt[5]{2}}|\), con las operaciones y funciones escritas exactamente en el orden dado, y a continuación, separado por un único espacio en blanco, copiad exactamente el resultado que ha dado R al evaluarla.
(3) Dad una expresión para calcular \(\sin(37^{\mathrm{o}})\), empleando la construcción explicada en esta lección para calcular funciones trigonométricas de ángulos dados en grados, y a continuación, separado por un único espacio en blanco, copiad exactamente el resultado que ha dado R al evaluarla.
(4) Dad una expresión para calcular \(3e-\pi\), con las operaciones escritas exactamente en la orden dado, y a continuación, separado por un único espacio en blanco, copiad exactamente el resultado que ha dado R al evaluarla.
(5) Dad una expresión para calcular \(e^{2/3}\) redondeado a 3 cifras decimales y a continuación, separado por un único espacio en blanco, copiad exactamente el resultado que ha dado R al evaluarla.
(6) En una sola línea, definid \(x\) como \(\sqrt{2}\) e \(y\) como \(\cos(3\pi)\) y calculad \(\ln(x^{y})\); separad las tres instrucciones con puntos y comas seguidos de un único espacio en blanco. A continuación, separado por un espacio en blanco (sin punto y coma), copiad exactamente el resultado que ha dado R al evaluar esta secuencia de instrucciones.
(7) Corresponde el número en notación científica 3.3333e10 al número 33333000000? Tenéis que contestar SI (sin acento) o NO.
Ejercicio
Si hubiéramos empezado a contar segundos a partir de las 12 campanadas que marcaron el inicio de 2015, ¿qué día de qué año llegaríamos a los 250 millones de segundos? ¡Cuidado con los años bisiestos!
Respuestas al test
(1) (2+7)*8+5/2-3^6+factorial(8) 39665.5
(2) abs(sin(sqrt(2))-exp(2^(1/5))) 2.166319
También sería correcto abs(sin(2^(1/2))-exp(2^(1/5))) 2.166319
(3) sin(37*pi/180) 0.601815
(4) 3*exp(1)-pi 5.013253
(5) round(exp(2/3),3) 1.948
(6) x=sqrt(2); y=cos(3*pi); log(x^y) -0.3465736
(7) SI