Lección 3 Un aperitivo: Introducción a la regresión lineal

En muchos libros de texto y artículos científicos encontraréis gráficos donde una línea recta o algún otro tipo de curva se ajusta a una serie de observaciones representadas por medio de puntos en el plano. La situación en general es la siguiente. Supongamos que tenemos una serie de puntos del plano cartesiano $\mathbb{R}^2$, \[ (x_1,y_1), (x_2,y_2),\ldots,(x_n,y_n), \] que representan pares de observaciones de dos variables numéricas: por ejemplo, $x=$ año e $y=$ población, o $x=$ longitud de una rama e $y=$ número de hojas en la rama. Queremos describir cómo depende la variable dependiente $y$ de la variable independiente $x$ a partir de estas observaciones. Para ello, buscaremos una función $y=f(x)$ cuya gráfica se aproxime lo máximo posible a los puntos $(x_i,y_i)_{i=1,\ldots,n}$. Esta función nos dará un modelo matemático del comportamiento de las observaciones realizadas que nos permitirá entender mejor los mecanismos que relacionan las variables estudiadas o hacer predicciones sobre futuras observaciones.

Una primera opción, y la más sencilla, es estudiar si los puntos $(x_i,y_i)_{i=1,\ldots,n}$ satisfacen una relación lineal. En este caso, se busca la recta de ecuación $y=b_1x+b_0$, con $b_0,b_1\in \mathbb{R}$, que aproxime mejor los puntos dados, en el sentido de que la suma de los cuadrados de las diferencias entre los valores $y_i$ y sus aproximaciones $b_1x_i+b_0$, \[ \sum_{i=1}^n (y_i-(b_1x_i+b_0))^2, \] sea mínima. A esta recta $y=b_1x+b_0$ se la llama recta de regresión por mínimos cuadrados; para abreviar, aquí la llamaremos simplemente recta de regresión, porque es la única que estudiaremos por ahora.

El objetivo de esta lección es ilustrar el uso de R mediante el cálculo de esta recta de regresión. Para ello, introduciremos algunas funciones de R que ya explicaremos con más detalle en otras lecciones. Utilizaremos también transformaciones logarítmicas para tratar casos en los que los puntos dados se aproximen mejor mediante una función potencial o exponencial.

3.1 Cálculo de rectas de regresión

Consideremos la Tabla 3.1, que da la altura media de los niños a determinadas edades. Los datos se han extraído de http://www.cdc.gov/growthcharts/clinical_charts.htm. Queremos determinar a partir de estos datos si hay una relación lineal entre la edad y la altura media de los niños.

Tabla 3.1: Alturas medias de niños por edad.
edad (años)	altura (cm)
1	76.11
2	86.45
3	95.27
5	109.18
7	122.03
9	133.73
11	143.73
13	156.41

Cuando tenemos una serie de observaciones emparejadas como las de esta tabla, la manera natural de almacenarlas en R es mediante una tabla de datos, un data frame en el argot de R. Aunque en este ejemplo concreto no sería necesario, lo haremos así para que empecéis a acostumbraros. La ventaja de tener los datos organizados en forma de data frame es que con ellos luego se pueden hacer muchas más cosas. Estudiaremos en detalle los data frames en la Lección 6.

Para crear este data frame, en primer lugar guardaremos cada fila de la Tabla 3.1 como un vector, es decir, como una lista ordenada de números, y le pondremos un nombre adecuado. Para definir un vector, podemos aplicar la función c a la secuencia ordenada de números, separados por comas:

edad=c(1,2,3,5,7,9,11,13)
altura=c(76.11,86.45,95.27,109.18,122.03,133.73,143.73,156.41)
edad
#> [1]  1  2  3  5  7  9 11 13
altura
#> [1]  76.11  86.45  95.27 109.18 122.03 133.73 143.73 156.41

Ahora vamos a construir un data frame de dos columnas, una para la edad y otra para la altura, y lo llamaremos datos1. Estas columnas serán las variables de nuestra tabla de datos. Para organizar diversos vectores de la misma longitud en un data frame, podemos aplicar la función data.frame a los vectores:

datos1=data.frame(edad, altura)
datos1
#>   edad altura
#> 1    1  76.11
#> 2    2  86.45
#> 3    3  95.27
#> 4    5 109.18
#> 5    7 122.03
#> 6    9 133.73
#> 7   11 143.73
#> 8   13 156.41

Observad que las filas del data frame resultante corresponden a los pares (edad, altura) de la Tabla 3.1.

Al analizar unos datos, siempre es conveniente empezar con una representación gráfica que nos permita hacernos una idea de sus características. En este caso, lo primero que haremos será dibujar los pares (edad,altura) usando la función plot. Esta función tiene muchos parámetros que permiten mejorar el resultado, pero ya los veremos al estudiarla en detalle en la Lección 7. Por ahora nos conformamos con un gráfico básico de estos puntos que nos muestre su distribución.

Dada una familia de puntos $(x_n,y_n)_{n=1,\ldots,k}$, si llamamos x al vector $(x_n)_{n=1,\ldots,k}$ de sus abscisas e y al vector $(y_n)_{n=1,\ldots,k}$ de sus ordenadas, podemos obtener el gráfico de los puntos $(x_n,y_n)_{n=1,\ldots,k}$ mediante la instrucción

plot(x, y)

Si los vectores x e y son, en este orden, la primera y la segunda columna de un data frame de dos variables, como es nuestro caso, es suficiente aplicar la función plot al data frame. Así, por ejemplo, para dibujar el gráfico de la Figura 3.1 de los puntos $(\mathrm{edad}_n,\textrm{altura}_n)_{n=1,\ldots,8}$, basta entrar la siguiente instrucción:

plot(datos1)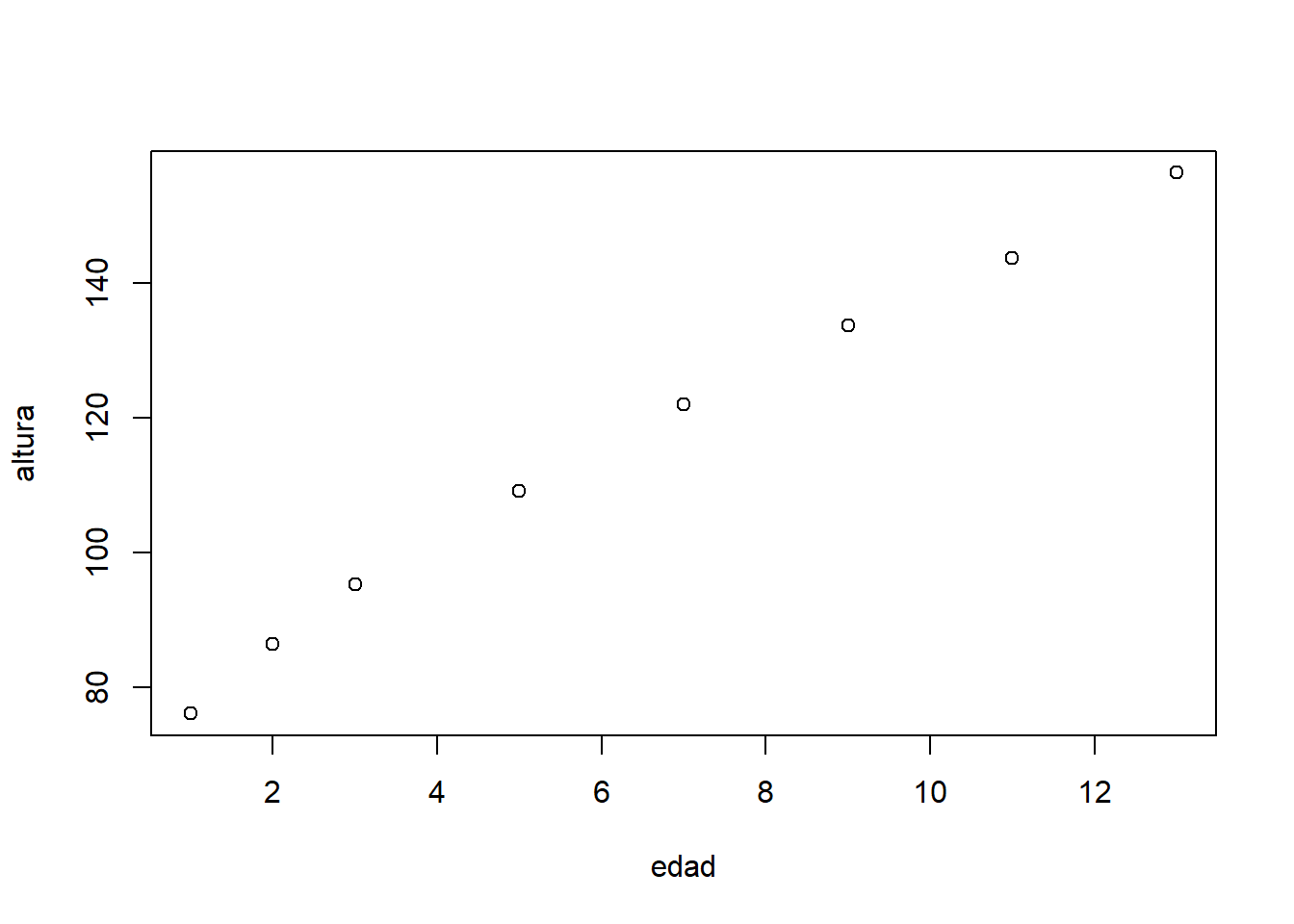

Figura 3.1: Representación gráfica de la altura media de los niños a determinadas edades.

Al ejecutar esta instrucción en la consola de Rstudio, el gráfico resultante se abrirá en la pestaña Plots, y en él se puede observar a simple vista que nuestros puntos siguen aproximadamente una recta. Vamos a calcular ahora su recta de regresión.

Dada una familia de puntos $(x_n,y_n)_{n=1,\ldots,k}$, si llamamos x al vector $(x_n)_{n=1,\ldots,k}$ de sus abscisas e y al vector $(y_n)_{n=1,\ldots,k}$ de sus ordenadas, su recta de regresión se calcula con R por medio de la instrucción

lm(y~x)

Fijaos en la sintaxis: dentro del argumento de lm, primero va el vector y, seguido del vector x conectado a y por una tilde ~. Para R, esta tilde significa en función de: es decir, lm(y~x) significa la recta de regresión de $y$ en función de $x$. Para obtener este signo, los usuarios de Windows y Linux tienen que pulsar Ctrl+Alt+4 seguido de un espacio en blanco y los de Mac OS X con teclado español pueden pulsar Alt+Ñ seguido de un espacio en blanco.

Si los vectores y y x son dos columnas de un data frame, para calcular la recta de regresión de $y$ en función de $x$ podemos usar la instrucción

lm(y~x, data=nombre del data frame)

Así pues, para calcular la recta de regresión de los puntos $(\mathrm{edad}_n,\textrm{altura}_n)_{n=1,\ldots,8}$, entramos la siguiente instrucción:

lm(altura~edad, data=datos1)
#> 
#> Call:
#> lm(formula = altura ~ edad, data = datos1)
#> 
#> Coefficients:
#> (Intercept)         edad  
#>      73.968        6.493

El resultado que hemos obtenido significa que la recta de regresión tiene término independiente 73.968 (el punto donde la recta interseca al eje de las $y$) y el coeficiente de $x$ es 6.493 (el coeficiente de la variable edad). Es decir, es la recta \[ y=6.493x+73.968. \] Ahora la podemos superponer al gráfico anterior, empleando la función abline. Esta función permite añadir una recta al gráfico activo en la pestaña Plots. Por lo tanto, si no hemos cerrado el gráfico anterior, la instrucción

abline(lm(altura~edad, data=datos1))

le añade la recta de regresión, produciendo la Figura 3.2. Se ve a simple vista que, efectivamente, esta recta aproxima muy bien los datos.

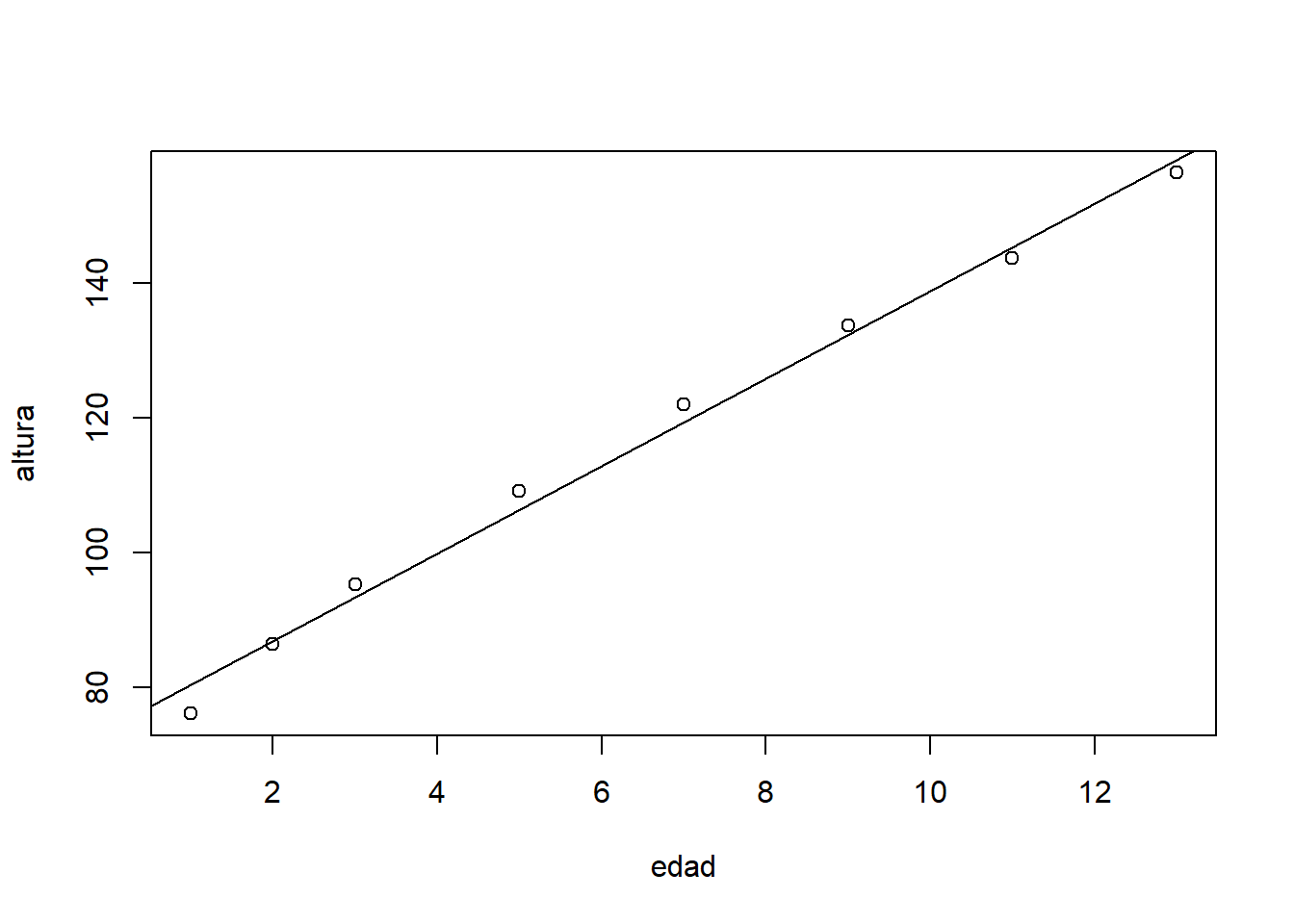
Figura 3.2: Ajuste mediante la recta de regresión de la altura media de los niños respecto de su edad.

Es importante tener presente que el análisis que hemos realizado de los pares de valores $(\mathrm{edad}_n, \textrm{altura}_n)_{n=1,\ldots,8}$ ha sido puramente descriptivo: hemos mostrado que estos datos son consistentes con una función lineal, pero no hemos demostrado que la altura media sea función aproximadamente lineal de la edad. Esto último requeriría una demostración matemática o un argumento biológico, no una simple comprobación numérica para una muestra pequeña de valores, que, al fin y al cabo, es lo único que hemos hecho.

Lo que sí que podemos hacer ahora es usar la relación lineal observada para predecir la altura media de los niños de otras edades. Por ejemplo, ¿qué altura media estimamos que tienen los niños de 10 años? Si aplicamos la regla

\[ \textrm{altura}=6.493\cdot \mathrm{edad}+73.968, \] podemos predecir que la altura media a los 10 años es 6.493·10+73.968=138.898, es decir, de unos 139 cm.

Para evaluar numéricamente si la relación lineal que hemos encontrado es significativa o no, podemos usar el coeficiente de determinación $R^2$. No explicaremos aquí cómo se define, ya lo haremos en la Lección ??. Es suficiente saber que es un valor entre 0 y 1 y que cuanto más se aproxime la recta de regresión al conjunto de puntos, más cercano será a 1. Por el momento, y como regla general, si este coeficiente de determinación $R^2$ es mayor que 0.9, consideraremos que el ajuste de los puntos a la recta es bueno.

Cuando R calcula la recta de regresión también obtiene este valor, pero no lo muestra si no se lo pedimos. Si queremos saber todo lo que ha calculado R con la función lm, tenemos que emplear la construcción summary(lm(...)). En general, la función summary aplicada a un objeto de R nos da un resumen de los contenidos de este objeto, resumen que depende de la clase de objeto que se trate.

Veamos cuál es el resultado de esta instrucción en nuestro ejemplo:

summary(lm(altura~edad, data=datos1))
#> 
#> Call:
#> lm(formula = altura ~ edad, data = datos1)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -4.351 -1.743  0.408  2.018  2.745 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  73.9681     1.7979   41.14 1.38e-08 ***
#> edad          6.4934     0.2374   27.36 1.58e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.746 on 6 degrees of freedom
#> Multiple R-squared:  0.992,  Adjusted R-squared:  0.9907 
#> F-statistic: 748.4 on 1 and 6 DF,  p-value: 1.577e-07

Por ahora podemos prescindir de casi toda esta información (en todo caso, observad que la columna Estimate nos da los coeficientes de la recta de regresión) y fijarnos sólo en el primer valor de la penúltima línea, Multiple R-squared. Éste es el coeficiente de determinación $R^2$ que nos interesa. En este caso ha sido de 0.992, lo que confirma que la recta de regresión aproxima muy bien los datos.

Podemos pedir a R que nos dé el valor Multiple R-squared sin tener que obtener todo el summary, añadiendo el sufijo $r.squared a la construcción summary(lm(...)).

summary(lm(altura~edad, data=datos1))$r.squared
#> [1] 0.9920466

Los sufijos que empiezan con $ suelen usarse en R para obtener componentes de un objeto. Por ejemplo, si al nombre de un data frame le añadimos el sufijo formado por $ seguido del nombre de una de sus variables, obtenemos el contenido de esta variable.

datos1$edad
#> [1]  1  2  3  5  7  9 11 13

Veamos otro ejemplo de cálculo de recta de regresión.

Ejemplo 3.1 Karl Pearson recopiló en 1903 las alturas de 1078 parejas formadas por un padre y un hijo. Hemos guardado en el url http://aprender.uib.es/Rdir/pearson.txt un fichero que contiene estas alturas. Si lo abrís en un navegador, veréis que es una tabla de dos columnas, etiquetadas Padres e Hijos (Figura 3.3). Cada fila contiene las alturas en pulgadas de un par Padre-Hijo.

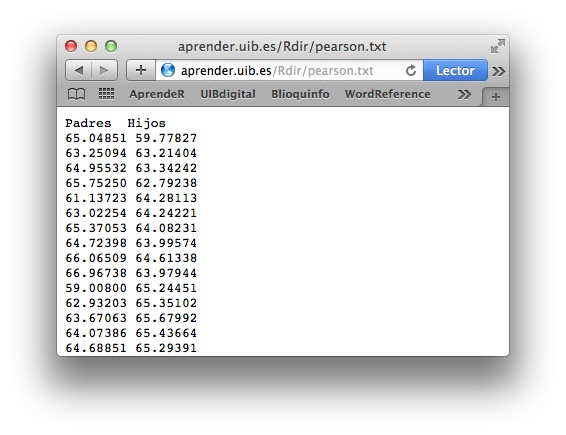
Figura 3.3: Vista en un navegador del fichero pearson.txt.

Vamos a usar estos datos para estudiar si hay dependencia lineal entre la altura de un hijo y la de su padre. Para ello, lo primero que haremos será cargarlos en un data frame. Esto se puede llevar a cabo de dos maneras:

Usando el menú Import Dataset de la pestaña Environment de la ventana superior derecha de RStudio, sobre el que volveremos en la Lección 6. Al pulsar sobre este menú, se nos ofrece la posibilidad de importar un fichero de diferentes maneras; en este ejemplo, vamos a usar From Text (readr)…, que es la adecuada para importar tablas de Internet. Al seleccionarla, se nos pide el url del fichero y se nos dan a escoger una serie de opciones donde podemos especificar el nombre del data frame que queremos crear, si el fichero tiene o no una primera fila con los nombres de las columnas, cuál es el signo usado para separar columnas, etc. Pulsando el botón Update podremos ver en el campo Data Preview de esta ventana de diálogo el aspecto del data frame que obtendremos con las opciones seleccionadas; se trata entonces de escoger las opciones adecuadas para que se cree la versión correcta del data frame. En el caso concreto de esta tabla pearson.txt, se tiene que seleccionar la casilla de First Row as Names y escoger el valor Whitespace en Delimiter (Figura 3.4). Al pulsar el botón Import, se importará el fichero en un data frame con el nombre especificado en el campo Name y se verá su contenido en la ventana de ficheros si se ha seleccionado la casilla Open Data Viewer.

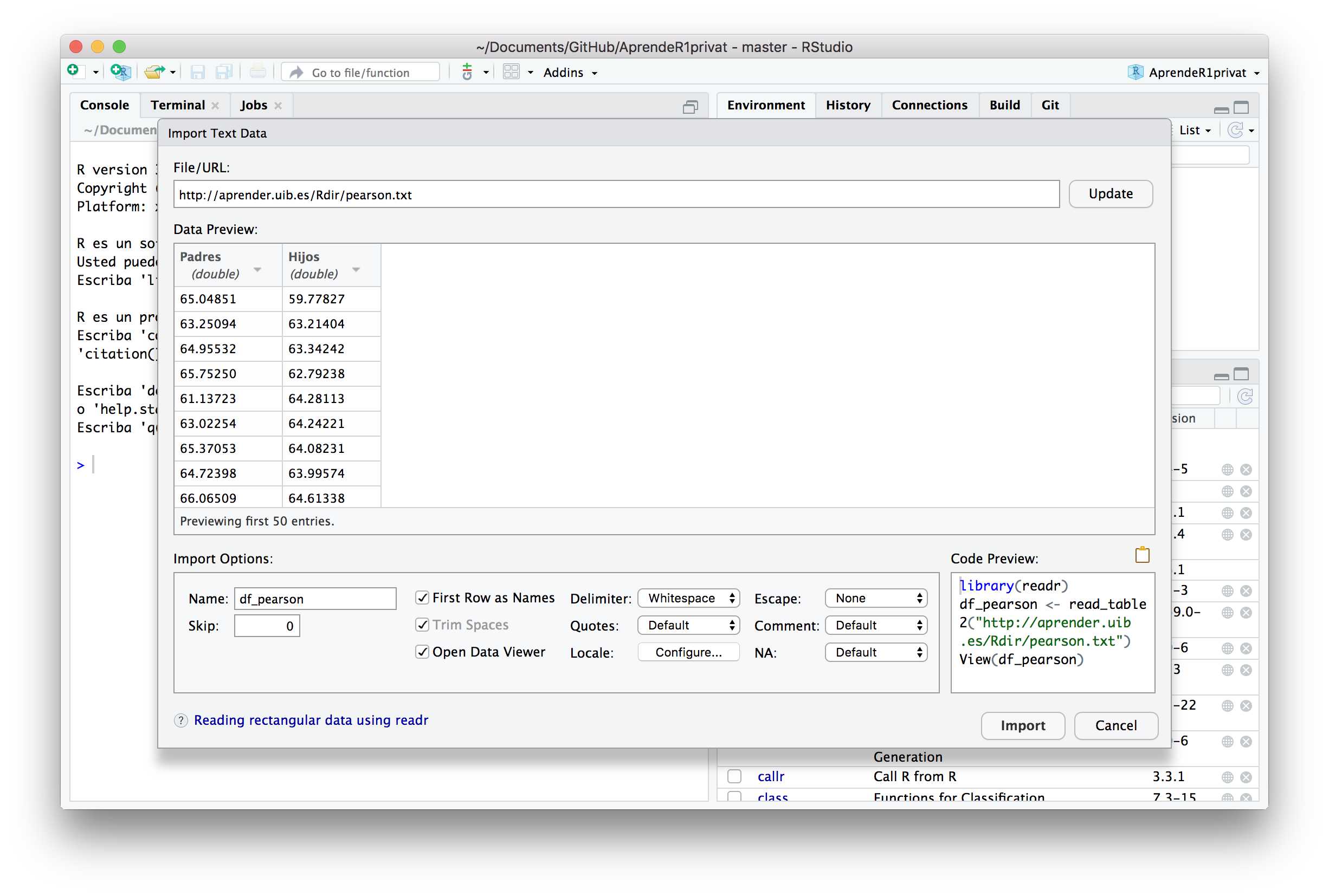
Figura 3.4: Opciones para guardar el fichero pearson.txt en un data frame llamado df_pearson usando el menú Import Dataset.

Usando la instrucción read.table, de la que también hablaremos en la Lección 6; por ahora simplemente hay que saber que se ha de aplicar al nombre del fichero entre comillas, si está en el directorio de trabajo, o a su url, también escrito entre comillas. Si además el fichero contiene una primera fila con los nombres de las columnas, hay que añadir el parámetro header=TRUE.

Así pues, para cargar esta tabla de datos concreta en un data frame llamado df_pearson, podemos usar el menú Import Dataset, o entrar la instrucción siguiente:

df_pearson=read.table("http://aprender.uib.es/Rdir/pearson.txt", header=TRUE)

En ambos casos, para comprobar que se ha cargado bien, podemos usar las funciones str, que muestra la estructura del data frame, y head, que muestra sus primeras filas.

str(df_pearson)
#> 'data.frame':    1078 obs. of  2 variables:
#>  $ Padres: num  65 63.3 65 65.8 61.1 ...
#>  $ Hijos : num  59.8 63.2 63.3 62.8 64.3 ...
head(df_pearson)
#>     Padres    Hijos
#> 1 65.04851 59.77827
#> 2 63.25094 63.21404
#> 3 64.95532 63.34242
#> 4 65.75250 62.79238
#> 5 61.13723 64.28113
#> 6 63.02254 64.24221

El resultado de str(df_pearson) nos dice que este data frame está formado por 1078 observaciones (filas) de dos variables (columnas) llamadas Padres e Hijos. El resultado de head(df_pearson) nos muestra sus primeras seis filas, que podemos comprobar que coinciden con las del fichero original mostrado en la Figura 3.3.

Calculemos la recta de regresión de las alturas de los hijos respecto de las de los padres: ahora las siguientes instrucciones:

lm(Hijos~Padres, data=df_pearson)
#> 
#> Call:
#> lm(formula = Hijos ~ Padres, data = df_pearson)
#> 
#> Coefficients:
#> (Intercept)       Padres  
#>     33.8866       0.5141
summary(lm(Hijos~Padres, data=df_pearson))$r.squared
#> [1] 0.2513401

Obtenemos la recta de regresión \[ y=33.8866+0.5141x, \] donde $y$ representa la altura de un hijo y $x$ la de su padre, y un coeficiente de determinación $R^2=0.25$, muy bajo. La regresión no es muy buena, como se puede observar en la Figura 3.5 que generamos con el código siguiente:

plot(df_pearson)
abline(lm(Hijos~Padres, data=df_pearson),col="red")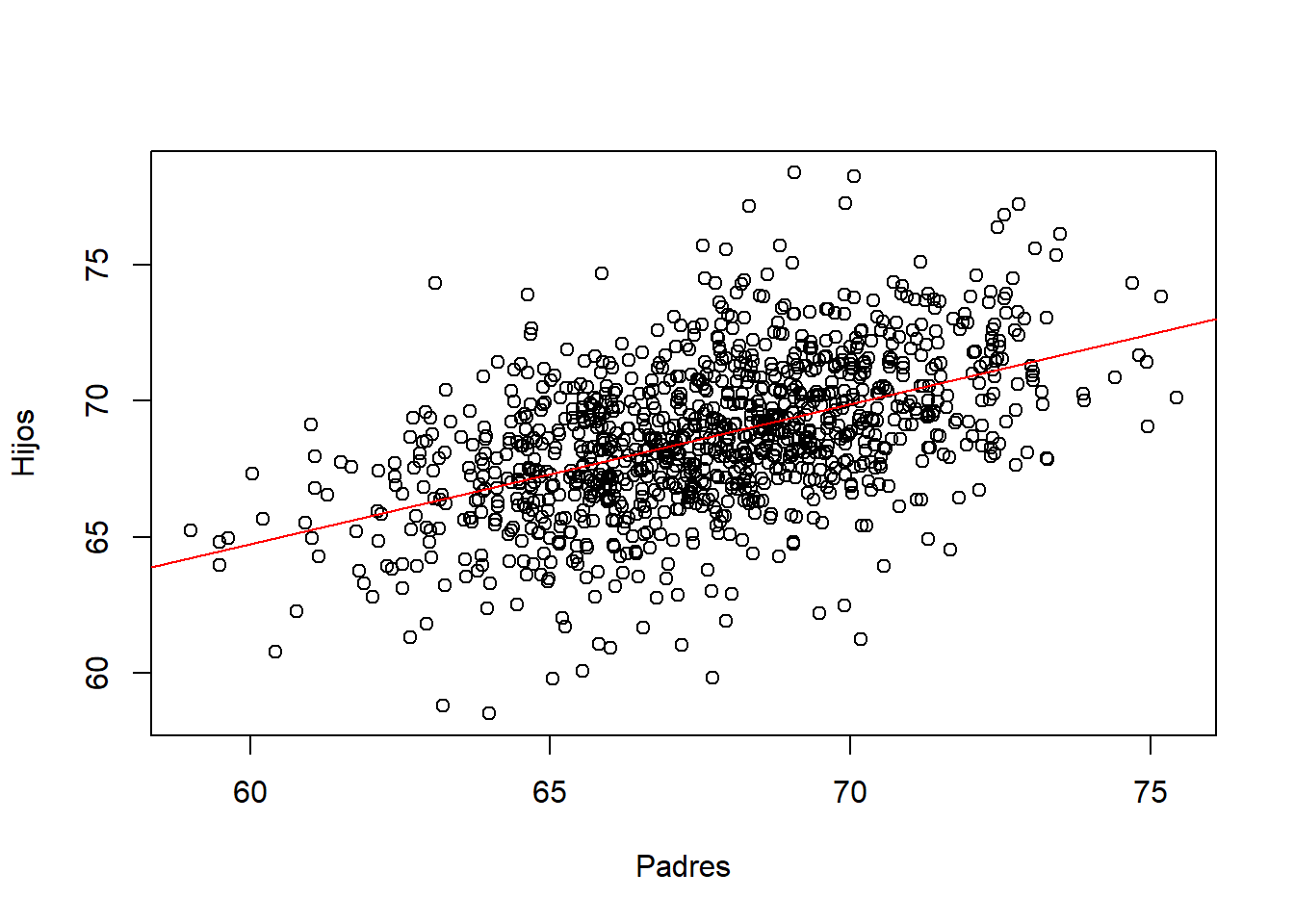

Figura 3.5: Representación gráfica de las alturas de los hijos en función de la de sus padres, junto con su recta de regresión.

Hemos usado el parámetro col="red" en el abline para que la recta de regresión sea roja y facilitar así su visualización en medio de la nube de puntos.

3.2 Rectas de regresión y transformaciones logarítmicas

La dependencia de un valor en función de otro no siempre es lineal. A veces podremos detectar otras dependencias (en concreto, exponenciales o potenciales) realizando un cambio de escala adecuado en el gráfico.

Cuando dibujamos un gráfico, lo normal es marcar cada eje de manera que la misma distancia entre marcas signifique la misma diferencia entre sus valores; por ejemplo, en el gráfico de la Figura 3.1, las marcas sobre cada uno de los ejes están igualmente espaciadas, de manera que entre cada par de marcas consecutivas en el eje de abscisas hay una diferencia de 2 años y entre cada par de marcas consecutivas en el eje de ordenadas hay una diferencia de 20 cm. Decimos entonces que los ejes están en escala lineal. Pero a veces es conveniente dibujar algún eje en escala logarítmica, situando las marcas de tal manera que la misma distancia entre marcas signifique el mismo cociente entre sus valores. Como el logaritmo transforma cocientes en restas, un eje en escala logarítmica representa el logaritmo de sus valores en escala lineal.

Decimos que un gráfico está en escala semilogarítmica cuando su eje de abscisas está en escala lineal y su eje de ordenadas en escala logarítmica. Salvo por los valores en las marcas sobre el eje de las $y$, esto significa que dibujamos en escala lineal el gráfico de $\log(y)$ en función de $x$. Así pues, si al representar unos puntos $(x,y)$ en escala semilogarítmica observamos que siguen aproximadamente una recta, esto querrá decir que los valores $\log(y)$ siguen una ley aproximadamente lineal en los valores $x$, y, por lo tanto, que $y$ sigue una ley aproximadamente exponencial en $x$. En efecto, si $\log(y)= ax+b$, entonces \[ y=10^{\log(y)}= 10^{ax+b}=10^{ax}\cdot 10^{b}=10^{b}\cdot (10^{a})^{x}=\beta\cdot \alpha^x, \] donde $\beta=10^b$ y $\alpha=10^a$.

De manera similar, decimos que un gráfico está en escala doble logarítmica cuando ambos ejes están en escala logarítmica. Esto es equivalente, de nuevo salvo por los valores en las marcas sobre los ejes, a dibujar en escala lineal el gráfico de $\log(y)$ en función de $\log(x)$. Por consiguiente, si al dibujar unos puntos $(x,y)$ en escala doble logarítmica observamos que siguen aproximadamente una recta, esto querrá decir que los valores $\log(y)$ siguen una ley aproximadamente lineal en los valores $\log(x)$, y, por lo tanto, que $y$ sigue una ley aproximadamente potencial en $x$. En efecto, si $\log(y)= a\log(x)+b$, entonces \[ y=10^{\log(y)}= 10^{a\log(x)+b}=10^{a\log(x)}\cdot 10^{b}=10^{b}\cdot (10^{\log(x)})^{a} =10^{b}\cdot x^{a}=\beta \cdot x^{a}, \] donde $\beta=10^b$.

Veamos algunos ejemplos de regresiones lineales con cambios de escala.

Ejemplo 3.2 La serotonina se asocia a la estabilidad emocional en el hombre. En un experimento (véase el artículo de B. Peskar y S. Spector “Serotonin: Radioimmunoassay” en Science 179 (1973), pp. 1340-1341) se midió, para algunas cantidades de serotonina (expresadas en nanogramos, la milmillonésima parte de un gramo), el porcentaje de inhibición de un cierto proceso bioquímico en el que se observaba su presencia. El objetivo era estimar la cantidad de serotonina presente en un tejido a partir del porcentaje de inhibición observado. Los datos que se obtuvieron son los de la Tabla 3.2.

Tabla 3.2: Porcentajes de inhibición de un cierto proceso bioquímico en presencia de serotonina.
serotonina (ng)	inhibición (%)
1.2	19
3.6	36
12.0	60
33.0	84

Como queremos predecir la cantidad de serotonina en función de la inhibición observada, consideraremos los pares (inhibición,serotonina). En esta ocasión, en vez de trabajar con un data frame, trabajaremos directamente con los vectores.

inh=c(19,36,60,84)
ser=c(1.2,3.6,12,33)

Con la instrucción siguiente obtenemos la Figura 3.6, donde vemos claramente que la cantidad de serotonina no es función lineal de la inhibición.

plot(inh, ser)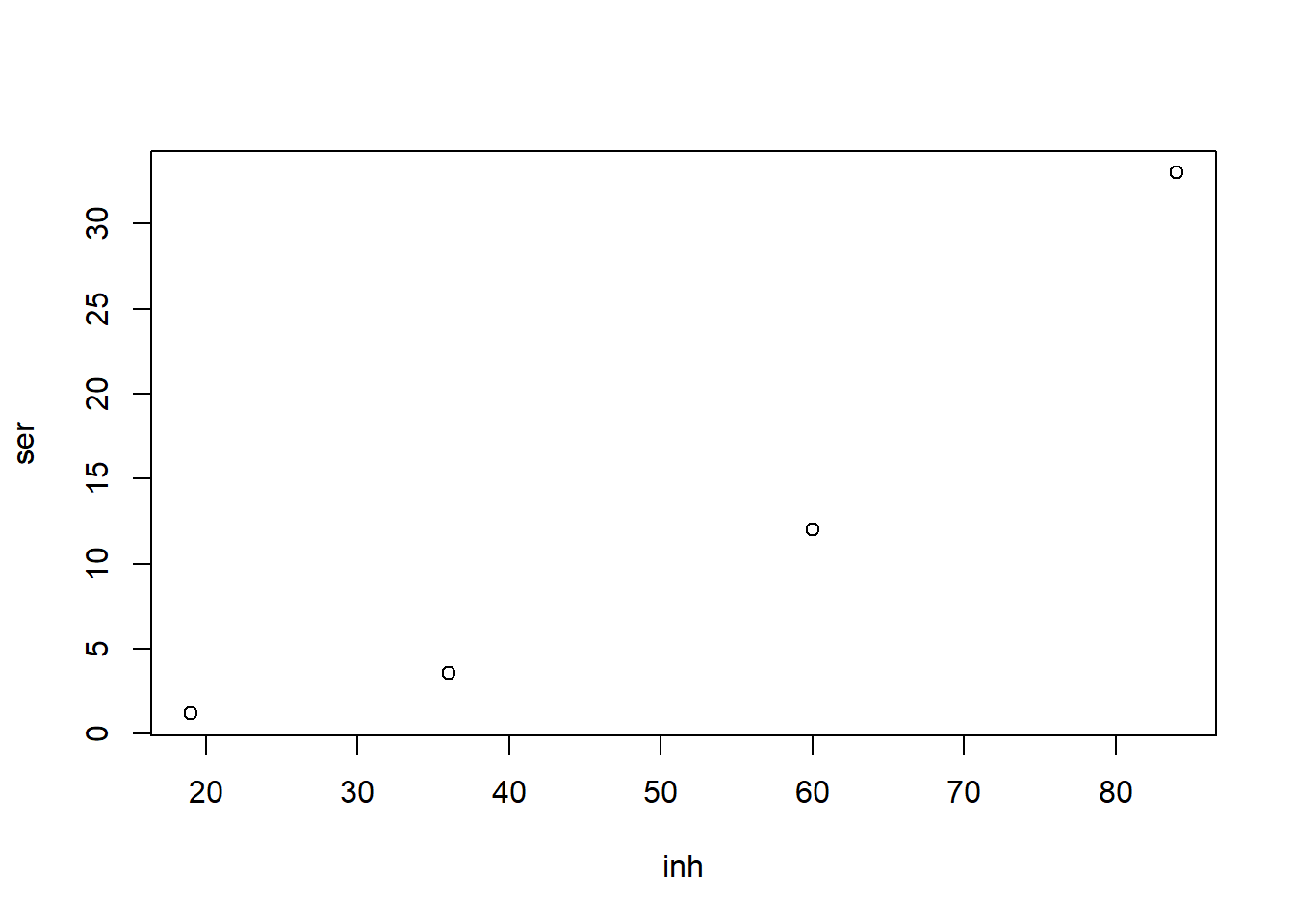

Figura 3.6: Representación gráfica en escala lineal del porcentaje de inhibición en función de la cantidad de serotonina.

Vamos a dibujar ahora el gráfico semilogarítmico de estos puntos, para ver si de esta manera quedan sobre una recta. Para ello, tenemos que añadir al argumento de plot el parámetro log="y".

plot(inh, ser, log="y")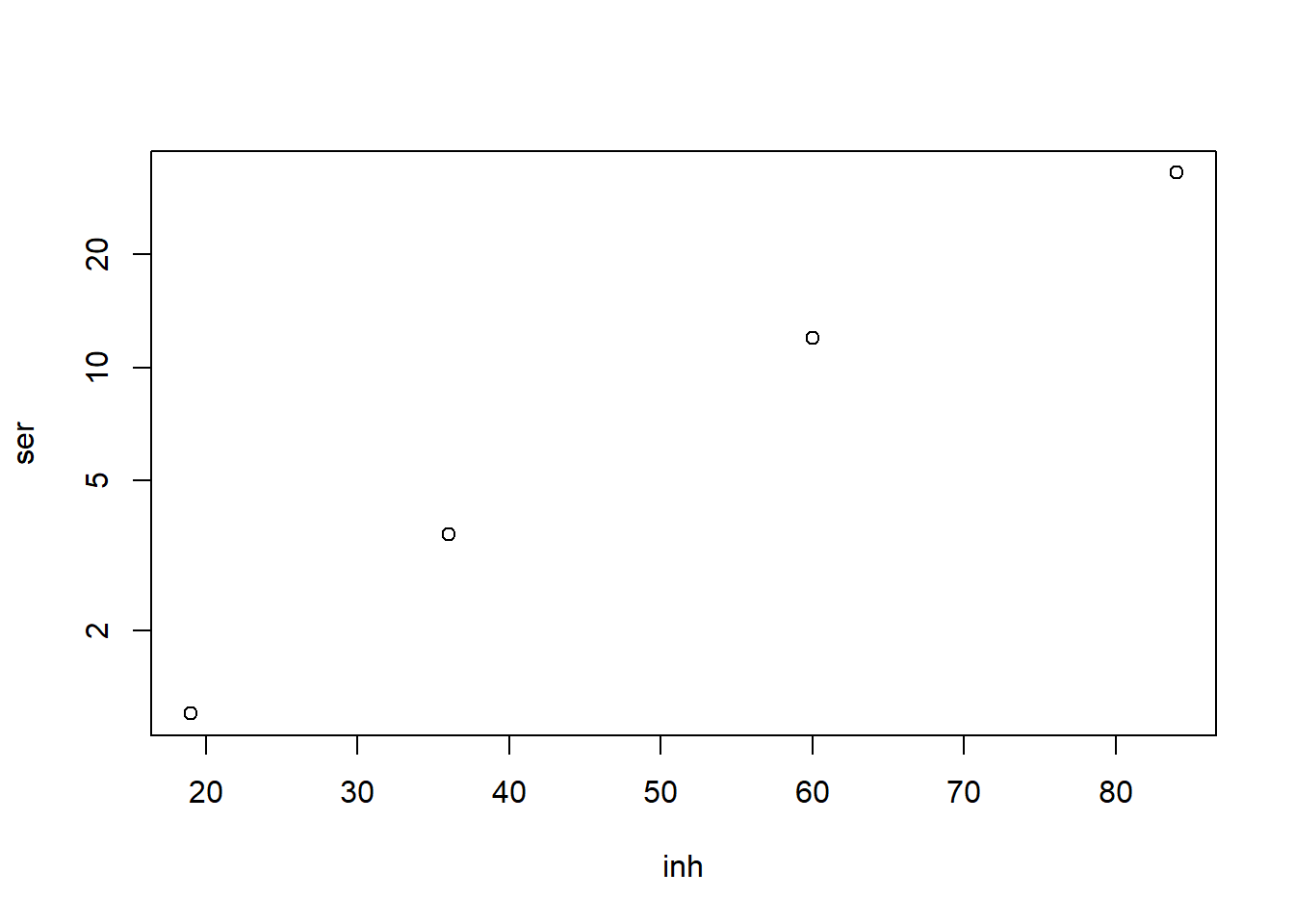

Figura 3.7: Representación gráfica en escala semilogarítmica del porcentaje de inhibición en función de la cantidad de serotonina.

Obtenemos la Figura 3.7. Observad cómo las marcas en el eje de ordenadas no están distribuidas de manera lineal: la distancia de 5 a 10 es la misma que de 10 a 20. Los puntos en este gráfico sí que parecen seguir una recta. Por lo tanto, parece que el logaritmo de la cantidad de serotonina es una función aproximadamente lineal del porcentaje de inhibición. Para confirmarlo, calcularemos la recta de regresión de los puntos

\[ (\textrm{inhibición}_n,\log(\textrm{serotonina}_n))_{n=1,\ldots,4}. \] Para calcular los logaritmos en base 10 de todas las cantidades de serotonina en un solo paso, podemos aplicar la función log10 directamente al vector ser.

log10(ser)
#> [1] 0.07918125 0.55630250 1.07918125 1.51851394
lm(log10(ser)~inh)
#> 
#> Call:
#> lm(formula = log10(ser) ~ inh)
#> 
#> Coefficients:
#> (Intercept)          inh  
#>    -0.28427      0.02196
summary(lm(log10(ser)~inh))$r.squared
#> [1] 0.9921146

El resultado indica que la recta de regresión de estos puntos es $y= 0.02196x-0.28427$, con un valor de $R^2$ de 0.992, muy bueno. Por lo tanto, podemos afirmar que, aproximadamente,

\[ \log(\textrm{serotonina})= 0.02196\cdot \mbox{inhibición}-0.28427. \] Elevando 10 a cada uno de los lados de esta identidad, obtenemos

\[\begin{align*} \textrm{serotonina} = & 10^{\log(\textrm{serotonina})}= 10^{-0.28427}\cdot 10^{0.02196\cdot \textrm{inhibición}} \\ = & 0.52\cdot 1.052^{\textrm{inhibición}}. \end{align*}\] Es decir, los puntos de partida siguen aproximadamente la función exponencial

\[ y=0.52\cdot 1.052^{x}. \]

Vamos ahora a dibujar en un mismo gráfico los puntos $(\textrm{inhibición}_n,\textrm{serotonina}_n)$ y esta función exponencial. Para añadir la gráfica de una función $y=f(x)$ al gráfico activo en la pestaña Plots podemos emplear la función

curve(f(x), add=TRUE)

Así, el código siguiente produce la Figura 3.8; fijaos en cómo hemos especificado la función $y=0.52\cdot 1.052^{x}$ dentro del curve.

plot(inh, ser)
curve(0.52*1.052^x, add=TRUE)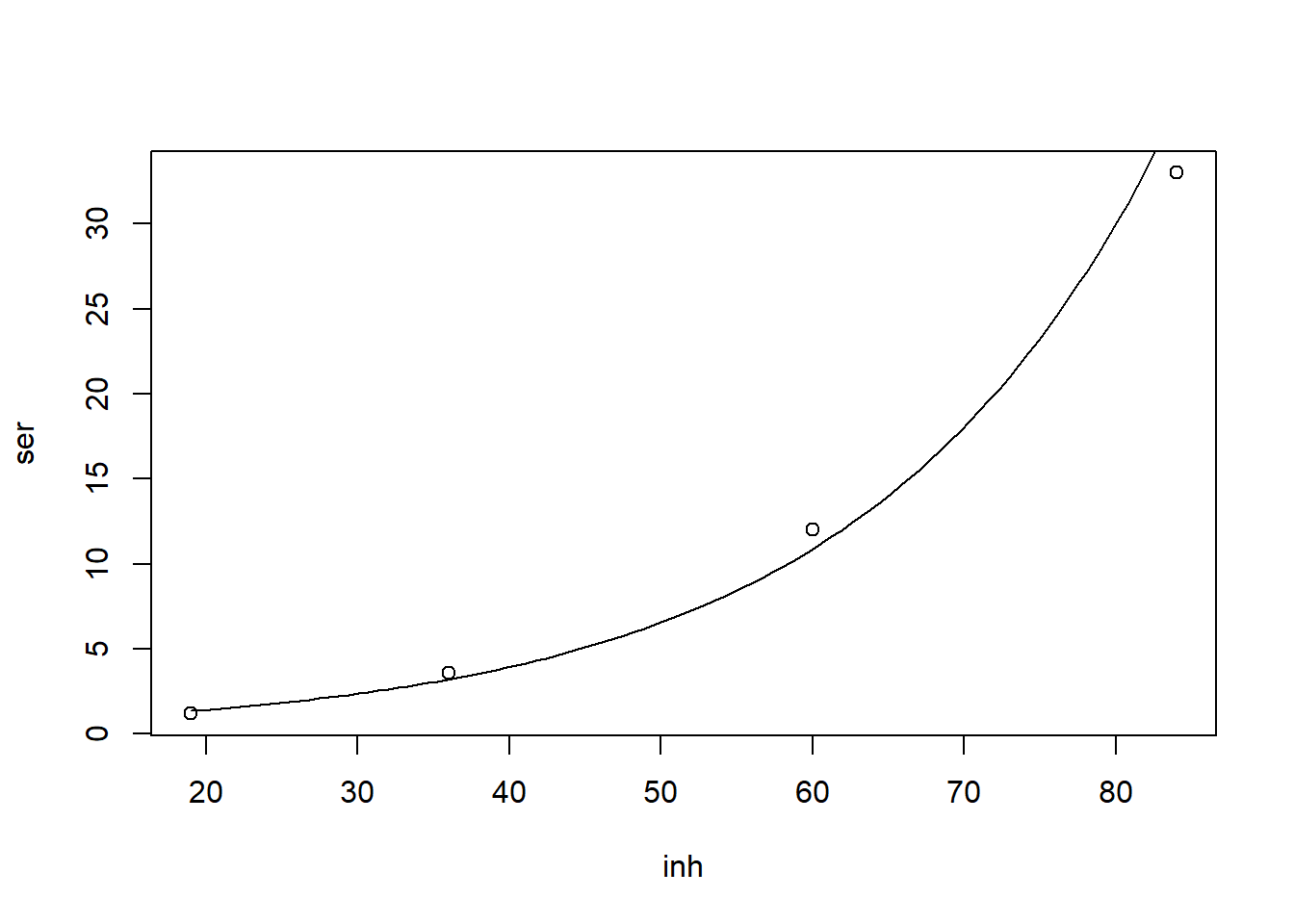

$Representación gráfica en escala lineal del porcentaje de inhibición en función de la cantidad de serotonina, junto con la función $y=0.52\cdot 1.052^x$.$

Figura 3.8: Representación gráfica en escala lineal del porcentaje de inhibición en función de la cantidad de serotonina, junto con la función $y=0.52\cdot 1.052^x$.

Ahora podemos usar la relación observada,

\[ \textrm{serotonina}= 0.52\cdot 1.052^{\textrm{inhibición}}, \] para estimar la cantidad de serotonina presente en el tejido a partir de una inhibición concreta. Por ejemplo, si hemos observado un 25% de inhibición, podemos estimar que la cantidad de serotonina es 0.52·1.052²⁵=1.84 ng

Ejemplo 3.3 Consideremos ahora los datos de la Tabla 3.3. Se trata de los números acumulados de casos de SIDA en los Estados Unidos desde 1981 hasta 1992, extraídos del HIV/AIDS Surveillance Report de 1993 (http://www.cdc.gov/hiv/topics/surveillance/resources/reports/index.htm). Acumulados significa que, para cada año, se da el número de casos detectados hasta entonces.

Tabla 3.3: Números acumulados anuales de casos de SIDA en los Estados Unidos, 1981 a 1992.
año	casos
1981	97
1982	709
1983	2698
1984	6928
1985	15242
1986	29944
1987	52902
1988	83903
1989	120612
1990	161711
1991	206247
1992	257085

Queremos estudiar el comportamiento de estos números acumulados de casos en función del tiempo expresado en años a partir de 1980. Lo primero que hacemos es cargar los datos en un data frame. Fijaos en que la lista de años va a ser la secuencia de números consecutivos entre 1 y 12. Para definir la secuencia de números consecutivos entre $a$ y $b$ podemos usar la construcción a:b. Esto nos ahorra trabajo y reduce las oportunidades de cometer errores al escribir los números.

tiempo=1:12
SIDA_acum=c(97,709,2698,6928,15242,29944,52902,83903,120612,161711,206247,257085)
df_SIDA=data.frame(tiempo, SIDA_acum)

Con la instrucción siguiente dibujamos estos datos:

plot(df_SIDA)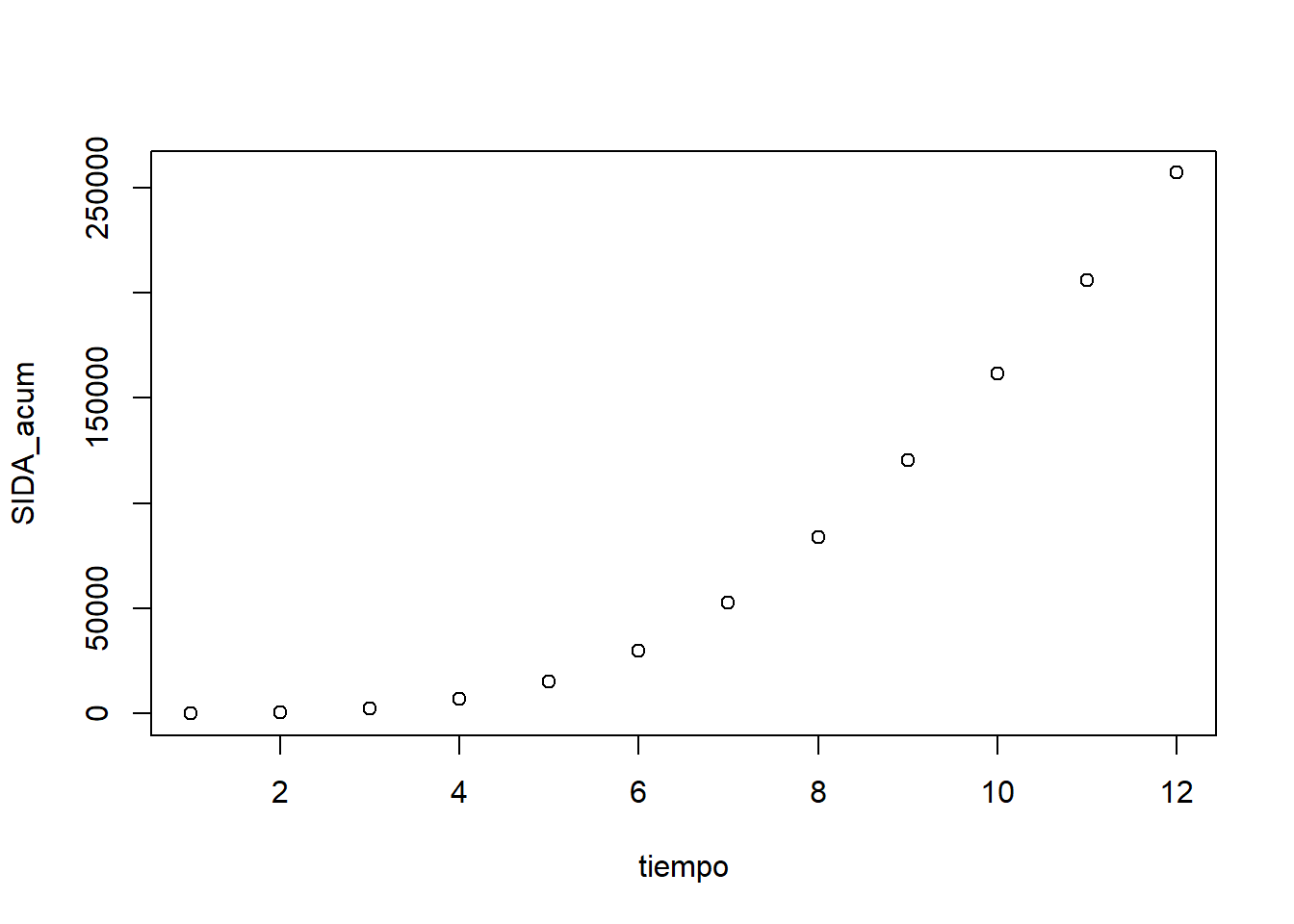

Representación gráfica en escala lineal del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Figura 3.9: Representación gráfica en escala lineal del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Obtenemos el gráfico de la Figura 3.9, y está claro que los puntos $(x_n,y_n)$, donde $x$ representa el año e $y$ el número acumulado de casos de SIDA, no se ajustan a una recta. De hecho, a simple vista se diría que el crecimiento de $y$ en función de $x$ es exponencial.

Para confirmar este crecimiento exponencial, dibujamos el gráfico semilogarítmico:

plot(df_SIDA, log="y")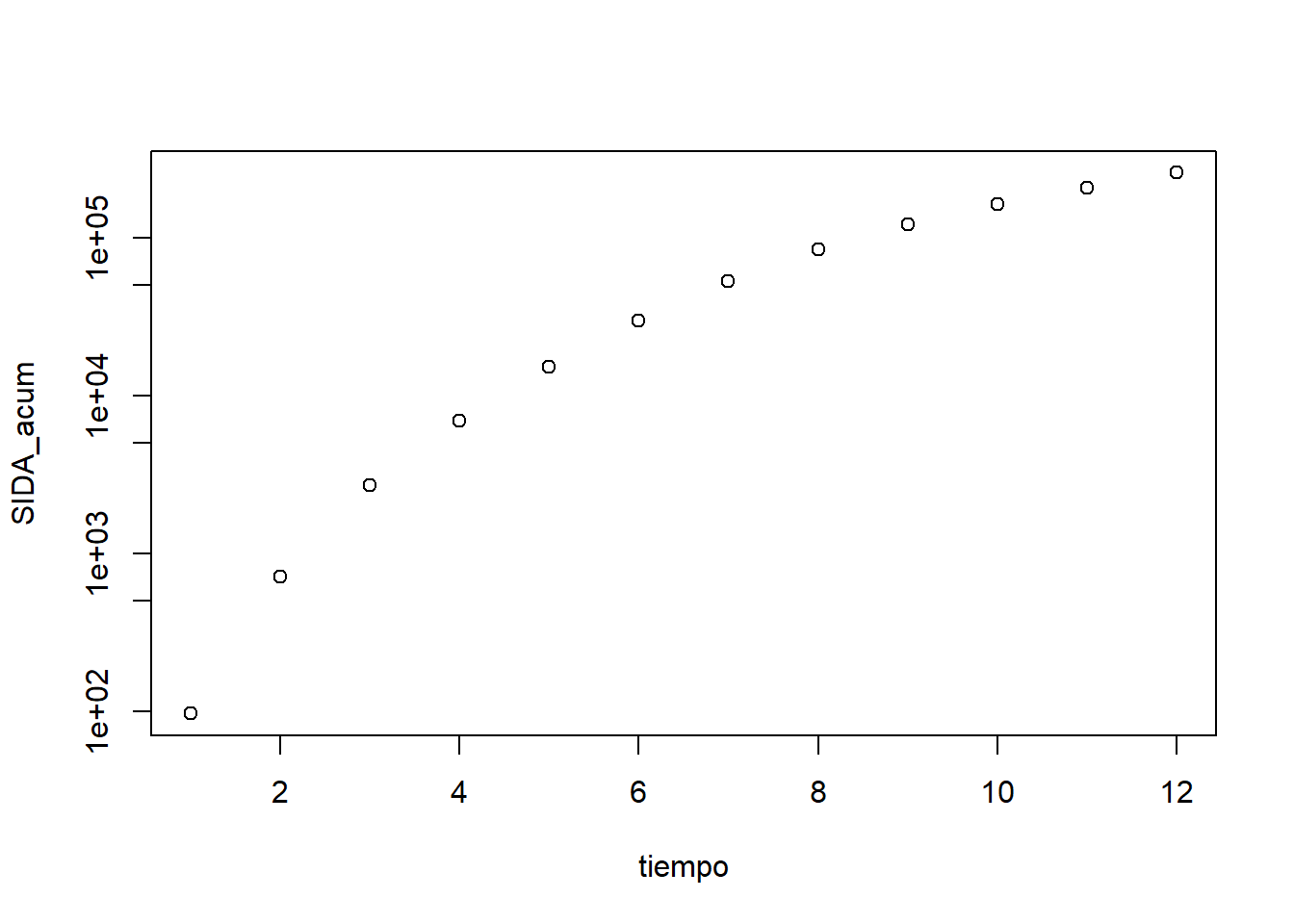

Representación gráfica en escala semilogarítmica del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Figura 3.10: Representación gráfica en escala semilogarítmica del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Obtenemos el gráfico de la Figura 3.10, donde los puntos tampoco siguen una recta. Así pues, resulta que $y$ tampoco parece ser función exponencial de $x$.

Vamos a ver si el crecimiento de $y$ en función de $x$ es potencial. Para ello, dibujaremos un gráfico doble logarítmico de los puntos $(x_n,y_n)$, especificando log="xy" dentro del argumento de plot.

plot(df_SIDA, log="xy")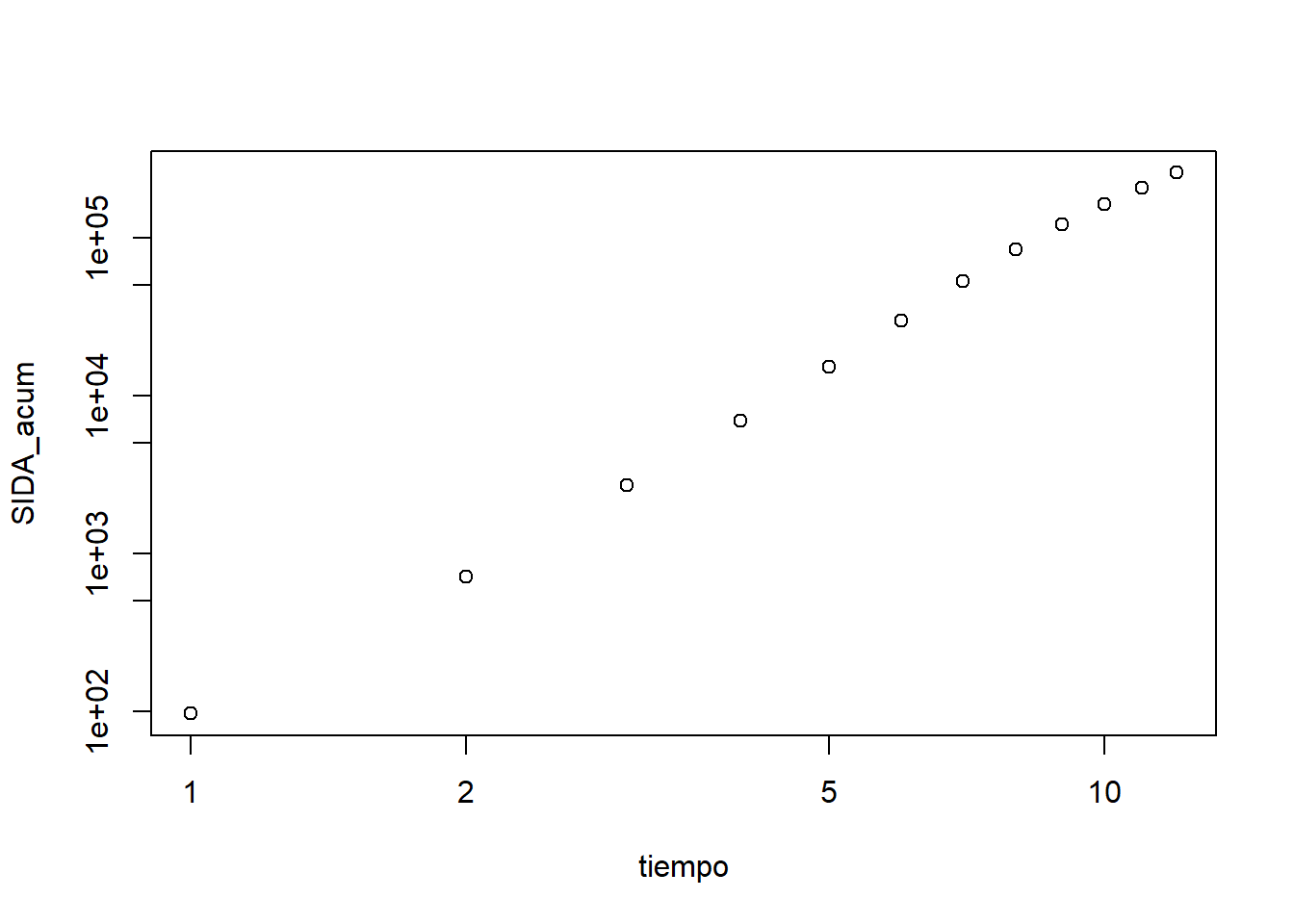

Representación gráfica en escala doble logarítmica del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Figura 3.11: Representación gráfica en escala doble logarítmica del número acumulado de casos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año.

Obtenemos el gráfico de la Figura 3.11, y ahora sí que parece lineal. Así que parece que los números acumulados de casos de SIDA crecieron potencialmente con el transcurso de los años.

Lo que haremos ahora será calcular la recta de regresión del logaritmo de SIDA_acum respecto del logaritmo de tiempo y mirar el coeficiente de determinación. Recordad que podemos aplicar una función a todas las entradas de un vector en un solo paso.

lm(log10(SIDA_acum)~log10(tiempo), data=df_SIDA)
#> 
#> Call:
#> lm(formula = log10(SIDA_acum) ~ log10(tiempo), data = df_SIDA)
#> 
#> Coefficients:
#>   (Intercept)  log10(tiempo)  
#>         1.918          3.274
summary(lm(log10(SIDA_acum)~log10(tiempo), data=df_SIDA))$r.squared
#> [1] 0.9983866

La regresión que obtenemos es $\log(y)=1.918 + 3.274\log(x)$, con un valor de $R^2$ de 0.998, muy alto. Elevando 10 a ambos lados de esta igualdad, obtenemos

\[\begin{align*} y=10^{\log(y)}= & 10^{1.918}\cdot 10^{3.274\log(x)}=10^{1.918}\cdot (10^{\log(x)})^{3.274} \\ = & 82.79422\cdot x^{3.274}. \end{align*}\] xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

\[ y=82.79422\cdot x^{3.274}, \] dibujaremos los puntos y la curva en un único gráfico (en escala lineal):

plot(df_SIDA)
curve(82.79422*x^3.274, add=TRUE)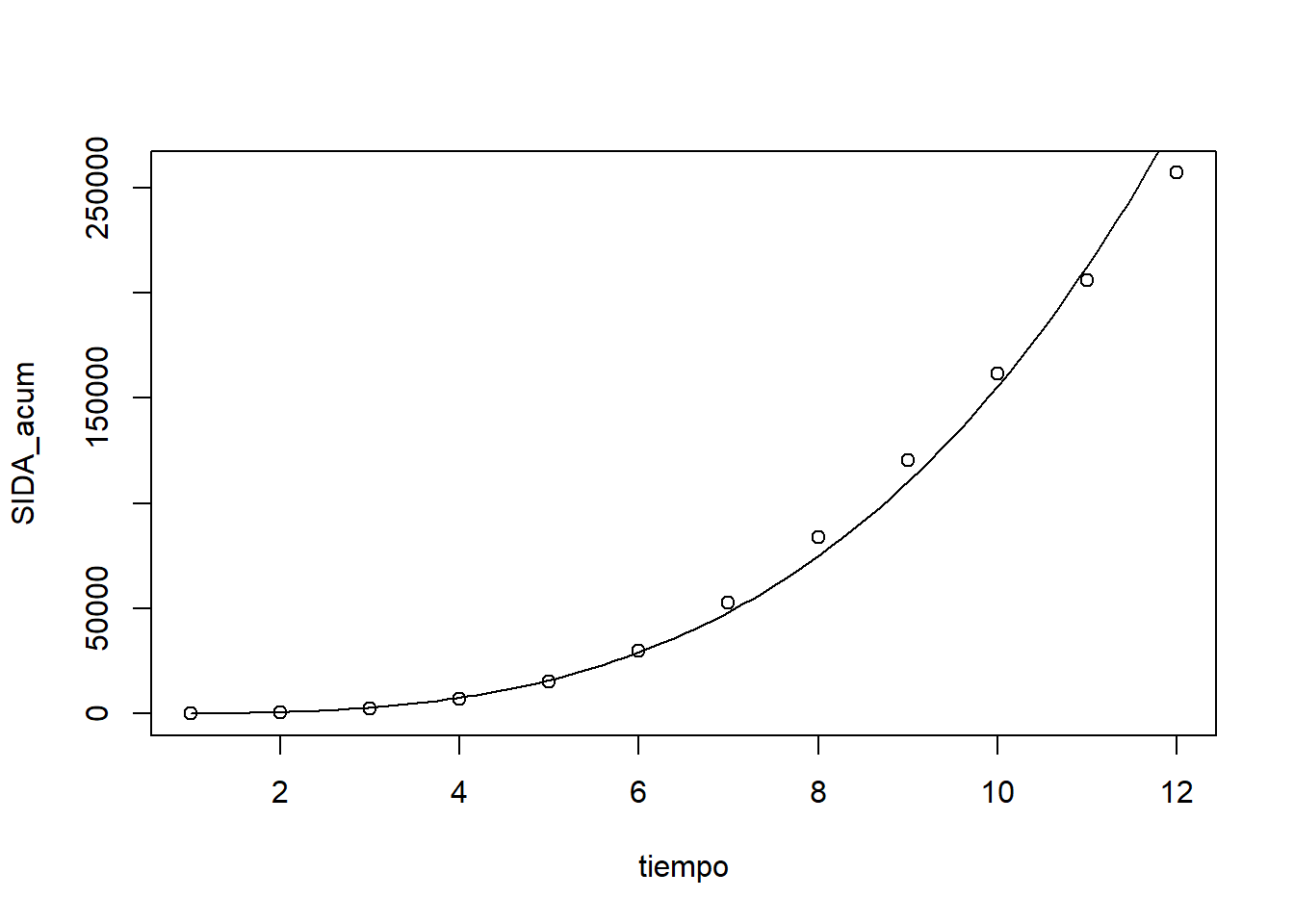

$Representación gráfica en escala lineal de la cantidad acumulada de enfermos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año, junto con su ajuste mediante la función potencial $82.79422 · x^{3.274}$.$

Figura 3.12: Representación gráfica en escala lineal de la cantidad acumulada de enfermos de SIDA en EEUU desde 1980 en función de los años transcurridos desde ese año, junto con su ajuste mediante la función potencial $82.79422 · x^{3.274}$.

Obtenemos la Figura 3.12, donde vemos que la curva se ajusta bastante bien a los puntos.

Hay que mencionar aquí que se han propuesto modelos matemáticos que predicen que, cuando se inicia una epidemia de SIDA en una población, los números acumulados de casos en los primeros años son proporcionales al cubo del tiempo transcurrido desde el inicio; véase, por ejemplo, el artículo de S.A. Colgate, E. A. Stanley, J. M. Hyman, S. P. Layne y C. Qualls “Risk behavior-based model of the cubic growth of acquired immunodeficiency syndrome in the United States”, en PNAS 86 (1989), pp. 4793-4797. El resultado del análisis que hemos realizado es consistente con esta predicción teórica.

3.3 Guía rápida

c sirve para definir vectores.
a:b, con a<b, define un vector con la secuencia a,a+1,a+2,…, b.
data.frame, aplicada a unos vectores de la misma longitud, define un data frame (el tipo de objetos de R en los que guardamos usualmente las tablas de datos) cuyas columnas serán estos vectores.
read.table define un data frame a partir de un fichero externo. También se puede usar el menú Import Dataset de la pestaña Environment en la ventana superior derecha de RStudio.
lm(y~x) calcula la recta de regresión del vector $y$ respecto del vector $x$. Si $x$ e $y$ son dos columnas de un data frame, éste se ha de especificar en el argumento mediante el parámetro data igualado al nombre del data frame.
summary sirve para obtener un resumen estadístico de un objeto. Este resumen depende del objeto. En el caso de una recta de regresión calculada con lm, muestra una serie de información estadística extra obtenida en dicho cálculo.
plot(x, y) produce el gráfico de los puntos $(x_n,y_n)$. Si $x$ e $y$ son, respectivamente, la primera y la segunda columna de un data frame de dos columnas, se le puede entrar directamente el nombre del data frame como argumento. El parámetro log sirve para indicar los ejes que se desea que estén en escala logarítmica: "x" (abscisas), "y" (ordenadas) o "xy" (ambos).
abline añade una recta al gráfico activo.
curve(función, add=TRUE) añade la gráfica de la función al gráfico activo.

3.4 Ejercicios

Ejercicio

Las larvas de Lymantria dispar, conocidas como orugas peludas del alcornoque, son una plaga en bosques y huertos. En un experimento se quiso determinar la capacidad de atracción de una cierta feromona sobre los machos de esta especie, con el objetivo de emplearla en trampas (véase el artículo de M. Beroza y E. F. Knipling “Gypsy moth control with the sex attractant pheromone” en Science 177 (1972), pp. 19-27). En la Tabla 3.4, $x$ representa la cantidad de feromona empleada, en microgramos (la millonésima parte de un gramo) y $N$ el número de machos atrapados en una trampa empleando esta cantidad de feromona para atraerlos.

Tabla 3.4: Cantidades de feromona empleadas en trampas y números de machos atrapados.
$x$	$N$
0.1	3
1.0	6
5.0	9
10.0	11
100.0	20

Decidid si, en los puntos $(x,N)$ dados en la Tabla 3.4, el valor de $N$ sigue una función aproximadamente lineal, exponencial o potencial en el valor de $x$.
En caso de ser una función de uno de estos tres tipos, calculadla.
Representad en un gráfico los puntos $(x,N)$ de la Tabla 3.4 y la función que hayáis calculado en el apartado anterior, para visualizar la bondad del ajuste de la curva a los puntos.
Estimad cuánta feromona tenemos que usar en una trampa para atraer a 50 machos.