Lección 12 Descripción de datos cuantitativos
Los datos cuantitativos son los que expresan cantidades que se representan mediante números, tales como los resultados de contar objetos o individuos o de medir pesos, distancias, tiempos o concentraciones, y se suelen clasificar en continuos y discretos. Los datos continuos son los que, si pudiéramos medirlos con precisión infinita, en principio podrían tomar todos los valores de un intervalo de la recta real: por ejemplo, el peso o la altura de un individuo o el tiempo que tarda un determinado proceso. En cambio, los datos discretos son los que pueden tomar solo un conjunto contable de valores: el resultado obtenido al lanzar un dado, el número de individuos en una población, el número de aminoácidos en una proteína… En todo caso, hay que tener en cuenta que esta distinción es solo teórica: en la práctica, todos los datos son discretos, ya que la precisión infinita no existe. Pero a veces es conveniente suponer que unos datos son continuos para poder usar técnicas específicas en su análisis.
Para estudiar una variable cuantitativa (un vector de datos cuantitativos), podemos usar las frecuencias y las frecuencias acumuladas de sus diferentes valores, como en las variables ordinales, puesto que podemos ordenar los datos cuantitativos con el orden natural de los números reales. Pero además de las frecuencias, disponemos de otras muchas técnicas descriptivas, ya que, como los datos cuantitativos son números reales y tienen el significado de números reales, podemos operar con ellos.
Los datos cuantitativos admiten dos tipos de tratamiento, según trabajemos con los datos originales o brutos (raw data) o los agrupemos en clases o intervalos (recordad el Ejemplo 11.6). En esta lección vamos a tratar solo la primera situación, y en la Lección ?? estudiaremos la descripción de datos agrupados.
12.1 Frecuencias
El tratamiento de las frecuencias de datos cuantitativos es similar al de los datos ordinales, excepto por un detalle: no se tienen en cuenta todos los niveles posibles, sino solo los observados.
Ejemplo 12.1 Hemos pedido las edades a un grupo de 15 voluntarios de una ONG. Las respuestas, en años, han sido las siguientes:
18, 22, 16, 19, 23, 18, 35, 16, 45, 20, 20, 22, 40, 18, 45.
Las diferentes edades que hemos observado son 16, 18, 19, 20, 22, 23, 35, 40 y 45, y por lo tanto solo nos interesan las frecuencias de estas edades. Las podemos calcular con R y así, de paso, recordaremos cómo se hace.
edades=c(18,22,16,19,23,18,35,16,45,20,20,22,40,18,45)- Tabla de frecuencias absolutas:
table(edades)
#> edades
#> 16 18 19 20 22 23 35 40 45
#> 2 3 1 2 2 1 1 1 2- Tabla de frecuencias relativas:
round(prop.table(table(edades)), 2)
#> edades
#> 16 18 19 20 22 23 35 40 45
#> 0.13 0.20 0.07 0.13 0.13 0.07 0.07 0.07 0.13- Tabla de frecuencias absolutas acumuladas:
cumsum(table(edades))
#> 16 18 19 20 22 23 35 40 45
#> 2 5 6 8 10 11 12 13 15- Tabla de frecuencias relativas acumuladas:
round(cumsum(prop.table(table(edades))), 2)
#> 16 18 19 20 22 23 35 40 45
#> 0.13 0.33 0.40 0.53 0.67 0.73 0.80 0.87 1.00Supongamos que realizamos \(n\) observaciones de una propiedad que se mide con un número real, y obtenemos la lista de datos cuantitativos (la variable cuantitativa) \[ x_1, \ldots, x_n. \] Sean \(X_1, \ldots, X_k\) los valores distintos que aparecen en esta lista de datos; los consideraremos ordenados \[ X_1 < X_2 < \cdots < X_k. \] Entonces, en esta variable cuantitativa:
La frecuencia absoluta de \(X_j\) es el número \(n_j\) de elementos que son iguales a \(X_j\).
La frecuencia absoluta acumulada de \(X_j\) es \(\displaystyle N_j=\sum\limits_{i=1}^j n_i.\)
La frecuencia relativa de \(X_j\) es \(\displaystyle f_j=\frac{n_j}{n}.\)
La frecuencia relativa acumulada de \(X_j\) es \(\displaystyle F_j=\frac{N_j}{n}=\sum\limits_{i=1}^j f_i.\)
Ejemplo 12.2 Lanzamos 10 veces un dado de seis caras al aire y anotamos los resultados:
2, 1, 4, 5, 6, 3, 5, 6, 3.
En este caso, \(n=10\), y los distintos valores observados son \[ X_1=1,\ X_2=2,\ X_3=3,\ X_4=4,\ X_5=5,\ X_6=6. \] Vamos a calcular las frecuencias de este experimento, y las organizaremos en forma de data frame para visualizarlas como una tabla:
dados=c(1,2,1,4,5,6,3,5,6,3)
table(dados)
#> dados
#> 1 2 3 4 5 6
#> 2 1 2 1 2 2
prop.table(table(dados))
#> dados
#> 1 2 3 4 5 6
#> 0.2 0.1 0.2 0.1 0.2 0.2
cumsum(table(dados))
#> 1 2 3 4 5 6
#> 2 3 5 6 8 10
cumsum(prop.table(table(dados)))
#> 1 2 3 4 5 6
#> 0.2 0.3 0.5 0.6 0.8 1.0
tabla_df=data.frame(Resultado=1:6,
Frec_Abs=as.vector(table(dados)),
Frec_Rel=as.vector(round(prop.table(table(dados)), 2)),
Frec_Abs_Acum=as.vector(cumsum(table(dados))),
Frec_Rel_Acum=as.vector(round(cumsum(prop.table(table(dados))), 2)))
tabla_df
#> Resultado Frec_Abs Frec_Rel Frec_Abs_Acum Frec_Rel_Acum
#> 1 1 2 0.2 2 0.2
#> 2 2 1 0.1 3 0.3
#> 3 3 2 0.2 5 0.5
#> 4 4 1 0.1 6 0.6
#> 5 5 2 0.2 8 0.8
#> 6 6 2 0.2 10 1.0Para entrar una tabla unidimensional como una variable en un data frame, es conveniente transformarla en vector con as.vector. De lo contrario, cada table y cada prop.table añadirían una columna extra con los nombres de los niveles. Comprobadlo.
12.2 Medidas de tendencia central
Las medidas de tendencia central son las que dan un valor representativo de todas las observaciones; las más importantes son:
La moda, que es el valor, o los valores, de máxima frecuencia (absoluta o relativa, tanto da).
La media aritmética, o valor medio, \[ \overline{x}=\frac{\sum_{i=1}^n x_i}{n}=\frac{\sum_{j=1}^k n_j\cdot X_j}{n}= \sum_{j=1}^k f_j\cdot X_j. \]
La mediana, que representa el valor central en la lista ordenada de observaciones y se define formalmente de la manera siguiente. Si denotamos por \[ x_{(1)}\leqslant x_{(2)}\leqslant\cdots \leqslant x_{(n)} \] los datos de la variable cuantitativa ordenados de menor a mayor, la mediana es:
- Si \(n\) es par, la media de los dos datos centrales: \[ \frac{x_{(n/2)}+x_{(n/2+1)}}{2}. \]
- Si \(n\) es impar, el dato central: \(x_{(n+1)/2}\).
En este curso, cuando hablemos de la media de unos datos nos referiremos siempre a su media aritmética. Hay otros tipos de media, como por ejemplo la media geométrica o la armónica, que no estudiaremos.
Ejemplo 8.2 En la situación del Ejemplo 12.1, la moda es 18 y la media es \[ \frac{18+22+16+19+23+18+35+16+45+20+20+22+40+18+45}{15}=25.1333. \] Si ordenamos los 15 resultados, quedan de la siguiente manera:
16, 16, 18, 18, 18, 19, 20, 20, 22, 22, 23, 35, 40, 45, 45.
Su mediana es la entrada central en esta lista, es decir, la octava: 20.
En la situación del Ejemplo 12.2, la moda es, de hecho, cuatro valores: 1, 3, 5 y 6. La media es \[ \frac{1+2+1+4+5+6+3+5+6+3}{10}=3.6. \] Como esta variable contiene 10 datos, su mediana es la media aritmética de sus dos resultados centrales (el quinto y el sexto) en la lista ordenada de resultados
1, 1, 2, 3, 3, 4, 5, 5, 6, 6.
Por lo tanto, su mediana es \((3+4)/2=3.5\).
Ya explicamos cómo se calcula la moda con R en la Lección 10. La única diferencia aquí es que, como trabajamos con datos cuantitativos, es conveniente que el resultado lo demos como un número, aplicándole as.numeric. En cuanto a la media y la mediana, se calculan aplicando las funciones mean y median, respectivamente, al vector de datos. Así:
- La moda de nuestro vector de edades es:
as.numeric(names(which(table(edades)==max(table(edades)))))
#> [1] 18- La media de nuestro vector de edades es:
mean(edades)
#> [1] 25.13333- La mediana de nuestro vector de edades es:
median(edades)
#> [1] 20- Las modas de nuestro vector de lanzamientos de dados son:
as.numeric(names(which(table(dados)==max(table(dados)))))
#> [1] 1 3 5 6- La media de nuestro vector de lanzamientos de dados es:
mean(dados)
#> [1] 3.6- La mediana de nuestro vector de lanzamientos de dados es:
median(dados)
#> [1] 3.512.3 Medidas de posición
Las medidas de posición estiman qué valores dividen la población en unas determinadas proporciones; los valores que determinan estas posiciones reciben el nombre de cuantiles. En este sentido, la mediana es también una medida de posición, puesto que divide la variable en dos mitades.
Dada una proporción \(0<p<1\), el cuantil de orden \(p\) de una variable cuantitativa, que denotaremos por \(Q_p\), es el valor más pequeño tal que su frecuencia relativa acumulada es mayor o igual que \(p\). En otras palabras, si tenemos un conjunto de datos \(x_1, \ldots, x_n\) y los ordenamos de menor a mayor, \(Q_p\) es el número más pequeño que deja a su izquierda (incluyéndolo a él) como mínimo la fracción \(p\) de los datos, es decir, \(p\cdot n\) datos. De esta manera, la mediana viene a ser el cuantil \(Q_{0.5}\).
Ejemplo 12.3 Consideremos otro experimento de lanzamientos de un dado. Esta vez lo lanzamos 30 veces y obtenemos los resultados siguientes:
2, 4, 5, 6, 3, 2, 4, 5, 1, 2, 1, 3, 4, 2, 3, 4, 1, 2, 5, 6, 5, 5, 3, 2, 1, 3, 4, 2, 2, 1.
Ordenamos estos resultados de menor a mayor.
dados2=c(2,4,5,6,3,2,4,5,1,2,1,3,4,2,3,4,1,2,5,6,5,5,3,2,1,3,4,2,2,1)
dados2=sort(dados2)
dados2
#> [1] 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5 6 6Si nos pidieran el cuantil \(Q_{0.2}\), sería el primer elemento en esta lista ordenada que fuera mayor o igual que, como mínimo, el 20% de los datos. Como el 20% de 30 es 6, sería el sexto elemento.
dados2[6]
#> [1] 2Si nos pidieran en cambio el cuantil \(Q_{0.65}\), sería el primer elemento en esta lista ordenada mayor o igual que, como mínimo, el 65% de los datos. Como el 65% de 30 es 19.5, sería el vigésimo elemento.
dados2[20]
#> [1] 4También podemos calcular los cuantiles \(Q_p\) comparando la proporción \(p\) con las frecuencias relativas acumuladas.
cumsum(prop.table(table(dados2)))
#> 1 2 3 4 5 6
#> 0.1666667 0.4333333 0.6000000 0.7666667 0.9333333 1.0000000El primer elemento con frecuencia relativa acumulada mayor o igual que 0.2 es 2, lo que implica que \(Q_{0.2}=2\), y el primer elemento con frecuencia relativa acumulada mayor o igual que 0.65 es 4, por lo que \(Q_{0.65}=4\).
Algunos cuantiles tienen nombre propio:
La mediana es el cuantil \(Q_{0.5}\).
Los cuartiles son los cuantiles \(Q_{0.25}\), \(Q_{0.5}\) y \(Q_{0.75}\), y reciben, respectivamente, los nombres de primer cuartil, segundo cuartil (o mediana) y tercer cuartil. \(Q_{0.25}\) será, pues, el menor valor que es mayor o igual que una cuarta parte de los datos, y \(Q_{0.75}\), el menor valor que es mayor o igual que tres cuartas partes de los datos.
Los deciles son los cuantiles \(Q_{p}\) con \(p\) un múltiplo entero de 0.1: el primer decil es \(Q_{0.1}\), el segundo decil es \(Q_{0.2}\), y así sucesivamente.
Los percentiles son los cuantiles \(Q_{p}\) con \(p\) un múltiplo entero de 0.01.
Ha llegado el momento de avisar que la definición de cuantil que hemos dado es más bien orientativa; en realidad, y salvo para el caso de la mediana, no hay un consenso sobre cómo se tienen que calcular los cuantiles, de manera que se han propuesto métodos diferentes que pueden dar resultados diferentes. La razón es que el objetivo final del cálculo de cuantiles puede no ser solo encontrar el primer valor cuya frecuencia relativa acumulada en la variable sea mayor o igual que \(p\), sino también estimar qué vale este valor para el total de la población.
Con R, los cuantiles de orden \(p\) de un vector \(x\) se calculan con la instrucción
quantile(x, p)Veamos algunos ejemplos:
x=c(1,2,3,4,5,6,2,3,2,3,4,2,2,3,2,2,5,7,3,4,2,1,3,6)
round(cumsum(prop.table(table(x))), 3)
#> 1 2 3 4 5 6 7
#> 0.083 0.417 0.667 0.792 0.875 0.958 1.000
quantile(x, 0.1)
#> 10%
#> 2
quantile(x, 0.25)
#> 25%
#> 2
quantile(x, 0.75)
#> 75%
#> 4R dispone de 9 métodos diferentes para calcular cuantiles, que se pueden especificar dentro de quantile con el parámetro type. En la mayoría de las ocasiones se obtiene el mismo resultado con todos los métodos, pero no siempre. Para saber en detalle las fórmulas que usa quantile para cada valor de type, se puede consultar la entrada correspondiente de la Wikipedia. El método que hemos usado en el Ejemplo 12.3 es el que corresponde a type=1, y siempre da un dato de los observados. El problema es que, entonces, quantile(x,0.5,type=1) y median(x) pueden dar resultados diferentes. El método que usa R por defecto si no especificamos otro es type=7.
x=c(1,2,3,4,5,6,2,3,2,3,4,2,2,3,2,2,5,7,3,4,2,1,3,6)
round(cumsum(prop.table(table(x))), 3)
#> 1 2 3 4 5 6 7
#> 0.083 0.417 0.667 0.792 0.875 0.958 1.000
quantile(x, 0.67)
#> 67%
#> 3.41
quantile(x, 0.67, type=1)
#> 67%
#> 4
dados=c(1,2,1,4,5,6,3,5,6,3)
round(cumsum(prop.table(table(dados))), 3)
#> 1 2 3 4 5 6
#> 0.2 0.3 0.5 0.6 0.8 1.0
median(dados)
#> [1] 3.5
quantile(dados, 0.5, type=1)
#> 50%
#> 3
quantile(dados, 0.5)
#> 50%
#> 3.5Seguramente os preguntáis: si los cuantiles se pueden calcular de diferentes maneras, ¿cómo lo tenéis que hacer vosotros? Como en el nivel de este curso no es necesario afinar tanto, aquí usaremos la función quantile sin especificar type, es decir, con su método por defecto; no hace falta que sepáis qué hace este método, lo importante es que entendáis el concepto de cuantil y qué representa, grosso modo, el resultado de quantile.
12.4 Medidas de dispersión
Las medidas de dispersión evalúan lo desperdigados que están los datos. Las más importantes son:
El rango, o recorrido, que es la diferencia entre el máximo y el mínimo de las observaciones.
El rango intercuartílico, que es la diferencia \(Q_{0.75}-Q_{0.25}\). También se llama a veces rango intercuartílico al intervalo intercuartílico: el intervalo \([Q_{0.25},Q_{0.75}]\).
La varianza, que es la media aritmética de las diferencias al cuadrado entre los datos \(x_i\) y la media \(\overline{x}\) de la variable; la denotamos por \(s^2\). Es decir, \[ s^2=\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n}=\frac{\sum_{i=1}^k n_i\cdot (X_i-\overline{x})^2}{n}=\sum_{i=1}^k f_i\cdot (X_i-\overline{x})^2. \]
La desviación típica, que es la raíz cuadrada positiva \(s\) de la varianza: \(s=\sqrt{s^2}\).
La varianza muestral, que es la corrección siguiente de la varianza: \[ \tilde{s}^2 =\frac{n}{n-1} \cdot s^2=\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n-1}. \] Esto es, la varianza muestral se calcula con la misma fórmula que la varianza salvo que el denominador es \(n-1\) en lugar de \(n\).
La desviación típica muestral, que es la raíz cuadrada positiva \(\tilde{s}\) de la varianza muestral: \(\tilde{s}=\sqrt{\tilde{s}^2}\).
La distinción entre la versión muestral y la “verdadera” de la varianza está motivada por la interrelación entre la estadística descriptiva y la inferencial de la que hablábamos en la introducción de la Lección 6. Por un lado, es natural medir la variabilidad de un conjunto de datos cuantitativos mediante su varianza “verdadera”, definida como la media de las distancias (al cuadrado) de los datos a su valor promedio; pero, por otro lado, nuestro conjunto de datos será, normalmente, una muestra de una población mucho mayor, de la que querremos estimar información, y en concreto su variabilidad. Por poner un ejemplo, las flores iris recogidas en la tabla de datos iris forman una muestra de la población de todas las flores iris. Con las técnicas de la estadística descriptiva, resumimos y representamos las características de esta muestra concreta; pero este estudio suele ser solo un paso previo al análisis inferencial de estos datos, cuyo objetivo no es analizar esta muestra en si misma, sino inferir información sobre todas las flores iris a partir de esta muestra. Así, lo más probable es que, en realidad, la variabilidad de las longitudes de los sépalos de las flores de iris setosa en esta muestra nos interese sobre todo como estimación de la variabilidad de las longitudes de los sépalos de todas las flores de esta especie.
Pues bien, resulta que la varianza “verdadera” de una muestra tiende a dar valores más pequeños que la varianza real de la población, mientras que la varianza muestral tiende a dar valores alrededor de la varianza real de la población. Para muestras grandes, la diferencia no es sustancial: si \(n\) es grande, dividir por \(n\) o por \(n-1\) no significa una gran diferencia, y sobre todo si tenemos en cuenta que se trata de estimar la varianza de la población, no de calcularla exactamente. Pero si el tamaño de la muestra es pequeño (pongamos, de menos de 25 individuos), la varianza muestral de una muestra aproxima significativamente mejor la varianza real de la población que su varianza “verdadera”. La justificación de este hecho se basa en la teoría de la estimación de parámetros y se sale de los objetivos de este curso.
¿Y por qué definimos la varianza y desviación típica, si ambas medidas dan una información equivalente? El motivo es que si los elementos de una variable cuantitativa tienen unidades (metros, años, individuos por metro cuadrado…), su varianza (sea “verdadera” o muestral) tiene estas unidades al cuadrado; por ejemplo, si los \(x_i\) son años, los valores de \(s^2\) y \(\tilde{s}^2\) representan años al cuadrado. En cambio, las desviaciones típicas tienen las mismas unidades que los datos, por lo que se pueden comparar con ellos, y de ahí su utilidad.
La varianza tiene las propiedades matemáticas siguientes:
\(s^2\geqslant 0\), porque es una suma de cuadrados de numeros reales.
Si \(s^2=0\), todos los sumandos \((x_i-\overline{x})^2\) son 0 y, por lo tanto, todos los datos son iguales a su media. En particular, \(s^2=0\) significa que todos los datos son iguales.
A partir de la fórmula dada para \(s^2\), se tiene que \[ \begin{array}{rl} n\cdot s^2 & \displaystyle = \sum_{i=1}^n (x_i-\overline{x})^2= \sum_{i=1}^n (x_i^2-2\overline{x}x_i+\overline{x}^2)= \sum_{i=1}^n x_i^2-2\sum_{i=1}^n\overline{x}x_i+\sum_{i=1}^n\overline{x}^2\\[2ex] & \displaystyle = \sum_{i=1}^n x_i^2-2\overline{x}\Big(\sum_{i=1}^n x_i\Big)+n\overline{x}^2= \sum_{i=1}^n x_i^2-2\overline{x}\cdot n\overline{x}+n\overline{x}^2= \sum_{i=1}^n x_i^2-n\overline{x}^2 \end{array} \] de donde deducimos que \[ s^2=\frac{\sum_{i=1}^n x_i^2-n\overline{x}^2}{n}= \frac{\sum_{i=1}^n x_i^2}{n}-\overline{x}^2. \] Es decir, la varianza es la media de los cuadrados de los datos, menos el cuadrado de la media de los datos.
Hay que ir con cuidado con la desviación típica y la desviación típica muestral. En los trabajos científicos es frecuente que se utilice una u otra sin especificar cuál es, y se la llame “desviación típica” (standard deviation) y se la denote por \(s\) independientemente de cuál sea en realidad. Asimismo, la mayoría de paquetes estadísticos llevan funciones para calcular la varianza y la desviación típica (sin más aclaraciones) que, en realidad, calculan sus versiones muestrales; como veremos en un momento, éste va ser justamente el caso de R. El motivo es que, como ya hemos comentado, suele interesar más su aspecto inferencial que el descriptivo.
Con R, podemos calcular la medidas de dispersión para un vector \(x\) definidas al principio de esta sección mediante las funciones siguientes:
La instrucción
range(x)nos da sus valores mínimo y máximo. Por lo tanto, su rango se puede calcular condiff(range(x)).Su rango intercuartílico se calcula con
IQR(x). Naturalmente, si se desea, se puede especificar el parámetrotypede los cuantiles.Su varianza muestral se obtiene con la función
var.Su desviación típica muestral se calcula con la función
sd.Para calcular su varianza, tenemos que multiplicar el resultado de
varpor \((n-1)/n\), donde \(n\) es el número de datos que contiene \(x\) (que podemos calcular conlength); por consiguiente, la varianza de \(x\) se puede calcular con la instrucción
var(x)*(length(x)-1)/length(x)- Para calcular su desviación típica, tenemos que efectuar la raíz cuadrada de la varianza, calculada con el procedimiento anterior:
sqrt(var(x)*(length(x)-1)/length(x))sd(...)=sqrt(var(...)), podemos usar:sd(x)*sqrt((length(x)-1)/length(x))¡Id con cuidado! Recordad que las funciones var y sd no calculan la varianza y la desviación típica, sino sus versiones muestrales.
Veamos algunos ejemplos. Consideremos el vector
x=c(1,2,3,4,5,6,2,3,2,3,4,2,2,3,2,2,5,7,3,4,2,1,3,6)- Su rango es
diff(range(x))
#> [1] 6- Su rango intercuartílico es
IQR(x)
#> [1] 2- Su varianza muestral es
var(x)
#> [1] 2.606884- Su desviación típica muestral es
sd(x)
#> [1] 1.614585- Su varianza es
var(x)*(length(x)-1)/length(x)
#> [1] 2.498264- Su desviación típica es
sd(x)*sqrt((length(x)-1)/length(x))
#> [1] 1.58059sqrt(var(x)*(length(x)-1)/length(x))
#> [1] 1.58059Si se aplica la función summary a un vector numérico, se obtiene un resumen estadístico que contiene sus valores mínimo y máximo, sus tres cuartiles y su media.
summary(x)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.000 2.000 3.000 3.208 4.000 7.000La función summary produce otros tipos de resúmenes para otras clases de objetos; por ejemplo, ya vimos en la Lección 3 el resultado de aplicar summary al resultado de una función lm.
Cuando aplicamos la función summary a un data frame, se aplica simultáneamente a todas sus variables, y así de manera rápida podemos observar si hay diferencias apreciables entre sus variables numéricas. A modo de ejemplo, si la aplicamos al data frame formado por las variables numéricas de la tabla iris, obtenemos lo siguiente:
summary(iris[,1:4])
#> Sepal.Length Sepal.Width Petal.Length Petal.Width
#> Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
#> 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
#> Median :5.800 Median :3.000 Median :4.350 Median :1.300
#> Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
#> 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
#> Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500De manera similar, si quisiéramos comparar numéricamente las longitudes de pétalos y sépalos de las flores de especie setosa con las de las flores de especie virgínica, podríamos entrar lo siguiente:
summary(subset(iris, Species=="setosa", c("Sepal.Length","Petal.Length")))
#> Sepal.Length Petal.Length
#> Min. :4.300 Min. :1.000
#> 1st Qu.:4.800 1st Qu.:1.400
#> Median :5.000 Median :1.500
#> Mean :5.006 Mean :1.462
#> 3rd Qu.:5.200 3rd Qu.:1.575
#> Max. :5.800 Max. :1.900
summary(subset(iris, Species=="virginica", c("Sepal.Length","Petal.Length")))
#> Sepal.Length Petal.Length
#> Min. :4.900 Min. :4.500
#> 1st Qu.:6.225 1st Qu.:5.100
#> Median :6.500 Median :5.550
#> Mean :6.588 Mean :5.552
#> 3rd Qu.:6.900 3rd Qu.:5.875
#> Max. :7.900 Max. :6.900y deducimos así a simple vista que los pétalos y sépalos de las iris virgínica son más grandes que los de las iris setosa.
La función by sirve para aplicar una función a algunas columnas de un data frame segmentándolas según los niveles de un factor. Su sintaxis es
by(columnas, factor, FUN=función)Por lo tanto, usando by con FUN=summary, podemos calcular este resumen estadístico en las subpoblaciones definidas por los niveles de un factor. Por ejemplo:
by(iris[, 1:4], iris$Species, FUN=summary)
#> iris$Species: setosa
#> Sepal.Length Sepal.Width Petal.Length Petal.Width
#> Min. :4.300 Min. :2.300 Min. :1.000 Min. :0.100
#> 1st Qu.:4.800 1st Qu.:3.200 1st Qu.:1.400 1st Qu.:0.200
#> Median :5.000 Median :3.400 Median :1.500 Median :0.200
#> Mean :5.006 Mean :3.428 Mean :1.462 Mean :0.246
#> 3rd Qu.:5.200 3rd Qu.:3.675 3rd Qu.:1.575 3rd Qu.:0.300
#> Max. :5.800 Max. :4.400 Max. :1.900 Max. :0.600
#> ------------------------------------------------------------
#> iris$Species: versicolor
#> Sepal.Length Sepal.Width Petal.Length Petal.Width
#> Min. :4.900 Min. :2.000 Min. :3.00 Min. :1.000
#> 1st Qu.:5.600 1st Qu.:2.525 1st Qu.:4.00 1st Qu.:1.200
#> Median :5.900 Median :2.800 Median :4.35 Median :1.300
#> Mean :5.936 Mean :2.770 Mean :4.26 Mean :1.326
#> 3rd Qu.:6.300 3rd Qu.:3.000 3rd Qu.:4.60 3rd Qu.:1.500
#> Max. :7.000 Max. :3.400 Max. :5.10 Max. :1.800
#> ------------------------------------------------------------
#> iris$Species: virginica
#> Sepal.Length Sepal.Width Petal.Length Petal.Width
#> Min. :4.900 Min. :2.200 Min. :4.500 Min. :1.400
#> 1st Qu.:6.225 1st Qu.:2.800 1st Qu.:5.100 1st Qu.:1.800
#> Median :6.500 Median :3.000 Median :5.550 Median :2.000
#> Mean :6.588 Mean :2.974 Mean :5.552 Mean :2.026
#> 3rd Qu.:6.900 3rd Qu.:3.175 3rd Qu.:5.875 3rd Qu.:2.300
#> Max. :7.900 Max. :3.800 Max. :6.900 Max. :2.500Usar by es equivalente a usar aggregate, pero el resultado se muestra de manera diferente. En este caso, era más conveniente usar by. Entrad la instrucción siguiente y lo comprobaréis.
aggregate(cbind(Sepal.Length,Sepal.Width,Petal.Length, Petal.Width)~Species, data=iris, FUN=summary)La mayoría de las instrucciones para calcular medidas estadísticas no admiten valores NA.
z=c(1,2,NA,4)
sum(z)
#> [1] NA
mean(z)
#> [1] NA
var(z)
#> [1] NAPara no tenerlos en cuenta a la hora de calcularlas, lo más conveniente es incluir el parámetro na.rm=TRUE en el argumento de la función.
sum(z, na.rm=TRUE)
#> [1] 7
mean(z, na.rm=TRUE)
#> [1] 2.333333
var(z, na.rm=TRUE)
#> [1] 2.333333Recordad de la Lección 4 que también podéis eliminar los NA de un vector con la función na.omit.
mean(na.omit(z))
#> [1] 2.33333312.5 Diagramas de caja
Un diagrama de caja, o box plot, es un gráfico que resume algunos datos estadísticos de una variable cuantitativa (véase la Figura 12.1). Este gráfico marca básicamente cinco valores:
Los lados inferior y superior de la caja representan el primer y el tercer cuartil, por lo que la altura de la caja es igual al rango intercuartílico.
La línea gruesa que divide la caja marca la mediana.
Los valores \(b_{inf}\) y \(b_{sup}\) son los bigotes (whiskers) del gráfico. Estos valores se calculan de la manera siguiente:
Sea \(m\) el mínimo del conjunto de datos. Si \(m\geqslant Q_{0.25}-1.5\cdot(Q_{0.75}-Q_{0.25})\) (es decir, si el mínimo está a menos de 1.5 veces el rango intercuartílico de \(Q_{0.25}\)), entonces \(b_{inf}=m\). Si, en cambio, \(m< Q_{0.25}-1.5\cdot(Q_{0.75}-Q_{0.25})\), entonces \(b_{inf}\) es el menor elemento del conjunto de datos que es mayor o igual que \(Q_{0.25}-1.5\cdot(Q_{0.75}-Q_{0.25})\).
Sea \(M\) el máximo del conjunto de datos. Si \(M\leqslant Q_{0.75}+1.5\cdot(Q_{0.75}-Q_{0.25})\) (es decir, si el máximo está a menos de 1.5 veces el rango intercuartílico de \(Q_{0.75}\)), entonces \(b_{sup}=M\). Si, en cambio, \(M> Q_{0.75}+1.5\cdot(Q_{0.75}-Q_{0.25})\), entonces \(b_{sup}\) es el mayor elemento del conjunto de datos que es menor o igual que \(Q_{0.75}+1.5\cdot(Q_{0.75}-Q_{0.25})\).
Es decir, los bigotes marcan el mínimo y el máximo de la variable, excepto cuando están muy alejados de la caja intercuartílica; en este caso, el bigote inferior marca el menor valor por debajo de la caja intercuartílica a distancia menor o igual que 1.5 veces la altura de dicha caja, y el superior marca el mayor valor por encima de la caja intercuartílica a distancia menor o igual que 1.5 veces la altura de dicha caja.
Si hay datos más allá de los bigotes (menores que \(b_{inf}\) o mayores que \(b_{sup}\)), se marcan como puntos aislados: son los valores atípicos (outliers) de la variable.
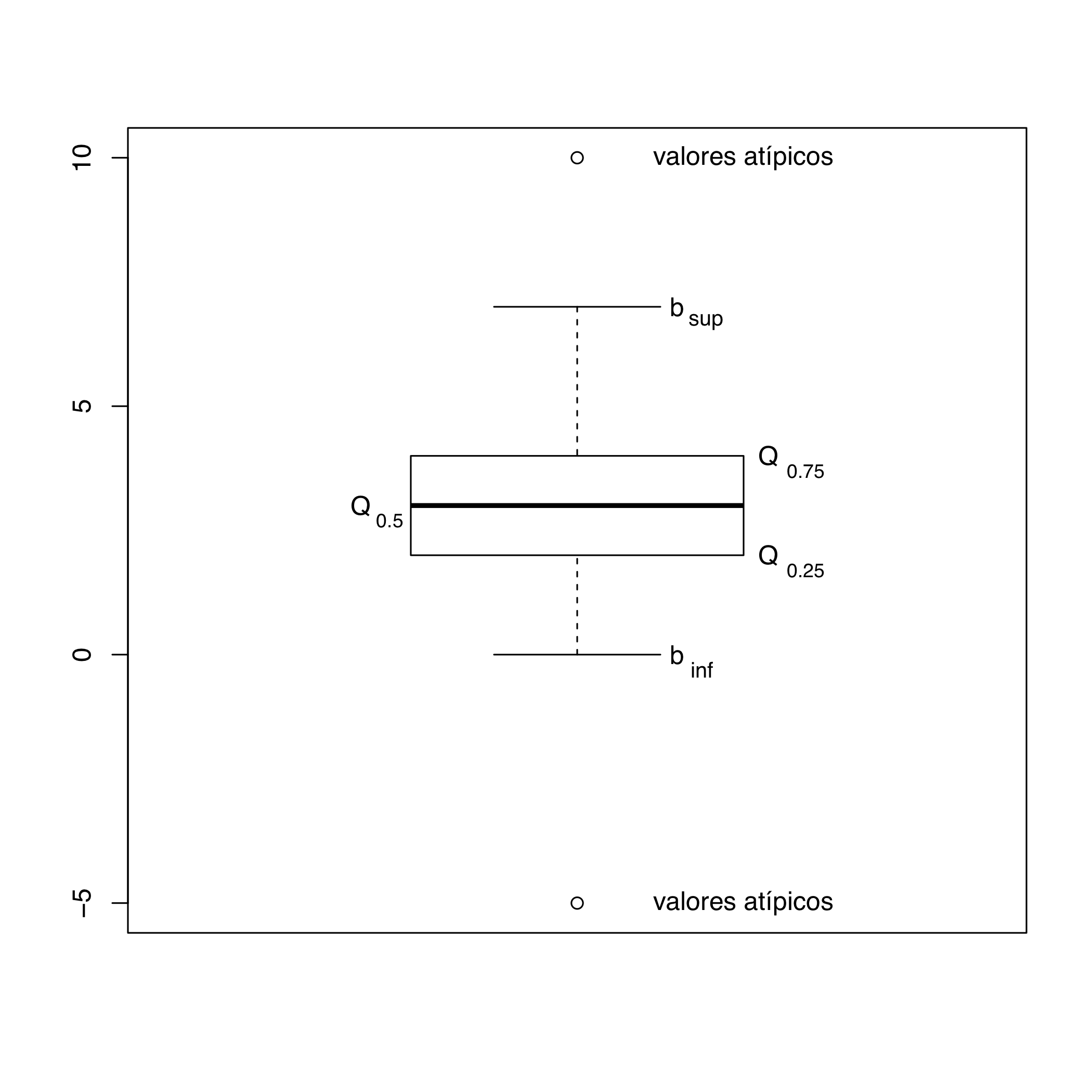
Figura 12.1: Esquema de un diagrama de caja.
La función básica para dibujar un diagrama de caja con R es boxplot. Por ejemplo,
x=c(1,2,3,4,5,6,2,3,2,3,4,2,2,3,2,2,5,7,3,4,2,1,3,6)
boxplot(x)produce la Figura 12.2.
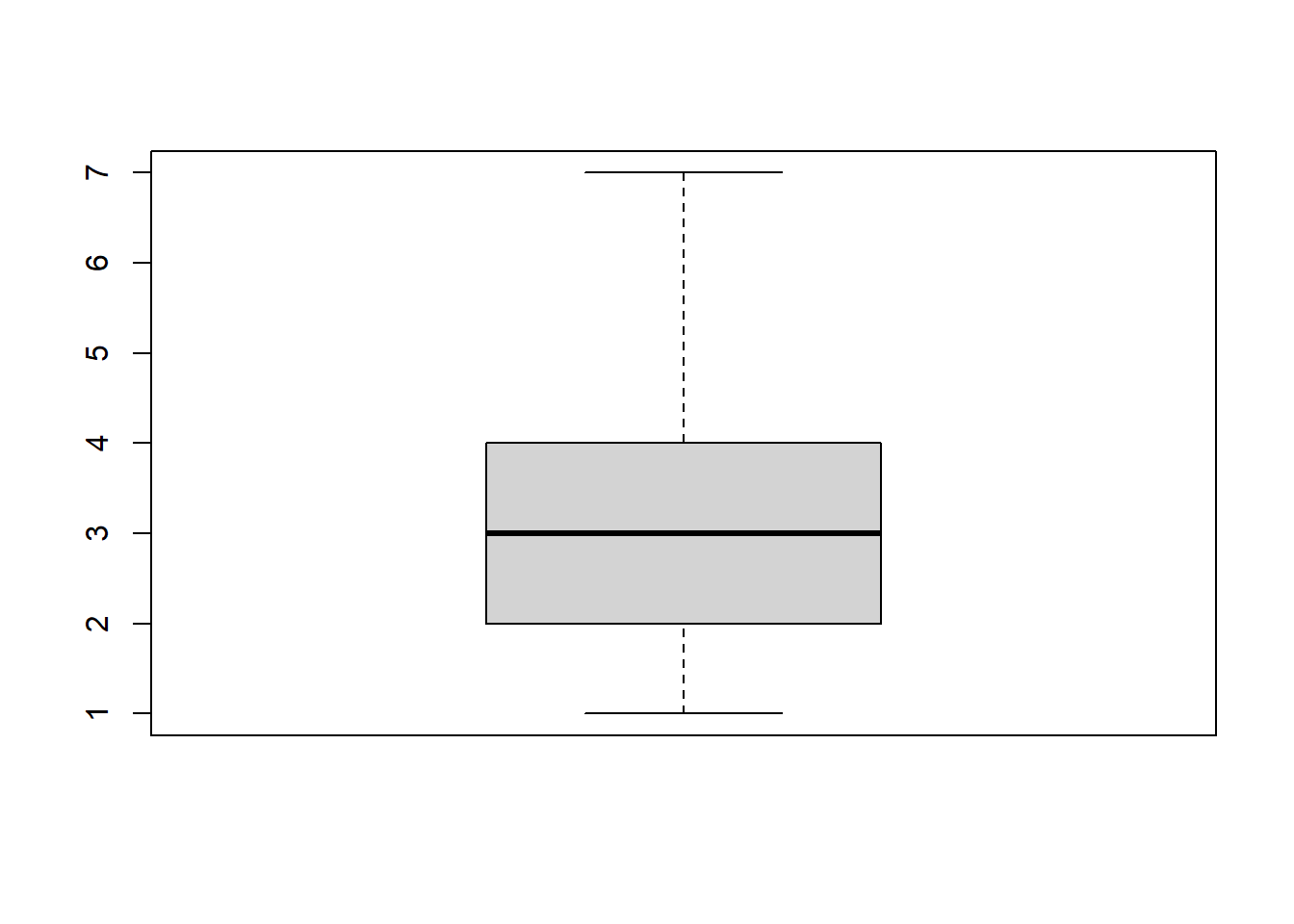
Figura 12.2: Un diagrama de caja.
La instrucción boxplot admite los parámetros usuales de plot para mejorar o hacer más informativo el resultado: main, xlab , ylim, yaxp, col, etc.; podéis consultarlos en su Ayuda. Por ejemplo, si queremos producir un diagrama de caja de las longitudes de pétalos de las flores de especie setosa recogidas en el data frame iris, con más marcas en el eje vertical para facilitar la lectura de los valores y un título oportuno, podemos entrar lo siguiente:
boxplot(iris[iris$Species=="setosa", ]$Petal.Length,
main="Longitudes de pétalos de las Iris setosa", yaxp=c(1,1.9,9)) 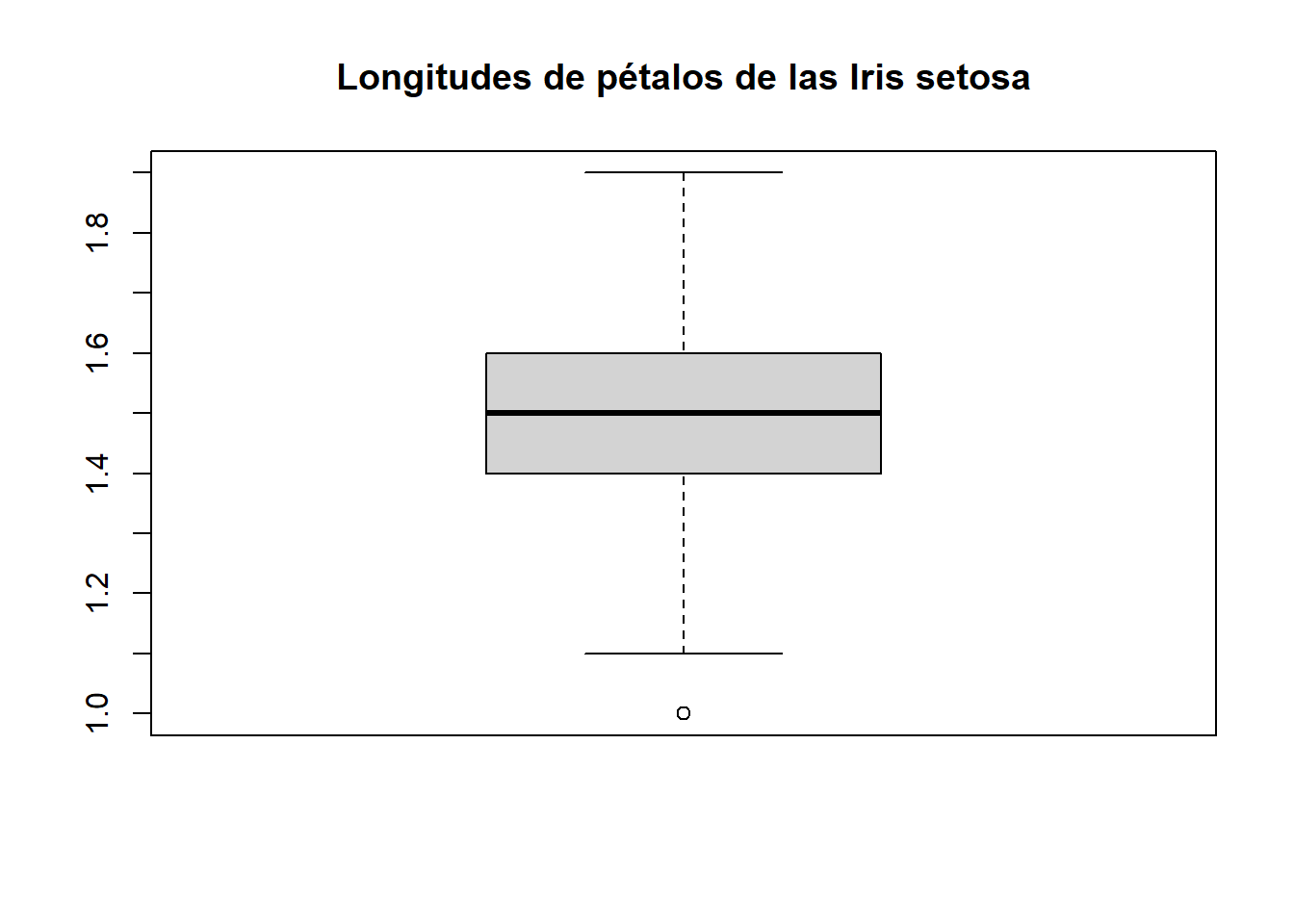
Para dibujar varios diagramas de caja en un mismo gráfico, por ejemplo para poder compararlos, basta aplicar la instrucción boxplot a todos los vectores simultáneamente. Por ejemplo:
x=c(1,2,3,4,5,6,2,3,2,3,4,2,2,3,2,2,5,7,3,4,2,1,3,6)
y=c(5,1,3,5,5,4,1,2,5,5,4,4,1,5,5,4,1,2,6,1)
z=c(3,5,6,1,2,3,1,2,5,1,5,2,4,2,6,5,2,1,4,4,1,6,5,5,4,6,4,5,4,5)
boxplot(x, y, z, names=c("x","y","z"))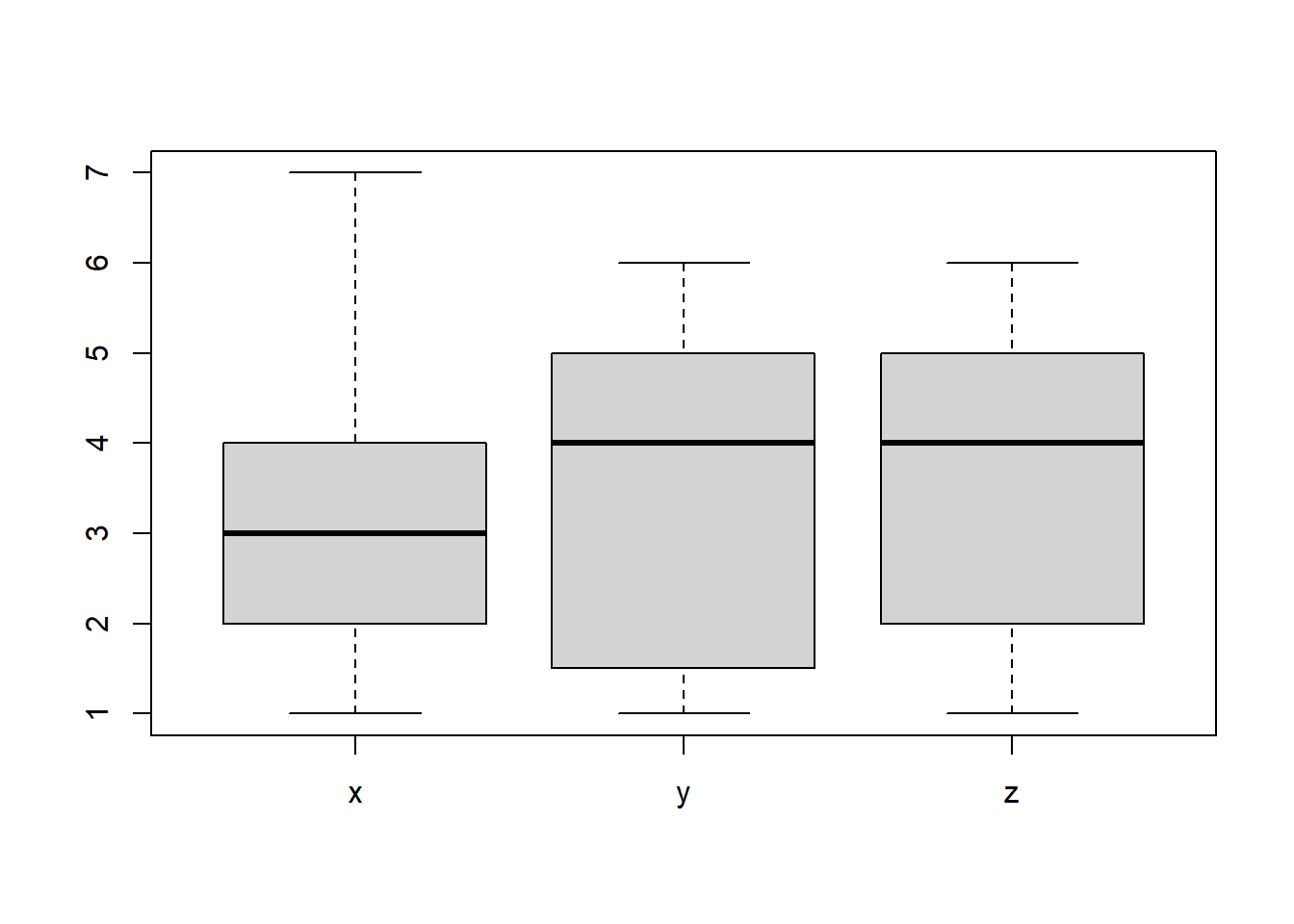
Observad que en la función boxplot del bloque anterior hemos usado el parámetro names para especificar las etiquetas de los diagramas de caja: de lo contrario, el gráfico hubiera sido más difícil de interpretar, probadlo.
Si preferís las cajas horizontales, podéis usar el parámetro horizontal=TRUE:
boxplot(x, y, z, names=c("x","y","z"), horizontal=TRUE)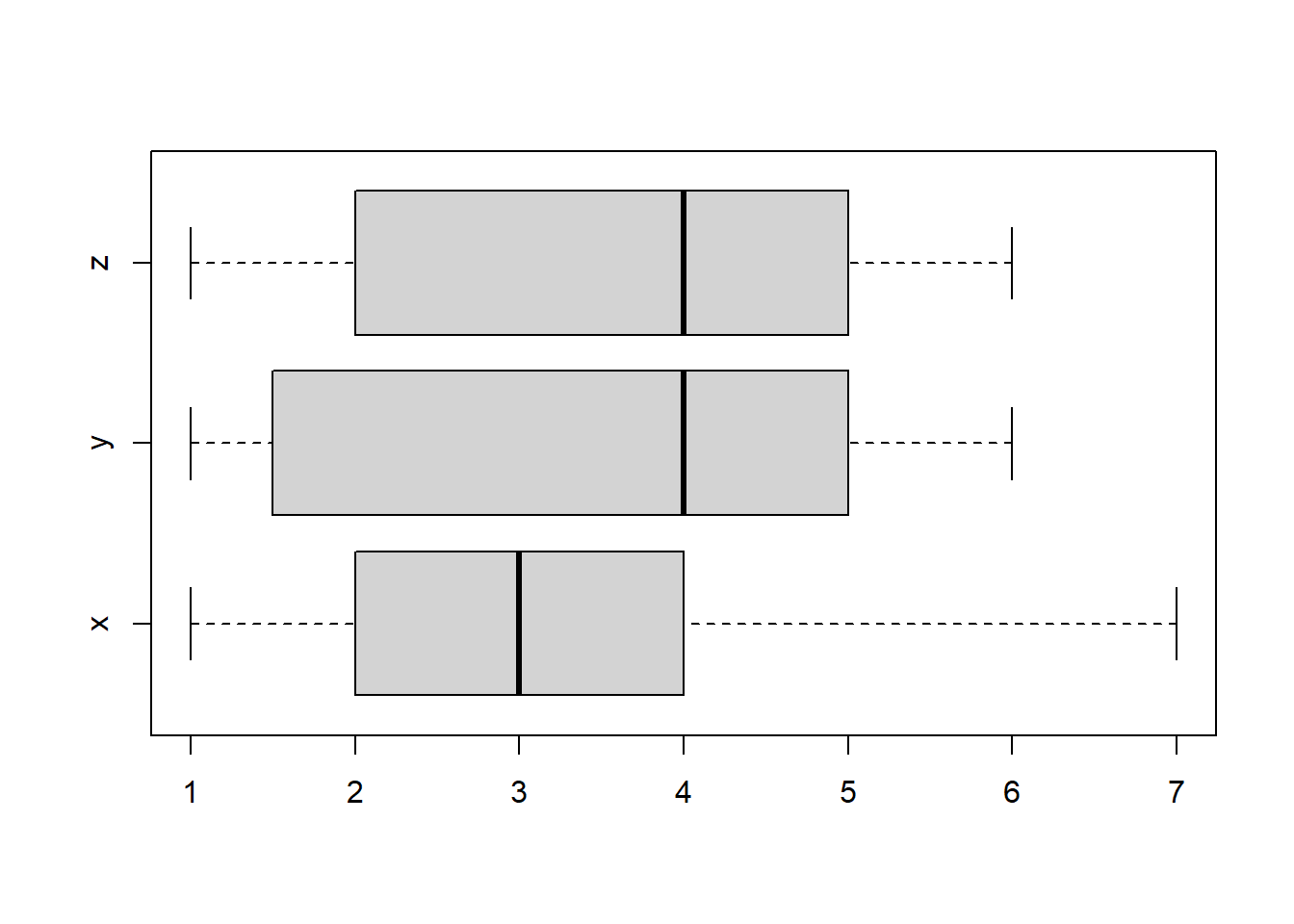
Podemos dibujar los diagramas de caja de todas las variables de un data frame en un solo paso, aplicando la función boxplot al data frame; por ejemplo:
boxplot(iris)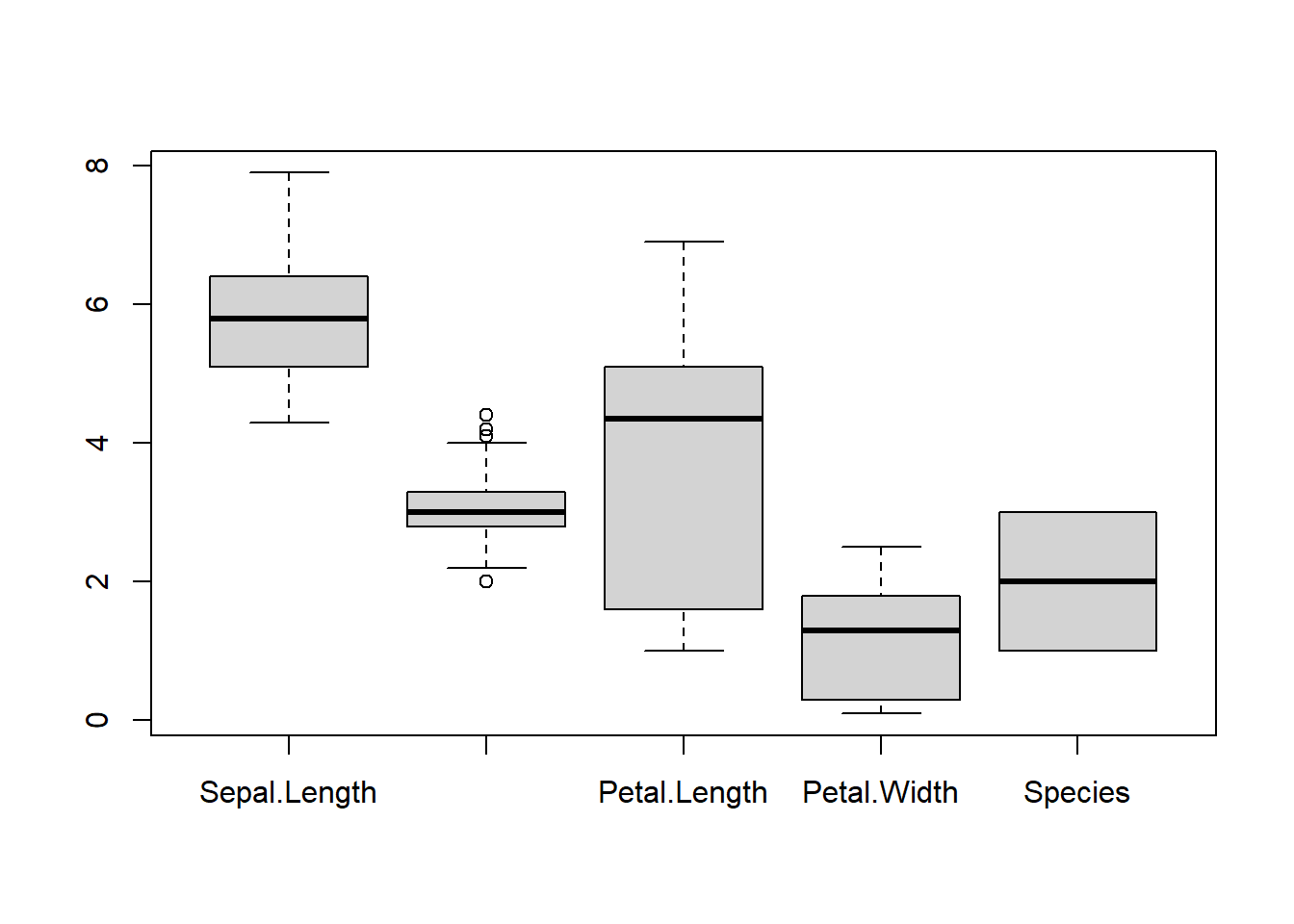
Observaréis que este gráfico no es muy satisfactorio. Dibujar el diagrama de caja de la variable Species, que es un factor, no tiene ningún sentido, y los nombres, además, no han quedado muy vistosos; podemos mejorar este gráfico, incluyendo solo las cuatro primeras variables y cambiando un poco los nombres, con la instrucción siguiente:
boxplot(iris[, 1:4], names=c("Sepal\n length","Sepal\n width","Petal\n length","Petal\n width"))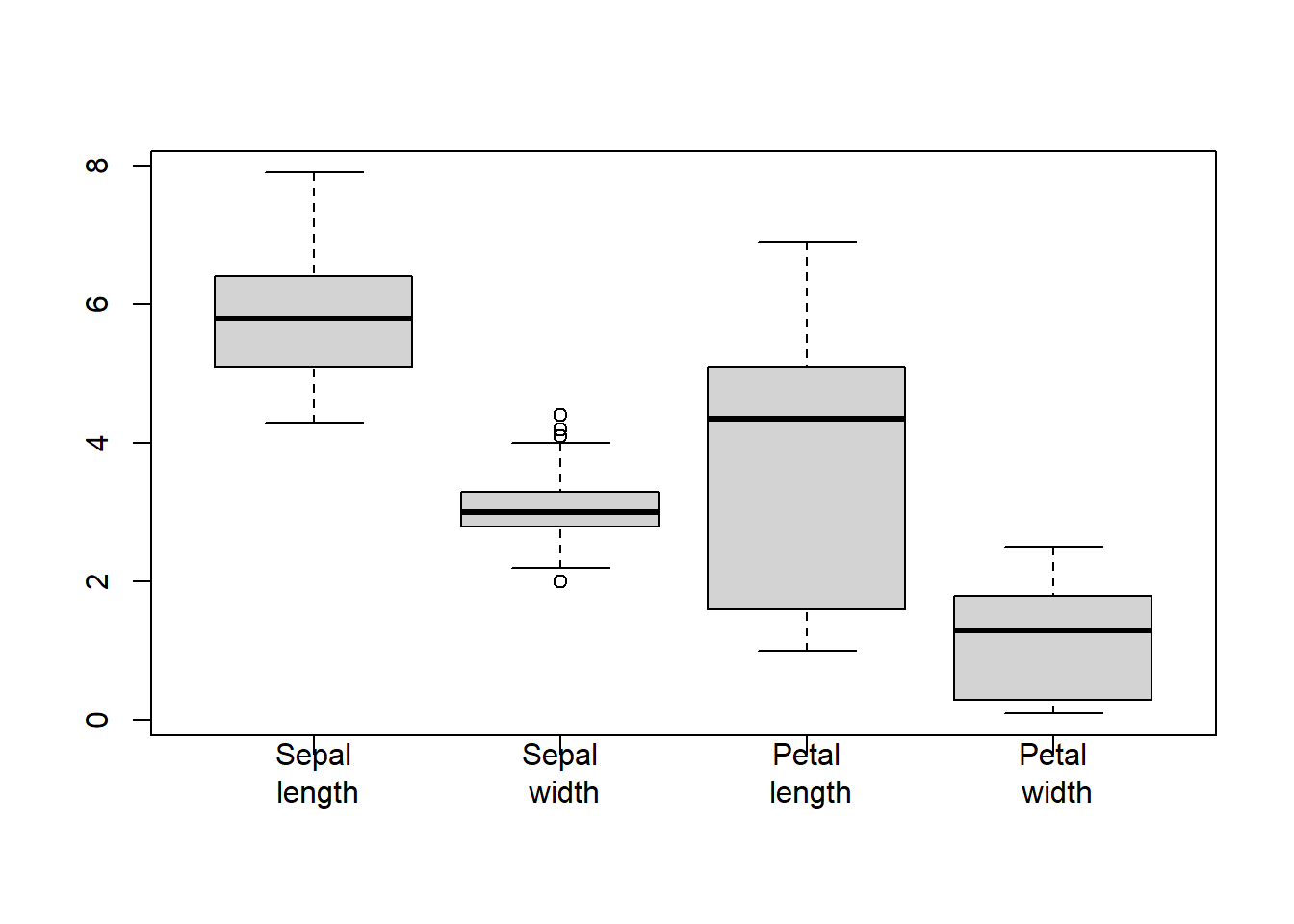
El objetivo de agrupar varios diagramas de caja en un único gráfico suele ser el poder compararlos visualmente, y esto normalmente solo tiene sentido cuando las variables tienen significados muy similares, o mejor, cuando son la misma variable sobre poblaciones diferentes. En concreto, a menudo querremos producir diagramas de caja de una variable cuantitativa segmentada por un factor, porque esto nos permitirá comparar el comportamiento de esta variable sobre cada uno de los niveles del factor. La manera más conveniente de hacerlo es partir de un data frame donde el factor sea una variable, digamos, F, y el vector de datos numéricos otra variable, digamos, X. Entonces, para cada nivel L de F, obtendremos un diagrama de caja de los valores que toma la variable X en los individuos de nivel L.
La sintaxis básica de la instrucción para dibujar en un único gráfico los diagramas de caja de una variable numérica de un data frame segmentada por un factor del data frame es
boxplot(variable numérica~factor, data=data frame)A modo de ejemplo, para dibujar en un único gráfico un diagrama de caja de la variable Sepal.Length del data frame iris para cada uno de los niveles del factor Species, podemos entrar
boxplot(Sepal.Length~Species, data=iris, ylab="Longitudes de sépalos (cm)")y obtenemos la Figura 12.3, donde podemos observar diferencias sustanciales entre las longitudes de los sépalos de las tres especies, y además un valor inusualmente pequeño en el conjunto de valores de las flores virgínica.
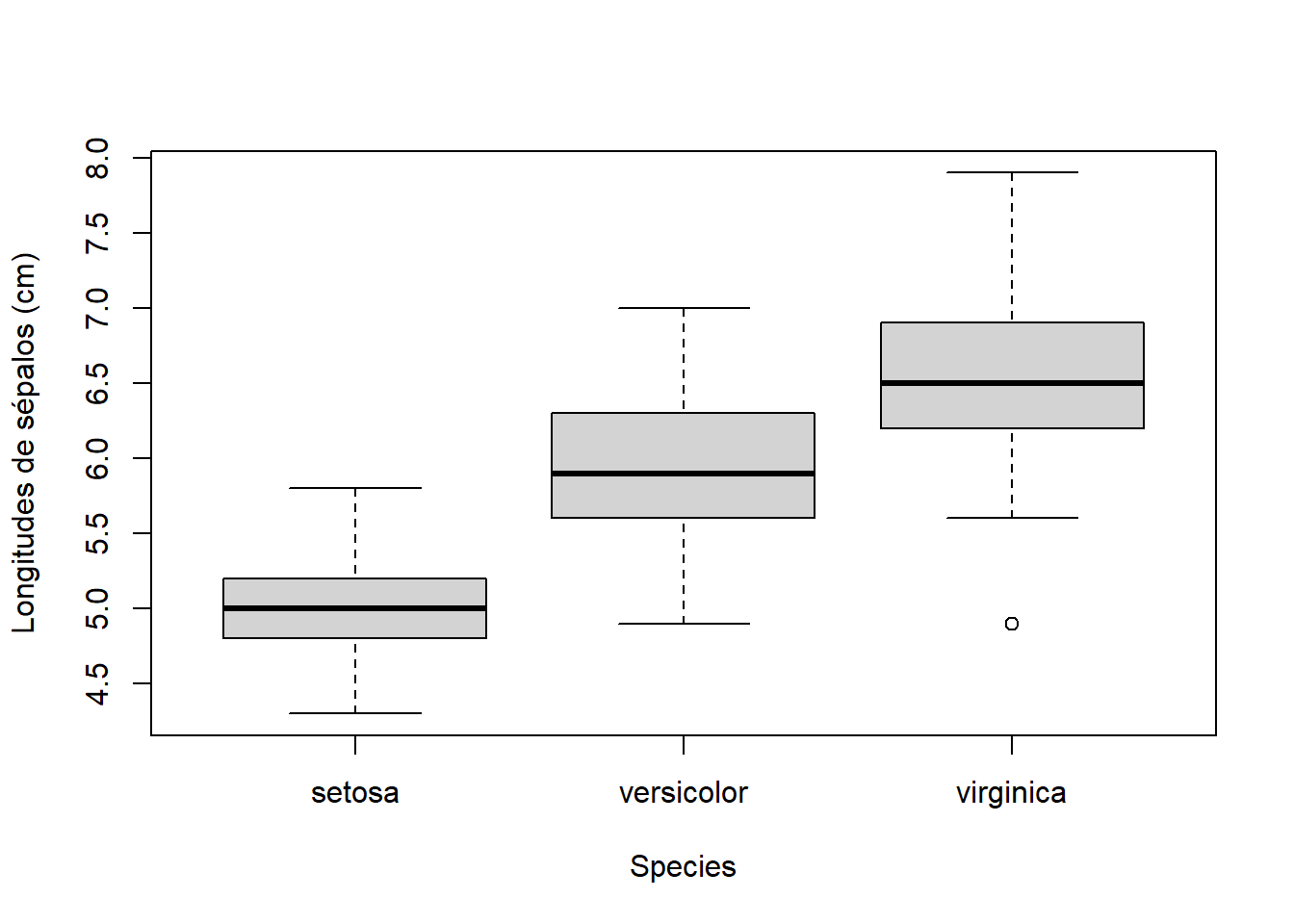
Figura 12.3: Diagramas de caja de las longitudes de sépalos de las flores iris agrupadas por especies.
Aparte de los parámetros de la función plot que tengan sentido,
la función boxplot dispone de algunos parámetros específicos. Destacamos el parámetro notch que, igualado a TRUE, añade una muesca en la mediana de cada caja. Estas muescas se calculan de tal manera que si las de dos diagramas de caja no se solapan, se puede tomar como evidencia significativa de que las medianas de las poblaciones correspondientes son diferentes; por ejemplo,
boxplot(Sepal.Length~Species, data=iris, notch=TRUE,
ylab="Longitudes de sépalos (cm)", col=c("red","blue","green"))produce el gráfico de la Figura 12.4 donde, colores aparte, vemos que las muescas no se solapan, lo que nos permite afirmar con un alto grado de confianza que las medianas de las longitudes de los sépalos de las tres especies de flores iris son diferentes (en general, y no solo para la muestra concreta recogida en el data frame). Este tipo de conclusiones son las que persigue la estadística inferencial.
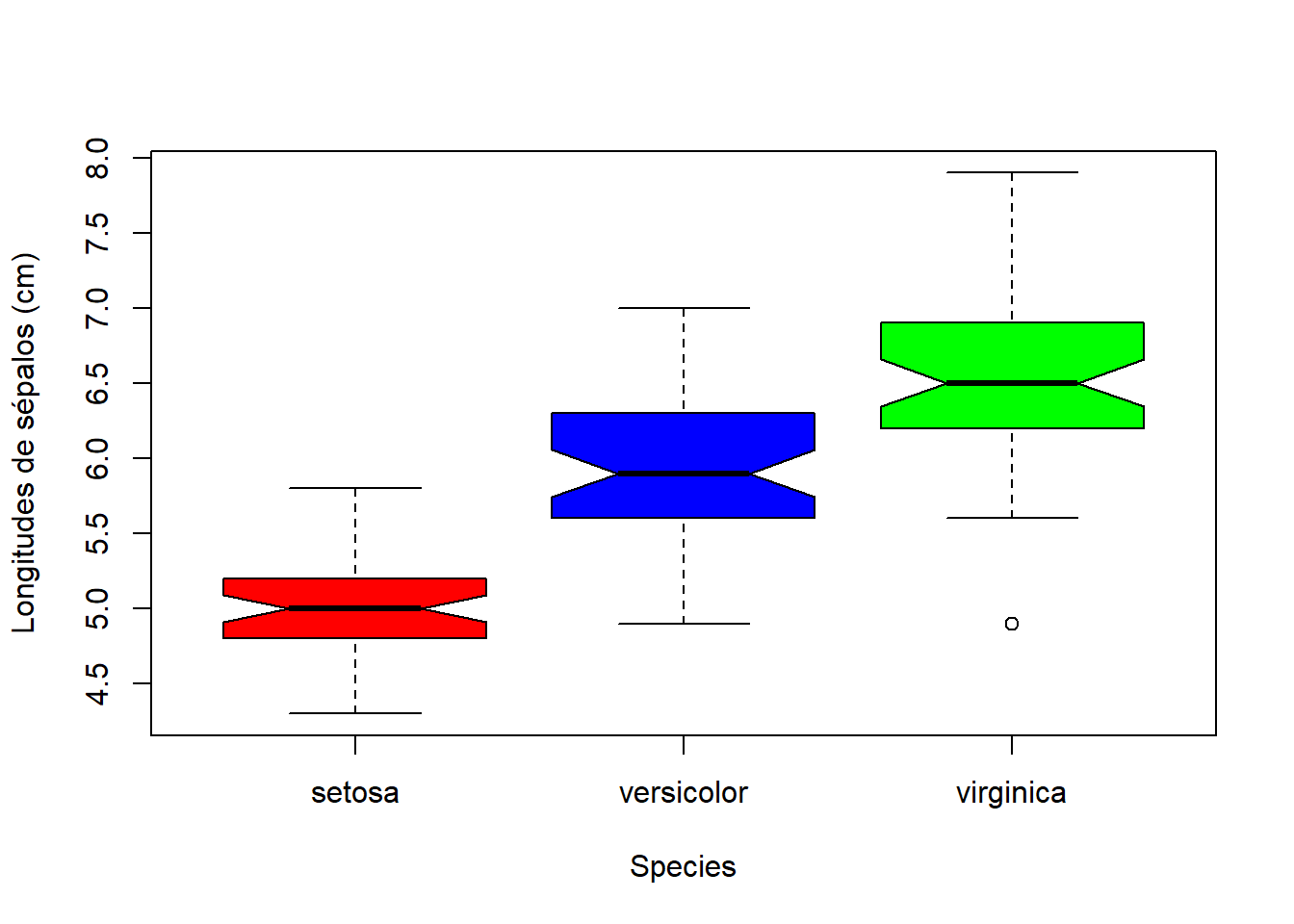
Figura 12.4: Diagramas de caja con muescas de las longitudes de sépalos de las flores iris agrupadas por especies.
A veces es útil superponer a un diagrama de caja una marca en el valor correspondiente a la media aritmética. Para ello se puede usar la función points. Considerad el bloque de código siguiente. Su primera instrucción produce el diagrama de caja de las longitudes de los sépalos de las flores iris agrupadas según la especie, de color gris claro; la segunda, calcula las medias de dichas longitudes para cada especie; finalmente, la tercera, añade al diagrama de caja de cada especie un diamante rojo en la ordenada correspondiente al valor de su media.
boxplot(Sepal.Length~Species, data=iris, col="lightgray")
medias=aggregate(Sepal.Length~Species, data=iris, FUN=mean)
points(medias, col="red", pch=18)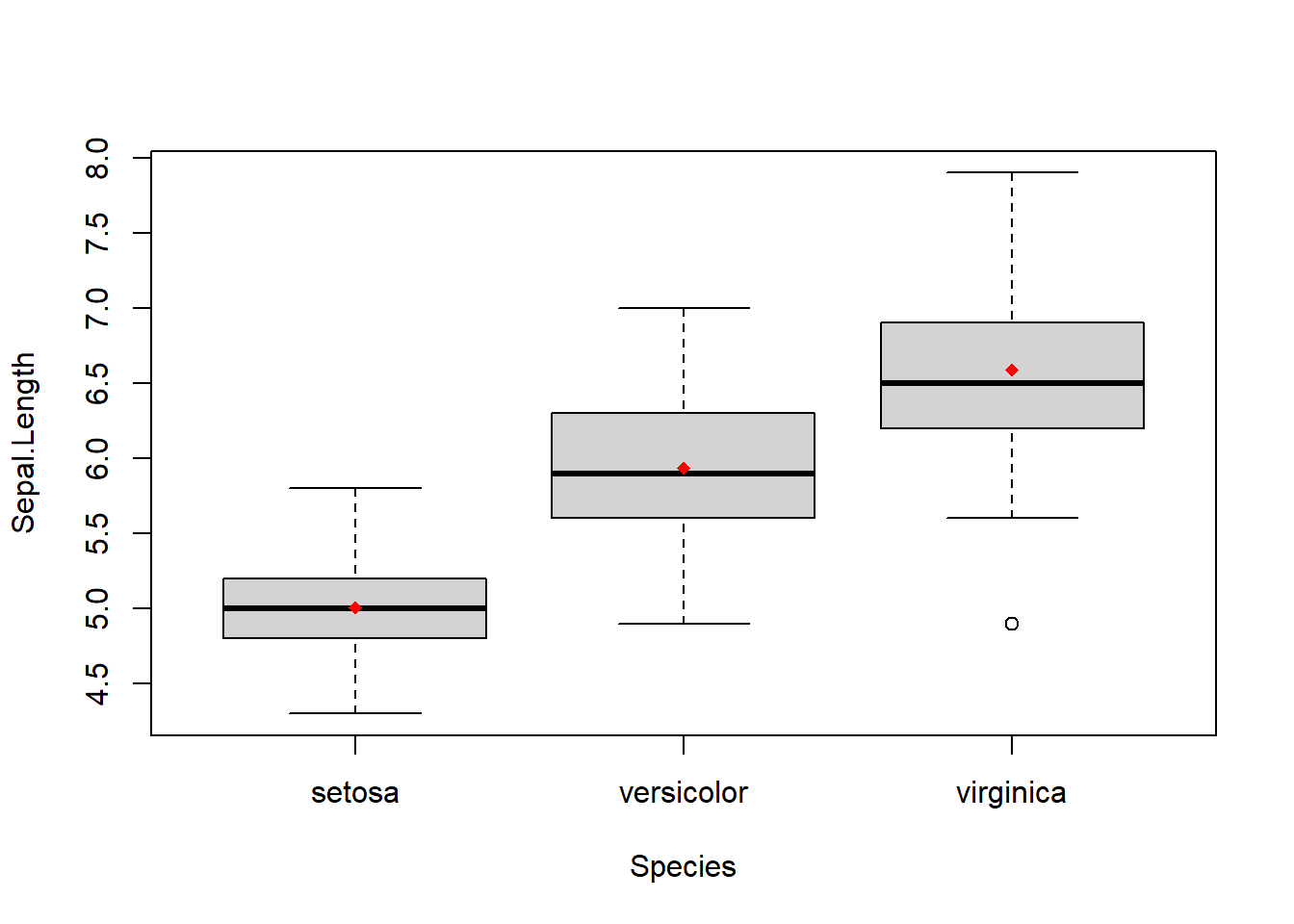
El resultado de una instrucción boxplot tiene una estructura interna que podemos aprovechar. Observemos, por ejemplo, el resultado de la instrucción siguiente (el parámetro plot=FALSE indica que no dibuje el boxplot):
str(boxplot(Sepal.Length~Species, data=iris, plot=FALSE))
#> List of 6
#> $ stats: num [1:5, 1:3] 4.3 4.8 5 5.2 5.8 4.9 5.6 5.9 6.3 7 ...
#> $ n : num [1:3] 50 50 50
#> $ conf : num [1:2, 1:3] 4.91 5.09 5.74 6.06 6.34 ...
#> $ out : num 4.9
#> $ group: num 3
#> $ names: chr [1:3] "setosa" "versicolor" "virginica"Esto muestra que un boxplot, como objeto de R, es en realidad una list. Los significados de sus componentes se pueden consultar en la Ayuda de la función. Aquí queremos destacar las siguientes:
statsnos da, para cada diagrama de caja en el gráfico, los valores corresondientes a sus cinco líneas horizontales: \(b_{inf}, Q_{0.25}, Q_{0.5}, Q_{0.75}, b_{sup}\).
boxplot(Sepal.Length~Species, data=iris, plot=FALSE)$stats
#> [,1] [,2] [,3]
#> [1,] 4.3 4.9 5.6
#> [2,] 4.8 5.6 6.2
#> [3,] 5.0 5.9 6.5
#> [4,] 5.2 6.3 6.9
#> [5,] 5.8 7.0 7.9outnos da los valores atípicos. Si hay más de un diagrama de caja, la componentegroupnos indica los diagramas a los que pertenecen estos valores atípicos.
boxplot(Sepal.Length~Species, data=iris, plot=FALSE)$out
#> [1] 4.9
boxplot(Sepal.Length~Species, data=iris, plot=FALSE)$group
#> [1] 3Ejemplo 12.4 Recordemos del Ejemplo 11.6 el data frame InsectSprays que viene predefinido en R. Este data frame tiene una variable factor spray con 6 niveles que corresponden a tipos de insecticidas, y una variable numérica count que contiene números de insectos recolectados en campos tratados con los insecticidas. En aquel ejemplo convertimos la variable count en una variable ordinal, pero está claro que se trata de una variable cuantitativa; por lo tanto, podemos usar las técnicas explicadas en esta lección para comparar de manera más significativa la efectividad de los insecticidas a partir de los datos brutos de esta variable.
En primer lugar, obtenemos un resumen estadístico de los números de insectos recogidos en los campos tratados con cada tipo de insecticida.
by(InsectSprays$count, InsectSprays$spray, FUN=summary)
#> InsectSprays$spray: A
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 7.00 11.50 14.00 14.50 17.75 23.00
#> ------------------------------------------------------------
#> InsectSprays$spray: B
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 7.00 12.50 16.50 15.33 17.50 21.00
#> ------------------------------------------------------------
#> InsectSprays$spray: C
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.000 1.000 1.500 2.083 3.000 7.000
#> ------------------------------------------------------------
#> InsectSprays$spray: D
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 2.000 3.750 5.000 4.917 5.000 12.000
#> ------------------------------------------------------------
#> InsectSprays$spray: E
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.00 2.75 3.00 3.50 5.00 6.00
#> ------------------------------------------------------------
#> InsectSprays$spray: F
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 9.00 12.50 15.00 16.67 22.50 26.00Echando un vistazo a las columnas de las medianas y medias vemos que los insecticidas C, D y E son, en término medio, más efectivos que A, B y F. Como una imagen vale más que mil palabras, a continuación dibujamos en un gráfico los diagramas de caja de los valores de count separados por los niveles de spray.
boxplot(count~spray, data=InsectSprays, ylab="Número de insectos",
xlab="Tipo de insecticida", col="pink")Obtenemos la Figura 12.5, que muestra a simple vista la diferencia en la efectividad de los insecticidas. También se ve en este gráfico que los números de insectos obtenidos en los campos tratados con los insecticidas C, D y E presentan una menor variabilidad que el resto, puesto que sus cajas intercuartílicas son mucho más cortas; lo podemos confirmar calculando las correspondientes desviaciones típicas muestrales.
aggregate(count~spray, data=InsectSprays, FUN=sd)
#> spray count
#> 1 A 4.719399
#> 2 B 4.271115
#> 3 C 1.975225
#> 4 D 2.503028
#> 5 E 1.732051
#> 6 F 6.213378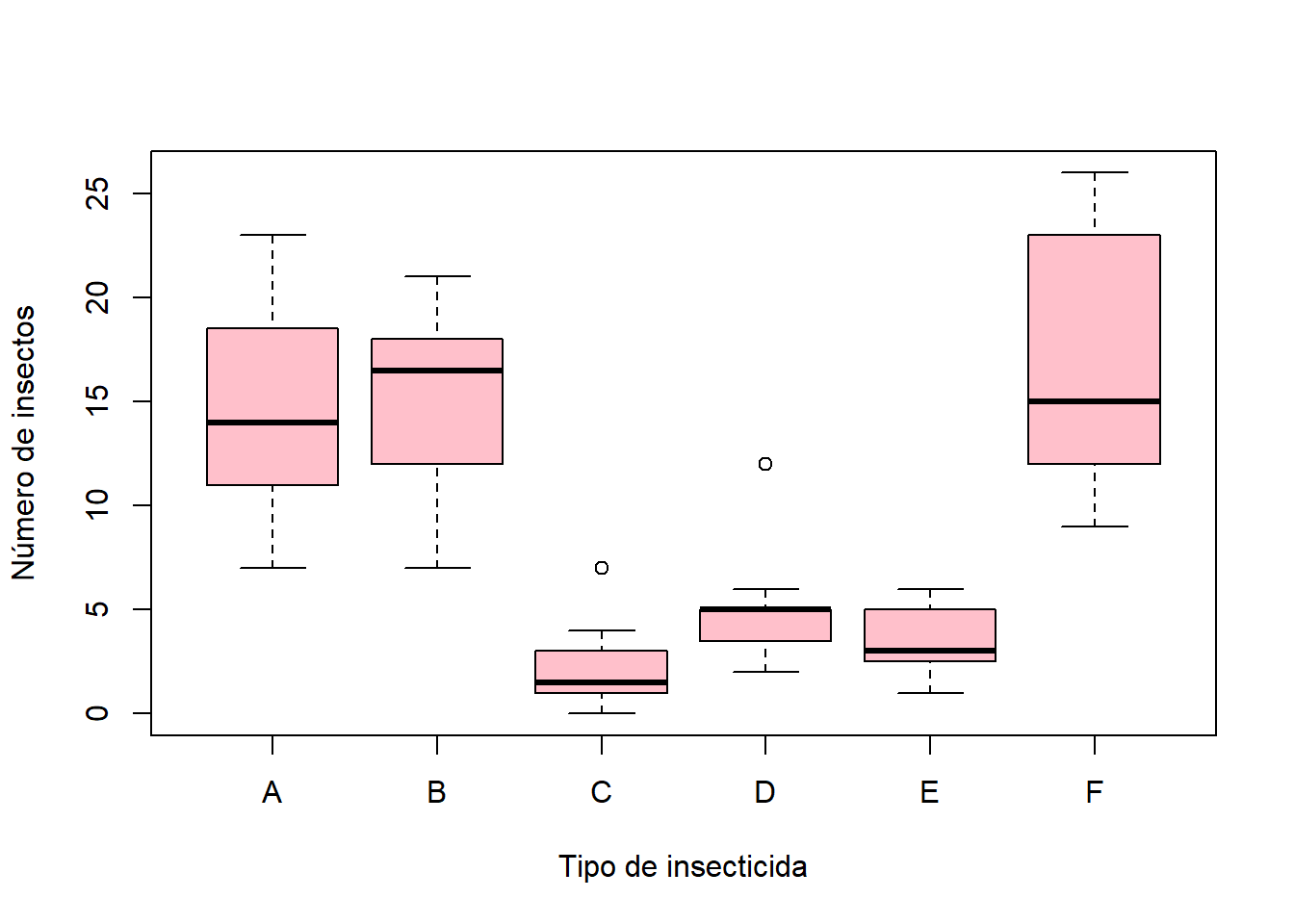
Figura 12.5: Diagramas de caja de los números de insectos en campos tratados con diferentes insecticidas.
12.6 Guía rápida de funciones
tablecalcula la tabla de frecuencias absolutas de un vector.prop.tablecalcula la tabla de frecuencias relativas de un vector a partir de su tabla de frecuencias absolutas.cumsumcalcula las sumas acumuladas de un vector.as.vectortransforma un objeto en un vector.meancalcula la media de un vector numérico.mediancalcula la mediana de un vector numérico.as.numeric(names(which(table(x)==max(table(x)))))calcula la moda del vector \(x\).quantile(x, p)calcula el cuantil de orden \(p\) del vector numérico \(x\). El parámetrotypepermite especificar el método.rangeproduce un vector con el mínimo y el máximo de un vector numérico.IQRcalcula el rango intercuartílico de un vector numérico. El parámetrotypepermite especificar el método de cálculo de los cuartiles.varcalcula la varianza muestral de un vector numérico.sdcalcula la desviación típica muestral de un vector numérico.summary, aplicado a un vector numérico, calcula sus extremos, sus cuartiles y su media; aplicado a un data frame, calcula resúmenes similares para todas sus variables.by(data frame,factor, FUN=función)aplica lafuncióna las variables del data frame segmentadas según el factor.boxplotdibuja los diagramas de caja de los vectores numéricos a los que se aplica. Algunos parámetros importantes:Los de
plotque tengan sentido.horizontal: igualado aTRUE, dibuja las cajas horizontales.names: sirve para especificar los nombres bajo los diagramas de caja en un gráfico que contenga varios.notch: dibuja cinturas alrededor de las medianas que permiten contrastar si las medianas poblacionales son diferentes.plot: igualado aFALSEcalcula el diagrama de caja, pero no lo dibuja.
Como objeto de datos, el resultado de esta función es una
listentre cuyas componentes destacamos:stats: contiene, para cada diagrama de caja en el gráfico, sus valores \(b_{inf}, Q_{0.25}, Q_{0.5}, Q_{0.75}, b_{sup}\).out: contiene los valores atípicos.group: indica los diagramas a los que pertenecen los valores atípicos.
12.7 Ejercicios
Test
(1) ¿Qué vale la mediana de la variable BH de la tabla http://aprender.uib.es/Rdir/ESD.txt?
(2) ¿Qué vale la varianza de la variable BH de la tabla http://aprender.uib.es/Rdir/ESD.txt? Dad su valor redondeado a 2 cifras decimales.
(3) La tabla DNase es uno de los data frames que lleva predefinidos R. Con una sola instrucción, dibujad un diagrama de cajas básico de la variable density de este data frames agrupada por su factor Run. Y antes de contestar, por favor, comprobad que funciona.
(4) Considerad la tabla de datos happy del paquete faraway. ¿Cuál de los cuatro valores de la variable work da un valor medio mayor de la variable money?
(5) Considerad de nuevo la tabla de datos happy del paquete faraway. ¿Qué vale la varianza, redondeada a 3 cifras decimales, de los valores que toma la variable happy entre los individuos de esta tabla que tienen una actividad sexual satisfactoria?
(6) Considerad de nuevo el data frame DNase que lleva predefinido R. Da el valor, redondeado a 3 cifras decimales, del bigote superior en el diagrama de caja de su variable density y responded, con SI o NO, si esta variable contiene valores atípicos por encima del bigote superior. Dad las dos respuestas en este orden y separadas por un espacio en blanco.
Ejercicio
Considerad de nuevo la tabla del ejercicio de la lección anterior, que se encuentra en http://aprender.uib.es/Rdir/Notas2011A.txt.
Definid un data frame con esta tabla, y comprobad con str y head que el data frame obtenido tiene la estructura deseada.
(a) Calculad la media, la mediana y la desviación típica (redondeadas a 2 cifras decimales) de las notas numéricas del examen, tanto globalmente como por grupos. ¿En qué grupo hay más variación de notas? ¿Qué grupo tiene la nota media más alta? ¿Hay mucha diferencia en estos dos valores entre los grupos?
(b) Dibujad en un único gráfico los diagramas de caja de las notas numéricas del examen de cada grupo; añadid marcas en las notas medias; poned nombres, título, etc., para que resulte más informativo. ¿Tiene algún grupo algún valor atípico? ¿Podéis decir a partir de este gráfico en qué grupo hay más variación de notas?
(c) Agrupad los estudiantes de los dos grupos de Biología, BLM y BLT, en uno solo, BL, y repetid los dos puntos anteriores para los grados BL y BQ.
(d) ¿Podéis extraer alguna conclusión sobre si el examen ha ido mejor en algún grupo que en los demás, o mejor en un grado que en el otro?
Respuestas al test
(1) 133
(2) 24.23
(3) boxplot(DNase$density~DNase$Run) o boxplot(density~Run,data=DNase)
(4) 4
(5) 3.097
(6) 2.003 NO