Lección 7 Gráficos básicos

El objetivo de esta lección es introducir los aspectos básicos de los gráficos que se obtienen por medio de la función plot. Muchos de los parámetros y funciones auxiliares que explicamos en esta lección se podrán usar más adelante en otras funciones que producen tipos específicos de gráficos en estadística descriptiva.

7.1 La función plot

Dada una familia de puntos \[ (x_1, y_1), \ldots, (x_n, y_n), \] podemos usar la función plot para dibujar su gráfico. La construcción básica para hacerlo es

plot(x, y)

donde \(x=(x_1, \ldots, x_n)\) es el vector de las primeras coordenadas de los puntos e \(y=(y_1, \ldots, y_n)\) el vector de sus segundas coordenadas. Por ejemplo, para dibujar el gráfico de los puntos

(2, 1), (5, 7), (6, 3), (3, 2), (4, 1),

basta entrar

x=c(2,5,6,3,4)
y=c(1,7,3,2,1)
plot(x, y)

y obtenemos la Figura 7.1.

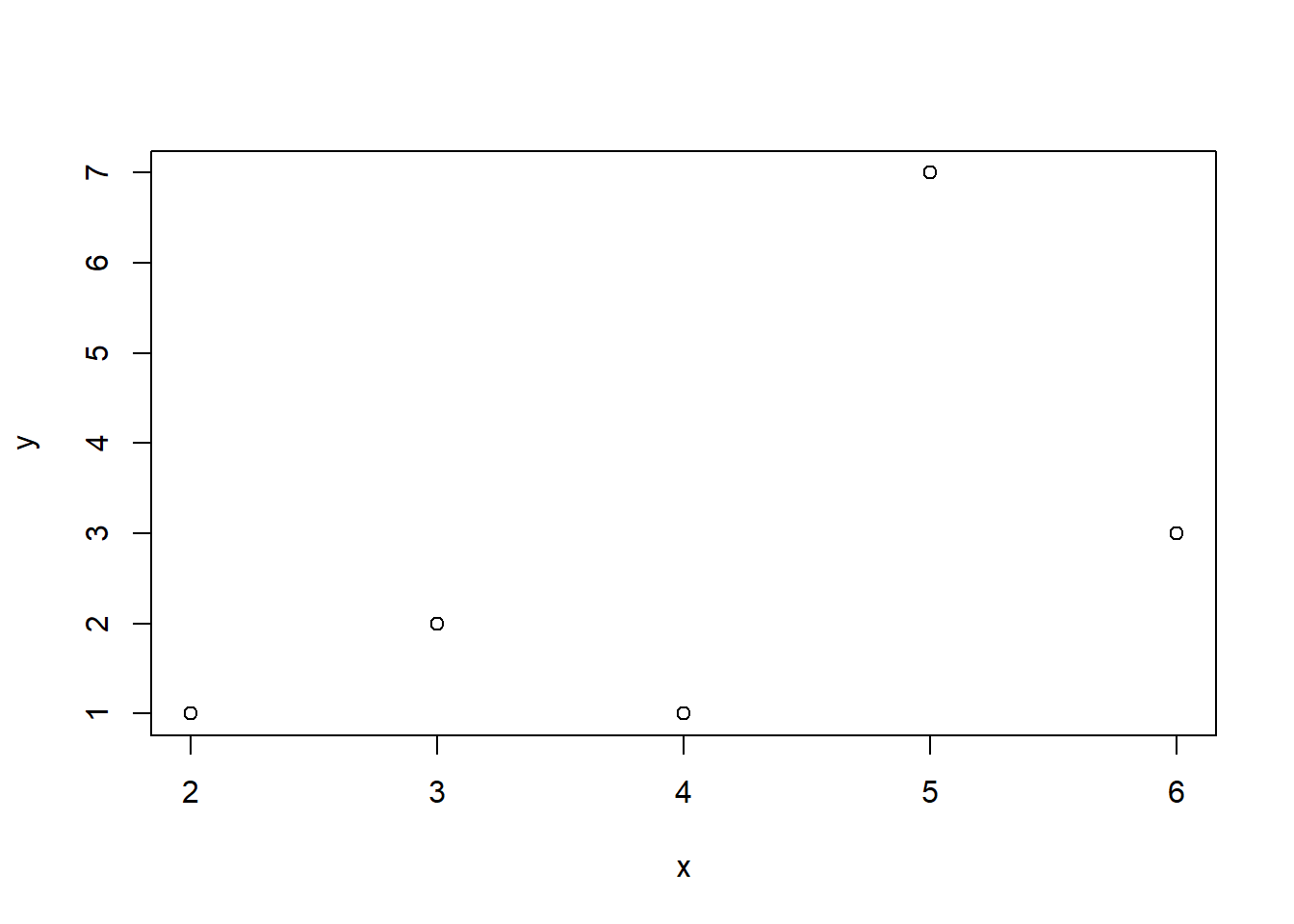
Gráfico básico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1).

Figura 7.1: Gráfico básico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1).

Cuando aplicamos plot a un solo vector \((x_1, \ldots, x_n)\), R produce el gráfico de los puntos \[ (1, x_1), \ldots, (n, x_n). \] Es decir, si el vector tiene longitud \(n\), plot(x) es una abreviatura de plot(1:n, x). Así, la Figura 7.2 se obtiene con la siguiente instrucción:

plot(2^(1:10))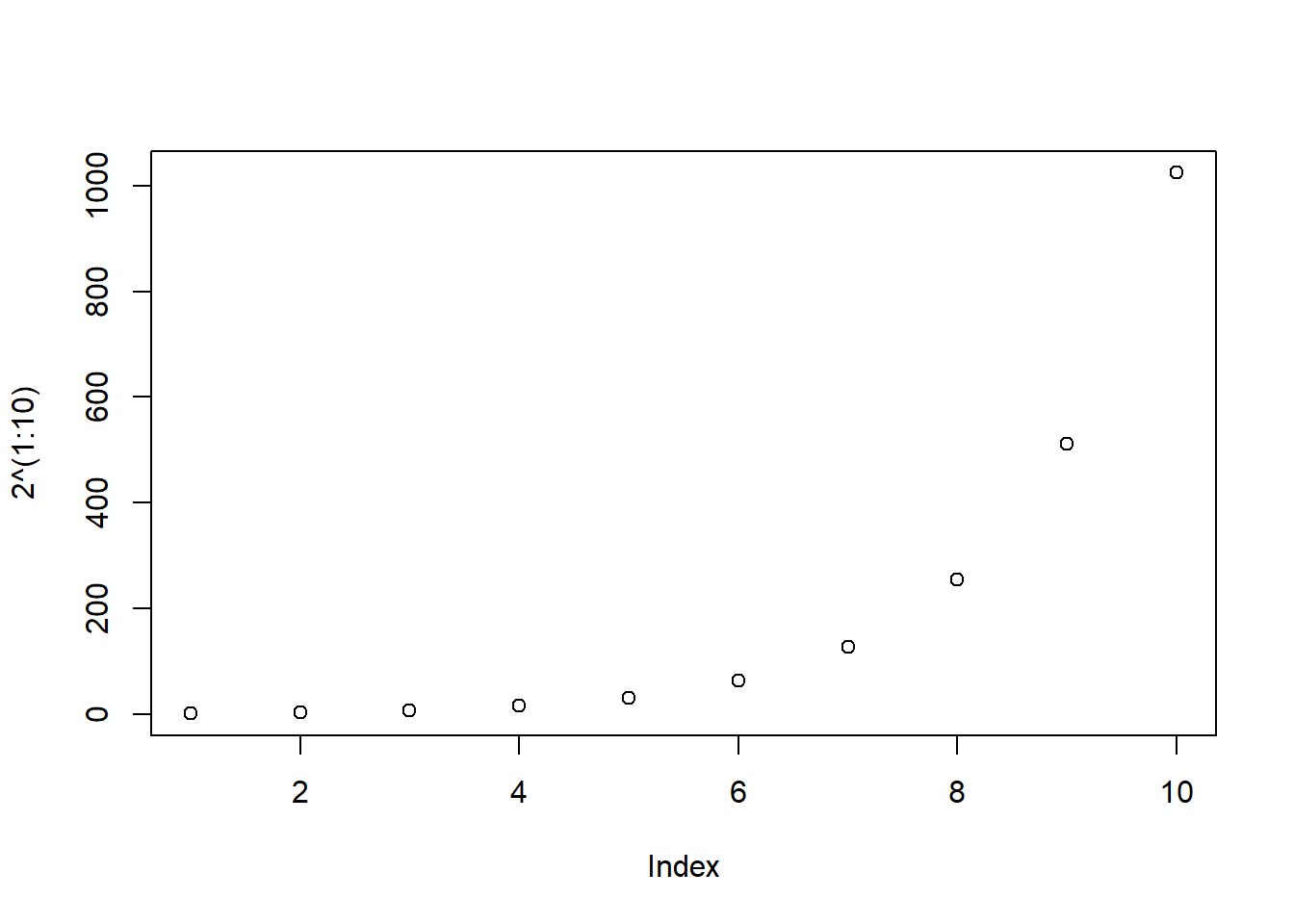
Gráfico básico de las diez primeras potencias de 2.

Figura 7.2: Gráfico básico de las diez primeras potencias de 2.

La función plot también sirve para dibujar el gráfico de una función definida mediante function. Por ejemplo, el código siguiente produce la gráfica de la parábola \(y=x^2\) entre \(x=0\) y \(x=1\) de la Figura 7.3:

f=function(x){x^2}
plot(f)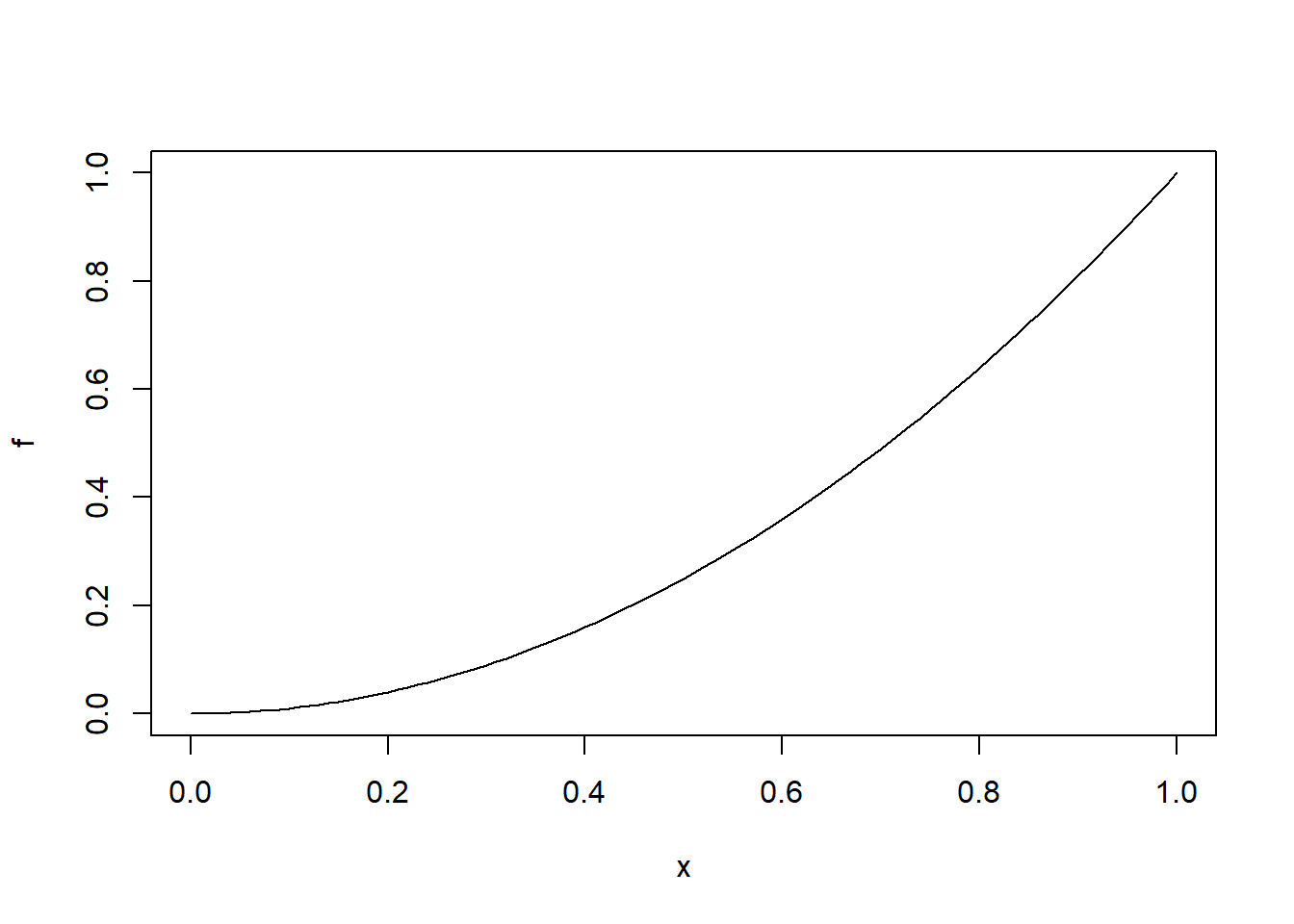
Gráfico básico de la curva $y=x^2$.

Figura 7.3: Gráfico básico de la curva \(y=x^2\).

7.2 Parámetros de plot

El aspecto de los gráficos que produce plot se puede modificar especificando parámetros en su argumento. Por ejemplo, ya vimos en la Lección 3 el parámetro log, que sirve para indicar si queremos algún eje en escala logarítmica.

Un primer grupo de parámetros permiten modificar el aspecto exterior del gráfico:

  • Para poner un título al gráfico, tenemos que especificarlo con el parámetro main.
  • Para modificar las etiquetas de los ejes de coordenadas, tenemos que usar los parámetros xlab e ylab.

Los valores de estos parámetros se tienen que entrar entre comillas o, si son fórmulas matemáticas, aplicarles la función expression, para que aparezcan en un formato matemático más adecuado.

Por ejemplo, suponemos que conocéis la sucesión \((F_n)_{n\geqslant 0}\) de los números de Fibonacci

1, 1, 2, 3, 5, 8, 13, 21 …

que empieza con \(F_0=F_1=1\) y a partir de aquí cada término es la suma de los dos anteriores. Esta sucesión está definida, para todo \(n\geqslant 0\), por la fórmula \[ F_n=\frac{1}{\sqrt{5}}\cdot\Biggl( \Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^{n+1}- \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^{n+1}\Biggl). \] Para comprobarlo para algunos valores, vamos a generar la parte inicial \((F_n)_{n=0, \ldots, 30}\) de la sucesión definida por esta fórmula.

n=0:30
Fib=(1/sqrt(5))*(((1+sqrt(5))/2)^(n+1)-((1-sqrt(5))/2)^(n+1))
Fib
#>  [1]       1       1       2       3       5       8      13      21      34
#> [10]      55      89     144     233     377     610     987    1597    2584
#> [19]    4181    6765   10946   17711   28657   46368   75025  121393  196418
#> [28]  317811  514229  832040 1346269

Para dibujar los pares \((n, F_n)_{n=0, \ldots, 30}\) en un gráfico titulado “Números de Fibonacci”, con el eje de abscisas etiquetado con \(n\) y el eje de ordenadas etiquetado con \(F_n\) igualado a su fórmula explícita, podemos entrar la instrucción siguiente. El resultado es la Figura 7.4.

plot(n, Fib, xlab="n", main="Números de Fibonacci", 
  ylab=expression(F[n]==(1/sqrt(5))*(((1+sqrt(5))/2)^(n+1)-((1-sqrt(5))/2)^(n+1))))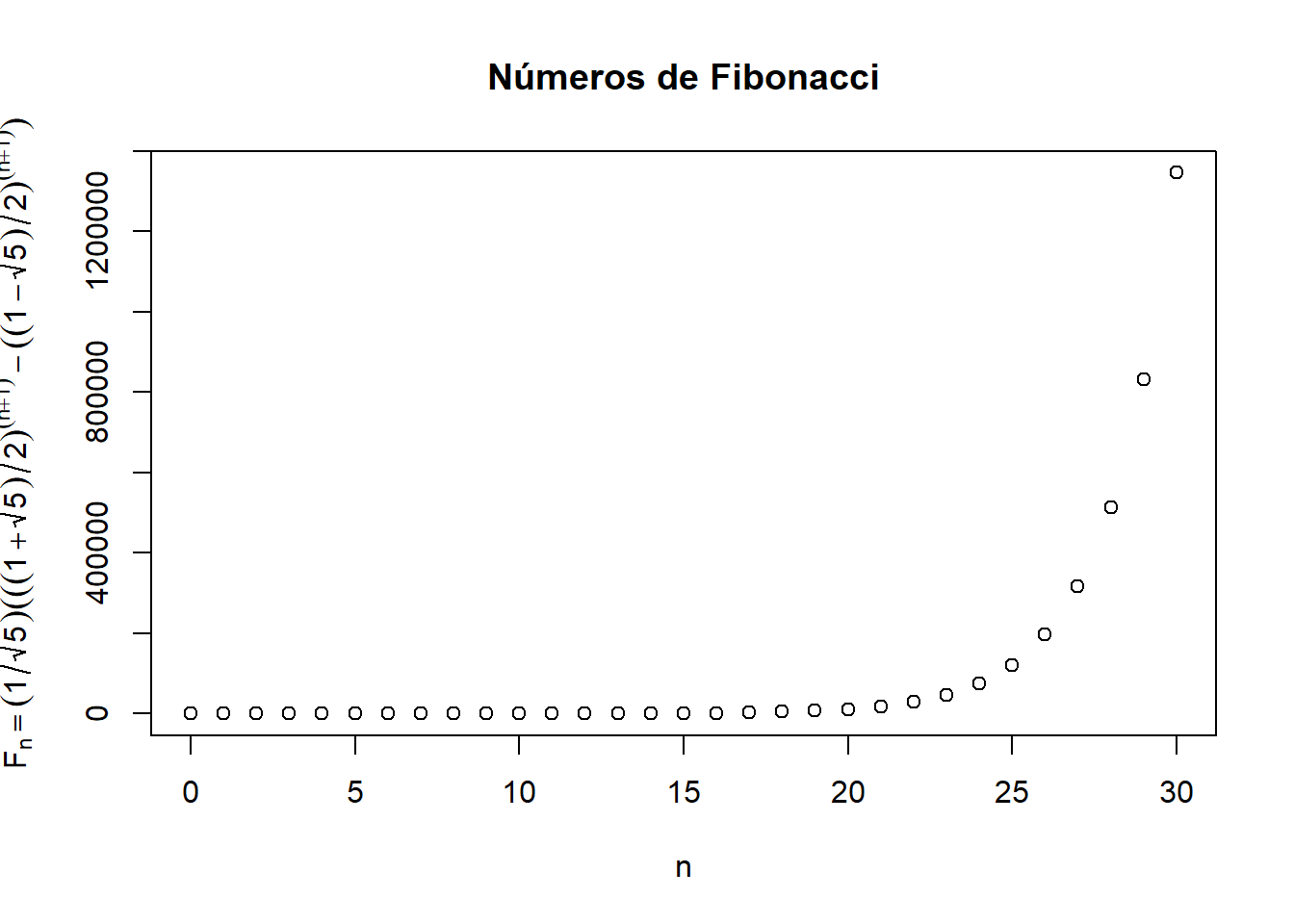
Gráfico de los 31 valores iniciales $F_n$ de la sucesión de Fibonacci.

Figura 7.4: Gráfico de los 31 valores iniciales \(F_n\) de la sucesión de Fibonacci.

Si os interesa información sobre cómo escribir las fórmulas dentro de expression, podéis consultar la Ayuda de plotmath.

Cómo podéis ver, por defecto plot dibuja los puntos como círculos vacíos. Esto se puede cambiar con el parámetro pch, que puede tomar como valor cualquier número natural entre 0 y 25. Con pch=0 obtenemos cuadrados, pch=1 produce los círculos que ya habéis visto (es el valor por defecto), pch=2 produce triángulos, etc. La Figura 7.5 muestra los signos correspondientes a los valores de pch. También se pueden usar letras para representar los puntos: hay que especificarlo igualando el parámetro pch a la letra entre comillas.

Signos correspondientes a los diferentes valores de `pch`.

Figura 7.5: Signos correspondientes a los diferentes valores de pch.

El tamaño de estos signos se puede modificar mediante el parámetro cex igualado al factor de escalado: cex=2 produce signos el doble de grandes que los que obtenemos por defecto, cex=0.5 produce signos de la mitad de tamaño, etc. Por ejemplo, el siguiente código produce la Figura 7.6.

plot(x, y, pch=20, cex=3)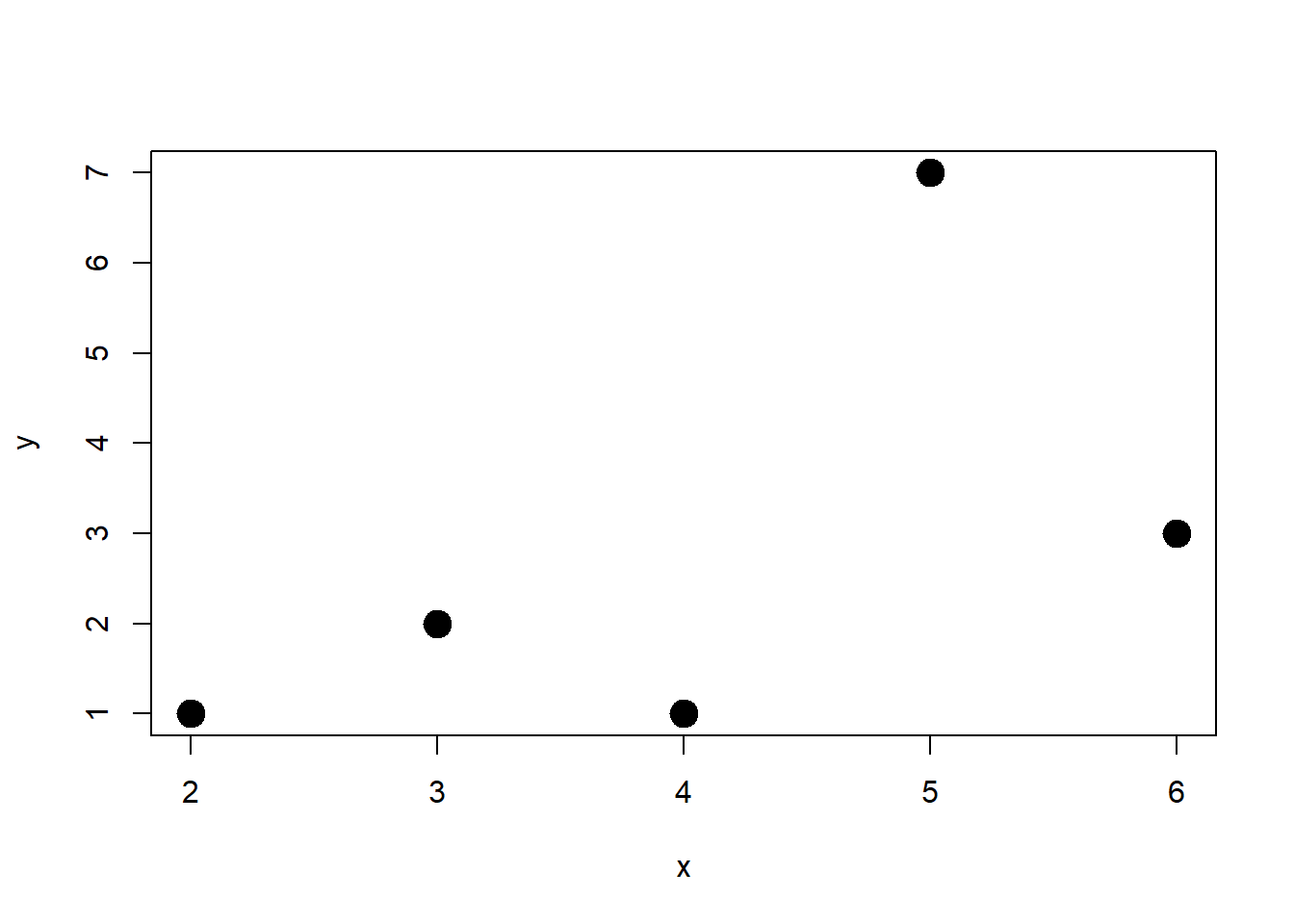
Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) con puntos de tamaño triple.

Figura 7.6: Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) con puntos de tamaño triple.

El color de los puntos se puede especificar mediante el parámetro col igualado al nombre del color en inglés. La paleta de colores de R consta de 502 colores diferentes. Podéis encontrar una presentación muy clara de esta paleta en el documento Rcolor.pdf que encontraréis en el url http://www.stat.columbia.edu/~tzheng/files/Rcolor.pdf

Así, por ejemplo, la función siguiente produce la Figura 7.7:

plot(x, y, col="red", pch=15)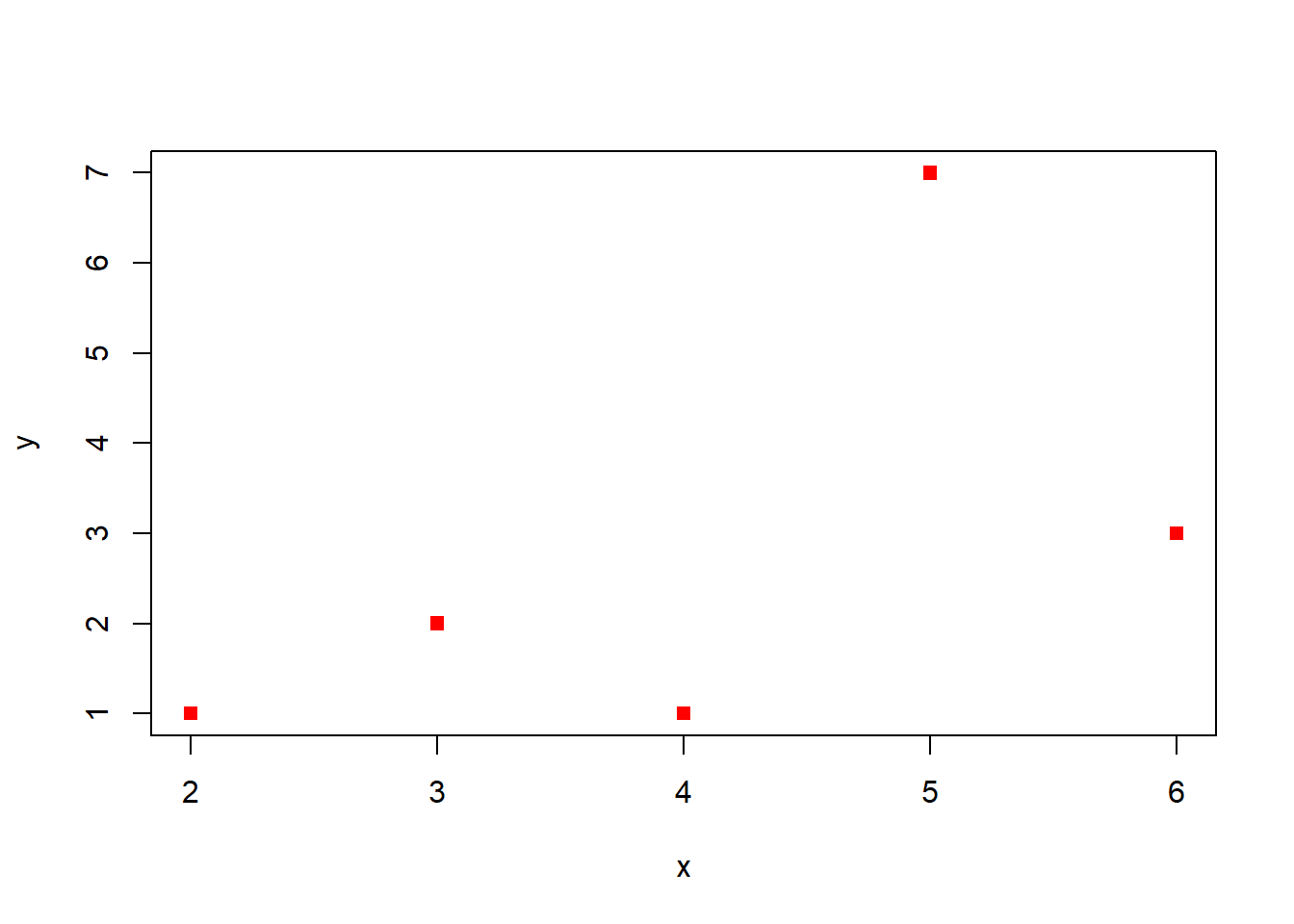
Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) como cuadrados rojos.

Figura 7.7: Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) como cuadrados rojos.

Los puntos que se obtienen con pch de 21 a 25 admiten un color para el borde (que se especifica con col) y uno de diferente para el relleno, que se especifica con bg. A modo de ejemplo, el gráfico de la Figura 7.8 se obtiene con el código siguiente:

plot(x, y, pch=21, col="blue", bg="red", cex=2)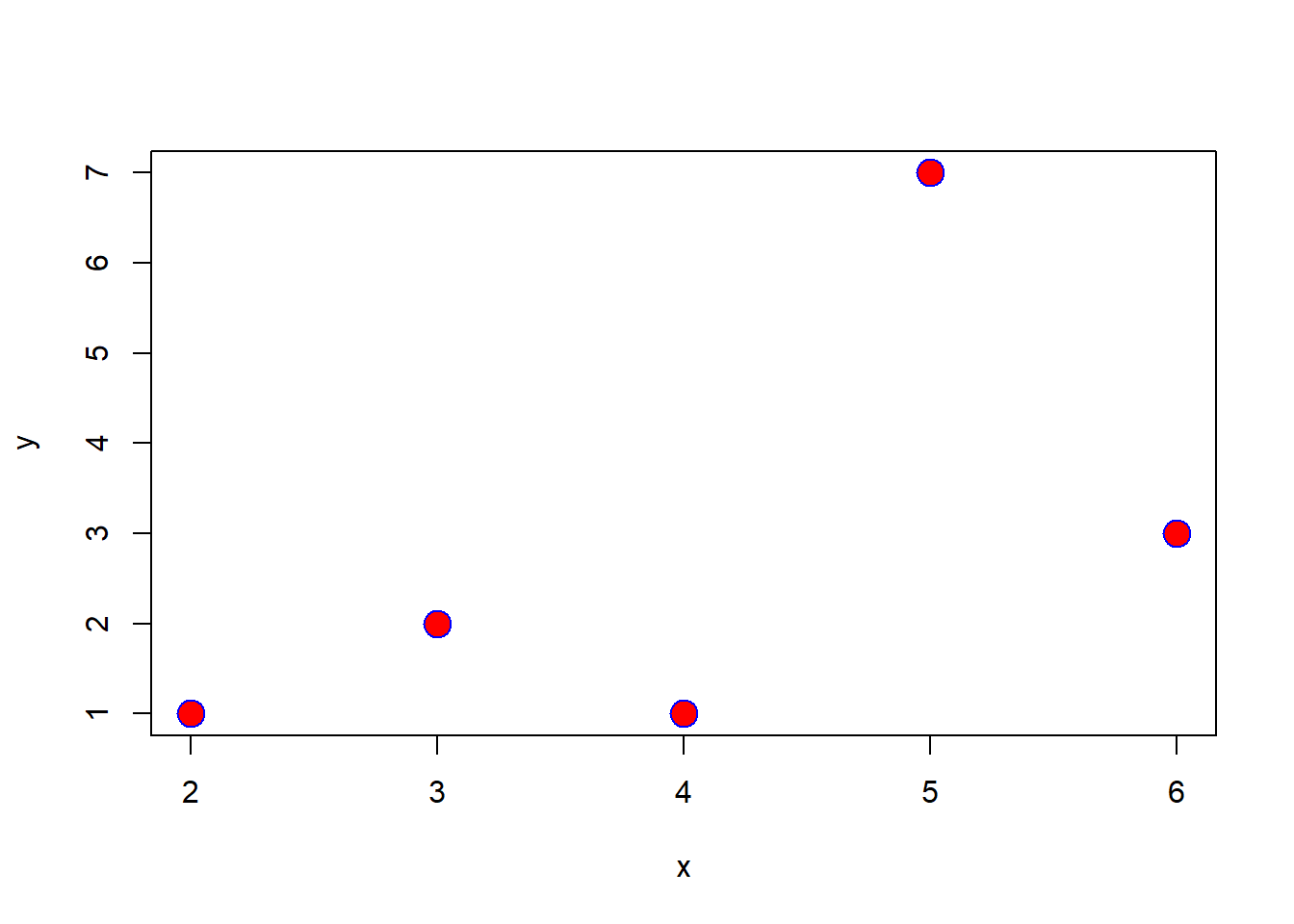
Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) bicolores.

Figura 7.8: Gráfico de los puntos (2,1), (5,7), (6,3), (3,2), (4,1) bicolores.

El parámetro type permite indicar el tipo de gráfico que queremos producir. El valor del parámetro se tiene que entrar entre comillas y puede ser:

  • "p", para dibujar los puntos como simples puntos, como hasta ahora; es el valor por defecto.
  • "l", para dibujar los puntos unidos por líneas rectas sin que se vean los puntos.
  • "b", para dibujar los puntos unidos por líneas rectas de manera que se vean los puntos (los dibuja ambos, both: rectas y puntos), pero sin que las rectas entren dentro de los signos que representan los puntos.
  • "o", que es como "b", pero ahora las rectas sí que entran dentro de los puntos.
  • "h", para dibujar líneas verticales desde el eje de abscisas a cada punto (un histograma de líneas).
  • "s", para dibujar un diagrama de escalones.
  • "n", para no dibujar los puntos, sólo el exterior del gráfico (ejes, título, etc.).

Veamos el efecto de los diferentes valores de type:

X=c(1,3,5,7,11)
Y=c(2,8,4,6,3)
plot(X, Y, type="p")  #Tipo por defecto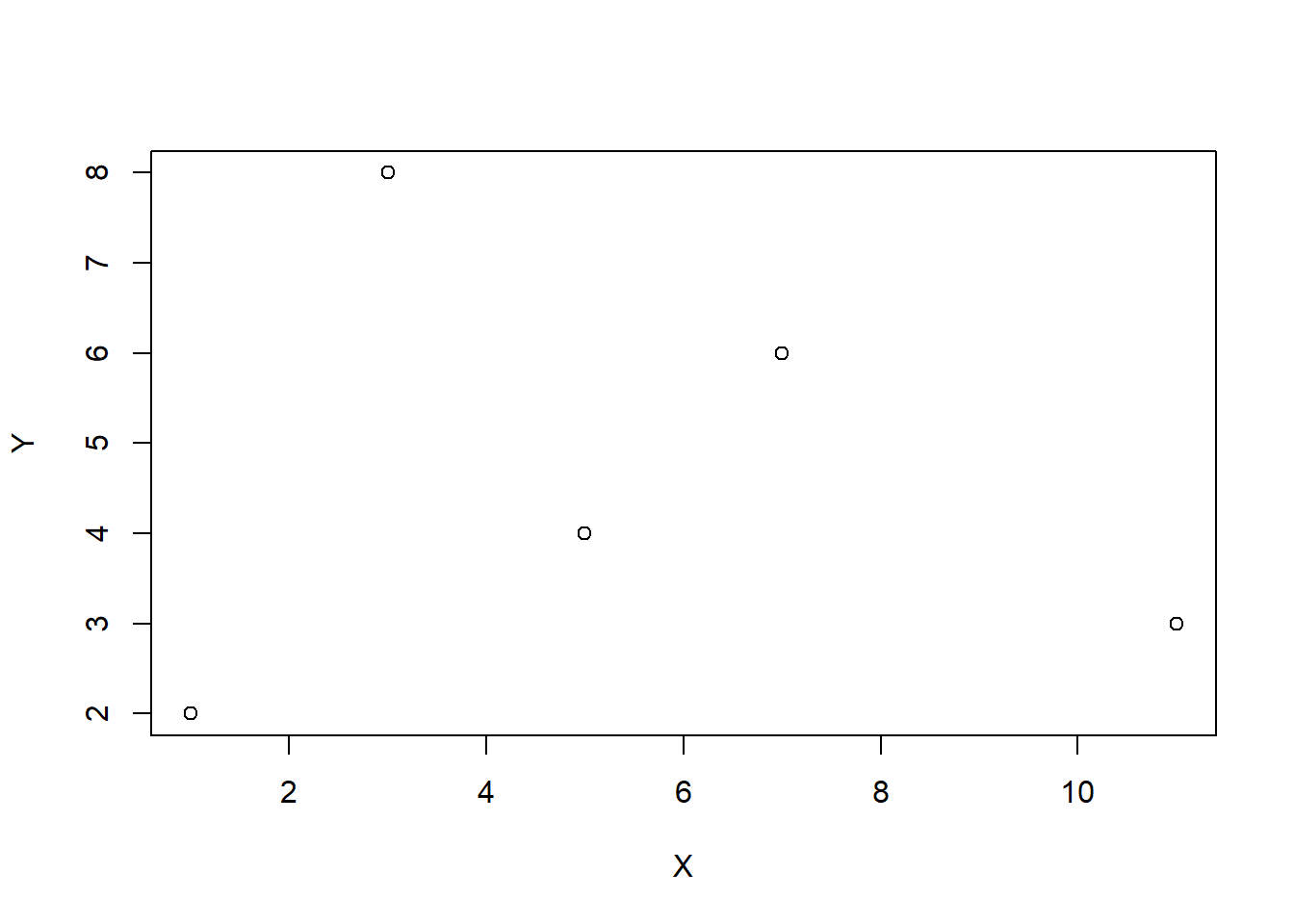

plot(X, Y, type="l")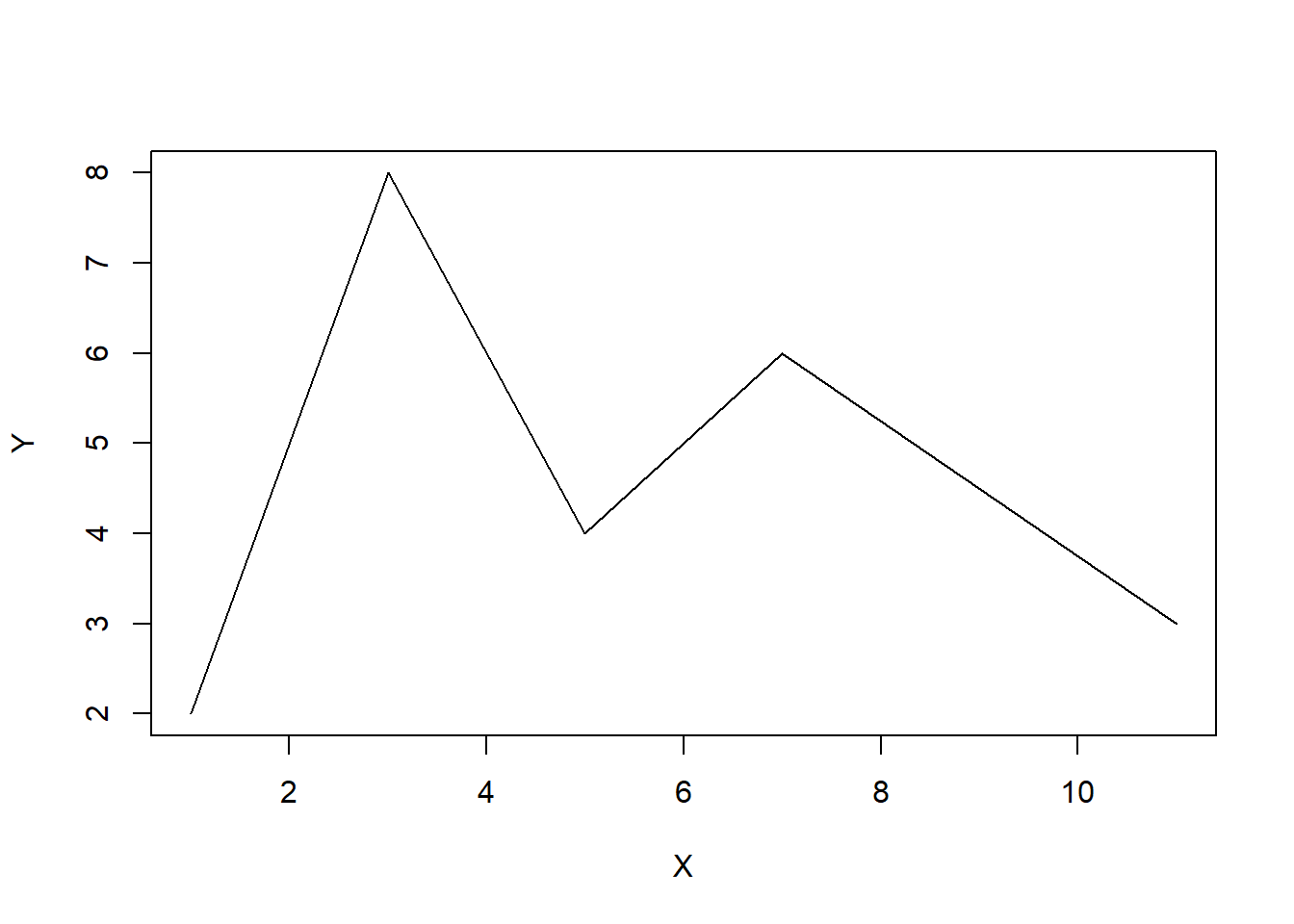

plot(X, Y, type="b")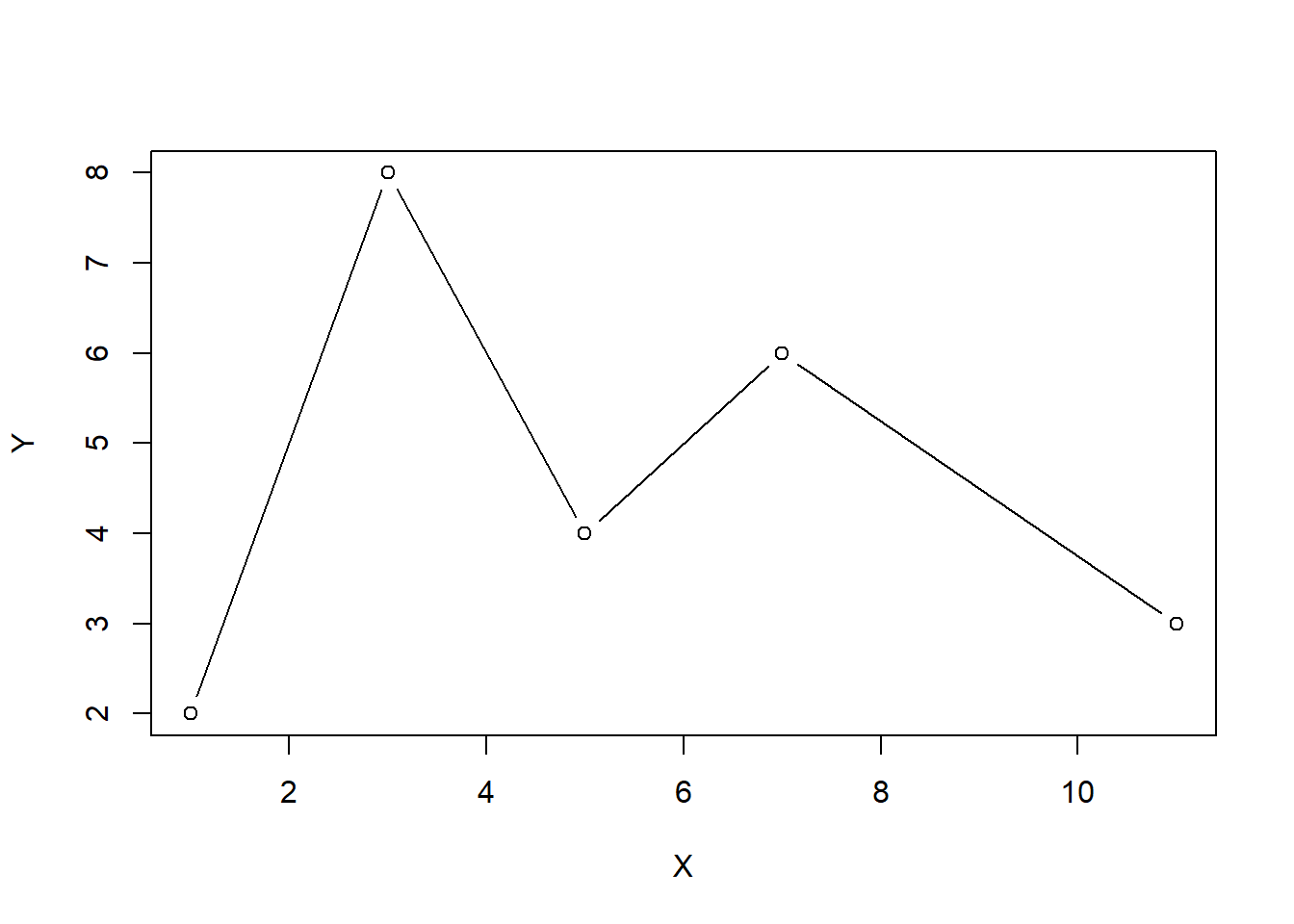

plot(X, Y, type="o")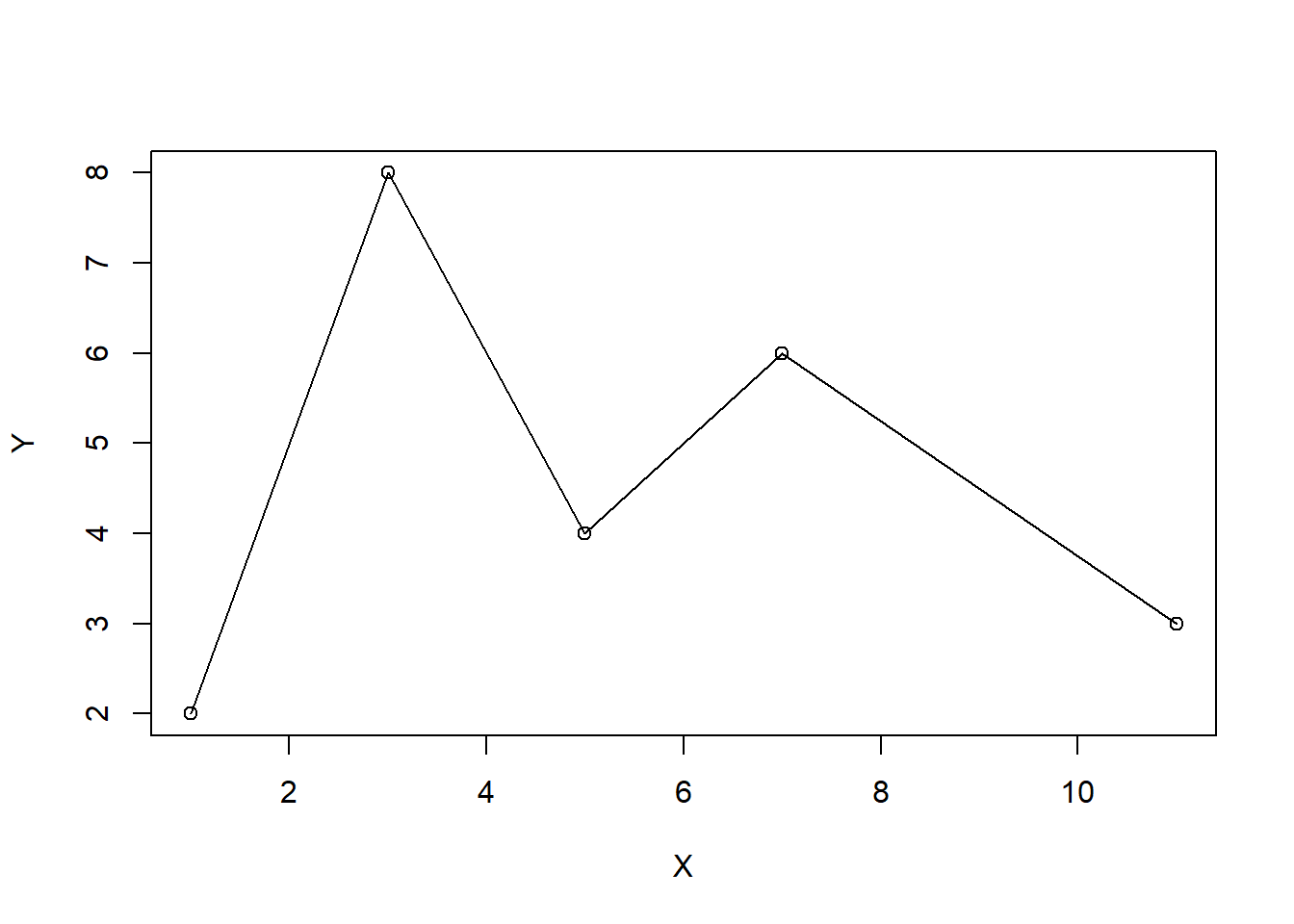

plot(X, Y, type="h")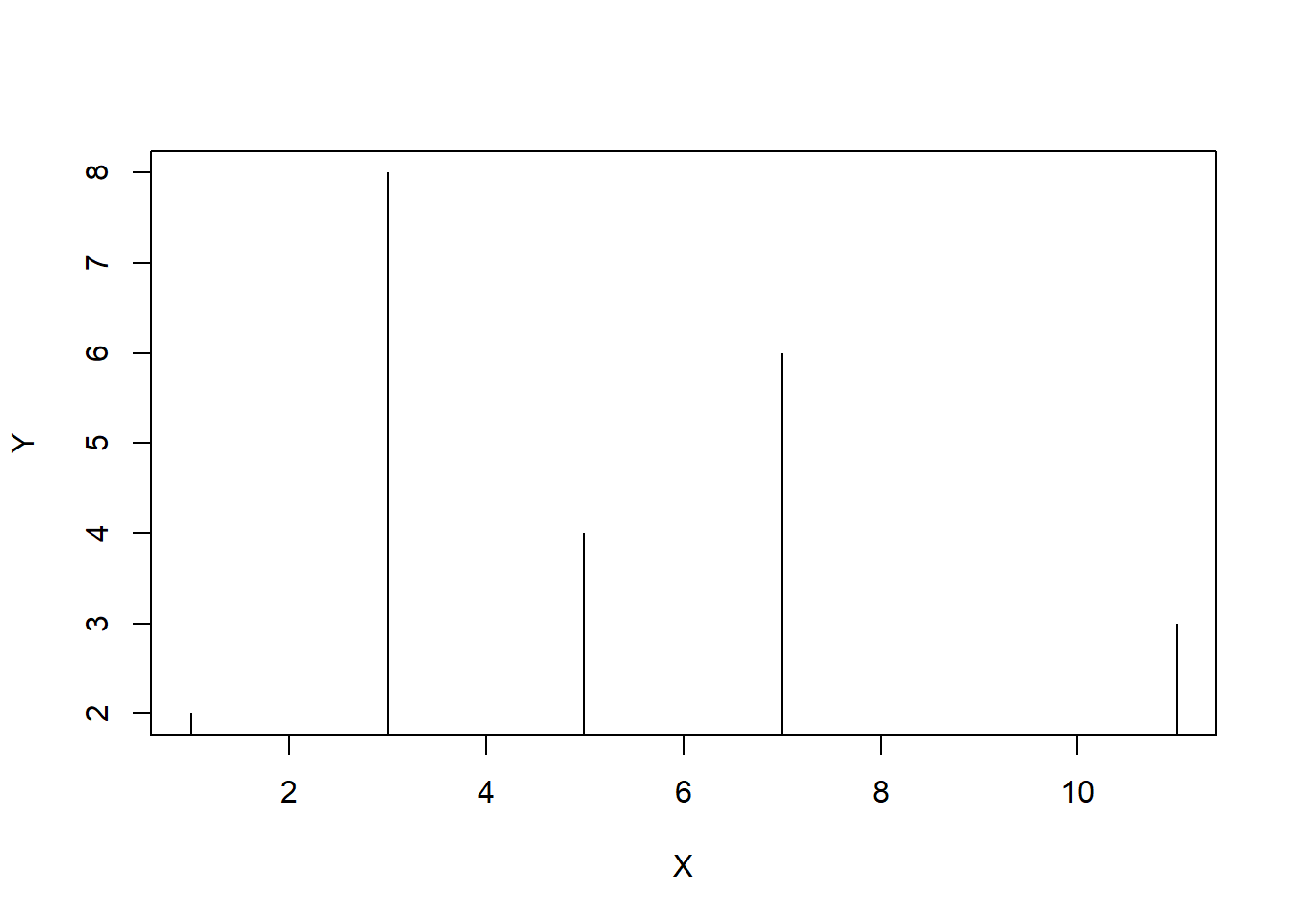

plot(X, Y, type="s")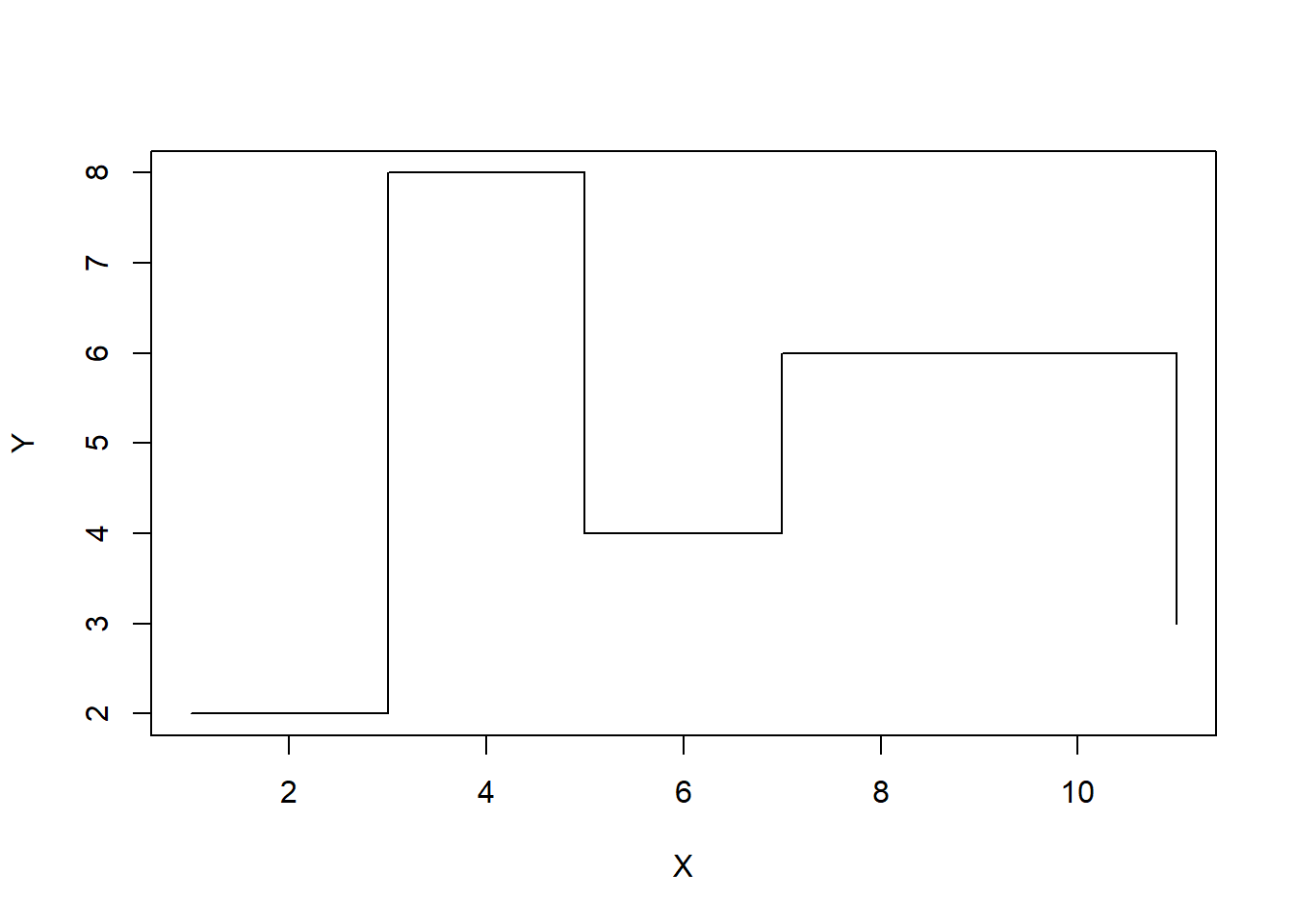

plot(X, Y, type="n")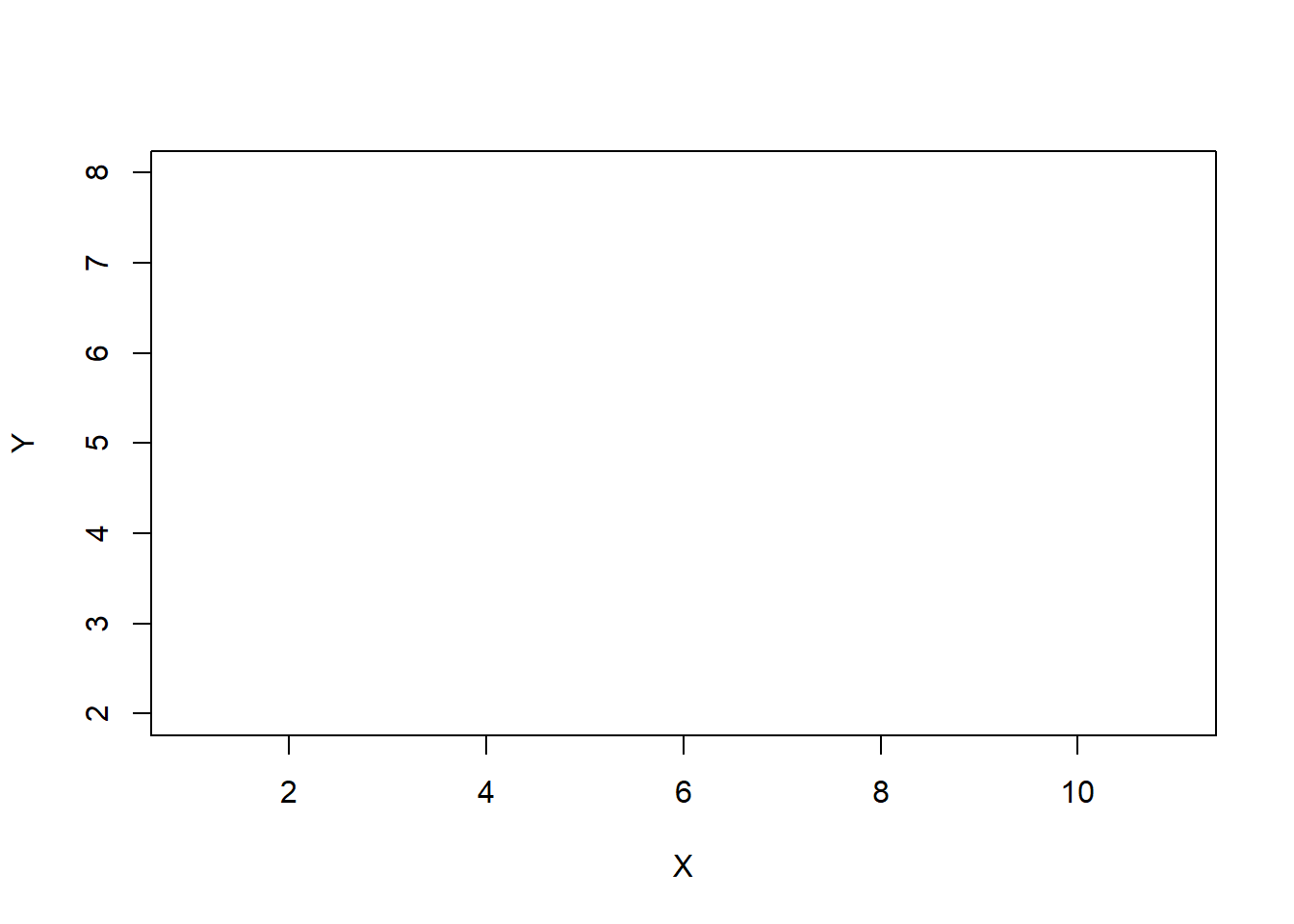

La función plot aplicada a una función \(f\) en realidad produce el gráfico de tipo "l" de una familia de puntos \((x, f(x))\) (por defecto, 101 puntos distribuidos uniformemente a lo largo del dominio; este valor se puede modificar con el parámetro n).

El estilo de las líneas usadas por plot se puede modificar con los parámetros siguientes:

  • El parámetro col especifica el color tanto de los puntos como de las líneas.

  • El tipo de línea se puede especificar con el parámetro lty igualado a uno de los valores siguientes: "solid", o 1, (el valor por defecto, que produce una línea continua); "dashed", o 2, (que produce una línea discontinua); "dotted", o 3, (que produce una línea de puntos); "dotdash", o 4, (que produce una línea que alterna puntos y rayas).

  • El grosor se puede especificar con el parámetro lwd, que igualado a r hace que el grosor de las líneas sea \(r\) veces su valor por defecto.

Veamos dos ejemplos:

plot(X, Y, type="o", col="blue", pch=19, lty="dotted")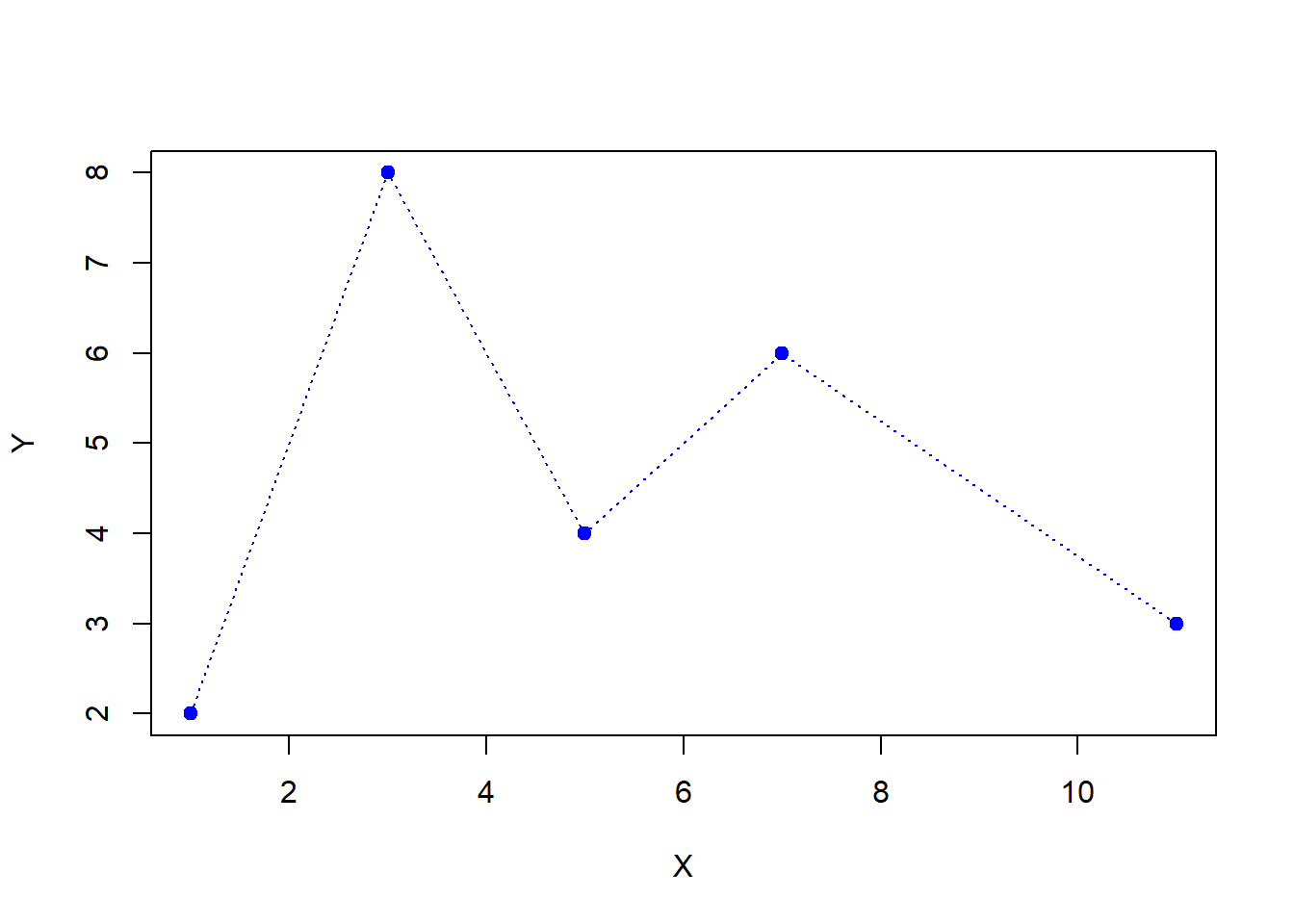

plot(X, Y, type="o", pch=19, lty="dashed", lwd=2)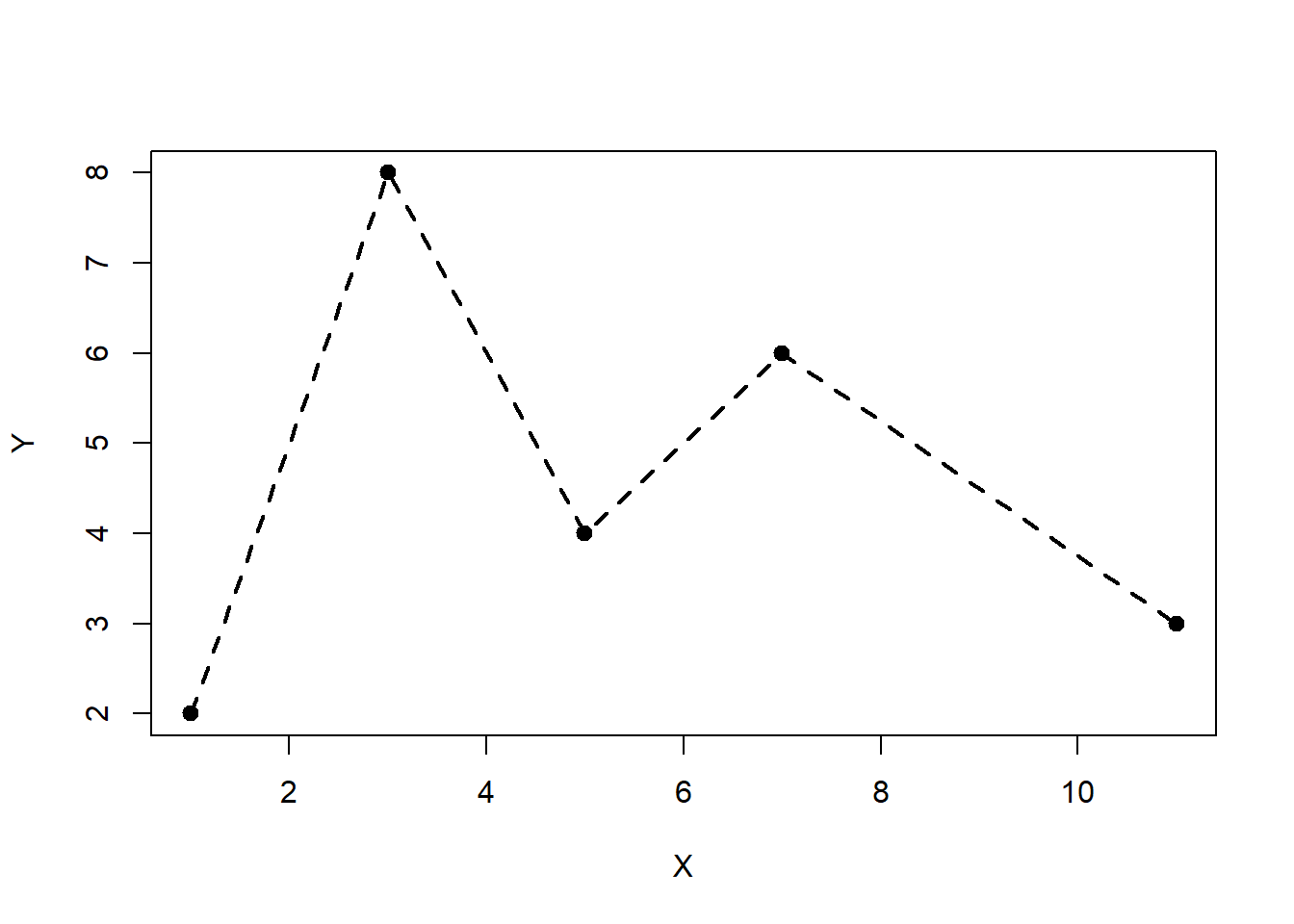

Si el argumento de plot son dos vectores, por norma general los rangos de los ejes de coordenadas van, por defecto, del mínimo al máximo de los vectores correspondientes. Si su argumento es una función \(f\), por defecto el rango del eje de abscisas es el intervalo \([0, 1]\) y el rango del eje de ordenadas va del valor mínimo de \(f\) sobre el rango de las abscisas al máximo. Si queremos modificar estos rangos, tenemos que usar los parámetros xlim e ylim, igualados cada uno a un vector de entradas los extremos del rango.

Veamos un ejemplo de uso de estos parámetros. Vamos a dibujar tres gráficas de la función \(f(x)=x\ln(x)\), variando los rangos de sus ejes.

  • Con los rangos por defecto:
f=function(x){x*log(x)}
plot(f)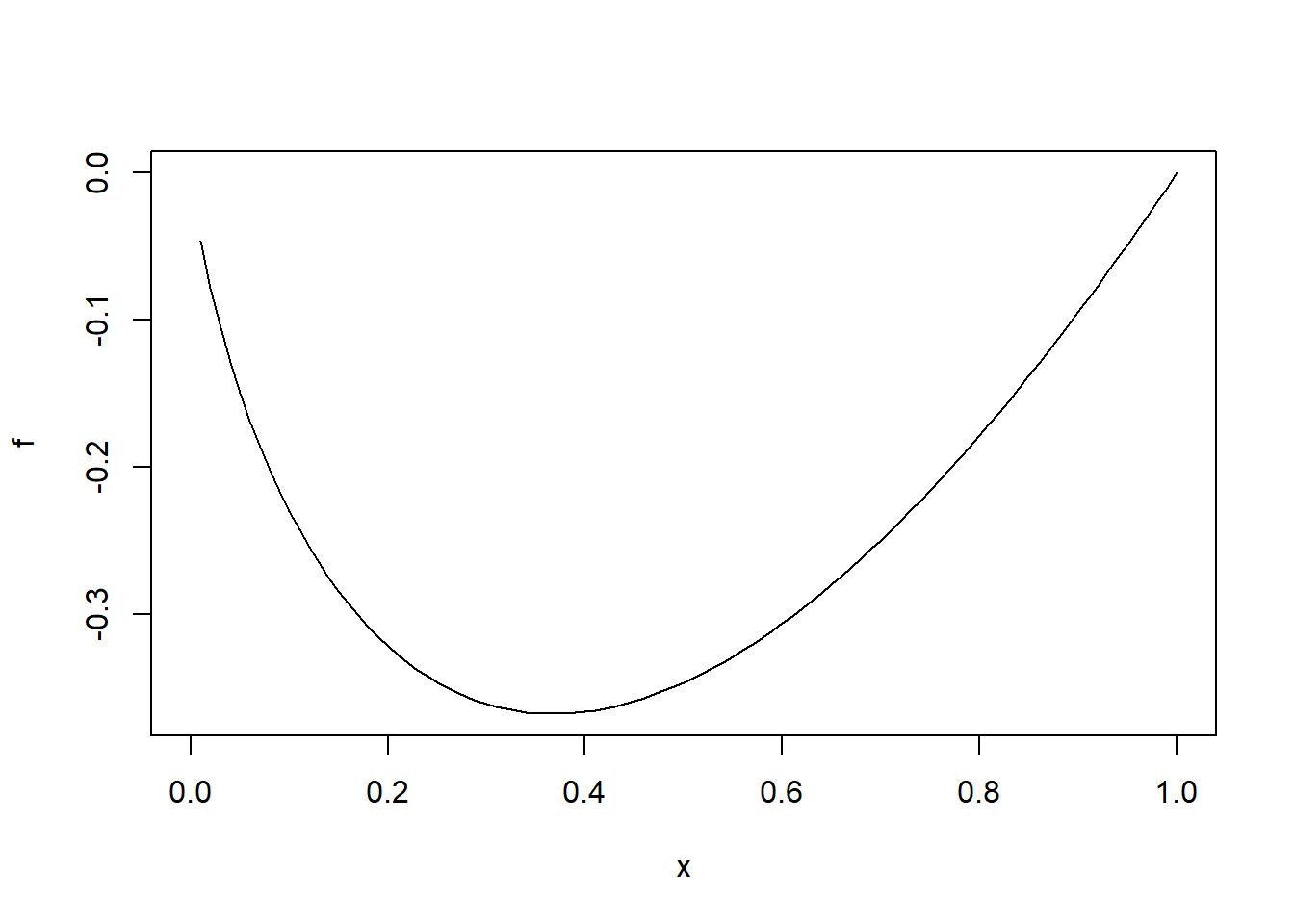

  • Modificando el rango del eje de abscisas:
plot(f, xlim=c(1, 10))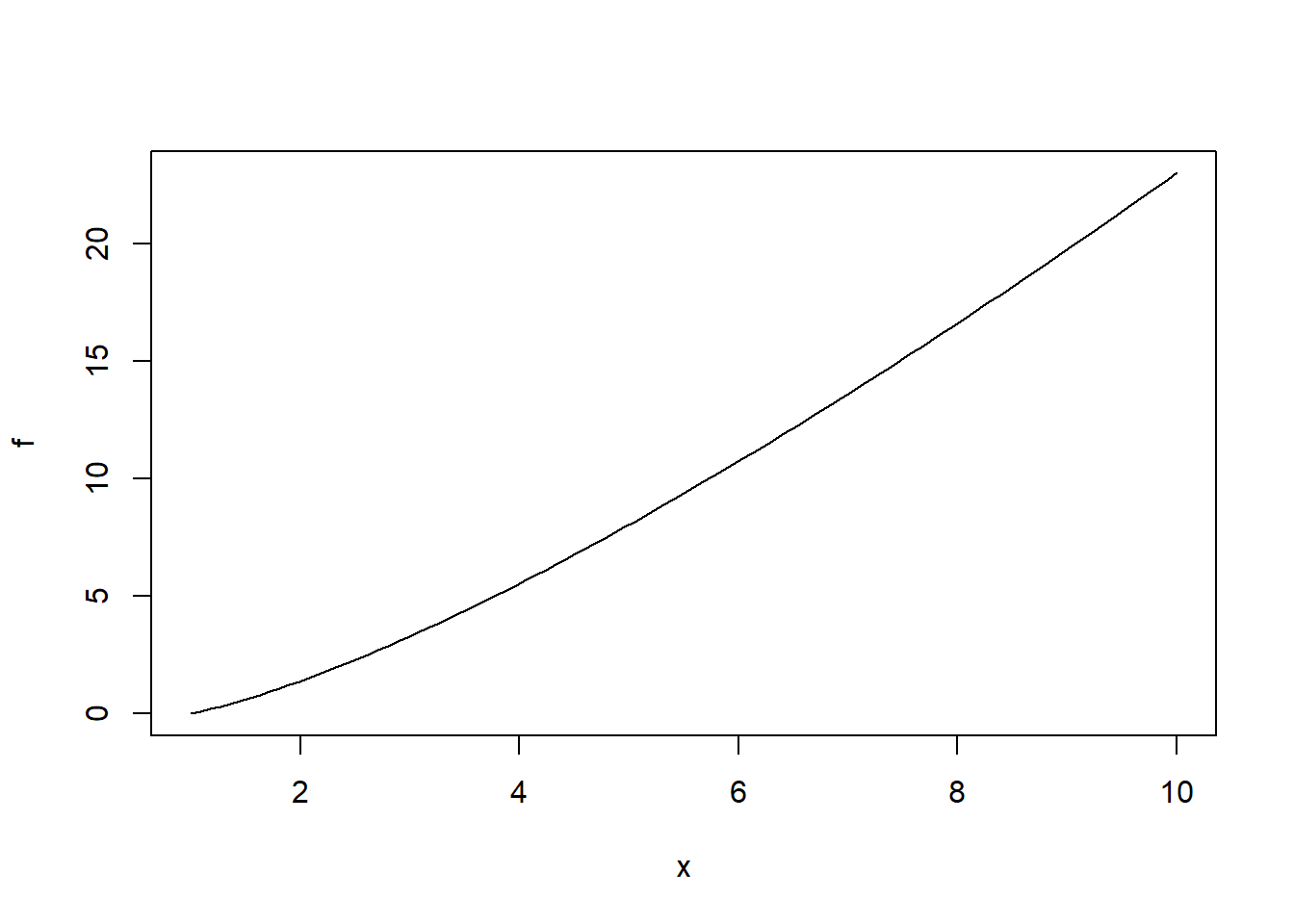

  • Modificando los rangos de ambos ejes:
plot(f, xlim=c(1, 10), ylim=c(0, 50))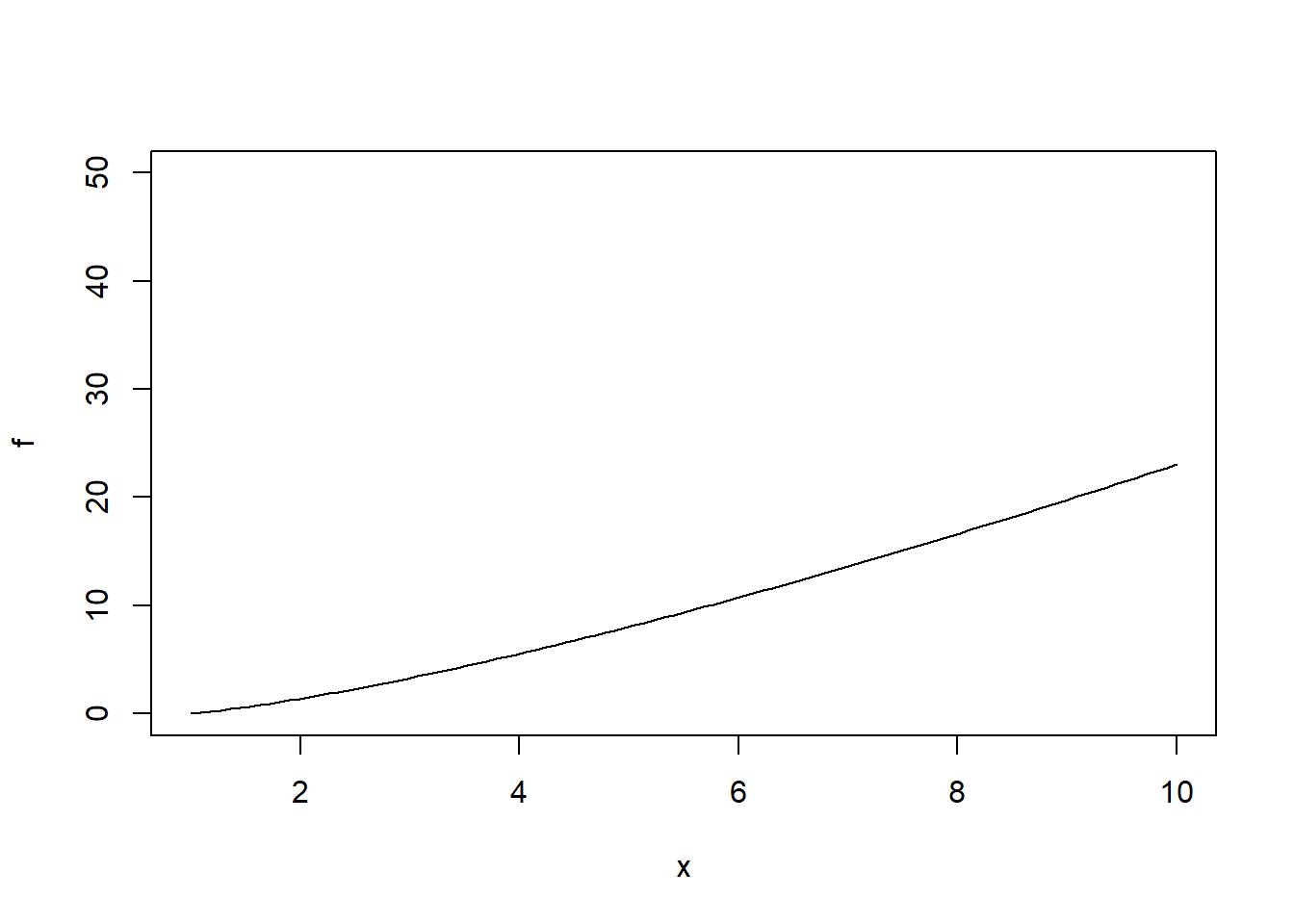

Para modificar las posiciones de las marcas en los ejes de abscisas y ordenadas podemos usar los parámetros xaxp e yaxp, respectivamente. Mediante la expresión xaxp=c(a, b, m), imponemos que R dibuje \(m+1\) marcas igualmente espaciadas entre los puntos \(a\) y \(b\) del eje de abscisas. La sintaxis para yaxp es la misma. Estas instrucciones no definen los rangos de los ejes de coordenadas, que se han de especificar con xlim e ylim si se quieren modificar. Veamos tres ejemplos:

  • Con las marcas por defecto:
plot(f, xlim=c(1, 10))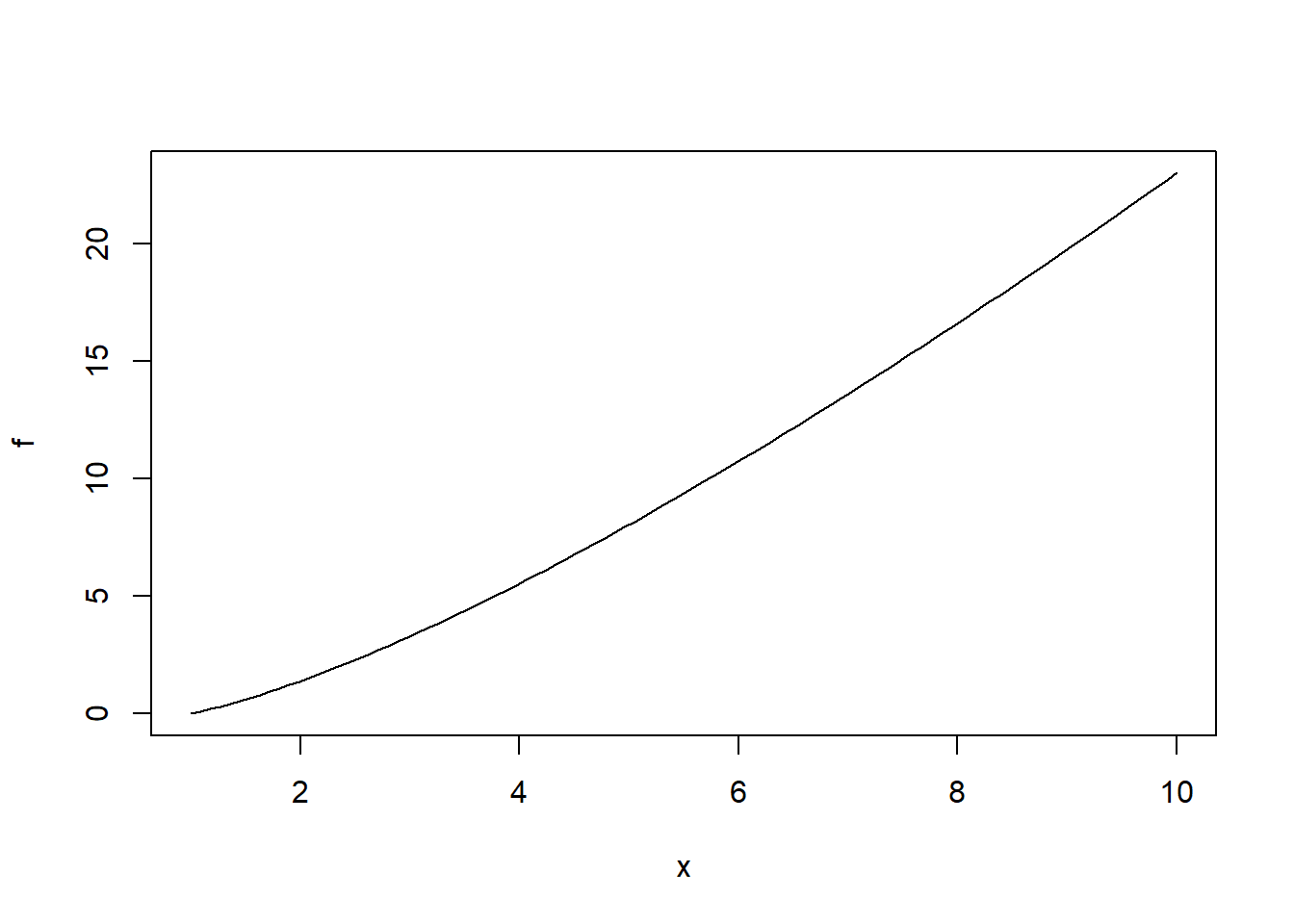

* Definiendo las marcas sobre el eje de abscisas:

plot(f, xlim=c(1, 10), xaxp=c(1, 10, 9))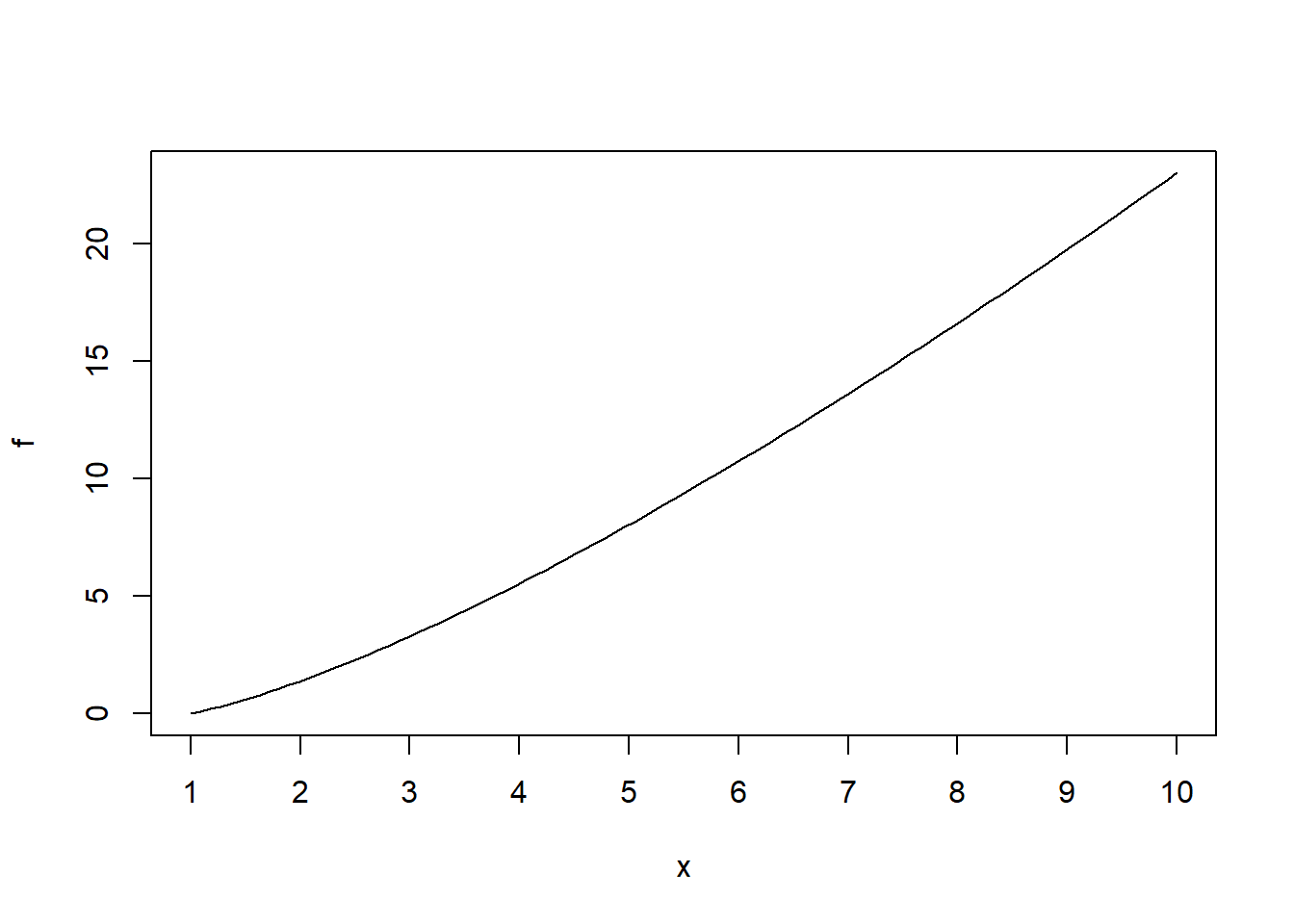

* Definiendo las marcas sobre ambos ejes:

plot(f, xlim=c(1, 10), xaxp=c(1, 10, 9), ylim=c(0, 25), yaxp=c(0, 25, 10))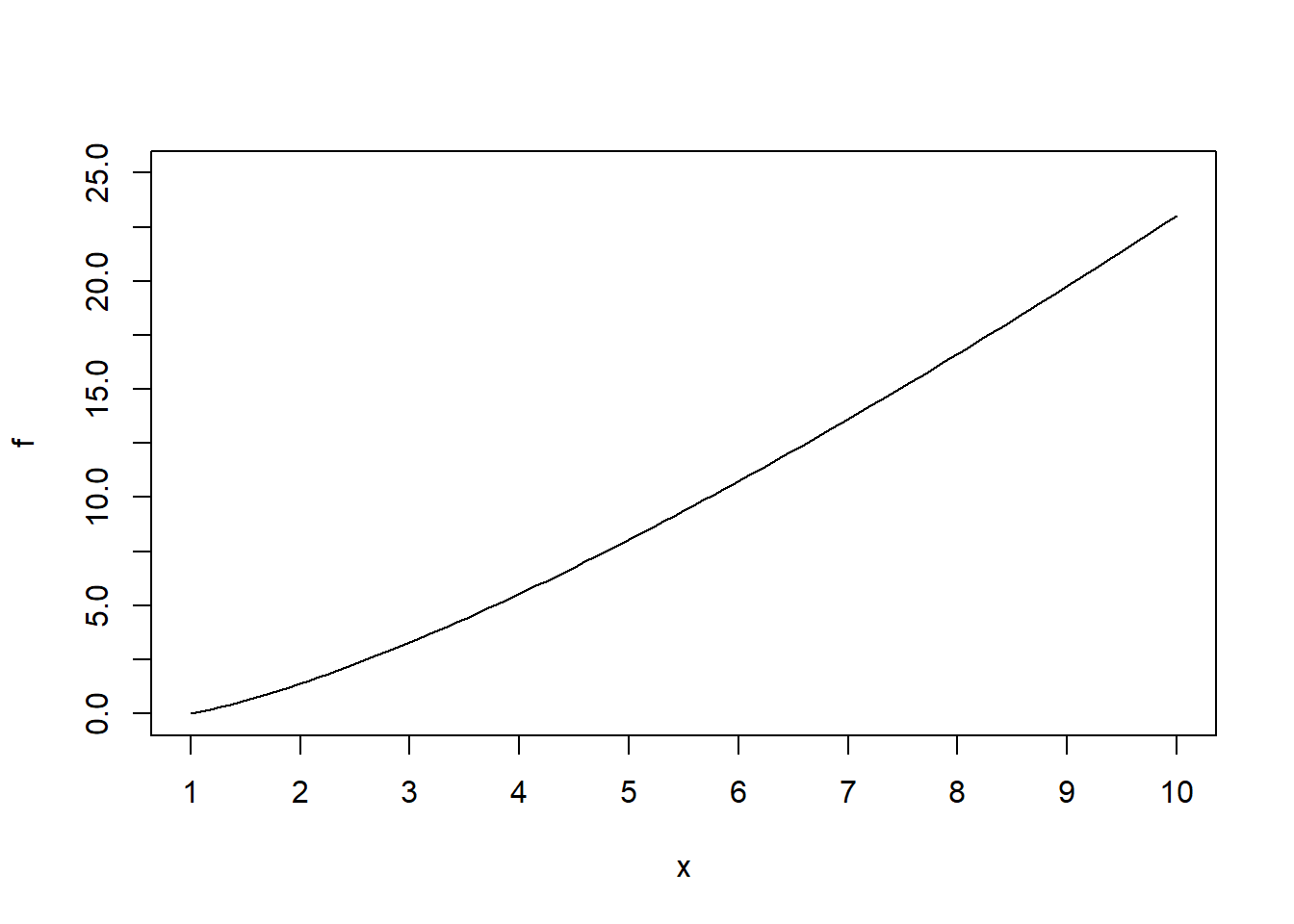

La función plot dispone de muchos otros parámetros, que podéis consultar en la Ayuda de plot y las de las funciones que se citan en su sección See Also. Son especialmente útiles los parámetros que se explican en la Ayuda de par.

7.3 Cómo añadir elementos a un gráfico

La función plot permite dibujar una sola cosa (una familia de puntos o una función) con un único estilo. Si queremos dibujar varios objetos en un gráfico, los tenemos que añadir uno a uno, usando las funciones adecuadas. En esta sección veremos algunas funciones que permiten añadir elementos a un gráfico.

Antes de empezar, queremos avisaros de algo muy importante. Cuando añadimos objetos a un gráfico, ya no podemos modificar su diseño general. Por ejemplo, los rangos de coordenadas de los ejes del gráfico final o sus etiquetas serán los del primer gráfico, aunque especifiquemos valores nuevos en el argumento de las funciones que usemos para añadir objetos.

La instrucción

points(x, y)

añade un punto de coordenadas \((x, y)\) al gráfico activo si x e y son números. Podemos declarar el color de este punto, el signo que lo represente, etc. mediante los parámetros usuales. Por ejemplo,

f=function(x){x^2}
plot(f, xlim=c(-3, 3))
points(0, 0, pch=19)

produce la Figura 7.9, en la que hemos dibujado la parábola \(y=x^2\) y hemos marcado su vértice con un punto.

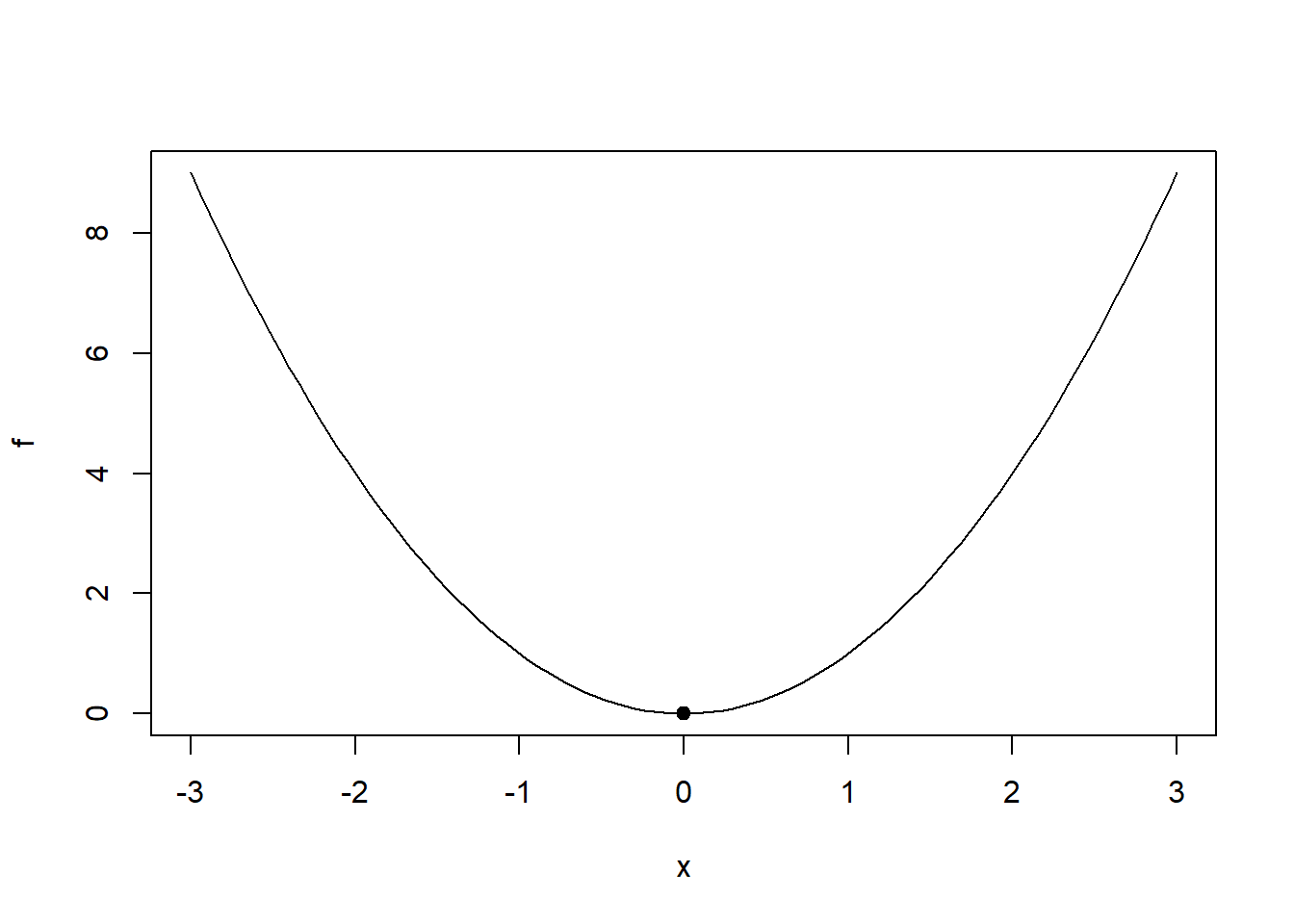
Gráfica de una parábola con su vértice marcado.

Figura 7.9: Gráfica de una parábola con su vértice marcado.

La función points también sirve para añadir una familia de puntos. En este caso, hay que entrar como x el vector de sus primeras coordenadas y como y el de sus segundas coordenadas, como lo haríamos en plot.

Veamos algunos ejemplos. El código

f=function(x){x^2}
plot(f, xlim=c(0, 10))
points(0:10, (0:10)^2, pch=19)

dibuja un trozo de la parábola \(y=x^2\) y añade los puntos \((n, n^2)_{n=0, \ldots, 10}\), produciendo la Figura 7.10.

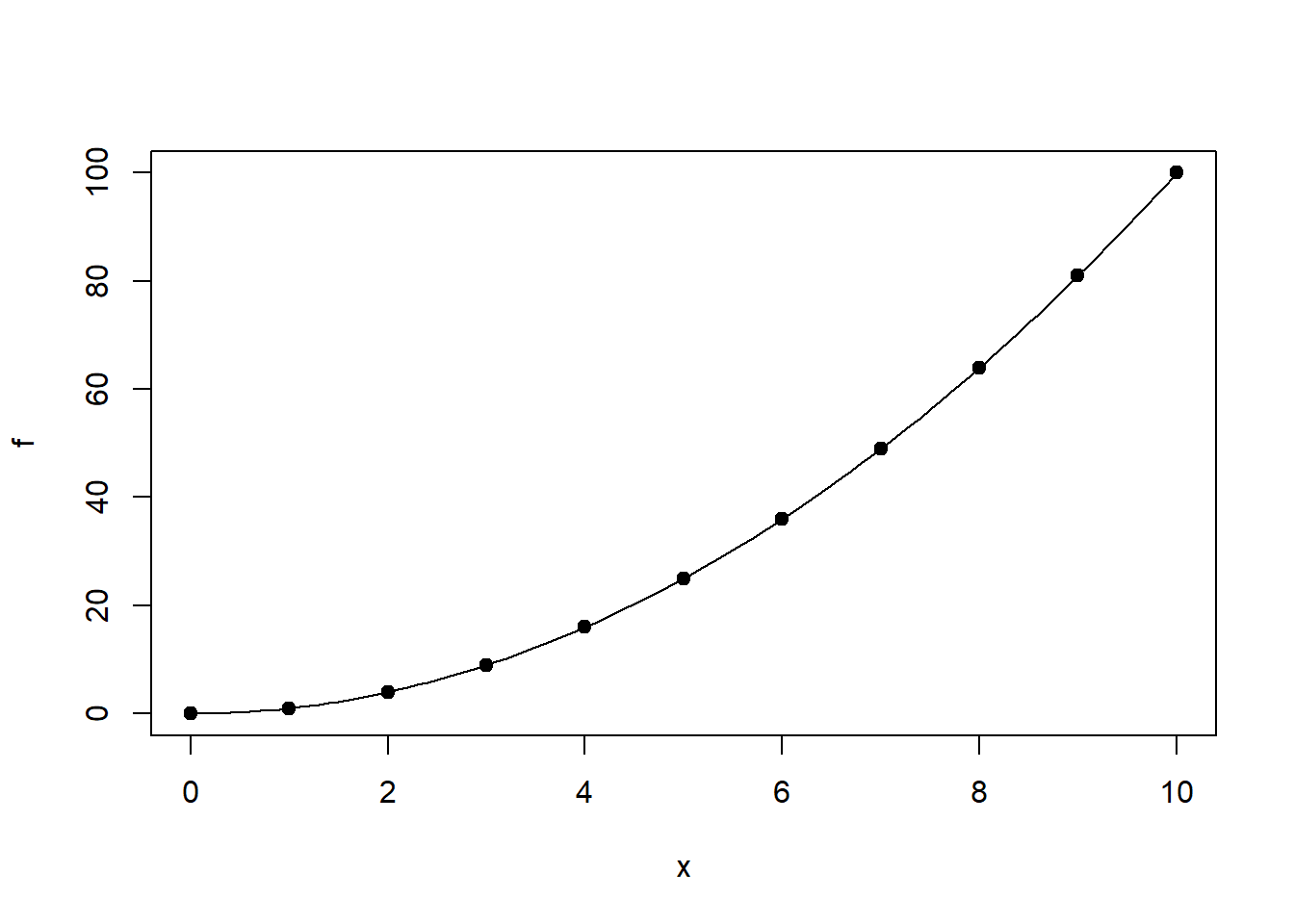
Gráfico de la función $f(x)=x^2$ con varios puntos marcados

Figura 7.10: Gráfico de la función \(f(x)=x^2\) con varios puntos marcados

Por su parte, el código

n=0:20
x=1.3^n-2*0.8^n
y=0.2*1.3^n+1.7*0.8^n
plot(n, x, col="blue")
points(n, y, pch=19, col="red")

primero dibuja los puntos \((n, 1.3^n-2\cdot 0.8^n)_{n=0, \ldots, 20}\) como circulitos azules vacíos, y después añade los puntos \((n, 0.2\cdot 1.3^n+1.7 \cdot 0.8^n)_{n=0, \ldots, 20}\) como circulitos rojos llenos, produciendo la Figura 7.11.

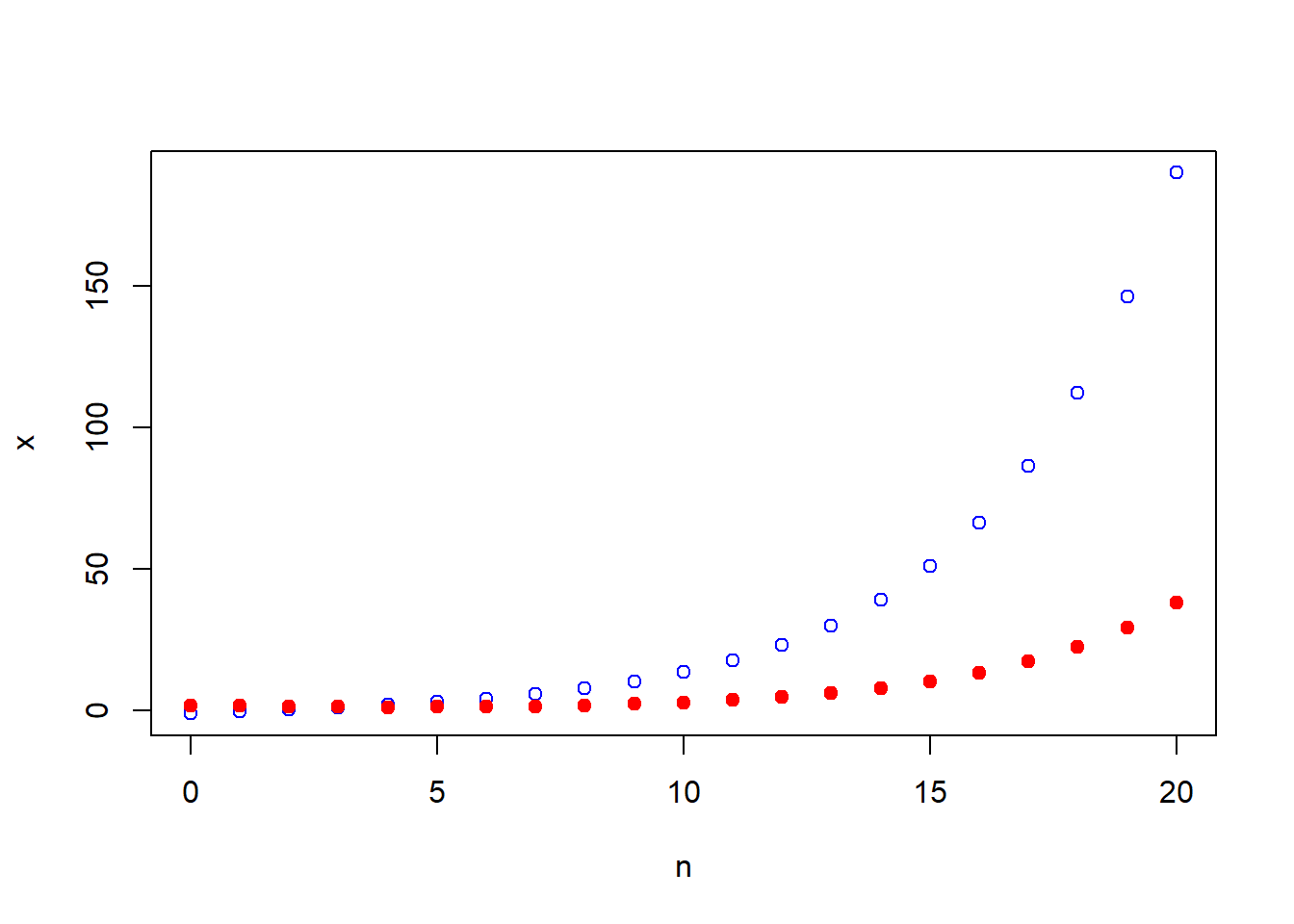
Gráfico de dos trozos de sucesiones.

Figura 7.11: Gráfico de dos trozos de sucesiones.

La función abline sirve para añadir una recta; ya la usamos en la Lección 3 para añadir a un gráfico una recta de regresión calculada con lm. Esta función tiene tres variantes:

  • abline(a, b) añade la recta \(y=a+bx\).
  • abline(v=a) añade la recta vertical \(x=a\).
  • abline(h=a) añade la recta horizontal \(y=a\).

Podemos especificar las características de estas rectas, como su grosor, su estilo o su color, mediante los parámetros pertinentes. Por ejemplo,

f=function(x){x^2}
plot(f, xlim=c(-3, 3), col="red")
points(0, 0, pch=19, col="blue")
points(1, 1, pch=19, col="blue")
abline(v=1, lty="dashed")
abline(h=0, lty="dotted")
abline(-1, 2, lty="dotdash")

produce la Figura 7.12. En este caso, hemos añadido a la gráfica de la parábola \(y=x^2\), dos puntos en (0, 0) y (1, 1), la recta horizontal \(y=0\) de puntos, la recta vertical \(x=1\) discontinua y la recta \(y=-1+2x\) de puntos y rayas.

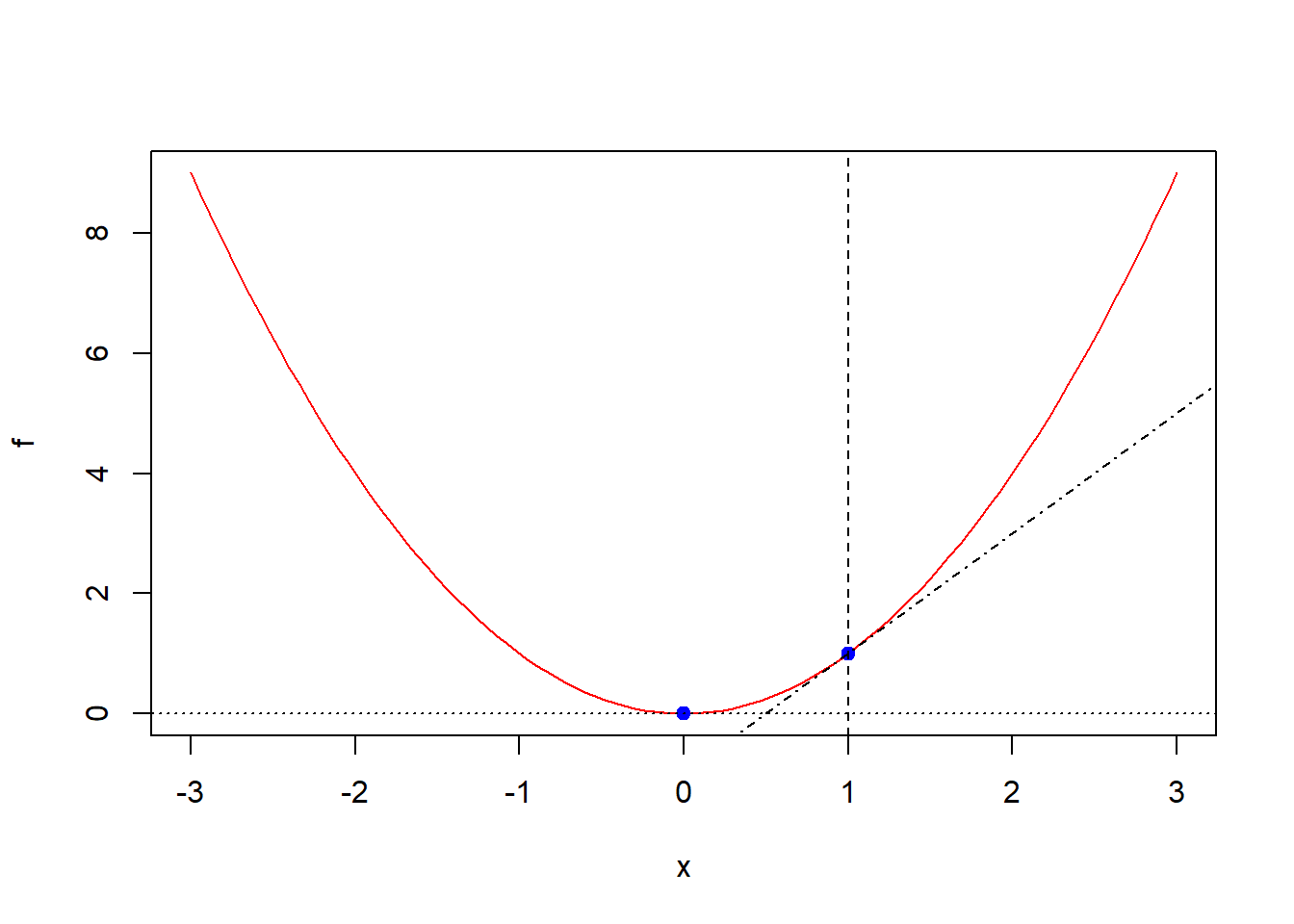
Gráfica conjunta de una parábola, dos puntos y tres rectas.

Figura 7.12: Gráfica conjunta de una parábola, dos puntos y tres rectas.

Los parámetros v y h de abline se pueden igualar a vectores numéricos, en cuyo caso la instrucción añade en un solo paso todas las rectas verticales u horizontales correspondientes, todas del mismo estilo. Incluso se pueden combinar los parámetros v y h en una misma función. Por ejemplo, el código siguiente produce la Figura 7.13:

f=function(x){x^2}
plot(f, xlim=c(-3, 3), col="red")
abline(h=0:9, v=-3:3, lty="dotted")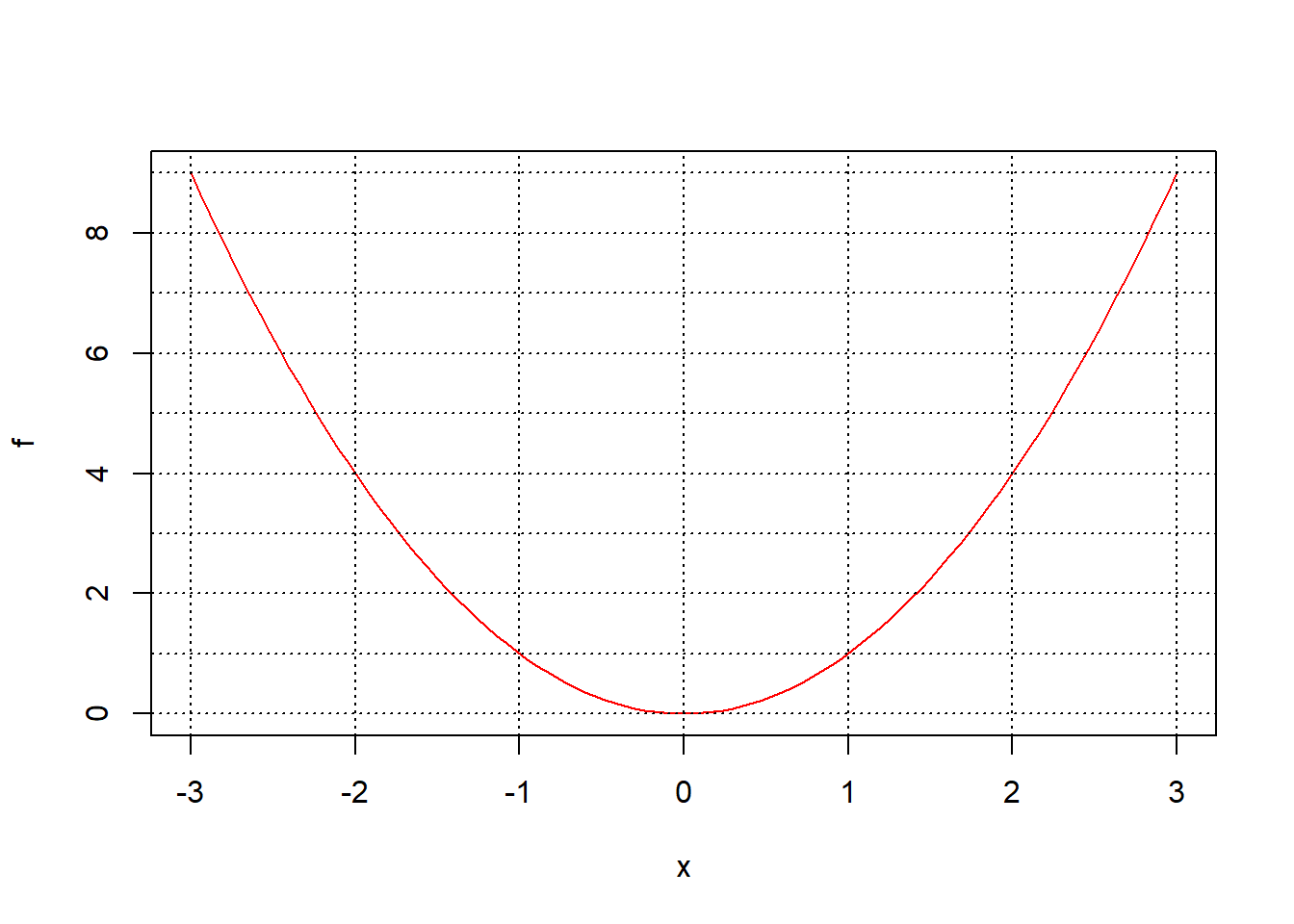
Gráfica de una parábola y una rejilla de rectas horizontales y verticales.

Figura 7.13: Gráfica de una parábola y una rejilla de rectas horizontales y verticales.

La instrucción

text(x, y, labels=...)

añade en el punto de coordenadas \((x, y)\) el texto especificado como argumento de labels. El texto se puede entrar entre comillas o en una expression. La función text admite un parámetro opcional, pos, que puede tomar valores 1, 2, 3 o 4 y permite indicar la posición del texto alrededor de las coordenadas \((x, y)\): 1 significa abajo, 2 a la izquierda, 3 arriba y 4 a la derecha. Sin especificar pos (o, equivalentemente, especificando pos=NULL, que es su valor por defecto), el texto se sitúa centrado en el punto \((x, y)\). El efecto de pos se ilustra en la Figura 7.14, producida con el código siguiente:

plot(0, 0, pch=19, xlab="", ylab="")
text(0, 0, labels="pos 1", pos=1)
text(0, 0, labels="pos 2", pos=2)
text(0, 0, labels="pos 3", pos=3)
text(0, 0, labels="pos 4", pos=4)
points(0, 0.5, pch=19)
text(0, 0.5, labels="no pos")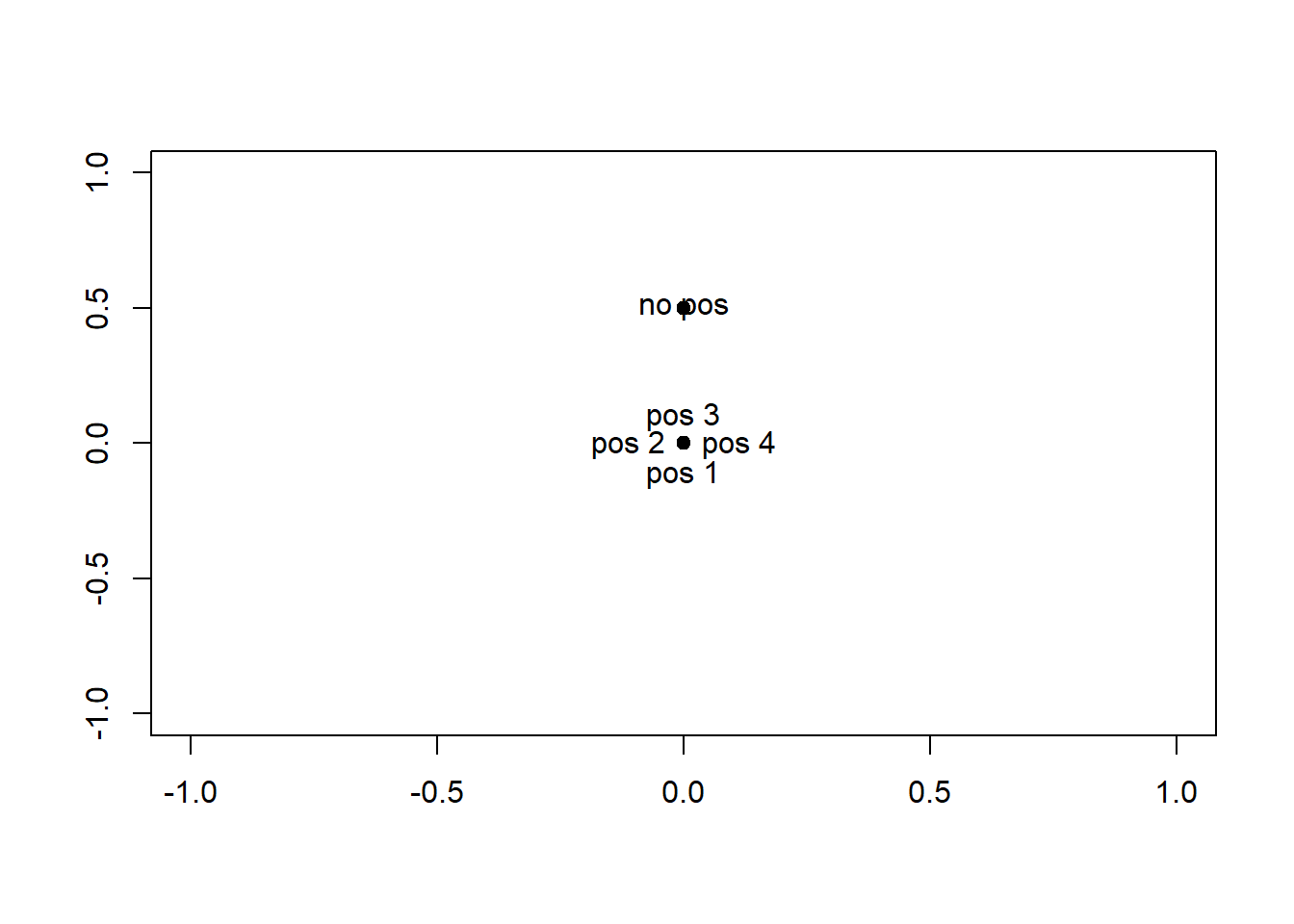
Significado del parámetro `pos` de la función `text`.

Figura 7.14: Significado del parámetro pos de la función text.

La función text se puede usar para añadir varios textos en un solo paso. En este caso, \(x\) e \(y\) han de ser los vectores de abscisas y ordenadas de los puntos donde se añadirán los textos, labels el vector de textos, y pos el vector de sus posiciones; en este vector, los textos que queremos centrados en su posición se han de indicar con NULL. Así, la Figura 7.14 también se hubiera podido obtener con el código siguiente, como podréis comprobar si lo ejecutáis:

plot(0, 0, pch=19, xlab="", ylab="")
points(0, 0.5, pch=19)
text(rep(0, 5), c(rep(0, 4), 0.5), pos=c(1, 2, 3, 4, NULL), 
     labels=c("pos 1", "pos 2", "pos 3", "pos 4", "no pos"))

La instrucción

lines(x, y)

donde \(x=(x_i)_{i=1, \ldots, n}\) e \(y=(y_i)_{i=1, \ldots, n}\) son dos vectores numéricos de la misma longitud, añade al gráfico una línea poligonal que une los puntos \((x_i, y_i)\) sucesivos. El efecto es como si añadiéramos un

plot(x, y, type="l")

Naturalmente, la apariencia de las líneas la podemos modificar con los parámetros usuales de grosor, color, estilo, etc. A modo de ejemplo, la Figura 7.15 se obtiene con el código siguiente:

f=function(x){x^2}
plot(f, xlim=c(0, 9))
lines(3*(0:3), (3*(0:3))^2, lwd=2, lty="dashed")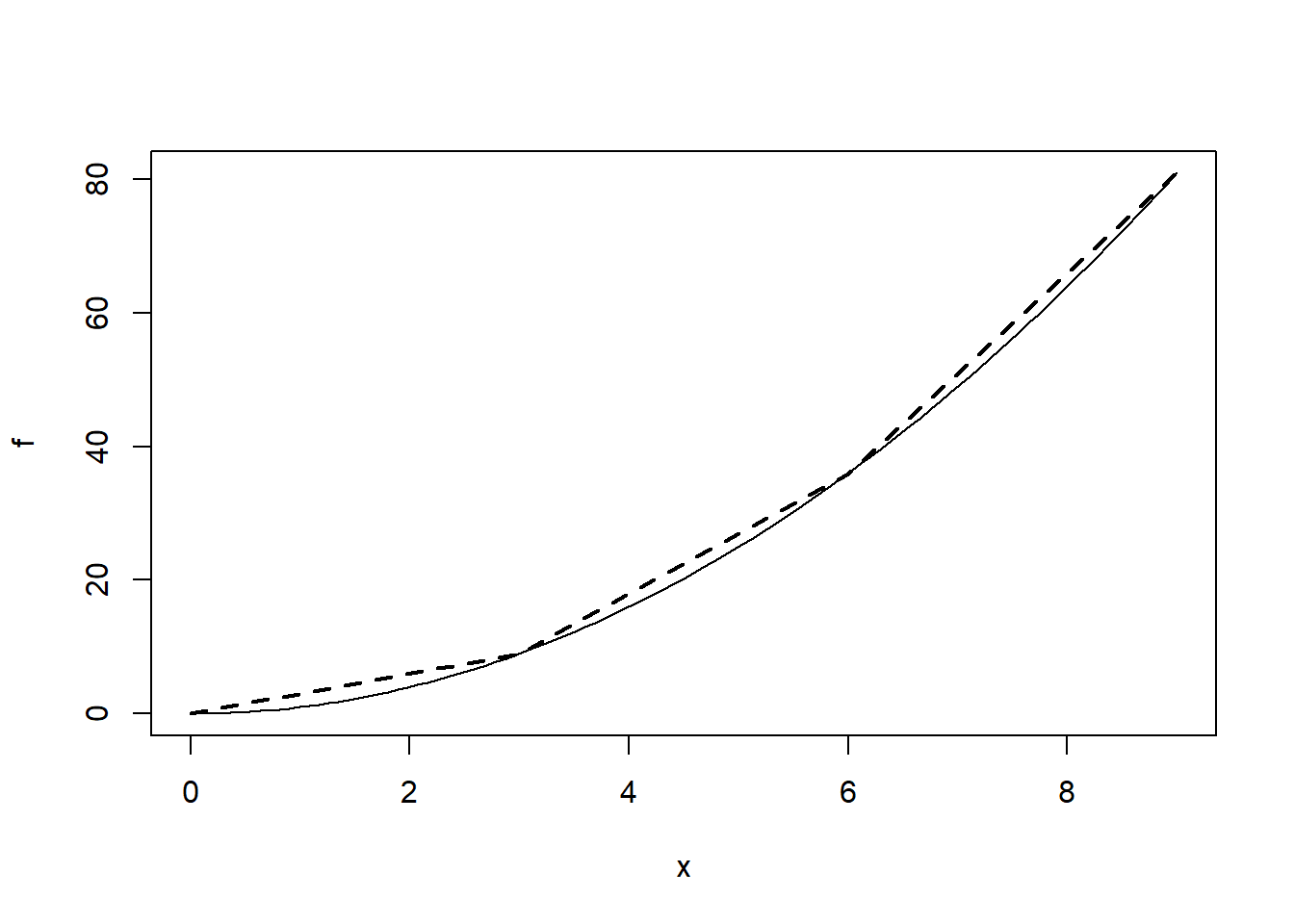
Gráfica conjunta de una función y una línea poligonal inscrita.

Figura 7.15: Gráfica conjunta de una función y una línea poligonal inscrita.

La instrucción curve con el parámetro add=TRUE permite añadir la gráfica de una curva a un gráfico anterior. La curva se puede especificar mediante una expresión algebraica con variable \(x\), o mediante su nombre si la hemos definido antes. Por ejemplo, el código siguiente produce el gráfico de la Figura 7.16.

f=function(x){x^2}
plot(f, xlim=c(-10, 10), xlab="x", ylab="y")
curve(x^3, lty="dashed", add=TRUE)
curve(x^4, lty="dotted", add=TRUE)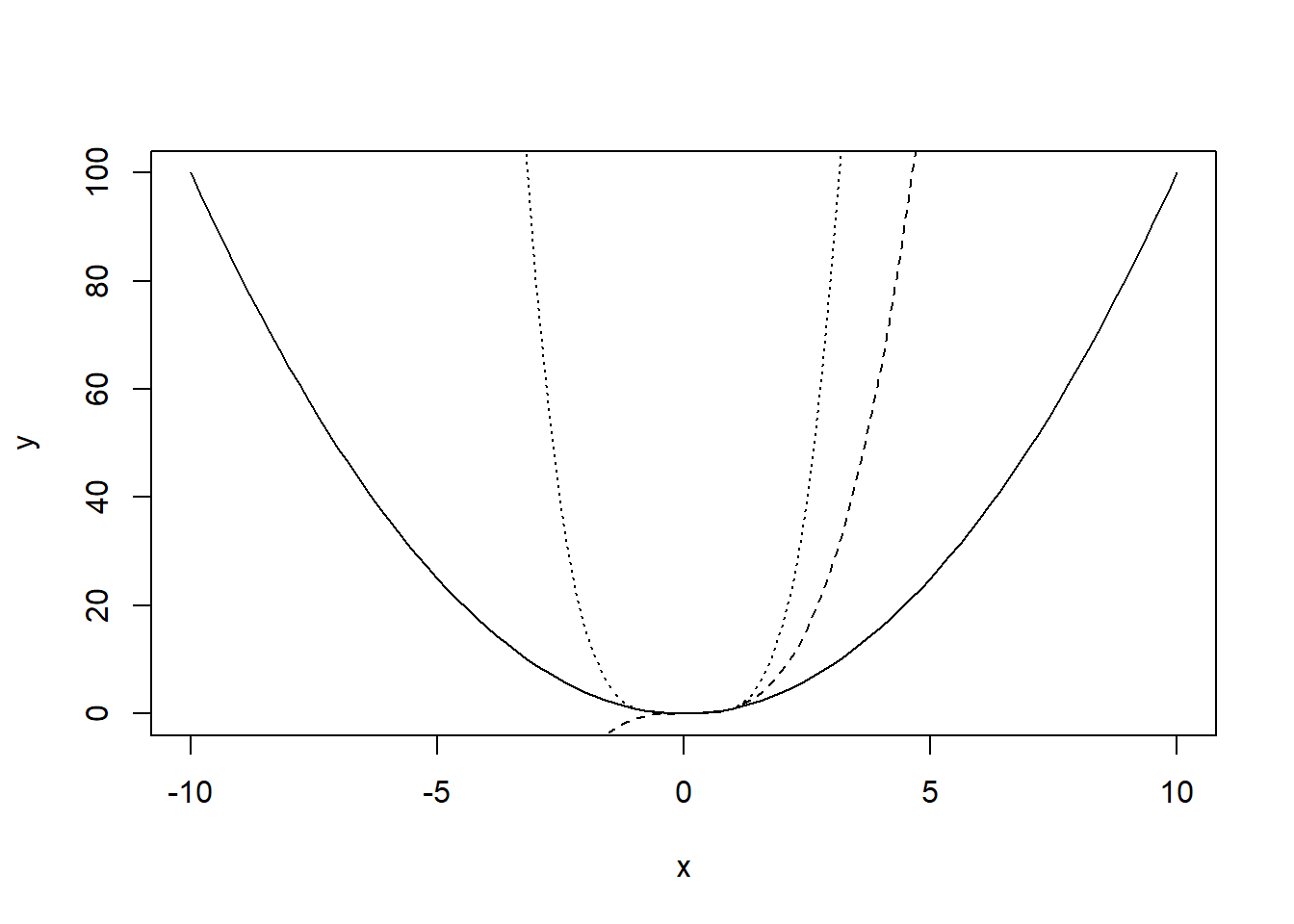
Gráfica conjunta de diferentes monomios.

Figura 7.16: Gráfica conjunta de diferentes monomios.

Las funciones points, abline, lines o text sólo sirven para añadir elementos a un gráfico. En cambio, la función curve también se puede usar para producir la gráfica de una función, como plot, con la ventaja sobre esta última que no sólo se puede aplicar a una función definida con function, sino también a una expresión algebraica. Además, la función curve admite todos los parámetros de plot. Así, el gráfico de la Figura 7.16 también se obtiene con el código siguiente:

curve(x^2, xlim=c(-10, 10), xlab="x", ylab="y")
curve(x^3, lty="dashed", add=TRUE)
curve(x^4, lty="dotted", add=TRUE)

Cuando dibujamos varias funciones en un gráfico, como el de la Figura 7.16, es conveniente usar una leyenda para distinguirlas. Para añadirla, se ha de usar la instrucción

legend(posición, legend=vector de nombres de las curvas, 
       parámetro=vector de  valores del parámetro, ..., 
       parámetro=vector de  valores del parámetro)

donde:

  • La posición indica dónde queremos situar la leyenda, y puede ser o bien dos números para especificar las coordenadas de su esquina superior izquierda, o bien una de las palabras siguientes: "bottomright" (esquina inferior derecha), "bottom" (centrada abajo), "bottomleft" (esquina inferior izquierda), "left" (centrada a la izquierda), "topleft" (esquina superior izquierda), "top" (centrada arriba), "topright" (esquina superior derecha), "right" (centrada a la derecha) o "center" (en el centro del gráfico).

  • El vector legend contiene los nombres (entre comillas o aplicándoles expression) con los que queremos identificar las curvas dentro de la leyenda.

  • Cada parámetro se usará para especificar el vector de sus valores sobre las diferentes curvas, en el orden en el que aparecen en el vector legend e incluyendo los valores por defecto. Se pueden usar varios parámetros. Si se quieren distinguir las curvas por su color, obligatoriamente también se ha de especificar algún otro parámetro, y en particular si sólo se distinguen por el color, se ha de añadir lty igualado al tipo de línea; por defecto, "solid".

  • Se puede usar también el parámetro cex dentro de la función legend para especificar el factor que queremos que se aplique al tamaño de la leyenda, si queremos modificar este último.

Por ejemplo,

curve(x^2, xlim=c(-10, 10), xlab="x", ylab="y")
curve(x^3, lty="dashed", add=TRUE)
curve(x^4, lty="dotted", add=TRUE) 
legend("bottomleft", legend=c(expression(x^2), expression(x^3), expression(x^4)), 
       lty=c("solid", "dashed", "dotted"))

produce el gráfico de la Figura 7.17. Observad que, aunque en el primer curve no hemos especificado el parámetro lty, y ha tomado su valor por defecto, en el parámetro lty del legend sí que hemos especificado su valor para la primera función.

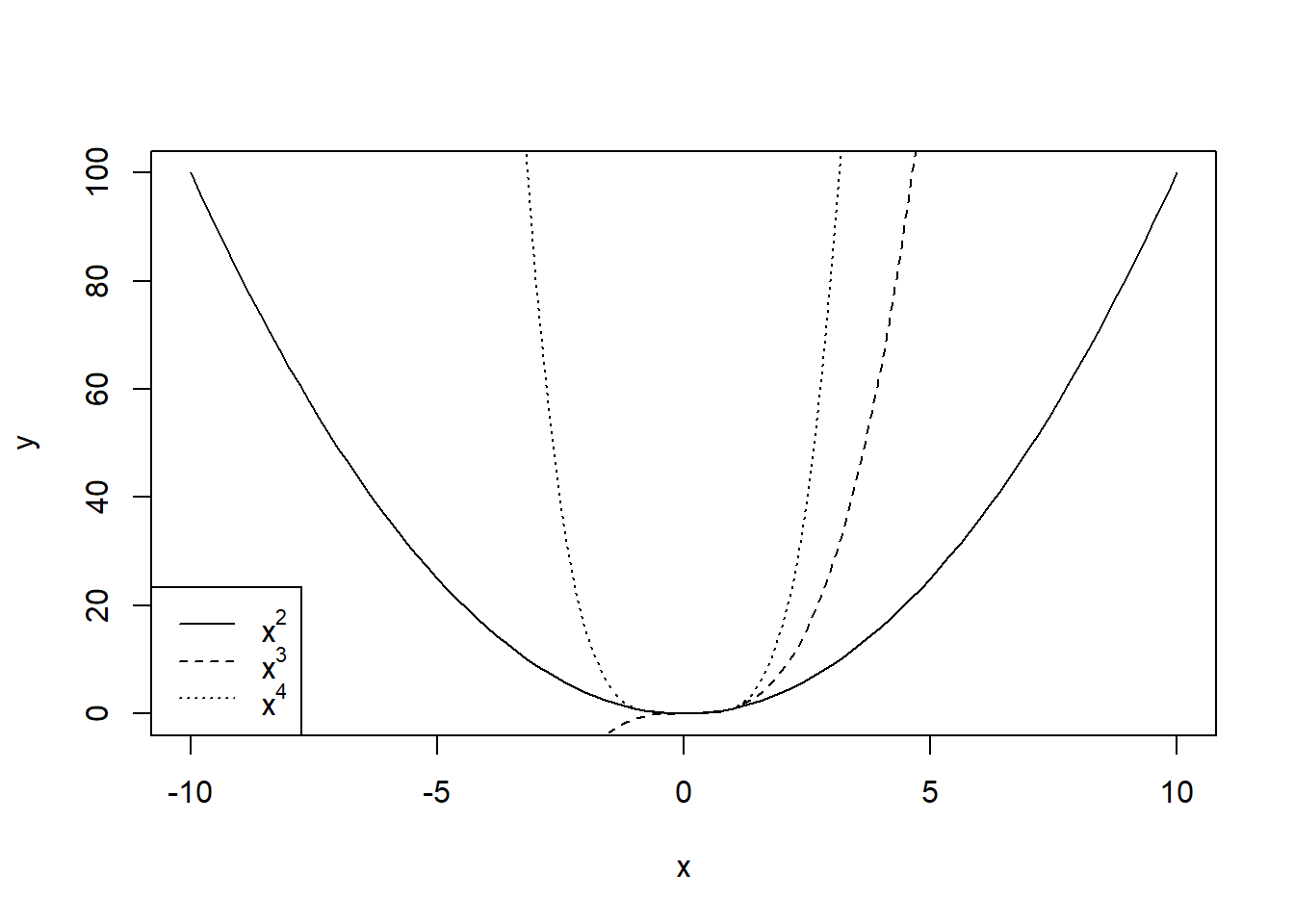
Ejemplo de gráfica conjunta de diferentes funciones con una leyenda.

Figura 7.17: Ejemplo de gráfica conjunta de diferentes funciones con una leyenda.

Veamos otro ejemplo:

curve(2*x+3, xlim=c(-10, 10), ylab="")
curve(2*x^2+3, col="red", lwd=2, add=TRUE)
curve(2*x^3+3, col="blue", lwd=3, add=TRUE)
legend("topleft", legend=c(expression(2*x+3), expression(2*x^2+3), expression(2*x^3+3)), 
       lwd=c(1, 2, 3), col=c("black", "red", "blue"), cex=0.5)

produce el gráfico de la Figura 7.18. Observad el efecto del parámetro cex comparando esta leyenda con la de la Figura 7.17.

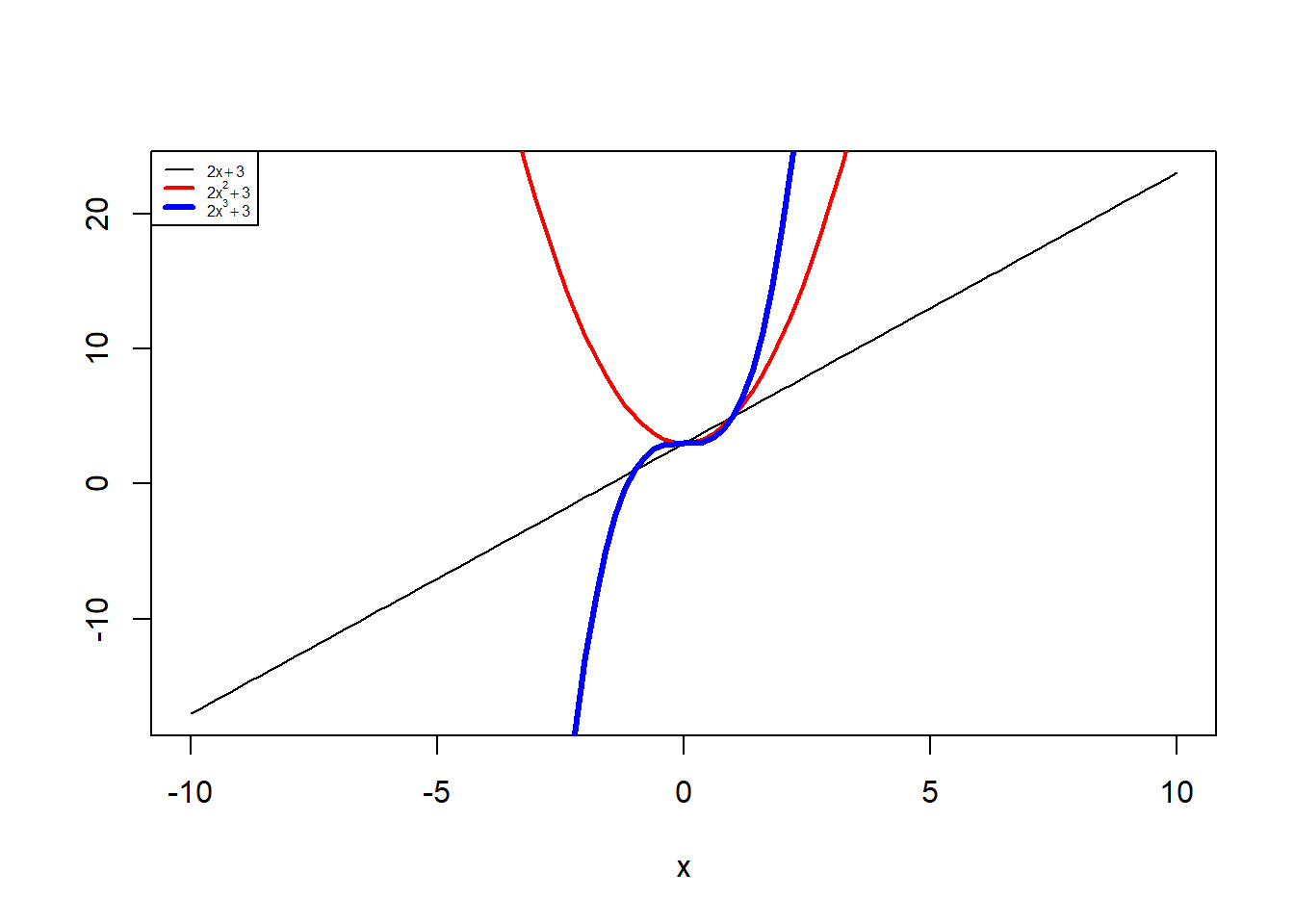
Ejemplo de gráfica conjunta de diferentes funciones con una leyenda reducida.

Figura 7.18: Ejemplo de gráfica conjunta de diferentes funciones con una leyenda reducida.

El código siguiente produce la Figura 7.19; en ella podemos observar que si el único parámetro que especificamos dentro del legend es el color, no se ven las líneas dentro de la leyenda.

curve(2*x+3, -10, 10, ylab="")
curve(2*x^2+3, col="red", add=TRUE)
curve(2*x^3+3, col="blue", add=TRUE)
legend("topleft", legend=c(expression(2*x+3), expression(2*x^2+3), 
                           expression(2*x^3+3)), col=c("black", "red", "blue"))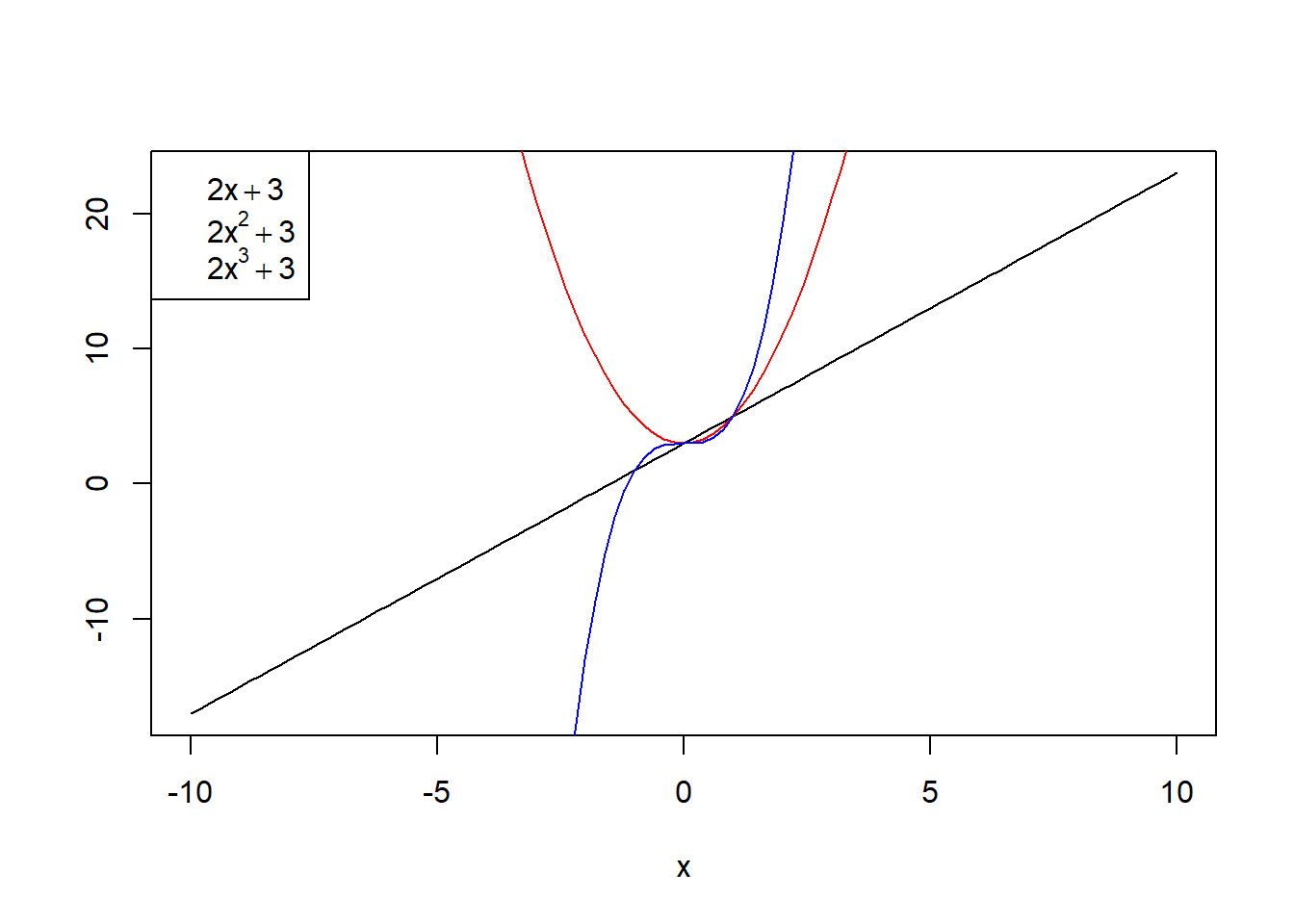
Ejemplo de gráfica conjunta de diferentes funciones con una leyenda inútil

Figura 7.19: Ejemplo de gráfica conjunta de diferentes funciones con una leyenda inútil

Si os interesan, también disponéis de las funciones segments (para añadir segmentos), arrows (para añadir flechas), symbols (para añadir signos, como estrellas, termómetros, …), polygon (para añadir polígonos cerrados especificando sus vértices), etc. Consultad las Ayudas de estas instrucciones para los detalles sobre cómo se usan.

7.4 Guía rápida

  • expression sirve para producir textos matemáticamente bien formateados.

  • par sirve para modificar el aspecto general de los gráficos. Consultad su Ayuda para conocer todos los parámetros que se pueden especificar en esta función.

  • plot es la función genérica para producir gráficos. Sus dos usos principales (por el momento) son:

    • plot(x, y), que dibuja el gráfico de los puntos con vector de primeras coordenadas x y vector de segundas coordenadas y.
    • plot(función), que dibuja la gráfica de la función.

    Algunos parámetros importantes:

    • main: sirve para especificar el título.
    • xlab e ylab: sirven para especificar las etiquetas de los ejes de coordenadas.
    • xlim e ylim: sirven para especificar los rangos de los ejes de coordenadas.
    • xaxp e yaxp: sirven para especificar las marcas en los ejes de coordenadas.
    • log: sirve para especificar los ejes de coordenadas que estarán en escala logarítmica.
    • type: sirve para especificar el tipo de gráfico.
    • pch: sirve para especificar el estilo de los puntos.
    • cex: sirve para especificar el tamaño de los puntos.
    • col: sirve para especificar el color del gráfico.
    • bg: sirve para especificar el color de relleno de los puntos de estilos pch de 21 a 25.
    • lty: sirve para especificar el tipo de las líneas.
    • lwd: sirve para especificar el grosor de la líneas.

    Los parámetros pch, cex, col, bg, type, lty y lwd también se pueden usar en las funciones que siguen.

  • points añade puntos al gráfico activo.

  • abline añade una recta al gráfico activo. Algunos parámetros específicos importantes:

    • v: la abscisa de una recta vertical.
    • h: la ordenada de una recta horizontal.

  • lines añade una línea poligonal al gráfico activo.

  • text añade textos al gráfico activo. Algunos parámetros específicos importantes:

    • pos: la posición del texto con respecto a sus coordenadas.
    • labels: el texto.

  • legend añade una leyenda al gráfico activo.

  • curve, con el parámetro add=TRUE, sirve para añadir la gráfica de una función al gráfico activo. Esta función admite todos los parámetros de plot.

7.5 Ejercicios

Test

(1) Dad una sola instrucción que dibuje un histograma de líneas de los puntos \((5\cdot 3^n)_{n=10,\ldots,20}\) (con las operaciones escritas exactamente en este orden). No dejéis espacios en blanco innecesarios. (Y antes de contestar, comprobad con R que la instrucción que dais hace el que os pedimos.)

(2) Dad dos instrucciones sucesivas, separadas por puntos y coma seguidos de un espacio en blanco, que definan la función \(f(x)=x^3-3x^2+5\) (con las operaciones en el orden dado) y a continuación dibujen su gráfica (usando la función plot) para \(x\) entre -15 y 15 y le pongan el título “Una cúbica”. No dejéis espacios en blanco innecesarios. (Y antes de contestar, comprobad con R que la instrucción que dais funciona.)

(3) Dad una sola instrucción (usando la función curve) que dibuje una gráfica de la función \(y=x^3-3x^2+5\) (con las operaciones en el orden dado) para \(x\) entre -15 y 15, deje sin etiquetar el eje de abscisas, etiquete con una y el eje de ordenadas y le ponga título “Una cúbica”. Los parámetros se tienen que especificar en el orden dado en el enunciado. No dejéis espacios en blanco innecesarios. (Y antes de contestar, comprobad con R que la instrucción que donau funciona.)

(4) Dad tres instrucciones sucesivas, separadas por puntos y coma seguidos de un espacio en blanco, de manera que las dos primeras dibujen (usando ambas la función curve) una gráfica conjunta de las rectas \(y=2x\) e \(y=3x\) para \(x\) entre -20 y 20, con ambos ejes de coordenadas sin etiquetar, con la primera recta roja y la segunda azul, y a continuación la tercera instrucción añada al gráfico producido por las dos primeras una leyenda en la esquina superior izquierda que indique que la función \(2x\) es roja y la \(3x\) azul. No dejéis espacios en blanco innecesarios. (Y antes de contestar, comprobad con R que las instrucciones que dais funcionan.)

(5) Dad dos instrucciones sucesivas, separadas por puntos y coma seguidos de un espacio en blanco, que dibujen un gráfico conjunto de las secuencias de puntos \((n,2n^2)_{n=5,\ldots,10}\) y \((n,3n^3)_{n=0,\ldots,5}\), con ambos ejes de coordenadas sin etiquetar y el rango del eje de ordenadas entre 0 y 500, con los puntos de la primera secuencia de estilo pch=18 y los de la segunda de estilo pch=20. No dejéis espacios en blanco innecesarios. (Y antes de contestar, comprobad con R que las instrucciones que dais hacen el que os pedimos.)

(6) Dad una instrucción que añada al gráfico inmediatamente anterior un punto en las coordenadas (2,3) de estilo pch=15. No dejéis espacios en blanco innecesarios.

(7) Dad una instrucción que añada al gráfico inmediatamente anterior la recta \(y=3x+5\) de triple grosor. No dejéis espacios en blanco innecesarios.

(8) Dad una instrucción que añad al gráfico inmediatamente anterior la recta horizontal \(y=2\) de color rojo. No dejéis espacios en blanco innecesarios.

(9) Dad una instrucción que añada al gráfico inmediatamente anterior el texto “(2,3)” a la derecha de las coordenadas (2,3). No dejéis espacios en blanco innecesarios.

Ejercicio

La función de Gompertz es \(G(t)=ae^{-be^{-ct}}\), con \(a, b, c\in \mathbb{R}\) estrictamente positivos, y se usa para modelar el crecimiento de tumores o de poblaciones con recursos limitados. Vamos a analizar gráficamente el efecto de los parámetros \(a, b, c\).

  • La recta \(y=a\) es una asíntota horizontal de \(G(t)\). Comprobadlo dibujando en un mismo gráfico dos funciones de Gompertz con los mismos valores de \(b\) y \(c\) y diferentes valores de \(a\), y las rectas horizontales definidas por estos valores de \(a\). Usad colores, tipos de líneas, textos, leyenda, todo lo que consideréis necesario para ayudar a que el gráfico muestre la información que se desea.
  • Para estudiar el efecto de \(b\), dibujad en un mismo gráfico tres funciones de Gompertz con los mismos valores de \(a\) y \(c\) y diferentes valores de \(b\). De nuevo, usad todo lo que consideréis necesario para mejorar la comprensión del gráfico. A partir de este gráfico, ¿qué efecto diríais que tiene el parámetro \(b\) sobre la gráfica de la función?
  • Para estudiar el efecto de \(c\), dibujad en un mismo gráfico tres funciones de Gompertz con los mismos valores de \(a\) y \(b\) y diferentes valores de \(c\). De nuevo, usad todo lo que consideréis necesario para mejorar la comprensión del gráfico. A partir de este gráfico, ¿qué efecto diríais que tiene el parámetro \(c\) sobre la gráfica de la función?

Respuestas al test

(1) plot(10:20,5*3^(10:20),type="h")

(2) f=function(x){x^3-3*x^2+5}; plot(f,xlim=c(-15,15),main="Una cúbica")

(3) curve(x^3-3*x^2+5,xlim=c(-15,15),xlab="",ylab="y",main="Una cúbica")

(4) curve(2*x,xlim=c(-20,20),xlab="",ylab="",col="red"); curve(3*x, col="blue",add=TRUE); legend("topleft",legend=c("2x","3x"),lty=c(1,1),col=c("red","blue"))

(5) plot(5:10,2*(5:10)^2,xlim=c(0,10),ylim=c(0,1000),xlab="",ylab="",pch=18); points(0:5,3*(0:5)^3,pch=20)

(6) points(2,3,pch=15)

(7) abline(5,3,lwd=3)

(8) abline(h=2,col="red")

(9) text(2,3,labels="(2,3)",pos=4)