Lección 10 Descripción de datos cualitativos

Los datos cualitativos corresponden a observaciones sobre cualidades de un objeto o individuo, tales como su especie o su sexo, que pueden ser iguales o diferentes, pero que no admiten ningún otro tipo de comparación significativa: por ejemplo, datos para los que no tenga ningún sentido preguntarse si uno es más grande que otro, ni efectuar operaciones aritméticas con ellos, aunque estén representados por números. Llamaremos variable cualitativa a una lista de observaciones de un tipo de datos cualitativos sobre un conjunto concreto de objetos, y niveles, como en los factores, a los diferentes valores que pueden tomar estos datos; por ejemplo, los dos niveles de una variable Sexo serían “Macho” y “Hembra”, o sinónimos.

Con R, usaremos vectores y factores para representar variables cualitativas. Los factores nos servirán para agrupar las observaciones según los niveles de la variable. De esta manera podremos segmentar la población que representa la variable en grupos o subpoblaciones, asignando un grupo a cada nivel, y podremos comparar el comportamiento de otras variables sobre estos grupos.

10.1 Frecuencias

Los estadísticos básicos para datos cualitativos son sencillos: dada una variable cualitativa, para cada uno de sus niveles podemos contar cuántos datos hay en ese nivel (la frecuencia absoluta del nivel) y qué fracción del total representan (la frecuencia relativa del nivel) y nada más.

Ejemplo 10.1 Supongamos que se ha realizado un seguimiento a 20 personas ingresadas en un geriátrico. Uno de los datos que se han recogido sobre estas personas ha sido su sexo. El resultado ha sido una variable cualitativa formada por las 20 observaciones siguientes:

Mujer, Mujer, Hombre, Mujer, Mujer, Mujer, Mujer, Mujer, Hombre, Mujer Hombre, Hombre, Mujer, Mujer, Hombre, Mujer, Mujer, Mujer, Mujer, Hombre.

Sus dos niveles son Hombre y Mujer. En esta variable hay 14 mujeres y 6 hombres. Por lo tanto, éstas son las frecuencias absolutas de estos niveles. Puesto que en total hay 20 individuos, sus frecuencias relativas son

Hombre: 6/20=0.3, Mujer: 14/20=0.7.

En general, supongamos que tenemos un tipo de datos cualitativos con niveles \[ l_1, l_2, \ldots, l_k. \] Efectuamos $n$ observaciones de este tipo de datos, y sean \[ x_1, x_2, \ldots, x_n \]

los resultados que obtenemos. Cada una de estas observaciones $x_j$ toma como valor alguno de los niveles $l_i$. Estas observaciones forman una variable cualitativa.

Así, en el ejemplo anterior tendríamos que $l_1$=Hombre y $l_2$=Mujer, que $n=20$ (el número de observaciones efectuadas), y $x_1, \ldots, x_{20}$ formarían la muestra de sexos.

Con estas notaciones:

La frecuencia absoluta del nivel $l_j$ en esta variable cualitativa, que denotaremos por $n_j$, es el número de observaciones en las que el resultado $x_i$ es igual al nivel $l_j$.
La frecuencia relativa del nivel $l_j$ en esta variable cualitativa es la fracción $f_j={n_j}/{n}$. Es decir, la fracción (en tanto por uno) de observaciones que corresponden a este nivel. El tanto por ciento de observaciones del nivel $l_j$ es entonces $f_j\cdot 100\%$.
La moda de esta variable cualitativa es su nivel, o niveles, de mayor frecuencia (absoluta o relativa, tanto da).

La tabla siguiente resume las frecuencias absolutas y relativas de la variable cualitativa del Ejemplo 10.1, con las notaciones que acabamos de introducir. Su moda es el nivel Mujer.

\[ \begin{array}{|c||rrr|} \hline \mathbf{Sexo} & n_j & f_j & \% \\\hline\hline \mbox{Hombre} & 6 & 0.3 & 30\% \\ \mbox{Mujer} & 14 & 0.7 & 70 \% \\\hline Total & 20 & 1 & 100\% \\\hline \end{array} \]

10.2 Tablas unidimensionales de frecuencias

Supongamos que tenemos una variable cualitativa guardada en un vector o un factor (para simplificar, en lo que queda de sección, diremos vector para referirnos genéricamente tanto a un vector como a un factor). Por ejemplo:

x=c(3,2,5,1,3,1,5,6,2,2,2,1,3,5,2)
x
#>  [1] 3 2 5 1 3 1 5 6 2 2 2 1 3 5 2
Respuestas=factor(c("No","No","Sí","No","Sí","No","No","Sí"))
Respuestas
#> [1] No No Sí No Sí No No Sí
#> Levels: No Sí

Con R, la tabla de frecuencias absolutas de un vector que representa una variable cualitativa se calcula con la función table. En nuestros ejemplos:

table(x)
#> x
#> 1 2 3 5 6 
#> 3 5 3 3 1
table(Respuestas)
#> Respuestas
#> No Sí 
#>  5  3

El resultado de una función table es un objeto de datos de un tipo nuevo: una tabla de contingencia, una table en el argot de R. Como vemos, al aplicar table a un vector obtenemos una tabla unidimensional formada por una fila con los niveles de la variable y una segunda fila donde, debajo de cada nivel, aparece su frecuencia absoluta en el vector.

Los nombres de las columnas de una tabla unidimensional se obtienen con la función names.

names(table(x))
#> [1] "1" "2" "3" "5" "6"
names(table(Respuestas))
#> [1] "No" "Sí"

Habréis observado que en la table de un vector sólo aparecen los nombres de los niveles presentes en el vector. Si el tipo de datos cualitativos usado tenía más niveles y queremos que aparezcan explícitamente en la tabla (con frecuencia 0), hay que transformar el vector en un factor con los niveles deseados.

z=factor(x, levels=1:7)  #Los niveles serán 1,2,3,4,5,6,7
z
#>  [1] 3 2 5 1 3 1 5 6 2 2 2 1 3 5 2
#> Levels: 1 2 3 4 5 6 7
table(z)
#> z
#> 1 2 3 4 5 6 7 
#> 3 5 3 0 3 1 0

A efectos prácticos, podemos pensar que una tabla unidimensional es como un vector de números donde cada entrada está identificada por un nombre: el de su columna. Para referirnos a una entrada de una tabla unidimensional, podemos usar tanto su posición como su nombre (entre comillas, aunque sea un número). Veamos algunos ejemplos.

La cuarta columna de table(x):

table(x)[4] 
#> 5 
#> 3

La columna de table(x) correspondiente al nivel 5:

table(x)["5"]
#> 5 
#> 3

El triple de la segunda columna de table(x):

3*table(x)[2]
#>  2 
#> 15

Las tablas de contingencia aceptan la mayoría de las funciones explicadas para vectores. Por ejemplo:

Suma de las entradas de table(x):

sum(table(x))
#> [1] 15

Raíces cuadradas de las entradas de table(Respuestas):

sqrt(table(Respuestas))
#> Respuestas
#>       No       Sí 
#> 2.236068 1.732051

La tabla de frecuencias relativas de un vector se puede calcular aplicando la función prop.table a su table. El resultado vuelve a ser una tabla de contingencia unidimensional.

prop.table(table(x))
#> x
#>          1          2          3          5          6 
#> 0.20000000 0.33333333 0.20000000 0.20000000 0.06666667
prop.table(table(Respuestas))
#> Respuestas
#>    No    Sí 
#> 0.625 0.375

¡Atención! La función prop.table se tiene que aplicar al resultado de table, no al vector original. Si aplicamos prop.table a un vector de palabras o a un factor, dará un error, pero si la aplicamos a un vector de números, nos dará una tabla. Esta tabla no es la tabla de frecuencias relativas de la variable cualitativa representada por el vector, sino la de una variable que tuviera como tabla de frecuencias absolutas este vector de números, entendiendo que cada entrada del vector representa la frecuencia de un nivel diferente. Por ejemplo, aplicando prop.table a nuestro vector x obtenemos:

prop.table(x)
#>  [1] 0.06976744 0.04651163 0.11627907 0.02325581 0.06976744 0.02325581
#>  [7] 0.11627907 0.13953488 0.04651163 0.04651163 0.04651163 0.02325581
#> [13] 0.06976744 0.11627907 0.04651163

que no es la tabla de frecuencias relativas de x. Veamos otro ejemplo aun más evidente:

X=c(1,1,1)
prop.table(table(X))
#> X
#> 1 
#> 1
prop.table(X)
#> [1] 0.3333333 0.3333333 0.3333333

También podemos calcular la tabla de frecuencias relativas de un vector dividiendo el resultado de table por el número de observaciones.

table(x)/length(x)
#> x
#>          1          2          3          5          6 
#> 0.20000000 0.33333333 0.20000000 0.20000000 0.06666667
table(x)/sum(table(x))
#> x
#>          1          2          3          5          6 
#> 0.20000000 0.33333333 0.20000000 0.20000000 0.06666667

Dados un vector x y un número natural n, la instrucción

names(which(table(x)==n)

nos da los niveles de x que tienen frecuencia absoluta n.

table(x)
#> x
#> 1 2 3 5 6 
#> 3 5 3 3 1
names(which(table(x)==3))
#> [1] "1" "3" "5"
names(which(table(x)==2))
#> character(0)

En particular, por lo tanto,

names(which(table(x)==max(table(x))))

nos da los niveles de frecuencia máxima en x: su moda.

names(which(table(x)==max(table(x))))
#> [1] "2"
names(which(table(Respuestas)==max(table(Respuestas))))
#> [1] "No"

Ejemplo 10.2 Continuamos en la situación del Ejemplo 10.1. Para calcular las frecuencias y la moda con R, definimos un vector con los datos y le aplicamos las funciones pertinentes:

Sexo_Ger=c("Mujer","Mujer","Hombre","Mujer","Mujer","Mujer","Mujer","Mujer","Hombre",
  "Mujer","Hombre","Hombre","Mujer","Mujer","Hombre","Mujer","Mujer","Mujer","Mujer","Hombre")
table(Sexo_Ger)  #Tabla de frecuencias absolutas
#> Sexo_Ger
#> Hombre  Mujer 
#>      6     14
prop.table(table(Sexo_Ger)) #Tabla de frecuencias relativas
#> Sexo_Ger
#> Hombre  Mujer 
#>    0.3    0.7
names(which(table(Sexo_Ger)==max(table(Sexo_Ger)))) #Moda
#> [1] "Mujer"

10.3 Tablas bidimensionales de frecuencias

La función table también permite construir tablas de frecuencias conjuntas de dos o más variables. A modo de ejemplo, supongamos que el vector Respuestas, de la sección anterior, contiene las respuestas a una pregunta dadas por unos individuos cuyos sexos tenemos almacenados en un vector Sexo, en el mismo orden que sus respuestas. En este caso, podemos construir una tabla que nos diga cuántos individuos de cada sexo han dado cada respuesta.

Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
Sexo=c("M","M","M","H","H","H","H","H") #H es hombre, M es mujer
table(Respuestas,Sexo)
#>           Sexo
#> Respuestas H M
#>         No 3 2
#>         Sí 2 1
table(Sexo,Respuestas)
#>     Respuestas
#> Sexo No Sí
#>    H  3  2
#>    M  2  1

El resultado es, en ambos casos, una tabla de contingencia como antes, pero ahora bidimensional, puesto que cada entrada tiene dos dimensiones, una por cada variable, como en una matriz.

Como podemos ver, en una tabla bidimensional producida aplicando table a dos vectores, los niveles del primer vector en el argumento definen las filas, y los del segundo, las columnas. Así, en table(Respuestas,Sexo), las filas corresponden a las respuestas y las columnas a los sexos. Para intercambiar filas por columnas, es decir, para “trasponer” la tabla sin tener que recalcularla, podemos usar la misma función t que usamos para trasponer matrices:

t(table(Respuestas,Sexo))
#>     Respuestas
#> Sexo No Sí
#>    H  3  2
#>    M  2  1

En la práctica, tenéis que decidir si alguna de las asignaciones de variables a dimensiones es más conveniente que la otra. Por ejemplo, y teniendo en cuenta que nuestra manera natural de leer una tabla es por filas, si lo que nos interesa son las frecuencias de las respuestas entre las personas de cada sexo, seguramente lo más adecuado será elegir el sexo como variable para las filas.

Para referirnos a una entrada de una tabla bidimensional podemos usar corchetes como si estuviéramos en una matriz o un data frame. Dentro de los corchetes, tanto podemos usar los índices como los nombres (entre comillas) de los niveles.

table(Respuestas,Sexo)[1,2]
#> [1] 2
table(Respuestas,Sexo)["No","M"]
#> [1] 2
table(Sexo,Respuestas)[1,2]
#> [1] 2
table(Sexo,Respuestas)["H","Sí"]
#> [1] 2

Como en el caso unidimensional, la función prop.table sirve para calcular tablas bidimensionales de frecuencias relativas conjuntas de pares de variables. Pero en el caso bidimensional tenemos dos tipos de frecuencias relativas, que definen, para cada par de variables, tres tablas diferentes:

Las frecuencias relativas globales: para cada par de niveles, uno de cada variable, la fracción de individuos que pertenecen a ambos niveles respecto del total de la muestra; por ejemplo, la fracción de mujeres que han contestado que sí respecto del total de la muestra sería la frecuencia relativa global del par (mujer, sí).
Las frecuencias relativas marginales: dentro de cada nivel de una variable, y para cada nivel de la otra, la fracción de individuos que pertenecen al segundo nivel respecto del total de la subpoblación definida por el primer nivel; por ejemplo, la fracción de mujeres que han contestado que sí respecto del total de mujeres sería una frecuencia relativa marginal.

Dadas dos variables, se pueden calcular dos familias de frecuencias relativas marginales, según cuál sea la variable que defina las subpoblaciones en las que calculemos las frecuencias relativas de los niveles de la otra variable; no es lo mismo la fracción de mujeres que han contestado que sí respecto del total de mujeres, que la fracción de mujeres que han contestado que sí respecto del total de personas que han dado esta misma respuesta.

La tabla de frecuencias relativas globales se calcula aplicando sin más la función prop.table a la table. Por lo que se refiere a las frecuencias relativas marginales, la variable que define las subpoblaciones en las que las calculamos se indica con el parámetro margin. Es decir, con margin=1 especificamos que la variable que define las subpoblaciones es la primera, y que, por lo tanto, las frecuencias relativas se calculan dentro de las filas; en cambio, con margin=2 especificamos que la variable que define las subpoblaciones es la segunda, por lo que las frecuencias relativas se calculan por columnas; margin=NULL es su valor por defecto y, por lo tanto, equivalente a no especificar este parámetro.

Así:

La tabla prop.table(table(Sexo,Respuestas)) nos da la fracción del total que representa cada pareja (sexo, respuesta).

prop.table(table(Sexo,Respuestas))
#>     Respuestas
#> Sexo    No    Sí
#>    H 0.375 0.250
#>    M 0.250 0.125

La tabla prop.table(table(Sexo,Respuestas), margin=1) nos da la fracción que representa cada respuesta dentro de cada sexo.

prop.table(table(Sexo,Respuestas), margin=1)
#>     Respuestas
#> Sexo        No        Sí
#>    H 0.6000000 0.4000000
#>    M 0.6666667 0.3333333

La tabla prop.table(table(Sexo,Respuestas), margin=2) nos da la fracción que representa cada sexo dentro de cada respuesta

prop.table(table(Sexo,Respuestas), margin=2)
#>     Respuestas
#> Sexo        No        Sí
#>    H 0.6000000 0.6666667
#>    M 0.4000000 0.3333333

De esta manera, por ejemplo, en la primera tabla podemos leer que un 25% del total de la muestra son mujeres que han contestado que no; en la segunda tabla, que un 66.67% de las mujeres han contestado que no; y en la tercera tabla, que las mujeres representan el 40% del total de las personas que han contestado que no.

La función CrossTable del paquete gmodels permite producir (especificando el parámetro prop.chisq=FALSE) un resumen de la tabla de frecuencias absolutas y las tres tablas de frecuencias relativas de dos variables en un formato adecuado para su visualización:

library(gmodels) 
CrossTable(Sexo, Respuestas, prop.chisq=FALSE)
#> 
#>  
#>    Cell Contents
#> |-------------------------|
#> |                       N |
#> |           N / Row Total |
#> |           N / Col Total |
#> |         N / Table Total |
#> |-------------------------|
#> 
#>  
#> Total Observations in Table:  8 
#> 
#>  
#>              | Respuestas 
#>         Sexo |        No |        Sí | Row Total | 
#> -------------|-----------|-----------|-----------|
#>            H |         3 |         2 |         5 | 
#>              |     0.600 |     0.400 |     0.625 | 
#>              |     0.600 |     0.667 |           | 
#>              |     0.375 |     0.250 |           | 
#> -------------|-----------|-----------|-----------|
#>            M |         2 |         1 |         3 | 
#>              |     0.667 |     0.333 |     0.375 | 
#>              |     0.400 |     0.333 |           | 
#>              |     0.250 |     0.125 |           | 
#> -------------|-----------|-----------|-----------|
#> Column Total |         5 |         3 |         8 | 
#>              |     0.625 |     0.375 |           | 
#> -------------|-----------|-----------|-----------|
#> 
#>

La leyenda Cell Contents explica los contenidos de cada celda de la tabla: en este caso, y en orden descendente, la frecuencia absoluta N, la frecuencia relativa por filas, la frecuencia relativa por columnas, y la frecuencia relativa global. Asimismo, se muestran las celdas de los márgenes, con las frecuencias absolutas y relativas de cada fila (en la columna Row Total) y cada columna (en la fila Column Total). Esta función dispone de muchos parámetros que permiten modificar el contenido de las celdas y que podéis consultar en su Ayuda.

Una tabla de contingencia bidimensional es, a efectos prácticos, una matriz con algunos atributos extra. En particular, podemos usar sobre estas tablas la mayoría de las funciones para matrices que tengan sentido para tablas; por ejemplo, rowSums y colSums se pueden aplicar a una tabla y suman sus filas y sus columnas, respectivamente:

table(Sexo,Respuestas)
#>     Respuestas
#> Sexo No Sí
#>    H  3  2
#>    M  2  1
colSums(table(Sexo,Respuestas))
#> No Sí 
#>  5  3
rowSums(table(Sexo,Respuestas))
#> H M 
#> 5 3
colSums(prop.table(table(Sexo,Respuestas)))
#>    No    Sí 
#> 0.625 0.375
rowSums(prop.table(table(Sexo,Respuestas)))
#>     H     M 
#> 0.625 0.375

También podemos usar sobre una tabla bidimensional (o, en general, multidimensional) la función apply con la misma sintaxis que para matrices; véase la próxima sección.

10.4 Tablas multidimensionales de frecuencias

En general, podemos calcular tablas de frecuencias de cualquier número de variables, no sólo de una o dos. El manejo de estas tablas multidimensionales es similar al caso bidimensional, simplemente recordando que ahora hay más variables que tener en cuenta en el momento, por ejemplo, de especificar entradas o de calcular frecuencias relativas marginales.

Veamos un ejemplo tridimensional. Supongamos que, además de los vectores

Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
Sexo=c("M","M","M","H","H","H","H","H")

tenemos un tercer vector con las nacionalidades de los individuos representados en estos dos vectores:

Pais=c("Francia","Alemania","Italia","Italia","Italia","Italia","Alemania","Francia")

Podemos calcular entonces una tabla de frecuencias absolutas para las ternas (sexo, respuesta, país).

table(Sexo,Respuestas,Pais)
#> , , Pais = Alemania
#> 
#>     Respuestas
#> Sexo No Sí
#>    H  1  0
#>    M  1  0
#> 
#> , , Pais = Francia
#> 
#>     Respuestas
#> Sexo No Sí
#>    H  0  1
#>    M  1  0
#> 
#> , , Pais = Italia
#> 
#>     Respuestas
#> Sexo No Sí
#>    H  2  1
#>    M  0  1

R muestra la tabla tridimensional que obtenemos como una lista de tablas bidimensionales table(Sexo,Respuestas), separando la población según los niveles de la tercera variable. Si no os gusta esta manera de visualizar una tabla tridimensional, una alternativa es usar la función ftable, que la mostrará en lo que se llama formato plano:

ftable(Sexo,Respuestas,Pais)
#>                 Pais Alemania Francia Italia
#> Sexo Respuestas                             
#> H    No                     1       0      2
#>      Sí                     0       1      1
#> M    No                     1       1      0
#>      Sí                     0       0      1

Los parámetros row.vars y col.vars de ftable permiten especificar qué variables queremos que aparezcan como filas o como columnas, respectivamente.

ftable(Sexo,Respuestas,Pais, col.vars=c("Sexo","Respuestas"))
#>          Sexo        H     M   
#>          Respuestas No Sí No Sí
#> Pais                           
#> Alemania             1  0  1  0
#> Francia              0  1  1  0
#> Italia               2  1  0  1

Para referirnos a una entrada, o a una subtabla, de una tabla podemos usar corchetes.

table(Sexo,Respuestas,Pais)["H","Sí","Italia"]
#> [1] 1
table(Sexo,Respuestas,Pais)[ , ,"Italia"]
#>     Respuestas
#> Sexo No Sí
#>    H  2  1
#>    M  0  1
table(Sexo,Respuestas,Pais)[  ,"Sí","Italia"]
#> H M 
#> 1 1
table(Sexo,Respuestas,Pais)["M", ,"Italia"]
#> No Sí 
#>  0  1

En una tabla multidimensional, podemos calcular frecuencias relativas marginales respecto de los niveles de una variable o respecto de combinaciones de niveles de varias variables: por ejemplo, las frecuencias relativas marginales de las respuestas en cada combinación (sexo, país). Como en el caso bidimensional, las tablas correspondientes se calculan aplicando prop.table a la tabla de frecuencias absolutas, y especificando con el parámetro margin las dimensiones, o combinaciones de dimensiones, respecto de las que calculamos las frecuencias relativas. Si no se especifica el parámetro margin, se obtiene la tabla de frecuencias relativas globales.

Así, por ejemplo:

La tabla prop.table(table(Sexo,Respuestas,Pais)) nos da la fracción que representa cada terna (sexo, respuesta, país) dentro del total de la muestra:

prop.table(table(Sexo,Respuestas,Pais)) 
#> , , Pais = Alemania
#> 
#>     Respuestas
#> Sexo    No    Sí
#>    H 0.125 0.000
#>    M 0.125 0.000
#> 
#> , , Pais = Francia
#> 
#>     Respuestas
#> Sexo    No    Sí
#>    H 0.000 0.125
#>    M 0.125 0.000
#> 
#> , , Pais = Italia
#> 
#>     Respuestas
#> Sexo    No    Sí
#>    H 0.250 0.125
#>    M 0.000 0.125

La tabla prop.table(table(Sexo,Respuestas,Pais), margin=3) nos da la fracción que representa cada pareja (sexo, respuesta) dentro de cada país:

prop.table(table(Sexo,Respuestas,Pais), margin=3)
#> , , Pais = Alemania
#> 
#>     Respuestas
#> Sexo   No   Sí
#>    H 0.50 0.00
#>    M 0.50 0.00
#> 
#> , , Pais = Francia
#> 
#>     Respuestas
#> Sexo   No   Sí
#>    H 0.00 0.50
#>    M 0.50 0.00
#> 
#> , , Pais = Italia
#> 
#>     Respuestas
#> Sexo   No   Sí
#>    H 0.50 0.25
#>    M 0.00 0.25

La tabla prop.table(table(Sexo,Respuestas,Pais), margin=c(1,3)) nos da la fracción que representa cada respuesta dentro de cada combinación de (sexo, país):

prop.table(table(Sexo,Respuestas,Pais), margin=c(1,3))
#> , , Pais = Alemania
#> 
#>     Respuestas
#> Sexo        No        Sí
#>    H 1.0000000 0.0000000
#>    M 1.0000000 0.0000000
#> 
#> , , Pais = Francia
#> 
#>     Respuestas
#> Sexo        No        Sí
#>    H 0.0000000 1.0000000
#>    M 1.0000000 0.0000000
#> 
#> , , Pais = Italia
#> 
#>     Respuestas
#> Sexo        No        Sí
#>    H 0.6666667 0.3333333
#>    M 0.0000000 1.0000000

De esta manera, por ejemplo, en la primera tabla podemos leer que los hombres españoles que han contestado afirmativamente forman un 12.5% del total de individuos; en la segunda, que los hombres que han contestado que sí representan un 25% del total de individuos españoles; y en la tercera, que un 33.33% del total de hombres españoles ha contestado que sí.

Al aplicar prop.table al resultado de una ftable, la tabla resultante sigue en formato plano:

prop.table(ftable(Sexo,Respuestas,Pais)) 
#>                 Pais Alemania Francia Italia
#> Sexo Respuestas                             
#> H    No                 0.125   0.000  0.250
#>      Sí                 0.000   0.125  0.125
#> M    No                 0.125   0.125  0.000
#>      Sí                 0.000   0.000  0.125

Podemos aplicar funciones a filas o columnas de una tabla multidimensional con la función apply, especificando en el parámetro FUN la función y en el parámetro MARGIN la variable o combinación de variables a la que aplicamos la función (son las variables que aparecerán en la tabla resultante). Observad las dos instrucciones siguientes y sus resultados:

Sumamos los números de respuestas agrupando por combinaciones (sexo,país):

apply(table(Sexo,Respuestas,Pais), MARGIN=c(1,3), FUN=sum)
#>     Pais
#> Sexo Alemania Francia Italia
#>    H        1       1      3
#>    M        1       1      1

Sumamos los números de respuestas agrupando por sexos:

apply(table(Sexo,Respuestas,Pais), MARGIN=2, FUN=sum)
#> No Sí 
#>  5  3

Hasta ahora hemos manipulado tablas de frecuencias que hemos construido nosotros mismos a partir de variables cualitativas. Todo lo que hemos hecho con estas tablas se puede también hacer con las tablas de frecuencias que lleva R predefinidas o que obtengamos de otra manera. Veamos un ejemplo.

Ejemplo 10.3 El objeto de datos HairEyeColor que lleva predefinido R es una tabla las frecuencias absolutas, en una muestra de personas, de tres variables cualitativas: color de cabello, Hair, color de los ojos, Eye, y sexo, Sex, en este orden.

str(HairEyeColor)
#>  'table' num [1:4, 1:4, 1:2] 32 53 10 3 11 50 10 30 10 25 ...
#>  - attr(*, "dimnames")=List of 3
#>   ..$ Hair: chr [1:4] "Black" "Brown" "Red" "Blond"
#>   ..$ Eye : chr [1:4] "Brown" "Blue" "Hazel" "Green"
#>   ..$ Sex : chr [1:2] "Male" "Female"
ftable(HairEyeColor)
#>             Sex Male Female
#> Hair  Eye                  
#> Black Brown       32     36
#>       Blue        11      9
#>       Hazel       10      5
#>       Green        3      2
#> Brown Brown       53     66
#>       Blue        50     34
#>       Hazel       25     29
#>       Green       15     14
#> Red   Brown       10     16
#>       Blue        10      7
#>       Hazel        7      7
#>       Green        7      7
#> Blond Brown        3      4
#>       Blue        30     64
#>       Hazel        5      5
#>       Green        8      8

Efectuemos algunas operaciones sobre esta tabla, para ilustrar como podemos trabajar con ella:

Número total de individuos en la muestra:

sum(HairEyeColor)
#> [1] 592

Subtabla de hombres:

HairEyeColor[ , ,"Male"]
#>        Eye
#> Hair    Brown Blue Hazel Green
#>   Black    32   11    10     3
#>   Brown    53   50    25    15
#>   Red      10   10     7     7
#>   Blond     3   30     5     8

Frecuencias relativas de las combinaciones (color de cabello, color de ojos) en cada sexo:

round(prop.table(HairEyeColor, margin=3), 3)
#> , , Sex = Male
#> 
#>        Eye
#> Hair    Brown  Blue Hazel Green
#>   Black 0.115 0.039 0.036 0.011
#>   Brown 0.190 0.179 0.090 0.054
#>   Red   0.036 0.036 0.025 0.025
#>   Blond 0.011 0.108 0.018 0.029
#> 
#> , , Sex = Female
#> 
#>        Eye
#> Hair    Brown  Blue Hazel Green
#>   Black 0.115 0.029 0.016 0.006
#>   Brown 0.211 0.109 0.093 0.045
#>   Red   0.051 0.022 0.022 0.022
#>   Blond 0.013 0.204 0.016 0.026

Frecuencias relativas de los sexos en cada combinación (color de cabello, color de ojos)

round(prop.table(HairEyeColor, margin=c(1,2)), 3)
#> , , Sex = Male
#> 
#>        Eye
#> Hair    Brown  Blue Hazel Green
#>   Black 0.471 0.550 0.667 0.600
#>   Brown 0.445 0.595 0.463 0.517
#>   Red   0.385 0.588 0.500 0.500
#>   Blond 0.429 0.319 0.500 0.500
#> 
#> , , Sex = Female
#> 
#>        Eye
#> Hair    Brown  Blue Hazel Green
#>   Black 0.529 0.450 0.333 0.400
#>   Brown 0.555 0.405 0.537 0.483
#>   Red   0.615 0.412 0.500 0.500
#>   Blond 0.571 0.681 0.500 0.500

Para cambiar el orden de las variables en una tabla multidimensional, se puede usar la instrucción

aperm(tabla, perm=...)

igualando el parámetro perm a la lista de las variables en el orden deseado. Por ejemplo, si queremos una tabla equivalente a HairEyeColor, pero con primera variable Sex, segunda variable Hair y tercera variable Eye, podemos hacer:

aperm(HairEyeColor, perm=c("Sex", "Hair", "Eye"))
#> , , Eye = Brown
#> 
#>         Hair
#> Sex      Black Brown Red Blond
#>   Male      32    53  10     3
#>   Female    36    66  16     4
#> 
#> , , Eye = Blue
#> 
#>         Hair
#> Sex      Black Brown Red Blond
#>   Male      11    50  10    30
#>   Female     9    34   7    64
#> 
#> , , Eye = Hazel
#> 
#>         Hair
#> Sex      Black Brown Red Blond
#>   Male      10    25   7     5
#>   Female     5    29   7     5
#> 
#> , , Eye = Green
#> 
#>         Hair
#> Sex      Black Brown Red Blond
#>   Male       3    15   7     8
#>   Female     2    14   7     8

10.5 Tablas a partir de data frames de variables cualitativas

Como ya hemos comentado en varias ocasiones, la manera natural de organizar datos multidimensionales en R es en forma de data frame. En esta sección explicaremos algunas instrucciones para calcular tablas de frecuencias absolutas a partir de un data frame de variables cualitativas. Para ilustrarla, usaremos el fichero que se encuentra en el url http://aprender.uib.es/Rdir/bebenerg.txt.

Este fichero consiste en una tabla de datos con la siguiente información sobre 122 estudiantes de la Escuela Politécnica Superior de la UIB: su sexo (variable sexo), el grado en el que están matriculados (variable estudio) y si consumen habitualmente bebidas energéticas (variable bebe). Como contiene letras acentuadas, al llerla con read.table vamos a usar el parámetro encoding.

Beb_Energ=read.table("http://aprender.uib.es/Rdir/bebenerg.txt",  header=TRUE, 
                     encoding="UTF-8")
str(Beb_Energ)
#> 'data.frame':    122 obs. of  3 variables:
#>  $ estudio: chr  "Informática" "Matemáticas" "Ing.Industrial" "Informática" ...
#>  $ bebe   : chr  "No" "No" "Sí" "Sí" ...
#>  $ sexo   : chr  "Mujer" "Hombre" "Mujer" "Hombre" ...
head(Beb_Energ)
#>          estudio bebe   sexo
#> 1    Informática   No  Mujer
#> 2    Matemáticas   No Hombre
#> 3 Ing.Industrial   Sí  Mujer
#> 4    Informática   Sí Hombre
#> 5 Ing.Industrial   No  Mujer
#> 6    Matemáticas   No  Mujer

Aplicando la función summary a un data frame de variables cualitativas, obtenemos, a modo de resumen, una tabla con las frecuencias absolutas de cada variable.

summary(Beb_Energ)
#>    estudio              bebe               sexo          
#>  Length:122         Length:122         Length:122        
#>  Class :character   Class :character   Class :character  
#>  Mode  :character   Mode  :character   Mode  :character

Esta tabla sólo sirve para ver la información, porque sus entradas son palabras.

summary(Beb_Energ)[,2]
#>                                                                
#> "Length:122        " "Class :character  " "Mode  :character  "

Para calcular en un solo paso la table de cada variable, podemos usar la función sapply de la manera siguiente:

sapply(Beb_Energ, FUN=table)
#> $estudio
#> 
#>    Informática Ing.Industrial    Matemáticas     Telemática 
#>             53             37             16             16 
#> 
#> $bebe
#> 
#> No Sí 
#> 97 25 
#> 
#> $sexo
#> 
#> Hombre  Mujer 
#>     83     39

De esta manera, hemos obtenido una list cuyas componentes son las tablas que queríamos.

sapply(Beb_Energ, FUN=table)$sexo
#> 
#> Hombre  Mujer 
#>     83     39
table(Beb_Energ$sexo)
#> 
#> Hombre  Mujer 
#>     83     39

Si aplicamos la función table a un data frame de variables cualitativas, obtenemos su tabla de frecuencias absolutas, con las variables ordenadas tal y como aparecen en el data frame

table(Beb_Energ)
#> , , sexo = Hombre
#> 
#>                 bebe
#> estudio          No Sí
#>   Informática    30  7
#>   Ing.Industrial 19  6
#>   Matemáticas     8  1
#>   Telemática     10  2
#> 
#> , , sexo = Mujer
#> 
#>                 bebe
#> estudio          No Sí
#>   Informática    11  5
#>   Ing.Industrial 10  2
#>   Matemáticas     6  1
#>   Telemática      3  1
table(Beb_Energ[c(1,3)])
#>                 sexo
#> estudio          Hombre Mujer
#>   Informática        37    16
#>   Ing.Industrial     25    12
#>   Matemáticas         9     7
#>   Telemática         12     4

Otra opción es usar la función ftable, que produce la misma tabla de frecuencias pero en formato plano.

ftable(Beb_Energ)
#>                     sexo Hombre Mujer
#> estudio        bebe                  
#> Informática    No            30    11
#>                Sí             7     5
#> Ing.Industrial No            19    10
#>                Sí             6     2
#> Matemáticas    No             8     6
#>                Sí             1     1
#> Telemática     No            10     3
#>                Sí             2     1

Las frecuencias relativas globales y marginales se obtienen aplicando prop.table como hasta ahora. Por ejemplo, las frecuencias relativas de bebedores y no bebedores para cada combinación (sexo, estudio) se obtienen con la función siguiente. Observad cómo cambiamos el orden de las variables para facilitar la comprensión: la primera tabla son las frecuencias relativas de no bebedores, la segunda de sí bebedores.

round(aperm(prop.table(table(Beb_Energ), margin=c(3,1)), perm=c("sexo","estudio","bebe")), 3)
#> , , bebe = No
#> 
#>         estudio
#> sexo     Informática Ing.Industrial Matemáticas Telemática
#>   Hombre       0.811          0.760       0.889      0.833
#>   Mujer        0.688          0.833       0.857      0.750
#> 
#> , , bebe = Sí
#> 
#>         estudio
#> sexo     Informática Ing.Industrial Matemáticas Telemática
#>   Hombre       0.189          0.240       0.111      0.167
#>   Mujer        0.312          0.167       0.143      0.250

10.6 Diagramas de barras

El tipo de gráfico más usado para representar variables cualitativas son los diagramas de barras (bar plots). Como su nombre indica, un diagrama de barras contiene, para cada nivel de la variable cualitativa, una barra de altura su frecuencia; por ejemplo, la Figura 10.1 es un diagrama de barras de las frecuencias absolutas de los dos niveles de la muestra de sexos del Ejemplo 10.1. El código que lo produce, y que explicaremos en esta sección, es el siguiente:

barplot(table(Sexo_Ger), col=c("lightblue","pink"), 
        main="Diagrama de barras de las frecuencias absolutas\n de la variable \"Sexo_Ger\"")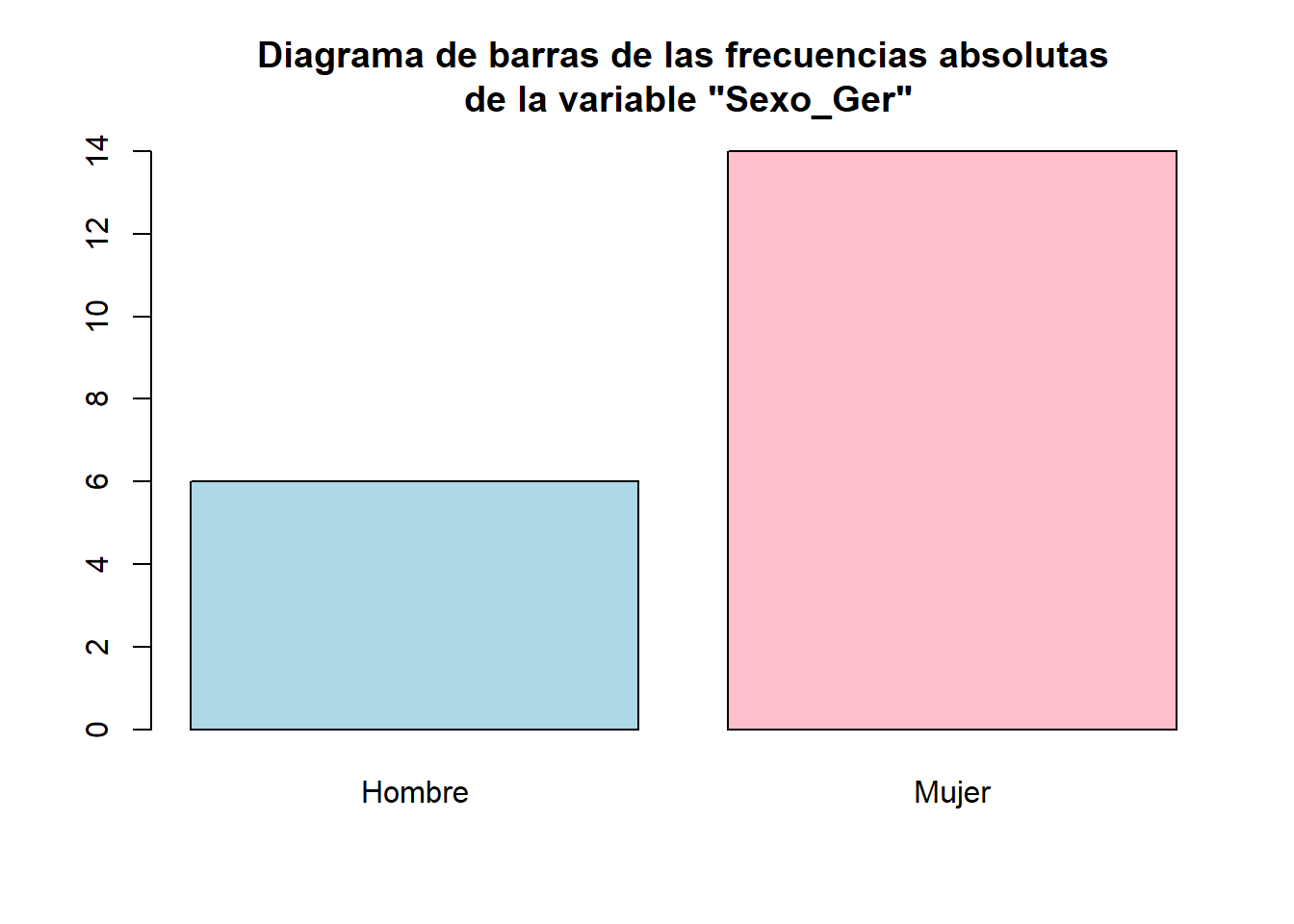

$Diagrama de barras de las frecuencias absolutas de los datos del Ejemplo \@ref(exm:ex1601).$

Figura 10.1: Diagrama de barras de las frecuencias absolutas de los datos del Ejemplo 10.1.

Antes de continuar con los diagramas de barras, vamos a comentar dos trucos usados en el título de este gráfico. Por un laod, la marca \n dentro de una frase entrada entre comillas introduce un cambio de línea. El mismo efecto se obtiene con un cambio de línea. Id con cuidado, porque ambos efectos se acumulan, así que si cambiais de línea después del \n, obtendréis una línea en blanco. Por otro lado, \\" escribe unas comillas en el texto entrado entre comillas.

La manera más sencilla de dibujar un diagrama de barras de las frecuencias absolutas o relativas de una variable cualitativa es usando la instrucción barplot aplicada a la tabla correspondiente. Veamos dos ejemplos más de diagramas de barras, uno de frecuencias absolutas y uno de relativas:

x=c(3,2,5,1,3,1,5,6,2,2,2,1,3,5,2)
Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
barplot(table(x), main="Diagrama de barras de frecuencias absolutas de la variable \"x\"")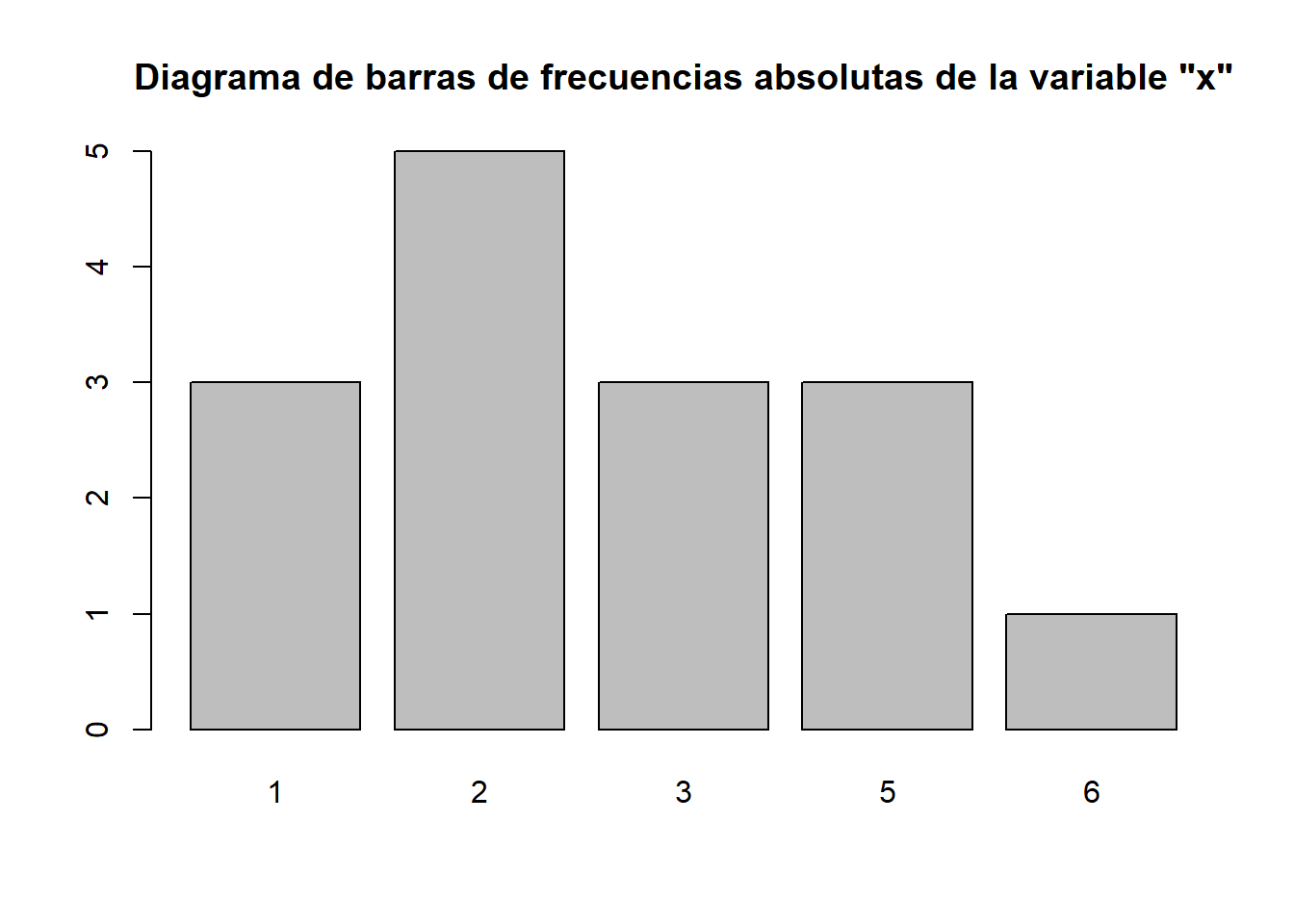

barplot(prop.table(table(Respuestas)), 
        main="Diagrama de barras de frecuencias relativas\n de la variable \"Respuestas\"")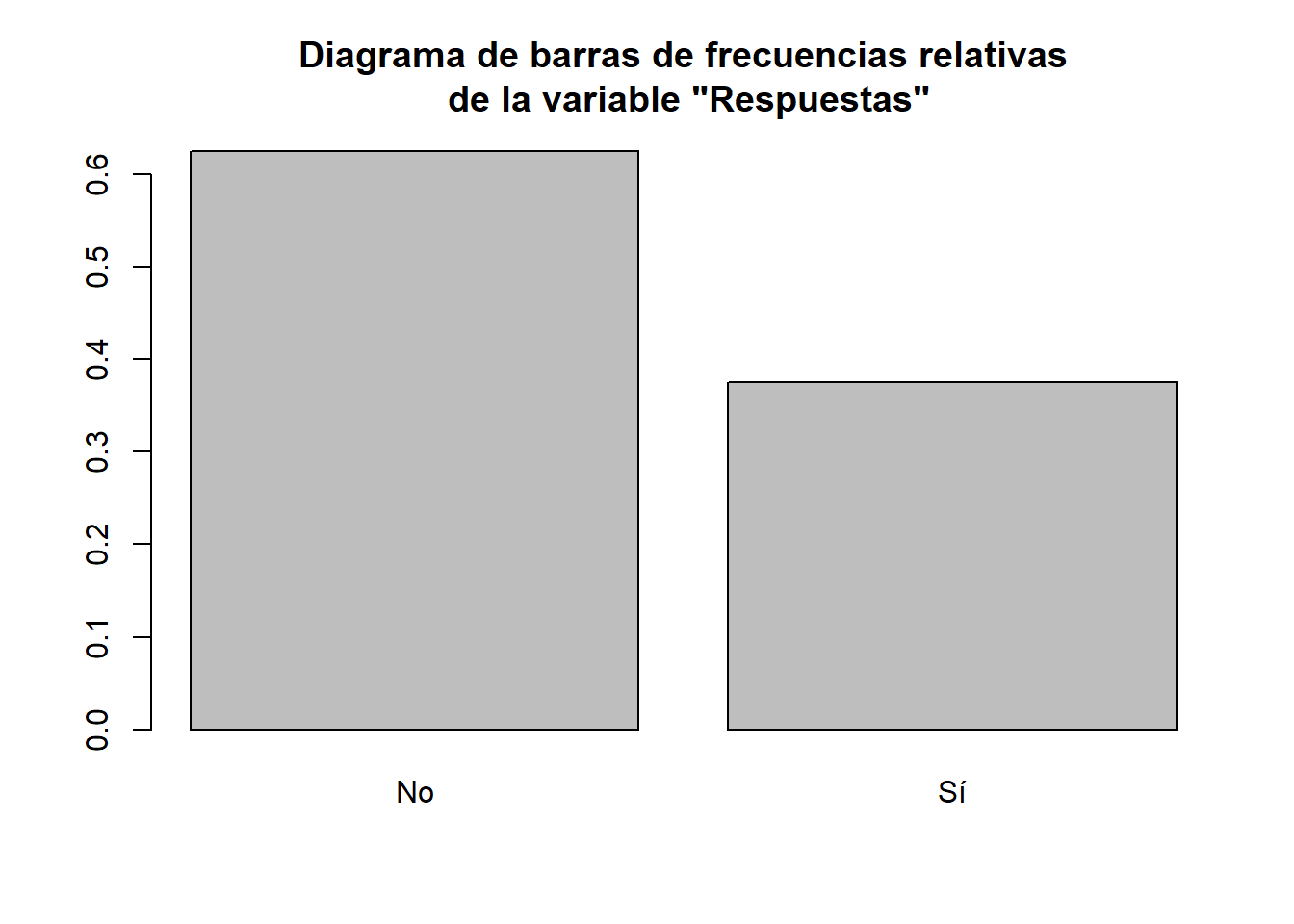

¡Atención! Como pasaba con prop.table, el argumento de barplot ha de ser una tabla, y, por consiguiente, se ha de aplicar al resultado de table o de prop.table, nunca al vector de datos original.

Habréis observado que en las funciones barplot anteriores hemos usado el parámetro main para poner título a los diagramas; en general, la función barplot admite los parámetros de plot que tienen sentido en el contexto de los diagramas de barras: xlab, ylab, main, etc. Los parámetros disponibles se pueden consultar en la Ayuda de barplot. Aquí sólo vamos a comentar algunos.

Se pueden especificar los colores de las barras usando el parámetro col. Si se iguala a un solo color, todas las barras serán de este color, pero también se puede especificar un color para cada barra, igualando col a un vector de colores. Veamos un ejemplo de cada.

barplot(table(Respuestas), col=c("green"))

barplot(table(Respuestas), col=c("red","blue"))

En un diagrama con muchas barras, es conveniente usar un esquema adecuado de colores para ellas. Para ello se puede usar el paquete RColorBrewer, del que hablaremos en detalle en la Sección ??.

Una opción interesante es dibujar las barras horizontales en vez de verticales: para hacerlo, se tiene que añadir el parámetro horiz=TRUE. Así, la Figura 10.2 se obtiene con la siguiente instrucción:

barplot(table(x), horiz=TRUE)

Figura 10.2: Un diagrama de barras horizontales.

Si se aplica barplot a una tabla bidimensional, por defecto dibuja las barras de la segunda variable cortadas por la frecuencia de la primera variable: se le llama un diagrama de barras apiladas. Por ejemplo, la función barplot del bloque de código siguiente produce la Figura 10.3.

Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
Sexo=c("M","M","M","H","H","H","H","H")
table(Sexo,Respuestas)
#>     Respuestas
#> Sexo No Sí
#>    H  3  2
#>    M  2  1
barplot(table(Sexo,Respuestas))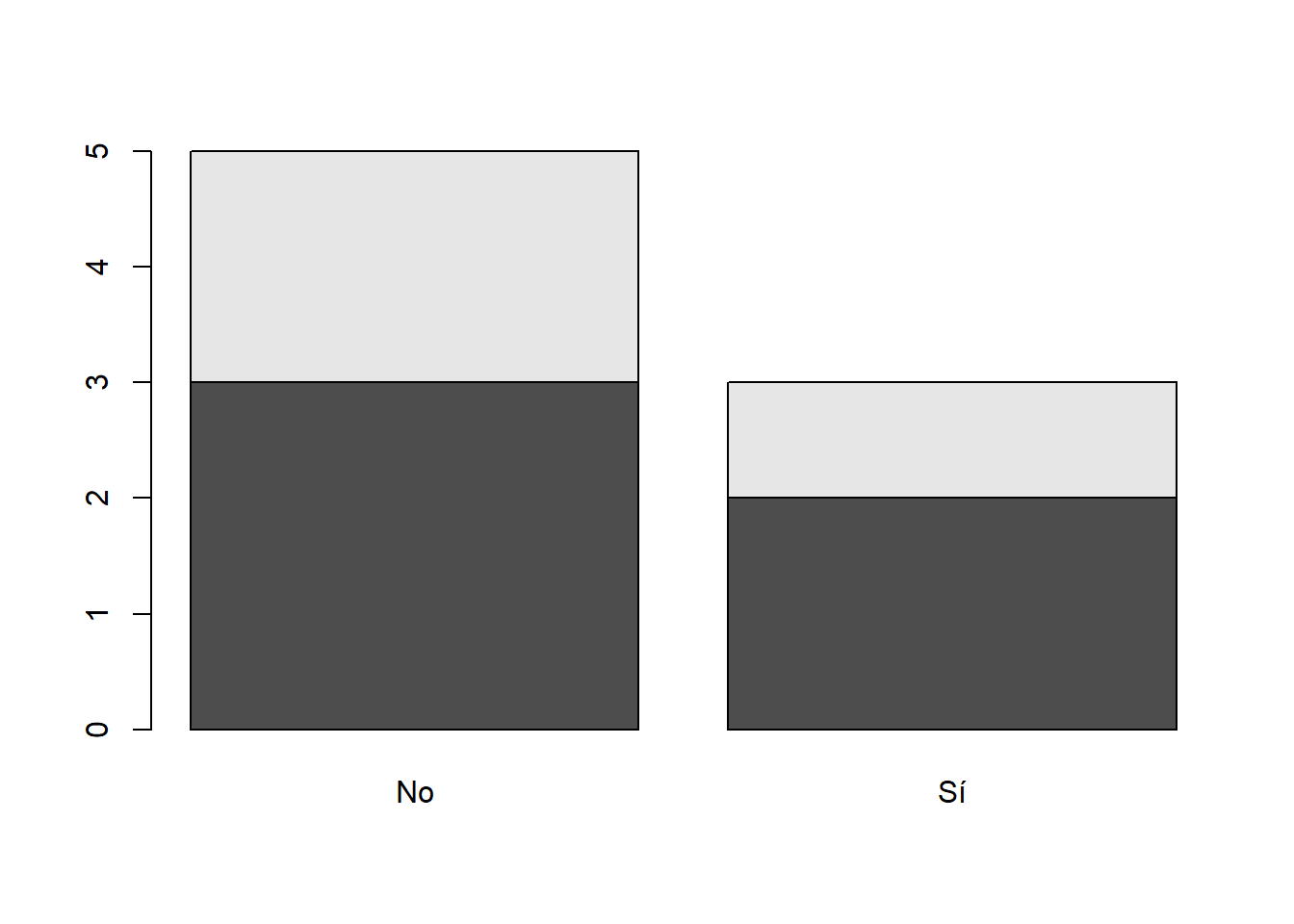

Figura 10.3: Un diagrama de barras apiladas.

En un diagrama de barras apiladas, las barras globales corresponden a los niveles de la variable que definen las columnas de la tabla, es decir, la segunda variable especificada dentro de table: en el de la Figura 10.3, se trata de la variable Respuestas, de niveles No y Si. Cada una de estas barras se divide verticalmente en sectores que representan los niveles de la otra variable, en orden ascendente: en el ejemplo que nos ocupa, la zona inferior de cada barra representa el nivel H de la variable Sexo y la zona superior su nivel M.

En vez de organizar las barras de la primera variable en una sola barra vertical, se pueden dibujar una junto a la otra añadiendo el parámetro beside=TRUE, obteniéndose de esta manera un diagrama de barras por bloques. Así,

barplot(table(Sexo,Respuestas), beside=TRUE)

produce el diagrama de barras de la Figura 10.4. En este diagrama, cada bloque de barras representa un nivel de la variable de las columnas (No y Si), y en cada uno de estos bloques las barras representan los niveles de las filas en su orden (en cada bloque, la barra de la izquierda corresponde a H y la de la derecha a M).

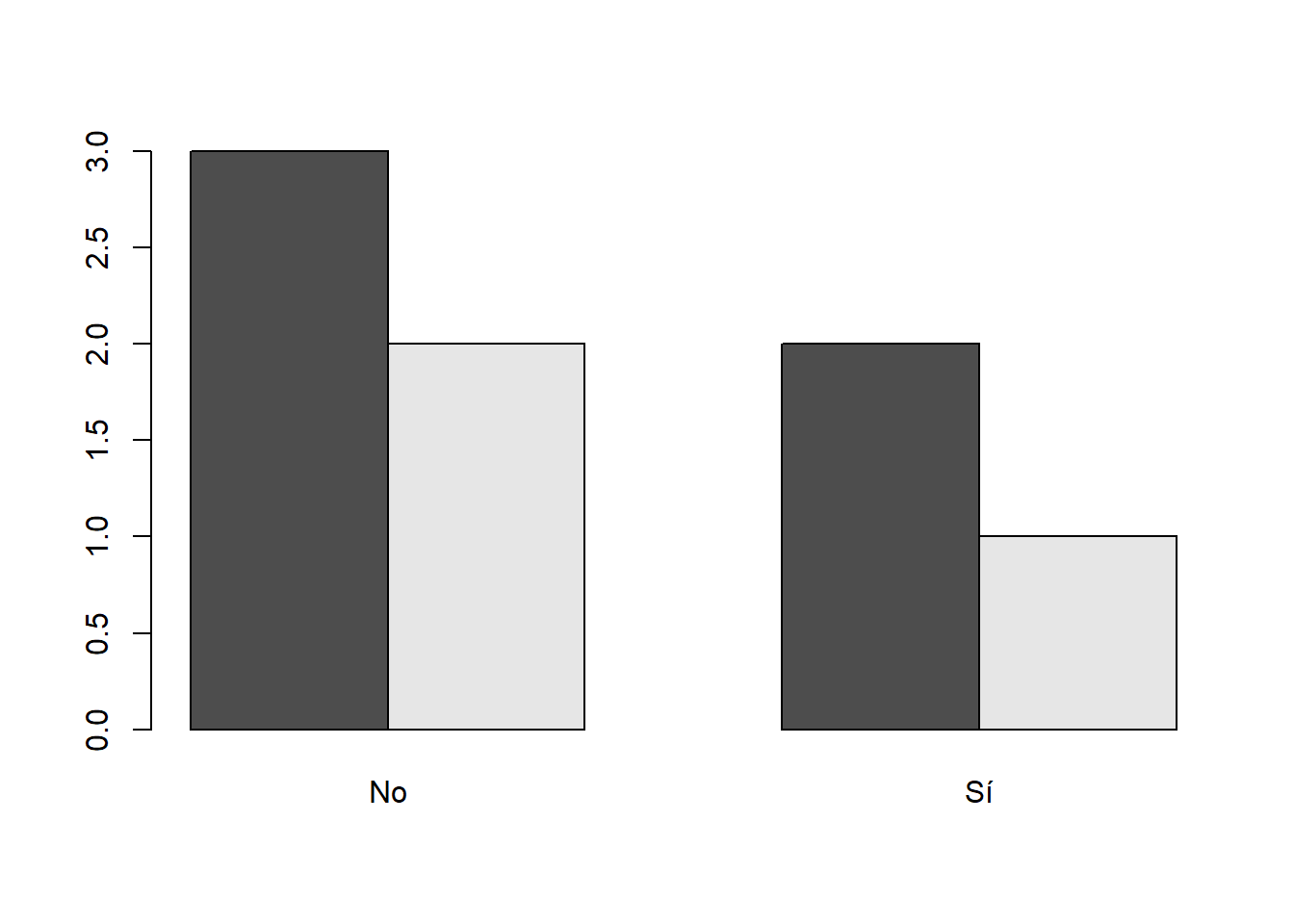
Figura 10.4: Un diagrama de barras por bloques.

Los diagramas de barras tienen que mostrar la información de la manera más adecuada. Por ejemplo, si lo que nos interesa es la distribución de las respuestas por sexo, los bloques de barras tienen que corresponder a los sexos y las barras dentro de cada bloque a las respuestas. En este caso, convendría cambiar el orden de los vectores dentro de la table a la que aplicamos barplot, o trasponer la tabla antes de aplicarle barplot.

barplot(table(Respuestas,Sexo), beside=TRUE)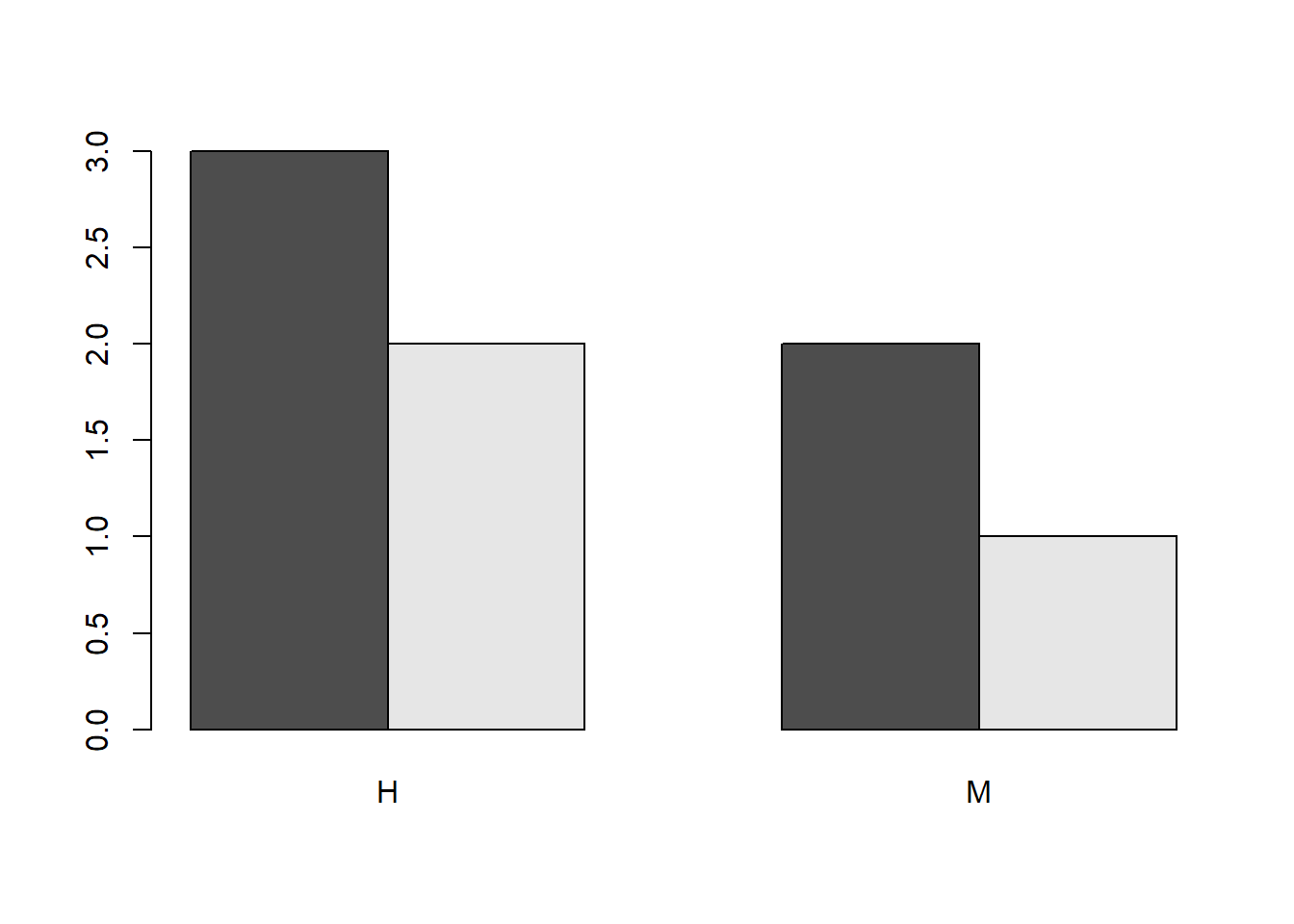

Suele ser conveniente añadir a un diagrama de barras de dos variables una leyenda que indique qué nivel representa cada sector (en los diagramas de barras apiladas) o cada barra (en los diagramas de barras por bloques). Esto se puede realizar entrando el parámetro legend.text igualado a TRUE, si no queremos modificar los nombres de los niveles de las filas, o igualado a un vector con los nombres que les queremos asignar (en el orden que toque). Por ejemplo,

barplot(table(Sexo,Respuestas), beside=TRUE, legend.text=TRUE)

produce el diagrama de la Figura 10.5, con el formato de leyenda por defecto.

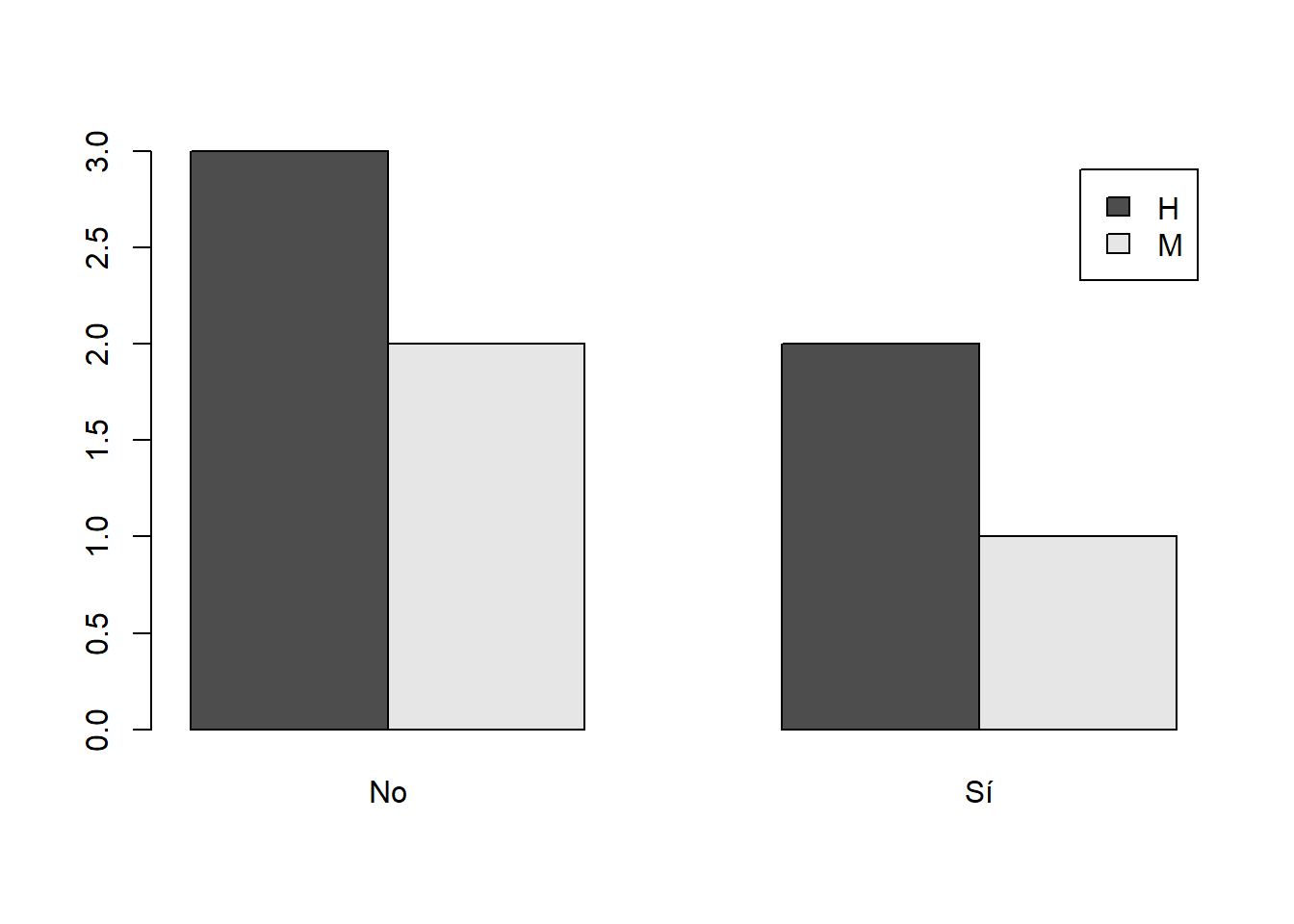
Figura 10.5: Un diagrama de barras por bloques con una leyenda.

La leyenda que genera R se puede modificar usando el parámetro args.legend igualado a una list con los parámetros que usaríamos en la función legend que explicamos en la Lección 7: x, para indicar la posición de la leyenda, cex para indicar el factor por el cual se quiere multiplicar su tamaño, etc. Podéis consultar los parámetros disponibles en la Ayuda de legend.

Se pueden cambiar los colores de las barras usando el parámetro col como en los diagramas de barras de tablas unidimensionales. La función legend.text importa estos colores, no hace falta especificarlos en el args.legend.

También puede ser conveniente poner nombres más informativos a los niveles de las variables. El parámetro names dentro de barplot permite cambiar los nombres de los niveles que muestra debajo del eje horizontal: en un diagrama de barras de una variable, los de sus niveles, y en un diagrama bidimensional, los de los niveles de la variable de las columnas.

Veamos un ejemplo usando col y con los nombres que se muestran de los niveles de ambas variables traducidos al inglés; el resultado es la Figura 10.6.

barplot(table(Respuestas,Sexo), beside=TRUE, names=c("Men","Women"),
        col=c("red","blue"), legend.text=c("No","Yes"))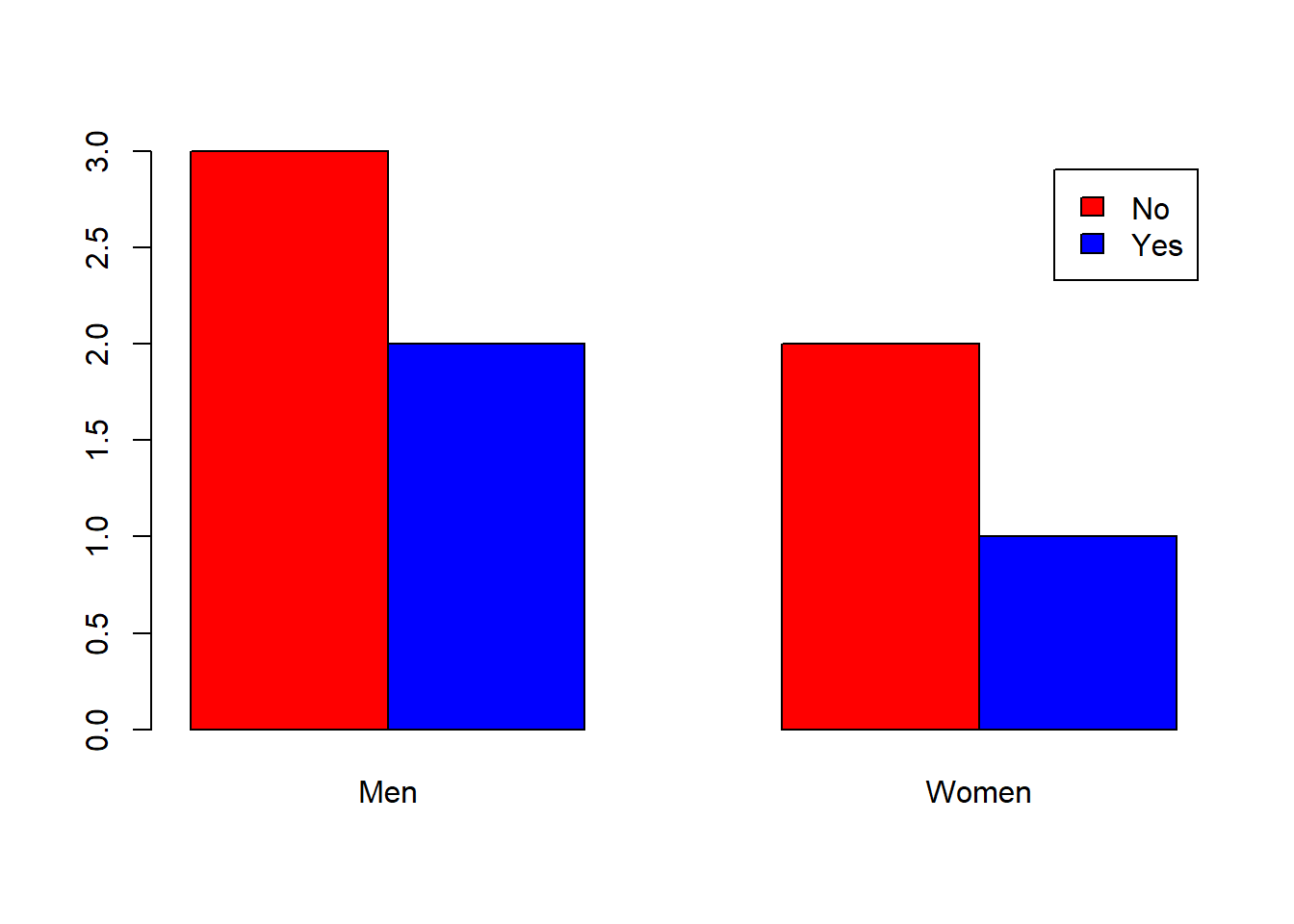

Figura 10.6: Diagrama de barras para visualizar la distribución de las respuestas por sexo.

10.7 Otros gráficos para datos cualitativos

Un tipo muy popular de representación gráfica de variables cualitativas son los diagramas circulares. En un diagrama circular (pie chart) se representan los niveles de una variable cualitativa como sectores circulares de un círculo, de manera que el ángulo (o equivalentemente, el área) de cada sector sea proporcional a la frecuencia del nivel al que corresponde. Con R, este tipo de diagramas se producen con la instrucción pie, de nuevo aplicada a una tabla de frecuencias y no al vector original. La función pie admite muchos parámetros para modificar el resultado: se pueden cambiar los colores con col, se pueden cambiar los nombres de los niveles con names, se puede poner un título con main, etc.; podéis consultar la lista completa de parámetros en su Ayuda. Así, por ejemplo,

Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
pie(table(Respuestas), main="Diagrama circular de la variable \"Respuestas\"")

produce el diagrama de la Figura 10.7.

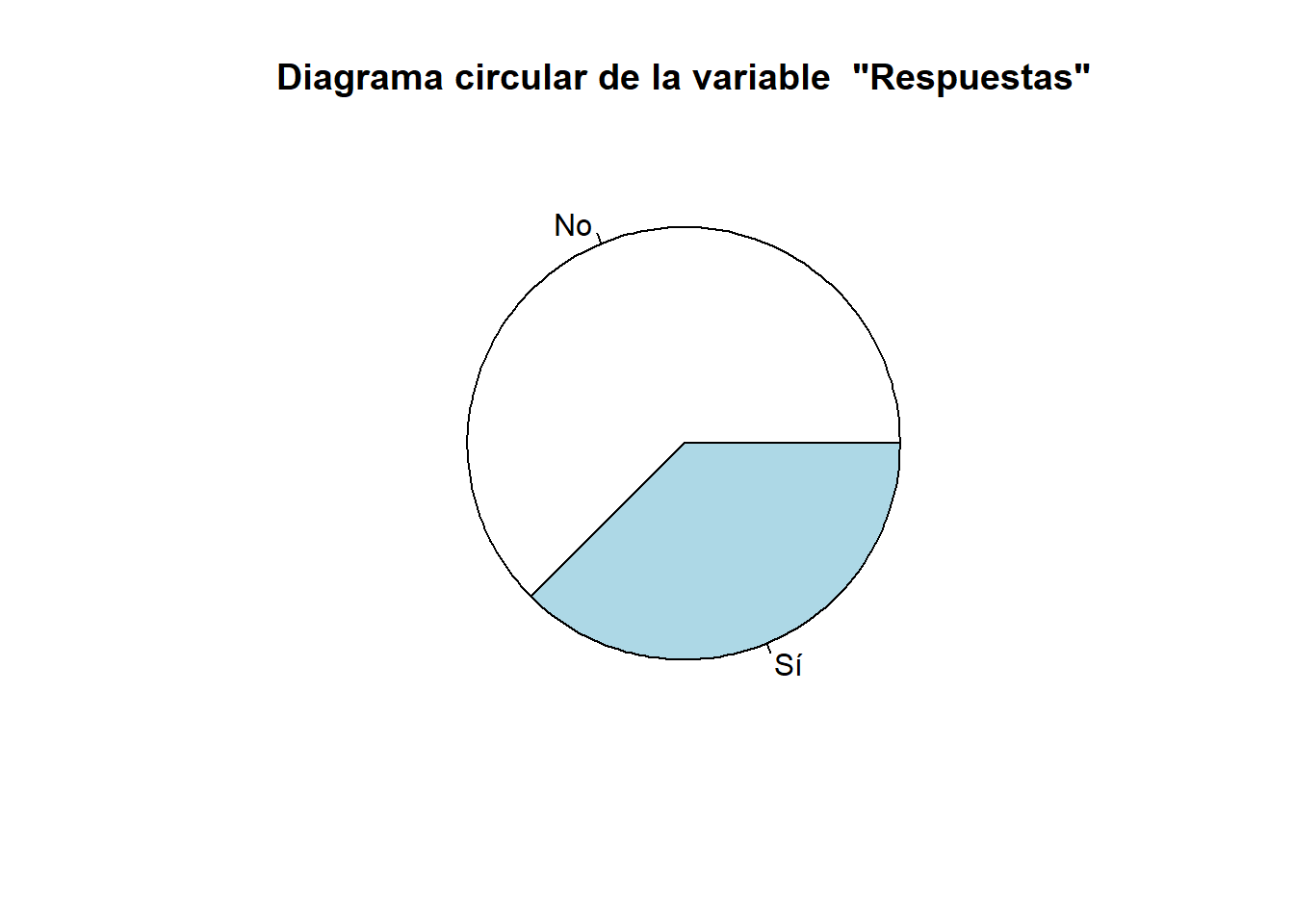
Figura 10.7: Un diagrama circular.

Pese a su popularidad, es poco recomendable usar diagramas circulares cuando manejamos más de dos niveles, porque a veces es difícil, a simple vista, comprender las relaciones entre las frecuencias que representan. Para convencerse, basta comparar los diagramas de barras y los diagramas circulares de la Figura 10.8 (extraída de la entrada sobre diagramas circulares de la Wikipedia).

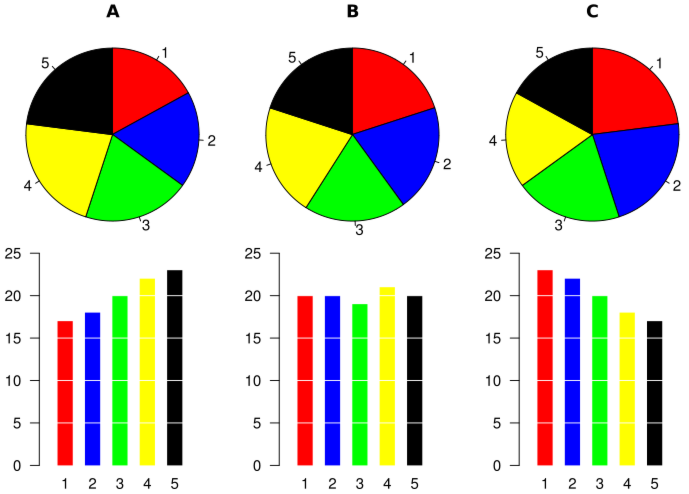
Figura 10.8: Diagramas de barras versus diagramas circulares.

Otra representación de las tablas multidimensionales de frecuencias son los diagramas de mosaico. Estos gráficos se obtienen sustituyendo cada entrada de la tabla de frecuencias por una región rectangular de área proporcional a su valor. En concreto, para obtener el diagrama de mosaico de una tabla bidimensional, se parte de un cuadrado de lado 1, primero se divide en barras verticales de amplitudes iguales a las frecuencias relativas de una variable, y luego cada barra se divide, a lo alto, en regiones de alturas proporcionales a las frecuencias relativas marginales de cada nivel de la otra variable dentro del nivel correspondiente de la primera variable.

Un diagrama de mosaico de una tabla se obtiene con R aplicando la función plot a la tabla, o también la función mosaicplot; esta última también se puede aplicar a matrices. Por ejemplo,

Respuestas=c("No","No","Sí","No","Sí","No","No","Sí")
Sexo=c("M","M","M","H","H","H","H","H")
plot(table(Sexo,Respuestas), main="Diagrama de mosaico de las variables \"Sexo\" y \"Respuestas\"")

produce el diagrama de mosaico de la Figura 10.9.

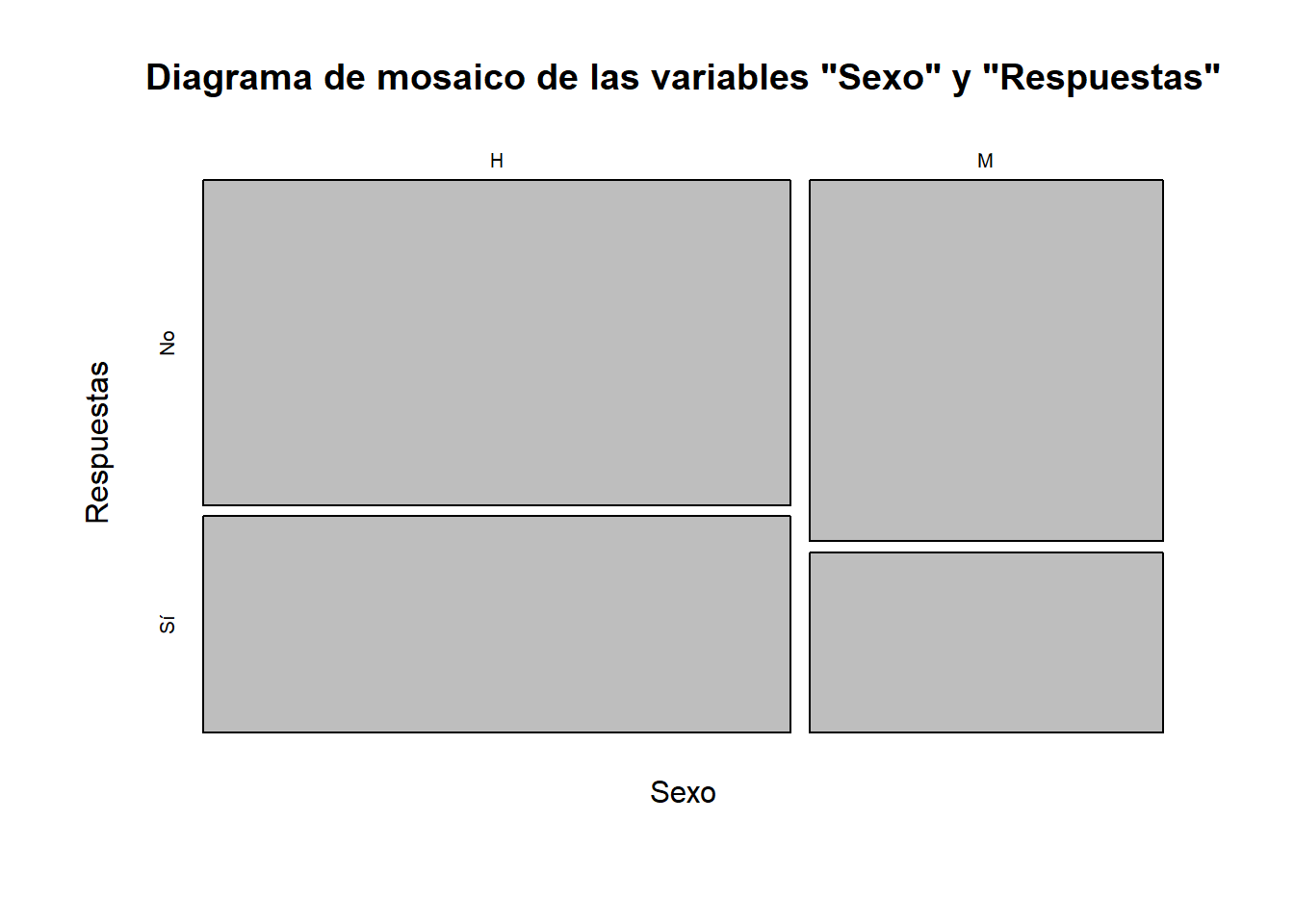
Figura 10.9: Un diagrama de mosaico bidimendiol.

En el diagrama de mosaico de una tabla tridimensional, primero se divide el cuadrado en barras verticales de amplitudes iguales a las frecuencias relativas de una variable; luego, cada barra se divide, a lo alto, en regiones de alturas proporcionales a las frecuencias relativas marginales de cada nivel de una segunda variable dentro del nivel correspondiente de la primera variable; y, finalmente, cada sector rectangular se vuelve a dividir a lo ancho en regiones de amplitudes proporcionales a las frecuencias relativas marginales de cada nivel de la tercera variable dentro de la combinación correspondiente de niveles de las otras dos. Por ejemplo,

plot(HairEyeColor,  main="Diagrama de mosaico de la tabla \"HairEyeColor\"", 
     col=c("pink","lightblue"))

produce el gráfico de la Figura 10.10.

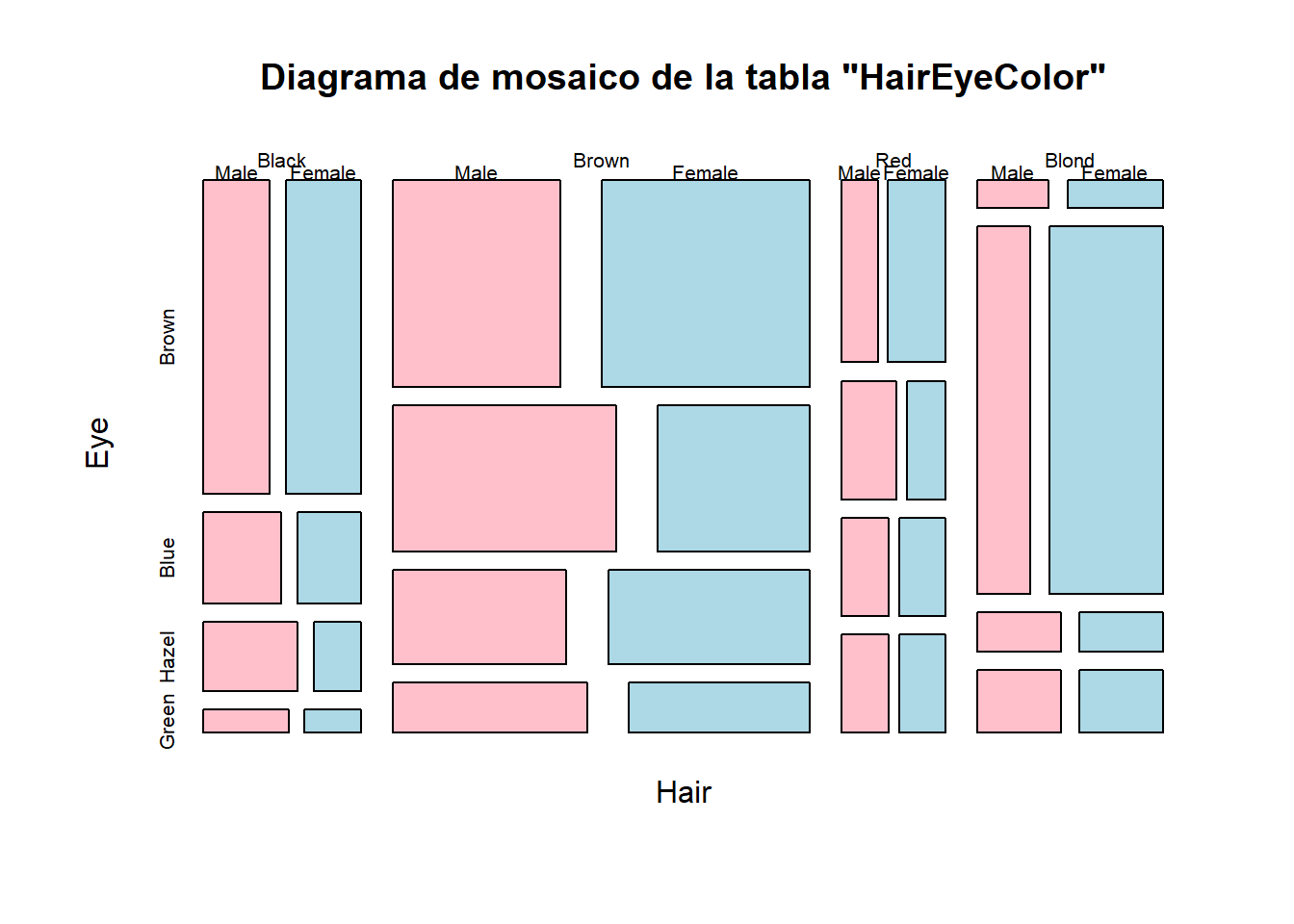
Figura 10.10: Un diagrama de mosaico tridimendiol.

Además de sus parámetros usuales, la función plot admite algunos parámetros específicos cuando se usa para producir el diagrama de mosaico de una tabla. Los más interesantes son:

col, que ya hemos usado en el diagrama de mosaico tridimensional anterior, asigna colores a los niveles de la última variable (en ese ejemplo, los sexos).
dir, igualado a un vector de direcciones "v" (vertical) y "h" (horizontal), sirve para especificar la dirección de las barras de cada variable (por defecto, como hemos comentado, alternan vertical y horizontal, empezando por vertical).

Estos y otros parámetros se pueden consultar en la Ayuda de mosaicplot.

El paquete vcd incorpora la función mosaic que sirve para producir diagramas de mosaico en los que se pueden controlar muchos más apsectos gráficos que con plot. Si la necesitáis, consultad su Ayuda.

Este paquete vcd también incluye la función cotabplot que produce un diagrama de mosaico para cada nivel de la tercera variable. Por ejemplo,

library(vcd)
cotabplot(table(Sexo,Respuestas,Pais))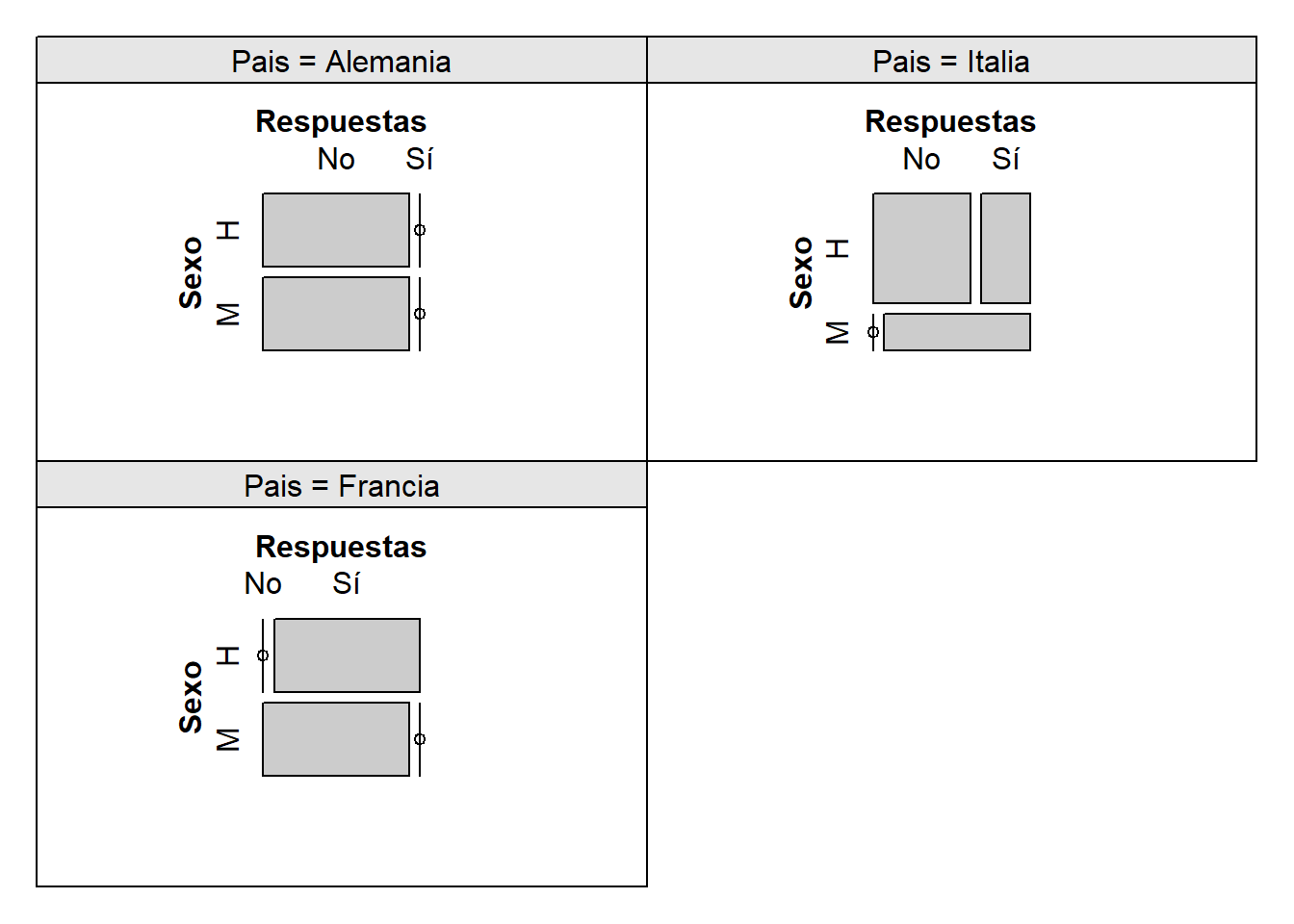

produce el gráfico de la Figura 10.11.

Figura 10.11: Diagrama de mosaico producido con cotabplot.

Finalmente, el paquete vcdExtra incluye la función mosaic3d que produce un diagrama de mosaico tridimensional en una ventana de una aplicación para gráficos 3D interactivos. Por ejemplo, el bloque de código

library(vcdExtra)
mosaic3d(HairEyeColor, type="expected", box=TRUE, col=c("pink","lightblue"))

produce el gráfico 3D de la Figura 10.12 en una ventana de gráficos interactivos donde lo podréis rotar, ampliar, etc.

knitr::include_graphics("AprendeR-Parte-I_files/figure-html/exmosaic3d.png")

Figura 10.12: Diagrama de mosaico 3D producido con mosaic3d.

10.8 Un ejemplo completo

Vamos a llevar a cabo un análisis completo de un ejemplo con lo que hemos aprendido en esta lección. Como ya hemos comentado, el objeto de datos HairEyeColor que lleva predefinido R es una tabla de frecuencias absolutas de tres variables cualitativas: Hair, Eye y Sex. Vamos a extraer de esta tabla una tabla bidimensional de frecuencias absolutas de las variables Eye y Hair, sin distinguir según el sexo. La manera más sencilla de obtener esta tabla es combinando la función apply con as.table, para que el resultado final sea una tabla de contingencia (sin esta instrucción, el resultado sería una matriz), de la manera siguiente:

HEC=as.table(apply(HairEyeColor, MARGIN=c(1,2), FUN=sum))
HEC
#>        Eye
#> Hair    Brown Blue Hazel Green
#>   Black    68   20    15     5
#>   Brown   119   84    54    29
#>   Red      26   17    14    14
#>   Blond     7   94    10    16

Vamos a traducir al castellano los nombres de las variables de esta tabla y de sus niveles. Esto lo podemos llevar a cabo en un solo paso con la función dimnames que ya usamos sobre data frames. El resultado de aplicar esta función a una table es una list cuyas componentes son los niveles de cada variable.

dimnames(HEC)
#> $Hair
#> [1] "Black" "Brown" "Red"   "Blond"
#> 
#> $Eye
#> [1] "Brown" "Blue"  "Hazel" "Green"

Por lo tanto, para reescribir los nombres de las variables y sus niveles, basta redefinir esta list de la manera siguiente:

dimnames(HEC)=list(Cabello=c("Negro","Castaño","Rojo","Rubio"), Ojos=c("Marrones","Azules","Pardos","Verdes"))
HEC
#>          Ojos
#> Cabello   Marrones Azules Pardos Verdes
#>   Negro         68     20     15      5
#>   Castaño      119     84     54     29
#>   Rojo          26     17     14     14
#>   Rubio          7     94     10     16

Vamos a dibujar un diagrama de mosaico de esta tabla.

plot(HEC,col=c("lightblue"),
     main="Diagrama de mosaico de la tabla bidimensional de frecuencias\n de colores de cabellos y ojo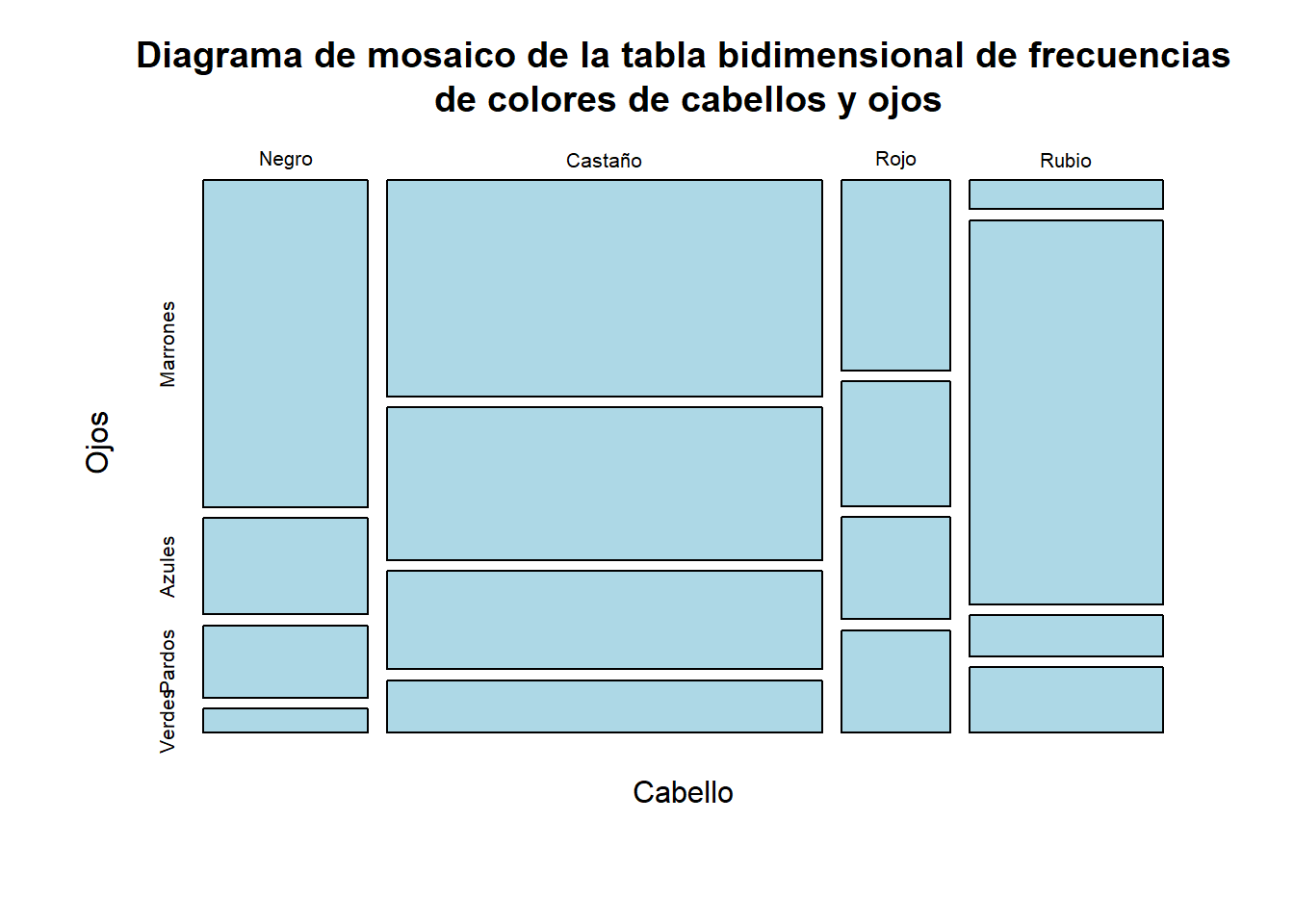s")

A simple vista, vemos que las combinaciones de colores de cabellos y ojos más frecuentes son los cabellos castaños con los ojos marrones, y los cabellos rubios con los ojos azules.

A continuación, vamos a calcular el número total de individuos representados en esta tabla, así como las tablas de frecuencias absolutas y relativas de cada variable, y representaremos estas últimas en sendos diagramas de barras.

Número total de individuos:

sum(HEC)
#> [1] 592

Tabla de frecuencias absolutas de colores de ojos:

colSums(HEC)
#> Marrones   Azules   Pardos   Verdes 
#>      220      215       93       64

Tabla de frecuencias absolutas de colores de cabello:

rowSums(HEC)       
#>   Negro Castaño    Rojo   Rubio 
#>     108     286      71     127

Tabla de frecuencias relativas de colores de ojos:

round(prop.table(colSums(HEC)),3)
#> Marrones   Azules   Pardos   Verdes 
#>    0.372    0.363    0.157    0.108

Tabla de frecuencias absolutas de colores de cabello:

round(prop.table(rowSums(HEC)),3)   #Frec. rel. de Cabello
#>   Negro Castaño    Rojo   Rubio 
#>   0.182   0.483   0.120   0.215

Diagrama de barras de frecuencias relativas de colores de ojos:

barplot(prop.table(colSums(HEC)), ylim=c(0,0.4),
  col=c("burlywood4","lightblue","orange3","lightgreen"))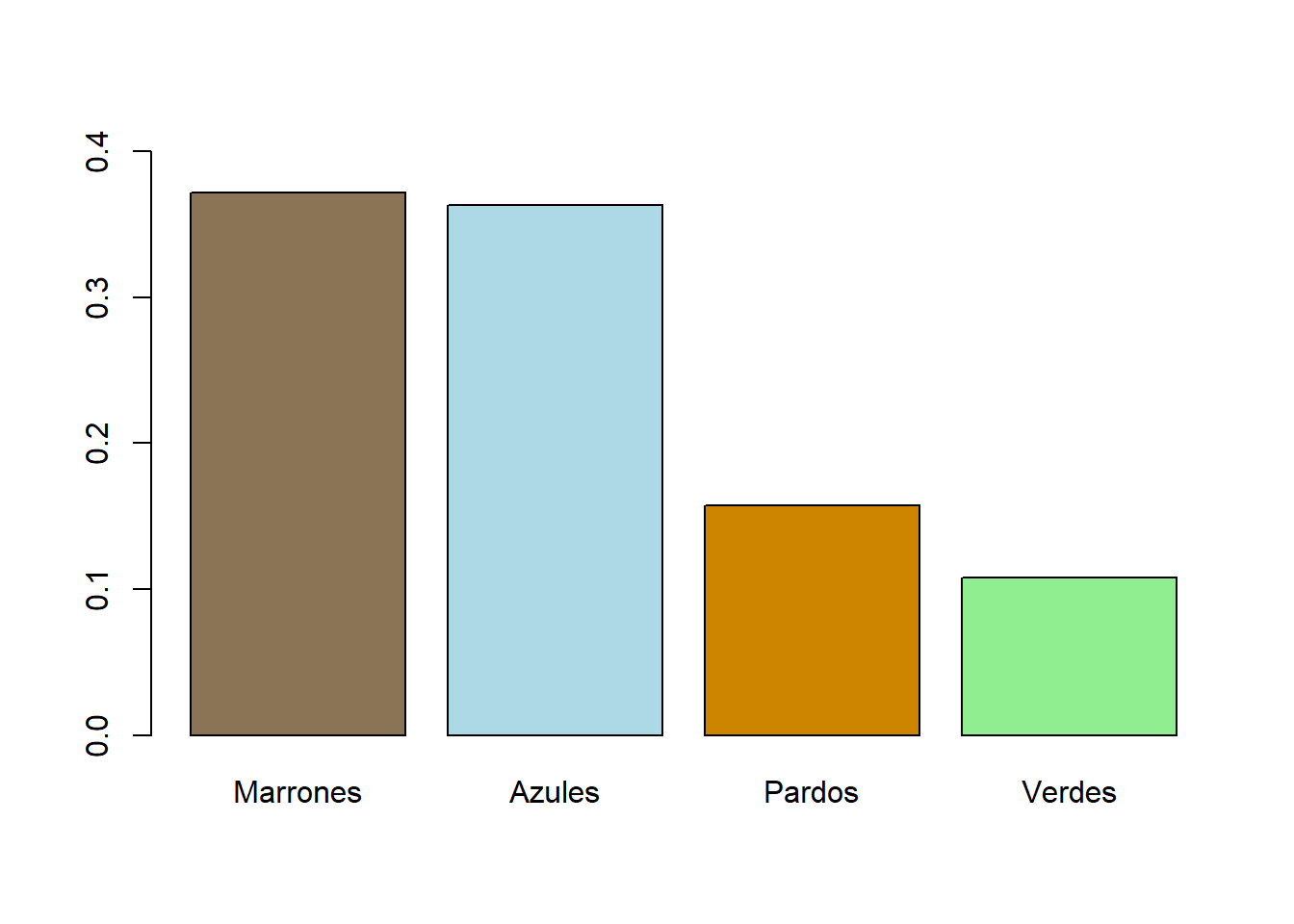

Diagrama de barras de frecuencias relativas de colores de cabello:

barplot(prop.table(rowSums(HEC)),
  col=c("black","brown","red","gold"), ylim=c(0,0.5))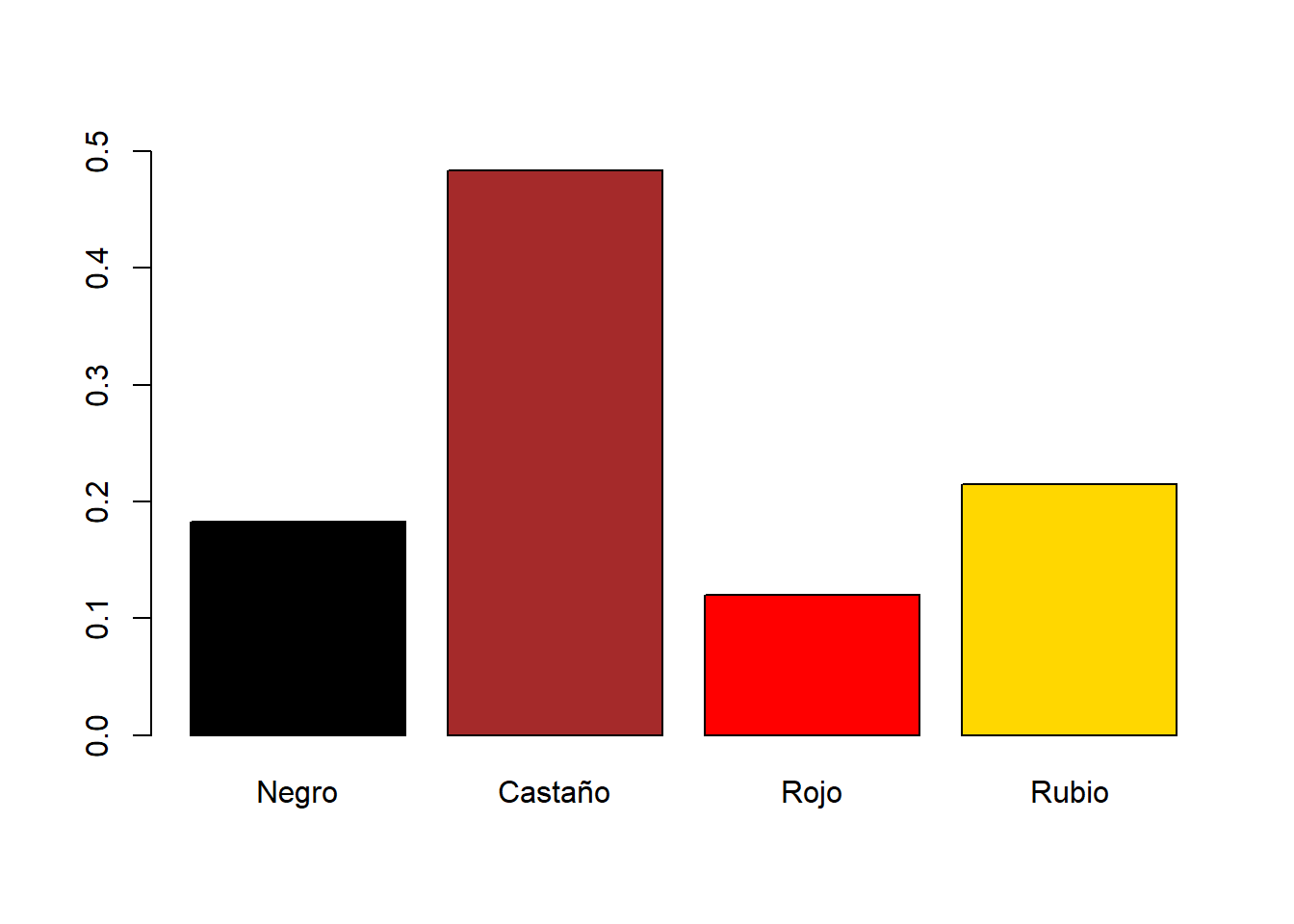

Vemos que el color dominante de cabellos es el castaño, mientras que en el color de ojos el marrón y el azul están prácticamente empatados.

Pasamos ahora a calcular las tablas de frecuencias relativas y dibujar los dos diagramas de barras de las frecuencias relativas marginales.

Tabla de frecuencias relativas globales:

round(prop.table(HEC), 3)  
#>          Ojos
#> Cabello   Marrones Azules Pardos Verdes
#>   Negro      0.115  0.034  0.025  0.008
#>   Castaño    0.201  0.142  0.091  0.049
#>   Rojo       0.044  0.029  0.024  0.024
#>   Rubio      0.012  0.159  0.017  0.027

Tabla de frecuencias relativas de los colores de cabello dentro de cada color de ojos:

round(prop.table(HEC, margin=1), 3)  
#>          Ojos
#> Cabello   Marrones Azules Pardos Verdes
#>   Negro      0.630  0.185  0.139  0.046
#>   Castaño    0.416  0.294  0.189  0.101
#>   Rojo       0.366  0.239  0.197  0.197
#>   Rubio      0.055  0.740  0.079  0.126

Tabla de frecuencias relativas de los colores de ojos dentro de cada color de cabellos:

round(prop.table(HEC, margin=2), 3)   
#>          Ojos
#> Cabello   Marrones Azules Pardos Verdes
#>   Negro      0.309  0.093  0.161  0.078
#>   Castaño    0.541  0.391  0.581  0.453
#>   Rojo       0.118  0.079  0.151  0.219
#>   Rubio      0.032  0.437  0.108  0.250

Diagrama de barras de frecuencias relativas de los colores de cabello dentro de cada color de ojos:

barplot(prop.table(HEC, margin=1), beside=TRUE, legend.text=TRUE,
   col=c("black","brown","red","gold"), ylim=c(0,0.8))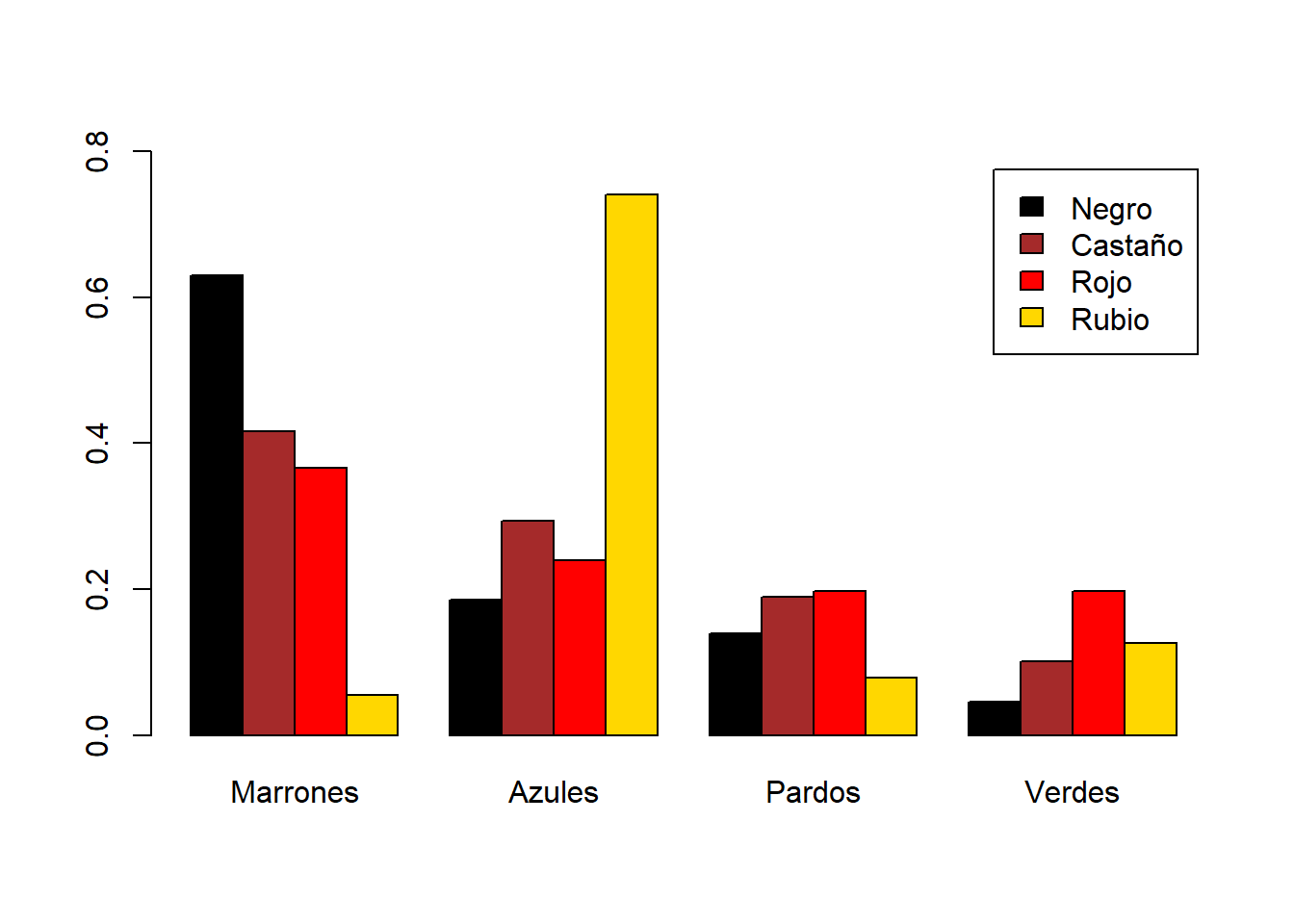

Diagrama de barras de frecuencias relativas de los colores de ojos dentro de cada color de cabello:

barplot(t(prop.table(HEC, margin=2)), beside=TRUE,
   legend.text=TRUE, ylim=c(0,0.6),
   col=c("burlywood4","lightblue","orange3","lightgreen"))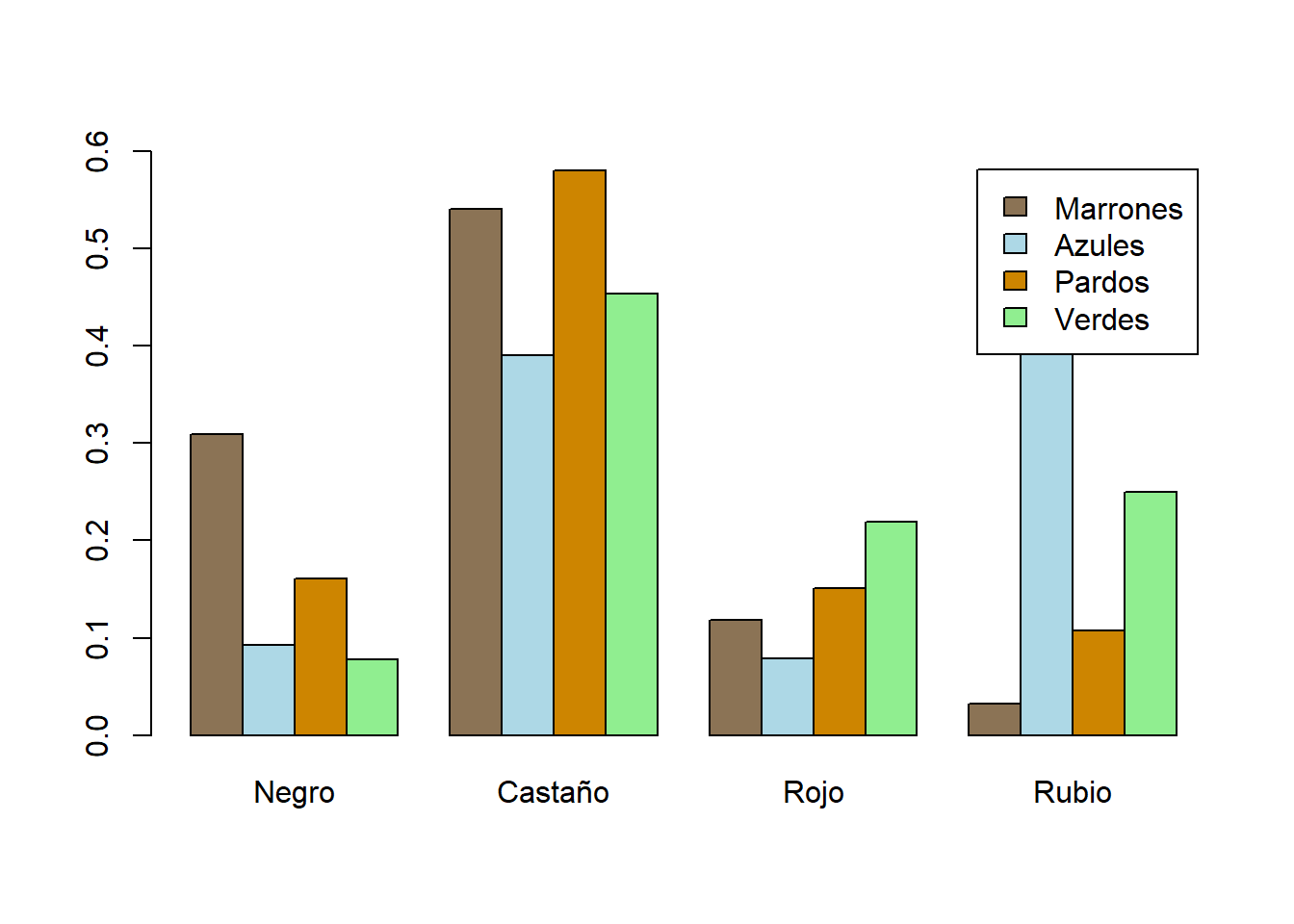

Vemos, por ejemplo, que entre las personas de ojos azules, los cabellos rubios son los más frecuentes, y que entre las personas castañas el color de ojos más frecuente es el pardo.

10.9 Guía rápida de funciones

table calcula la tabla de frecuencias absolutas de un vector o un factor.
as.table convierte un objeto (por ejemplo, una matriz) en una tabla de contingencia.
ftable muestra una tabla multidimensional en formato plano.
t sirve para trasponer una tabla bidimensional.
aperm sirve para permutar las variables de una tabla multidimensional. La permutación se especifica con el parámetro perm.
prop.table calcula la tabla de frecuencias relativas de un vector o un factor a partir de su tabla de frecuencias absolutas. El parámetro margin sirve para especificar las dimensiones en cuyos niveles se calcularán las frecuencias relativas marginales. Si no se especifica, se calculan las frecuencias relativas globales.
CrossTable del paquete gmodels, produce, en el caso bidimensional, una tabla conjunta de frecuencias absolutas y de frecuencias relativas globales y marginales.
names da los nombres de las columnas de una tabla unidimensional, y sirve también para modificar estos nombres.
dimnames da una list con los vectores de los nombres de los niveles de las diferentes variables de una tabla multidimensional, y sirve también para modificar los nombres tanto de las variables como de sus niveles.
tabla[...] se usa para especificar un elemento, una fila, una columna o una subtabla de la tabla.
barplot dibuja el diagrama de barras de un vector o un factor a partir de una tabla de frecuencias. Algunos parámetros importantes:
- col: sirve para especificar los colores de las barras.
- horiz=TRUE: sirve para dibujar el diagrama horizontal.
- beside=TRUE: sirve para especificar que el diagrama sea por bloques.
- legend.text: sirve para añadir una leyenda que explique qué barras corresponden a cada uno de los niveles de la primera variable.
- args.legend: sirve para modificar las características de esta leyenda, igualándolo a una list con los valores de los parámetros de la función legend que queramos especificar.
- names: sirve para cambiar en el diagrama los nombres de los niveles de la segunda variable.
- main, xlab, ylab y el resto de parámetros de plot que tengan sentido para diagramas de barras.
pie dibuja el diagrama circular de un vector o un factor a partir de una tabla de frecuencias. Algunos parámetros importantes:
- col: sirve para especificar los colores de los sectores.
- names: sirve para cambiar en el diagrama los nombres de los niveles.
- main, xlab, ylab y el resto de parámetros de plot que tengan sentido para diagramas circulares.
plot y mosaicplot dibujan el diagrama de mosaico de una tabla de frecuencias. Algunos parámetros relevantes (aparte de los usuales de plot):
- col: asigna colores a los niveles de la última variable.
- dir: igualado a un vector de direcciones "v" (vertical) y "h" (horizontal), sirve para especificar la dirección de las barras de cada variable.
mosaic del paquete vcd, también dibuja el diagrama de mosaico de una tabla de frecuencias. Algunos parámetros importantes:
- dir: como en mosaicplot.
- highlighting: sirve para destacar una variable.
- highlighting_fill: sirve para asignar colores a los niveles de la variable destacada.
cotabplot del paquete vcd, produce una tabla con un diagrama de mosaico para cada nivel de la última variable.
mosaic3d del paquete vcdExtra, produce un diagrama de mosaico tridimensional.
\n indica un cambio de línea en un título o etiqueta.
\" escribe unas comillas en el texto de un título o etiqueta.

10.10 Ejercicios

Test

(1) Dad una instrucción que defina la tabla de frecuencias absolutas de un vector llamado flores.

(2) Dad una instrucción que defina la tabla de frecuencias relativas de un vector llamado flores usando la función prop.table.

(3) Dad una instrucción que defina la tabla bidimensional conjunta de frecuencias absolutas de dos vectores llamados flores y zona de forma que las filas correspondan a flores y las columnas a zona.

(4) Dad una instrucción que defina la tabla bidimensional conjunta de frecuencias relativas, calculadas dentro del total, de dos vectores llamados flores y zona, de forma que las filas correspondan a zona y las columnas a flores.

(5) Dad una instrucción que dibuje un diagrama de barras básico de un vector llamado flores.

(6) Dad una instrucción que dibuje un diagrama circular básico de un vector llamado flores.

(7) Definid un data frame a partir de la tabla de datos contenida en el url http://aprender.uib.es/Rdir/ESD.txt y dad la moda de la variable MB. Tenéis que dar el resultado final, no cómo lo habéis obtenido, y sin las comillas. Si la frecuencia máxima se logra en dos o más valores de esta variable, dad todos estos valores, ordenados de menor a mayor, separados por un espacio en blanco.

(8) Definid un data frame a partir de la tabla de datos contenida en el url http://aprender.uib.es/Rdir/ESD.txt y dad la frecuencia relativa (redondeada a 2 cifras decimales) del valor 135 en la variable MB. Tenéis que dar el resultado final, no cómo lo habéis obtenido.

(9) Definid un data frame a partir de la tabla de datos contenida en el url http://aprender.uib.es/Rdir/ESD.txt y dad la frecuencia relativa (calculada dentro del total y redondeada a 4 cifras decimales) de los individuos que en la variable MB tienen el valor 126 y en la variable BH tienen el valor 124.

(10) La tabla DNase es uno de los data frames que lleva predefinidos R. Dad una instrucción que dibuje un diagrama de barras básico de la variable density de este data frame. Y antes de contestar, comprobad que funciona.

(11) Considerad el objeto de datos HairEyeColor que lleva predefinido R y que ya hemos usado en esta lección. ¿Qué porcentaje de hombres en esta tabla son pelirrojos y tienen los ojos verdes? Dad el valor del porcentaje redondeado a dos cifras decimales y sin el signo %.

Ejercicio

Instalad y cargad el paquete MASS. Este paquete lleva una tabla de datos llamada birthwt sobre factores que pueden incidir en el peso de los niños al nacer. Antes de empezar, con str, View, head … explorad su estructura y consultad en su Ayuda el significado de cada variable.

(a) Calculad una tabla bidimensional de frecuencias relativas marginales de los pares (raza de la madre, peso inferior a 2.5 kg o no) que permita ver, fácilmente, si la raza de la madre influye en el peso del bebé. Dibujad un diagrama de mosaico de esta tabla.

Asimismo, dibujad un diagrama de barras por bloques e estas frecuencias relativas que permita visualizar esta información. Poned nombres adecuados a los bloques, colores a las barras, y añadid una leyenda que explique qué representa cada barra. ¿Se puede obtener alguna conclusión de esta tabla y de este diagrama de barras?

(b) Repetid el punto anterior para los pares (madre fumadora o no, peso inferior a 2.5 kg o no) y para los pares (madre hipertensa o no, peso inferior a 2.5 kg o no).

(c) Calculad una tabla de frecuencias relativas marginales de las ternas (raza de la madre, madre fumadora o no, peso inferior a 2.5 kg o no) que permita ver, fácilmente, si la combinación de la raza de la madre y su condición de fumadora o no fumadora influye en el peso del bebé. Dibujad un diagrama de mosaico de esta tabla tridimensional.

Asimismo, dibujad un diagrama de barras por bloques que permita visualizar esta información (pensad cómo pasaréis de la tabla tridimensional a un diagrama de barras bidimensional que muestre la información deseada). Poned nombres adecuados a los bloques, colores a las barras, y añadid una leyenda que explique qué representa cada barra. ¿Se puede obtener alguna conclusión de esta tabla y de este diagrama de barras?

Respuestas al test

(1) table(flores)

(2) prop.table(table(flores))

(3) table(flores,zona)

(4) prop.table(table(zona,flores))

(5) barplot(table(flores))

(6) pie(table(flores))

(7) 131 138

(8) 0.07

(9) 0.0067

(10) barplot(table(DNase$density))

(11) 2.51